Construyendo un modelo deterministico simple

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

¿Cómo construir un modelo simplificado de zika?

Objetivos

Al final de este taller usted podrá:

Reconocer cómo se construye un modelo determinístico simple mediante ecuaciones diferenciales ordinarias.
Identificar parámetros relevantes para modelar epidemias de ETV.
Diagramar la interacción entre los diferentes compartimentos del sistema mediante los parámetros.
Traducir ecuaciones matemáticas del modelo determinístico a código de lenguaje R.
Explorar el uso de las simulaciones del modelo para proyectar escenarios de transmisión y potencial impacto de las intervenciones

Pre requisito

Esta unidad tiene como prerequisitos:

Introducción a R y RStudio
Introducción a la teoría epidémica
Historia de las epidemias y las pandemias
Visualización de datos en R con ggplot

Tabla de contenido

Tema 1: Enfermedades transmitidas por vectores: Biología del vector, virus del Zika, diagnóstico e intervenciones
Tema 2: Repaso ¿Qué es un modelo determinístico simple?
Tema 3: Modelo SIR simple Zika
Tema 4: Elaborando diagramas y ecuaciones del modelo Zika
Tema 5. Elaborando la tabla de parámetros del modelo simple de Zika.
Tema 6: Modelo Zika en R
Tema 7: Parametrización de intervenciones de control para Zika

Introducción

En esta unidad abordaremos la construcción de un modelo determinístico simple, específicamente para el virus del Zika, una enfermedad que desencadenó una gran epidemia en Latinoamérica y el Caribe, y que fue declarada como emergencia de salud pública de importancia internacional. Utilizando los conocimientos previos de teoría epidémica, construiremos un modelo determinístico tipo SIR que incorpora aspectos demográficos.

Para la construcción de este modelo, aprenderemos sobre la dinámica de interacción entre humanos y vectores, así como de los parámetros fundamentales que rigen estos procesos biológicos. Mediante la construcción de un diagrama, examinaremos estas relaciones y formularemos ecuaciones que describen el comportamiento del sistema. Estas ecuaciones serán la base para simular el modelo en el lenguaje de programación R. A su vez propondremos y modelaremos estrategias de intervención.

Mediante el análisis del modelo, evaluaremos el potencial impacto de esta epidemia en la sociedad, contextualizando algunas de estas intervenciones en América Latina. Además, reforzaremos y aplicaremos temas clave como son: Modelo SIR, Inmunidad de rebaño, Parámetros e intervenciones de control (fumigación, mosquiteros y vacunación) para una Enfermedad transmitida por vectores (ETV).

Tema 6: Modelo Zika en R

En esta sección pondremos en uso el conocimiento adquirido sobre el Zika, los mecanismos involucrados en la transmisión y las ecuaciones del modelo. El objetivo es construirlo en R.

El único paquete que se requiere para el modelamiento es deSolve, el cual permite resolver las ecuaciones diferenciales. Adicionalmente para manejar los datos y graficar los resultados recomendamos usar tidyverse y cowplot.

6.1 Inicio práctica en R

Para iniciar nuestra práctica en R, por favor abra un proyecto de R y cree un nuevo documento. En este documento debemos cargar las funciones que acabamos de explicar. Si tiene dificultades con este proceso por favor repase la unidad Introducción a R.

install.packages(deSolve) # Paquete deSolve para resolver las ecuaciones diferenciales

Una vez instalado el paquete deSolve por favor cárgue los paquetes con las siguientes líneas de código, cópielas en su script de R y ejecútelas.

R

library(deSolve)

library(tidyverse)

library(cowplot)

Recordemos que para crear un modelo necesitamos compartimentos, condiciones iniciales, parámetros y ecuaciones.

Para este modelo en R empezaremos por definir los parámetros, es decir, todos aquellos valores que a través de la investigación se han recopilado y hacen parte del comportamiento de la enfermedad. En la sección anterior hablamos sobre ellos y los completamos en una tabla. Es hora de ingresarlos en R.

Instrucción: Por favor, tome la tabla que trabajó anteriormente e ingrese el valor de cada uno de estos parámetros.

NOTA:

Es importante recordar que en R, puede utilizar objetos previamente creados para realizar cálculos. Por ejemplo, el parámetro muv es el inverso del parámetro Lv, es decir, muv = 1/Lv. Por lo tanto, en R se puede asignar este valor directamente con muv <- 1/Lv. No es necesario realizar la división y asignar el resultado manualmente.

Desafío 1

Instrucción: Por favor, tome la tabla que trabajó anteriormente e ingrese el valor de cada uno de estos parámetros.

R

Lv       <-        # Esperanza de vida de los mosquitos (en días)
Lh       <-        # Esperanza de vida de los humanos (en días)
PIh      <-        # Periodo infeccioso en humanos (en días)
PIv      <-        # Periodo infeccioso en vectores (en días)
PEI      <-        # Período extrínseco de incubación en mosquitos adultos (en días)
muv      <-        # Tasa per cápita de mortalidad de la población de mosquitos (1/Lv)
muh      <-        # Tasa per cápita de mortalidad de la población de humanos (1/Lh)
alphav   <-        # Tasa per cápita de natalidad de la población de mosquitos. Por ahora asumiremos que es la misma de tasa de mortalidad.
alphah   <-        # Tasa per cápita de natalidad de la población de humanos.  Por ahora asumiremos que es la misma de tasa de mortalidad
gamma    <-        # Tasa de recuperación en humanos (1/PIh)
delta    <-        # Tasa extrínseca de incubación (1/PEI)
Nh       <-        # Número de humanos. Para este ejercicio proponemos 100.000 humanos. Puede cambiarlos si desea de acuerdo a su contexto.
m        <-        # Densidad de mosquitos hembra por humano
Nv       <-        # Número de mosquitos (m * Nh)
R0       <-        # Número reproductivo básico
ph       <-        # Probabilidad de transmisión de un mosquito infeccioso a un humano susceptible después de una picadura.
pv       <-        # Probabilidad de transmisión de un humano infeccioso a un mosquito susceptible después de una picadura.
b        <-        sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
                   (m * ph * pv * delta)) # Tasa de picadura
betah    <-        # Coeficiente de transmisión de un mosquito infeccioso a un humano susceptible después de una picadura (ph*b)
betav    <-        # Coeficiente de transmisión de un humano infeccioso a un mosquito susceptible después de una picadura (pv*b)
TIME     <-  1      # Número de años que se va a simular. Para este ejercicio iniciaremos con el primer año de la epidemia.

6.2 Ecuaciones del modelo

Ahora que ya ingresamos al script los parámetros es hora de emplear las ecuaciones que se escribieron antes, las cuales permiten conocer el número de individuos en cada uno de los seis compartimentos en función del tiempo. Tres compartimentos para los humanos y tres compartimentos para los mosquitos, los cuales están identificados por una h (para humanos) y una v (para mosquitos). Para los humanos tenemos los compartimentos; susceptibles, infectados y recuperados (de ahí la palabra SIR) y para los mosquitos los compartimientos son: susceptibles, expuestos e infecciosos (SEI).

Compartimentos

$S_h$ : Humanos susceptibles
$I_h$ : Humanos infecciosos
$R_h$ : Humanos recuperados de la infección (inmunizados frente a nueva infección)
$S_v$ : Vectores susceptibles
$E_v$ : Vectores expuestos
$I_v$ : Vectores infecciosos

Para este modelo emplearemos las siguientes ecuaciones diferenciales:

6.2.1 Humanos

\[\ \frac{dSh}{dt} = \alpha_h N_h - \beta_h \frac {I_v}{N_h}S_h - \mu_h S_h \]

\[\ \frac{dIh}{dt} = \beta_h \frac {I_v}{N_h}S_h - (\gamma + \mu_h) I_h \]

\[\ \frac{dRh}{dt} = \gamma I_h - \mu_h R_h\]

6.2.2 Vectores

\[\ \frac{dSv}{dt} = \alpha_v N_v - \beta_v \frac{ I_h} {N_h}S_v - \mu_v Sv\]

\[\ \frac{dE_v}{dt} = \beta_v \frac{I_h} {N_h}S_v- (\delta + \mu_v) Ev\]

\[\ \frac{dI_v}{dt} = \delta Ev - \mu_v I_v\]

6.3 Fórmula para calcular $R_0$ (Número reproductivo básico)

Fórmula necesaria para estimar $R_0$:

\[ R_0 = \frac{mb^2 p_h p_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma)} \]

Desafío

Instrucción: Traduzca las ecuaciones a R

R

# Humanos
         dSh   <-  alphah * Nh - betah * (Iv/Nh) * Sh - muh * Sh   
         dIh   <-______ * (Iv/Nh) * Sh - (____ + _____) * Ih
         dRh   <-  ______ * Ih  - ______ * Rh
         
 # Mosquitos
         dSv  <-  alphav * Nv - _____ * (Ih/Nh) * Sv - _____ * Sv 
         dEv  <-  _____ * (Ih/Nh) * Sv - (____ + _____)* Ev
         dIv  <-  _____ * Ev - _____ * Iv

Una vez sepamos traducir las ecuaciones a código, se procederá a ejecutar el modelo. Para esto se usará la función ode del paquete deSolve.

Se empezará por crear la función (que luego se usará en el argumento fun). Para ello es necesario traducir las ecuaciones del modelo de Zika a R. Abajo encontrará la función ya construida modelo_zika para que usted reemplace las ecuaciones que ya completó arriba.

Desafío 3

Instrucción: Reemplace las ecuaciones incompletas del siguiente código por las ecuaciones completas del modelo Zika que trabajó en la instrucción anterior.

R

# Modelo determinístico simple (fun)
modelo_zika <- function(tiempo, variable_estado, parametros) {
  
  with(as.list(c(variable_estado, parametros))
, # entorno local para evaluar derivados
       {
         # Humanos
         dSh   <-  ____ * Nh - ____ * (Iv/Nh) * Sh - ____ * Sh   
         dIh   <-  ____ * (Iv/Nh) * Sh - (____ + ____) * Ih
         dRh   <-  ____ * Ih  - ____ * Rh
         
         # Mosquitos
         dSv  <-  alphav * Nv - ____ * (Ih/Nh) * Sv - ____ * Sv 
         dEv  <-  ____ * (Ih/Nh) * Sv - (____ + ____)* Ev
         dIv  <-  ____ * Ev - ____ * Iv
         
         list(c(dSh, dIh, dRh, dSv, dEv, dIv))
       }
  )
}

6.4 Resolviendo el Sistema

Para resolver el sistema es necesario crear los tres argumentos faltantes (times, parms y y) para usar la función ode.

Desafío 4

Instrucción: Para times y parms, copie el código que se encuentra a continuación y ejecútelo.

R

# Secuencia temporal (times)
tiempo <- seq(1, 365 * TIME , by = 1)
# Los parámetros (parms)
params <- c(
  muv      = muv,     
  muh      = muh, 
  alphav   = alphav,
  alphah   = alphah,
  gamma    = gamma,   
  delta    = delta,   
  betav    = betav,       
  betah    = betah,   
  Nh       = Nh,      
  Nv       = Nv
)

En el código que ejecutó se creó tiempo (times) y parametros (params). Aún nos falta crear el argumento y, el cual desarrollaremos en la siguiente sección.

6.4.1. Condiciones iniciales del sistema (y)

Para definir las condiciones iniciales, recuerde que el escenario a modelar en este ejercicio es para una fecha antes del reporte del primer caso. Por lo tanto estos valores deben reflejar ese contexto.

Discusión

Reflexión: ¿Qué condiciones iniciales tendrían cada uno de los compartimientos?

Desafío 5

Instrucción: Complete los espacios según lo aprendido en el tutorial.

R

# Condiciones iniciales del sistema (y)
inicio <- c(Sh = _______ ,        # COMPLETE Y COMENTE
            Ih = _______ ,        # COMPLETE Y COMENTE
            Rh = _______ ,        # COMPLETE Y COMENTE
            Sv = _______ ,        # COMPLETE Y COMENTE
            Ev = _______ ,        # COMPLETE Y COMENTE
            Iv = _______ )        # COMPLETE Y COMENTE

6.4.2 Función ode

Una vez creados todos los argumentos necesarios, es hora de ingresarlos a ode. Recordemos los cuatro argumentos de ode y a que corresponden a:

y:inicio. Vector creado con las condiciones iniciales de los seis compartimentos.
times:tiempo. Vector con la secuencia temporal
fun:modelo_zika. Función que contiene las ecuaciones necesarias para simular el modelo.
parms:parametros. Vector en el cual se recopilaron los parámetros necesarios para simular el modelo.

Desafío 6

Instrucción: Complete los espacios en blanco según lo trabajado hasta el momento.

R

# Resuelva las ecuaciones
salida <- ode(y      =   _______ , # COMPLETE Y COMENTE
              times  = _______ ,   # COMPLETE Y COMENTE
              fun    = _______ ,   # COMPLETE Y COMENTE
              parms  = _______  # COMPLETE Y COMENTE
) %>%
  as.data.frame() # Convertir a data frame

6.4.3 Introduciendo el primer caso

Ahora que tenemos todos los compartimentos definidos, es hora de ingresar al modelo un individuo infeccioso para iniciar la epidemia.

Discusión

Reflexión: ¿Qué cree que es más probable, que a una población (en otro país) ingrese un humano infeccioso o un mosquito infeccioso?

Para nuestro caso hipotético, vamos a suponer que una persona se infectó en Brasil mientras estaba de turismo y regresó posteriormente a la ciudad ______________ (la ciudad que usted definió al comienzo del ejercicio) siendo el primer sujeto infeccioso en esta población. En este contexto, el compartimento de humanos infecciosos tendrá entonces un individuo, Ih = 1 y el compartimento de humanos susceptibles tendrá un individuo menos, Sh = Nh - 1.

Desafío

Pista: Cambie en R las condiciones iniciales (inicio) de forma que Ih = 1 y Sh = Nh - 1.

6.5 ¡Ahora ejecutaremos el modelo!

Hasta este punto, usted ha completado toda la información faltante en el script para poder ejecutar el modelo.

Aviso

Instrucción: Ejecute cada conjunto de las líneas del script vistas anteriormente, es decir, ejecute las secciones: Lista de parámetros, la sección Modelo determinístico simple (donde construyó el modelo), las secciones Secuencia temporal (tiempo (times)), Los parámetros (parametros (parms)), la sección Condiciones iniciales del sistema (inicio (y)) y la sección final Resuelva las ecuaciones.

Instrucción: Verifique que no aparezca ningún error. En caso de error por favor verifique la escritura del código y que no haya quedado en el código otros caracteres que no corresponden como por ejemplo “_____” los guiones de los espacios para completar.

6.6 Visualizando los resultados

En nuestro curso usaremos ggplot para la visualización de datos. Es importante que repase la Unidad 4. Visualización de datos en ggplot

Hay que recordar que la unidad de tiempo del modelo de Zika está ya definida desde los parámetros como días.

Sin embargo, si usted quisiera visualizar los resultados en semanas, meses o años puede hacerlo a partir de los resultados del modelo (salida$time). Para hacerlo, puede usar el siguiente código.

Desafío 7

Para tener una visualización más significativa de los resultados, convierta las unidades de tiempo de días a años y a semanas.

R

# Cree las opciones de tiempo para años y semanas 
salida$años <- salida$time/365
salida$semanas <- salida$time/7

6.7 Visualice y analice la primer epidemia

Empecemos realizando una visualización de la primera epidemia. Dado que es un periodo de un año visualicemos las gráficas en semanas.

Instrucción: Ejecute el código a continuación y analice las gráficas resultantes.

R

# Revise la primera epidemia
p1e <- ggplot(data = salida, aes(y = Ih, x = semanas)) +
  geom_line(color = 'firebrick', linewidth = 1) +
  ggtitle('Población de humanos infecciosos') +
  theme_bw() + ylab('Número') + xlab('Semanas') +
 coord_cartesian(ylim = c(0,10000)) #creamos gráfico de población humana infecciosa
p2e <- ggplot(data = salida, aes(y = Rh, x = semanas)) +
  geom_line(color = 'olivedrab', linewidth = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Número') + xlab('Semanas') +
 coord_cartesian(ylim = c(0,100000))  #creamos gráfico de población humana recuperada


plot_grid(p1e, p2e) #creamos gráfico comparativo de la gráfica de población humana infecciosa y población humana recuperada

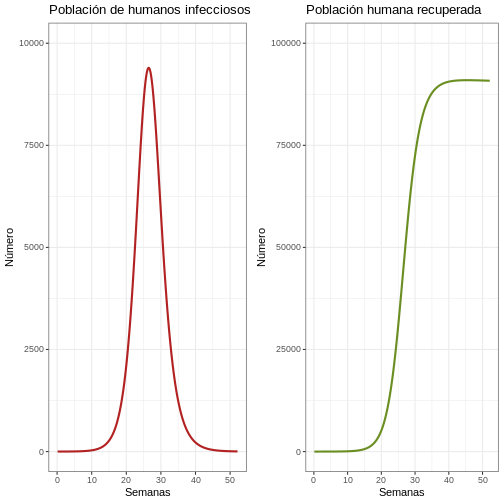
Discusión

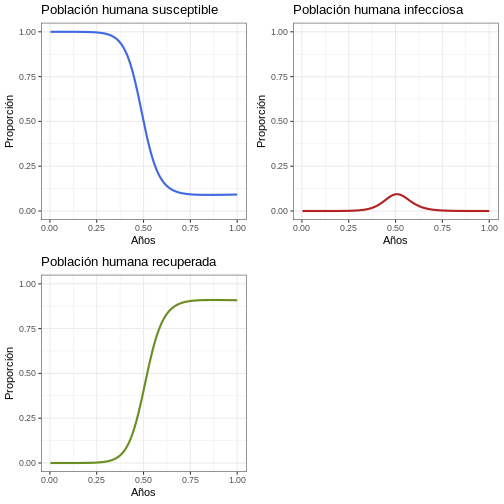
Reflexión: ¿Qué puede observar en la gráfica? Observe bien el eje Y. ¿Qué proporción de humanos son infecciosos al mismo tiempo?

Para tener mayor claridad de esto podemos crear gráficas de las proporciones:

R

# Revise la primera epidemia con proporciones
p1p <- ggplot(data = salida, aes(y = Ih/(Sh+Ih+Rh), x = semanas)) +
  geom_line(color = 'firebrick', linewidth = 1) +
  ggtitle('Población de humanos infecciosos') +
  theme_bw() + ylab('Proporción') + xlab('Semanas') +
 coord_cartesian(ylim = c(0,1)) #creamos gráfico de población humana infecciosa
p2p <- ggplot(data = salida, aes(y = Rh/(Sh+Ih+Rh), x = semanas)) +
  geom_line(color = 'olivedrab', linewidth = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Proporción') + xlab('Semanas') +
 coord_cartesian(ylim = c(0,1))  #creamos gráfico de población humana recuperada


plot_grid(p1p, p2p) #creamos gráfico comparativo de la gráfica de población humana infecciosa y población humana recuperada

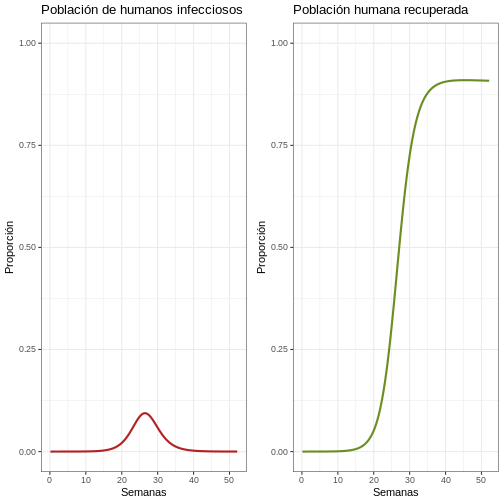
Comportamiento general (Población humana)

Ya observamos la primera epidemia es momento de proyectar la epidemia a un tiempo superior.

Instrucción: Regrese a los parámetros y modifique el parámetro TIME a 100 años. Ejecute el siguiente bloque de código y observe cuántos brotes se producen en la población humana y el tamaño de cada brote.

R

# # Revise el comportamiento general del modelo para 100 años
p1h <- ggplot(data = salida, aes(y = (Rh + Ih + Sh), x = años)) +
  geom_line(color = 'grey68', linewidth = 1) +
  ggtitle('Población humana total') +
  theme_bw() + ylab('Número') + xlab('Años')
p2h <- ggplot(data = salida, aes(y = Sh, x = años)) +
  geom_line(color = 'royalblue', linewidth = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('Número') + xlab('Años')
p3h <- ggplot(data = salida, aes(y = Ih, x = años)) +
  geom_line(color = 'firebrick', linewidth = 1) +
  ggtitle('Población humana infecciosa') +
  theme_bw() + ylab('Número') + xlab('Años')
p4h <- ggplot(data = salida, aes(y = Rh, x = años)) +
  geom_line(color = 'olivedrab', linewidth = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1h, p2h, p3h, p4h, ncol = 2)

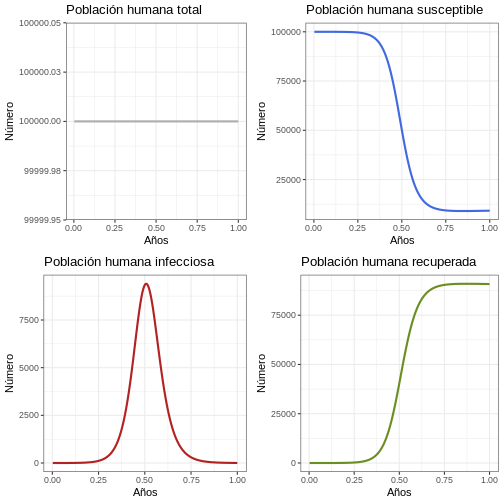
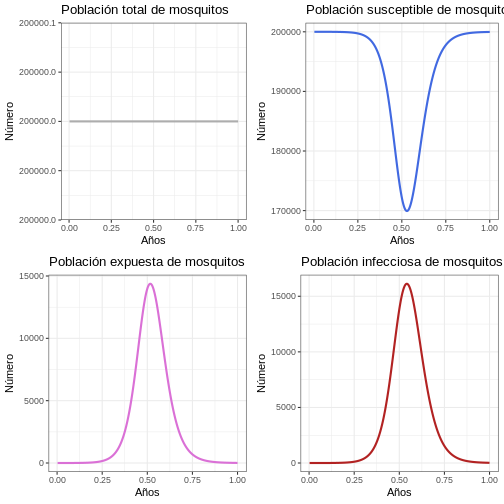
Comportamiento General (Población de mosquitos)

Instrucción: Ejecute el siguiente bloque de código y observe cuántos brotes se producen en la población de mosquitos y el tamaño de cada brote. Compare las gráficas con las gráficas de la población humana.

R

# Revise el comportamiento general del modelo
p1v <- ggplot(data = salida, aes(y = (Sv + Ev + Iv), x = años)) +
  geom_line(color = 'grey68', linewidth = 1) +
  ggtitle('Población total de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p2v <- ggplot(data = salida, aes(y = Sv, x = años)) +
  geom_line(color = 'royalblue', linewidth = 1) +
  ggtitle('Población susceptible de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p3v <- ggplot(data = salida, aes(y = Ev, x = años)) +
  geom_line(color = 'orchid', linewidth = 1) +
  ggtitle('Población expuesta de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p4v <- ggplot(data = salida, aes(y = Iv, x = años)) +
  geom_line(color = 'firebrick', linewidth = 1) +
  ggtitle('Población infecciosa de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1v, p2v, p3v, p4v, ncol = 2)

Proporción

Instrucción: Ejecute el siguiente bloque de código y compárelo con las gráficas generadas para la población humana.

R

p1 <- ggplot(data = salida, aes(y = Sh/(Sh+Ih+Rh), x = años)) +
  geom_line(color = 'royalblue', linewidth = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
p2 <- ggplot(data = salida, aes(y = Ih/(Sh+Ih+Rh), x = años)) +
  geom_line(color = 'firebrick', linewidth = 1) +
  ggtitle('Población humana infecciosa') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
p3 <- ggplot(data = salida, aes(y = Rh/(Sh+Ih+Rh), x = años)) +
  geom_line(color = 'olivedrab', linewidth = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
plot_grid(p1, p2, p3, ncol = 2)

Puntos Clave

Revise si al final de esta lección adquirió estas competencias:

Aplicar conceptos como parámetros, $R_0$ e inmunidad de rebaño, aprendidos en la sesión A del taller
Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
Realizar un modelo simple en R para una enfermedad transmitida por vector
Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección

Contribuciones

Zulma Cucunuba & Pierre Nouvellet: Versión inicial
Kelly Charinga & Zhian N. Kamvar: Edición
José M. Velasco-España: Traducción de Inglés a Español y Edición
Andree Valle-Campos: Ediciones menores

Asuntos legales

Referencias

de Carvalho, S. S., Rodovalho, C. M., Gaviraghi, A., Mota, M. B. S., Jablonka, W., Rocha-Santos, C., Nunes, R. D., Sá-Guimarães, T. da E., Oliveira, D. S., Melo, A. C. A., Moreira, M. F., Fampa, P., Oliveira, M. F., da Silva-Neto, M. A. C., Mesquita, R. D., & Atella, G. C. (2021). Aedes aegypti post-emergence transcriptome: Unveiling the molecular basis for the hematophagic and gonotrophic capacitation. PLoS Neglected Tropical Diseases, 15(1), 1–32. https://doi.org/10.1371/journal.pntd.0008915

Chang, C., Ortiz, K., Ansari, A., & Gershwin, M. E. (2016). The Zika outbreak of the 21st century. Journal of Autoimmunity, 68, 1–13. https://doi.org/10.1016/j.jaut.2016.02.006

Cori, A., Ferguson, N. M., Fraser, C., & Cauchemez, S. (2013). A new framework and software to estimate time-varying reproduction numbers during epidemics. American Journal of Epidemiology, 178(9), 1505–1512. https://doi.org/10.1093/aje/kwt133

Duffy, M. R., Chen, T.-H., Hancock, W. T., Powers, A. M., Kool, J. L., Lanciotti, R. S., Pretrick, M., Marfel, M., Holzbauer, S., Dubray, C., Guillaumot, L., Griggs, A., Bel, M., Lambert, A. J., Laven, J., Kosoy, O., Panella, A., Biggerstaff, B. J., Fischer, M., & Hayes, E. B. (2009). Zika Virus Outbreak on Yap Island, Federated States of Micronesia. New England Journal of Medicine, 360(24), 2536–2543. https://doi.org/10.1056/nejmoa0805715

Ferguson, N. M., Cucunubá, Z. M., Dorigatti, I., Nedjati-Gilani, G. L., Donnelly, C. A., Basáñez, M. G., Nouvellet, P., & Lessler, J. (2016). Countering the Zika epidemic in Latin America. Science, 353(6297). https://doi.org/10.1126/science.aag0219

Heesterbeek, J. A. P. (2002). A brief history of R0 and a recipe for its calculation. Acta Biotheoretica, 50(3). https://doi.org/10.1023/A:1016599411804

Lee, E. K., Liu, Y., & Pietz, F. H. (2016). A Compartmental Model for Zika Virus with Dynamic Human and Vector Populations. AMIA … Annual Symposium Proceedings. AMIA Symposium, 2016, 743–752.

Pettersson, J. H. O., Eldholm, V., Seligman, S. J., Lundkvist, Å., Falconar, A. K., Gaunt, M. W., Musso, D., Nougairède, A., Charrel, R., Gould, E. A., & de Lamballerie, X. (2016). How did zika virus emerge in the Pacific Islands and Latin America? MBio, 7(5). https://doi.org/10.1128/mBio.01239-16

Construyendo un modelo deterministico simple

Hoja de ruta

Preguntas

Objetivos

Pre requisito

Tabla de contenido

Introducción

Tema 6: Modelo Zika en R

6.1 Inicio práctica en R

R

NOTA:

Desafío 1

R

6.2 Ecuaciones del modelo

Compartimentos

6.2.1 Humanos

6.2.2 Vectores

6.3 Fórmula para calcular \(R_0\) (Número reproductivo básico)

Desafío

R

Desafío 3

R

6.4 Resolviendo el Sistema

Desafío 4

R

6.4.1. Condiciones iniciales del sistema (y)

Discusión

Desafío 5

R

6.4.2 Función ode

Desafío 6

R

6.4.3 Introduciendo el primer caso

Discusión

Desafío

6.5 ¡Ahora ejecutaremos el modelo!

Aviso

6.6 Visualizando los resultados

Desafío 7

R

6.7 Visualice y analice la primer epidemia

R

Discusión

R

R

R

R

Puntos Clave

Contribuciones

Asuntos legales

Referencias