Projecting infectious disease incidence: a COVID-19 example

Overview

Branching processes can be used to project stochastic infectious disease trends in time provided we can characterize the distribution of times between successive cases (serial interval), and the distribution of secondary cases produced by a single individual (offspring distribution). Such simulations can be achieved in epichains with the simulate_chains() function and Pearson et al. (2020), and Abbott et al. (2020) illustrate its application to COVID-19.

The purpose of this vignette is to use early data on COVID-19 in South Africa (Marivate and Combrink 2020) to illustrate how epichains can be used to project an outbreak.

Let’s load the required packages

library("epichains")
library("dplyr")
library("ggplot2")
library("lubridate")

Data

Included in epichains is a cleaned time series of the first 15 days of the COVID-19 outbreak in South Africa. This can be loaded into memory as follows:

data("covid19_sa", package = "epichains")

We will use the first $5$ observations for this demonstration. We will assume that all the cases in that subset are imported and did not infect each other.

Let us subset and view that aspect of the data.

seed_cases <- covid19_sa[1:5, ]
head(seed_cases)
#> # A tibble: 5 × 2
#>   date       cases
#>   <date>     <int>
#> 1 2020-03-05     1
#> 2 2020-03-07     1
#> 3 2020-03-08     1
#> 4 2020-03-09     4
#> 5 2020-03-11     6

Setting up the inputs

We will now proceed to set up simulate_chains() for the simulations.

Onset times

simulate_chains() requires a vector of seeding times, t0, for each chain/individual/simulation.

To get this, we will use the observation date of the index case as the reference and find the difference between the other observed dates and the reference.

days_since_index <- as.integer(seed_cases$date - min(seed_cases$date))
days_since_index
#> [1] 0 2 3 4 6

Using the vector of start times from the time series, we will then create a corresponding seeding time for each individual, which we’ll call t0.

t0 <- rep(days_since_index, seed_cases$cases)
t0
#>  [1] 0 2 3 4 4 4 4 6 6 6 6 6 6

Generation time

In epidemiology, the generation time (also called the generation interval) is the duration between successive infectious events in a chain of transmission. Similarly, the serial interval is the duration between observed symptom onset times between successive cases in a transmission chain. The generation interval is often hard to observe because exact times of infection are hard to measure hence, the serial interval is often used instead. Here, we use the serial interval and interpret the simulated case data to represent symptom onset.

In this example, we will assume based on COVID-19 literature that the serial interval, S, is log-normal distributed with parameters, $\mu = 4.7$ and $\sigma = 2.9$ (Pearson et al. 2020). The log-normal distribution is commonly used in epidemiology to characterise quantities such as the serial interval because it has a large variance and can only be positive-valued (Nishiura 2007; Limpert, Stahel, and Abbt 2001).

Note that when the distribution is described this way, it means $\mu$ and $\sigma$ are the expected value and standard deviation of the natural logarithm of the serial interval. Hence, in order to sample the “back-transformed” measured serial interval with expectation/mean, $E[S]$ and standard deviation, $SD [S]$ , we can use the following parametrisation:

$\begin{align} E[S] &= \ln \left( \dfrac{\mu^2}{(\sqrt{\mu^2 + \sigma^2}} \right) \\ SD [S] &= \sqrt {\ln \left(1 + \dfrac{\sigma^2}{\mu^2} \right)} \end{align}$

See “log-normal_distribution” on Wikipedia for a detailed explanation of this parametrisation.

We will now set up the generation time function with the appropriate inputs. We adopt R’s random lognormal distribution generator (rlnorm()) that takes meanlog and sdlog as arguments, which we define with the parametrisation above as log_mean() and log_sd() respectively and wrap it in the generation_time_fn() function. Moreover, generation_time_fn() takes one argument n as is required by epichains (See ?epichains::simulate_chains), which is further passed to rlnorm() as the first argument to determine the number of observations to sample (See ?rlnorm).

mu <- 4.7
sgma <- 2.9

log_mean <- log((mu^2) / (sqrt(sgma^2 + mu^2))) # log mean
log_sd <- sqrt(log(1 + (sgma / mu)^2)) # log sd

#' serial interval function
generation_time <- function(n) {
  gt <- rlnorm(n, meanlog = log_mean, sdlog = log_sd)
  return(gt)
}

Offspring distribution

Let us now set up the offspring distribution, that is the distribution that drives the mechanism behind how individual cases infect other cases. The appropriate way to model the offspring distribution is to capture both the population-level transmissibility ( $R0$ ) and the individual-level heterogeneity in transmission (“superspreading”). The negative binomial distribution is commonly used in this case (Lloyd-Smith et al. 2005).

For this example, we will assume that the offspring distribution is characterised by a negative binomial with $mu = 2.5$ (Abbott et al. 2020) and $size = 0.58$ (Wang et al. 2020).

mu <- 2.5
size <- 0.58

In this parameterization, $mu$ represents the $R_0$ , which is defined as the average number of cases produced by a single individual in an entirely susceptible population. The parameter $size$ represents superspreading, that is, the degree of heterogeneity in transmission by single individuals.

Simulation controls

For this example, we will simulate outbreaks that end $21$ days after the last date of observations in the seed_cases dataset.

#' Date to end simulation
projection_window <- 21
tf <- max(days_since_index) + projection_window
tf
#> [1] 27

simulate_chains() is stochastic, meaning the results are different every time it is run for the same set of parameters. We will, therefore, run the simulations $100$ times and aggregate the results.

Let us specify that.

#' Number of simulations
sim_rep <- 100

Lastly, since, we have specified that $R0 > 1$ , it means the epidemic could potentially grow without end. Hence, we must specify an end point for the simulations.

simulate_chains() provides the stat_threshold argument for this purpose. Above stat_threshold, the simulation is cut off. If this value is not specified, it assumes a value of infinity. Here, we will assume a maximum chain size of $1000$ .

#' Maximum chain size allowed
stat_threshold <- 1000

Modelling assumptions

This exercise makes the following simplifying assumptions:

All cases are observed.
Cases are observed exactly at the time of infection.
There is no reporting delay.
Reporting rate is constant through the course of the epidemic.
No interventions have been implemented.
Population is homogeneous and well-mixed.

To summarise the whole set up so far, we are going to simulate each chain 100 times, projecting cases over 21 days after the first 6 days, and assuming that no outbreak size exceeds 1000 cases.

Running the simulations

We will use the function lapply() to run the simulations and bind them by rows with dplyr::bind_rows().

set.seed(1234)
sim_chain_sizes <- lapply(
  seq_len(sim_rep),
  function(sim) {
    simulate_chains(
      n_chains = length(t0),
      offspring_dist = rnbinom,
      mu = mu,
      size = size,
      statistic = "size",
      stat_threshold = stat_threshold,
      generation_time = generation_time,
      t0 = t0,
      tf = tf
    ) %>%
      mutate(sim = sim)
  }
)

sim_output <- bind_rows(sim_chain_sizes)

Let us view the first few rows of the simulation results.

head(sim_output)
#>    chain infector infectee generation      time sim
#> 14     3        1        2          2  8.123133   1
#> 15     3        1        3          2  6.842933   1
#> 16     3        1        4          2  7.260639   1
#> 17     3        1        5          2 11.244838   1
#> 18     7        1        2          2  7.022334   1
#> 19     7        1        3          2 12.182368   1

Post-processing

Now, we will summarise the simulation results.

We want to plot the individual simulated daily time series and show the median cases per day aggregated over all simulations.

First, we will create the daily time series per simulation by aggregating the number of cases per day of each simulation.

# Daily number of cases for each simulation
incidence_ts <- sim_output %>%
  mutate(day = ceiling(time)) %>%
  count(sim, day, name = "cases") %>%
  as_tibble()

head(incidence_ts)
#> # A tibble: 6 × 3
#>     sim   day cases
#>   <int> <dbl> <int>
#> 1     1     0     1
#> 2     1     2     1
#> 3     1     3     1
#> 4     1     4     4
#> 5     1     6     6
#> 6     1     7     1

Next, we will add a date column to the results of each simulation set. We will use the date of the first case in the observed data as the reference start date.

# Get start date from the observed data
index_date <- min(seed_cases$date)
index_date
#> [1] "2020-03-05"

# Add a dates column to each simulation result
incidence_ts_by_date <- incidence_ts %>%
  group_by(sim) %>%
  mutate(date = index_date + days(seq(0, n() - 1))) %>%
  ungroup()

head(incidence_ts_by_date)
#> # A tibble: 6 × 4
#>     sim   day cases date      
#>   <int> <dbl> <int> <date>    
#> 1     1     0     1 2020-03-05
#> 2     1     2     1 2020-03-06
#> 3     1     3     1 2020-03-07
#> 4     1     4     4 2020-03-08
#> 5     1     6     6 2020-03-09
#> 6     1     7     1 2020-03-10

Now we will aggregate the simulations by day and evaluate the median daily cases across all simulations.

# Median daily number of cases aggregated across all simulations
median_daily_cases <- incidence_ts_by_date %>%
  group_by(date) %>%
  summarise(median_cases = median(cases)) %>%
  ungroup() %>%
  arrange(date)

head(median_daily_cases)
#> # A tibble: 6 × 2
#>   date       median_cases
#>   <date>            <dbl>
#> 1 2020-03-05            1
#> 2 2020-03-06            1
#> 3 2020-03-07            1
#> 4 2020-03-08            4
#> 5 2020-03-09            5
#> 6 2020-03-10            8

Visualization

We will now plot the individual simulation results alongside the median of the aggregated results.

# since all simulations may end at a different date, we will find the minimum
# final date for all simulations for the purposes of visualisation.
final_date <- incidence_ts_by_date %>%
  group_by(sim) %>%
  summarise(final_date = max(date), .groups = "drop") %>%
  summarise(min_final_date = min(final_date)) %>%
  pull(min_final_date)

incidence_ts_by_date <- incidence_ts_by_date %>%
  filter(date <= final_date)

median_daily_cases <- median_daily_cases %>%
  filter(date <= final_date)

ggplot(data = incidence_ts_by_date) +
  geom_line(
    aes(
      x = date,
      y = cases,
      group = sim
    ),
    color = "grey",
    linewidth = 0.2,
    alpha = 0.25
  ) +
  geom_line(
    data = median_daily_cases,
    aes(
      x = date,
      y = median_cases
    ),
    color = "tomato3",
    linewidth = 1.8
  ) +
  geom_point(
    data = covid19_sa,
    aes(
      x = date,
      y = cases
    ),
    color = "black",
    size = 1.75,
    shape = 21
  ) +
  geom_line(
    data = covid19_sa,
    aes(
      x = date,
      y = cases
    ),
    color = "black",
    linewidth = 1
  ) +
  scale_x_continuous(
    breaks = seq(
      min(incidence_ts_by_date$date),
      max(incidence_ts_by_date$date),
      5
    ),
    labels = seq(
      min(incidence_ts_by_date$date),
      max(incidence_ts_by_date$date),
      5
    )
  ) +
  scale_y_continuous(
    breaks = seq(
      0,
      max(incidence_ts_by_date$cases),
      30
    ),
    labels = seq(
      0,
      max(incidence_ts_by_date$cases),
      30
    )
  ) +
  geom_vline(
    mapping = aes(xintercept = max(seed_cases$date)),
    linetype = "dashed"
  ) +
  labs(x = "Date", y = "Daily cases")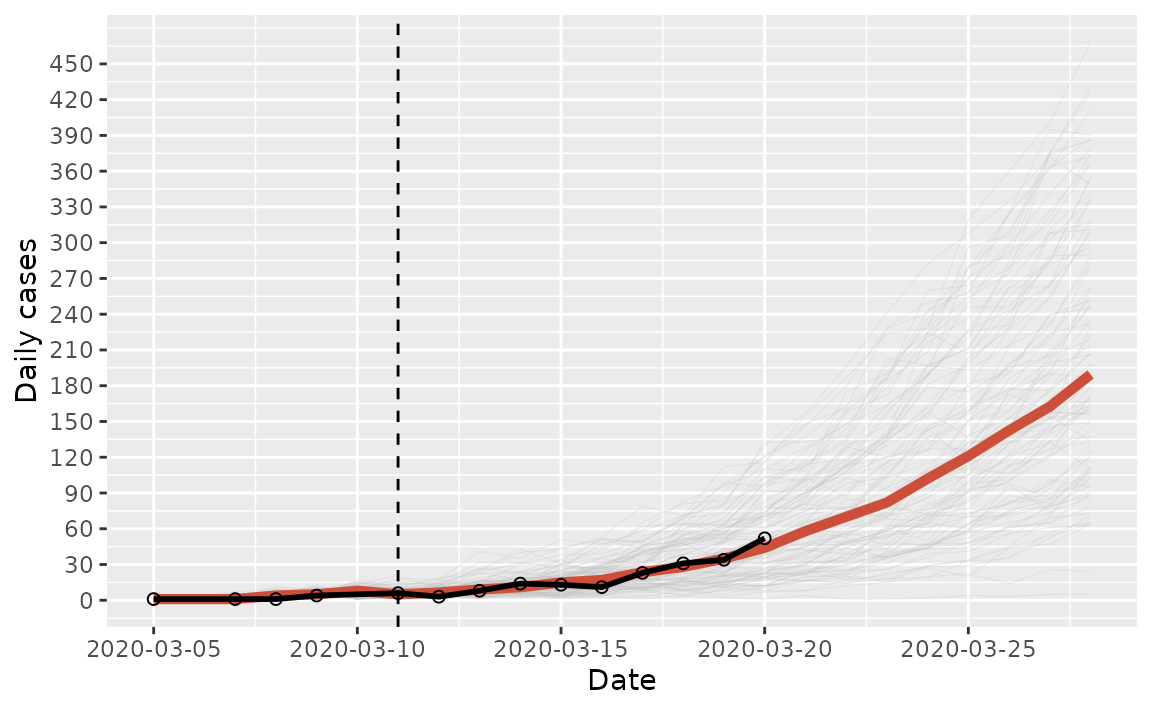

COVID-19 incidence in South Africa projected over a two week window in 2020. The light gray lines represent the individual simulations, the red line represents the median daily cases across all simulations, the black connected dots represent the observed data, and the dashed vertical line marks the beginning of the projection.

References

Abbott, Sam, Joel Hellewell, James Munday, Sebastian Funk, CMMID nCoV working group, et al. 2020. “The Transmissibility of Novel Coronavirus in the Early Stages of the 2019-20 Outbreak in Wuhan: Exploring Initial Point-Source Exposure Sizes and Durations Using Scenario Analysis.” Wellcome Open Research 5.

Limpert, Eckhard, Werner A. Stahel, and Markus Abbt. 2001. “Log-Normal Distributions Across the Sciences: Keys and Clues.” BioScience 51 (5): 341–52. https://doi.org/10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2.

Lloyd-Smith, J. O., S. J. Schreiber, P. E. Kopp, and W. M. Getz. 2005. “Superspreading and the Effect of Individual Variation on Disease Emergence.” Nature 438 (7066): 355–59. https://doi.org/10.1038/nature04153.

Marivate, Vukosi, and Herkulaas MvE Combrink. 2020. “Use of Available Data to Inform the COVID-19 Outbreak in South Africa: A Case Study.” arXiv Preprint arXiv:2004.04813.

Nishiura, Hiroshi. 2007. “Early Efforts in Modeling the Incubation Period of Infectious Diseases with an Acute Course of Illness.” Emerging Themes in Epidemiology 4: 1–12. https://doi.org/10.1186/1742-7622-4-2.

Pearson, Carl A.B., Cari van Schalkwyk, Anna M. Foss, Kathleen M. O’Reilly, and Juliet R.C. Pulliam. 2020. “Projected Early Spread of COVID-19 in Africa Through 1 June 2020.” Eurosurveillance 25 (18): 1–6. https://doi.org/10.2807/1560-7917.ES.2020.25.18.2000543.

Wang, Liang, Xavier Didelot, Jing Yang, Gary Wong, Yi Shi, Wenjun Liu, George F. Gao, and Yuhai Bi. 2020. “Inference of Person-to-Person Transmission of COVID-19 Reveals Hidden Super-Spreading Events During the Early Outbreak Phase.” Nature Communications 11 (1): 1–6. https://doi.org/10.1038/s41467-020-18836-4.

James Azam, Sebastian Funk