Introduction to delays

Last updated on 2025-04-12 | Edit this page

Overview

Questions

  • How to fit a probability distribution to delay data?
  • How to interpret distribution parameters?
  • How to access distribution parameters from fitting objects

Objectives

  • Fit a probability distribution to data using fitdistrplus
  • Extract a single column using pull(), dollar sign $, or square brackets [].

Introduction

Delays are key for downstream task in outbreak analytics. To estimate the outbreak severity, we need to assume a known delay from onset to death. To quantify transmission, we need to consider delays from the moment of infection to the time of data collection. In order to account for epidemiological delays when estimating indicators of severity or transmission, in our analysis we need to input delays as Probability Distributions.

Let’s start by loading the package dplyr to manipulate data. We’ll use the pipe %>% to connect some of their functions, including others from the package ggplot2, so let’s call to the package tidyverse that loads them all. We will also use fitdistrplus to fit probability distributions to delays:

R 

# Load packages
library(tidyverse) # loads dplyr, the pipe, and ggplot2
library(fitdistrplus)

Checklist

The double-colon

The double-colon :: in R let you call a specific function from a package without loading the entire package into the current environment.

For example, dplyr::filter(data, condition) uses filter() from the dplyr package.

This helps us remember package functions and avoid namespace conflicts.

Fit a probability distribution to delays

We fit a probability distribution to data (like delays) to make inferences about it. These inferences can be useful for Public health interventions and decision making. For example:

  • From the incubation period distribution we can inform the length of active monitoring or quarantine. We can infer the time by which 99% of infected individuals are expected to show symptoms (Lauer et al., 2020).

  • From the serial interval distribution we can optimize contact tracing. We can evaluate the need to expand the number of days pre-onset to consider in the contact tracing to include more backwards contacts (Claire Blackmore, 2021; Davis et al., 2020).

A schematic of the relationship of different time periods of transmission between a primary case and a secondary case in a transmission pair. Adapted from Zhao et al, 2021
A schematic of the relationship of different time periods of transmission between a primary case and a secondary case in a transmission pair. Adapted from Zhao et al, 2021

Callout

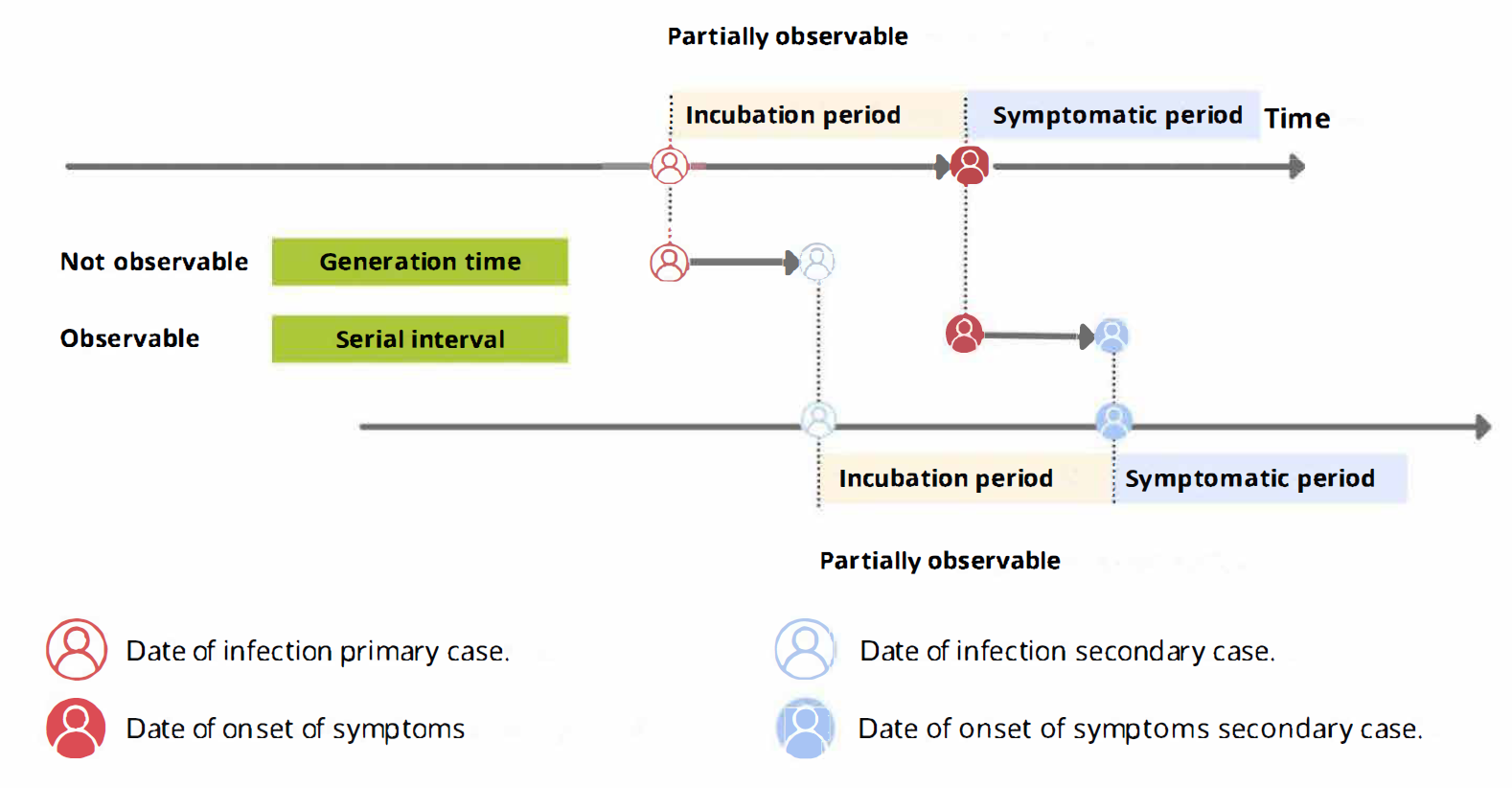
From time periods to probability distributions

When we calculate the serial interval, we see that not all case pairs have the same time length. We will observe this variability for any case pair and individual time period.

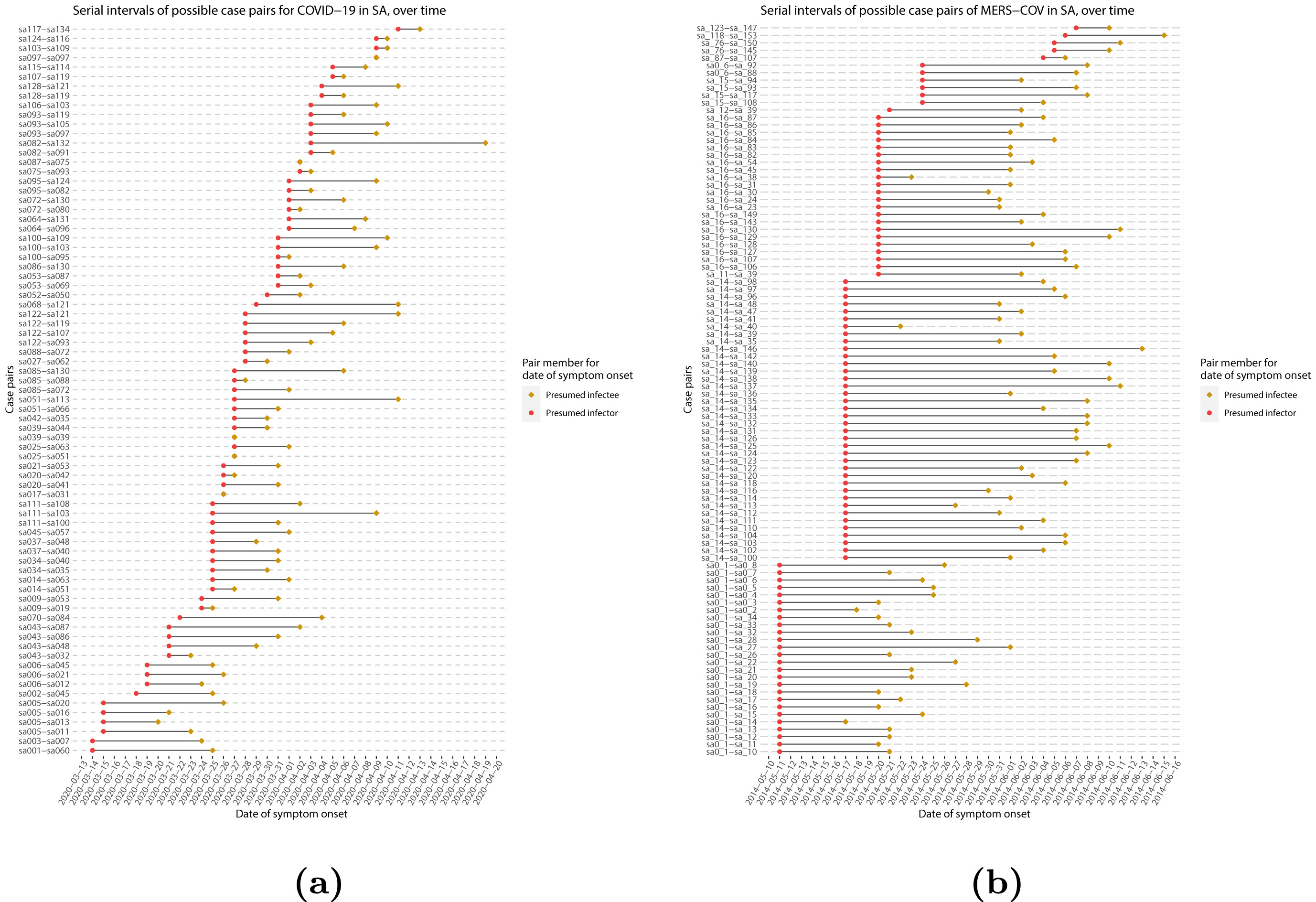
Serial intervals of possible case pairs in (a) COVID-19 and (b) MERS-CoV. Pairs represent a presumed infector and their presumed infectee plotted by date of symptom onset (Althobaity et al., 2022).
Serial intervals of possible case pairs in (a) COVID-19 and (b) MERS-CoV. Pairs represent a presumed infector and their presumed infectee plotted by date of symptom onset (Althobaity et al., 2022).

To summarise these data from individual and pair time periods, we can find the statistical distributions that best fit the data (McFarland et al., 2023).

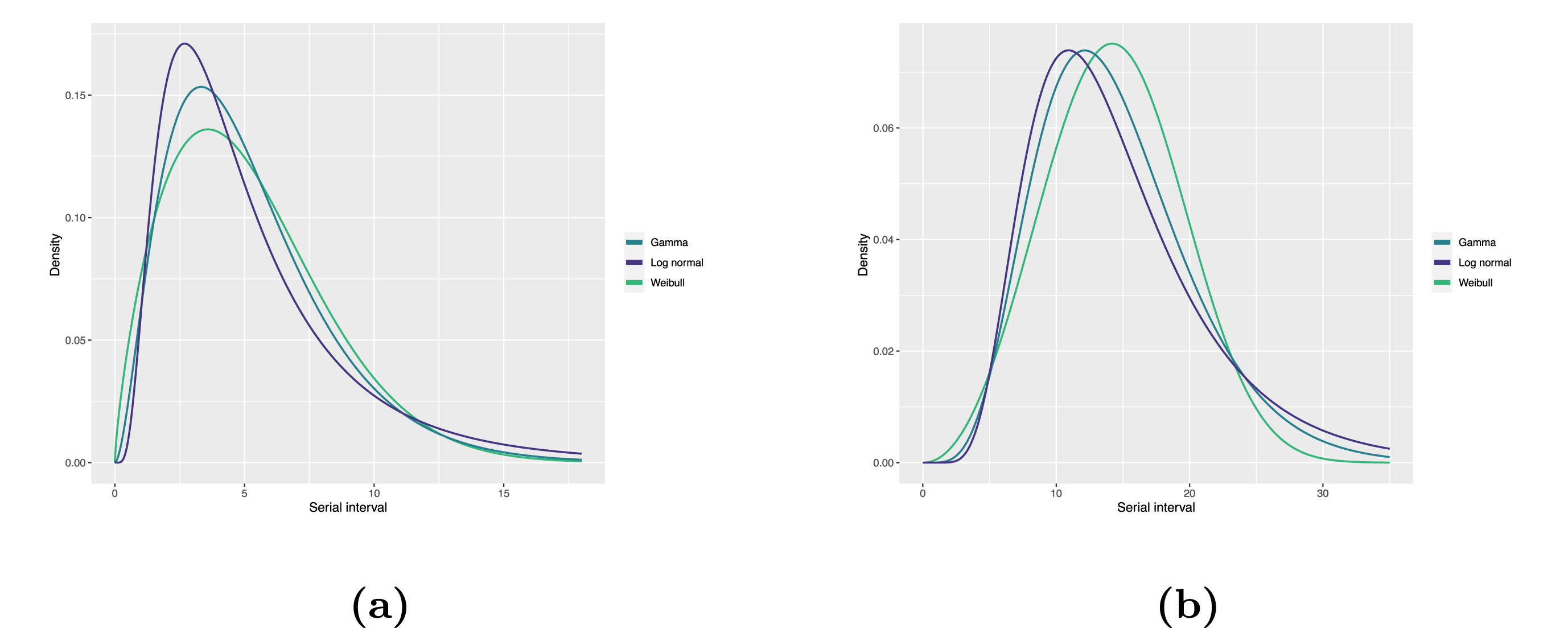
Fitted serial interval distribution for (a) COVID-19 and (b) MERS-CoV based on reported transmission pairs in Saudi Arabia. We fitted three commonly used distributions, Log normal, Gamma, and Weibull distributions, respectively (Althobaity et al., 2022).
Fitted serial interval distribution for (a) COVID-19 and (b) MERS-CoV based on reported transmission pairs in Saudi Arabia. We fitted three commonly used distributions, Log normal, Gamma, and Weibull distributions, respectively (Althobaity et al., 2022).

Statistical distributions are summarised in terms of their summary statistics like the location (mean and percentiles) and spread (variance or standard deviation) of the distribution, or with their distribution parameters that inform about the form (shape and rate/scale) of the distribution. These estimated values can be reported with their uncertainty (95% confidence intervals).

Gamma mean shape rate/scale
MERS-CoV 14.13(13.9–14.7) 6.31(4.88–8.52) 0.43(0.33–0.60)
COVID-19 5.1(5.0–5.5) 2.77(2.09–3.88) 0.53(0.38–0.76)
Weibull mean shape rate/scale
MERS-CoV 14.2(13.3–15.2) 3.07(2.64–3.63) 16.1(15.0–17.1)
COVID-19 5.2(4.6–5.9) 1.74(1.46–2.11) 5.83(5.08–6.67)
Serial interval estimates using Gamma, Weibull, and Log Normal distributions. 95% confidence intervals for the shape and scale (logmean and sd for Log Normal) parameters are shown in brackets (Althobaity et al., 2022).
Log normal mean mean-log sd-log
MERS-CoV 14.08(13.1–15.2) 2.58(2.50–2.68) 0.44(0.39–0.5)
COVID-19 5.2(4.2–6.5) 1.45(1.31–1.61) 0.63(0.54–0.74)

To illustrate this, let’s continue with the same line list from the previous episode:

R 

# Read data
# e.g.: if path to file is data/linelist.csv then:
cases <- readr::read_csv(
  here::here("data", "linelist.csv")
)

From the cases object we can use:

  • dplyr::mutate() to transform the reporting_delay class object from <time> to <numeric>,
  • dplyr::filter() to keep the positive values,
  • dplyr::pull() to extract a single column,
  • fitdistrplus::fitdist() to fit a probability distribution using Maximum Likelihood. We can test distributions like the Log Normal ("lnorm"), "gamma", or "weibull".

R 

cases %>%
  dplyr::select(case_id, date_of_onset, date_of_hospitalisation) %>%
  dplyr::mutate(reporting_delay = date_of_hospitalisation - date_of_onset) %>%
  dplyr::mutate(reporting_delay_num = as.numeric(reporting_delay)) %>%
  dplyr::filter(reporting_delay_num > 0) %>%
  dplyr::pull(reporting_delay_num) %>%
  fitdistrplus::fitdist(distr = "lnorm")

OUTPUT 

Fitting of the distribution ' lnorm ' by maximum likelihood
Parameters:
         estimate Std. Error
meanlog 1.0488098 0.06866105
sdlog   0.8465102 0.04855039

Use summary() to find goodness-of-fit statistics from the Maximum likelihood. Use plot() to visualize the fitted density function and other quality control plots. To compare multiple distributions you can use superspreading::ic_tbl(). We’ll explore that package later!

Now we can do inferences from the probability distribution fitted to the epidemiological delay! Want to learn how? Read the “Show details” :)

Making inferences from probability distributions

From probability distributions we can infer estimates like cumulative probability, maximum values, or generate random values. We can access to them using R probability functions.

We recommend you read the definitions of the R probability functions for the Normal distribution. From it we can relate with any other family of statistical distributions!

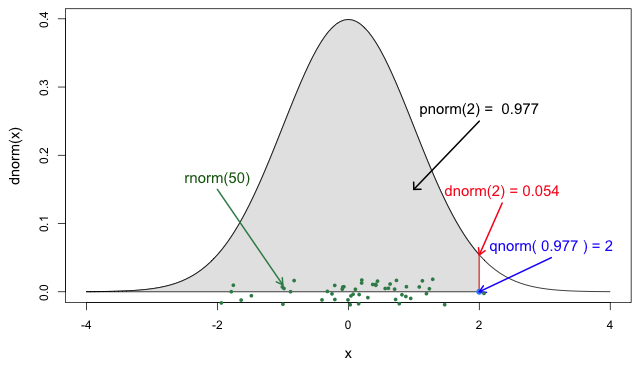
The four probability functions for the normal distribution (Jack Weiss, 2012)
The four probability functions for the normal distribution (Jack Weiss, 2012)

Each probability distribution has a unique set of parameters and probability functions. Read the Distributions in the stats package or ?stats::Distributions to find the ones available in R.

For example, assuming that the reporting delay follows a Log Normal distribution, we can use plnorm() to calculate the probability of observing a reporting delay of 14 days or less:

R 

plnorm(q = 14, meanlog = 1.0488098, sdlog = 0.8465102)

OUTPUT 

[1] 0.9698499

Or the amount of time by which 99% of symptomatic individuals are expected to be reported in the hospitalization record:

R 

qlnorm(p = 0.99, meanlog = 1.0488098, sdlog = 0.8465102)

OUTPUT 

[1] 20.45213

You will find more examples of how to use delays for decision-making at the Use delay distributions in analysis at Tutorials Middle!

To interactively explore probability distributions, their parameters and access to their distribution functions, we suggest to explore a shinyapp called The Distribution Zoo: https://ben18785.shinyapps.io/distribution-zoo/

Checklist

Let’s review some operators used until now:

  • Assignment <- assigns a value to a variable from right to left.
  • Double colon :: to call a function from a specific package.
  • Pipe %>% to structure sequences of data operations left-to-right

We need to add two more to the list:

  • Dollar sign $
  • Square brackets []

Last step is to access to this parameters. Most modeling outputs from R functions will be stored as list class objects. In R, the dollar sign operator $ is used to access elements (like columns) within a data frame or list by name, allowing for easy retrieval of specific components.

Testimonial

A code completion tip

If we write the square brackets [] next to the object reporting_delay_fit$estimate[], within [] we can use the Tab key ↹ for code completion feature

This gives quick access to "meanlog" and "sdlog". We invite you to try this out in code chunks and the R console!

R 

# 1. Place the cursor within the square brackets
# 2. Use the Tab key
# 3. Explore the completion list
# 4. Select for "meanlog" or "sdlog"
reporting_delay_fit$estimate[]

Callout

Estimating epidemiological delays is CHALLENGING!

Epidemiological delays need to account for biases like censoring, right truncation, or epidemic phase (Charniga et al., 2024).

Additionally, at the beginning of an outbreak, limited data or resources exist to perform this during a real-time analysis. Until we have more appropriate data for the specific disease and region of the ongoing outbreak, we can reuse delays from past outbreaks from the same pathogens or close in its phylogeny, independent of the area of origin.

In the following tutorial episodes, we will:

  • Access to epidemiological delay distributions to estimate delay-adjusted transmission and severity metrics (e.g. reproduction number and case fatality risk). Find more in Tutorials Middle!
  • Use parameter values like the basic reproduction number, and delays like the latent period and infectious period to simulate transmission trajectories and intervention scenarios. Find more in Tutorials Late!

Challenges

Challenge

Relevant delays when estimating transmission

  • Review the definition of the incubation period in our glossary page.

  • Calculate the summary statistics of the incubation period distribution observed in the line list.

  • Visualize the distribution of the incubation period from the line list.

  • Fit a log-normal distribution to get the probability distribution parameters of the the observed incubation period.

  • (Optional) Infer the time by which 99% of infected individuals are expected to show symptoms.

Calculate the summary statistics:

R 

cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  skimr::skim(incubation_period)
Data summary
Name Piped data
Number of rows 166
Number of columns 4
_______________________
Column type frequency:
difftime 1
________________________
Group variables None

Variable type: difftime

skim_variable n_missing complete_rate min max median n_unique
incubation_period 61 0.63 1 days 37 days 5 days 25

Visualize the distribution:

R 

cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  ggplot(aes(x = incubation_period)) +
  geom_histogram(binwidth = 1)

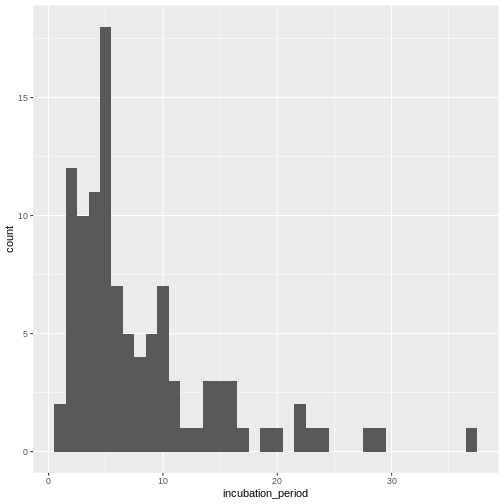
Fit a log-normal distribution:

R 

incubation_period_dist <- cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  mutate(incubation_period_num = as.numeric(incubation_period)) %>%
  filter(!is.na(incubation_period_num)) %>%
  pull(incubation_period_num) %>%
  fitdistrplus::fitdist(distr = "lnorm")

incubation_period_dist

OUTPUT 

Fitting of the distribution ' lnorm ' by maximum likelihood
Parameters:
         estimate Std. Error
meanlog 1.8037993 0.07381350
sdlog   0.7563633 0.05219361

(Optional) Infer the time by which 99% of infected individuals are expected to show symptoms:

R 

qlnorm(
  p = 0.99,
  meanlog = incubation_period_dist$estimate["meanlog"],
  sdlog = incubation_period_dist$estimate["sdlog"]
)

OUTPUT 

[1] 35.28167

With the distribution parameters of the incubation period we can infer the length of active monitoring or quarantine. Lauer et al., 2020 estimated the incubation period of Coronavirus Disease 2019 (COVID-19) from publicly reported confirmed cases.

Key Points

  • Epidemiological delays condition the estimation of indicators for severity or transmission.
  • Fit probability distribution to delays to make inferences from them for decision-making.
  • Fitting epidemiological delays need to account for biases like censoring, right truncation, or epidemic phase.

References