Content from Introduction to outbreak analytics

Last updated on 2025-04-08 | Edit this page

Overview

Questions

  • How to calculate delays from line list data?
  • Why it is important to account for delays in outbreak analytics?

Objectives

  • Use the pipe operator %>% to structure sequences of data operations.
  • Count observations in each group using count() function.
  • Create new columns from existing columns using mutate() function.
  • Keep or drop columns by their names using select().
  • Keep rows that match a condition using filter().
  • Create graphics declaratively using ggplot2.

Prerequisite

Setup an RStudio project and folder

Checklist

RStudio projects

The directory of an RStudio Project named, for example training, should look like this:

training/
|__ data/
|__ training.Rproj

RStudio Projects allows you to use relative file paths with respect to the R Project, making your code more portable and less error-prone. Avoids using setwd() with absolute paths like "C:/Users/MyName/WeirdPath/training/data/file.csv".

Challenge

Let’s starts by creating New Quarto Document!

  1. In the RStudio IDE, go to: File > New File > Quarto Document
  2. Accept the default options
  3. Save the file with the name 01-report.qmd
  4. Use the Render button to render the file and preview the output.

Introduction

A new Ebola Virus Disease (EVD) outbreak has been notified in a country in West Africa. The Ministry of Health is coordinating the outbreak response and has contracted you as a consultant in epidemic analysis to inform the response in real-time. The available report of cases is coming from hospital admissions.

Let’s start by loading the package readr to read .csv data, dplyr to manipulate data, tidyr to rearrange it, and here to write file paths within your RStudio project. We’ll use the pipe %>% to connect some of their functions, including others from the package ggplot2, so let’s call to the package tidyverse that loads them all:

R 

# Load packages
library(tidyverse) # loads readr, dplyr, tidyr and ggplot2

OUTPUT 

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.0.4
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Checklist

The double-colon

The double-colon :: in R let you call a specific function from a package without loading the entire package into the current environment.

For example, dplyr::filter(data, condition) uses filter() from the dplyr package.

This helps us remember package functions and avoid namespace conflicts.

Explore data

For the purpose of this episode, we will read a pre-cleaned line list data. Following episodes will tackle how to solve cleaning tasks.

R 

# Read data
# e.g.: if path to file is data/linelist.csv then:
cases <- readr::read_csv(
  here::here("data", "linelist.csv")
)

Checklist

Why should we use the {here} package?

The package here simplifies file referencing in R projects. It allows them to work across different operating systems (Windows, Mac, Linux). This feature, called cross-environment compatibility, eliminates the need to adjust file paths. For example:

  • On Windows, paths are written using backslashes ( \ ) as the separator between folder names: "data\raw-data\file.csv"
  • On Unix based operating system such as macOS or Linux the forward slash ( / ) is used as the path separator: "data/raw-data/file.csv"

The here package adds one more layer of reproducibility to your work. For more, read this tutorial about open, sustainable, and reproducible epidemic analysis with R

R 

# Print line list data
cases

OUTPUT 

# A tibble: 166 × 11
   case_id generation date_of_infection date_of_onset date_of_hospitalisation
   <chr>        <dbl> <date>            <date>        <date>
 1 d1fafd           0 NA                2014-04-07    2014-04-17
 2 53371b           1 2014-04-09        2014-04-15    2014-04-20
 3 f5c3d8           1 2014-04-18        2014-04-21    2014-04-25
 4 e66fa4           2 NA                2014-04-21    2014-05-06
 5 49731d           0 2014-03-19        2014-04-25    2014-05-02
 6 0f58c4           2 2014-04-22        2014-04-26    2014-04-29
 7 6c286a           2 NA                2014-04-27    2014-04-27
 8 881bd4           3 2014-04-26        2014-05-01    2014-05-05
 9 d58402           2 2014-04-23        2014-05-01    2014-05-10
10 f9149b           3 NA                2014-05-03    2014-05-04
# ℹ 156 more rows
# ℹ 6 more variables: date_of_outcome <date>, outcome <chr>, gender <chr>,
#   hospital <chr>, lon <dbl>, lat <dbl>

Discussion

Take a moment to review the data and its structure..

  • Do the data and format resemble line lists you’ve encountered before?
  • If you were part of the outbreak investigation team, what additional information might you want to collect?

You may notice that there are missing entries.

We can also explore missing data with summary a visualization:

R 

cases %>%
  visdat::vis_miss()

Discussion

Why do we have more missings on date of infection or date of outcome?

Calculate severity

A frequent indicator for measuring severity is the Case Fatality Risk (CFR).

CFR is defined as the conditional probability of death given confirmed diagnosis, calculated as the cumulative number of deaths from an infectious disease over the number of confirmed diagnosed cases.

We can use the function dplyr::count() to count the observations in each group of the variable outcome:

R 

cases %>%
  dplyr::count(outcome)

OUTPUT 

# A tibble: 3 × 2
  outcome     n
  <chr>   <int>
1 Death      65
2 Recover    59
3 <NA>       42

Discussion

Report:

  • What to do with cases whose outcome is <NA>?

  • Should we consider missing outcomes to calculate the CFR?

Data of today will not include outcomes from patients that are still hospitalised. Then, one relevant question to ask is: In average, how much time it would take to know the outcomes of hospitalised cases? For this we can calculate delays!

Calculate delays

The time between sequence of dated events can vary between subjects. For example, we would expect the date of infection to always be before the date of symptom onset, and the later always before the date of hospitalization.

In a random sample of 30 observations from the cases data frame we observe variability between the date of hospitalization and date of outcome:

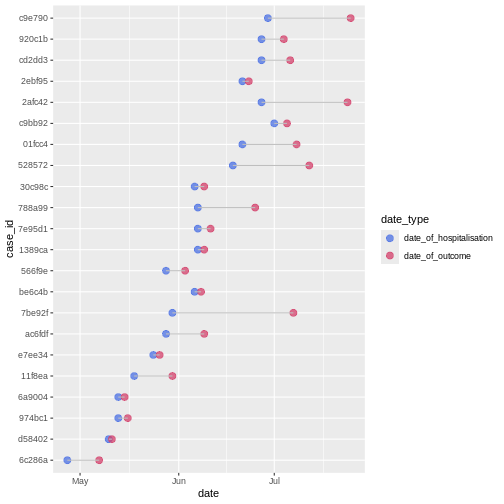
We can calculate the average time from hospitalisation to outcome from the line list.

From the cases object we will use:

  • dplyr::select() to keep columns using their names,
  • dplyr::mutate() to create one new column outcome_delay as a function of existing variables date_of_outcome and date_of_hospitalisation,
  • dplyr::filter() to keep the rows that match a condition like outcome_delay > 0,
  • skimr::skim() to get useful summary statistics

R 

# delay from report to outcome
cases %>%
  dplyr::select(case_id, date_of_hospitalisation, date_of_outcome) %>%
  dplyr::mutate(outcome_delay = date_of_outcome - date_of_hospitalisation) %>%
  dplyr::filter(outcome_delay > 0) %>%
  skimr::skim(outcome_delay)
Data summary
Name Piped data
Number of rows 123
Number of columns 4
_______________________
Column type frequency:
difftime 1
________________________
Group variables None

Variable type: difftime

skim_variable n_missing complete_rate min max median n_unique
outcome_delay 0 1 1 days 55 days 7 days 29

Callout

Inconsistencies among sequence of dated-events?

Wait! Is it consistent to have negative time delays from primary to secondary observations, i.e., from hospitalisation to death?

In the next episode called Clean data we will learn how to check sequence of dated-events and other frequent and challenging inconsistencies!

Challenge

To calculate a delay-adjusted Case Fatality Risk (CFR), we need to assume a known delay from onset to death.

Using the cases object:

  • Calculate the summary statistics of the delay from onset to death.

Keep the rows that match a condition like outcome == "Death":

R 

# delay from onset to death
cases %>%
  dplyr::filter(outcome == "Death") %>%
  ...() # replace ... with downstream code

Is it consistent to have negative delays from onset of symptoms to death?

R 

# delay from onset to death
cases %>%
  dplyr::select(case_id, date_of_onset, date_of_outcome, outcome) %>%
  dplyr::filter(outcome == "Death") %>%
  dplyr::mutate(delay_onset_death = date_of_outcome - date_of_onset) %>%
  dplyr::filter(delay_onset_death > 0) %>%
  skimr::skim(delay_onset_death)
Data summary
Name Piped data
Number of rows 46
Number of columns 5
_______________________
Column type frequency:
difftime 1
________________________
Group variables None

Variable type: difftime

skim_variable n_missing complete_rate min max median n_unique
delay_onset_death 0 1 2 days 17 days 7 days 15

Where is the source of the inconsistency? Let’s say you want to keep the rows with negative delay values to investigate them. How would you do it?

We can use dplyr::filter() again to identify the inconsistent observations:

R 

# keep negative delays
cases %>%
  dplyr::select(case_id, date_of_onset, date_of_outcome, outcome) %>%
  dplyr::filter(outcome == "Death") %>%
  dplyr::mutate(delay_onset_death = date_of_outcome - date_of_onset) %>%
  dplyr::filter(delay_onset_death < 0)

OUTPUT 

# A tibble: 6 × 5
  case_id date_of_onset date_of_outcome outcome delay_onset_death
  <chr>   <date>        <date>          <chr>   <drtn>
1 c43190  2014-05-06    2014-04-26      Death   -10 days
2 bd8c0e  2014-05-17    2014-05-09      Death    -8 days
3 49d786  2014-05-20    2014-05-11      Death    -9 days
4 e85785  2014-06-03    2014-06-02      Death    -1 days
5 60f0c2  2014-06-07    2014-05-30      Death    -8 days
6 a48f5d  2014-06-15    2014-06-10      Death    -5 days

More on estimating a delay-adjusted Case Fatality Risk (CFR) on the episode about Estimating outbreak severity!

Epidemic curve

The first question we want to know is simply: how bad is it? The first step of the analysis is descriptive. We want to draw an epidemic curve or epicurve. This visualises the incidence over time by date of symptom onset.

From the cases object we will use:

  • ggplot() to declare the input data frame,
  • aes() for the variable date_of_onset to map to geoms,
  • geom_histogram() to visualise the distribution of a single continuous variable with a binwidth equal to 7 days.

R 

# incidence curve
cases %>%
  ggplot(aes(x = date_of_onset)) +
  geom_histogram(binwidth = 7)

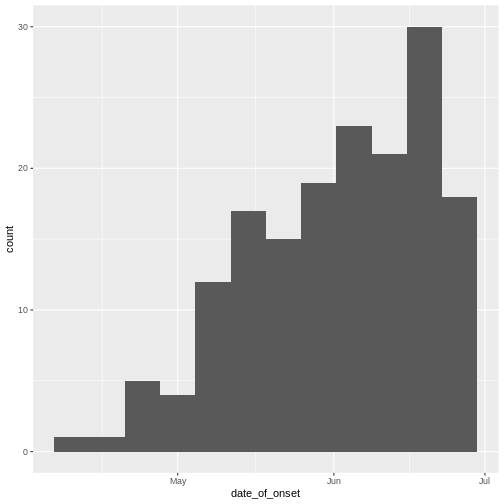
Discussion

The early phase of an outbreak usually growths exponentially.

  • Why exponential growth may not be observed in the most recent weeks?

You may want to examine how long after onset of symptoms cases are hospitalised; this may inform the reporting delay from this line list data:

R 

# reporting delay
cases %>%
  dplyr::select(case_id, date_of_onset, date_of_hospitalisation) %>%
  dplyr::mutate(reporting_delay = date_of_hospitalisation - date_of_onset) %>%
  ggplot(aes(x = reporting_delay)) +
  geom_histogram(binwidth = 1)

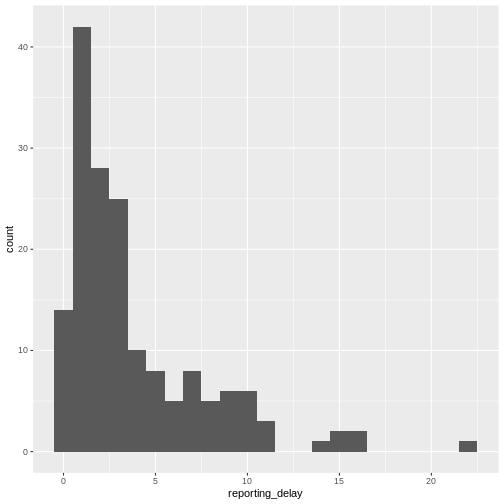
The distribution of the reporting delay in day units is heavily skewed. Symptomatic cases may take up to two weeks to be reported.

From reports (hospitalisations) in the most recent two weeks, we completed the exponential growth trend of incidence cases within the last four weeks:

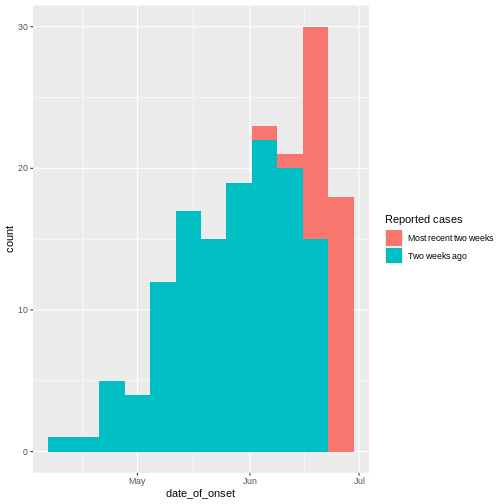
Given to reporting delays during this outbreak, it seemed that two weeks ago we had a decay of cases during the last three weeks. We needed to wait a couple of weeks to complete the incidence of cases on each week.

Challenge

Report:

  • What indicator can we use to estimate transmission from the incidence curve?
  • The growth rate! by fitting a linear model.
  • The reproduction number accounting for delays from secondary observations to infection.

More on this topic on episodes about Aggregate and visualize and Quantifying transmission.

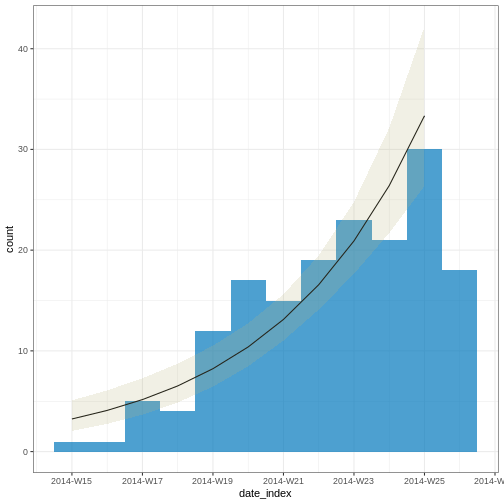
OUTPUT 

# A tibble: 2 × 6
  count_variable term        estimate std.error statistic  p.value
  <chr>          <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 date_of_onset  (Intercept) -537.      70.1        -7.67 1.76e-14
2 date_of_onset  date_index     0.233    0.0302      7.71 1.29e-14

Note: Due to the diagnosed reporting delay, We conveniently truncated the epidemic curve one week before to fit the model! This improves the fitted model to data when quantifying the growth rate during the exponential phase.

In order to account for these epidemiological delays when estimating indicators of severity or transmission, in our analysis we need to input delays as Probability Distributions. We will learn how to fit and access them in the next episodes.

Challenges

Challenge

Relevant delays when estimating transmission

  • Review the definition of the incubation period in our glossary page.

  • Calculate the summary statistics of the incubation period distribution observed in the line list.

  • Visualize the distribution of the incubation period from the line list.

Calculate the summary statistics:

R 

cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  skimr::skim(incubation_period)
Data summary
Name Piped data
Number of rows 166
Number of columns 4
_______________________
Column type frequency:
difftime 1
________________________
Group variables None

Variable type: difftime

skim_variable n_missing complete_rate min max median n_unique
incubation_period 61 0.63 1 days 37 days 5 days 25

Visualize the distribution:

R 

cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  ggplot(aes(x = incubation_period)) +
  geom_histogram(binwidth = 1)

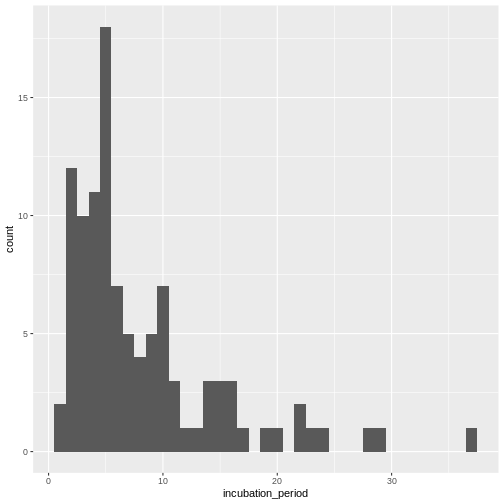
In coming episode we will learn how to fit statistical distribution paramaters to a distribution, or access to the most appropriate estimates.

With the distribution parameters of the incubation period we can infer the length of active monitoring or quarantine. Lauer et al., 2020 estimated the incubation period of Coronavirus Disease 2019 (COVID-19) from publicly reported confirmed cases.

Key Points

  • Use packages from the tidyverse like dplyr, tidyr, and ggplot2 for exploratory data analysis.
  • Epidemiological delays condition the estimation of indicators for severity or transmission.

References

Content from Introduction to delays

Last updated on 2025-04-08 | Edit this page

Overview

Questions

  • How to fit a probability distribution to delay data?
  • How to interpret distribution parameters?
  • How to access distribution parameters from fitting objects

Objectives

  • Fit a probability distribution to data using fitdistrplus
  • Extract a single column using pull(), dollar sign $, or square brackets [].

Introduction

Delays are key for downstream task in outbreak analytics. To estimate the outbreak severity, we need to assume a known delay from onset to death. To quantify transmission, we need to consider delays from the moment of infection to the time of data collection. In order to account for epidemiological delays when estimating indicators of severity or transmission, in our analysis we need to input delays as Probability Distributions.

Let’s start by loading the package dplyr to manipulate data. We’ll use the pipe %>% to connect some of their functions, including others from the package ggplot2, so let’s call to the package tidyverse that loads them all. We will also use fitdistrplus to fit probability distributions to delays:

R 

# Load packages
library(tidyverse) # loads dplyr, the pipe, and ggplot2
library(fitdistrplus)

Checklist

The double-colon

The double-colon :: in R let you call a specific function from a package without loading the entire package into the current environment.

For example, dplyr::filter(data, condition) uses filter() from the dplyr package.

This helps us remember package functions and avoid namespace conflicts.

Fit a probability distribution to delays

We fit a probability distribution to data (like delays) to make inferences about it. These inferences can be useful for Public health interventions and decision making. For example:

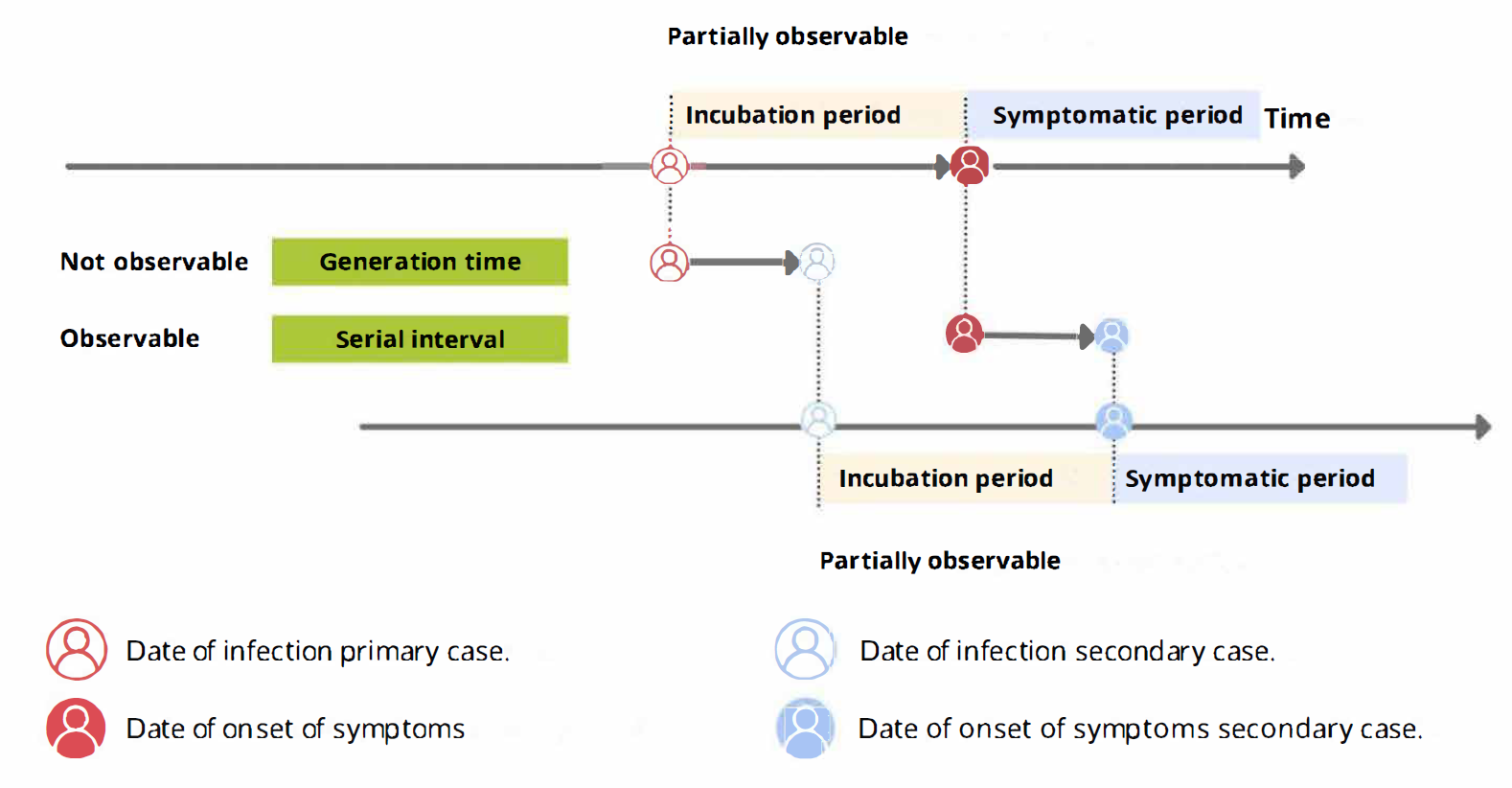
  • From the incubation period distribution we can inform the length of active monitoring or quarantine. We can infer the time by which 99% of infected individuals are expected to show symptoms (Lauer et al., 2020).

  • From the serial interval distribution we can optimize contact tracing. We can evaluate the need to expand the number of days pre-onset to consider in the contact tracing to include more backwards contacts (Claire Blackmore, 2021; Davis et al., 2020).

A schematic of the relationship of different time periods of transmission between a primary case and a secondary case in a transmission pair. Adapted from Zhao et al, 2021
A schematic of the relationship of different time periods of transmission between a primary case and a secondary case in a transmission pair. Adapted from Zhao et al, 2021

Callout

From time periods to probability distributions

When we calculate the serial interval, we see that not all case pairs have the same time length. We will observe this variability for any case pair and individual time period.

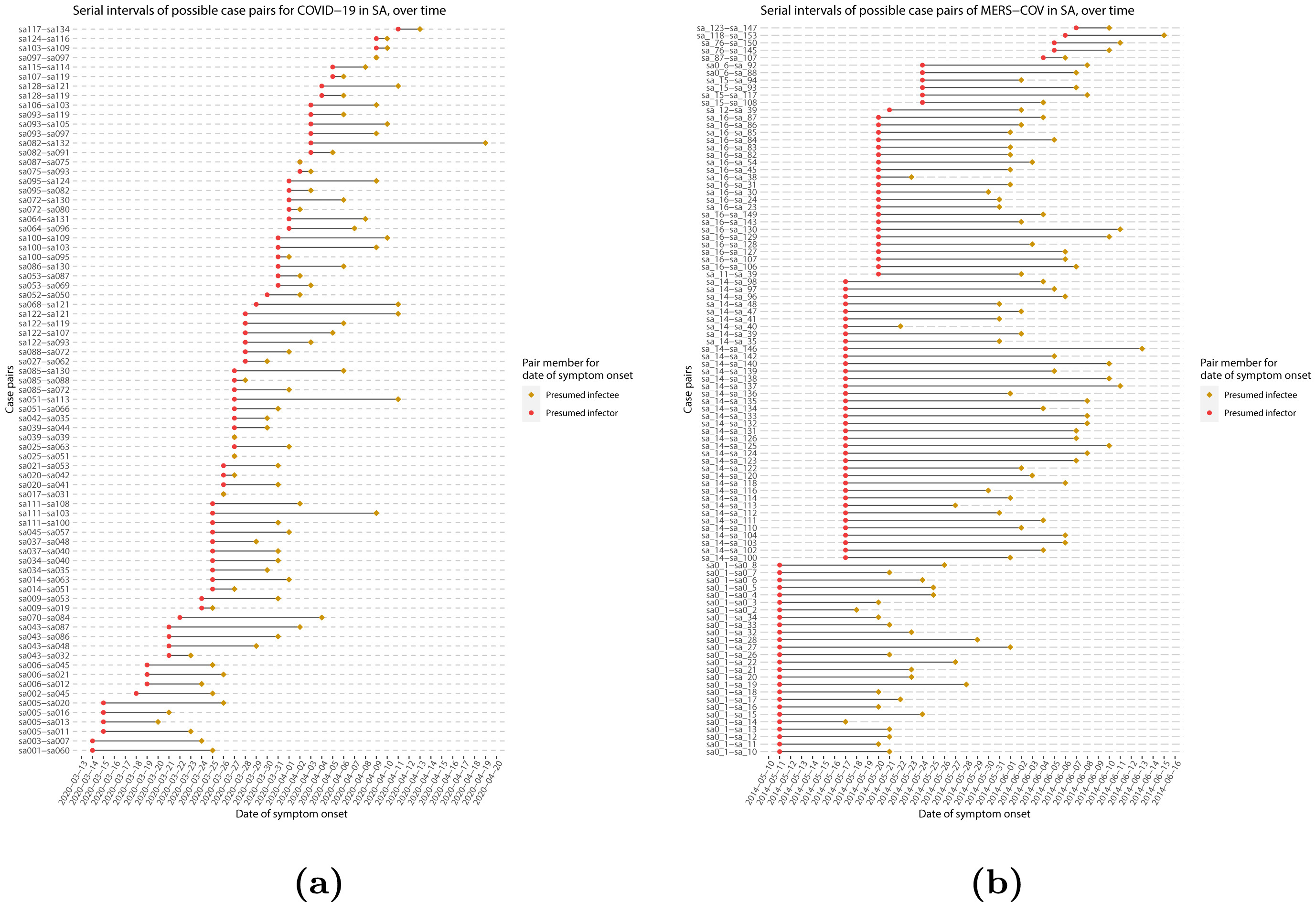
Serial intervals of possible case pairs in (a) COVID-19 and (b) MERS-CoV. Pairs represent a presumed infector and their presumed infectee plotted by date of symptom onset (Althobaity et al., 2022).
Serial intervals of possible case pairs in (a) COVID-19 and (b) MERS-CoV. Pairs represent a presumed infector and their presumed infectee plotted by date of symptom onset (Althobaity et al., 2022).

To summarise these data from individual and pair time periods, we can find the statistical distributions that best fit the data (McFarland et al., 2023).

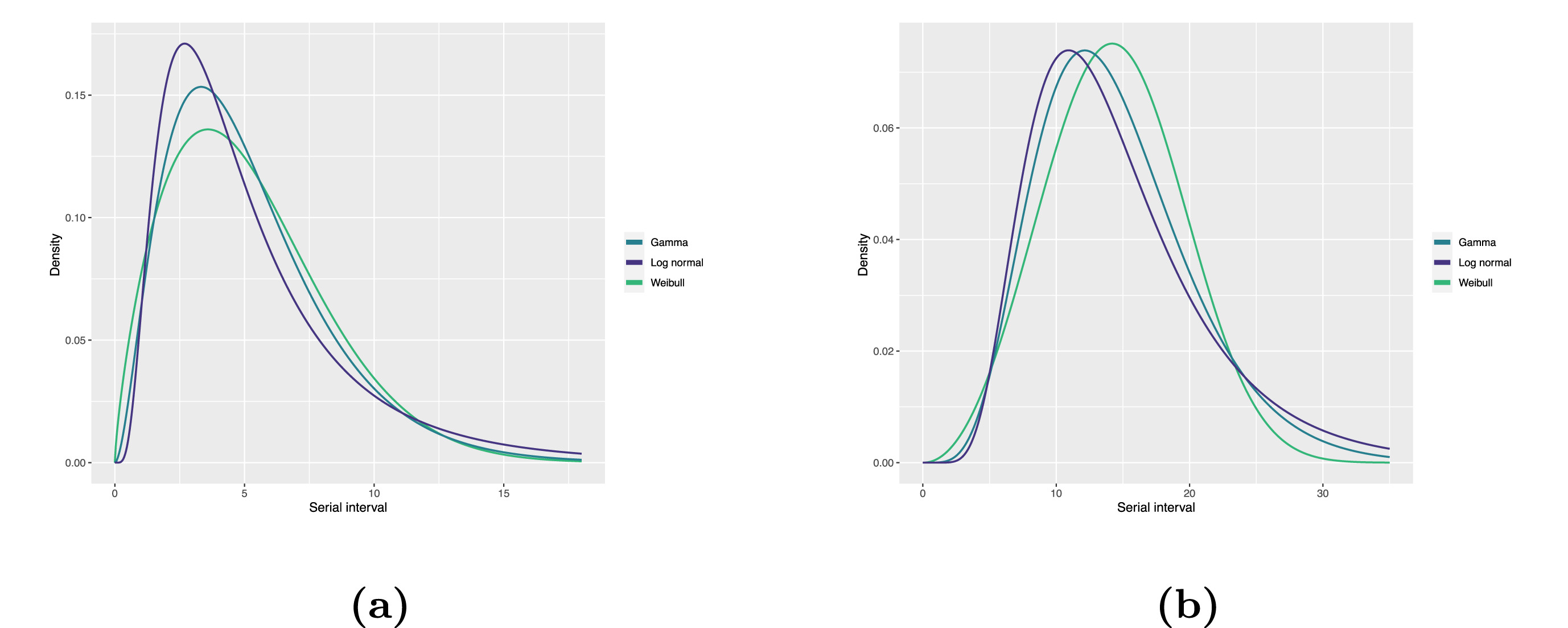
Fitted serial interval distribution for (a) COVID-19 and (b) MERS-CoV based on reported transmission pairs in Saudi Arabia. We fitted three commonly used distributions, Log normal, Gamma, and Weibull distributions, respectively (Althobaity et al., 2022).
Fitted serial interval distribution for (a) COVID-19 and (b) MERS-CoV based on reported transmission pairs in Saudi Arabia. We fitted three commonly used distributions, Log normal, Gamma, and Weibull distributions, respectively (Althobaity et al., 2022).

Statistical distributions are summarised in terms of their summary statistics like the location (mean and percentiles) and spread (variance or standard deviation) of the distribution, or with their distribution parameters that inform about the form (shape and rate/scale) of the distribution. These estimated values can be reported with their uncertainty (95% confidence intervals).

Gamma mean shape rate/scale
MERS-CoV 14.13(13.9–14.7) 6.31(4.88–8.52) 0.43(0.33–0.60)
COVID-19 5.1(5.0–5.5) 2.77(2.09–3.88) 0.53(0.38–0.76)
Weibull mean shape rate/scale
MERS-CoV 14.2(13.3–15.2) 3.07(2.64–3.63) 16.1(15.0–17.1)
COVID-19 5.2(4.6–5.9) 1.74(1.46–2.11) 5.83(5.08–6.67)
Serial interval estimates using Gamma, Weibull, and Log Normal distributions. 95% confidence intervals for the shape and scale (logmean and sd for Log Normal) parameters are shown in brackets (Althobaity et al., 2022).
Log normal mean mean-log sd-log
MERS-CoV 14.08(13.1–15.2) 2.58(2.50–2.68) 0.44(0.39–0.5)
COVID-19 5.2(4.2–6.5) 1.45(1.31–1.61) 0.63(0.54–0.74)

To illustrate this, let’s continue with the same line list from the previous episode:

R 

# Read data
# e.g.: if path to file is data/linelist.csv then:
cases <- readr::read_csv(
  here::here("data", "linelist.csv")
)

From the cases object we can use:

  • dplyr::mutate() to transform the reporting_delay class object from <time> to <numeric>,
  • dplyr::filter() to keep the positive values,
  • dplyr::pull() to extract a single column,
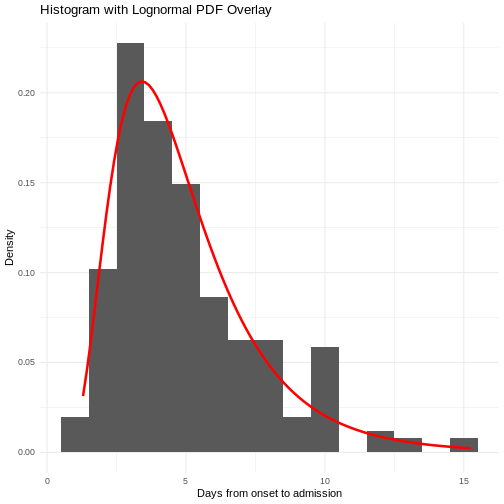
  • fitdistrplus::fitdist() to fit a probability distribution using Maximum Likelihood. We can test distributions like the Log Normal ("lnorm"), "gamma", or "weibull".

R 

cases %>%
  dplyr::select(case_id, date_of_onset, date_of_hospitalisation) %>%
  dplyr::mutate(reporting_delay = date_of_hospitalisation - date_of_onset) %>%
  dplyr::mutate(reporting_delay_num = as.numeric(reporting_delay)) %>%
  dplyr::filter(reporting_delay_num > 0) %>%
  dplyr::pull(reporting_delay_num) %>%
  fitdistrplus::fitdist(distr = "lnorm")

OUTPUT 

Fitting of the distribution ' lnorm ' by maximum likelihood
Parameters:
         estimate Std. Error
meanlog 1.0488098 0.06866105
sdlog   0.8465102 0.04855039

Use summary() to find goodness-of-fit statistics from the Maximum likelihood. Use plot() to visualize the fitted density function and other quality control plots. To compare multiple distributions you can use superspreading::ic_tbl(). We’ll explore that package later!

Now we can do inferences from the probability distribution fitted to the epidemiological delay! Want to learn how? Read the “Show details” :)

Making inferences from probability distributions

From probability distributions we can infer estimates like cumulative probability, maximum values, or generate random values. We can access to them using R probability functions.

We recommend you read the definitions of the R probability functions for the Normal distribution. From it we can relate with any other family of statistical distributions!

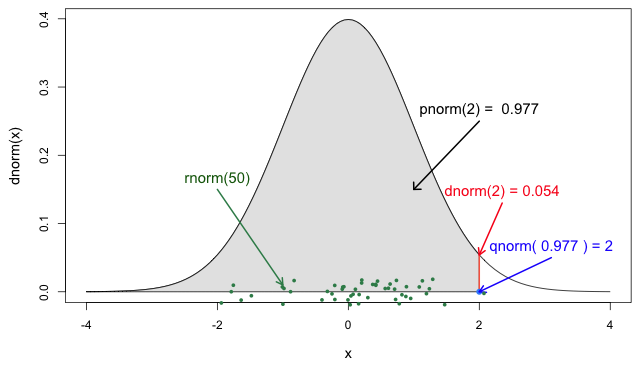
The four probability functions for the normal distribution (Jack Weiss, 2012)
The four probability functions for the normal distribution (Jack Weiss, 2012)

Each probability distribution has a unique set of parameters and probability functions. Read the Distributions in the stats package or ?stats::Distributions to find the ones available in R.

For example, assuming that the reporting delay follows a Log Normal distribution, we can use plnorm() to calculate the probability of observing a reporting delay of 14 days or less:

R 

plnorm(q = 14, meanlog = 1.0488098, sdlog = 0.8465102)

OUTPUT 

[1] 0.9698499

Or the amount of time by which 99% of symptomatic individuals are expected to be reported in the hospitalization record:

R 

qlnorm(p = 0.99, meanlog = 1.0488098, sdlog = 0.8465102)

OUTPUT 

[1] 20.45213

You will find more examples of how to use delays for decision-making at the Use delay distributions in analysis at Tutorials Middle!

To interactively explore probability distributions, their parameters and access to their distribution functions, we suggest to explore a shinyapp called The Distribution Zoo: https://ben18785.shinyapps.io/distribution-zoo/

Checklist

Let’s review some operators used until now:

  • Assignment <- assigns a value to a variable from right to left.
  • Double colon :: to call a function from a specific package.
  • Pipe %>% to structure sequences of data operations left-to-right

We need to add two more to the list:

  • Dollar sign $
  • Square brackets []

Last step is to access to this parameters. Most modeling outputs from R functions will be stored as list class objects. In R, the dollar sign operator $ is used to access elements (like columns) within a data frame or list by name, allowing for easy retrieval of specific components.

Testimonial

A code completion tip

If we write the square brackets [] next to the object reporting_delay_fit$estimate[], within [] we can use the Tab key ↹ for code completion feature

This gives quick access to "meanlog" and "sdlog". We invite you to try this out in code chunks and the R console!

R 

# 1. Place the cursor within the square brackets
# 2. Use the Tab key
# 3. Explore the completion list
# 4. Select for "meanlog" or "sdlog"
reporting_delay_fit$estimate[]

Callout

Estimating epidemiological delays is CHALLENGING!

Epidemiological delays need to account for biases like censoring, right truncation, or epidemic phase (Charniga et al., 2024).

Additionally, at the beginning of an outbreak, limited data or resources exist to perform this during a real-time analysis. Until we have more appropriate data for the specific disease and region of the ongoing outbreak, we can reuse delays from past outbreaks from the same pathogens or close in its phylogeny, independent of the area of origin.

In the following tutorial episodes, we will:

  • Access to epidemiological delay distributions to estimate delay-adjusted transmission and severity metrics (e.g. reproduction number and case fatality risk). Find more in Tutorials Middle!
  • Use parameter values like the basic reproduction number, and delays like the latent period and infectious period to simulate transmission trajectories and intervention scenarios. Find more in Tutorials Late!

Challenges

Challenge

Relevant delays when estimating transmission

  • Review the definition of the incubation period in our glossary page.

  • Calculate the summary statistics of the incubation period distribution observed in the line list.

  • Visualize the distribution of the incubation period from the line list.

  • Fit a log-normal distribution to get the probability distribution parameters of the the observed incubation period.

  • (Optional) Infer the time by which 99% of infected individuals are expected to show symptoms.

Calculate the summary statistics:

R 

cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  skimr::skim(incubation_period)
Data summary
Name Piped data
Number of rows 166
Number of columns 4
_______________________
Column type frequency:
difftime 1
________________________
Group variables None

Variable type: difftime

skim_variable n_missing complete_rate min max median n_unique
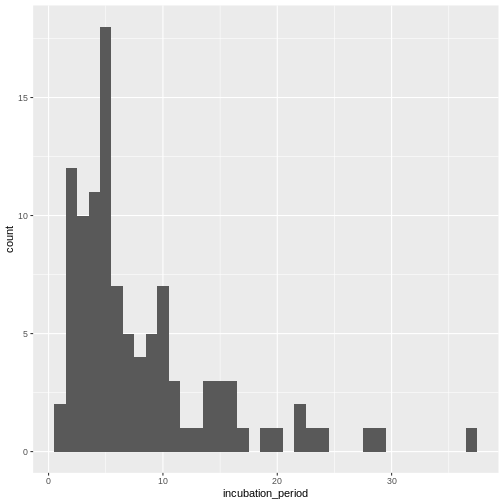
incubation_period 61 0.63 1 days 37 days 5 days 25

Visualize the distribution:

R 

cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  ggplot(aes(x = incubation_period)) +
  geom_histogram(binwidth = 1)

Fit a log-normal distribution:

R 

incubation_period_dist <- cases %>%
  dplyr::select(case_id, date_of_infection, date_of_onset) %>%
  dplyr::mutate(incubation_period = date_of_onset - date_of_infection) %>%
  mutate(incubation_period_num = as.numeric(incubation_period)) %>%
  filter(!is.na(incubation_period_num)) %>%
  pull(incubation_period_num) %>%
  fitdistrplus::fitdist(distr = "lnorm")

incubation_period_dist

OUTPUT 

Fitting of the distribution ' lnorm ' by maximum likelihood
Parameters:
         estimate Std. Error
meanlog 1.8037993 0.07381350
sdlog   0.7563633 0.05219361

(Optional) Infer the time by which 99% of infected individuals are expected to show symptoms:

R 

qlnorm(
  p = 0.99,
  meanlog = incubation_period_dist$estimate["meanlog"],
  sdlog = incubation_period_dist$estimate["sdlog"]
)

OUTPUT 

[1] 35.28167

With the distribution parameters of the incubation period we can infer the length of active monitoring or quarantine. Lauer et al., 2020 estimated the incubation period of Coronavirus Disease 2019 (COVID-19) from publicly reported confirmed cases.

Key Points

  • Epidemiological delays condition the estimation of indicators for severity or transmission.
  • Fit probability distribution to delays to make inferences from them for decision-making.
  • Fitting epidemiological delays need to account for biases like censoring, right truncation, or epidemic phase.

References