Notas de la instructora

This is a placeholder file. Please add content here.

Introducción a la analítica de brotes

Solución 1

R 

muertes <- sum(casos$desenlace %in% "Muerte") 

casos_desenlace_final_conocido <- sum(casos$desenlace %in% c("Muerte", "Recuperacion")) 

CFR <- muertes / casos_desenlace_final_conocido

print(CFR)

SALIDA 

[1] 0.5825243

Solución 2

R 

CFR_con_CI <- binom.confint(muertes, 
                                       casos_desenlace_final_conocido, method = "exact") %>%
  kable(caption = "**CFR con intervalos de confianza**")

CFR_con_CI
CFR con intervalos de confianza
method x n mean lower upper
exact 60 103 0.5825243 0.4812264 0.6789504

Solución 3

R 

incidencia_diaria <- incidence(casos$fecha_inicio_sintomas)
incidencia_diaria

SALIDA 

<incidence object>
[166 cases from days 2014-04-07 to 2014-06-29]

$counts: matrix with 84 rows and 1 columns
$n: 166 cases in total
$dates: 84 dates marking the left-side of bins
$interval: 1 day
$timespan: 84 days
$cumulative: FALSE

Ideas discusión:

Usualmente al inicio de la transmisión en la fase exponencial, y dependiendo el periodo de incubación y el intervalo serial, se van a ver días sin casos. Eso no significa que la curva no sea creciente. Usualmente, al agrupar por semana ya no se verá la ausencia de casos.


Solución 4

R 

incidencia_semanal <- incidence(casos$fecha_inicio_sintomas, 
                                interval = 7, 
                                last_date = max(casos$fecha_de_hospitalizacion,
                                              na.rm = TRUE))
incidencia_semanal

SALIDA 

<incidence object>
[166 cases from days 2014-04-07 to 2014-06-30]
[166 cases from ISO weeks 2014-W15 to 2014-W27]

$counts: matrix with 13 rows and 1 columns
$n: 166 cases in total
$dates: 13 dates marking the left-side of bins
$interval: 7 days
$timespan: 85 days
$cumulative: FALSE

R 

plot(incidencia_semanal, border = "black")

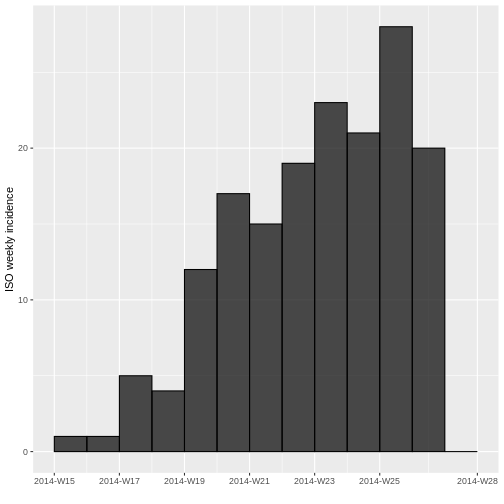
Ideas para responder:

Es preferible estimar la tasa de crecimiento diaria utilizando el ajuste de la incidencia semanal en lugar de la incidencia diaria debido a que los datos diarios pueden ser muy volátiles en los primeros días de la curva exponencial. Esto puede suceder por varias razones:

  • Las fluctuaciones naturales, ciclos de informes, retrasos en el reporte y los errores de medición, que pueden no reflejar cambios reales en la transmisión de la enfermedad.

  • Los datos diarios pueden tener más lagunas o inexactitudes.

  • Eventos de superdispersión o las intervenciones de control.

El uso de datos semanales puede suavizar estas fluctuaciones, dando una mejor idea de la tendencia subyacente. Al utilizar una media móvil semanal, se suavizan estas fluctuaciones, lo que proporciona una imagen más clara de la tendencia subyacente. Esto permite mejorar la precisión de la estimación y evitar el sesgo de los días de la semana, así como mejorar el modelo al reducir el número total de puntos, dado que puede ayudar a evitar el sobreajuste y mejorar la generalización del modelo.

Ejemplo: Algunos fenómenos pueden variar sistemáticamente según el día de la semana. Por ejemplo, el número de pruebas de COVID-19 realizadas podría ser menor los fines de semana, lo que podría afectar a la incidencia reportada. Al utilizar una media móvil semanal, se evita este tipo de sesgo.


Notas de la instructora

Si se grafica por fecha de inicio de síntomas mientras el brote está creciendo, siempre se va a ver un descenso artificial en la curva de la incidencia en fechas recientes. Este descenso sólo corresponde al rezago administrativo (del diagnóstico y reporte de casos), pero no indica necesariamente una reducción de la incidencia real.


Solución 6

R 

ajuste_modelo_truncado <- incidence::fit(incidencia_semanal_truncada)
ajuste_modelo_truncado

SALIDA 

<incidence_fit object>

$model: regression of log-incidence over time

$info: list containing the following items:
  $r (daily growth rate):
[1] 0.05224047

  $r.conf (confidence interval):
          2.5 %    97.5 %
[1,] 0.03323024 0.0712507

  $doubling (doubling time in days):
[1] 13.2684

  $doubling.conf (confidence interval):
        2.5 %   97.5 %
[1,] 9.728286 20.85893

  $pred: data.frame of incidence predictions (10 rows, 5 columns)

R 

AjusteR2modelo <- summary(ajuste_modelo_truncado$model)$adj.r.squared 

cat("El R cuadrado ajustado es:", AjusteR2modelo, "\n")

SALIDA 

El R cuadrado ajustado es: 0.8131106

Solución 7

R 

plot(incidencia_semanal_truncada, fit = ajuste_modelo_truncado)

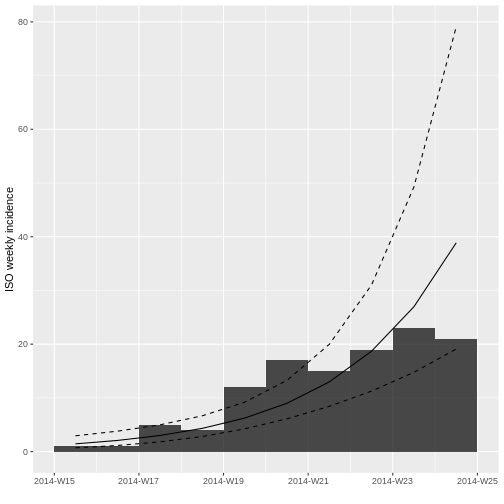
Solución 8

R 

# Estimación de la tasa de crecimiento diaria
tasa_crecimiento_diaria <- ajuste_modelo_truncado$info$r

cat("La tasa de crecimiento diaria es:", tasa_crecimiento_diaria, "\n")

SALIDA 

La tasa de crecimiento diaria es: 0.05224047

R 

# Intervalo de confianza de la tasa de crecimiento diaria
tasa_crecimiento_IC <- ajuste_modelo_truncado$info$r.conf

cat("Intervalo de confianza de la tasa de crecimiento diaria (95%):", tasa_crecimiento_IC, "\n")

SALIDA 

Intervalo de confianza de la tasa de crecimiento diaria (95%): 0.03323024 0.0712507

Solución 9

R 

# Estimación del tiempo de duplicación en días
tiempo_duplicacion_dias <- ajuste_modelo_truncado$info$doubling
cat("El tiempo de duplicación de la epidemia es", tiempo_duplicacion_dias, "días\n")

SALIDA 

El tiempo de duplicación de la epidemia es 13.2684 días

R 

# Intervalo de confianza del tiempo de duplicación
tiempo_duplicacion_IC <- ajuste_modelo_truncado$info$doubling.conf
cat("Intervalo de confianza del tiempo de duplicación (95%):", tiempo_duplicacion_IC, "\n")

SALIDA 

Intervalo de confianza del tiempo de duplicación (95%): 9.728286 20.85893

Construyendo un modelo matemático simple para Zika

Solución 1

R 

# Parámetros
ph       <- 0.7       # Probabilidad de transmisión del vector al hospedador dada una picadura por un mosquito infeccioso a un humano susceptible
pv       <- 0.7       # Probabilidad de transmisión del hospedador al vector dada una picadura por un mosquito susceptible a un humano infeccioso
Lv       <- 10        # Esperanza de vida de los mosquitos (en días)
Lh       <- 50 * 365  # Esperanza de vida de los humanos (en días)
Iph      <- 7         # Periodo infeccioso en humanos (en días)
IP       <- 6         # Periodo infeccioso en vectores (en días)
EIP      <- 8.4       # Período extrínseco de incubación en mosquitos adultos
muv      <- 1/Lv      # Tasa per capita de mortalidad del vector (1/Lv)
muh      <- 1/Lh      # Tasa per capita de mortalidad del hospedador (1/Lh)
alphav   <- muv       # Tasa per capita de natalidad del vector
alphah   <- muh       # Tasa per capita de natalidad del hospedador
gamma    <- 1/Iph     # Tasa de recuperación en humanos
delta    <- 1/EIP     # Tasa extrínseca de incubación



# Tamaño de la población
Nh       <- 100000   # Número de humanos
m        <- 2         # Proporción vector a humano
Nv       <- m * Nh    # Número de vectores
R0       <- 3         # Número reproductivo
b        <- sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
                   (m * ph * pv * delta)) # tasa de picadura

betah    <- ph*b     # Coeficiente de transmisión del mosquito al humano
betav    <- pv*b     # Coeficiente de transmisión del humano al mosquito

TIME     <- 100       # Número de años a simular

Solución 2

R 

arbovmodel <- function(t, x, params) {
  
  Sh <- x[1]    # Humanos susceptibles
  Ih <- x[2]    # Humanos infecciosos 
  Rh <- x[3]    # Humanos recuperados
  Sv <- x[4]    # Vectores susceptibles
  Ev <- x[5]    # Vectores expuestos
  Iv <- x[6]    # Vectores infecciosos
  
  with(as.list(params), # entorno local para evaluar derivados
       {
         # Humanos
         dSh   <-  alphah * Nh - betah * (Iv/Nh) * Sh - muh * Sh
         dIh   <-  betah * (Iv/Nh) * Sh  - (gamma + muh) * Ih
         dRh   <-  gamma * Ih  - muh * Rh
         
         # Vectores
         dSv   <-  alphav * Nv - betav * (Ih/Nh) * Sv - muv * Sv 
         dEv   <-  betav * (Ih/Nh) * Sv - (delta + muv)* Ev
         dIv   <-  delta * Ev - muv * Iv
         
         dx    <- c(dSh, dIh, dRh, dSv, dEv, dIv)
         list(dx)
       }
  )
}

Solución 3

R 

# ----------- Resuelva el modelo
#Tiempo
times  <- seq(1, 365 * TIME , by = 1)
# Especifique los parámetros
params <- c(
  muv      = muv,     
  muh      = muh, 
  alphav   = alphav,
  alphah   = alphah,
  gamma    = gamma,   
  delta    = delta,   
  betav    = betav,       
  betah    = betah,   
  Nh       = Nh,      
  Nv       = Nv
)
# Condiciones iniciales del sistema
xstart<- c(Sh = Nh ,      # Número inicial de Sh en T0
           Ih = 0,        # Número inicial de Ih en T0
           Rh = 0,        # Número inicial de Rh en T0
           Sv = Nv-1,     # Número inicial de Sv en T0
           Ev = 0,        # Número inicial de Ev en T0
           Iv = 1)        # Número inicial de Iv en TO
# Resuelva las ecuaciones
out <- as.data.frame(ode(y      = xstart,     # Condiciones iniciales
                         times  = times,      # Tiempo
                         fun    = arbovmodel, # Modelo
                         parms  = params))    # Parámetros

Solución 4

R 

# Cree las opciones de tiempo a mostrar 
out$years <- out$time / 365
out$weeks <- out$time / 7

Estimación de las distribuciones de rezagos epidemiológicos: Enfermedad X_______Pausa 1 ________________Pausa 2 ________________Pausa 3 _________

Generar reportes a partir de bases de datos de vigilancia epidemiológica usando sivirep

Estima la fuerza de infección a partir de encuestas serológicas usando serofoi

Notas de la instructora

Comparación de los modelos:

El poder predictivo de un modelo Bayesiano se puede caracterizar por medio del elpd (Expected Log Predictive Density), el cuál corresponde al valor esperado de la log-verosimilitud (log-likelihood) de un único dato nuevo \(y'\) respecto a su distribución real (la cual queremos aproximar con el modelo):

\[ \text{elpd} = \mathbb{E}_{\text{real}}[\log(p(y'|\vec{y}))] = \int p^{\text{real}}(y') \log(p(y'|\vec{y})) \, dy' \]

donde \(\vec{y}\) corresponde a los datos.

Existen varios métodos para estimar el elpdque permiten aproximar la precisión predictiva de un modelo Bayesiano. El criterio de información de Watanabe-Akaike (WAIC) es uno de ellos:

\[ \text{WAIC} = -2 \hat{lpd} + 2 p_{\text{waic}} \]

donde \(p_{\text{waic}}\) es el número efectivo de parámetros y \(\hat{lpd}\) corresponde al logaritmo del promedio de la verosimilitud respecto a la distribución posterior para un dato \(y_i \in \vec{y}\):

\[ \hat{lpd} = \log(\mathbb{E}_{\text{post}}[p(y_i|\theta)]) \]

El objetivo de restar el número efectivo de parámetros del modelo es dar cuenta de la posibilidad de sobreajustar el modelo (overfitting). El WAIC nos permite caracterizar la capacidad predictiva del modelo: cuanto más bajo sea su valor, mejor.

Similarmente, podemos computar el looic (leave-one-out information criterion), también conocido como loo-cv (leave-one-out cross-validation), el cual consiste en utilizar un único punto de los datos para probar el poder predictivo del modelo usando el resto de la muestra como muestra de entrenamiento. Este proceso se repite con cada dato de la muestra y sus respectivas densidades posteriores logarítmicas se suman (Lambert 2018), es decir:

\[ \text{looic} = \sum_{y_i} \log(p(y_i | \vec{y}_{i})) \]

donde \(\vec{y}_{i}\) representa a la muestra de datos extrayendo \(y_i\).


Notas de la instructora

Desafío: caso simulado

El desafío se realiza con 4 equipos (cada uno de 4-5 personas), que contarán con el apoyo de un coordinador y 4 monitores.

Cada equipo debe generar un diagnóstico de la situación en las diferentes regiones, así como comparar la evolución de la enfermedad con el fin de evaluar las estrategías de control en cada región.

Fuente: Reto


Notas de la instructora

Muestra de la solución para una base de datos:

R 

virus_serosurvey %>%
  serofoi::plot_serosurvey()

R 

virus_serosurvey %>%
  serofoi::fit_seromodel(model_type = "time", iter = 1000) %>% 
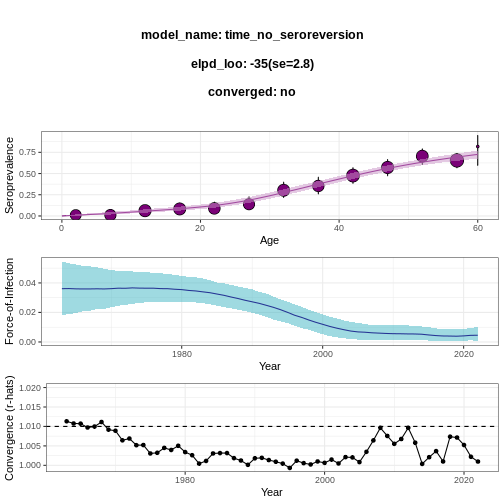
  serofoi::plot_seromodel(serosurvey = virus_serosurvey)

SALIDA 


SAMPLING FOR MODEL 'time_no_seroreversion' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 0.000107 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 1.07 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration:   1 / 1000 [  0%]  (Warmup)
Chain 1: Iteration: 100 / 1000 [ 10%]  (Warmup)
Chain 1: Iteration: 200 / 1000 [ 20%]  (Warmup)
Chain 1: Iteration: 300 / 1000 [ 30%]  (Warmup)
Chain 1: Iteration: 400 / 1000 [ 40%]  (Warmup)
Chain 1: Iteration: 500 / 1000 [ 50%]  (Warmup)
Chain 1: Iteration: 501 / 1000 [ 50%]  (Sampling)
Chain 1: Iteration: 600 / 1000 [ 60%]  (Sampling)
Chain 1: Iteration: 700 / 1000 [ 70%]  (Sampling)
Chain 1: Iteration: 800 / 1000 [ 80%]  (Sampling)
Chain 1: Iteration: 900 / 1000 [ 90%]  (Sampling)
Chain 1: Iteration: 1000 / 1000 [100%]  (Sampling)
Chain 1:
Chain 1:  Elapsed Time: 4.123 seconds (Warm-up)
Chain 1:                2.657 seconds (Sampling)
Chain 1:                6.78 seconds (Total)
Chain 1:

SAMPLING FOR MODEL 'time_no_seroreversion' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 0.0001 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 1 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration:   1 / 1000 [  0%]  (Warmup)
Chain 2: Iteration: 100 / 1000 [ 10%]  (Warmup)
Chain 2: Iteration: 200 / 1000 [ 20%]  (Warmup)
Chain 2: Iteration: 300 / 1000 [ 30%]  (Warmup)
Chain 2: Iteration: 400 / 1000 [ 40%]  (Warmup)
Chain 2: Iteration: 500 / 1000 [ 50%]  (Warmup)
Chain 2: Iteration: 501 / 1000 [ 50%]  (Sampling)
Chain 2: Iteration: 600 / 1000 [ 60%]  (Sampling)
Chain 2: Iteration: 700 / 1000 [ 70%]  (Sampling)
Chain 2: Iteration: 800 / 1000 [ 80%]  (Sampling)
Chain 2: Iteration: 900 / 1000 [ 90%]  (Sampling)
Chain 2: Iteration: 1000 / 1000 [100%]  (Sampling)
Chain 2:
Chain 2:  Elapsed Time: 4.177 seconds (Warm-up)
Chain 2:                4.061 seconds (Sampling)
Chain 2:                8.238 seconds (Total)
Chain 2:

SAMPLING FOR MODEL 'time_no_seroreversion' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 9.8e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.98 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration:   1 / 1000 [  0%]  (Warmup)
Chain 3: Iteration: 100 / 1000 [ 10%]  (Warmup)
Chain 3: Iteration: 200 / 1000 [ 20%]  (Warmup)
Chain 3: Iteration: 300 / 1000 [ 30%]  (Warmup)
Chain 3: Iteration: 400 / 1000 [ 40%]  (Warmup)
Chain 3: Iteration: 500 / 1000 [ 50%]  (Warmup)
Chain 3: Iteration: 501 / 1000 [ 50%]  (Sampling)
Chain 3: Iteration: 600 / 1000 [ 60%]  (Sampling)
Chain 3: Iteration: 700 / 1000 [ 70%]  (Sampling)
Chain 3: Iteration: 800 / 1000 [ 80%]  (Sampling)
Chain 3: Iteration: 900 / 1000 [ 90%]  (Sampling)
Chain 3: Iteration: 1000 / 1000 [100%]  (Sampling)
Chain 3:
Chain 3:  Elapsed Time: 4.037 seconds (Warm-up)
Chain 3:                4.257 seconds (Sampling)
Chain 3:                8.294 seconds (Total)
Chain 3:

SAMPLING FOR MODEL 'time_no_seroreversion' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 9.9e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.99 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration:   1 / 1000 [  0%]  (Warmup)
Chain 4: Iteration: 100 / 1000 [ 10%]  (Warmup)
Chain 4: Iteration: 200 / 1000 [ 20%]  (Warmup)
Chain 4: Iteration: 300 / 1000 [ 30%]  (Warmup)
Chain 4: Iteration: 400 / 1000 [ 40%]  (Warmup)
Chain 4: Iteration: 500 / 1000 [ 50%]  (Warmup)
Chain 4: Iteration: 501 / 1000 [ 50%]  (Sampling)
Chain 4: Iteration: 600 / 1000 [ 60%]  (Sampling)
Chain 4: Iteration: 700 / 1000 [ 70%]  (Sampling)
Chain 4: Iteration: 800 / 1000 [ 80%]  (Sampling)
Chain 4: Iteration: 900 / 1000 [ 90%]  (Sampling)
Chain 4: Iteration: 1000 / 1000 [100%]  (Sampling)
Chain 4:
Chain 4:  Elapsed Time: 4.296 seconds (Warm-up)
Chain 4:                3.555 seconds (Sampling)
Chain 4:                7.851 seconds (Total)
Chain 4:

ADVERTENCIA 

Warning: There were 1 chains where the estimated Bayesian Fraction of Missing Information was low. See
https://mc-stan.org/misc/warnings.html#bfmi-low

ADVERTENCIA 

Warning: Examine the pairs() plot to diagnose sampling problems

ADVERTENCIA 

Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess

ADVERTENCIA 

Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess

Introducción al cálculo de efectividad vacunal con cohortes usando vaccineff

Indicadores demográficos, canales endémicos y clusters de incidencia usando epiCoepiCo