Unidad de Estadística y probabilidad

Última actualización: 2024-11-19 | Mejora esta página

Tiempo estimado: 44 minutos

Hoja de ruta

Preguntas

¿Cómo se pueden utilizar la estadística y la probabilidad para resolver preguntas en la epidemiología de enfermedades infecciosas?

Objetivos

Al final de este taller usted podrá:

Comprender el rol de la estadística en el estudio de las enfermedades infecciosas.
Comprender las medidas estadísticas para resumir y analizar la información.
Familiarizarse con el concepto de variable aleatoria y reconocer las principales distribuciones de probabilidad.
Identificar y comprender el proceso del problema estadístico como un problema de inferencia desde una muestra.
Comprender el concepto de intervalo de confianza y el procedimiento de las pruebas de hipótesis.

Pre requisito

Esta unidad tiene como prerequisitos:

Introducción a R y RStudio
Visualización con ggplot2

Esta unidad es un complemento al Curso en ciencia de datos en salud pública y modelamiento de enfermedades infecciosas

Tabla de contenido

Tema 1: Introducción al Pensamiento Estadístico (Ver en plataforma del curso)
Tema 2: Estadística Descriptiva (Ver complemento en plataforma del curso)
Tema 3: Probabilidad (Ver complemento en plataforma del curso)
Tema 4: Principales distribuciones de probabilidad (Ver complemento en plataforma del curso)
Tema 5: Introducción a la inferencia estadística (Ver complemento en plataforma del curso)

Antes de comenzar

Por favor revise que tenga instaladas las librerías tidyverse, pak, epiparameter e infer, en caso de que no estén instaladas ejecute el código a continuación de acuerdo a su necesidad:

R

#Para instalar el paquete de epiparameter si aún no lo tiene (o no tiene seguridad de tenerlo) ejercute el siguiente código

if(!require("pak")) install.packages("pak")
if(!require("epiparameter")) pak::pak("epiverse-trace/epiparameter")

# Para instalar el paquete de tidyverse si aún no lo tiene (o no tiene seguridad de tenerlo)  ejercute el siguiente código

if(!require("tidyverse")) install.packages("tidyverse")


# Para instalar el paquete de infer si aún no lo tiene (o no tiene seguridad de tenerlo)  ejercute el siguiente código

if(!require("infer")) install.packages("infer")

# Para instalar el paquete de epitools si aún no lo tiene (o no tiene seguridad de tenerlo)  ejercute el siguiente código

if (!require(epitools)) install.packages("epitools")

# Para instalar el paquete de cfr si aún no lo tiene (o no tiene seguridad de tenerlo)  ejercute el siguiente código

if (!require("cfr")) install.packages("cfr")

Tema 2: Estadística Descriptiva

Ejercicio: Visualizando y Analizando Datos en R

Existen muchos gráficos de acuerdo al tipo de escala de la variable que se desea analizar. A continuación presentaremos algunos ejemplos para comprender estos conceptos.

Tenga en cuenta realizar previamente la unidad de introducción a R y la unidad de visualización de datos. La tabla de datos para este ejercicio puede encontrarla en: https://github.com/TRACE-LAC/TRACE-LAC-data/raw/main/otros/muestra_covid.RDS
Cuando ya tenga los datos descargados en su computador y en la carpeta de data de su proyecto puede ejecutar el siguiente comando:

R

muestra_covid <- 
  base::readRDS("data/muestra_covid.RDS")

Histograma y Boxplot

Los dos tipos de gráficos más comunes para visualizar la distribución de las variables cuantitativas son los histogramas y los boxplot o gráfico de caja y bigotes.

Los histogramas permiten describir visualmente la distribución de los datos agrupando los datos en intervalos en el eje x, los cuales son generalmente de igual tamaño, y luego para cada intervalo describe la frecuencia absoluta, la frecuencia relativa o la densidad en el eje y. Un histograma de densidad ajusta la frecuencia relativa de cada intervalo de acuerdo a la amplitud del mismo. En R puede ser construido de la siguiente manera:

R

library(ggplot2)
library(dplyr)

SALIDA


Attaching package: 'dplyr'

SALIDA

The following objects are masked from 'package:stats':

    filter, lag

SALIDA

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

R

# Histograma con frecuencia absoluta

ggplot(muestra_covid, aes(x = edad)) +
  geom_histogram(color = "darkblue", 
                 fill = "lightblue") +
  labs(y = "Frecuencia Absoluta", x = "Edad en años",
       title = "Distribución de la edad")

SALIDA

`stat_bin()` using `bins = 30`. Pick better value with `binw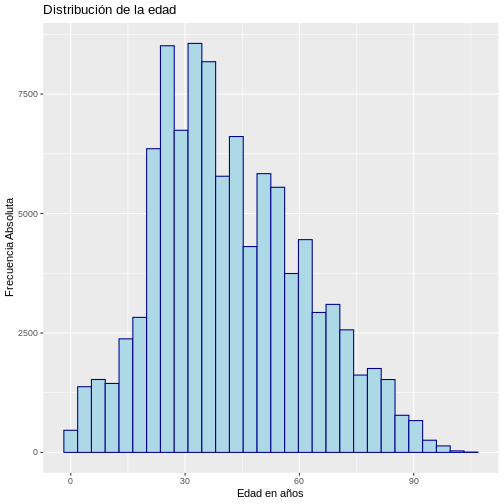idth`.

R

# Histograma con densidad

ggplot(muestra_covid, aes(x = edad)) +
  geom_histogram(aes(y = after_stat(density)),
                 color = "darkblue",
                 fill = "lightblue") +
  labs(y = "Densidad", x = "Edad en años",
       title = "Distribución de la edad")

SALIDA

`stat_bin()` using `bins = 30`. Pick better value with `binw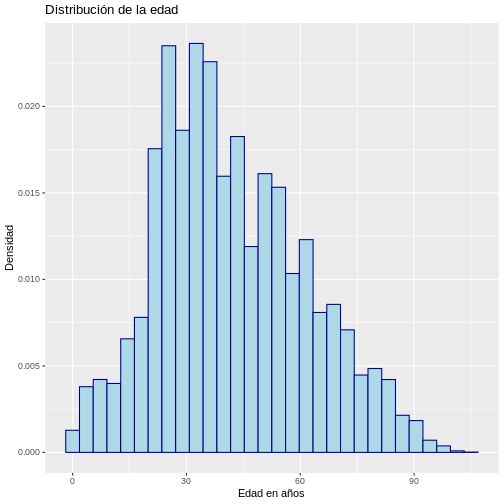idth`.

Los Boxplot se construyen a partir de la visualización en sentido horizontal o vertical de los siguientes estadísticos:

Primer cuartil Q1 (percentil 25): Valor que deja por debajo el 25% de los datos. “Primera Línea”
Segundo cuartil Q2 (percentil 50 o mediana): Valor que deja por debajo el 50% de los datos. “línea de la mitad”
Tercer cuartil Q3 (percentil 50 o mediana): Valor que deja por debajo el 75% de los datos. “Tercera Línea”

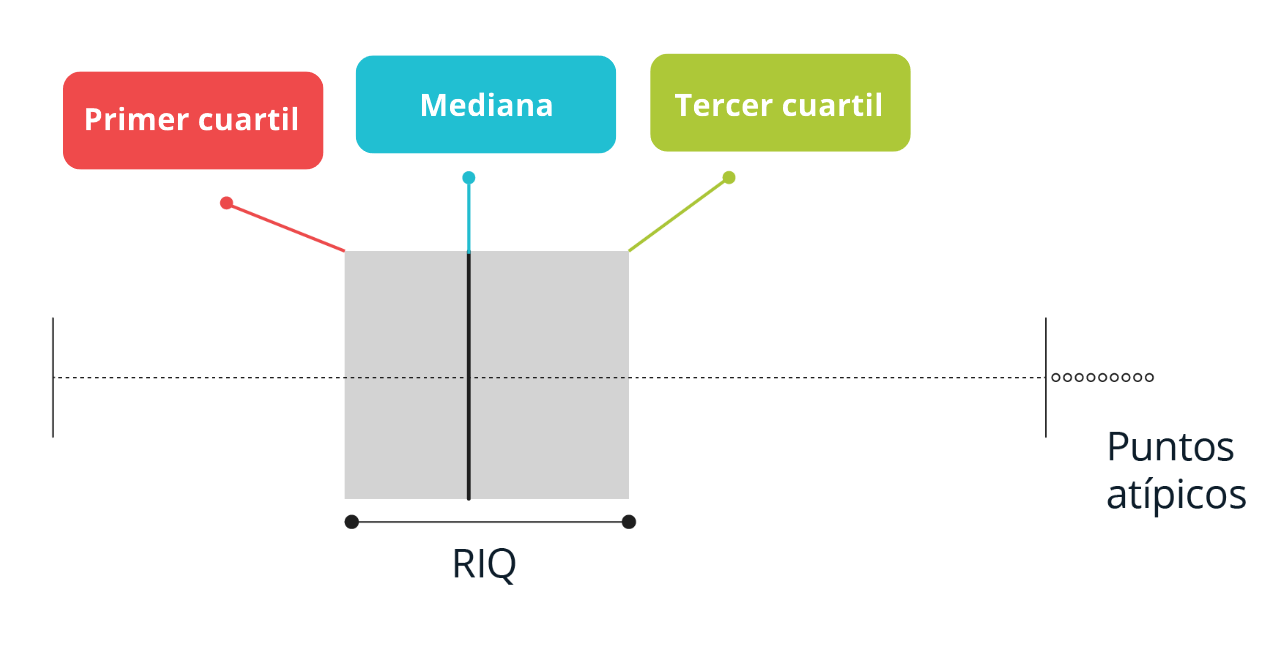
Adicionalmente, estos gráficos son útiles para detectar puntos atípicos o outliers al establecer un límite inferior (Q1-1.5×RIQ) y un límite superior (Q3+1.5×RIQ) basado en el RIQ=Q3-Q1. Los datos por fuera de estos límites son catalogados como inusuales y deben ser revisados. En presencia de datos atípicos, las líneas o bigotes van hasta los límites inferior o superior, en caso contrario van hasta el valor mínimo y máximo, respectivamente.

Otra utilidad de los boxplot y los histogramas es que ayudan a conocer la forma de la distribución con el objetivo de decidir el mejor indicador de tendencia central. De esta manera, una distribución puede ser simétrica o asimétrica positiva/negativa. Cuando existe simetría, se recomienda utilizar la media acompañada de la desviación estándar y en caso contrario, la mediana y el rango intercuartílico debido a que la media puede ser influenciada por los datos extremos de la distribución. Recuerde que un indicador de tendencia central siempre debe ir acompañado de un juez, es decir, su respectivo indicador de variabilidad.

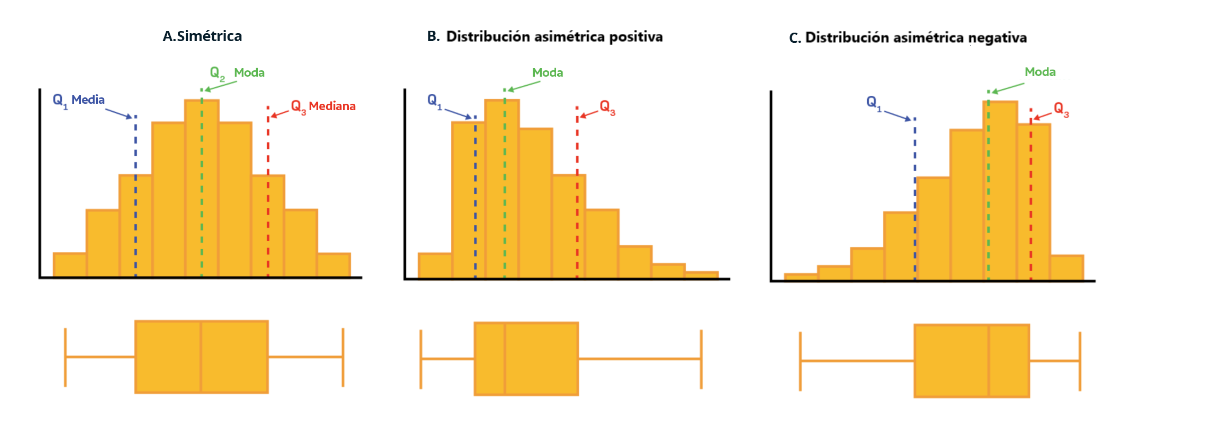
Leyenda explicativa A: En una distribución simétrica, la media, la moda y la mediana toman el mismo valor y los datos se encuentran distribuidos equitativamente alrededor del valor central. Para este tipo de distribuciones se recomienda describir la serie de datos con media y desviación estándar.
Leyenda explicativa B: Distribución asimétrica positiva o sesgada hacia la derecha. Este tipo de distribuciones se caracterizan por tener una mayor concentración de datos hacia el mínimo de la distribución, pero algunos valores se concentran hacia el valor máximo de la misma. El comportamiento esperado es que la media>mediana>moda puesto que la media se deja influenciar por los valores extremos positivos de la distribución. Se recomienda realizar la descripción de los datos por medio de la mediana y rango intercuartílico.
Leyenda explicativa C: Distribución asimétrica negativa o sesgada hacia la izquierda. Este tipo de distribuciones se caracterizan por tener una mayor concentración de datos hacia el máximo de la distribución, pero algunos valores se concentran hacia el valor mínimo de la misma (valores hacia la izquierda). El comportamiento esperado es que la moda>mediana>media dado que esta última se deja influenciar por los valores extremos del costado izquierdo. Se recomienda realizar la descripción de los datos por medio de la mediana y rango intercuartílico.

A continuación realizaremos la visualización de la edad de los casos de COVID-19 a través de un boxplot.

R

# Boxplot

ggplot(muestra_covid, aes(x = "", y = edad)) +
  geom_boxplot(outlier.shape = NA)

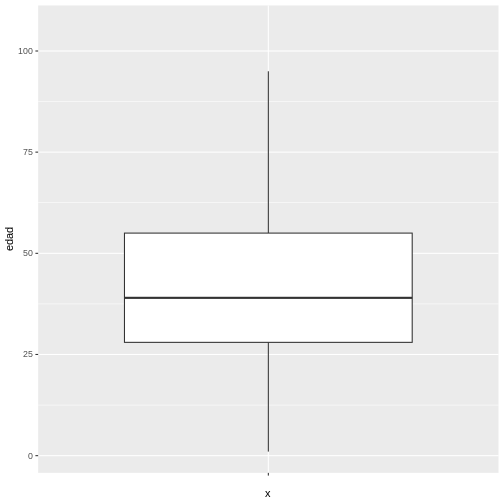
De acuerdo con el boxplot de la edad de la muestra de los casos de COVID-19 es posible concluir que la distribución de los datos es asimétrica positiva, dado que existe una mayor cercanía entre los valores del Q1 y la mediana, por lo que es recomendar describir el comportamiento de la misma por medio de la mediana y rango intercuartílico, esto en R puede ser encontrado de la siguiente manera utilizando las funciones resaltadas en azul:

R

# Estadísticas Descriptivas Variables cuantitativas

muestra_covid %>%
  dplyr::summarise(
  n = n (), # Número de observaciones
  media = mean(edad), #Media
  sd = sd(edad), #Desviación estándar
  mediana = quantile(edad, 0.50), # Mediana-Percentil 50
  P25 = quantile(edad, 0.25), # Percentil 25
  P75 = quantile(edad, 0.75)) # Percentil 75

SALIDA

       n    media       sd mediana P25 P75
1 100000 41.99912 19.51872      39  28  55

Finalmente, para la variable edad se puede concluir que la mitad de los pacientes con covid-19 tienen edades entre 27 y 52 años (“RIQ”) con una mediana de 38 años, lo que indica que la mitad de los casos tienen una edad por debajo de este valor. Es importante resaltar que, debido a la asimetría de la distribución, la media y la mediana no coinciden, comportamiento esperado en las distribuciones asimétricas.

Gráfico de Barras y Tablas de Frecuencia

Las variables cualitativas se recomiendan que sean representadas por medio de gráficos de barras. Generalmente, estos se construyen indicando en el X las categorías de las variables y en el eje Y el valor de las frecuencias absolutas, relativas o porcentajes de acuerdo a las necesidades, es decir, siempre es necesario primero evaluar la tabla de frecuencia de la variable. Supongamos que se desea conocer el tipo de contagio de COVID-19. Esto en R puede realizarse utilizando el siguiente comando:

R

tabla <- muestra_covid %>% # se crea la tabla de frecuencia
  dplyr::count(tipo_de_contagio) %>% #conteo de frecuencia para la variable estado
  dplyr::mutate(prop = base::prop.table(n), #proporción
                perc = base::prop.table(n)*100) #porcentaje

tabla

SALIDA

  tipo_de_contagio     n    prop   perc
1      Comunitaria 69985 0.69985 69.985
2        Importado    63 0.00063  0.063
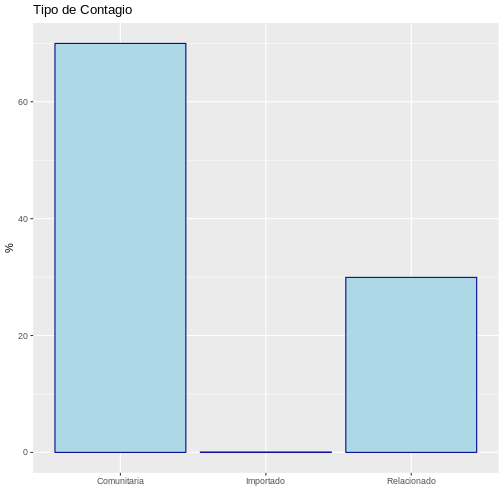
3      Relacionado 29952 0.29952 29.952

Con esta información se puede concluir que el 70% de los casos de covid-19 fueron de la comunidad y sólo el 0.06% fueron importados de otros lugares. Esto puede ser visualizado por medio de un gráfico de barras:

R

ggplot(data = tabla, aes(x = tipo_de_contagio, y = perc)) +
  geom_bar(stat = "identity", color = "darkblue", fill = "lightblue")+
  labs(y = "%", x = " ",title = "Tipo de Contagio")

Tema 3: Probabilidad

En un estudio publicado en el NEJM en el año 2014. titulado “Ebola Virus Disease in West Africa- The First 9 Months of the Epidemic and Forward Projections” (DOI: 10.1056/NEJMoa1411100), se describieron las características clínicas y epidemiológicas de los casos de ébola reportados durante la epidemia que afectó a los países de Guinea, Liberia, Nigeria y Sierra Leona desde diciembre del 2013. En ese estudio se describió que aquellos sujetos mayores de 44 años tenían una mayor probabilidad de morir a causa de la enfermedad. De manera similar al artículo de referencia, se llega a una conclusión comparable si realizamos un cálculo equivalente utilizando medidas de asociación vistas en la Unidad de Epidemiología General aplicada a enfermedades infecciosas, como Riesgos relativos (RR) del la Razón de riesgos o Riesgo relativo (RR). Para ello, se puede reconstruir una tabla 2x2, donde el RR puede ser medido por la razón entre el CFR de un grupo A (p.e., casos con 45 años o más) y un grupo B (p.e., casos con 44 años o menos), donde el CFR es el riesgo de muerte en casos (del inglés Case Fatality Risk).

De esta forma, obtenemos que el riesgo de muerte en casos con 45 años o más es 1.20 veces el riesgo de muerte en casos con 44 años o menos, con un intervalo de confianza del 95% de 1.13 a 1.27, y un valor p menor a 0.01. Para reproducir este cálculo puede usar la librería epitools como se muestra acontinuación.

R

library(epitools)

tabla2x2 <- matrix(c(311, 51, 768, 299),nrow = 2, ncol = 2)

epitools::riskratio(tabla2x2)

SALIDA

$data
          Outcome
Predictor  Disease1 Disease2 Total
  Exposed1      311      768  1079
  Exposed2       51      299   350
  Total         362     1067  1429

$measure
          risk ratio with 95% C.I.
Predictor  estimate    lower    upper
  Exposed1 1.000000       NA       NA
  Exposed2 1.200227 1.133086 1.271346

$p.value
          two-sided
Predictor    midp.exact fisher.exact   chi.square
  Exposed1           NA           NA           NA
  Exposed2 3.179312e-08 4.200177e-08 9.982161e-08

$correction
[1] FALSE

attr(,"method")
[1] "Unconditional MLE & normal approximation (Wald) CI"

En el Tema 5 de esta Unidad encontrará una introducción a la inferencia estadística e intervalos de confianza.

Tema 4: Principales distribuciones de probabilidad

Cómo se describió en el Tema 3, la probabilidad estudia el comportamiento de fenómenos aleatorios “eventos”. En este proceso se observan variables aleatorias (v.a), denotadas usualmente como X que tienen comoobjetivo asignar un número real a cada evento que puede suceder en el espacio muestral.

Para la explicación y ejemplos de las principales distribuciones es importante que instale y cargue los paquetes epiparameter del Epiverse.

R

#cargue la librería epiparameter
library(epiparameter)

Modelos Discretos

La distribución binomial permite describir la probabilidad de ocurrencia de un evento con dos posibles resultados, éxito (p) o fracaso (1-p), en un número determinado de ensayos independientes n con probabilidad constante de éxito p. La variable aleatoria en estudio corresponde a:

X: Número de éxitos en n ensayos

El modelo binomial puede ser de utilidad para conocer la probabilidad de observar un número determinado de eventos (ej. casos, muertes, reinfecciones) en una población de tamaño n bajo el supuesto que la probabilidad del evento es constante. La distribución binomial depende de dos parámetros: la probabilidad de éxito p y el número de ensayos independientes n.

Si X tiene una distribución binomial entonces se representa de la siguiente manera. X~Bin(n,p)

Y su función de densidad, media, esperanza y varianza corresponden a:

$f(x)=P(X=x)=(n x )$

$p^x (1-p)^{(n-x)}$

$E(x)=np$
$Var(x)=np(1-p)$

Ejemplo: Sí en una comunidad de 20 individuos se introduce un virus con una tasa de ataque del 60% ¿Cuál es la probabilidad de que en esta comunidad se infecten 10 o menos individuos?

Sea $X~Bin(n=20,p=0.60)$, entonces se necesita calcular la siguiente expresión:

$P(X≤10)=∑_(x=0)^10 (20 x ) 〖0.60〗^x (1-0.60)^(20-x)$

En R esto puede ser calculado de la siguiente forma:

R

p <- 0.60 
n <- 20 
x <- 10 

pbinom(x,n,p, lower.tail = TRUE)

SALIDA

[1] 0.2446628

Por lo tanto, la probabilidad de que máximo 10 individuos se infecten es del 24.5%.

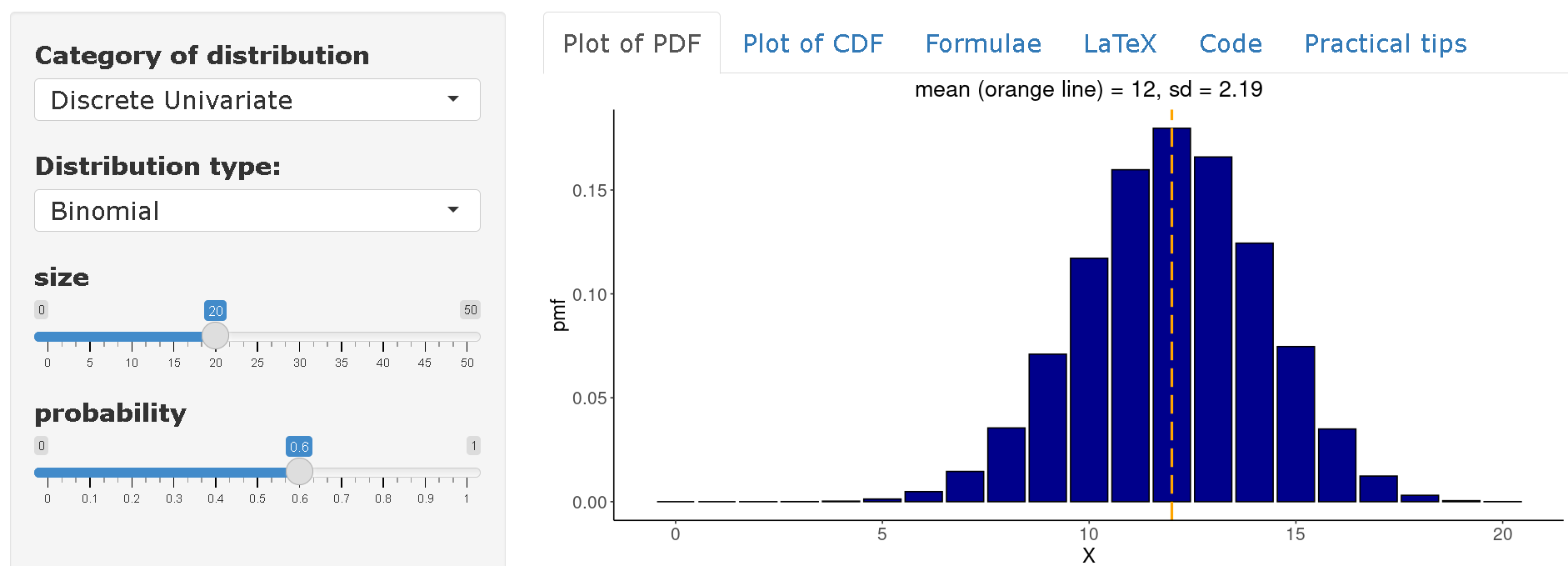
En distribution-zoo se puede visualizar la distribución completa de la variable

$X~Bin(n=20,p=0.60)$. Así, se puede concluir que en promedio se esperaría encontrar 12 infectados en una comunidad de 20 individuos partiendo de una tasa de ataque del 60%.

Distribución Poisson

La distribución de Poisson modela el comportamiento de variables aleatorias que describen el número de eventos, “conteos”, que ocurren en un intervalo de observación fijo, ejemplo, tiempo (número de infecciones ocurridas en una hora, día, semana, año, etc), o área (número de infecciones ocurridas en un municipio, hospital, etc).

Esta distribución tiene un parámetro llamado lambda ($λ$), $λ>0$, que describe el número promedio de eventos que suceden en el intervalo fijo de observación. Si $X$ tiene una distribución de Poisson, entonces, se representa de la siguiente manera:

$X$~$Poisson(λ)$

Su función de densidad, esperanza, media y varianza corresponde a:

$fx=P(X=x)=\frac{e^{-λ}λ^x}{x!}, x=0,1,2,..,$

$E(x)=λ Var(x)=λ$

En enfermedades infecciosas, la distribución de Poisson puede ser utilizada para modelar el número de casos secundarios generados por un caso primario. En este contexto, el parámetro está en función del número efectivo de reproducción R que representa el promedio de infecciones secundarias causadas por cada caso primario en el tiempo en una población compuesta por individuos susceptibles y no susceptibles.

Desafío

Ejemplo

Supongamos que se desea estudiar la propagación de un brote con base en un modelo de Poisson a medida que transcurren los días (t). La variable aleatoria de interés es:

$X_{(t )}$: Número de casos secundarios causados por cada caso primario al día t

Este es un modelo de Poisson dado que existe un intervalo fijo de observación “cada caso primario” y se desea estudiar el número de casos secundarios observados “eventos”. Así, se podría construir el siguiente modelo:

$X_{(t )}∼Poisson (λ= R X_{(t-1)})$

Lo anterior expresa que el número promedio de casos secundarios al día t depende del número de reproducción $R$ y del número de casos observados $X$ el día anterior $(t-1)$. No obstante, R es difícil de conocer en la vida real y podría ser de interés aproximar su valor con base en los datos observados durante el brote con el fin de generar estrategias de control.

Supongamos que al día 1 del brote $(t=1)$ se presentaron un total de 5 casos nuevos y que al siguiente día $(t=2)$ se presentaron 10 casos nuevos. Con la anterior información nos interesa estudiar el número de casos secundarios en el día 2, lo que equivale a:

$X_{(2 )}$: Número de casos secundarios causados por cada caso primario en el día 2

La cual tiene la siguiente distribución:

$X_{(2 )}∼Poisson (λ= R *5)$

De aquí, podríamos estimar el valor de $R$ al descubrir cuál valor maximiza la probabilidad de observar este número específico de casos secundarios en el día 2, es decir:

$P(X_{(2 )}=10)=\frac{e^{-(R *5)} (R *5)^{10}}{10!}$

En R lo podríamos descubrir al variar diferentes valores del número de reproducción (R) de la siguiente manera:

R

# Calculo probabilidad de poisson
prob_poisson <- function(x1, x2, r){
  dpois(x2, r*x1)
}

 # Aplicar la función con los datos observados

numeros_reproduccion <- base::seq(0,5,0.01) # Diferentes valores de R
resultados_poisson <- base::vector(length = base::length(numeros_reproduccion))

#crear un vector vacío 

for (i in seq_along(numeros_reproduccion)){
 resultados_poisson[i] <- prob_poisson(x1 = 5, x2 = 10, r = numeros_reproduccion[i])
}

datos_resultados <- base::data.frame(numeros_reproduccion, resultados_poisson)
numero_mas_probable <- datos_resultados %>%  dplyr::filter(resultados_poisson == max(resultados_poisson)) %>%  dplyr::pull(numeros_reproduccion) 

p <- ggplot(data = datos_resultados, aes(x = numeros_reproduccion, y = resultados_poisson)) + geom_line() +  geom_vline(xintercept = numero_mas_probable ,color = "red", size=1)

ADVERTENCIA

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.
This warning is displayed once every 8 hours.
Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
generated.

R

p+labs(y = "Probabilidad", x = "Número Reproductivo (R) ",title = "Modelo de Poisson")

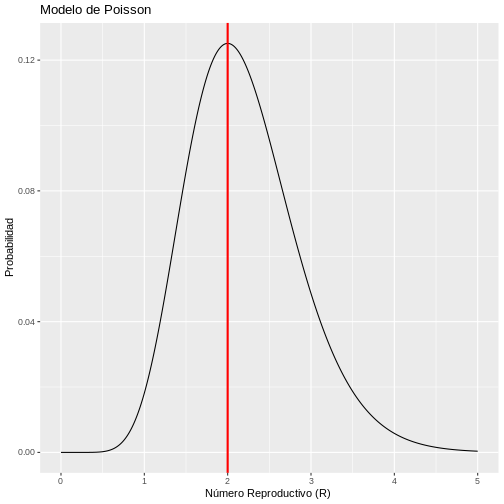
Por lo tanto, si el número de casos secundarios se comporta de acuerdo a una distribución de Poisson, existe una alta probabilidad de que el número de casos nuevos observados en el día 2 hayan sido generados con un número de reproducción de R=2. Lo que implica que el promedio de casos secundarios por cada caso primario es de 2. No obstante, este modelo simple supone que el número de casos secundarios generados por cada caso primario tienen igual media y varianza, lo que implica que todos los casos primarios generan el promedio un número similar de casos secundarios. Este supuesto puede ser difícil de asumir en algunas enfermedades infecciosas en especial cuando siguen un patrón de sobredispersión (20% de los casos causan el 80% de la transmisión) por lo que el modelo de Poisson tiene limitaciones en su aplicación.

Distribución Binomial Negativa

Al igual que la distribución de Poisson, la distribución binomial negativa permite modelar el número de eventos que ocurren “conteos”. Si $X$ tiene una distribución Binomial Negativa, entonces, se representa de la siguiente manera.

$X $~$ BN(μ,k)$

Donde, $μ$ representa la media de la distribución y $k$ es el parámetro de dispersión que permite que la media y la varianza de los eventos no sean iguales. Este parámetro $k$ permite introducir al modelo el grado de dispersión en cómo se generan los eventos. Así, $k$ mide inversamente el grado de variación de los eventos ocurridos dado que la media y la varianza de la distribución corresponden a:

$E(x)=μ$

$Var(x)=μ(1+\frac{μ}{k})$

Con función de densidad:

$f(x)=\frac{Γ(x+k)}{Γ(k)Γ(x+1)} (\frac{μ}{μ+k})^x (\frac{k}{μ+k})^k,x=0,1,2...$

Desafío

Ejemplo

En el estudio de las enfermedades infecciosas, la distribución binomial negativa juega un rol relevante dado que permite modelar la distribución del número de casos secundarios generados por un caso primario, es decir, permite conocer la distribución del número de reproducción básico R_0. En este contexto, la media de la distribución corresponde a $R_0$(Número de casos secundarios en una población totalmente susceptible) y el parámetro $k$ controla la variación entre los casos primarios. Así, valores pequeños de k sugieren que los casos secundarios son generados por un grupo pequeño de casos primarios, mientras que valores grandes sugieren que la propagación del virus es alta. Así, siendo $X$ el número de casos secundarios, entonces:

$X \sim Bn(R_0,k)$

$E(x)=R_0$

$Var(x)=R_0 (\frac{1+R_0}{k})$

En el artículo de Lloyd-Smith et al. se muestra cómo la distribución binomial negativa permite modelar la distribución de casos secundarios de varios patógenos. Con base en los casos reportados durante el brote de SARS ocurrido en Singapur en el año 2023, se logró estimar los parámetros de la distribución binomial negativa encontrando un $R_0=1.630$ y $k=0.160$. Estas estimaciones se encuentran disponibles en el paquete epiparameter, el cual es un paquete disponible en R que recopila las principales estimaciones para varios parámetros epidemiológicos de interés en el estudio de las enfermedades infecciosas.

R

SARS_R <- epiparameter::epiparameter_db(
    disease = "SARS",
    epi_name = "offspring distribution",
    single_epiparameter = TRUE
)

SALIDA

Using Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>..
To retrieve the citation use the 'get_citation' function

R

SARS_R

SALIDA

Disease: SARS
Pathogen: SARS-Cov-1
Epi Parameter: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom
Parameters:
  mean: 1.630
  dispersion: 0.160

Con estos resultados sería posible graficar la distribución del número de casos secundarios del SARS para poder sugerir medidas de control. Esto también está disponible en el paquete epiparameter con la función plot.

R

plot(SARS_R)

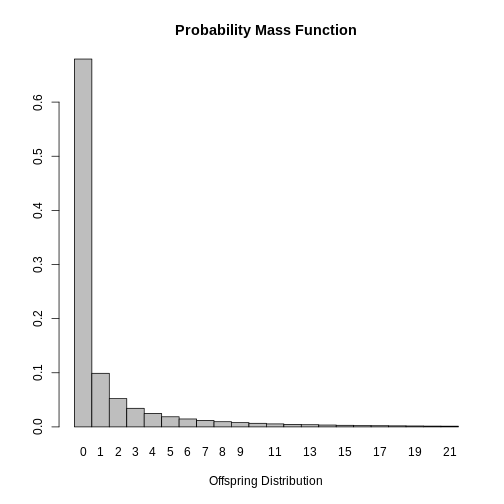
Finalmente, es posible concluir que la mayoría de casos infectados con SARS no propagan la enfermedad dado que la moda de la distribución es $0$. Este resultado es esperado dado que $k<1$, lo que indica que los casos secundarios son generados por un pequeño grupo de infectados y que el valor estimado de $R_0$ varía para los casos.

Distribución geométrica

Otra distribución discreta de interés que puede ser utilizada para modelar conteos o número de eventos es la distribución geométrica. En enfermedades infecciosas su principal uso surge cuando el parámetro de dispersión de la distribución negativa es igual a 1. Esta distribución depende de la probabilidad de que ocurra el evento de interés y se representa de la siguiente manera.

$X \sim Geom(p)$

donde p representa la probabilidad de éxito o la probabilidad de que ocurra el evento de interés con media igual a:

$E(x)=\frac{1}{p}$

Desafío

Ejemplo

Si en el caso del brote de SARS de Singapur en el año 2023, el valor estimado de $k$ hubiera sido $1$, entonces, la distribución de casos secundarios podría ser modelado con una distribución geométrica de tal manera que su media sea igual al $R_0$ estimado, es decir se debe cumplir que:

$E(x)=\frac{1}{p}=1.630$ y por lo tanto, $p=\frac{1}{1.630}$

Por lo que la distribución del número de contactos secundarios se podría escribir como:

$X \sim Geom(p=0.613)$

En R podríamos simular el comportamiento del número de casos secundarios con el siguiente código:

R

# Distribución Geométrica
x <- base::seq(0,20,1) # Diferentes valores de R
prob <- 1/(1.630)
datos_geome <- base::data.frame(x, probg = dgeom(x, prob))

ggplot(data = datos_geome, aes(x = x, y = probg)) +
  geom_bar(stat = "identity") +
  labs(y = "Probabilidad", x = "Casos secundarios",
       title = "Distribución Geométrica")

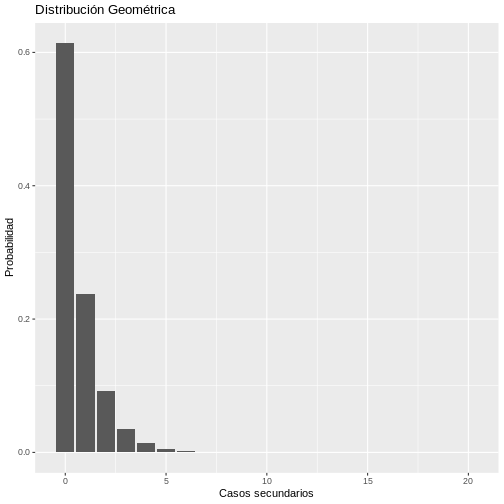
Bajo la distribución geométrica, entonces existe una mayor probabilidad de que un caso primario pueda transmitir el virus dado que la probabilidad de que un caso primario genere 1,2, o más casos secundarios es mayor con este modelo en comparación de lo estimado con el modelo binomial negativo.

Modelos Continuos

Distribución Uniforme

La distribución uniforme modela una variable continua que toma valores dentro de un intervalo $[a,b]$ con igual probabilidad. Esta distribución suele utilizarse en la simulación de números aleatorios. Si $X$ sigue una distribución uniforme, esto se puede representar por:

$X ∼U(a,b)$

Sus parámetros a y b, representan el valor mínimo y máximo que puede tomar la variable, respectivamente. Su función de densidad está determinada por:

$f(x)=\frac{1}{b-a}$,con $a<x<b$

La media y varianza está determinada por:

$E(x)=\frac{a+b}{2}$ y $V(x)=\frac{(b-a)^2}{12}$

Desafío

Ejemplo

Un investigador desea simular el comportamiento del COVID-19 y necesita generar aleatoriamente el valor que puede tomar el número básico de reproducción $R_0$ para luego utilizarlo dentro de su modelo de propagación. Para esto, él supone que el $R_0$ del COVID-19 sigue una distribución uniforme entre 2 y 5:

$R0∼U[2,5]$

Para su simulación necesita generar cinco posibles valores de $R_0$ con igual probabilidad, lo anterior en R se resuelve utilizando el siguiente código:

R

# Generación de números aleatorios con la distribución uniforme
n <- 5
a <- 2
b <- 5
stats::runif(n, a, b)

SALIDA

[1] 3.296493 2.735185 2.097067 2.509185 4.294340

Distribución Normal

La distribución normal es sin duda el modelo probabilístico más importante en la teoría estadística debido a que permite modelar múltiples problemas de la vida real y a su relevante rol en el campo de la inferencia. Esta distribución intenta modelar variables aleatorias que pueden estar influenciadas por múltiples factores, cuyos efectos al ser sumados hacen que los valores de la distribución tiendan hacia el centro (media). Por ejemplo, la temperatura corporal puede seguir una distribución normal dado que esta es influenciada por múltiples factores biológicos y ambientales, los cuales al sumar sus efectos hacen que la mayoría de los individuos se encuentran alrededor de un valor central.

Para expresar matemáticamente que una variable continua tiene distribución normal se escribe:

$X ∼N(μ,σ)$

La cual tendrá asociada la siguiente función de densidad de probabilidad:

$f(x)=\frac{1}{ σ\sqrt{2\pi}}exp[-\frac{1}{2 σ^2}(x-u)^2]$

Donde $μ$ y $σ$ son los parámetros de la distribución y representan respectivamente la media y la desviación estándar de la variable aleatoria, es decir, el valor central y la dispersión de los datos respecto a este. Estos parámetros corresponden a los valores que se obtendría si se logrará estudiar toda la población y no una muestra de la misma.

Cuando $μ=0$ y $σ=1$, recibe el nombre de distribución normal estándar. Sin embargo, existen muchas distribuciones normales de acuerdo a los valores que tomen sus parámetros, pero sin importar el valor de estos, la forma de la distribución siempre es simétrica y siempre puede ser transformada a una distribución normal estándar por medio de un procedimiento de estandarización aplicando la siguiente fórmula:

$Z=\frac{X-μ}{σ}∼N(0,1)$

Desafío

Ejemplo,

Si se sabe que en una comunidad la edad de los casos que fallecieron por COVID-19 tiene una distribución normal con media 67.8 y desviación estándar de 15.4 años. ¿Cuál es la probabilidad de que un fallecido sea menor de 40 años?

Primero se define la variable a estudiar, la cual tiene una distribución normal

$X∼N(67.8,15.4)$

$X$: La edad de los casos fallecidos por COVID-19

En R, podemos usar la función pnorm() de la siguiente manera para encontrar:

$P(X<40)=?$

R

mu <- 67.8
sigma <- 15.4 
x <- 40 
stats::pnorm(x, mean = mu, sd = sigma)

SALIDA

[1] 0.0355221

Por lo tanto, la probabilidad de que un fallecido por COVID-19 sea menor de 40 años es del 3.5%.

Distribución Log-normal

La distribución log-normal surge cuando se consideran variables aleatorias continuas que no toman el valor de cero o números negativos cuya distribución tiene una forma asimétrica y su variación es generada por múltiples factores cuyos efectos no son simétricos. Si una v.a sigue una distribución lognormal, su transformación al aplicar la función logaritmo generará una variable normal y de ahí surge su nombre. En el campo de las enfermedades infecciosas, la distribución log-normal tiene gran utilidad para modelar los periodos de incubación (tiempo desde la infección hasta el inicio de síntomas).

Si $X ∼LogN(μ,σ)$, entonces, se cumple que $Y=log (X) ∼N(μ,σ)$ y la función de densidad de $X$ está dada por:

$f(x)=\frac{1}{ xσ\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{ln(x)-u}{σ})^2}$

A diferencia de la distribución normal, en la distribución log-normal el parámetro μ cumple el rol de un parámetro de escala dado que aumenta la dispersión de los datos al incrementar su grado de amplitud y el parámetro σ controla la forma, es decir, el grado de asimetría.

Desafío

Ejemplo

En el año 2009 en el artículo de Lessler et al. se modelaron los periodos de incubación de varios patógenos con base en una distribución lognormal. El interés principal era estimar los parámetros de $(μ,σ)$. Por ejemplo en el caso del SARS se encontró una estimación de $μ=0.660$, y $σ=1.205$, lo que implica que en promedio un caso infectado desarrolla síntomas en 0.7 días. Esta información puede ser obtenida en el paquete epiparameter con el siguiente comando:

R

SARS_incubacion <- epiparameter::epiparameter_db(
    disease = "SARS",
    epi_name = "incubation period",
    single_epiparameter = TRUE
)

SALIDA

Using Lessler J, Reich N, Brookmeyer R, Perl T, Nelson K, Cummings D (2009).
"Incubation periods of acute respiratory viral infections: a systematic
review." _The Lancet Infectious Diseases_.
doi:10.1016/S1473-3099(09)70069-8
<https://doi.org/10.1016/S1473-3099%2809%2970069-8>..
To retrieve the citation use the 'get_citation' function

R

SARS_incubacion

SALIDA

Disease: SARS
Pathogen: SARS-Cov-1
Epi Parameter: incubation period
Study: Lessler J, Reich N, Brookmeyer R, Perl T, Nelson K, Cummings D (2009).
"Incubation periods of acute respiratory viral infections: a systematic
review." _The Lancet Infectious Diseases_.
doi:10.1016/S1473-3099(09)70069-8
<https://doi.org/10.1016/S1473-3099%2809%2970069-8>.
Distribution: lnorm
Parameters:
  meanlog: 1.386
  sdlog: 0.593

La distribución completa del periodo de incubación para SARS puede graficarse por medio de:

R

plot(SARS_incubacion)

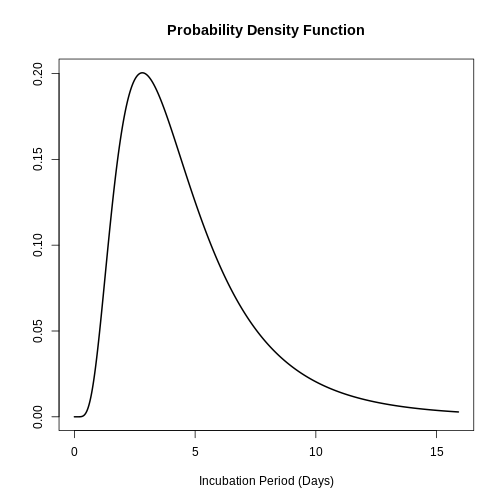
Lo anterior es útil para responder preguntas tipo: ¿Cuál es la probabilidad de que un caso de SARS desarrolle síntomas dos días después de la infección?

R

stats::plnorm(2, meanlog = 0.660, sdlog = 1.205, lower.tail = FALSE)

SALIDA

[1] 0.4890273

Distribución Gamma

Cuando estamos estudiando variables aleatorias de Poisson, generalmente, nos interesa estudiar el número de eventos que ocurren con media $λ$ por un intervalo de tiempo definido. La distribución Gamma se centra en estudiar la v.a $X$: el tiempo que transcurre hasta que ocurra un determinado número de eventos $α^th$. Por ejemplo, si estamos evaluando el número de contagios por hora y queremos estudiar cuánto tiempo puede transcurrir hasta encontrar α contagios, gráficamente $X$ corresponde a:

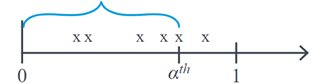
La distribución Gamma es ampliamente utilizada en análisis de supervivencia debido a su flexibilidad que viene dada por sus parámetros de forma $α$ y escala $θ$, que determinan su función de densidad, la cual tiene un comportamiento asimétrico. Aquí, $θ$ representan el tiempo promedio de espera hasta que el primer evento ocurre y $α$ es el número de eventos que se espera ocurran. Esta distribución se denota de la siguiente manera:

$X ∼Gamma(α,θ)$

$f(x)=\frac{1}{(α-1)!θ^α}e^{\frac{-x}{θ}} x^{α-1}$

$E(x)=αθ$

$Var(x)=αθ^2$

Cuando $θ$ aumenta su valor, la concentración de la probabilidad se corre hacia la derecha, lo mismo ocurre al esperar un mayor número de eventos $α$ dado que el tiempo de espera $X$ puede ser mayor.

Desafío

Ejemplo

Una posible aplicación de la distribución Gamma es en el modelamiento del intervalo serial de las enfermedades infecciosas. El intervalo serial (s) se define como el tiempo que transcurre entre el inicio de síntomas del caso primario y el inicio de síntomas del caso secundario. En el estudio de Ghani et al. se describió la distribución del intervalo serial de la influenza Influenza-A-H1N1Pdm por medio de la distribución gamma encontrando los siguientes parámetros:

$s ∼Gamma( α=2.622,θ=0.957)$

Esta información puede ser obtenida también en el paquete epiparameter con el siguiente comando:

R

influenza_s <- epiparameter::epiparameter_db(
  disease = "Influenza",
  epi_name = "serial_interval",
  single_epiparameter = TRUE
)

SALIDA

Using Ghani A, Baguelin M, Griffin J, Flasche S, van Hoek A, Cauchemez S,
Donnelly C, Robertson C, White M, Truscott J, Fraser C, Garske T, White
P, Leach S, Hall I, Jenkins H, Ferguson N, Cooper B (2009). "The Early
Transmission Dynamics of H1N1pdm Influenza in the United Kingdom."
_PLoS Currents_. doi:10.1371/currents.RRN1130
<https://doi.org/10.1371/currents.RRN1130>..
To retrieve the citation use the 'get_citation' function

R

influenza_s

SALIDA

Disease: Influenza
Pathogen: Influenza-A-H1N1Pdm
Epi Parameter: serial interval
Study: Ghani A, Baguelin M, Griffin J, Flasche S, van Hoek A, Cauchemez S,
Donnelly C, Robertson C, White M, Truscott J, Fraser C, Garske T, White
P, Leach S, Hall I, Jenkins H, Ferguson N, Cooper B (2009). "The Early
Transmission Dynamics of H1N1pdm Influenza in the United Kingdom."
_PLoS Currents_. doi:10.1371/currents.RRN1130
<https://doi.org/10.1371/currents.RRN1130>.
Distribution: gamma
Parameters:
  shape: 2.622
  scale: 0.957

R

graphics::plot(influenza_s)

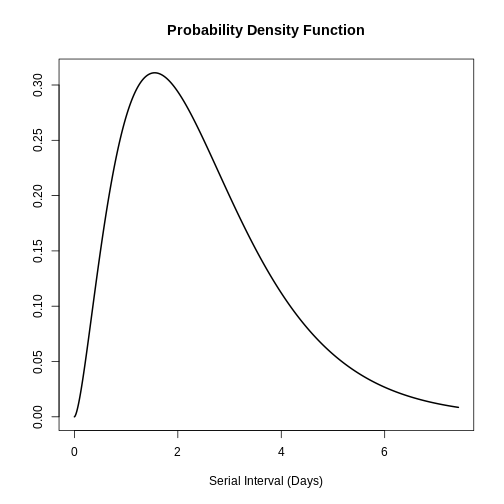
Con esta información se podría encontrar la media y desviación estándar de la distribución con base en la aplicación de la distribución gamma:

R

shape <- 2.622
scale <- 0.957
mean <- shape*scale
sd <- sqrt(shape*scale^2)
print(c(mean, sd))

SALIDA

[1] 2.509254 1.549631

Por lo tanto, el promedio del intervalo serial de la influenza es de 5.51 días con una desviación estándar de 1.55 días.

Distribución Weibull

Al igual que la distribución Gamma, la distribución Weibull es de gran utilidad en el análisis de v.a´s que representan tiempos de espera hasta observar un evento en particular. La distribución Weibull tiene dos parámetros y su función de densidad está definida por:

$f(x)= \frac{β}{η}(\frac{x}{η})^{β-1}{e^{-(x/η)}}^β$

Aquí, $η$ es el parámetro de escala y $β$ el de forma. El parámetro de forma $β$ también es conocido como pendiente e intenta modelar la relación entre la probabilidad y los tiempos de espera. Así cuando $β>1$ la tasa de ocurrencia de eventos incrementa con el tiempo, mientras si $β<1$ describe que el riesgo del evento disminuye con el tiempo. El parámetro de escala maneja el grado de variabilidad de la distribución y se encuentra en las mismas unidades de $X$.

Desafío

Ejemplo

En el estudio de Virlogeux et al. se describió la distribución del tiempo de incubación de la influenza por medio de la distribución Weibull encontrando los siguientes parámetros:

$x∼Gamma( β=2.101,η=3.839)$

Esta información puede ser obtenida también en el paquete epiparameter con el siguiente comando:

R

influenza_incubacion <- epiparameter::epiparameter_db(
  disease = "Influenza",
  epi_name = "incubation period",
  single_epiparameter = TRUE
)

SALIDA

Using Virlogeux V, Li M, Tsang T, Feng L, Fang V, Jiang H, Wu P, Zheng J, Lau
E, Cao Y, Qin Y, Liao Q, Yu H, Cowling B (2015). "Estimating the
Distribution of the Incubation Periods of Human Avian Influenza A(H7N9)
Virus Infections." _American Journal of Epidemiology_.
doi:10.1093/aje/kwv115 <https://doi.org/10.1093/aje/kwv115>..
To retrieve the citation use the 'get_citation' function

R

influenza_incubacion

SALIDA

Disease: Influenza
Pathogen: Influenza-A-H7N9
Epi Parameter: incubation period
Study: Virlogeux V, Li M, Tsang T, Feng L, Fang V, Jiang H, Wu P, Zheng J, Lau
E, Cao Y, Qin Y, Liao Q, Yu H, Cowling B (2015). "Estimating the
Distribution of the Incubation Periods of Human Avian Influenza A(H7N9)
Virus Infections." _American Journal of Epidemiology_.
doi:10.1093/aje/kwv115 <https://doi.org/10.1093/aje/kwv115>.
Distribution: weibull
Parameters:
  shape: 2.101
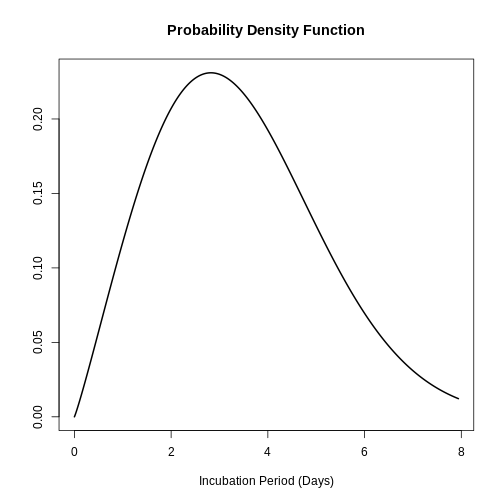
  scale: 3.839

R

plot(influenza_incubacion)

Tema 5: Introducción a la inferencia estadística

La estadística puede dividirse en dos grandes ramas: descriptiva e inferencial. Cómo lo vimos en unidades anteriores, la primera comúnmente busca resumir y explorar los datos que han sido recolectados en una muestra seleccionada de una población. En cambio, la segunda tiene por objetivo realizar generalizaciones y concluir sobre toda la población a partir de la información o datos provenientes de una muestra.

Por la naturaleza del proceso inferencial que es basado en la toma de muestras aleatorias de la población, un estimador puede tomar múltiples valores dado que depende de las unidades que fueron seleccionadas en la muestra. Esta variación debida al azar, denominada variación muestral, debe ser involucrada al proceso de inferencia como lo veremos más adelante.

Es importante recalcar que la variación muestral dependerá del tamaño de la muestra. Por ejemplo, si tomamos muestras de tamaño 10 y calculamos la CFR en cada una de ellas, estas estimaciones se parecerán más entre sí en comparación con las obtenidas cuando se seleccionan sólo 5 individuos por muestra. Lo anterior, puede ser comprobado al realizar una simulación en R y seleccionar 1000 muestras de tamaño 5 y 10, respectivamente. Como se observa en la siguiente figura, las CFR estimadas al incrementar el tamaño de la muestra de 5 a 10 fueron más similares con un menor RIQ.

R

library(infer)

SALIDA


Attaching package: 'infer'

SALIDA

The following object is masked from 'package:epiparameter':

    generate

R

set.seed(200)
poblacion <- base::data.frame(muerto=c(base::rep(1,40), base::rep(0,160)))
muestrasn5 <- poblacion %>%
  infer::rep_sample_n(size = 5, reps = 100, replace = FALSE)

cfrn5 <-muestrasn5 %>%
  dplyr::group_by(replicate) %>%
  dplyr::summarise(cfr = mean(muerto))

muestrasn10 <- poblacion %>%
  infer::rep_sample_n(size = 10, reps = 100, replace = FALSE)

cfrn10<-muestrasn10 %>%
  dplyr::group_by(replicate) %>%
  dplyr::summarise(cfr = mean(muerto))

cfr <- dplyr::bind_rows(cfrn5, cfrn10)
cfr <- cfr %>% 
  dplyr::mutate(size = base::as.factor(c(base::rep(5,100), base::rep(10, 100))))


# Plot sampling distribution
ggplot(cfr, aes(x =size, y=cfr, fill=size)) +
  geom_boxplot(show.legend = FALSE) +
  labs(x = "Tamaño muestral", y = "CFR estimación",
       title = " ") + scale_fill_brewer(palette="Blues")

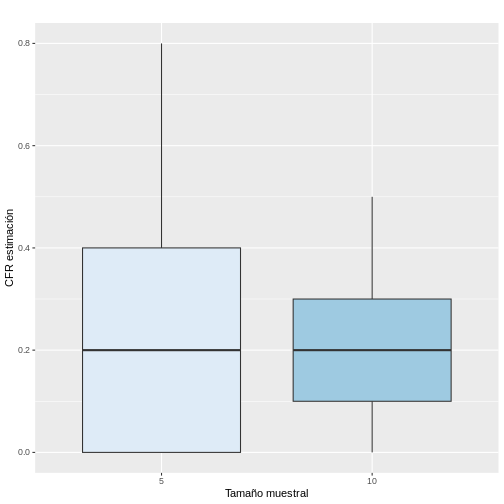
Si calculamos la media y desviación estándar de los valores estimados de la CRF con las muestras de tamaño 5 y tamaño 10, vemos que efectivamente la desviación estándar de las estimaciones es menor al incrementar el tamaño de la muestra, pero en ambos casos en promedio las muestras se acercaron al verdadero valor del parámetro del 0.20.

R

cfr %>%
  group_by(size) %>%
  summarise(
    media = mean(cfr),
    sd = sd(cfr),
    mediana = median(cfr),
    P25 = quantile(cfr, 0.25),
    P75 = quantile(cfr, 0.75)
  )

SALIDA

# A tibble: 2 × 6
  size  media    sd mediana   P25   P75
  <fct> <dbl> <dbl>   <dbl> <dbl> <dbl>
1 5     0.208 0.180     0.2   0     0.4
2 10    0.197 0.116     0.2   0.1   0.3

Pero, si en la vida real solo podemos tomar una muestra aleatoria, esto significa que solo vamos a tener una única oportunidad de calcular un estadístico que será el estimador puntual del parámetro. No obstante, ese único valor no va a poder proveer información sobre la variabilidad inmersa en la selección aleatoria de la muestra. Adicionalmente, como vimos en el ejemplo anterior, existe una alta probabilidad de que muchas de las posibles configuraciones de las muestras den estimaciones que se encuentren alejadas del verdadero valor del parámetro. Por lo tanto, debemos intentar involucrar la variabilidad muestral en el proceso de estimación.

Estimación por intervalos de confianza

El objetivo de la estimación por intervalos de confianza es proveer un rango de valores, un límite inferior y superior (a; b), que con una elevada probabilidad “confianza” contenga el verdadero valor del parámetro que se desea estimar. Aunque con cada muestra aleatoria que pueda ser seleccionada se obtendrían límites diferentes, este procedimiento garantiza que un $(1-α) \%$ determinado de los intervalos construidos, contendrán el verdadero valor del parámetro. Lo anterior, también implica que un $α\%$ de los intervalos no contendrán el verdadero valor. El símbolo α es conocido como nivel de significancia.

De manera general un intervalo de confianza se construye con los siguientes ingredientes:

$\text{Estimador} ±(\text{coeficiente de confiabilidad})*(\text{error estándar})$

Desafío

Ejemplo

En el paquete CFR de la iniciativa Epiverse-TRACE se encuentra disponible la información de un brote de ébola que sucedió en 1976 en Zaire, ahora llamada República del Congo, documentando el número de casos y muertes durante 73 días. Finalmente, se reportaron 245 casos de ébola y de estos 234 fueron casos fatales. Si el interés es realizar una estimación por intervalo de la CFR al 95%. ¿Cuál debería ser el procedimiento a realizar?

● Paso 1-Estimador: se debe iniciar por encontrar la estimación en la muestra observada:

$\hat{p} = \widehat{\text{CFR}} = \frac{234}{245}= 0.955$

Por lo que la CFR estimada fue del 95.5%

● Paso 2-Coeficiente de confiabilidad basado en la distribución normal para un 95% de confianza correspondería a 1.96

● Paso 3-Error estándar:

$\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}=\sqrt{\frac{0.955 (1-0.955)}{245}}$

● Paso 4-Juntar los ingredientes

Como hasta ahora se han dado cuenta este paso a paso puede llegar a ser engorroso por los cálculos, pero en R podemos obtener todo de una manera más rápida y eficaz de la siguiente manera:

${\left[p ̂±z_{\frac{α}{2}} \sqrt{\frac{p ̂(1-p ̂)}{n}}\right]}={\left[0.955±1,96\sqrt{\frac{0.955 (1-0.955)}{245}}\right]}$

Como hasta ahora se han dado cuenta este paso a paso puede llegar a ser engorroso por los cálculos, pero en R podemos obtener todo de una manera más rápida y eficaz de la siguiente manera:

R

#Cargue librería cfr
library(cfr)
# Cargue los datos de Ebola 1976 
utils::data(ebola1976)
ebola1976%>%  dplyr::summarise(
    n=sum(cases), #Total de casos
    muertes = sum(deaths), #Total de muertes
    cfr_est = muertes/n, # Estimación 
    error = sqrt((cfr_est*(1-cfr_est))/n),
    lim_inf = cfr_est -1.96*error, #Limite inferior del IC
    lim_sup = cfr_est +1.96*error #Limite superior del IC
)

SALIDA

    n muertes  cfr_est      error   lim_inf   lim_sup
1 245     234 0.955102 0.01322986 0.9291715 0.9810326

Finalmente, podemos concluir que con una confianza del 95%, la CFR de ébola en la epidemia de 1976 en la República Democrática del Congo se encuentra contenida en el intervalo entre 92.9% y 98.1%.

El paquete CFR también tiene una función incorporada para estimar automáticamente con su respectivo intervalo al 95% la CFR durante una epidemia por medio de la función:

R

cfr::cfr_static(data = ebola1976)

SALIDA

  severity_estimate severity_low severity_high
1          0.955102    0.9210866     0.9773771

Cómo pueden observar existen ligeras diferencias entre el IC construido paso a paso y el reportado por la función cfr_static. Esto se debe a que el paquete CFR realiza la construcción del IC por el método basado en máxima verosimilitud y diferentes distribuciones estadísticas según el número total de casos, pero la interpretación no cambia.

Puntos Clave

Al final de la sesión revise si alcanzo los objetivos:

Comprender el rol de la estadística en el estudio de las enfermedades infecciosas.
Comprender las medidas estadísticas para resumir y analizar la información.
Familiarizarse con el concepto de variable aleatoria y reconocer las principales distribuciones de probabilidad.
Identificar y comprender el proceso del problema estadístico como un problema de inferencia desde una muestra.
Comprender el concepto de intervalo de confianza y el procedimiento de las pruebas de hipótesis.

Contribuciones

Erika Cantor: Versión inicial
Zulma M. Cucunuba: Edición
Laura Gómez-Bermeo: Edición
Andree Valle-Campo: Ediciones menores
José M. Velasco-España: Ediciones menores