Spatiotemporal analyses with epiCo

epiCo’s spatiotemporal module is a tool to analyze the spatial correlation of cases based on their coordinates of notification and the real travel times within Colombian territory.

The spatiotemporal module allows users to:

• Define the neighbors of a municipality based on a travel time threshold that accounts for real connectivity and infrastructure in Colombia.
• Perform a Moran’s Index autocorrelation analysis on the defined neighborhood and the provided incidence data (internally converted to incidence rate).
• Plot a map with the High (spatial correlation) - High (incidence rate) clusters, as well as Low (spatial correlation) - Low (incidence rate) clusters.

In the following vignette, you will learn:

1. How real travel times were estimated from Colombian connectivity and infrastructure.
2. To obtain the neighbors of a municipality from real travel times using the neighborhoods function.
3. To use epiCo’s morans_index function.
4. How to interpret and communicate the results.

1. Real travel times among Colombian municipalities

Several approaches to estimating the proximity and neighborhood of a point (or region) are developed in the literature. Some rely on euclidean distances among the centroids of the areas, whereas others rely on contiguity approaches between their boundaries.

epiCo aims to propose a new approach to neighborhood estimation by defining the proximity among municipalities based on the real available infrastructure in the territory. This is important in countries like Colombia, where topology shapes the connectivity and interaction between municipalities and where Euclidean distances and boundaries may lead to an overestimation of nearness when in reality one of the three mountain ranges or one of the several rivers in the country may lead to large travel distances and times.

To estimate real travel times among Colombian municipalities, a travel times matrix was calculated based on the Bravo-Vega C., Santos-Vega M., & Cordovez J.M. (2022) study. The travel times account for the fastest path to connect one municipality to all municipalities in a friction map that provides different speeds according to the presence and quality of the roads, fluvial transport, or walking possibilities.

2. Defining a neighborhood with epiCo

Since epiCo stores all travel times among municipalities in Colombia, the definition of a neighborhood has to be based on the expertise and knowledge of the user regarding the maximum travel time for which a municipality is considered a neighbor.

The neighborhoods function receives as parameters a vector of DIVIPOLA codes accounting for the municipalities to consider as potential neighbors and a threshold that accounts for the maximum travel time (in hours) that a municipality can be from another.

library(epiCo)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(incidence)
data(divipola_table)
cundinamarca_data <- dplyr::filter(
  divipola_table,
  NOM_DPTO == "CUNDINAMARCA"
) %>%
  select(COD_MPIO, LATITUD, LONGITUD)

cundinamarca_neighborhood <- neighborhoods(
  query_vector = cundinamarca_data$COD_MPIO,
  threshold = 0.5
)$neighbours
#> Warning in spdep::mat2listw(distance, style = "W", zero.policy = TRUE):
#> neighbour object has 5 sub-graphs
#> Municipalities 25572, 25653, 25885 are not part of the neighborhood according to the selected threshold in hours. It wil be displayed as 'Not significant' but it was not included in the local moran's index analysis.

plot(cundinamarca_neighborhood, cbind(
  cundinamarca_data$LATITUD,
  cundinamarca_data$LONGITUD
))

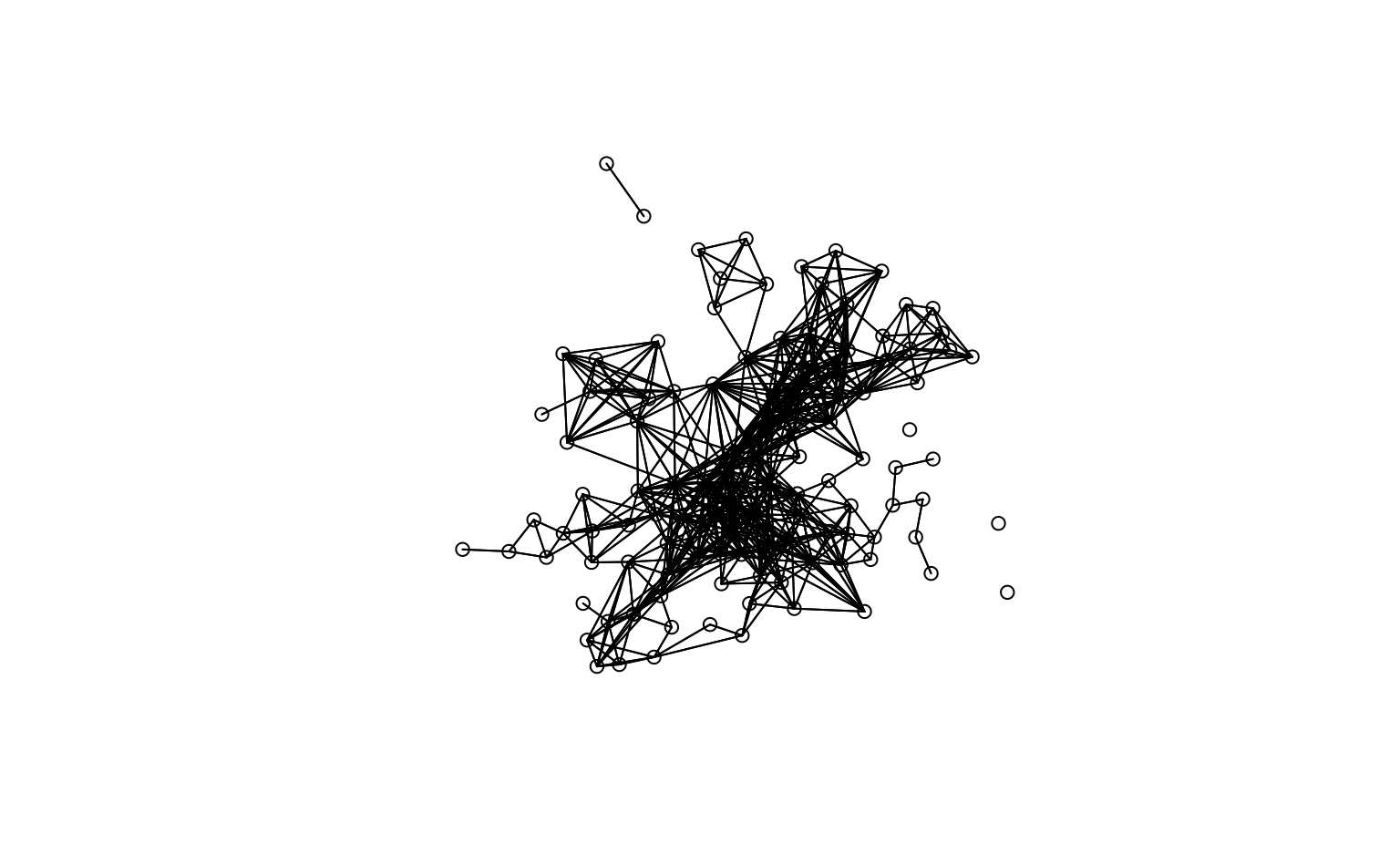
Neighbor municipalities of Cundinamarca with a 0.5-hour threshold.

3. epiCo’s morans_index function

epiCo provides a function to perform a Local Moran’s index analysis from an incidence object with unique observations for a set of Colombian municipalities.

Internally, the function reads the incidence object’s groups as the DIVIPOLA codes to:

1. Estimate incidence rates using epiCo’s incidence_rate function.
2. Evaluate them on the epiCo’s neighborhoods function.

It is necessary for the user to provide the travel time threshold for the neighborhood definition.

The following example uses the cases of the municipalities of Tolima for the year 2019.

data("epi_data")

data_tolima <- epi_data[lubridate::year(epi_data$fec_not) == 2019, ]
incidence_object <- incidence(
  dates = data_tolima$fec_not,
  groups = data_tolima$cod_mun_o,
  interval = "12 months"
)

morans_tolima <- morans_index(
  incidence_object = incidence_object
)
#> Significant municipalities are:
#> 73024 with Low-High (incidence - spatial correlation)
#> 73226 with High-High (incidence - spatial correlation)
#> 73555 with High-High (incidence - spatial correlation)
#> 73675 with High-High (incidence - spatial correlation)
morans_tolima$plot

Local Moran’s index clusters for the incidence of Tolima municipalities in 2019.

4. Interpretation and communication of epiCo’s morans_index results

High-high clusters represent areas with high incidence rate surrounded by other areas with high incidence rates, suggesting a spatial cluster of elevated risk (e.g., a disease hotspot).

Similarly, low-low clusters indicate areas with low incidence rates surrounded by other low incidence rates areas.

High-low or low-high clusters represent areas with dissimilar values neighboring each other and may not lead to significant conclusions regarding spatial behavior of the disease.

Nevertheless, is important to recall that a cluster map (as the one created by the epiCo’s morans_index function) is a complementary tool to understand the spatiotemporal behavior of a disease, but is limited to provide explicit information regarding (for example) allocation of resources. Comparisons with other methodologies and with epidemiology experience should be done to address epidemic responses.

In addition, risk communication should share simple and interpretable results. If public opinion may be misleaded or confused by the clusters analysis, simpler visualization of disease behavior as heatmaps should be used.