Epidemic Risk

New to the {superspreading} package?

See the Get started vignette for an introduction to the concepts discussed below and some of the functions included in the R package.

During the early stages of an infectious disease outbreak information on transmission clusters and heterogeneity in individual-level transmission can provide insight into the occurrence of superspreading events and from this the probability an outbreak will cause an epidemic. This has implications for policy decisions on how to bring disease transmission under control (e.g. $R$ < 1) and increase the probability that an outbreak goes extinct.

A recent example of where individual-level transmission and superspreading were analysed to understand disease transmission was by the Scientific Advisory Group for Emergencies (SAGE) for the UK’s COVID-19 response.

This vignette explores the applications of the functions included in the {superspreading} package and their visualisation in understanding and informing decision-makers for a variety of outbreak scenarios.

library(superspreading)
library(ggplot2)
library(ggtext)

Early in the COVID-19 epidemic, a number of studies including Kucharski et al. (2020) investigated whether data on SARS-CoV-2 incidence had evidence of superspreading events. These events are often estimated as some measure of overdispersion. This was in light of evidence that other coronavirus outbreaks (Severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS)) had superspreading events. The detection of variability in individual-transmission is important in understanding or predicting the likelihood of transmission establishing when imported into a new location (e.g. country).

First we set up the parameters to use for calculating the probability of an epidemic. In this case we are varying the heterogeneity of transmission (k) and number of initial infections (num_init_infect).

epidemic_params <- expand.grid(
  R = 2.35,
  R_lw = 1.5,
  R_up = 3.2,
  k = seq(0, 1, 0.1),
  num_init_infect = seq(0, 10, 1)
)

Then we calculate the probability of an epidemic for each parameter combination. The results are combined with the the parameters.

# results are transposed to pivot to long rather than wide data
prob_epidemic <- t(apply(epidemic_params, 1, function(x) {
  central <- probability_epidemic(
    R = x[["R"]],
    k = x[["k"]],
    num_init_infect = x[["num_init_infect"]]
  )
  lower <- probability_epidemic(
    R = x[["R_lw"]],
    k = x[["k"]],
    num_init_infect = x[["num_init_infect"]]
  )
  upper <- probability_epidemic(
    R = x[["R_up"]],
    k = x[["k"]],
    num_init_infect = x[["num_init_infect"]]
  )
  c(prob_epidemic = central, prob_epidemic_lw = lower, prob_epidemic_up = upper)
}))
epidemic_params <- cbind(epidemic_params, prob_epidemic)

To visualise the influence of transmission variation (k) we subset the results to only include those with a single initial infection seeding transmission (num_init_infect = 1).

# subset data for a single initial infection
homogeneity <- subset(epidemic_params, num_init_infect == 1)

# plot probability of epidemic across dispersion
ggplot(data = homogeneity) +
  geom_ribbon(
    mapping = aes(
      x = k,
      ymin = prob_epidemic_lw,
      ymax = prob_epidemic_up
    ),
    fill = "grey70"
  ) +
  geom_line(mapping = aes(x = k, y = prob_epidemic)) +
  geom_vline(
    mapping = aes(xintercept = 0.2),
    linetype = "dashed"
  ) +
  annotate(geom = "text", x = 0.15, y = 0.75, label = "SARS") +
  geom_vline(
    mapping = aes(xintercept = 0.4),
    linetype = "dashed"
  ) +
  annotate(geom = "text", x = 0.45, y = 0.75, label = "MERS") +
  scale_y_continuous(
    name = "Probability of large outbreak",
    limits = c(0, 1)
  ) +
  scale_x_continuous(name = "Extent of homogeneity in transmission") +
  theme_bw()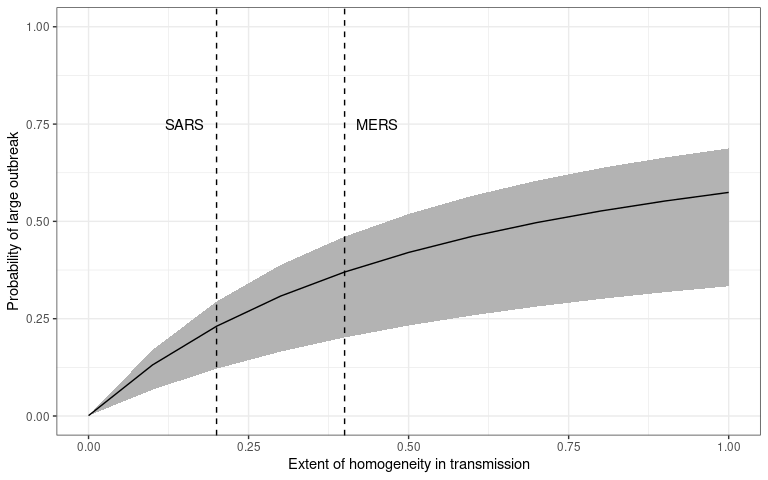

A graph showing the relationship between extent of homogeneity in transmission (x-axis, from 0 to 1) and probability of a large outbreak (y-axis, from 0 to 1). A black curved line shows an increasing relationship, starting near 0 and rising to 0.57, with the curve flattening as homogeneity increases. A grey shaded area around the line indicates confidence intervals, widening toward higher homogeneity values. Two vertical dashed lines mark specific diseases: SARS at 0.2 extent of homogeneity (corresponding to a 0.23 probability of large outbreak), and MERS at 0.4 extent of homogeneity (corresponding to 0.37 probability of large outbreak). The graph illustrates that diseases with more homogeneous transmission patterns have higher probabilities of causing large outbreaks.

The probability that an initial infection (introduction) will cause a sustained outbreak (transmission chain). The dispersion of the individual-level transmission is plotted on the x-axis and probability of outbreak – calculated using probability_epidemic() – is on the y-axis. This plot is reproduced from Kucharski et al. (2020) figure 3A.

The degree of variability in transmission increases as $k$ decreases (Lloyd-Smith et al. 2005). So the probability of a large outbreak is smaller for smaller values of $k$ , for a given value of $R$ , meaning that if COVID-19 is more similar to SARS than MERS it will be less likely to establish and cause an outbreak if introduced into a newly susceptible population.

However, this probability of establishment and continued transmission will also depend on the number of initial introductions to that populations. The more introductions, the higher the chance one will lead to an epidemic.

introductions <- subset(epidemic_params, k == 0.5)

# plot probability of epidemic across introductions
ggplot(data = introductions) +
  geom_pointrange(
    mapping = aes(
      x = num_init_infect,
      y = prob_epidemic,
      ymin = prob_epidemic_lw,
      ymax = prob_epidemic_up
    )
  ) +
  scale_y_continuous(
    name = "Probability of large outbreak",
    limits = c(0, 1)
  ) +
  scale_x_continuous(name = "Number of introductions", n.breaks = 6) +
  theme_bw()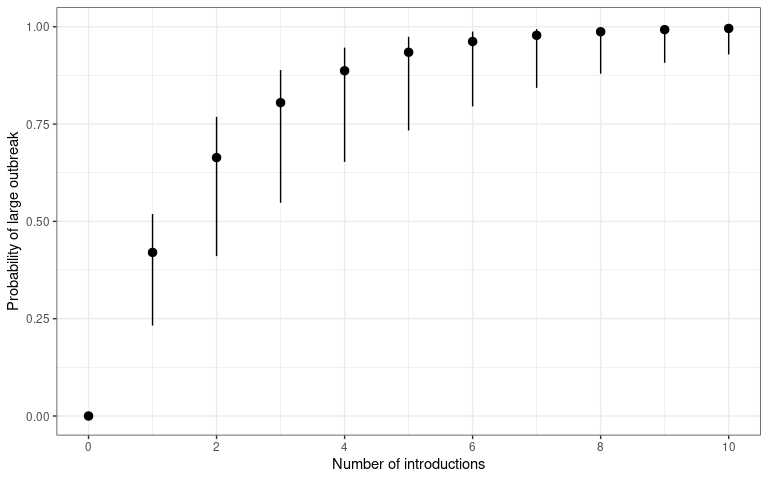

A scatter plot showing the relationship between the number of introductions of an infectious disease (x-axis, ranging from 0 to 10) and the probability of large outbreak (y-axis, ranging from 0 to 1). Each point estimate has vertical error bars showing confidence intervals. The plot shows a clear increasing trend: starting at 0 introductions with 0% probability of large outbreak, rising to 42% at 1 introduction, 66% at 2 introductions, 81% at 3 introductions, 89% at 4 introductions, 93% at 5 introductions, 96% at 6 introductions, and plateauing near 99% for 7-10 introductions. The confidence intervals are widest at intermediate values (1-5 introductions). The pattern demonstrates the more introduction increase the probability of a large outbreak but has minimal impact once the probability approaches 1.

The probability that a number of introduction events will cause a sustained outbreak (transmission chain). The number of disease introductions is plotted on the x-axis and probability of outbreak – calculated using probability_epidemic() – is on the y-axis. This plot is reproduced from Kucharski et al. (2020) figure 3B.

Different levels of heterogeneity in transmission will produce different probabilities of epidemics.

# plot probability of epidemic across introductions for multiple k
ggplot(data = epidemic_params) +
  geom_point(
    mapping = aes(
      x = num_init_infect,
      y = prob_epidemic,
      colour = k
    )
  ) +
  scale_y_continuous(
    name = "Probability of large outbreak",
    limits = c(0, 1)
  ) +
  labs(colour = "Dispersion (*k*)") +
  scale_x_continuous(name = "Number of introductions", n.breaks = 6) +
  scale_colour_continuous(type = "viridis") +
  theme_bw() +
  theme(legend.title = element_markdown())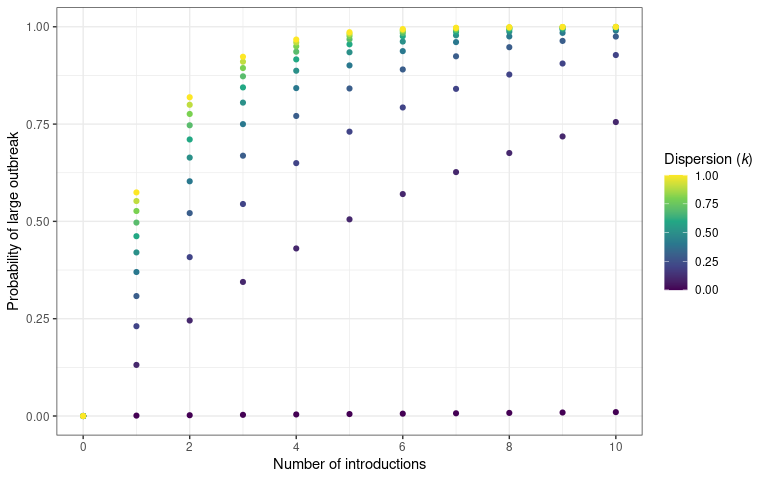

A scatter plot showing the relationship between the number of introductions (x-axis, ranging from 0 to 10) and the probability of a large outbreak (y-axis, ranging from 0 to 1). Points are coloured according to a dispersion parameter (k) ranging from 0 (purple) to 1.00 (yellow), as shown in the legend. The plot demonstrates that higher dispersion values (yellow and green points) consistently show higher probabilities of large outbreaks across all numbers of introductions. For any given number of introductions, there is a clear gradient from low outbreak probability (purple points at bottom) to high outbreak probability (yellow points at top). The relationship shows that both the number of introductions and the dispersion parameter influence outbreak probability, with the steepest increases occurring between 1-4 introductions.

The probability that an a number of introduction events will cause a sustained outbreak (transmission chain). The number of disease introductions is plotted on the x-axis and probability of outbreak – calculated using probability_epidemic() – is on the y-axis. Different values of dispersion are plotted to show the effect of increased transmission variability on an epidemic establishing

In the above plot we drop the uncertainty around each point and assume a known value of $R$ in order to more clearly show the pattern.

These calculations enable us to understand epidemics and applications, such as Shiny apps, to explore this functionality and compare between existing parameter estimates of offspring distributions are also useful. An example application called Probability of a large 2019-nCoV outbreak following introduction of cases, that is no longer maintained, was developed by the Centre for Mathematical Modelling of Infectious diseases at the London School of Hygiene and Tropical Medicine, for comparing SARS-like and MERS-like scenarios, as well as random mixing during the COVID-19 pandemic.

Conversely to the probability of an epidemic, the probability that an outbreak will go extinct (i.e. transmission will subside), can also be plotted for different values of $R$ .

extinction_params <- expand.grid(
  R = seq(0, 5, 0.1),
  k = c(0.01, 0.1, 0.5, 1, 4, Inf),
  num_init_infect = 1
)
# results are transposed to pivot to long rather than wide data
prob_extinct <- apply(extinction_params, 1, function(x) {
  central <- probability_extinct(
    R = x[["R"]],
    k = x[["k"]],
    num_init_infect = x[["num_init_infect"]]
  )
  central
})
extinction_params <- cbind(extinction_params, prob_extinct)

# plot probability of extinction across R for multiple k
ggplot(data = extinction_params) +
  geom_point(
    mapping = aes(
      x = R,
      y = prob_extinct,
      colour = factor(k)
    )
  ) +
  scale_y_continuous(
    name = "Probability of extinction",
    limits = c(0, 1)
  ) +
  labs(colour = "Dispersion (*k*)") +
  scale_x_continuous(
    name = "Reproductive number (*R*)",
    n.breaks = 6
  ) +
  scale_colour_viridis_d() +
  theme_bw() +
  theme(
    axis.title.x = element_markdown(),
    legend.title = element_markdown()
  )

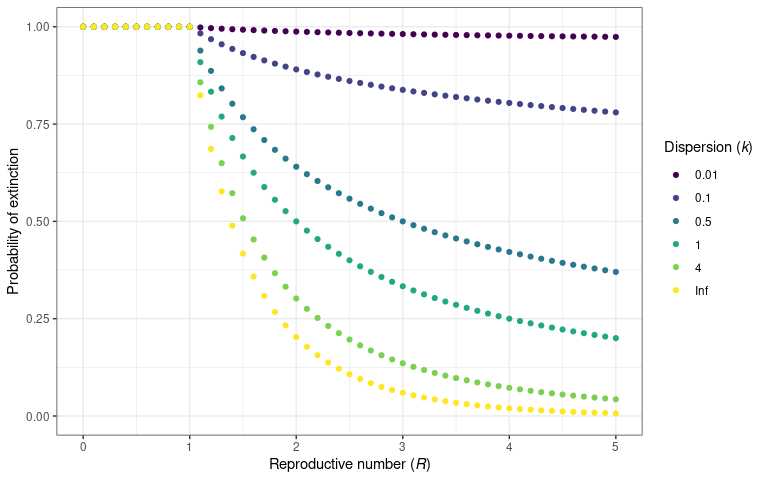
A scatter plot showing the relationship between the reproduction number (R) (x-axis, ranging from 0 to 5) and the probability of extinction (y-axis, ranging from 0 to 1). Points are discretely coloured according to a dispersion parameter (k) ranging from 0.01 (purple) to infinite (yellow), with intermediate values of 0.1, 0.5, 1 and 4, as shown in the legend. The plot demonstrates that higher dispersion values (yellow and green points) consistently show lower probabilities of extinction across all reproduction numbers greater than 1. All points for reproduction numbers below 1 have a probability of extinction at 1. The probability of extinction declines sharply in an exponential-like fashion for higher dispersion values, whereas smaller values of dispersion have a more gradual decline with higher reproduction numbers.

The probability that an infectious disease will go extinct for a given value of $R$ and $k$ . This is calculated using probability_extinct() function. This plot is reproduced from Lloyd-Smith et al. (2005) figure 2B.

Superspreading in decision making

One of the first tasks in an outbreak is to establish whether estimates of individual-level transmission variability have been reported, either for this outbreak or a previous outbreak of the same pathogen. Alternatively, if it is an outbreak of a novel pathogen, parameters for similar pathogens can be searched for.

This is accomplished by another Epiverse-TRACE R package: {epiparameter}. This package contains a library of epidemiological parameters included offspring distribution parameter estimates and uncertainty obtained from published literature. This aids the collation and establishes a baseline understanding of transmission. Similar to the collation of transmission clusters for COVID-19.

Equipped with these parameter estimates, metrics that provide an intuitive understanding of transmission patterns can be tabulated. For example the proportion of transmission events in a given cluster size can be calculated using the {superspreading} function proportion_cluster_size().

This calculates the proportion of new cases that originate within a transmission cluster of a given size. In other words, what proportion of all transmission events were part of secondary case clusters (i.e. from the same primary case) of at least, for example, five cases. This calculation is useful to inform backwards contact tracing efforts.

In this example we look at clusters of at least 5, 10 and 25 secondary cases, at different numbers of initial infections and for two reproduction numbers to see how this affects cluster sizes.

# For R = 0.8
proportion_cluster_size(
  R = 0.8,
  k = seq(0.1, 1, 0.1),
  cluster_size = c(5, 10, 25)
)
#>      R   k prop_5 prop_10 prop_25
#> 1  0.8 0.1  66.8%   38.7%   7.36%
#> 2  0.8 0.2  48.6%     18%  0.786%
#> 3  0.8 0.3  37.7%   9.37%  0.197%
#> 4  0.8 0.4  30.3%   5.24% 0.0324%
#> 5  0.8 0.5  24.5%   3.07%      0%
#> 6  0.8 0.6  21.2%   1.68%      0%
#> 7  0.8 0.7  18.2%   1.11%      0%
#> 8  0.8 0.8    16%  0.925%      0%
#> 9  0.8 0.9  14.5%    0.6%      0%
#> 10 0.8 1.0  12.7%  0.445%      0%

# For R = 3
proportion_cluster_size(
  R = 3,
  k = seq(0.1, 1, 0.1),
  cluster_size = c(5, 10, 25)
)
#>    R   k prop_5 prop_10 prop_25
#> 1  3 0.1  90.3%   78.4%   50.5%
#> 2  3 0.2  84.1%   64.8%   27.1%
#> 3  3 0.3  79.5%   55.2%   15.8%
#> 4  3 0.4  75.9%   47.6%   9.35%
#> 5  3 0.5  73.1%   42.1%   6.09%
#> 6  3 0.6  70.5%   36.8%   3.57%
#> 7  3 0.7  68.2%   32.7%   2.04%
#> 8  3 0.8  66.3%   29.6%   1.63%
#> 9  3 0.9  64.7%   26.7%   0.95%
#> 10 3 1.0  63.1%   23.9%  0.695%

These results show that as the level of heterogeneity in individual-level transmission increases, a larger percentage of cases come from larger cluster sizes, and that large clusters can be produced when $R$ is higher even with low levels of transmission variation.

It indicates whether preventing gatherings of a certain size can reduce the epidemic by preventing potential superspreading events.

When data on the settings of transmission is known, priority can be given to restricting particular types of gatherings to most effectively bring down the reproduction number.

Controls on transmission

In their work on identifying the prevalence of overdispersion in individual-level transmission, Lloyd-Smith et al. (2005) also showed the effect of control measures on the probability of containment. They defined containment as the size of a transmission chain not reaching 100 cases. They assumed the implementation of control measures at the individual or population level. {superspreading} provides probability_contain() to calculate the probability that an outbreak will go extinct before reaching a threshold size.

contain_params <- expand.grid(
  R = 3, k = c(0.1, 0.5, 1, Inf), num_init_infect = 1, control = seq(0, 1, 0.05)
)
prob_contain <- apply(contain_params, 1, function(x) {
  probability_contain(
    R = x[["R"]],
    k = x[["k"]],
    num_init_infect = x[["num_init_infect"]],
    pop_control = x[["control"]]
  )
})
contain_params <- cbind(contain_params, prob_contain)

# plot probability of epidemic across introductions for multiple k
ggplot(data = contain_params) +
  geom_point(
    mapping = aes(
      x = control,
      y = prob_contain,
      colour = factor(k)
    )
  ) +
  scale_y_continuous(
    name = "Probability of containment",
    limits = c(0, 1)
  ) +
  scale_x_continuous(name = "Control measures (*c*)", n.breaks = 6) +
  labs(colour = "Dispersion (*k*)") +
  scale_colour_viridis_d() +
  theme_bw() +
  theme(
    axis.title.x = element_markdown(),
    legend.title = element_markdown()
  )

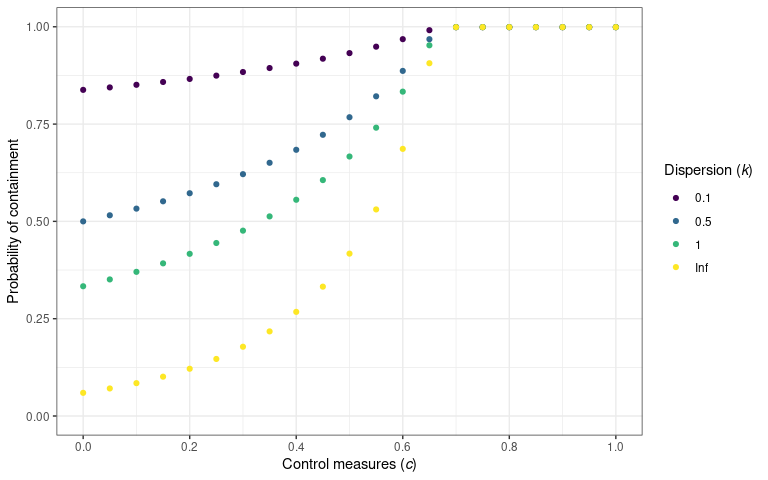
A scatter plot showing the relationship between the strength of outbreak control measures (c) (x-axis, ranging from 0 to 1) and the probability of containment (y-axis, ranging from 0 to 1). Points are discretely coloured according to a dispersion parameter (k) ranging from 0.1 (purple) to infinite (yellow), with intermediate values of 0.5 and 1, as shown in the legend. The plot demonstrates that the probability of outbreak containment increases with greater control measures, with lower dispersion values having a higher probability of containment than higher dispersion values for each control measure value. Once control measures reach 0.7 all dispersion values converge to a probability of containment of 1.

The probability that an outbreak will be contained (i.e. not exceed 100 cases) for a variety of population-level control measures. The probability of containment is calculated using probability_contain(). This plot is reproduced from Lloyd-Smith et al. (2005) figure 3C.

References

Kucharski, Adam J, Timothy W Russell, Charlie Diamond, Yang Liu, John Edmunds, Sebastian Funk, Rosalind M Eggo, et al. 2020. “Early Dynamics of Transmission and Control of COVID-19: A Mathematical Modelling Study.” The Lancet Infectious Diseases 20 (5): 553–58. https://doi.org/10.1016/S1473-3099(20)30144-4.

Lloyd-Smith, J. O., S. J. Schreiber, P. E. Kopp, and W. M. Getz. 2005. “Superspreading and the Effect of Individual Variation on Disease Emergence.” Nature 438 (7066): 355–59. https://doi.org/10.1038/nature04153.

Superspreading on policy, decision making and control measures

Superspreading in decision making

Controls on transmission

References