Methods for calculating the proportion of transmission • superspreading

This vignette explores the proportion_transmission() function in {superspreading}. The function calculates what proportion of cases we would expect to cause a certain proportion of transmission for a particular infectious disease (e.g. “how much transmission comes from the top 10% of infectious individuals?”)

To perform this calculation, we assume that the offspring distribution of disease transmission depends both on the distribution of individual variability in transmissibility, which we define using a Gamma distribution with mean $R$ , as well as stochastic transmission within a population, which we define using a Poisson process, following Lloyd-Smith et al. (2005).

If we put a Gamma distributed individual transmissibility into a Poisson distribution, the result a negative binomial distribution. This is defined by two parameters: $R$ , the mean of the negative binomial distribution and the average number of secondary cases caused by a typical primary case; and $k$ , the dispersion parameter of the negative binomial distribution and controls the heterogeneity in transmission. A smaller $k$ results is more variability (overdispersion) in transmission and thus superspreading events are more likely.

Poisson and geometric offspring distributions are special cases of the negative binomial offspring distribution. By setting $k$ to Inf (or approximately infinite, $> 10^5$ ) then the offspring distribution is a Poisson distribution. By setting $k$ to 1 the offspring distribution is a geometric distribution.

It is currently not possible to calculate the proportion transmission using the Poisson-Lognormal and Poisson-Weibull distributions (whose density and cumulative distribution functions are included in the {superspreading} package).

The proportion of transmission can be calculated using two methods, both of which are included in the proportion_transmission() function and can be changed using the method argument. The first method focuses on transmission as it occurs in reality, accounting both for variation in the mean number of secondary cases at the individual and the stochastic nature of onwards transmission within a population; the second method focuses only on variation in the mean number of secondary cases at the individual level. The first method is denoted $p_{80}$ and the second $t_{20}$ . The $p_{80}$ method is the default (method = "p_80").

The output of method = "p_80" and method = "t_20" have different interpretations and cannot be used interchangeably without understanding the differences in what they are measuring.

The output of method = "p_80" gives the proportion of cases that generate a certain proportion of realised transmission. The most common use case is calculating what proportion of cases would cause 80% of transmission during an outbreak of the infection. Thus a small proportion in the output <data.frame> means that there is a lot of overdispersion in individual-level transmission. The percent_transmission argument when method = "p_80" is to set the proportion of transmission.

The output of method = "t_20" gives the proportion of cases that we would expected to produced by a certain proportion of the most infectious individuals. This is commonly used to calculate what proportion of cases are expected to be caused by the most infectious 20% of individuals. A high proportion in the output <data.frame> means that there is a lot of overdispersion in the transmission. The percent_transmission argument when method = "t_20" is to set the proportion of most infectious cases to calculate their proportion of total transmission.

The key difference is that in a realised large outbreak (i.e. one that includes stochastic transmission), it is highly likely that some individuals will generate no secondary cases. This is because even a non-zero expected number of secondary cases can produce a zero when drawn from a Poisson process.

Definitions

The formula for the $p_{80}$ method as stated in Endo et al. (2020) is:

$1 - p_{80} = \int^{X}_{0} \text{NB} ( \lfloor x \rfloor; k, \left( \frac{k}{(R_0) + k} \right) dx$ where $X$ satisfies

$1 - 0.8 = \frac{1}{R_0} \int^{X}_{0} \lfloor x \rfloor \text{NB} \left( \lfloor x \rfloor; k, \frac{k}{R_0 + k} \right) dx$ Additionally, Endo et al. (2020) showed that:

$\frac{1}{R_0} \int^{X}_{0} \lfloor x \rfloor \text{NB} \left( \lfloor x \rfloor; k, \frac{k}{R_0 + k} \right) dx = \int^{X-1}_{0} \text{NB} \left( \lfloor x \rfloor; k + 1, \frac{k}{R_0 + k} \right)$

The $t_{20}$ method calculates, as stated by Lloyd-Smith et al. (2005): “the expected proportion of transmission due to the most infectious 20% of cases, $t_{20}$ ”, given by $t_{20} = 1 - F_{trans}(x_{20})$ , where $F_{trans}$ is defined as:

$F_{trans}(x) = \frac{1}{R_0} \int^{x}_{0} u f_v (u) du$

$f_\nu(x)$ is the probability density function (pdf) of the gamma distribution of the individual reproduction number $\nu$ .

For both methods the proportion of transmission can be modified using the percent_transmission argument in proportion_transmission() so they are not fixed at 80 and 20, respectively, for $p_{80}$ and $t_{20}$ .

There are two methods for calculating the $p_{80}$ method, analytically as given by Endo et al. (2020), or numerically by sampling from a negative binomial distribution (proportion_transmission(..., simulate = TRUE). For the purpose of this vignette to compare all of the methods we will term the analytical calculation $p_{80}$ , and the numerical calculation $p_{80}^{sim}$ .

Now that the $p_{80}$ and $t_{20}$ methods have been defined we’ll explore the functionality of each, their characteristics and compare them, making note of any unexpected behaviour to watch out for.

First we load the {superspreading}, {ggplot2}, {purrr} and {dplyr} R packages.

library(superspreading)
library(ggplot2)
library(purrr)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union

Exploring each method

To show the proportion of transmission using both methods we can load the estimates of $R$ and $k$ estimated from Lloyd-Smith et al. (2005), which are stored in the library of epidemiological parameters in the {epiparameter} R package, and the interoperability of {epiparameter} and {superspreading} to directly supply the parameters for the offspring distributions (<epiparameter> objects) to the offspring_dist argument in proportion_transmission().

library(epiparameter)
offspring_dists <- epiparameter_db(
  epi_name = "offspring distribution"
)
#> Returning 10 results that match the criteria (10 are parameterised). 
#> Use subset to filter by entry variables or single_epiparameter to return a single entry. 
#> To retrieve the citation for each use the 'get_citation' function

Here we create a table with the estimates of the mean ( $R$ ) and dispersion ( $k$ ) for each disease from Lloyd-Smith et al. (2005).

diseases <- vapply(offspring_dists, `[[`, FUN.VALUE = character(1), "disease")
offspring_dists <- offspring_dists[!duplicated(diseases)]
diseases <- diseases[!duplicated(diseases)]

offspring_dist_params <- vapply(
  offspring_dists, get_parameters, FUN.VALUE = numeric(2)
)

offspring_dist_params <- data.frame(
  disease = diseases,
  t(offspring_dist_params)
)
offspring_dist_params
#>                         disease mean dispersion
#> 1                          SARS 1.63       0.16
#> 2                      Smallpox 3.19       0.37
#> 3                          Mpox 0.32       0.58
#> 4              Pneumonic Plague 1.32       1.37
#> 5 Hantavirus Pulmonary Syndrome 0.70       1.66
#> 6           Ebola Virus Disease 1.50       5.10

Using these parameter estimates for the negative binomial offspring distribution of each disease we can append the calculated proportion of transmission caused by the most infectious 20% of cases, using the $t_{20}$ method, and the calculated proportion of transmission causing 80% of onward transmission, using the $p_{80}$ method.

offspring_dist_params$t20 <- do.call(
  rbind,
  apply(
    offspring_dist_params,
    MARGIN = 1,
    function(x) {
      proportion_transmission(
        R = as.numeric(x[2]), k = as.numeric(x[3]), percent_transmission = 0.2,
        method = "t_20", format_prop = FALSE
      )
    }
  )
)[, 3]

offspring_dist_params$p80 <- do.call(
  rbind,
  apply(
    offspring_dist_params,
    MARGIN = 1,
    function(x) {
      proportion_transmission(
        R = as.numeric(x[2]), k = as.numeric(x[3]), percent_transmission = 0.8,
        method = "p_80", format_prop = FALSE
      )
    }
  )
)[, 3]
offspring_dist_params
#>                         disease mean dispersion       t20       p80
#> 1                          SARS 1.63       0.16 0.8825175 0.1300095
#> 2                      Smallpox 3.19       0.37 0.7125723 0.2405781
#> 3                          Mpox 0.32       0.58 0.6201376 0.1609538
#> 4              Pneumonic Plague 1.32       1.37 0.4737949 0.3392229
#> 5 Hantavirus Pulmonary Syndrome 0.70       1.66 0.4476538 0.3023708
#> 6           Ebola Virus Disease 1.50       5.10 0.3363023 0.4315065

It can be seen in the table above that when an offspring distribution has a smaller dispersion ( $k$ ) parameter the proportion of cases produced by the most infectious 20% of cases is high, and the proportion of cases that produce 80% of transmission is low. The estimates for SARS demonstrate this point. Both metrics lead to the same conclusion that disease transmission dynamics for the 2003 SARS outbreak in Singapore are heterogeneous and superspreading is a important aspect of the outbreak.

The variability in individual-level transmission comes from modelling the individual reproduction number, $\nu$ as a gamma distribution, instead of assuming that the individual-level reproduction number is equal for all individuals, which would result in a Poisson offspring distribution (see Lloyd-Smith et al. (2005) Supplementary Material for more information). To visualise the inherent variability resulting from the gamma-distributed reproduction number and how that compares to the assumption of a homogeneous population we can plot the expected proportion of transmission against the proportion of infectious cases.

For this we will need to write a couple of custom functions.

# nolint start for `:::`
get_infectious_curve <- function(R, k) {
  # upper limit of x when y = 0
  upper_u <- superspreading:::solve_for_u(prop = 0, R = R, k = k)
  upper_u <- round(upper_u)
  u_seq <- superspreading:::lseq(from = 1e-5, to = upper_u, length.out = 500)
  res <- lapply(u_seq, function(upper) {
    integrate(
      function(u) u * superspreading:::fvx(x = u, R, k),
      lower = 0, upper = upper
    )$value / R
  })
  expected_v_more_than_x <- 1 - unlist(res)
  proportion_more_than_x <- 1 - superspreading:::pgammaRk(u_seq, R = R, k = k)
  data.frame(
    exp_t = expected_v_more_than_x,
    prop_i = proportion_more_than_x
  )
}
# nolint end

We can now reproduce Figure 1b in Lloyd-Smith et al. (2005) using the offspring distribution parameters obtained above.

infect_curve <- map(offspring_dist_params %>%
      group_split(disease), function(x) {
        get_infectious_curve(R = x$mean, k = x$dispersion) %>%
          mutate(
            disease = x$disease,
            R = x$mean, k = x$dispersion
          )
      })

infect_curve <- do.call(rbind, infect_curve)

ggplot(
  data = infect_curve,
  aes(x = prop_i, y = exp_t, colour = disease)
) +
  geom_line() +
  geom_abline(slope = 1) +
  geom_vline(xintercept = 0.2, linetype = 2, alpha = 0.2) +
  scale_x_continuous(breaks = seq(0, 1, by = 0.2)) +
  theme_classic() +
  theme(
    aspect.ratio = 1,
    legend.position = "right"
  ) +
  annotate(
    geom = "text",
    angle = 45,
    size = 2.5,
    x = 0.5,
    y = 0.5,
    vjust = 1.5,
    label = "Homogeneous population"
  ) +
  labs(
    x = "Proportion of infectious cases (ranked)",
    y = "Expected proportion of transmission",
    colour = ""
  ) +
  coord_cartesian(expand = FALSE)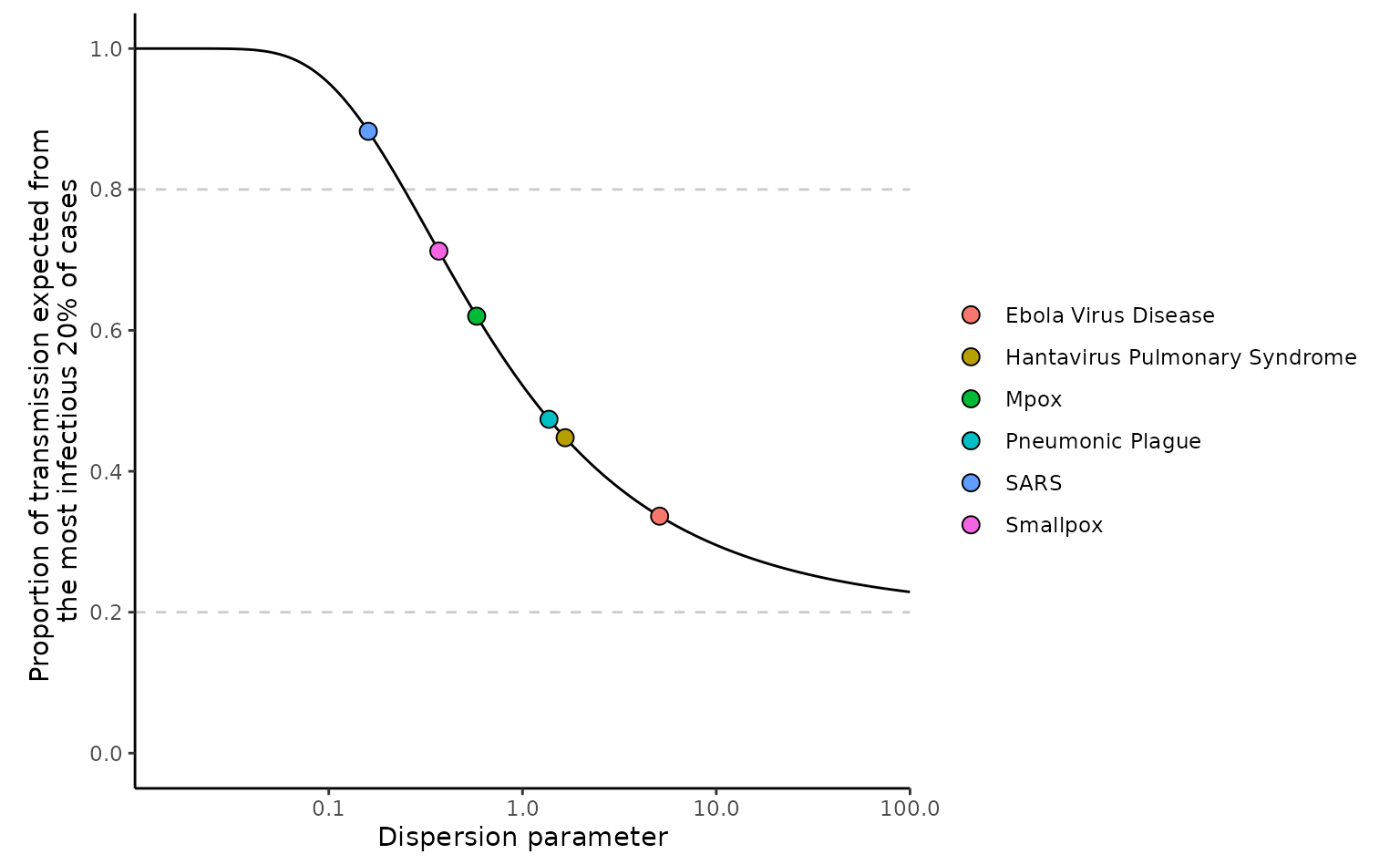

This plot shows the variability in transmission owing to the gamma-distributed individual reproduction number ( $\nu$ ). If we take a slice through the above plot when the proportion of infectious cases equals 0.2 (shown by the dashed line) we can calculate the proportion of transmission caused by the most infectious 20% of cases using the proportion_tranmission(..., method = "t_20") function.

k_seq <- superspreading:::lseq(from = 0.01, to = 100, length.out = 1000) # nolint
y <- map_dbl(
  k_seq,
  function(x) {
    proportion_transmission(
      R = 2, k = x, percent_transmission = 0.2,
      method = "t_20", format_prop = FALSE
    )[, 3]
  }
)
prop_t20 <- data.frame(k_seq, y)

ggplot() +
  geom_line(data = prop_t20, mapping = aes(x = k_seq, y = y)) +
  geom_point(
  data = offspring_dist_params,
    mapping = aes(
      x = dispersion,
      y = t20,
      fill = disease
    ),
    shape = 21,
    size = 3
  ) +
  geom_hline(yintercept = c(0.2, 0.8), linetype = 2, alpha = 0.2) +
  theme_classic() +
  theme(
    aspect.ratio = 1
  ) +
  scale_y_continuous(
    name = paste(
      "Proportion of transmission expected from",
      "the most infectious 20% of cases",
      sep = " \n"
    ),
    limits = c(0, 1),
    breaks = seq(0, 1, by = 0.2)
  ) +
  scale_x_log10(name = "Dispersion parameter", expand = c(0, 0)) +
  labs(fill = "")

The above plot replicates Figure 1c from Lloyd-Smith et al. (2005). It shows how different diseases have different proportion of transmission from the most infectious 20% owing to varying degrees of overdispersion ( $k$ ).

The plot uses an $R$ of 2, however, one characteristic of the $t_{20}$ method is that different values of $R$ do not influence the proportion of transmission, so the plot would look identical with other value of $R$ . This is because as shown the equation defining the $t_{20}$ method above the integral is divided by $R_0$ so that only $f_{\nu}(u)$ control the proportion of transmission.

# For k = 0.5
proportion_transmission(
  R = 0.1, k = 0.5, percent_transmission = 0.8, method = "t_20"
)
#>     R   k prop_80
#> 1 0.1 0.5   99.6%
proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.8, method = "t_20"
)
#>   R   k prop_80
#> 1 1 0.5   99.6%
proportion_transmission(
  R = 5, k = 0.5, percent_transmission = 0.8, method = "t_20"
)
#>   R   k prop_80
#> 1 5 0.5   99.6%

# For k = 2
proportion_transmission(
  R = 0.1, k = 2, percent_transmission = 0.8, method = "t_20"
)
#>     R k prop_80
#> 1 0.1 2   94.9%
proportion_transmission(
  R = 1, k = 2, percent_transmission = 0.8, method = "t_20"
)
#>   R k prop_80
#> 1 1 2   94.9%
proportion_transmission(
  R = 5, k = 2, percent_transmission = 0.8, method = "t_20"
)
#>   R k prop_80
#> 1 5 2   94.9%

This is not the case for $p_{80}$ , where changes in both $R$ and $k$ influence the proportion of transmission.

# For k = 0.5
proportion_transmission(
  R = 0.1, k = 0.5, percent_transmission = 0.8, method = "p_80"
)
#>     R   k prop_80
#> 1 0.1 0.5   6.71%
proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.8, method = "p_80"
)
#>   R   k prop_80
#> 1 1 0.5   22.6%
proportion_transmission(
  R = 5, k = 0.5, percent_transmission = 0.8, method = "p_80"
)
#>   R   k prop_80
#> 1 5 0.5   29.3%

# For k = 2
proportion_transmission(
  R = 0.1, k = 2, percent_transmission = 0.8, method = "p_80"
)
#>     R k prop_80
#> 1 0.1 2    7.3%
proportion_transmission(
  R = 1, k = 2, percent_transmission = 0.8, method = "p_80"
)
#>   R k prop_80
#> 1 1 2   35.6%
proportion_transmission(
  R = 5, k = 2, percent_transmission = 0.8, method = "p_80"
)
#>   R k prop_80
#> 1 5 2   48.9%

One thing that was mentioned above is that the interpretation of the $p_{80}$ and $t_{20}$ methods are not interchangeable, additionally, $t_{80}$ and $p_{20}$ are not equal. Stated differently, the $p_{80}$ method to calculate the proportion of transmission that cause 20% of cases, and the $t_{20}$ method to calculate the proportion of transmission caused by the most infectious 80% are not equivalent. It is also the case that $1 - p_{80} \neq t_{20}$ , thus $1 - t_{20} \neq p_{80}$ .

Here we vary $R$ and $k$ and show that by setting the $p_{80}$ method to percent_transmission = 0.2, and the $t_{20}$ method to percent_transmission = 0.8 the two cannot be interchangeably interpreted as outlined in the box above.

# R = 1, k = 0.5
proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.2, method = "p_80"
)
#>   R   k prop_20
#> 1 1 0.5   2.45%
proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.8, method = "t_20"
)
#>   R   k prop_80
#> 1 1 0.5   99.6%

# R = 3, k = 2
proportion_transmission(
  R = 3, k = 2, percent_transmission = 0.2, method = "p_80"
)
#>   R k prop_20
#> 1 3 2   5.86%
proportion_transmission(
  R = 3, k = 2, percent_transmission = 0.8, method = "t_20"
)
#>   R k prop_80
#> 1 3 2   94.9%

Here we show that $1 - p_{80} \neq t_{20}$ and $1 - t_{20} \neq p_{80}$ .

1 - proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.8, method = "p_80",
  format_prop = FALSE
)[, 3]
#> [1] 0.7735753
proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.2, method = "t_20"
)
#>   R   k prop_20
#> 1 1 0.5     65%

1 - proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.2, method = "t_20",
  format_prop = FALSE
)[, 3]
#> [1] 0.3501798
proportion_transmission(
  R = 1, k = 0.5, percent_transmission = 0.8, method = "p_80"
)
#>   R   k prop_80
#> 1 1 0.5   22.6%

The $t_{20}$ method allows for true homogeneity when $k \rightarrow \infty$ ( $t_{20} = 20\%$ ), whereas the $p_{80}$ method does not allow for true homogeneity ( $p_{80} \neq 80\%$ ).

proportion_transmission(
  R = 1, k = Inf, percent_transmission = 0.8, method = "p_80"
)
#> Infinite values of k are being approximated by 1e+05 for calculations.
#>   R     k prop_80
#> 1 1 1e+05   43.2%
proportion_transmission(
  R = 1, k = Inf, percent_transmission = 0.8, method = "t_20"
)
#> Infinite values of k are being approximated by 1e+05 for calculations.
#>   R     k prop_80
#> 1 1 1e+05   80.1%

Endo, Akira, Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group, Sam Abbott, Adam J. Kucharski, and Sebastian Funk. 2020. “Estimating the Overdispersion in COVID-19 Transmission Using Outbreak Sizes Outside China.” Wellcome Open Research 5 (July): 67. https://doi.org/10.12688/wellcomeopenres.15842.3.

Lloyd-Smith, J. O., S. J. Schreiber, P. E. Kopp, and W. M. Getz. 2005. “Superspreading and the Effect of Individual Variation on Disease Emergence.” Nature 438 (7066): 355–59. https://doi.org/10.1038/nature04153.