Matrices de contact

Dernière mise à jour le 2025-10-13 | Modifier cette page

Durée estimée : 50 minutes

Vue d'ensemble

Questions

  • Qu’est-ce qu’une matrice de contact ?
  • Comment les matrices de contact sont-elles estimées ?
  • Comment les matrices de contact sont-elles utilisées dans l’analyse épidémiologique ?

Objectifs

  • Utilisez le package R socialmixr pour estimer une matrice de contact
  • Comprendre les différents types d’analyse pour lesquels les matrices de contact peuvent être utilisées

Introduction

Certains groupes d’individus ont plus de contacts que d’autres ; l’écolier moyen a beaucoup plus de contacts quotidiens que la personne âgée moyenne, par exemple. Cette hétérogénéité des schémas de contact entre les différents groupes peut avoir un impact sur la transmission des maladies, car certains groupes sont plus susceptibles de transmettre la maladie à d’autres membres de ce groupe, ainsi qu’à d’autres groupes. La vitesse à laquelle les individus d’un même groupe et d’un groupe à l’autre entrent en contact avec d’autres personnes peut être résumée dans une matrice de contact. Dans ce tutoriel, nous allons apprendre comment les matrices de contact peuvent être utilisées dans différentes analyses et comment le package socialmixr peut être utilisé pour estimer les matrices de contact.

R 

library(socialmixr)

La matrice de contact

La matrice de contact de base représente la quantité de contacts, ou de mélanges, au sein de différents sous-groupes d’une population et entre ces sous-groupes. Les sous-groupes sont souvent des catégories d’âge, mais peuvent aussi être.. :

  • des zones géographiques (par exemple, différentes régions ou différents pays)
  • Groupes à risque (par exemple, professions à haut/faible risque)
  • Milieux sociaux (ménage, lieu de travail, école, etc.)

Par exemple, une matrice de contact hypothétique représentant le nombre moyen de contacts par jour entre les enfants et les adultes pourrait être la suivante :

\[ \begin{bmatrix} 2 & 2\ 1 & 3 \end{bmatrix} \] Dans cet exemple, cela signifie que les enfants rencontrent en moyenne 2 autres enfants et 2 adultes par jour (première ligne), et que les adultes rencontrent en moyenne 1 enfant et 3 autres adultes par jour (deuxième ligne). Nous pouvons utiliser ce type d’information pour rendre compte du rôle que joue l’hétérogénéité des contacts dans la transmission des maladies infectieuses.

Note sur la notation

Pour une matrice de contact avec des lignes \(i\) et des colonnes \(j\):

  • $C [i,j] $ représente le nombre moyen de contacts que les individus du groupe \(i\) ont avec les individus du groupe \(j\)
  • Cette moyenne est calculée comme le nombre total de contacts entre les groupes. \(i\) et \(j\), divisé par le nombre d’individus dans le groupe \(i\)

L’utilisation socialmixr

Les matrices de contact sont généralement estimées à partir des études qui utilisent des journaux pour enregistrer les interactions. Par exemple, l’enquête POLYMOD a mesuré les schémas de contact dans 8 pays européens en utilisant des données sur le lieu et la durée des contacts signalés par les participants à l’étude. (Mossong et al. 2008).

Le package R socialmixr contient des fonctions permettant d’estimer les matrices de contact à partir de POLYMOD et d’autres enquêtes. Nous pouvons charger les données de l’enquête POLYMOD :

R 

polymod <- socialmixr::polymod

Nous pouvons alors obtenir la matrice de contact pour les catégories d’âge souhaitées en spécifiant age.limits.

R 

contact_data <- contact_matrix(
  survey = polymod,
  countries = "United Kingdom",
  age.limits = c(0, 20, 40),
  symmetric = TRUE
)

SORTIE 

Removing participants that have contacts without age information. To change this behaviour, set the 'missing.contact.age' option

R 

contact_data

SORTIE 

$matrix
         contact.age.group
age.group   [0,20)  [20,40)      40+
  [0,20)  7.883663 3.120220 3.063895
  [20,40) 2.794154 4.854839 4.599893
  40+     1.565665 2.624868 5.005571

$demography
   age.group population proportion  year
      <char>      <num>      <num> <int>
1:    [0,20)   14799290  0.2454816  2005
2:   [20,40)   16526302  0.2741283  2005
3:       40+   28961159  0.4803901  2005

$participants
   age.group participants proportion
      <char>        <int>      <num>
1:    [0,20)          404  0.3996044
2:   [20,40)          248  0.2453017
3:       40+          359  0.3550940

Remarque : bien que la matrice de contact contact_data$matrix ne soit pas elle-même mathématiquement symétrique, elle satisfait à la condition selon laquelle le nombre total de contacts d’un groupe avec un autre est le même que l’inverse. En d’autres termes : contact_data$matrix[j,i]*contact_data$demography$proportion[j] = contact_data$matrix[i,j]*contact_data$demography$proportion[i]. Pour l’explication mathématique, voir la section correspondante dans la documentation de socialmixr.

Pourquoi une matrice de contact serait-elle non symétrique ?

L’un des arguments que nous avons donné à la fonction contact_matrix() est symmetric=TRUE. Cela garantit que le nombre total de contacts d’un groupe à l’autre est égal au nombre total de contacts du second groupe au premier (voir la section socialmixr vignette pour plus de détails).

Cependant, lorsque les matrices de contact sont estimées à partir d’enquêtes ou d’autres sources, le nombre de contacts signalés peut différer selon le groupe d’âge pour plusieurs raisons :

  • Biais de mémorisation : Les différents groupes d’âge pourraient avoir des capacités différentes à se souvenir des contacts et à les décrire avec précision.
  • Biais de déclaration : certains groupes pourraient systématiquement surestimer ou sous-estimer leurs contacts.
  • Incertitude de l’échantillonnage : La taille limitée des échantillons pourrait entraîner des variations statistiques (Prem et al 2021)

Si symmetric est réglé sur VRAI, la fonction contact_matrix() utilisera une moyenne des contacts signalés pour s’assurer que le nombre total de contacts obtenu est symétrique.

L’exemple ci-dessus utilise l’enquête POLYMOD. Il existe un certain nombre d’enquêtes disponibles dans socialmixr Pour obtenir la liste des enquêtes disponibles, utilisez list_surveys(). Pour télécharger une enquête, vous pouvez utiliser get_survey()

R 

zambia_sa_survey <- get_survey(
  "https://doi.org/10.5281/zenodo.3874675"
)

Vous pouvez explorer toutes les enquêtes disponibles dans le référentiel Zenodo à l’adresse https://zenodo.org/communities/social_contact_data/. Si vous souhaitez accéder à une URL spécifique dans R, vous pouvez essayer :

R 

library(socialmixr)
library(tidyverse)

# Get URL for Zambia contact survey data from {socialmixr}
socialmixr::list_surveys() %>%
  dplyr::filter(stringr::str_detect(title, "Zambia")) %>%
  dplyr::pull(url)

Matrice des contacts en Zambie

Le package R {socialmixr} contient des fonctions permettant d’estimer les matrices de contacts à partir de POLYMOD et d’autres enquêtes. Les résultats comprennent des informations démographiques telles que la taille de la population et le nombre de participants à l’étude. En utilisant {socialmixr}:

  • Téléchargé l’enquête de la Zambie

  • Générez une matrice de contact symétrique pour la Zambie en utilisant les tranches d’âge suivantes :

    • [0,20)
    • 20+

  • Accédez au vecteur représentant la taille de la population par tranche d’âge à partir du tableau de données démographiques dans la matrice de contact.

L’objet d’enquête zambia_sa_survey contient des données provenant de deux pays. Si vous avez besoin d’estimer la matrice des contacts sociaux à partir des données spécifiques à la Zambie, identifiez l’argument dont vous avez besoin dans socialmixr::contact_matrix() pour cela.

R 

# Inspect the countries within the survey object
levels(zambia_sa_survey$participants$country)

SORTIE 

[1] "South Africa" "Zambia"

Comme dans le code ci-dessus, pour accéder aux valeurs vectorielles dans un dataframe, vous pouvez utiliser l’opérateur signe dollar : $

R 

# Generate the contact matrix for Zambia only
contact_data_zambia <- socialmixr::contact_matrix(
  survey = zambia_sa_survey,
  countries = "Zambia", # key argument
  age.limits = c(0, 20),
  symmetric = TRUE
)

SORTIE 

Removing participants without age information. To change this behaviour, set the 'missing.participant.age' option

SORTIE 

Removing participants that have contacts without age information. To change this behaviour, set the 'missing.contact.age' option

R 

# Print the contact matrix for Zambia only
contact_data_zambia

SORTIE 

$matrix
         contact.age.group
age.group   [0,20)      20+
   [0,20) 3.650000 1.451168
   20+    1.988136 2.461856

$demography
   age.group population proportion  year
      <char>      <num>      <num> <int>
1:    [0,20)    8006201  0.5780636  2010
2:       20+    5843835  0.4219364  2010

$participants
   age.group participants proportion
      <char>        <int>      <num>
1:    [0,20)          180 0.08490566
2:       20+         1940 0.91509434

R 

# Print the vector of population size for {epidemics}
contact_data_zambia$demography$population

SORTIE 

[1] 8006201 5843835

Matrices de contact synthétiques

Les matrices de contact peuvent être estimées à partir de données obtenues des journaux (tels que POLYMOD), d’enquêtes ou de données de contact. Prem et al. 2021 ont utilisé les données POLYMOD dans le cadre d’un modèle hiérarchique bayésien pour projeter les matrices de contact de 177 autres pays.

Analyses avec des matrices de contact

On peut utiliser les matrices de contact pour effectuer de nombreuses analyses épidémiologiques différentes :

  • pour calculer le nombre de reproduction de base tout en tenant compte des différents taux de contacts entre les groupes d’âge (Funk et al. 2019),
  • pour calculer la taille finale d’une épidémie, comme dans le package R finalsize,
  • pour évaluer l’impact des interventions en déterminant le changement relatif entre les matrices de contact avant et après l’intervention pour calculer la différence relative dans le nombre de cas. \(R_0\) (Jarvis et al. 2020),
  • et dans les modèles mathématiques de transmission au sein d’une population, afin de tenir compte des schémas de contact propres à chaque groupe.

Cependant, toutes ces applications nous obligent à effectuer des calculs supplémentaires à l’aide de la matrice de contact. Plus précisément, nous devons souvent effectuer deux calculs principaux :

  1. Convertir la matrice de contact en nombre attendu de cas secondaires

Si les contacts varient entre les groupes, le nombre moyen de cas secondaires ne sera pas simplement égal au nombre moyen de contacts multiplié par la probabilité de transmission par contact. En effet, la quantité moyenne de transmission dans chaque génération d’infection ne dépend pas seulement des personnes avec lesquelles un groupe est entré en contact, mais aussi des personnes avec lesquelles ces contacts sont ensuite entrés en contact. La fonction r_eff dans le package finalsize peut effectuer cette conversion, en prenant une matrice de contact, la démographie et la proportion de personnes sensibles et en la convertissant en une estimation du nombre moyen de cas secondaires générés par un individu infectieux typique (c’est-à-dire le nombre de reproduction effectif).

  1. Convertir la matrice des contacts en taux de contact

Alors qu’une matrice de contacts donne le nombre moyen de contacts qu’un groupe a avec un autre, la dynamique épidémique dans différents groupes dépend du taux auquel un groupe en infecte un autre. Nous devons donc mettre à l’échelle le taux d’interaction entre les différents groupes (c’est-à-dire le nombre de contacts par unité de temps) pour obtenir le taux de transmission. Cependant, nous devons veiller à définir correctement la transmission vers et depuis chaque groupe dans n’importe quel modèle. Plus précisément, l’entrée \((i,j)\) dans la matrice des contacts d’un modèle mathématique représente les contacts du groupe \(i\) avec le groupe \(j\). Mais si nous voulons connaître le taux auquel un groupe \(i\) est infecté, nous devons multiplier le nombre de contacts des personnes sensibles dans le groupe \(i\) (\(S_i\)) avec le groupe \(j\) ( $C [i,j] \() avec la proportion de ces contacts qui sont infectieux (\)I_j/N_j\() et le risque de transmission par contact (\)$).

Dans les modèles mathématiques

Considérons le modèle SIR dans lequel les individus sont catégorisés comme étant soit sensibles \(S\), infectés mais pas encore infectieux \(E\), contagieux \(I\), ou guéri \(R\). Le schéma ci-dessous montre les processus qui décrivent le flux d’individus entre les différents états \(S\), \(I\) et \(R\) et les paramètres clés de chaque processus.

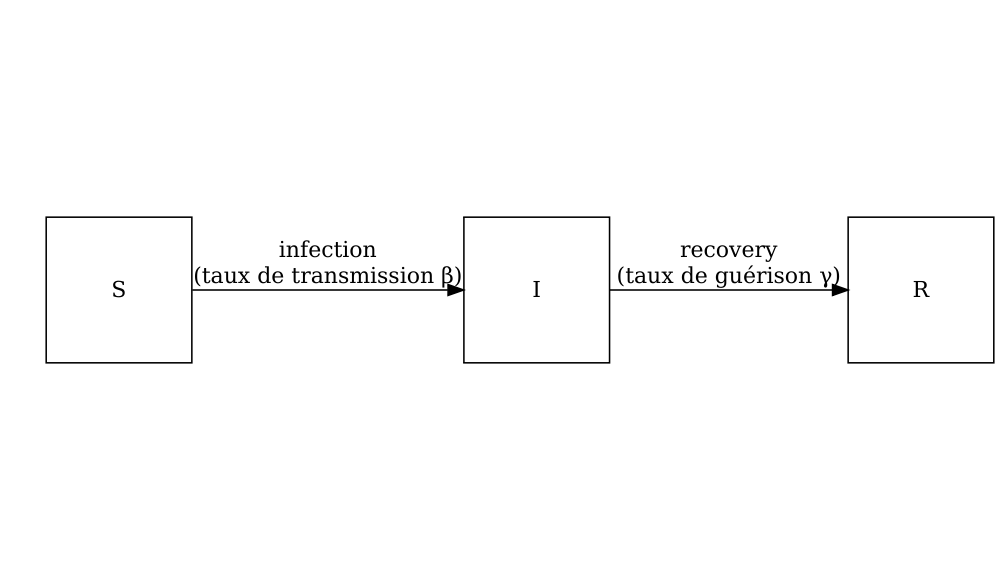
Les équations différentielles ci-dessous décrivent comment les individus passent d’un état à un autre (Bjørnstad et al. 2020).

\[ \begin{aligned} \frac{dS}{dt} & = - \beta S I /N \ \frac{dI}{dt} &= \beta S I /N - \gamma I \ \frac{dR}{dt} &=\gamma I \ \end{aligned} \] Pour ajouter une structure d’âge à notre modèle, nous devons ajouter des équations supplémentaires pour les états d’infection \(S\), \(I\) et \(R\) pour chaque groupe d’âge \(i\). Si nous voulons supposer qu’il existe une hétérogénéité dans les contacts entre les groupes d’âge, nous devons adapter le terme de transmission \(\beta SI\) pour inclure la matrice de contact \(C\) comme suit :

\[ \beta S_i \sum_j C_{i,j} I_j/N_j. \]

Individus susceptibles dans le groupe d’âge \(i\) sont infectés en fonction de leur taux de contact avec les individus de chaque groupe d’âge. Pour chaque état (\(S\), \(E\), \(I\) et \(R\)) et le groupe d’âge (\(i\)), nous avons une équation différentielle décrivant le taux de changement par rapport au temps.

\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j \ \frac{dI_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \gamma I_i \ \frac{dR_i}{dt} &=\gamma I_i \ \end{aligned} \]

La normalisation de la matrice des contacts pour garantir la valeur correcte de \(R_0\)

Lors de la simulation d’une épidémie, nous voulons souvent nous assurer que le nombre moyen de cas secondaires générés par un individu infectieux typique (c’est-à-dire \(R_0\)) soit cohérent avec les valeurs connues pour le pathogène que nous analysons. Dans le modèle ci-dessus, nous mettons à l’échelle la matrice des contacts par le facteur \(\beta\) pour convertir les données brutes d’interaction en taux de transmission. Mais comment définir la valeur de \(\beta\) pour garantir une certaine valeur de \(R_0\)?

Plutôt que d’utiliser le nombre brut de contacts, nous pouvons normaliser la matrice des contacts afin de faciliter le travail en termes de \(R_0\). En particulier, nous normalisons la matrice en la mettant à l’échelle de sorte que si nous devions calculer le nombre moyen de cas secondaires sur la base de cette matrice normalisée, le résultat serait 1 (en termes mathématiques, nous mettons la matrice à l’échelle de sorte que la plus grande valeur propre soit 1). Cette transformation met à l’échelle les entrées mais préserve leurs valeurs relatives.

Dans le cas du modèle ci-dessus, nous voulons définir \(\beta C_{i,j}\) afin que le modèle ait une valeur spécifiée de \(R_0\). Si l’entrée de la matrice de contact $C [i,j] $ représente les contacts de la population \(i\) avec \(j\), il est équivalent à contact_data$matrix[i,j] et la valeur propre maximale de cette matrice représente l’ampleur typique des contacts, et non l’ampleur typique de la transmission. Nous devons donc normaliser la matrice \(C\) de manière à ce que la valeur propre maximale soit égale à un ; nous appelons cette matrice \(C_{normalised}\). Comme le taux de récupération est \(\gamma\), les individus seront infectieux en moyenne pendant \(1/\gamma\) jours. Ainsi, \(\beta\) en tant qu’entrée du modèle est calculée à partir de \(R_0\), le facteur d’échelle, et la valeur de \(\gamma\) (c’est-à-dire que, mathématiquement, nous utilisons le fait que la valeur propre dominante de la matrice \(R_0 \times C_{normalised}\) est égale à \(\beta / \gamma\)).

R 

contact_matrix <- t(contact_data$matrix)
scaling_factor <- 1 / max(eigen(contact_matrix)$values)
normalised_matrix <- contact_matrix * scaling_factor

Par conséquent, si nous multiplions la matrice mise à l’échelle par \(R_0\) puis la multiplions en nombre de cas secondaires attendus, nous obtenons \(R_0\), comme requis.

R 

infectious_period <- 7.0
basic_reproduction <- 1.46
transmission_rate <- basic_reproduction * scaling_factor / infectious_period
# check the dominant eigenvalue of R0 x C_normalised is R0
max(eigen(basic_reproduction * normalised_matrix)$values)

SORTIE 

[1] 1.46

Normalisation à l’aide de socialmixr

La normalisation peut être effectuée par la fonction contact_matrix() dans socialmixr. Pour obtenir la matrice normalisée, nous devons spécifier que nous voulons séparer les différentes composantes de la matrice de contact à l’aide de l’argument split = TRUE. Nous pouvons alors obtenir la matrice normalisée de la manière suivante :

R 

contact_data_split <- contact_matrix(
  survey = polymod,
  countries = "United Kingdom",
  age.limits = c(0, 20, 40),
  symmetric = TRUE,
  split = TRUE
)

# extraire les composants de la matrice de contact
contacts_d <- contact_data_split$contacts
matrix_a <- contact_data_split$matrix
demography_n <- contact_data_split$demography$proportion

# calculer la matrice normalisée
normalised_matrix_split <- contacts_d * matrix_a * demography_n

Pour plus de détails sur les différentes composantes de la matrice de contact, voir la vignette du package sur la division des matrices de contact.

Vérifiez la dimension de \(\beta\)

Dans le modèle SIR sans structure d’âge, le taux de contact fait partie du taux de transmission. \(\beta\) alors que dans le modèle avec structure d’âge, nous avons séparé le taux de contact, et donc le taux de transmission. Pour cette raison, \(\beta\) dans le modèle structuré par âge aura une valeur différente.

Nous pouvons utiliser les matrices de contact de socialmixr avec des modèles mathématiques dans le package R {epidemics}. Regarder le tutoriel Simuler la transmission pour des exemples et une introduction à epidemics.

Groupes de contact

Dans l’exemple ci-dessus, la dimension de la matrice de contact sera la même que le nombre de groupes d’âge, c’est-à-dire que s’il y a 3 groupes d’âge, la matrice de contact aura 3 lignes et 3 colonnes. Les matrices de contact peuvent être utilisées pour d’autres groupes, à condition que la dimension de la matrice corresponde au nombre de groupes.

Par exemple, nous pourrions avoir un méta-modèle de population avec deux zones géographiques. Notre matrice de contact serait alors une matrice 2 x 2 dont les entrées représenteraient les contacts entre les zones géographiques et à l’intérieur de celles-ci.

Résumé

Dans ce tutoriel, nous avons appris la définition de la matrice de contact, comment elle est estimée et comment accéder aux données de contact social à partir de socialmixr. Dans le prochain tutoriel, nous apprendrons à utiliser le package R {epidemics} pour générer des trajectoires de maladies à partir de modèles mathématiques avec des matrices de contact provenant de socialmixr.

Points clés

  • Les matrices de contact quantifient les schémas de mélange entre différents groupes de population.
  • socialmixr fournit des outils pour estimer les matrices de contact à partir de données d’enquête
  • Les matrices de contact peuvent être utilisées dans diverses analyses épidémiologiques, qu’il s’agisse du du calcul de \(R_0\) à la modélisation des interventions.
  • Une normalisation adéquate est cruciale lors de l’utilisation des matrices de contact dans les modèles de transmission.