Content from Matrices de contact
Dernière mise à jour le 2025-11-23 | Modifier cette page
Durée estimée : 50 minutes
Vue d'ensemble
Questions
- Qu’est-ce qu’une matrice de contact ?
- Comment les matrices de contact sont-elles estimées ?
- Comment les matrices de contact sont-elles utilisées dans l’analyse épidémiologique ?
Objectifs
- Utilisez le package R
socialmixrpour estimer une matrice de contact - Comprendre les différents types d’analyse pour lesquels les matrices de contact peuvent être utilisées
Introduction
Certains groupes d’individus ont plus de contacts que d’autres ; l’écolier moyen a beaucoup plus de contacts quotidiens que la personne âgée moyenne, par exemple. Cette hétérogénéité des schémas de contact entre les différents groupes peut avoir un impact sur la transmission des maladies, car certains groupes sont plus susceptibles de transmettre la maladie à d’autres membres de ce groupe, ainsi qu’à d’autres groupes. La vitesse à laquelle les individus d’un même groupe et d’un groupe à l’autre entrent en contact avec d’autres personnes peut être résumée dans une matrice de contact. Dans ce tutoriel, nous allons apprendre comment les matrices de contact peuvent être utilisées dans différentes analyses et comment le package socialmixr peut être utilisé pour estimer les matrices de contact.
R
library(socialmixr)
La matrice de contact
La matrice de contact de base représente la quantité de contacts, ou de mélanges, au sein de différents sous-groupes d’une population et entre ces sous-groupes. Les sous-groupes sont souvent des catégories d’âge, mais peuvent aussi être.. :
- des zones géographiques (par exemple, différentes régions ou différents pays)
- Groupes à risque (par exemple, professions à haut/faible risque)
- Milieux sociaux (ménage, lieu de travail, école, etc.)
Par exemple, une matrice de contact hypothétique représentant le nombre moyen de contacts par jour entre les enfants et les adultes pourrait être la suivante :
\[ \begin{bmatrix} 2 & 2\\ 1 & 3 \end{bmatrix} \]
Dans cet exemple, cela signifie que les enfants rencontrent en moyenne 2 autres enfants et 2 adultes par jour (première ligne), et que les adultes rencontrent en moyenne 1 enfant et 3 autres adultes par jour (deuxième ligne). Nous pouvons utiliser ce type d’information pour rendre compte du rôle que joue l’hétérogénéité des contacts dans la transmission des maladies infectieuses.
Note sur la notation
Pour une matrice de contact avec des lignes \(i\) et des colonnes \(j\):
- $C [i,j] $ représente le nombre moyen de contacts que les individus du groupe \(i\) ont avec les individus du groupe \(j\)
- Cette moyenne est calculée comme le nombre total de contacts entre les groupes. \(i\) et \(j\), divisé par le nombre d’individus dans le groupe \(i\)
L’utilisation socialmixr
Les matrices de contact sont généralement estimées à partir des études qui utilisent des journaux pour enregistrer les interactions. Par exemple, l’enquête POLYMOD a mesuré les schémas de contact dans 8 pays européens en utilisant des données sur le lieu et la durée des contacts signalés par les participants à l’étude. (Mossong et al. 2008).
Le package R socialmixr contient des fonctions permettant d’estimer les matrices de contact à partir de POLYMOD et d’autres enquêtes. Nous pouvons charger les données de l’enquête POLYMOD :
R
polymod <- socialmixr::polymod
Nous pouvons alors obtenir la matrice de contact pour les catégories
d’âge souhaitées en spécifiant age.limits.
R
contact_data <- contact_matrix(
survey = polymod,
countries = "United Kingdom",
age.limits = c(0, 20, 40),
symmetric = TRUE
)
SORTIE
Removing participants that have contacts without age information. To change this behaviour, set the 'missing.contact.age' optionR
contact_data
SORTIE
$matrix
contact.age.group
age.group [0,20) [20,40) 40+
[0,20) 7.883663 3.120220 3.063895
[20,40) 2.794154 4.854839 4.599893
40+ 1.565665 2.624868 5.005571
$demography
age.group population proportion year
<char> <num> <num> <int>
1: [0,20) 14799290 0.2454816 2005
2: [20,40) 16526302 0.2741283 2005
3: 40+ 28961159 0.4803901 2005
$participants
age.group participants proportion
<char> <int> <num>
1: [0,20) 404 0.3996044
2: [20,40) 248 0.2453017
3: 40+ 359 0.3550940Remarque : bien que la matrice de contact
contact_data$matrix ne soit pas elle-même mathématiquement
symétrique, elle satisfait à la condition selon laquelle le nombre total
de contacts d’un groupe avec un autre est le même que l’inverse. En
d’autres termes :
contact_data$matrix[j,i]*contact_data$demography$proportion[j] = contact_data$matrix[i,j]*contact_data$demography$proportion[i].
Pour l’explication mathématique, voir la
section correspondante dans la documentation de
socialmixr.
Pourquoi une matrice de contact serait-elle non symétrique ?
L’un des arguments que nous avons donné à la fonction
contact_matrix() est symmetric=TRUE. Cela
garantit que le nombre total de contacts d’un groupe à l’autre est égal
au nombre total de contacts du second groupe au premier (voir la section
socialmixr vignette
pour plus de détails).
Cependant, lorsque les matrices de contact sont estimées à partir d’enquêtes ou d’autres sources, le nombre de contacts signalés peut différer selon le groupe d’âge pour plusieurs raisons :
- Biais de mémorisation : Les différents groupes d’âge pourraient avoir des capacités différentes à se souvenir des contacts et à les décrire avec précision.
- Biais de déclaration : certains groupes pourraient systématiquement surestimer ou sous-estimer leurs contacts.
- Incertitude de l’échantillonnage : La taille limitée des échantillons pourrait entraîner des variations statistiques (Prem et al 2021)
Si symmetric est réglé sur VRAI, la fonction
contact_matrix() utilisera une moyenne des contacts
signalés pour s’assurer que le nombre total de contacts obtenu est
symétrique.
L’exemple ci-dessus utilise l’enquête POLYMOD. Il existe un certain
nombre d’enquêtes disponibles dans socialmixr Pour obtenir
la liste des enquêtes disponibles, utilisez list_surveys().
Pour télécharger une enquête, vous pouvez utiliser
get_survey()
R
zambia_sa_survey <- get_survey(
"https://doi.org/10.5281/zenodo.3874675"
)
Vous pouvez explorer toutes les enquêtes disponibles dans le référentiel Zenodo à l’adresse https://zenodo.org/communities/social_contact_data/. Si vous souhaitez accéder à une URL spécifique dans R, vous pouvez essayer :
R
library(socialmixr)
library(tidyverse)
# Get URL for Zambia contact survey data from {socialmixr}
socialmixr::list_surveys() %>%
dplyr::filter(stringr::str_detect(title, "Zambia")) %>%
dplyr::pull(url)
Matrice des contacts en Zambie
Le package R {socialmixr} contient des fonctions permettant d’estimer les matrices de contacts à partir de POLYMOD et d’autres enquêtes. Les résultats comprennent des informations démographiques telles que la taille de la population et le nombre de participants à l’étude. En utilisant {socialmixr}:
Téléchargé l’enquête de la Zambie
-
Générez une matrice de contact symétrique pour la Zambie en utilisant les tranches d’âge suivantes :
- [0,20)
- 20+
Accédez au vecteur représentant la taille de la population par tranche d’âge à partir du tableau de données démographiques dans la matrice de contact.
L’objet d’enquête zambia_sa_survey contient des données
provenant de deux pays. Si vous avez besoin d’estimer la matrice des
contacts sociaux à partir des données spécifiques à la Zambie,
identifiez l’argument dont vous avez besoin dans
socialmixr::contact_matrix() pour cela.
R
# Inspect the countries within the survey object
levels(zambia_sa_survey$participants$country)
SORTIE
[1] "South Africa" "Zambia" Comme dans le code ci-dessus, pour accéder aux valeurs vectorielles
dans un dataframe, vous pouvez utiliser l’opérateur signe dollar :
$
R
# Generate the contact matrix for Zambia only
contact_data_zambia <- socialmixr::contact_matrix(
survey = zambia_sa_survey,
countries = "Zambia", # key argument
age.limits = c(0, 20),
symmetric = TRUE
)
SORTIE
Removing participants without age information. To change this behaviour, set the 'missing.participant.age' optionSORTIE
Removing participants that have contacts without age information. To change this behaviour, set the 'missing.contact.age' optionR
# Print the contact matrix for Zambia only
contact_data_zambia
SORTIE
$matrix
contact.age.group
age.group [0,20) 20+
[0,20) 3.650000 1.451168
20+ 1.988136 2.461856
$demography
age.group population proportion year
<char> <num> <num> <int>
1: [0,20) 8006201 0.5780636 2010
2: 20+ 5843835 0.4219364 2010
$participants
age.group participants proportion
<char> <int> <num>
1: [0,20) 180 0.08490566
2: 20+ 1940 0.91509434R
# Print the vector of population size for {epidemics}
contact_data_zambia$demography$population
SORTIE
[1] 8006201 5843835Matrices de contact synthétiques
Les matrices de contact peuvent être estimées à partir de données obtenues des journaux (tels que POLYMOD), d’enquêtes ou de données de contact. Prem et al. 2021 ont utilisé les données POLYMOD dans le cadre d’un modèle hiérarchique bayésien pour projeter les matrices de contact de 177 autres pays.
Analyses avec des matrices de contact
On peut utiliser les matrices de contact pour effectuer de nombreuses analyses épidémiologiques différentes :
- pour calculer le nombre de reproduction de base tout en tenant compte des différents taux de contacts entre les groupes d’âge (Funk et al. 2019),
- pour calculer la taille finale d’une épidémie, comme dans le package R finalsize,
- pour évaluer l’impact des interventions en déterminant le changement relatif entre les matrices de contact avant et après l’intervention pour calculer la différence relative dans le nombre de cas. \(R_0\) (Jarvis et al. 2020),
- et dans les modèles mathématiques de transmission au sein d’une population, afin de tenir compte des schémas de contact propres à chaque groupe.
Cependant, toutes ces applications nous obligent à effectuer des calculs supplémentaires à l’aide de la matrice de contact. Plus précisément, nous devons souvent effectuer deux calculs principaux :
- Convertir la matrice de contact en nombre attendu de cas secondaires
Si les contacts varient entre les groupes, le nombre moyen de cas
secondaires ne sera pas simplement égal au nombre moyen de contacts
multiplié par la probabilité de transmission par contact. En effet, la
quantité moyenne de transmission dans chaque génération d’infection ne
dépend pas seulement des personnes avec lesquelles un groupe est entré
en contact, mais aussi des personnes avec lesquelles ces contacts sont
ensuite entrés en contact. La fonction r_eff dans le
package finalsize peut effectuer cette conversion, en
prenant une matrice de contact, la démographie et la proportion de
personnes sensibles et en la convertissant en une estimation du nombre
moyen de cas secondaires générés par un individu infectieux typique
(c’est-à-dire le nombre de reproduction effectif).
- Convertir la matrice des contacts en taux de contact
Alors qu’une matrice de contacts donne le nombre moyen de contacts qu’un groupe a avec un autre, la dynamique épidémique dans différents groupes dépend du taux auquel un groupe en infecte un autre. Nous devons donc mettre à l’échelle le taux d’interaction entre les différents groupes (c’est-à-dire le nombre de contacts par unité de temps) pour obtenir le taux de transmission. Cependant, nous devons veiller à définir correctement la transmission vers et depuis chaque groupe dans n’importe quel modèle. Plus précisément, l’entrée \((i,j)\) dans la matrice des contacts d’un modèle mathématique représente les contacts du groupe \(i\) avec le groupe \(j\). Mais si nous voulons connaître le taux auquel un groupe \(i\) est infecté, nous devons multiplier le nombre de contacts des personnes sensibles dans le groupe \(i\) (\(S_i\)) avec le groupe \(j\) ( $C [i,j] \() avec la proportion de ces contacts qui sont infectieux (\)I_j/N_j\() et le risque de transmission par contact (\)$).
Dans les modèles mathématiques
Considérons le modèle SIR dans lequel les individus sont catégorisés comme étant soit sensibles \(S\), infectés mais pas encore infectieux \(E\), contagieux \(I\), ou guéri \(R\). Le schéma ci-dessous montre les processus qui décrivent le flux d’individus entre les différents états \(S\), \(I\) et \(R\) et les paramètres clés de chaque processus.
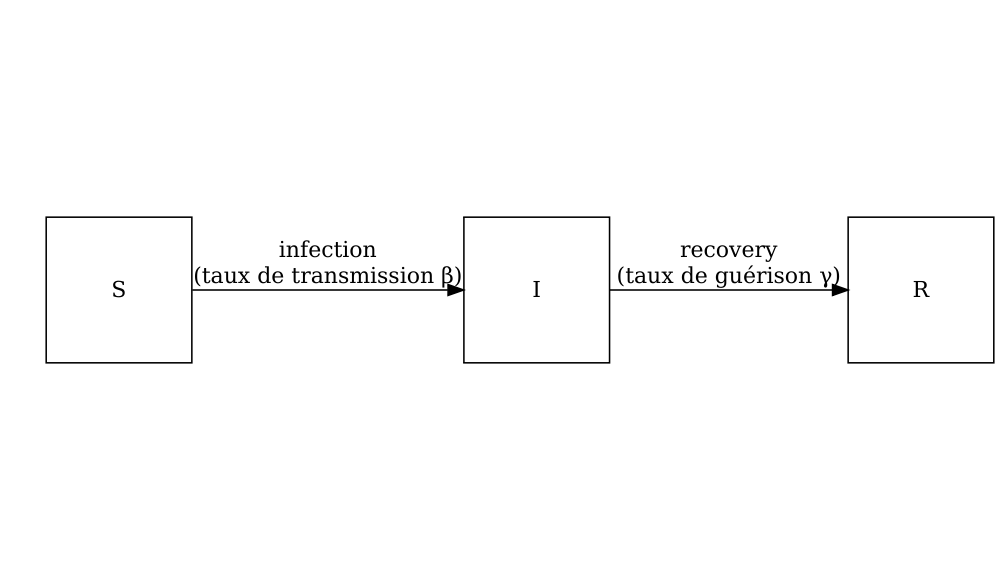
Les équations différentielles ci-dessous décrivent comment les individus passent d’un état à un autre (Bjørnstad et al. 2020).
\[ \begin{aligned} \frac{dS}{dt} & = - \beta S I /N \\ \frac{dI}{dt} &= \beta S I /N - \gamma I \\ \frac{dR}{dt} &=\gamma I \\ \end{aligned} \]
Pour ajouter une structure d’âge à notre modèle, nous devons ajouter des équations supplémentaires pour les états d’infection \(S\), \(I\) et \(R\) pour chaque groupe d’âge \(i\). Si nous voulons supposer qu’il existe une hétérogénéité dans les contacts entre les groupes d’âge, nous devons adapter le terme de transmission \(\beta SI\) pour inclure la matrice de contact \(C\) comme suit :
\[ \beta S_i \sum_j C_{i,j} I_j/N_j. \]
Individus susceptibles dans le groupe d’âge \(i\) sont infectés en fonction de leur taux de contact avec les individus de chaque groupe d’âge. Pour chaque état (\(S\), \(E\), \(I\) et \(R\)) et le groupe d’âge (\(i\)), nous avons une équation différentielle décrivant le taux de changement par rapport au temps.
\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j \\ \frac{dI_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \gamma I_i \\ \frac{dR_i}{dt} &=\gamma I_i \\ \end{aligned} \]
La normalisation de la matrice des contacts pour garantir la valeur correcte de \(R_0\)
Lors de la simulation d’une épidémie, nous voulons souvent nous assurer que le nombre moyen de cas secondaires générés par un individu infectieux typique (c’est-à-dire \(R_0\)) soit cohérent avec les valeurs connues pour le pathogène que nous analysons. Dans le modèle ci-dessus, nous mettons à l’échelle la matrice des contacts par le facteur \(\beta\) pour convertir les données brutes d’interaction en taux de transmission. Mais comment définir la valeur de \(\beta\) pour garantir une certaine valeur de \(R_0\)?
Plutôt que d’utiliser le nombre brut de contacts, nous pouvons normaliser la matrice des contacts afin de faciliter le travail en termes de \(R_0\). En particulier, nous normalisons la matrice en la mettant à l’échelle de sorte que si nous devions calculer le nombre moyen de cas secondaires sur la base de cette matrice normalisée, le résultat serait 1 (en termes mathématiques, nous mettons la matrice à l’échelle de sorte que la plus grande valeur propre soit 1). Cette transformation met à l’échelle les entrées mais préserve leurs valeurs relatives.
Dans le cas du modèle ci-dessus, nous voulons définir \(\beta C_{i,j}\) afin que le modèle ait une
valeur spécifiée de \(R_0\). Si
l’entrée de la matrice de contact $C [i,j] $ représente les contacts de
la population \(i\) avec \(j\), il est équivalent à
contact_data$matrix[i,j] et la valeur propre maximale de
cette matrice représente l’ampleur typique des contacts, et non
l’ampleur typique de la transmission. Nous devons donc normaliser la
matrice \(C\) de manière à ce que la
valeur propre maximale soit égale à un ; nous appelons cette matrice
\(C_{normalised}\). Comme le taux de
récupération est \(\gamma\), les
individus seront infectieux en moyenne pendant \(1/\gamma\) jours. Ainsi, \(\beta\) en tant qu’entrée du modèle est
calculée à partir de \(R_0\), le
facteur d’échelle, et la valeur de \(\gamma\) (c’est-à-dire que,
mathématiquement, nous utilisons le fait que la valeur propre dominante
de la matrice \(R_0 \times
C_{normalised}\) est égale à \(\beta /
\gamma\)).
R
contact_matrix <- t(contact_data$matrix)
scaling_factor <- 1 / max(eigen(contact_matrix)$values)
normalised_matrix <- contact_matrix * scaling_factor
Par conséquent, si nous multiplions la matrice mise à l’échelle par \(R_0\) puis la multiplions en nombre de cas secondaires attendus, nous obtenons \(R_0\), comme requis.
R
infectious_period <- 7.0
basic_reproduction <- 1.46
transmission_rate <- basic_reproduction * scaling_factor / infectious_period
# check the dominant eigenvalue of R0 x C_normalised is R0
max(eigen(basic_reproduction * normalised_matrix)$values)
SORTIE
[1] 1.46Vérifiez la dimension de \(\beta\)
Dans le modèle SIR sans structure d’âge, le taux de contact fait partie du taux de transmission. \(\beta\) alors que dans le modèle avec structure d’âge, nous avons séparé le taux de contact, et donc le taux de transmission. Pour cette raison, \(\beta\) dans le modèle structuré par âge aura une valeur différente.
Nous pouvons utiliser les matrices de contact de
socialmixr avec des modèles mathématiques dans le package R
{epidemics}. Regarder le tutoriel Simuler la transmission pour des
exemples et une introduction à epidemics.
Groupes de contact
Dans l’exemple ci-dessus, la dimension de la matrice de contact sera la même que le nombre de groupes d’âge, c’est-à-dire que s’il y a 3 groupes d’âge, la matrice de contact aura 3 lignes et 3 colonnes. Les matrices de contact peuvent être utilisées pour d’autres groupes, à condition que la dimension de la matrice corresponde au nombre de groupes.
Par exemple, nous pourrions avoir un méta-modèle de population avec deux zones géographiques. Notre matrice de contact serait alors une matrice 2 x 2 dont les entrées représenteraient les contacts entre les zones géographiques et à l’intérieur de celles-ci.
Résumé
Dans ce tutoriel, nous avons appris la définition de la matrice de
contact, comment elle est estimée et comment accéder aux données de
contact social à partir de socialmixr. Dans le prochain
tutoriel, nous apprendrons à utiliser le package R
{epidemics} pour générer des trajectoires de maladies à
partir de modèles mathématiques avec des matrices de contact provenant
de socialmixr.
Points clés
- Les matrices de contact quantifient les schémas de mélange entre différents groupes de population.
-
socialmixrfournit des outils pour estimer les matrices de contact à partir de données d’enquête - Les matrices de contact peuvent être utilisées dans diverses analyses épidémiologiques, qu’il s’agisse du du calcul de \(R_0\) à la modélisation des interventions.
- Une normalisation adéquate est cruciale lors de l’utilisation des matrices de contact dans les modèles de transmission.
Content from Simulation de la transmission
Dernière mise à jour le 2025-11-23 | Modifier cette page
Durée estimée : 75 minutes
Vue d'ensemble
Questions
- Comment simuler la propagation d’une maladie à l’aide d’un modèle mathématique ?
- Quels sont les données nécessaires à la simulation d’un modèle ?
- Comment tenir compte de l’incertitude ?
Objectifs
- Chargez une structure de modèle existante à partir de la librairie
{epidemics} - Chargez une matrice de contacts sociaux existante avec socialmixr
- Générer une simulation de modèle de propagation d’une maladie avec
{epidemics} - Générer des simulations de plusieurs modèles et visualiser l’incertitude
Pré-requis
- Compléter le tutoriel sur Matrices de contact.
Les apprenants doivent se familiariser avec les concepts suivants pour mieux comprendre les notions abordées dans ce cours.
Modélisation mathématique : Introduction aux modèles de maladies infectieuses, variables d’état, paramètres du modèle, conditions initiales, équations différentielles.
Théorie des épidémies : Transmission, Nombre de reproduction.
R packages installés: {epidemics},
socialmixr, scales,
tidyverse.
Installer les packages si elles ne le sont pas déjà:
R
if (!base::require("pak")) install.packages("pak")
pak::pak(c("epiverse-trace/epidemics", "socialmixr", "scales", "tidyverse"))
Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.
Introduction
Les modèles mathématiques sont des outils essentiels pour générer des
trajectoires futures de propagation de maladies. a librairie
{epidemics} de R contient des fonctionnalités que nous
allons utiliser dans ce tutoriel pour générer des trajectoires de
maladie d’une souche de grippe à potentiel pandémique. À la fin de ce
tutoriel, vous serez en mesure de générer les trajectoires illustrées
ci-dessous, montrant le nombre d’individus infectieux dans différentes
catégories d’âge au cours du temps.
Dans les sections qui vont suivrent, nous allons apprendre à utiliser
la librairie {epidemics} pour simuler des trajectoires
d’une maladie et à accéder aux données de contacts sociaux à travers le
package socialmixr. Nous utiliserons
dplyr, ggplot2 et l’opérateur pipe
(%>%) de la librairie magrittr pour
relier certaines de leurs fonctions. Ainsi, nous chargerons la librairie
tidyverse qui contient l’ensemble de ces trois
packages.
R
library(epidemics)
library(socialmixr)
library(tidyverse)
Use slides to introduce the topics of:
- Scenario modelling and
- Contact matrix.
Then start with the livecoding.
Simuler la propagation d’une maladie
Pour simuler les trajectoires des maladies infectieuses, il faut
d’abord choisir un modèle mathématique. La librairie
{epidemics} contient une bibliothèque de modèles parmi
lesquels vous pouvez choisir celui qui conviendrai à la maladie
d’intéret. Les noms de ces modèles commencent par model_*
et se terminent par le nom de la maladie (par exemple
model_ebola pour Ebola) ou d’un identifiant différent (par
exemple model_default).
Dans ce tutoriel, nous utiliserons le modèle par défaut appelé
model_default() de la librairie {epidemics}.
Il s’agit d’un modèle structuré par âge qui classe les individus en
fonction de leur statut infectieux. Dans chaque groupe d’âge \(i\) les individus sont classés dans les
compartiments suivants: sensibles \(S\), infectés mais pas encore contagieux
\(E\), infectieux \(I\) et guéris \(R\). Nous devons ensuite définir le
processus par lequel les individus passent d’un compartiment à l’autre.
Cela peut se faire en définissant un ensemble d’ équations différentielles qui
spécifient comment le nombre d’individus dans chaque compartiment évolue
dans le temps.
Le schéma ci-dessous montre les processus qui décrivent le flux d’individus entre les états pathologiques \(S\), \(E\), \(I\) et \(R\) et les paramètres clés de chaque processus.
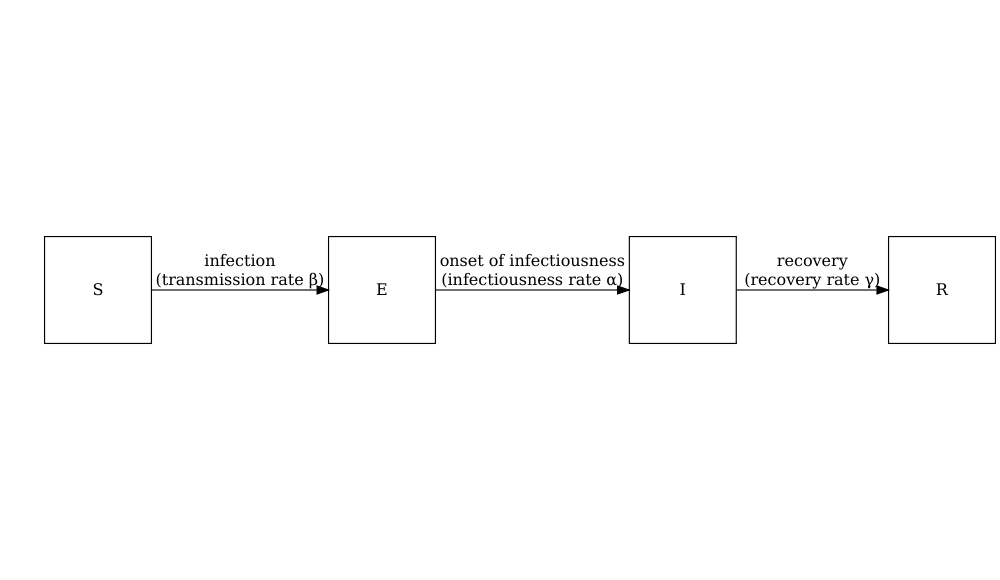
Paramètres du modèle : les taux
Dans les modèles au niveau de la population définis par des équations différentielles, les paramètres du modèle sont souvent (mais pas toujours) spécifiés sous forme de taux. Le taux auquel un événement se produit est l’inverse du temps moyen jusqu’à cet événement. Par exemple, dans le modèle SEIR, le taux de guérrison \(\gamma\) est l’inverse de la période infectieuse moyenne.
Les valeurs de ces taux peuvent être déterminées à partir de l’histoire naturelle de la maladie. Par exemple, si les personnes sont en moyenne infectieuses pendant 8 jours, alors dans le modèle, une personnes sur huits (1/8) actuellement infectieuses se rétablissent chaque jour (c’est-à-dire le taux de guèrrison \(\gamma=1/8=0.125\)).
Pour chaque état pathologique (\(S\), \(E\), \(I\) et \(R\)) dans le groupe d’âge (\(i\)), nous avons une équation différentielle décrivant le taux de changement par rapport au temps.
\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j \\ \frac{dE_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \alpha E_i \\ \frac{dI_i}{dt} &= \alpha E_i - \gamma I_i \\ \frac{dR_i}{dt} &=\gamma I_i \\ \end{aligned} \]
Les individus de la tranche d’âge (\(i\)) quittent l’état sensible (\(S_i\)) pour l’état exposé (\(E_i\)) par le biais de contacts spécifiques à l’âge avec des individus infectieux dans tous les groupes \(\beta S_i \sum_j C_{i,j} I_j/N_j\). La matrice de contact \(C\) permet de tenir compte de l’hétérogénéité des contacts entre les groupes d’âge. Ils passent ensuite à l’état infectieux à un taux \(\alpha\) et se rétablissent à un taux \(\gamma\). Notez que ce modèle suppose qu’il n’y a pas de perte d’immunité (il n’y a pas de flux sortant de l’état de guérison), ce qui peut ne pas être le cas pour toutes les maladies, car certains individus guerris peuvent redevenir infectés à la suite de leur guérison dans la cadre de certaines maladies.
Les paramètres du modèle sont les suivants
- taux de transmission \(\beta\) (dérivé du nombre de reproduction de base \(R_0\) et du taux de guérison \(\gamma\)),
- matrice de contact \(C\) contenant la fréquence des contacts entre les groupes d’âge (une matrice carrée \(i \times j\)),
- le taux d’infectiosité \(\alpha\) (période pré-infectieuse, ou période de latence =\(1/\alpha\)), et
- taux de guérison \(\gamma\) (période infectieuse = \(1/\gamma\)).
Exposé, infecté, infectieux
Les termes “exposé”, “infecté” et “infectieux” dans la modélisation mathématique prêtent parfois à confusion. L’infection se produit après qu’une personne a été exposée, mais en termes de modélisation, les individus “exposés” sont considérés comme déjà infectés.
Nous utiliserons les définitions suivantes pour nos variables d’état :
- \(E\) = Exposé : infecté mais pas encore infectieux,
- \(I\) = infectieux : infecté et infectieux.
Pour générer des trajectoires à l’aide de notre modèle, nous devons préparer les données d’entrée suivantes :
- Matrice de contact
- Conditions initiales
- Structure de la population
- Paramètres du modèle
1. Matrice de contact
Une matrice de contacts représente le nombre moyen de contacts entre les individus de différents groupes d’âge. Il s’agit d’une composante essentielle des modèles structurés par âge, car elle permet de savoir la manière dont les différents groupes d’âge interagissent et se transmettent potentiellement l’infections. Nous utiliserons le package R socialmixr pour charger une matrice de contacts estimée à partir des données de l’enquête POLYMOD (Mossong et al. 2008).
Charger les données de contact et de démographie
En utilisant la librairie socialmixr, obtenir la matrice de contact du Royaume-Uni pour les tranches d’âge suivantes :
- âge entre 0 et 20 ans,
- âge compris entre 20 et 40 ans,
- 40 ans et plus.
Utilisez le sondage disponible sur
socialmixr::polymod.
- Compléter le tutoriel sur Matrices de contact.
R
# Access the contact survey data
polymod <- socialmixr::polymod
# Generate the contact matrix
contact_data <- socialmixr::contact_matrix(
polymod,
countries = "United Kingdom",
age.limits = c(0, 20, 40),
symmetric = TRUE
)
# prepare contact matrix
socialcontact_matrix <- t(contact_data$matrix)
# print
socialcontact_matrix
SORTIE
age.group
contact.age.group [0,20) [20,40) 40+
[0,20) 7.883663 2.794154 1.565665
[20,40) 3.120220 4.854839 2.624868
40+ 3.063895 4.599893 5.005571N’oubliez pas que la matrice satisfait à la condition
symmetric = TRUE au niveau du nombre total de contacts.
Le nombre total de contacts entre les groupes \(i\) et \(j\) est calculé comme étant le nombre moyen
de contacts (contact_data$matrix) multiplié par le nombre
d’individus dans le groupe \(i\)
(contact_data$demography$population).
R
contact_data$matrix * contact_data$demography$population
SORTIE
contact.age.group
age.group [0,20) [20,40) 40+
[0,20) 116672620 46177038 45343471
[20,40) 46177038 80232531 76019216
40+ 45343471 76019216 144967139Le résultat est une matrice carrée avec des lignes et des colonnes
pour chaque groupe d’âge. Les matrices de contact peuvent être chargées
à partir d’autres sources, mais elles doivent être formatées de sorte à
être utilisées par les fonctions de la librairies
{epidemics}.
Normalisation
Dans le cadre de {epidemics} la normalisation de la
matrice de contact se fait durant l’appel de la fonction, nous n’avons
donc pas besoin de normaliser la matrice de contact avant de la passer à
la fonction epidemics::population() (voir section 3.
Structure de la population). Pour plus de détails sur la normalisation,
consultez le tutoriel sur les matrices
de contact .
Make a pause.
Use slides to introduce the topics of:
- Initial conditions and
- Population structure.
Then continue with the livecoding.
2. Conditions initiales
Les conditions initiales sont la proportion d’individus dans chaque état pathologique \(S\), \(E\), \(I\) et \(R\) pour chaque groupe d’âge au temps 0. Dans cet exemple, nous avons trois groupes d’âge : âge entre 0 et 20 ans, âge entre 20 et 40 ans et plus. Supposons que dans la catégorie d’âge la plus jeune, un individu sur un million soit infectieux, et que les autres catégories d’âge soient exemptes d’infection.
Les conditions initiales dans la première catégorie d’âge sont les suivantes \(S(0)=1-\frac{1}{1,000,000}\), \(E(0) =0\), \(I(0)=\frac{1}{1,000,000}\), \(R(0)=0\). Il est spécifié sous la forme d’un vecteur comme suit :
R
# 1 in 1,000,000 is equivalent to 1e-6
initial_i <- 1e-6
initial_conditions_inf <- c(
S = 1 - initial_i, E = 0, I = initial_i, R = 0, V = 0
)
Notez que R utilise la notation scientifique e, où
e vous indique de multiplier le nombre de base par 10 élevé
à la puissance indiquée (DataKwery,
2020). L’expression \(1 \times
10^{-6}\) équivaut à 1e-6.
Pour les catégories d’âge exemptes d’infection, les conditions initiales sont les suivantes \(S(0)=1\), \(E(0) =0\), \(I(0)=0\), \(R(0)=0\). Nous spécifions ceci comme suit,
R
initial_conditions_free <- c(
S = 1, E = 0, I = 0, R = 0, V = 0
)
Nous combinons les trois vecteurs de conditions initiales en une seule matrice,
R
# combiner les conditions initiales dans un objet de classe matricielle
initial_conditions <- rbind(
initial_conditions_inf, # groupe d'age 1 (seul groupe infectieux)
initial_conditions_free, # groupe d'age 2
initial_conditions_free # groupe d'age 3
)
# utiliser la matrice de contact pour renommer les noms de lignes de la matrice
# des conditions initiales
rownames(initial_conditions) <- rownames(socialcontact_matrix)
initial_conditions
SORTIE
S E I R V
[0,20) 0.999999 0 1e-06 0 0
[20,40) 1.000000 0 0e+00 0 0
40+ 1.000000 0 0e+00 0 03. Structure de la population
L’objet de la classe contact_data
que nous avons obtenu à l’aide de la librairie
socialmixr.
R
# extraire le vecteur démographique
demography_vector <- contact_data$demography$population
# utiliser la matrice de contact pour renommer les noms
# des lignes du vecteur démographique
names(demography_vector) <- rownames(socialcontact_matrix)
demography_vector
SORTIE
[0,20) [20,40) 40+
14799290 16526302 28961159 Pour créer notre objet de classe {epidemics}, nous utiliserons la fonction
epidemics::population() en spécifiant le nom du pays, la
matrice de contact, le vecteur démographique et les conditions
initiales.
R
library(epidemics)
uk_population <- epidemics::population(
name = "UK",
contact_matrix = socialcontact_matrix,
demography_vector = demography_vector,
initial_conditions = initial_conditions
)
Make a pause.
Use slides to introduce the topics of:
- Model parameters and
- New infections.
Then continue with the livecoding.
4. Paramètres du modèle
Pour exécuter notre modèle, nous devons spécifier les paramètres :
- le taux de transmission \(\beta\),
- taux d’infectiosité \(\alpha\) (période préinfectieuse=\(1/\alpha\)),
- taux de guérison \(\gamma\) (période infectieuse=\(1/\gamma\)).
Dans {epidemics} nous spécifions les paramètres du
modèle comme étant :
-
transmission_rate\(\beta = R_0 \gamma\), -
infectiousness_rate= \(\alpha\), -
recovery_rate= \(\gamma\),
Nous simulerons une souche de grippe à potentiel pandémique ayant les caractéristiques suivantes \(R_0=1.46\) avec une période pré-infectieuse de 3 jours et une période infectieuse de 7 jours. Nos données d’entrée seront donc les suivantes
R
# les délais
preinfectious_period <- 3.0
infectious_period <- 7.0
basic_reproduction <- 1.46
R
# les taux
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
transmission_rate <- basic_reproduction / infectious_period
Le nombre de reproduction de base \(R_0\)
Le nombre de reproduction de base, \(R_0\) pour le modèle SEIR est le suivant :
\[ R_0 = \frac{\beta}{\gamma}.\]
Par conséquent, nous pouvons réécrire le taux de transmission \(\beta\) comme suit :
\[ \beta = R_0 \gamma.\]
Exécution du modèle
Exécution (résolution) du modèle
Pour les modèles décrits par les équations différentielles, “exécuter” le modèle signifie en fait prendre le système d’équations différentielles et le “résoudre” pour découvrir comment le nombre de personnes dans les compartiments sous-jacents évolue dans le temps. Étant donné que les équations différentielles décrivent le taux de changement des états pathologiques en fonction du temps, plutôt que le nombre d’individus dans chacun de ces états, nous devons généralement utiliser des méthodes numériques pour résoudre les équations.
Un solveur ODE est le logiciel utilisé pour trouver des
solutions numériques aux équations différentielles. Si vous souhaitez
savoir comment un système d’équations différentielles est résolu dans
{epidemics} nous vous suggérons de lire la section sur Systèmes
et modèles d’EDO de la vignette “Design principles”.
Nous sommes maintenant prêts à exécuter notre modèle en utilisant
epidemics::model_default() de la librairies
{epidemics}.
Précisons time_end=600 pour exécuter le modèle pendant
600 jours.
R
output <- epidemics::model_default(
# population
population = uk_population,
# les taux
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# duree de l'épidémie
time_end = 600,
increment = 1.0
)
head(output)
SORTIE
time demography_group compartment value
<num> <char> <char> <num>
1: 0 [0,20) susceptible 14799275
2: 0 [20,40) susceptible 16526302
3: 0 40+ susceptible 28961159
4: 0 [0,20) exposed 0
5: 0 [20,40) exposed 0
6: 0 40+ exposed 0Remarque : ce modèle permet également d’inclure la vaccination et de suivre le nombre d’individus vaccinés au fil du temps. Même si nous n’avons pas spécifié de vaccination, il y a toujours un compartiment vacciné dans le résultat (ne contenant aucun individu). Nous aborderons l’utilisation de la vaccination dans le prochain tutoriel.
Le résultat de notre modèle est le nombre d’individus dans chaque compartiment de chaque groupe d’âge au cours du temps. Nous pouvons visualiser uniquement les individus infectieux (ceux qui se trouvent dans le compartiment \(I\)) au cours du temps.
R
library(tidyverse)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
geom_line(
aes(
x = time,
y = value,
colour = demography_group
)
) +
scale_y_continuous(
labels = scales::comma
) +
theme_bw() +
labs(
x = "Durée de la simulation (en jours)",
linetype = "Compartiment",
y = "nombre d'invidus"
)
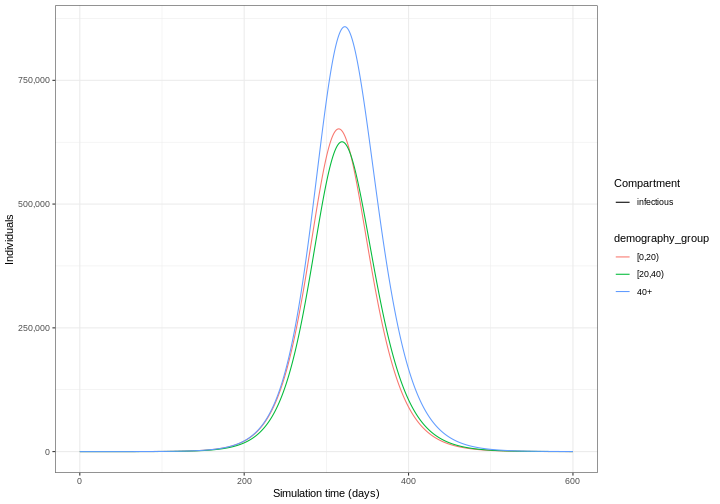
Incréments de temps
Notez qu’il existe une valeur par défaut de l’argument
increment = 1. Il s’agit du pas de temps du solveur ODE.
Lorsque les paramètres sont spécifiés sur une échelle de temps
quotidienne et la limite de temps (time_end) est de jours,
le pas de temps par défaut du solveur ODE est d’un jour.
Le choix de l’incrément dépend de l’échelle de temps des paramètres et de la vitesse à laquelle les événements peuvent se produire. En général, l’incrément doit être plus petit que l’événement le plus rapide qui puisse se produire. Par exemple, l’incrément doit être plus petit que l’événement le plus rapide qui peut se produire :
- si les paramètres se situent sur une échelle de temps quotidienne et que tous les événements sont signalés quotidiennement, l’incrément doit être égal à un jour ;
- si les paramètres se situent sur une échelle de temps mensuelle, mais que certains événements se produisent au cours d’un mois, l’incrément doit être inférieur à un mois.
Témoignage
Deux fonctions d’aide dans
{epidemics}
Utilisez epidemics::epidemic_peak() pour obtenir l’heure
et la taille du pic le plus élevé d’un compartiment pour tous les
groupes démographiques. Par défaut, cela calculera pour le compartiment
infectieux.
R
epidemics::epidemic_peak(data = output)
SORTIE
demography_group compartment time value
<char> <char> <num> <num>
1: [0,20) infectious 315 651944.3
2: [20,40) infectious 319 625863.8
3: 40+ infectious 322 858259.1Utilisez epidemics::epidemic_size() pour obtenir la
taille de l’épidémie à n’importe quel stade entre le début et la fin.
Celle-ci est calculée comme le nombre d’individus guéris de
l’infection à ce stade de l’épidémie.
R
epidemics::epidemic_size(data = output)
SORTIE
[1] 9285873 9040679 12540088Ces fonctions de synthèse peuvent vous aider à obtenir des résultats pertinents pour comparer des scénarios ou pour toute autre analyse en aval.
La figure ci-dessus montre le nombre total ou le nombre cumulé
d’individus dans le compartiment infectieux à chaque instant. Si vous
souhaitez montrer la charge totale de la maladie, le
compartiment infectious est le plus approprié. En revanche,
si vous souhaitez montrer la charge quotidienne, vous pouvez
utiliser epidemics::new_infections() pour obtenir
l’incidence quotidienne.
Notez que le nombre de nouveaux cas infectés à chaque instant (comme dans la figure ci-dessous) est inférieur au nombre cumulé de personnes infectieuses à chaque instant (comme dans la figure ci-dessus).
R
# New infections
newinfections_bygroup <- epidemics::new_infections(data = output)
# Visualise the spread of the epidemic in terms of new infections
newinfections_bygroup %>%
ggplot(aes(x = time, y = new_infections, colour = demography_group)) +
geom_line() +
scale_y_continuous(
breaks = scales::breaks_pretty(n = 5),
labels = scales::comma
) +
theme_bw()
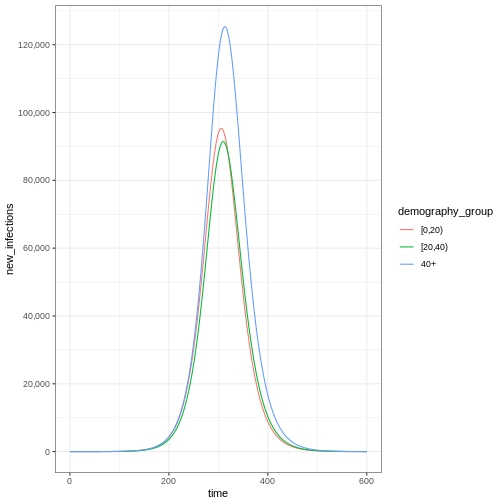
Stop the livecoding.
Suggest learners to read the rest of the episode.
Return to slides.
Prise en compte de l’incertitude
Le modèle épidémique est déterministe, c’est-à-dire qu’il fonctionne comme une horloge : les mêmes paramètres conduiront toujours à la même trajectoire. Un modèle déterministe est un modèle dont le résultat est entièrement déterminé par les conditions et les paramètres initiaux, sans aucune variation aléatoire. Cependant, la réalité n’est pas aussi prévisible à cause de ces deux raisons principales : le processus de transmission peut être aléatoire et nous pouvons ne pas connaître les caractéristiques épidémiologiques exactes de l’agent pathogène qui nous intéresse. Dans le prochain épisode, nous examinerons les modèles “stochastiques” (c’est-à-dire les modèles dans lesquels nous pouvons définir le processus qui crée un caractère aléatoire dans la transmission). Entre-temps, nous pouvons inclure l’incertitude dans la valeur des paramètres qui entrent dans le modèle déterministe. Pour tenir compte de cette incertitude, nous devons exécuter notre modèle pour différentes combinaisons de paramètres.
Nous avons exécuté notre modèle avec \(R_0 = 1.5\). Cependant, nous pensons que \(R_0\) suit une distribution normale avec une moyenne de 1,5 et un écart-type de 0,05. Pour tenir compte de l’incertitude, nous exécuterons le modèle pour différentes valeurs de \(R_0\). Les étapes à suivre pour ce faire sont les suivantes :
- Obtenir 100 valeurs aléatoires de \(R_0\) à partir d’une distribution normale.
R
# spécifier la moyenne et l'écart-type de R0
r_estimate_mean <- 1.5
r_estimate_sd <- 0.05
# Générer 100 R0 de façon aléatoire
r_samples <- withr::with_seed(
seed = 1,
rnorm(
n = 100, mean = r_estimate_mean, sd = r_estimate_sd
)
)
infectious_period <- 7
beta <- r_samples / infectious_period
- Exécutez le modèle 100 fois en variant \(R_0\) à chaque itération
R
output_samples <- epidemics::model_default(
population = uk_population,
transmission_rate = beta,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 600,
increment = 1
)
- Calculez la moyenne et les quantiles à 95 % du nombre d’individus infectieux pour chaque simulation du modèle et visualisez les résultats.
R
output_samples %>%
mutate(r_value = r_samples) %>%
unnest(data) %>%
filter(compartment == "infectious") %>%
ggplot() +
geom_line(
aes(time, value, color = r_value, group = param_set),
alpha = 3
) +
scale_color_fermenter(
palette = "RdBu",
name = "R"
) +
scale_y_continuous(
labels = scales::comma
) +
facet_grid(
cols = vars(demography_group)
) +
theme_bw() +
labs(
x = "Durée de simulation (en jours)",
y = "Nombre d'individus"
)
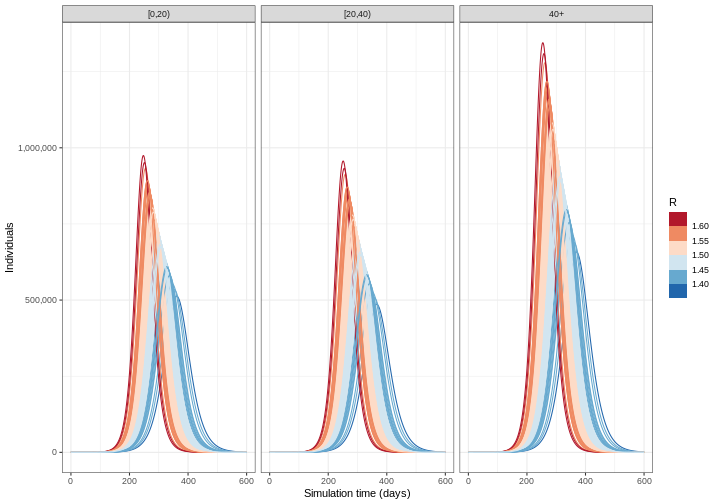
Le choix des paramètres dans lesquels inclure l’incertitude dépend de plusieurs facteurs : le degré d’information sur la valeur d’un paramètre, par exemple la cohérence des estimations tirées de la littérature ; la sensibilité des résultats du modèle aux changements de valeur des paramètres ; et l’objectif de la tâche de modélisation. Voir aussi McCabe et al. 2021 pour en savoir plus sur les différents types d’incertitude dans la modélisation des maladies infectieuses.
Résumé
Dans ce tutoriel, nous avons appris à simuler la propagation d’une maladie à l’aide d’un modèle mathématique. Une fois qu’un modèle a été choisi, les paramètres et autres données d’entrées doivent être spécifiés de manière correcte pour effectuer les simulations du modèle. Dans le prochain tutoriel, nous verrons comment choisir le modèle approprié pour différentes tâches.
Points clés
- Les trajectoires de la maladie peuvent être générées à l’aide du
package
{epidemics}de R. - L’incertitude devrait être incluse dans les trajectoires du modèle en utilisant une gamme de valeurs des paramètres du modèle.
Content from Choisir un modèle approprié
Dernière mise à jour le 2025-11-24 | Modifier cette page
Durée estimée : 30 minutes
Vue d'ensemble
Questions
- Comment choisir un modèle mathématique approprié pour bien faire ma tâche d’analyse ?
Objectifs
- Comprendre les exigences du modèle pour une question de recherche spécifique
::::::::::::::::::::::::::::::::::::: prereq
- Compléter le tutoriel Simuler la transmission :::::::::::::::::::::::::::::::::
Introduction
Il existe des modèles mathématiques pour différentes infections, interventions et schémas de transmission qui peuvent être utilisés pour répondre à de nouvelles questions. Dans ce tutoriel, nous apprendrons à choisir un modèle existant pour accomplir une tâche donnée.
L’objectif de ce tutoriel est de comprendre les modèles existants afin de décider s’ils sont appropriés pour une question donnée.
Choisir un modèle
Lorsqu’il s’agit de choisir le modèle mathématique à utiliser, un certain nombre de questions se posent :
Il se peut qu’un modèle existe déjà pour la maladie que vous étudiez, ou qu’il existe un modèle pour une infection dont les voies de transmission et les caractéristiques épidémiologiques sont similaires et qui peut être adapté. Par exemple, les maladies ayant des voies de transmission similaires (par exemple, transmission par voie aérienne, par gouttelettes ou par contact) et une histoire naturelle similaire (par exemple, période d’incubation, période infectieuse) peuvent utiliser des structures de modèle similaires.
Les structures des modèles diffèrent en fonction de l’ampleur et de la nature de l’épidémie. Lorsque le nombre d’infections simulées est faible, la variation stochastique (c’est-à-dire le caractère aléatoire que nous pouvons définir mathématiquement) des résultats peut avoir une incidence significative sur le déclenchement ou non d’une épidémie. Les épidémies localisés peuvent être mieux modélisées à l’aide d’approches stochastiques afin de saisir l’incertitude de la dynamique de transmission précoce. Les épidémies à plus grande échelle, peuvent souvent être modélisées efficacement à l’aide d’approches déterministes, car la variation stochastique devient moins importante par rapport à la dynamique globale.
Le résultat d’intérêt est généralement une quantité mesurable dérivée du modèle mathématique. Il peut s’agir de
- le nombre d’infections au fil du temps
- Le nombre maximal d’hospitalisations
- Le nombre total de cas de maladies graves
- L’ampleur finale de l’épidémie
- Le moment des pics épidémiques
Par exemple, directes ou indirecte, par voie aérienne ou à transmission vectorielle.
Pour une même infection ou un même type d’épidémie, il peut y avoir des différences subtiles dans les structures des modèles, qui peuvent passer inaperçues si l’on n’étudie pas les équations. Par exemple, les paramètres de transmissibilité peuvent être spécifiés sous forme de taux ou de probabilités. Si vous souhaitez utiliser les valeurs des paramètres d’autres modèles publiés, vous devez vérifier que la transmission est formulée de la même manière.
Il se peut que nous nous intéressions aux interventions telles que la vaccination, la distanciation physique ou les programmes de traitement. Les capacités d’intégration des interventions varient d’un modèle à l’autre :
- Certains modèles peuvent simuler des interventions continues (par exemple, des programmes de vaccination délivrés en continu).
- D’autres traitent les interventions discrètes (par exemple, les fermetures ponctuelles d’écoles).
- Certains modèles ne comprennent aucune fonctionnalité permettant de modéliser les interventions.
Nous discutons des interventions en détail dans le tutoriel Modélisation des interventions.
Modèles disponibles en {epidemics}
Le package R {epidemics} contient des fonctions
permettant d’exécuter les modèles existants. Pour plus de détails sur
les modèles disponibles, consultez le package Guide
de référence des “Fonctions de modèle”. Tous les noms des fonctions
des modèles commencent par model_*(). Pour apprendre
comment exécuter les modèles dans R, lisez le document suivant Vignettes
sur les “Guides pour les modèles de la bibliothèque”.
Quel modèle ?
On vous a demandé d’étudier la variation du nombre de personnes infectieuses dans les premières phases d’une épidémie d’Ebola.
Parmi les modèles suivants, lequel serait le plus approprié pour cette tâche ?
model_default()model_ebola()
Réfléchissez aux questions suivantes :
Liste de vérification
- Quelle est l’infection ou la maladie en question ?
- Avons-nous besoin d’un modèle déterministe ou stochastique ?
- Quel est le résultat qui nous intéresse ?
- Des interventions seront-elles modélisées ?
- Quelle est l’infection ou la maladie concernée ? Ebola
- Faut-il un modèle déterministe ou stochastique ? Un modèle stochastique nous permettrait d’étudier les variations au cours des premières phases de l’épidémie
- Quel est le résultat qui vous intéresse ? Nombre d’infections
- Des interventions seront-elles modélisées ? Non
model_default()
Un modèle SEIR (S: susceptible, E: exposé; I: infectieux; R: récupéré) déterministe avec une transmission directe spécifique à l’âge.
Le modèle est capable de simuler une épidémie de type Ebola, mais comme il est déterministe, nous ne sommes pas en mesure d’étudier les variations stochastiques au cours des premières phases de l’épidémie.
model_ebola()
Un modèle stochastique SEIHFR (Susceptible, Exposé, Infectieux, Hospitalisé, Funéraire, Retiré) développé spécifiquement pour la maladie à virus Ebola. Le modèle comprend des compartiments pour les états Hospitalisé et Funéraire, qui sont essentiels pour comprendre la dynamique de transmission du virus Ebola en raison du risque élevé de transmission dans les établissements de soins de santé et pendant les pratiques funéraires traditionnelles. Le modèle présente une stochasticité dans les temps de passage entre les états, qui sont modélisés avec des distributions d’Erlang.
Les paramètres clés affectant la transition entre les états sont les suivants :
- \(R_0\) le nombre de reproduction de base,
- \(\rho^I\) la période infectieuse moyenne,
- \(\rho^E\) la période préinfectieuse moyenne,
- \(p_{hosp}\) la probabilité d’être transféré dans le compartiment hospitalisé.
**Note : la relation fonctionnelle entre la période préinfectieuse (\(\rho^E\)) et le taux de transition entre exposé et infectieux (\(\gamma^E\)) est la suivante \(\rho^E = k^E/\gamma^E\) où \(k^E\) est le paramètre de forme de la distribution d’Erlang. De même, pour la période infectieuse \(\rho^I = k^I/\gamma^I\). Pour plus de détails sur la formulation du modèle stochastique, vous pourriez regarder la section sur les Modèle à temps discret de la maladie à virus Ebola dans la vignette “Modélisation des réponses à une épidémie stochastique de virus Ebola”. **
Le modèle comporte des paramètres supplémentaires décrivant le risque de transmission dans les hôpitaux et les les funérailles :
- \(p_{ETU}\) la proportion de cas hospitalisés contribuant à l’infection de personnes sensibles (ETU = unités de traitement du virus Ebola),
- \(p_{funeral}\) la proportion de funérailles au cours desquelles le risque de transmission est le même que pour les personnes infectieuses dans la communauté.
Ce modèle étant stochastique, il constitue le choix le plus approprié pour étudier la variation du nombre de personnes infectées au cours des premières phases d’une épidémie d’Ebola.
Devrais-je utiliser un modèle mathématique ?
Les modèles mathématiques peuvent être utilisés pour générer des trajectoires de maladie, qui peuvent ensuite être utilisées pour calculer la taille finale de l’épidémie. Si seule la taille finale vous intéresse, il est possible d’utiliser la théorie mathématique pour calculer directement cette quantité, sans avoir à simuler le modèle complet puis déterminer le nombre d’individus infectés. Ces calculs mathématiques sont effectués à l’aide de fonctions R dans le paquetage finalsize.
L’avantage d’utiliser finalsize est que moins de
paramètres sont nécessaires. Il suffit de définir la transmissibilité et
la susceptibilité de la population, ainsi qu’une matrice de contacts si
pertinent, plutôt que des paramètres tels que la période infectieuse,
qui sont nécessaires dans le cadre du package {epidemics} pour simuler
la dynamique dans le temps. Consultez la page vignettes
du paquet pour plus d’informations sur l’utilisation de
finalsize pour calculer la taille de l’épidémie.
Défi : Analyse de l’épidémie d’Ebola
Exécution du modèle
Vous avez été chargé de générer les trajectoires initiales d’une
épidémie d’Ebola en Guinée. En utilisant model_ebola() et
les informations détaillées ci-dessous, effectuez les tâches suivantes
:
- Exécutez le modèle une fois et représentez graphiquement le nombre d’individus infectieux au fil du temps.
- Exécutez le modèle 100 fois et représentez la moyenne, les quantiles supérieurs et inférieurs à 95 % du nombre d’individus infectieux en fonction du temps.
- Taille de la population : 14 millions
- Nombre initial d’individus exposés : 10
- Nombre initial d’individus infectieux : 5
- Durée de la simulation : 120 jours
- Valeurs des paramètres :
-
\(R_0\) (
r0) = 1.1, -
\(p^I\)
(
infectious_period) = 12, -
\(p^E\)
(
preinfectious_period) = 5, - \(k^E=k^I = 2\),
-
\(1-p_{hosp}\)
(
prop_community) = 0.9, -
\(p_{ETU}\) (
etu_risk) = 0.7, -
\(p_{funeral}\)
(
funeral_risk) = 0.5
-
\(R_0\) (
R
# définir la taille de la population
population_size <- 14e6
E0 <- 10
I0 <- 5
# préparer les conditions initiales sous forme de proportions.
initial_conditions <- c(
S = population_size - (E0 + I0), E = E0, I = I0, H = 0, F = 0, R = 0
) / population_size
guinea_population <- population(
name = "Guinea",
contact_matrix = matrix(1), # note dummy value
demography_vector = population_size, # 14 million, no age groups
initial_conditions = matrix(
initial_conditions,
nrow = 1
)
)
Adaptez le code de la section prise en compte de l’incertitude
- Exécutez le modèle une fois et représentez le nombre d’individus infectieux en fonction du temps.
R
output <- model_ebola(
population = guinea_population,
transmission_rate = 1.1 / 12,
infectiousness_rate = 2.0 / 5,
removal_rate = 2.0 / 12,
prop_community = 0.9,
etu_risk = 0.7,
funeral_risk = 0.5,
time_end = 100,
replicates = 1 # replicates argument
)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
geom_line(
aes(time, value),
linewidth = 1.2
) +
scale_y_continuous(
labels = scales::comma
) +
labs(
x = "Simulation time (days)",
y = "Individuals"
) +
theme_bw(
base_size = 15
)
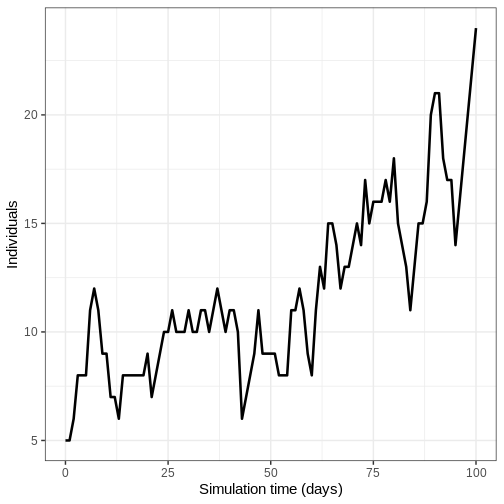
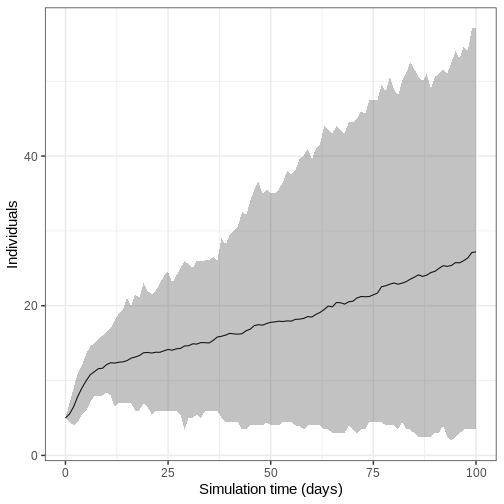
- Exécutez le modèle 100 fois et représentez la moyenne, les quantiles supérieurs et inférieurs à 95 % du nombre d’individus infectieux en fonction du temps.
Nous exécutons le modèle 100 fois avec les même valeurs des paramètres.
R
output_replicates <- model_ebola(
population = guinea_population,
transmission_rate = 1.1 / 12,
infectiousness_rate = 2.0 / 5,
removal_rate = 2.0 / 12,
prop_community = 0.9,
etu_risk = 0.7,
funeral_risk = 0.5,
time_end = 100,
replicates = 100 # replicates argument
)
output_replicates %>%
filter(compartment == "infectious") %>%
ggplot(
aes(time, value)
) +
stat_summary(geom = "line", fun = mean) +
stat_summary(
geom = "ribbon",
fun.min = function(z) {
quantile(z, 0.025)
},
fun.max = function(z) {
quantile(z, 0.975)
},
alpha = 0.3
) +
labs(
x = "Simulation time (days)",
y = "Individuals"
) +
theme_bw(
base_size = 15
)
Points clés
- Les modèles mathématiques existants doivent être sélectionnés en fonction de la question de recherche.
- Il est important de vérifier qu’un modèle repose sur des hypothèses appropriées concernant la transmission, le potentiel épidémique, les résultats et les interventions.
Content from Modélisation des interventions
Dernière mise à jour le 2025-11-23 | Modifier cette page
Durée estimée : 75 minutes
Vue d'ensemble
Questions
- Comment étudier l’effet des interventions sur les trajectoires des maladies ?
Objectifs
- Ajoutez les interventions pharmaceutiques et non pharmaceutiques à
la liste des interventions d’un modèle crée avec le package
{epidemics}
Pré-requis
- Compléter le tutoriel sur La simulation de la transmission.
Les apprenants doivent également se familiariser avec les dépendances des concepts suivants avant de travailler sur ce tutoriel :
Réponse à l’épidémie : Types d’intervention.
R packages installés: {epidemics},
socialmixr, scales,
tidyverse.
Installer les packages si elles ne le sont pas déjà:
R
if (!base::require("pak")) install.packages("pak")
pak::pak(c("epiverse-trace/epidemics", "socialmixr", "scales", "tidyverse"))
Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.
Introduction
Les modèles mathématiques peuvent être utilisés pour générer des trajectoires de propagation de maladies dans le cadre de la mise en œuvre d’interventions à différents stades d’une épidémie. Ces trajectoires peuvent être utilisées pour prendre des décisions sur les interventions à mettre en place pour ralentir la propagation des maladies.
Les interventions sont généralement incorporées dans les modèles mathématiques en manipulant les valeurs des paramètres pertinents, par exemple la réduction de la transmission, ou en introduisant un nouvel état de la maladie, par exemple la classe vaccinée, où nous supposons que les individus qui appartiennent à cette classe ne sont plus susceptibles d’être infectés.
Dans ce tutoriel, nous apprendrons à utiliser le package
{epidemics} pour modéliser les interventions et l’accès aux
données de contact social avec socialmixr. Nous
utiliserons dplyr, ggplot2 et le tuyau
%>% pour relier certaines de leurs fonctions, alors
appelons aussi tidyverse:
R
library(epidemics)
library(socialmixr)
library(tidyverse)
Dans ce tutoriel, on introduit différents types d’intervention et la manière dont ils peuvent être modélisés. Les apprenants devraient être en mesure de comprendre le mécanisme sous-jacent de ces interventions (par exemple, réduire le taux de contact) ainsi que la manière d’implémenter le code pour inclure de telles interventions.
Share with learners the code for the baseline model.
It has different disease parameters than previous episode.
Then start with the livecoding directly with interventions.
Modèle de référence
Nous étudierons l’effet des interventions sur une épidémie de
COVID-19 à l’aide d’un modèle SEIR (model_default() dans le
paquetage R {epidemics}). Pour être en mesure de voir
l’effet de notre intervention, nous exécutons également une variante de
base du modèle, c’est-à-dire sans intervention.
Le modèle SEIR divise la population en quatre compartiments : Susceptible (S), Exposé (E), Infectieux (I) et Rétabli (R). Nous définirons les paramètres suivants pour notre modèle : \(R_0 = 2.7\) (nombre de reproduction de base), période de latence ou période pré-infectieuse \(= 4\) jours, et la période infectieuse \(= 5.5\) jours (paramètres adaptés de Davies et al. (2020)). Nous adoptons une matrice de contact avec des tranches d’âge 0-18, 18-65, 65 ans et plus en utilisant socialmixr et supposons qu’un individu sur un million dans chaque groupe d’âge est contagieux au début de l’épidémie.
R
# charger les données de l'enquête
survey_data <- socialmixr::polymod
# générer une matrice de contacts
cm_results <- socialmixr::contact_matrix(
survey = survey_data,
countries = "United Kingdom",
age.limits = c(0, 15, 65),
symmetric = TRUE
)
# prépare la matrice de contact
cm_matrix <- t(cm_results$matrix)
# prépare le vecteur de la démographie
demography_vector <- cm_results$demography$population
names(demography_vector) <- rownames(cm_matrix)
# conditions initiales: une personne sur un million est infecté
initial_i <- 1e-6
initial_conditions <- c(
S = 1 - initial_i,
E = 0,
I = initial_i,
R = 0,
V = 0
)
# crée la matrice de conditions initiales pour chaque tranche d'âge
initial_conditions <- base::rbind(
initial_conditions,
initial_conditions,
initial_conditions
)
rownames(initial_conditions) <- rownames(cm_matrix)
# prépare la population à modéliser comme étant touchée par l'épidémie
uk_population <- epidemics::population(
name = "UK",
contact_matrix = cm_matrix,
demography_vector = demography_vector,
initial_conditions = initial_conditions
)
En utilisant le taux d’infectiosité \(= 1/4\), le taux de guérison \(= 1/5.5\) et le taux de transmission \(= 2.7/5.5\) (rappelez-vous que taux de transmission = \(R_0\)* taux de guérison) comme suit :
R
# périodes de temp
preinfectious_period <- 4.0
infectious_period <- 5.5
basic_reproduction <- 2.7
# taux
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
transmission_rate <- basic_reproduction * recovery_rate
# exécuter une variante de base du modèle sans intervention
output_baseline <- epidemics::model_default(
population = uk_population,
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0
)
Make a pause.
Use slides to introduce the topics of:
- Non pharmaceutical interventions.
Then continue with the livecoding.
Interventions non-pharmaceutiques
Interventions non-pharmaceutiques Les interventions non pharmaceutiques (INP) sont des mesures mises en place pour réduire la transmission qui n’incluent pas l’administration de médicaments ou de vaccins. Les IPN visent à réduire les contacts entre les personnes infectieuses et les personnes sensibles en fermant les écoles et les lieux de travail et en prenant d’autres mesures pour empêcher la propagation de la maladie, par exemple en se lavant les mains et en portant des masques.
Effet des fermetures d’écoles sur la propagation de COVID-19
Le premier IPN que nous examinerons est l’effet des fermetures d’écoles sur la réduction du nombre de personnes infectées par le COVID-19 au fil du temps. Nous supposons qu’une fermeture d’école réduit la fréquence des contacts au sein des différents groupes d’âge et entre eux. Sur la base d’études empiriques, nous supposons que les fermetures d’écoles réduiront de 50 % les contacts entre enfants d’âge scolaire (0-15 ans) et entraîneront une faible réduction (1 %) des contacts entre adultes (15 ans et plus).
Pour inclure une intervention dans notre modèle, nous devons créer un
objet intervention. Les données d’entrée sont le nom de
l’intervention (name), le type d’intervention
(contacts ou rate), l’heure de début
(time_begin), l’heure de fin (time_end) et la
réduction (reduction). Les valeurs de la matrice de
réduction sont spécifiées dans le même ordre que les groupes d’âge dans
la matrice de contact.
R
rownames(cm_matrix)
SORTIE
[1] "[0,15)" "[15,65)" "65+" Par conséquent, nous spécifions
reduction = matrix(c(0.5, 0.01, 0.01)). Nous supposons que
les fermetures d’écoles commencent le 50e jour et se poursuivent pendant
100 jours supplémentaires. Notre objet d’intervention est donc :
R
close_schools <- epidemics::intervention(
name = "School closure",
type = "contacts",
time_begin = 50,
time_end = 50 + 100,
reduction = matrix(c(0.5, 0.01, 0.01))
)
Effet des interventions sur les contacts
Dans le cadre de {epidemics} la matrice des contacts est
réduite par des proportions pour la période pendant laquelle
l’intervention est en place. Pour comprendre comment la réduction est
calculée dans les fonctions du modèle, considérons une matrice de
contacts pour deux groupes d’âge avec un nombre égal de contacts :
SORTIE
[,1] [,2]
[1,] 1 1
[2,] 1 1Si la réduction est de 50 % dans le groupe 1 et de 10 % dans le groupe 2, la matrice des contacts pendant l’intervention sera la suivante :
SORTIE
[,1] [,2]
[1,] 0.25 0.45
[2,] 0.45 0.81Les contacts au sein du groupe 1 sont réduits de 50 % deux fois pour tenir compte d’une réduction de 50 % des contacts sortants et entrants (\(1\times 0.5 \times 0.5 = 0.25\)). De même, les contacts au sein du groupe 2 sont réduits deux fois de 10 %. Les contacts entre le groupe 1 et le groupe 2 sont réduits de 50 %, puis de 10 % (\(1 \times 0.5 \times 0.9= 0.45\)).
Nous exécutons le modèle avec
intervention = list(contacts = close_schools) comme suit
:
R
output_school <- epidemics::model_default(
# population
population = uk_population,
# taux
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
intervention = list(contacts = close_schools),
# temps
time_end = 300, increment = 1.0
)
Pour observer l’effet de notre intervention, nous combinerons les
sorties du modèle de référence et celles de l’intervention dans un seul
tableau de données, puis nous tracerons les résultats. Ici, nous
représentons le nombre total d’individus infectieux dans tous les
groupes d’âge en utilisant les données suivantes
ggplot2::stat_summary() fonction :
R
# créer une colonne intervention_type pour le graphique
output_school$intervention_type <- "school closure"
output_baseline$intervention_type <- "baseline"
output <- base::rbind(output_school, output_baseline)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
close_schools$time_begin,
close_schools$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
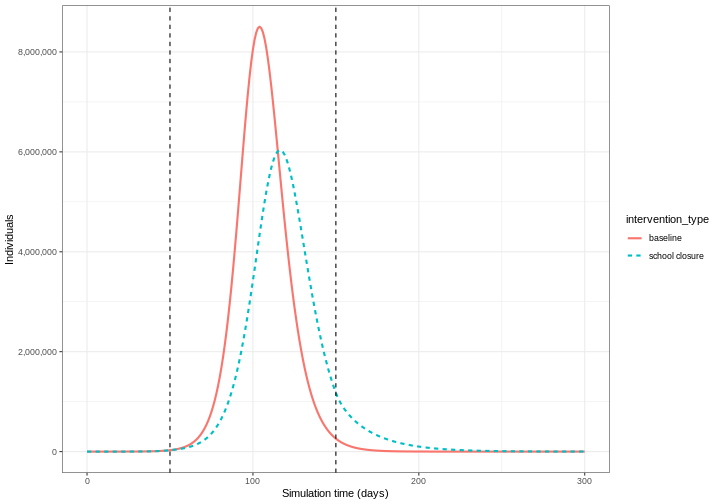
Nous pouvons constater qu’avec l’intervention en place, l’infection se propage toujours dans la population et que l’accumulation de l’immunité contribue à l’éventuel pic et déclin. Toutefois, le nombre maximal de personnes infectées est inférieur (ligne pointillée verte) à la ligne de base sans intervention (ligne continue rouge), ce qui montre une réduction du nombre absolu de cas.
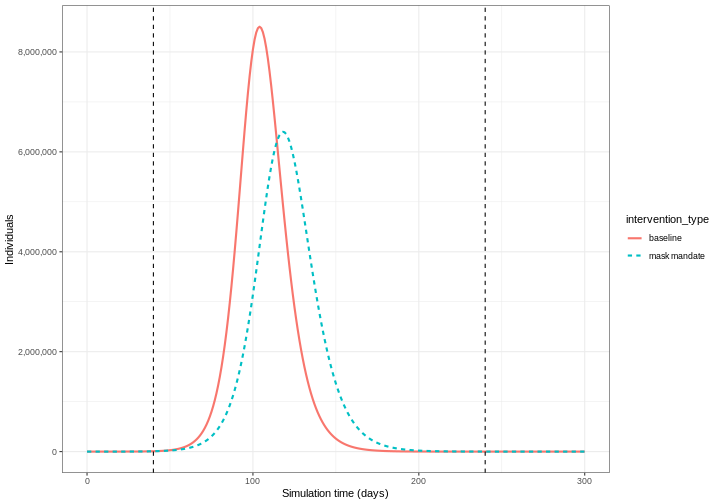
Effet du port du masque sur la propagation de COVID-19
Nous pouvons également modéliser l’effet d’autres IPN en réduisant la valeur des paramètres pertinents. Par exemple, étudier l’effet du port du masque sur le nombre de personnes infectées par COVID-19 au fil du temps.
Nous nous attendons à ce que le port du masque réduise la contagiosité d’un individu, sur la base de nombreuses études montrant l’efficacité des masques dans la réduction de la transmission. Comme nous utilisons un modèle basé sur la population, nous ne pouvons pas modifier les comportements individuels et nous supposons donc que le taux de transmission \(\beta\) est réduit par une proportion due au port du masque dans la population. Nous spécifions cette proportion, \(\theta\) comme le produit de la proportion de personnes portant un masque multiplié par la proportion de réduction du taux de transmission (adapté de Li et al. 2020).
Nous créons un objet d’intervention avec type = "rate"
et reduction = 0.161. En utilisant des paramètres adaptés
de Li et
al. 2020 nous avons la proportion de personnes portant des masques =
couverture \(\times\) disponibilité =
\(0.54 \times 0.525 = 0.2835\) et la
proportion de réduction du taux de transmission = \(0.575\). Par conséquent, \(\theta = 0.2835 \times 0.575 = 0.163\).
Nous supposons que l’obligation de porter un masque commence au 40e jour
et reste en vigueur pendant 200 jours.
R
mask_mandate <- epidemics::intervention(
name = "mask mandate",
type = "rate",
time_begin = 40,
time_end = 40 + 200,
reduction = 0.163
)
Pour mettre en œuvre cette intervention sur le taux de transmission
\(\beta\) nous spécifions
intervention = list(transmission_rate = mask_mandate).
R
output_masks <- epidemics::model_default(
# population
population = uk_population,
# taux
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
intervention = list(transmission_rate = mask_mandate),
# temps
time_end = 300, increment = 1.0
)
R
# créer une colonne intervention_type pour le graphique
output_masks$intervention_type <- "mask mandate"
output_baseline$intervention_type <- "baseline"
output <- base::rbind(output_masks, output_baseline)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
mask_mandate$time_begin,
mask_mandate$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
Types d’intervention
Il existe deux types d’intervention pour
model_default(). Interventions sur les paramètres du modèle
(transmission_rate \(\beta\), infectiousness_rate
\(\sigma\) et
recovery_rate \(\gamma\))
et les réductions des matrices de contact (contacts).
Pour mettre en œuvre les interventions sur les contacts et les taux
dans la même simulation, elles doivent être transmises sous la forme
d’une liste, par exemple,
intervention = list(transmission_rate = mask_mandate, contacts = close_schools).
Toutefois, si plusieurs interventions ciblent les taux de contact, elles
doivent être transmises sous la forme d’une seule entrée du modèle
contacts. Voir la vignette
sur la modélisation des interventions qui se chevauchent pour plus
de détails.
Make a pause.
Use slides to introduce the topics of:
- Pharmaceutical interventions.
Then continue with the livecoding.
Interventions pharmaceutiques
Les interventions pharmaceutiques (IP) sont des mesures telles que les programmes de vaccination et de traitement de masse. Dans la section précédente, nous avons intégré les interventions dans le modèle en réduisant les valeurs des paramètres pendant une période spécifique de la fenêtre temporelle au cours de laquelle ces interventions doivent avoir lieu. Dans le cas de la vaccination, nous supposons qu’après l’intervention, les individus ne sont plus sensibles et doivent être classés dans un état pathologique différent. Par conséquent, nous spécifions le taux auquel les individus sont vaccinés et suivons le nombre d’individus vaccinés au fil du temps.
Le diagramme ci-dessous montre le modèle SEIRV mis en œuvre à l’aide
de model_default() où les individus sensibles sont vaccinés
et passent ensuite à l’étape de la vaccination. \(V\) classe.
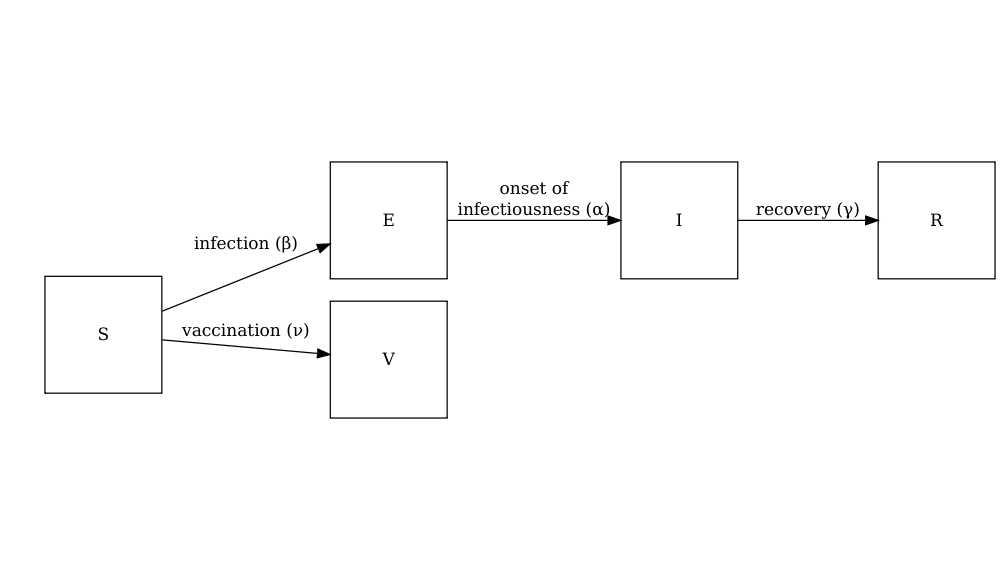
Les équations décrivant ce modèle sont les suivantes :
\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j -\nu_{t} S_i \\ \frac{dE_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \alpha E_i \\ \frac{dI_i}{dt} &= \alpha E_i - \gamma I_i \\ \frac{dR_i}{dt} &=\gamma I_i \\ \frac{dV_i}{dt} & =\nu_{i,t} S_i\\ \end{aligned} \]
Les individus de la tranche d’âge (\(i\)) à un moment spécifique (\(t\)) sont vaccinés à un taux (\(\nu_{i,t}\)). Les autres composantes SEIR de ces équations sont décrites dans le tutoriel simuler la transmission.
Pour étudier l’effet de la vaccination, nous devons créer un objet de
vaccination que nous transmettrons en tant qu’entrée à la fonction
model_default() qui comprend le taux de vaccination pour
chaque tranche d’âge nu et les dates de début et de fin du
programme de vaccination pour chaque tranche d’âge
(time_begin et time_end).
Nous supposerons ici que tous les groupes d’âge sont vaccinés au même taux (0,01) et que le programme de vaccination commence au 40e jour et se poursuit pendant 150 jours.
R
# prépare un object de vaccination
vaccinate <- epidemics::vaccination(
name = "vaccinate all",
time_begin = matrix(40, nrow(cm_matrix)),
time_end = matrix(40 + 150, nrow(cm_matrix)),
nu = matrix(c(0.01, 0.01, 0.01))
)
Nous passons notre objet de vaccination dans le modèle en utilisant
l’argument vaccination = vaccinate:
R
output_vaccinate <- epidemics::model_default(
# population
population = uk_population,
# rate
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
vaccination = vaccinate,
# time
time_end = 300, increment = 1.0
)
Comparez les interventions
Représentez sur un même graphique les trois interventions (vaccination, fermeture des écoles et obligation de porter un masque) et la simulation de référence sans intervention. Quelle intervention réduit le plus le nombre maximal de personnes infectieuses ?
R
# create intervention_type column for plotting
output_vaccinate$intervention_type <- "vaccination"
output <- base::rbind(
output_school,
output_masks,
output_vaccinate,
output_baseline
)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
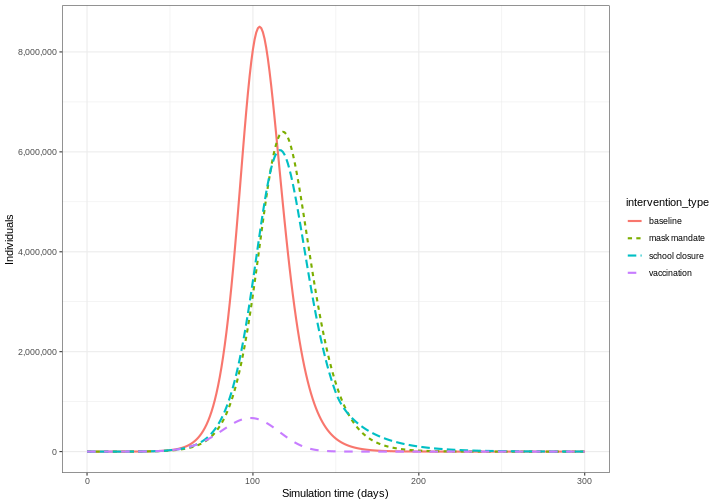
Le graphique montre que le pic du nombre total d’individus infectieux en cas de vaccination est beaucoup plus faible que lors des fermetures d’écoles et des interventions avec port du masque.
Enfin, si vous souhaitez représenter graphiquement les nouvelles
infections à partir d’un object de
epidemics::model_default() qui inclut la
vaccination, vous devez ajouter un argument à
epidemics::new_infections() : définissez
exclude_compartments = "vaccinated" pour indiquer à la
fonction que les personnes passant de « susceptibles » à « vaccinées »
ne sont pas infectées. Cela garantit que les personnes vaccinées ne
seront pas comptées comme des infections.
Notez que si nous ajoutons by_group = FALSE dans epidemics::new_infections(), nous obtenons un résumé des nouvelles infections dans la population.
R
infections_baseline <- epidemics::new_infections(
data = output_baseline,
exclude_compartments = "vaccinated", # if vaccination
by_group = FALSE
)
infections_intervention <- epidemics::new_infections(
data = output_vaccinate,
exclude_compartments = "vaccinated", # if vaccination
by_group = FALSE
)
# Assigner les noms des scénarios
infections_baseline$scenario <- "Baseline"
infections_intervention$scenario <- "Vaccination"
# Combiner les données des deux scénarios
infections_baseline_interv <- dplyr::bind_rows(
infections_baseline,
infections_intervention
)
infections_baseline_interv %>%
ggplot(aes(x = time, y = new_infections, colour = scenario)) +
geom_line() +
geom_vline(
xintercept = c(vaccinate$time_begin, vaccinate$time_end),
linetype = "dashed",
linewidth = 0.2
) +
scale_y_continuous(labels = scales::comma) +
theme_bw()
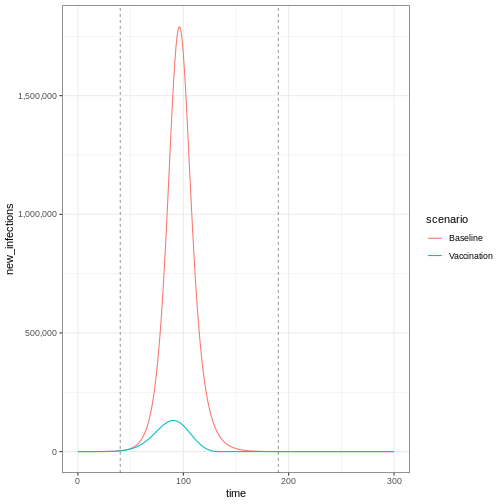
Pour obtenir un graphique stratifié par âge, conservez la valeur par
défaut by_group = TRUE, puis ajoutez
linetype = demography_group lors de la déclaration des
variables dans ggplot(aes(...)).
Stop the livecoding.
Suggest learners to read the next episode.
Return to slides.
Résumé
Différents types d’intervention peuvent être mis en œuvre à l’aide de la modélisation mathématique. La modélisation des interventions nécessite des hypothèses sur les paramètres du modèle qui sont affectés (par exemple, les matrices de contact, le taux de transmission), ainsi que sur l’ampleur et le moment de la simulation d’une épidémie.
L’étape suivante consiste à quantifier l’effet d’une intervention. Si vous souhaitez apprendre à comparer les interventions, veuillez suivre le tutoriel suivant Comparer les résultats des interventions en matière de santé publique.
Points clés
- L’effet des NPI peut être modélisé comme une réduction des taux de contact entre les groupes d’âge ou une réduction du taux de transmission de l’infection.
- La vaccination peut être modélisée en supposant que les individus passent à un état pathologique différent \(V\).
Références
Davies, N. G., Klepac, P., Liu, Y., Prem, K., Jit, M. et Eggo, R. M. (2020). Age-dependent effects in the transmission and control of COVID-19 epidemics (Effets dépendants de l’âge dans la transmission et le contrôle des épidémies de COVID-19). Nature Medicine, 26(8), 1205-1211. https://doi.org/10.1016/S2468-2667\(20\)30133-X
Li, Y., Liang, M., Gao, L., Ahmed, M. A., Uy, J. P., Cheng, C., … & Sun, C. (2020). Masques de protection pour prévenir la transmission du COVID-19 : A systematic review and meta-analysis. American Journal of Infection Control, 49(7), 900-906. https://doi.org/10.1371/journal.pone.0237691
Mossong, J., Hens, N., Jit, M., Beutels, P., Auranen, K., Mikolajczyk, R., … & Edmunds, W. J. (2008). Social contacts and mixing patterns relevant to the spread of infectious diseases (contacts sociaux et modèles de mélange pertinents pour la propagation des maladies infectieuses). PLoS medicine, 5(3), e74. https://doi.org/10.1371/journal.pmed.0050074
Content from Comparer les résultats des interventions de santé publique
Dernière mise à jour le 2025-11-23 | Modifier cette page
Durée estimée : 75 minutes
Vue d'ensemble
Questions
- Comment puis-je quantifier l’effet d’une intervention ?
Objectifs
- Comparez les scénarios d’intervention
Pré-requis
- Compléter les tutoriels Simuler la transmission et Modélisation des interventions
Les apprenants doivent se familiariser avec les dépendances conceptuelles suivantes avant de travailler sur ce didacticiel :
Réponse à l’épidémie : Types d’intervention.
Introduction
Dans ce tutoriel, nous allons comparer des scénarios d’intervention les uns par rapport aux autres. Pour quantifier l’effet d’une intervention, nous devons comparer notre scénario d’intervention à un scénario contrefactuel (de référence). Le scénario contrefactuel est le scénario dans lequel rien ne change, souvent appelé “scénario du statu quo”. Le scénario contrefactuel peut consister de :
- Aucune intervention, ou
- Interventions existantes (si nous étudions l’impact potentiel d’une intervention supplémentaire)
Nous devons également définir nos résultat d’intérêt afin d’établir des comparaisons entre les scénarios d’intervention et les scénarios contrefactuels. Le résultat d’intérêt peut être :
- Les résultats directs du modèle (par exemple, le nombre d’infections, d’hospitalisations)
- Mesures épidémiologiques (par exemple, période de pic de l’épidémie, sa taille finale)
- Mesures de l’impact sur la santé (par exemple, années de vie ajustée par la qualité [AVAQs] ou les années de vie corrigées de l’incapacité [AVCI] )
- Mesures économiques (par exemple, coûts des soins de santé, pertes de productivité)
Dans ce tutoriel, nous allons apprendre à utiliser le package
{epidemics} dans R pour comparer l’effet de différentes
interventions sur des trajectoires d’épidémies simulées. Nous
utiliserons socialmixr pour les données sur les contacts
sociaux et tidyverse (y compris dplyr,
ggplot2 et le tuyau %>%) pour la
manipulation et la visualisation des données.
R
library(epidemics)
library(socialmixr)
library(tidyverse)
Dans ce tutoriel, nous introduisons le concept de contrefactuel et la manière de comparer des scénarios (contrefactuel versus intervention) les uns par rapport aux autres.
Visualiser l’effet des interventions
Pour comparer le scénario de base aux scénarios d’intervention, nous pouvons visualiser le résultat qui nous intéresse. Ce résultat peut être simplement la sortie du modèle ou une mesure agrégée de la sortie du modèle.
Si nous voulons étudier le changementdu pic épidémique après l’application d’une intervention, nous pouvons tracer les trajectoires du modèle dans le temps :
R
output_baseline <- epidemics::model_default(
population = uk_population,
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0
)
output_school <- epidemics::model_default(
# population
population = uk_population,
# rate
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
intervention = list(contacts = close_schools),
# time
time_end = 300, increment = 1.0
)
# create intervention_type column for plotting
output_school$intervention_type <- "school closure"
output_baseline$intervention_type <- "baseline"
output <- rbind(output_school, output_baseline)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
close_schools$time_begin,
close_schools$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
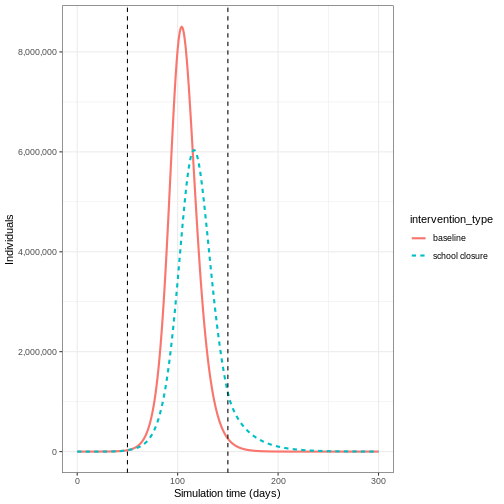
Si nous voulons quantifier l’impact de l’intervention sur les résultats du modèle dans le temps, nous pouvons considérer le nombre cumulé de personnes infectieuses dans le scénario de base par rapport au scénario d’intervention :
R
output %>%
filter(compartment == "infectious") %>%
group_by(time, intervention_type) %>%
summarise(value_total = sum(value)) %>%
group_by(intervention_type) %>%
mutate(cum_value = cumsum(value_total)) %>%
ggplot() +
geom_line(
aes(
x = time,
y = cum_value,
color = intervention_type,
linetype = intervention_type
),
linewidth = 1.2
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
close_schools$time_begin,
close_schools$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Cumulative number of infectious individuals"
)
SORTIE
`summarise()` has grouped output by 'time'. You can override using the
`.groups` argument.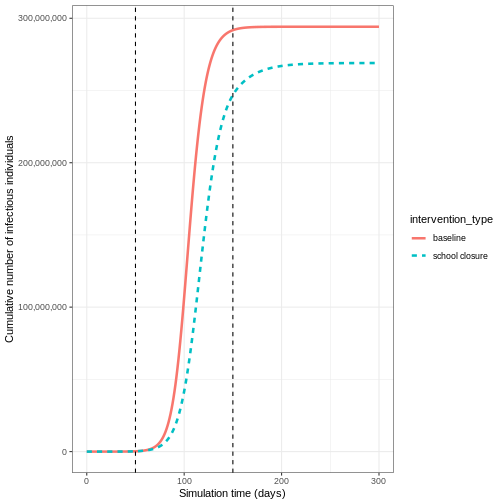
Modèle Vacamole
Le modèle Vacamole est un modèle déterministe basé sur un système d’équations différentielles ordinaires (ODE) développé par Ainslie et al. (2022) pour décrire l’effet de la vaccination sur la dynamique de COVID-19. Le modèle se compose de 11 compartiments, dans lesquels les individus sont classés comme suit :
- Susceptibles (\(S\))
- Partiellement vacciné (\(V_1\))
- Totalement vacciné (\(V_2\))
- Exposé (\(E\)) et exposé alors qu’ils sontvacciné (\(E_V\))
- Infectieux (\(I\)) et infectieux en cas de vaccination (\(I_V\))
- Hospitalisé (\(H\)) et hospitalisé alors qu’ils étaient vacciné (\(H_V\))
- Mort (\(D\))
- Récupéré (\(R\))
Le schéma ci-dessous décrit le flux d’individus à travers les différents compartiments.
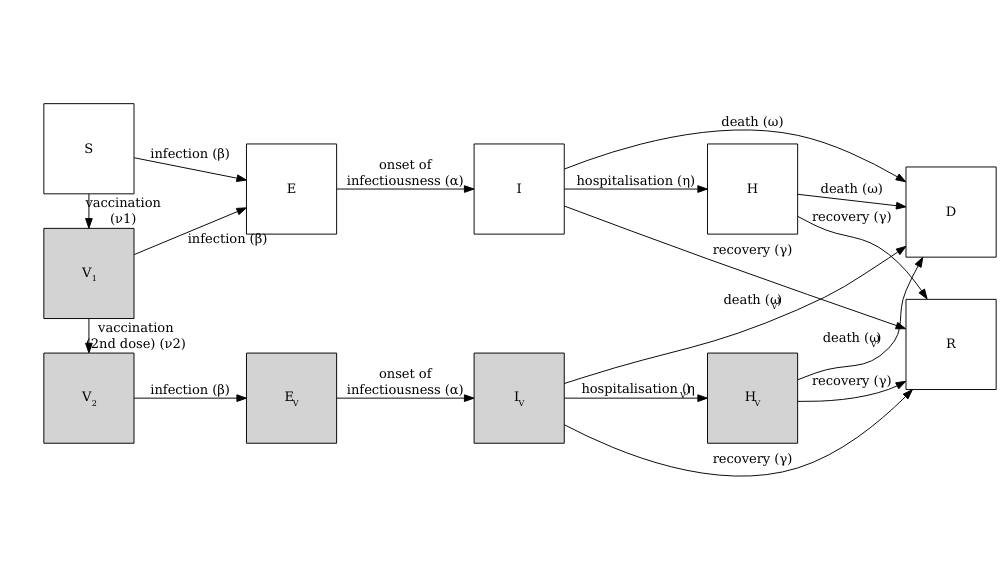
Exécution d’un scénario contrefactuel à l’aide du modèle Vacamole
- Exécutez le modèle avec les valeurs par défaut de paramètres pour la population britannique en supposant que :
- un individu sur un million (0,0001 %) est contagieux (et non vacciné) au début de la simulation.
- La matrice des contacts pour le Royaume-Uni comporte les tranches
d’âge suivantes :
- 0-20 ans
- 20-40 ans
- 40 ans et plus
Pour les scénarios suivants :
- Scénario de base : Programme de vaccination à deux doses
- La dose 1 (taux de vaccination 0,01) commence à partir du jour 30.
- La dose 2 (taux de vaccination 0,01) est administrée à partir du 60e jour.
- Les deux programmes durent 300 jours
- Intervention : Mandat de masque
- Commence à partir du jour 60
- Durée de 100 jours
- Réduit le taux de transmission de 16,3 % (d’après des études empiriques sur l’efficacité des masques)
Il n’y a pas de programme de vaccination en place
- À l’aide du résultat, tracez le nombre cumulé de décès au fil du temps.
Nous pouvons exécuter le modèle Vacamole avec les valeurs par défaut de paramètres en spécifiant simplement l’objet de la population et le nombre de pas de temps pour lesquels le modèle doit être exécuté :
R
output <- epidemics::model_vacamole(
population = uk_population,
time_end = 300
)
- Exécutez le modèle
R
polymod <- socialmixr::polymod
contact_data <- socialmixr::contact_matrix(
survey = polymod,
countries = "United Kingdom",
age.limits = c(0, 20, 40),
symmetric = TRUE
)
SORTIE
Removing participants that have contacts without age information. To change this behaviour, set the 'missing.contact.age' optionR
# prepare contact matrix
contact_matrix <- t(contact_data$matrix)
# extract demography vector
demography_vector <- contact_data$demography$population
names(demography_vector) <- rownames(contact_matrix)
# prepare initial conditions
initial_i <- 1e-6
initial_conditions_vacamole <- c(
S = 1 - initial_i,
V1 = 0, V2 = 0,
E = 0, EV = 0,
I = initial_i, IV = 0,
H = 0, HV = 0, D = 0, R = 0
)
initial_conditions_vacamole <- rbind(
initial_conditions_vacamole,
initial_conditions_vacamole,
initial_conditions_vacamole
)
rownames(initial_conditions_vacamole) <- rownames(contact_matrix)
# prepare population object
uk_population_vacamole <- epidemics::population(
name = "UK",
contact_matrix = contact_matrix,
demography_vector = demography_vector,
initial_conditions = initial_conditions_vacamole
)
# prepare two vaccination objects
# dose 1 vaccination
dose_1 <- epidemics::vaccination(
name = "two-dose vaccination", # name given to first dose
nu = matrix(0.01, nrow = 3),
time_begin = matrix(30, nrow = 3),
time_end = matrix(300, nrow = 3)
)
# prepare the second dose with a 30 day interval in start date
dose_2 <- epidemics::vaccination(
name = "two-dose vaccination", # name given to first dose
nu = matrix(0.01, nrow = 3),
time_begin = matrix(30 + 30, nrow = 3),
time_end = matrix(300, nrow = 3)
)
# use `c()` to combine the two doses
double_vaccination <- c(dose_1, dose_2)
# run baseline model
output_baseline_vc <- epidemics::model_vacamole(
population = uk_population_vacamole,
vaccination = double_vaccination,
time_end = 300
)
# create mask intervention
mask_mandate <- epidemics::intervention(
name = "mask mandate",
type = "rate",
time_begin = 60,
time_end = 60 + 100,
reduction = 0.163
)
# run intervention model
output_intervention_vc <- epidemics::model_vacamole(
population = uk_population_vacamole,
vaccination = double_vaccination,
intervention = list(
transmission_rate = mask_mandate
),
time_end = 300
)
- Tracez le nombre cumulé de décès au fil du temps
R
# create intervention_type column for plotting
output_intervention_vc$intervention_type <- "mask mandate"
output_baseline_vc$intervention_type <- "baseline"
output_vacamole <- rbind(output_intervention_vc, output_baseline_vc)
output_vacamole %>%
filter(compartment == "dead") %>%
group_by(time, intervention_type) %>%
summarise(value_total = sum(value)) %>%
group_by(intervention_type) %>%
mutate(cum_value = cumsum(value_total)) %>%
ggplot() +
geom_line(
aes(
x = time,
y = cum_value,
color = intervention_type,
linetype = intervention_type
),
linewidth = 1.2
) +
scale_y_continuous(
labels = scales::comma
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Cumulative number of deaths"
)
SORTIE
`summarise()` has grouped output by 'time'. You can override using the
`.groups` argument.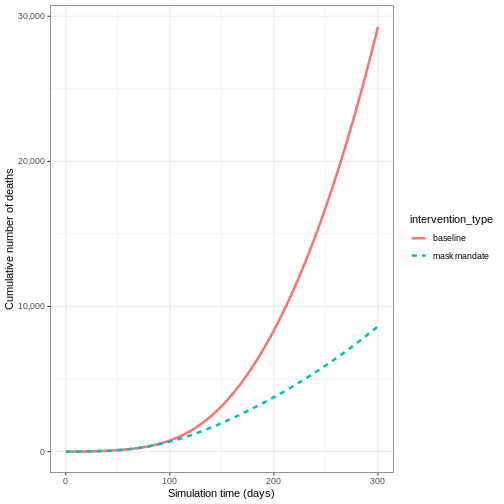
Calcul des résultats évités
Si les visualisations sont utiles pour comparer les scénarios d’intervention dans le temps, nous avons également besoin des mesures pour quantifier l’impact de l’intervention. Une de ces mesures est le nombre d’infections évitées, qui nous aide à comprendre la différence entre les scénarios d’intervention.
Le package {epidemics} de R fournit l’outil
outcomes_averted() pour calculer les infections évitées en
tenant compte de l’incertitude des paramètres. Étendons notre exemple
COVID-19 de Modélisation des
interventions pour tenir compte de l’incertitude concernant le
nombre de reproduction de base (\(R_0\)).
R
# time periods
preinfectious_period <- 4.0
infectious_period <- 5.5
# specify the mean and standard deviation of R0
r_estimate_mean <- 2.7
r_estimate_sd <- 0.05
# generate 100 R samples
r_samples <- withr::with_seed(
seed = 1,
rnorm(
n = 100, mean = r_estimate_mean, sd = r_estimate_sd
)
)
beta <- r_samples / infectious_period
# rates
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
Nous utilisons ces valeurs de paramètres en même temps que la structure de la population et la matrice de contact utilisées dans le Modélisation des interventions afin d’exécuter le modèle pour le scénario de base :
R
output_baseline <- epidemics::model_default(
population = uk_population,
transmission_rate = beta,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0
)
Ensuite, nous créons une liste de toutes les interventions que nous voulons inclure dans notre comparaison. Nous définissons nos scénarios comme suit :
- scénario 1 : fermer les écoles
- scénario 2 : mandat de masque
- scénario 3 : fermeture des écoles et mandat de masque.
Dans R, nous spécifions ceci comme :
R
intervention_scenarios <- list(
scenario_1 = list(
contacts = close_schools
),
scenario_2 = list(
transmission_rate = mask_mandate
),
scenario_3 = list(
contacts = close_schools,
transmission_rate = mask_mandate
)
)
Nous utilisons cette liste comme entrée pour
intervention dans model_default
R
output <- epidemics::model_default(
uk_population,
transmission_rate = beta,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0,
intervention = intervention_scenarios
)
head(output)
SORTIE
transmission_rate infectiousness_rate recovery_rate time_end param_set
<num> <num> <num> <num> <int>
1: 0.4852141 0.25 0.1818182 300 1
2: 0.4852141 0.25 0.1818182 300 1
3: 0.4852141 0.25 0.1818182 300 1
4: 0.4925786 0.25 0.1818182 300 2
5: 0.4925786 0.25 0.1818182 300 2
6: 0.4925786 0.25 0.1818182 300 2
population intervention vaccination time_dependence increment scenario
<list> <list> <list> <list> <num> <int>
1: <population[4]> <list[1]> [NULL] <list[1]> 1 1
2: <population[4]> <list[1]> [NULL] <list[1]> 1 2
3: <population[4]> <list[2]> [NULL] <list[1]> 1 3
4: <population[4]> <list[1]> [NULL] <list[1]> 1 1
5: <population[4]> <list[1]> [NULL] <list[1]> 1 2
6: <population[4]> <list[2]> [NULL] <list[1]> 1 3
data
<list>
1: <data.table[4515x4]>
2: <data.table[4515x4]>
3: <data.table[4515x4]>
4: <data.table[4515x4]>
5: <data.table[4515x4]>
6: <data.table[4515x4]>Maintenant que nous avons des résultats de notre modèle pour tous nos scénarios, nous voulons comparer les résultats des interventions à notre base de référence.
Nous pouvons le faire en utilisant outcomes_averted()
dans {epidemics}. Cette fonction calcule la taille finale
de l’épidémie pour chaque scénario, puis le nombre d’infections évitées
dans chaque scénario par rapport à la ligne de base. Pour utiliser cette
fonction, il faut spécifier :
- le résultat du scénario de base
- les résultats des scénario(s) d’intervention.
R
intervention_effect <- epidemics::outcomes_averted(
baseline = output_baseline, scenarios = output
)
intervention_effect
SORTIE
scenario demography_group averted_median averted_lower averted_upper
<int> <char> <num> <num> <num>
1: 1 65+ 405810.5 383340.3 414044.8
2: 1 [0,15) 2890964.4 2577490.7 3082420.9
3: 1 [15,65) 1288482.1 1257862.4 1290841.4
4: 2 65+ 900819.9 882242.1 912790.7
5: 2 [0,15) 517742.8 478431.1 558631.8
6: 2 [15,65) 2413423.7 2259624.9 2566010.9
7: 3 65+ 1004123.7 864726.7 1100018.0
8: 3 [0,15) 1974788.9 1494800.2 2415088.5
9: 3 [15,65) 2908140.6 2546313.2 3129329.3Le résultat nous donne le nombre d’infections évitées dans chaque
scénario par rapport à la ligne de base. Pour obtenir le nombre total
d’infections évitées, nous spécifions by_group = FALSE:
R
intervention_effect <- epidemics::outcomes_averted(
baseline = output_baseline, scenarios = output,
by_group = FALSE
)
intervention_effect
SORTIE
scenario averted_median averted_lower averted_upper
<int> <num> <num> <num>
1: 1 4587505 4220698 4770734
2: 2 3831986 3620298 4037433
3: 3 5887053 4905840 6644436Vignettes de paquets
Nous vous recommandons de lire la vignette sur Modélisation des réponses à une épidémie stochastique de virus Ebola pour utiliser un modèle compartimental stochastique à temps discret d’Ebola utilisé lors de l’épidémie de MVE de 2014 en Afrique de l’Ouest.
Défi : Analyse de l’épidémie d’Ebola
Vous avez été chargé d’étudier l’impact potentiel d’une intervention
sur une épidémie d’Ebola en Guinée (par exemple, une réduction des
contacts à haute risque avec les cas). En utilisant
model_ebola() et les informations détaillées ci-dessous,
trouvez le nombre d’infections évitées lorsque :
- une intervention est appliquée pour réduire le taux de transmission de 50 % à partir du jour 60 et,
- une intervention est appliquée pour réduire la transmission de 10 % à partir du jour 30.
Pour les deux interventions, nous supposons qu’il existe une certaine incertitude quant au taux de transmission de base. Nous capturons cette incertitude en la tirant d’une distribution normale avec une moyenne = 1,1 / 12 (c.-à-d. \(R_0=1.1\) et la période infectieuse = 12 jours) et un écart-type = 0,01.
Remarque : selon le nombre de réplicats utilisés, l’exécution de cette simulation peut prendre plusieurs minutes.
- Taille de la population : 14 millions
- Nombre initial d’individus exposés : 10
- Nombre initial d’individus infectieuses : 5
- Durée de la simulation : 120 jours
- Valeurs des paramètres :
-
\(R_0\) (
r0) = 1.1, -
\(p^I\)
(
infectious_period) = 12, -
\(p^E\)
(
preinfectious_period) = 5, - \(k^E=k^I = 2\),
-
\(1-p_{hosp}\)
(
prop_community) = 0.9, -
\(p_{ETU}\) (
etu_risk) = 0.7, -
\(p_{funeral}\)
(
funeral_risk) = 0.5
-
\(R_0\) (
R
population_size <- 14e6
E0 <- 10
I0 <- 5
# prepare initial conditions as proportions
initial_conditions <- c(
S = population_size - (E0 + I0), E = E0, I = I0, H = 0, F = 0, R = 0
) / population_size
# set up population object
guinea_population <- population(
name = "Guinea",
contact_matrix = matrix(1), # note dummy value
demography_vector = population_size, # 14 million, no age groups
initial_conditions = matrix(
initial_conditions,
nrow = 1
)
)
# generate 100 beta samples
beta <- withr::with_seed(
seed = 1,
rnorm(
n = 100, mean = 1.1 / 12, sd = 0.01
)
)
# run the baseline
output_baseline <- epidemics::model_ebola(
population = guinea_population,
transmission_rate = beta,
infectiousness_rate = 2.0 / 5,
removal_rate = 2.0 / 12,
prop_community = 0.9,
etu_risk = 0.7,
funeral_risk = 0.5,
time_end = 100,
replicates = 100 # replicates argument
)
# create intervention objects
reduce_transmission_1 <- epidemics::intervention(
type = "rate",
time_begin = 60, time_end = 100, reduction = 0.5
)
reduce_transmission_2 <- epidemics::intervention(
type = "rate",
time_begin = 30, time_end = 100, reduction = 0.1
)
# create intervention list
intervention_scenarios <- list(
scenario_1 = list(
transmission_rate = reduce_transmission_1
),
scenario_2 = list(
transmission_rate = reduce_transmission_2
)
)
# run model
output_intervention <- epidemics::model_ebola(
population = guinea_population,
transmission_rate = beta,
infectiousness_rate = 2.0 / 5,
removal_rate = 2.0 / 12,
prop_community = 0.9,
etu_risk = 0.7,
funeral_risk = 0.5,
time_end = 100,
replicates = 100, # replicates argument,
intervention = intervention_scenarios
)
AVERTISSEMENT
Warning: Running 2 scenarios and 100 parameter sets with 100 replicates each, for a
total of 20000 model runs.R
# calculate outcomes averted
intervention_effect <- epidemics::outcomes_averted(
baseline = output_baseline, scenarios = output_intervention,
by_group = FALSE
)
intervention_effect
SORTIE
scenario averted_median averted_lower averted_upper
<int> <num> <num> <num>
1: 1 31 1 112
2: 2 20 -22 105Note : Le nombre d’infections évitées peut être négatif. Cela est dû à la variation stochastique des trajectoires de la maladie pour un taux de transmission donné, qui peut entraîner une épidémie de taille différente.
Points clés
- Un scénario contrefactuel (de référence) doit être clairement défini pour permettre des comparaisons significatives.
- Les scénarios peuvent être comparés à l’aide de visualisations et de mesures quantitatives.
- La fonction outcomes_averted() permet de quantifier les effets des interventions.
- L’incertitude des paramètres doit être prise en compte dans l’analyse des interventions.
