Simulation de la transmission
Dernière mise à jour le 2025-11-23 | Modifier cette page
Durée estimée : 75 minutes
Vue d'ensemble
Questions
- Comment simuler la propagation d’une maladie à l’aide d’un modèle mathématique ?
- Quels sont les données nécessaires à la simulation d’un modèle ?
- Comment tenir compte de l’incertitude ?
Objectifs
- Chargez une structure de modèle existante à partir de la librairie
{epidemics} - Chargez une matrice de contacts sociaux existante avec socialmixr
- Générer une simulation de modèle de propagation d’une maladie avec
{epidemics} - Générer des simulations de plusieurs modèles et visualiser l’incertitude
Pré-requis
- Compléter le tutoriel sur Matrices de contact.
Les apprenants doivent se familiariser avec les concepts suivants pour mieux comprendre les notions abordées dans ce cours.
Modélisation mathématique : Introduction aux modèles de maladies infectieuses, variables d’état, paramètres du modèle, conditions initiales, équations différentielles.
Théorie des épidémies : Transmission, Nombre de reproduction.
R packages installés: {epidemics},
socialmixr, scales,
tidyverse.
Installer les packages si elles ne le sont pas déjà:
R
if (!base::require("pak")) install.packages("pak")
pak::pak(c("epiverse-trace/epidemics", "socialmixr", "scales", "tidyverse"))
Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.
Introduction
Les modèles mathématiques sont des outils essentiels pour générer des
trajectoires futures de propagation de maladies. a librairie
{epidemics} de R contient des fonctionnalités que nous
allons utiliser dans ce tutoriel pour générer des trajectoires de
maladie d’une souche de grippe à potentiel pandémique. À la fin de ce
tutoriel, vous serez en mesure de générer les trajectoires illustrées
ci-dessous, montrant le nombre d’individus infectieux dans différentes
catégories d’âge au cours du temps.
Dans les sections qui vont suivrent, nous allons apprendre à utiliser
la librairie {epidemics} pour simuler des trajectoires
d’une maladie et à accéder aux données de contacts sociaux à travers le
package socialmixr. Nous utiliserons
dplyr, ggplot2 et l’opérateur pipe
(%>%) de la librairie magrittr pour
relier certaines de leurs fonctions. Ainsi, nous chargerons la librairie
tidyverse qui contient l’ensemble de ces trois
packages.
R
library(epidemics)
library(socialmixr)
library(tidyverse)
Use slides to introduce the topics of:
- Scenario modelling and
- Contact matrix.
Then start with the livecoding.
Simuler la propagation d’une maladie
Pour simuler les trajectoires des maladies infectieuses, il faut
d’abord choisir un modèle mathématique. La librairie
{epidemics} contient une bibliothèque de modèles parmi
lesquels vous pouvez choisir celui qui conviendrai à la maladie
d’intéret. Les noms de ces modèles commencent par model_*
et se terminent par le nom de la maladie (par exemple
model_ebola pour Ebola) ou d’un identifiant différent (par
exemple model_default).
Dans ce tutoriel, nous utiliserons le modèle par défaut appelé
model_default() de la librairie {epidemics}.
Il s’agit d’un modèle structuré par âge qui classe les individus en
fonction de leur statut infectieux. Dans chaque groupe d’âge \(i\) les individus sont classés dans les
compartiments suivants: sensibles \(S\), infectés mais pas encore contagieux
\(E\), infectieux \(I\) et guéris \(R\). Nous devons ensuite définir le
processus par lequel les individus passent d’un compartiment à l’autre.
Cela peut se faire en définissant un ensemble d’ équations différentielles qui
spécifient comment le nombre d’individus dans chaque compartiment évolue
dans le temps.
Le schéma ci-dessous montre les processus qui décrivent le flux d’individus entre les états pathologiques \(S\), \(E\), \(I\) et \(R\) et les paramètres clés de chaque processus.
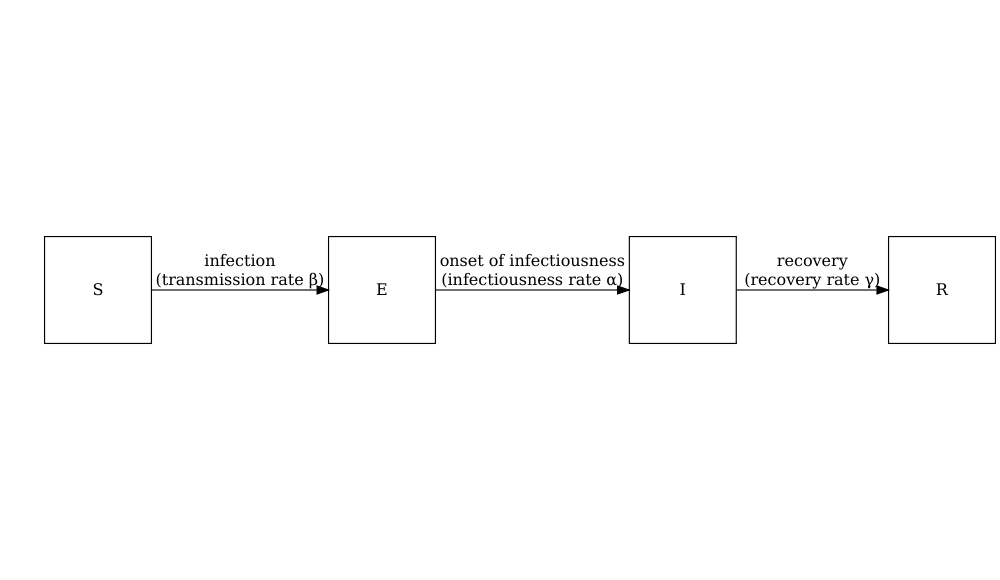
Paramètres du modèle : les taux
Dans les modèles au niveau de la population définis par des équations différentielles, les paramètres du modèle sont souvent (mais pas toujours) spécifiés sous forme de taux. Le taux auquel un événement se produit est l’inverse du temps moyen jusqu’à cet événement. Par exemple, dans le modèle SEIR, le taux de guérrison \(\gamma\) est l’inverse de la période infectieuse moyenne.
Les valeurs de ces taux peuvent être déterminées à partir de l’histoire naturelle de la maladie. Par exemple, si les personnes sont en moyenne infectieuses pendant 8 jours, alors dans le modèle, une personnes sur huits (1/8) actuellement infectieuses se rétablissent chaque jour (c’est-à-dire le taux de guèrrison \(\gamma=1/8=0.125\)).
Pour chaque état pathologique (\(S\), \(E\), \(I\) et \(R\)) dans le groupe d’âge (\(i\)), nous avons une équation différentielle décrivant le taux de changement par rapport au temps.
\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j \\ \frac{dE_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \alpha E_i \\ \frac{dI_i}{dt} &= \alpha E_i - \gamma I_i \\ \frac{dR_i}{dt} &=\gamma I_i \\ \end{aligned} \]
Les individus de la tranche d’âge (\(i\)) quittent l’état sensible (\(S_i\)) pour l’état exposé (\(E_i\)) par le biais de contacts spécifiques à l’âge avec des individus infectieux dans tous les groupes \(\beta S_i \sum_j C_{i,j} I_j/N_j\). La matrice de contact \(C\) permet de tenir compte de l’hétérogénéité des contacts entre les groupes d’âge. Ils passent ensuite à l’état infectieux à un taux \(\alpha\) et se rétablissent à un taux \(\gamma\). Notez que ce modèle suppose qu’il n’y a pas de perte d’immunité (il n’y a pas de flux sortant de l’état de guérison), ce qui peut ne pas être le cas pour toutes les maladies, car certains individus guerris peuvent redevenir infectés à la suite de leur guérison dans la cadre de certaines maladies.
Les paramètres du modèle sont les suivants
- taux de transmission \(\beta\) (dérivé du nombre de reproduction de base \(R_0\) et du taux de guérison \(\gamma\)),
- matrice de contact \(C\) contenant la fréquence des contacts entre les groupes d’âge (une matrice carrée \(i \times j\)),
- le taux d’infectiosité \(\alpha\) (période pré-infectieuse, ou période de latence =\(1/\alpha\)), et
- taux de guérison \(\gamma\) (période infectieuse = \(1/\gamma\)).
Exposé, infecté, infectieux
Les termes “exposé”, “infecté” et “infectieux” dans la modélisation mathématique prêtent parfois à confusion. L’infection se produit après qu’une personne a été exposée, mais en termes de modélisation, les individus “exposés” sont considérés comme déjà infectés.
Nous utiliserons les définitions suivantes pour nos variables d’état :
- \(E\) = Exposé : infecté mais pas encore infectieux,
- \(I\) = infectieux : infecté et infectieux.
Pour générer des trajectoires à l’aide de notre modèle, nous devons préparer les données d’entrée suivantes :
- Matrice de contact
- Conditions initiales
- Structure de la population
- Paramètres du modèle
1. Matrice de contact
Une matrice de contacts représente le nombre moyen de contacts entre les individus de différents groupes d’âge. Il s’agit d’une composante essentielle des modèles structurés par âge, car elle permet de savoir la manière dont les différents groupes d’âge interagissent et se transmettent potentiellement l’infections. Nous utiliserons le package R socialmixr pour charger une matrice de contacts estimée à partir des données de l’enquête POLYMOD (Mossong et al. 2008).
Charger les données de contact et de démographie
En utilisant la librairie socialmixr, obtenir la matrice de contact du Royaume-Uni pour les tranches d’âge suivantes :
- âge entre 0 et 20 ans,
- âge compris entre 20 et 40 ans,
- 40 ans et plus.
Utilisez le sondage disponible sur
socialmixr::polymod.
- Compléter le tutoriel sur Matrices de contact.
R
# Access the contact survey data
polymod <- socialmixr::polymod
# Generate the contact matrix
contact_data <- socialmixr::contact_matrix(
polymod,
countries = "United Kingdom",
age.limits = c(0, 20, 40),
symmetric = TRUE
)
# prepare contact matrix
socialcontact_matrix <- t(contact_data$matrix)
# print
socialcontact_matrix
SORTIE
age.group
contact.age.group [0,20) [20,40) 40+
[0,20) 7.883663 2.794154 1.565665
[20,40) 3.120220 4.854839 2.624868
40+ 3.063895 4.599893 5.005571N’oubliez pas que la matrice satisfait à la condition
symmetric = TRUE au niveau du nombre total de contacts.
Le nombre total de contacts entre les groupes \(i\) et \(j\) est calculé comme étant le nombre moyen
de contacts (contact_data$matrix) multiplié par le nombre
d’individus dans le groupe \(i\)
(contact_data$demography$population).
R
contact_data$matrix * contact_data$demography$population
SORTIE
contact.age.group
age.group [0,20) [20,40) 40+
[0,20) 116672620 46177038 45343471
[20,40) 46177038 80232531 76019216
40+ 45343471 76019216 144967139Le résultat est une matrice carrée avec des lignes et des colonnes
pour chaque groupe d’âge. Les matrices de contact peuvent être chargées
à partir d’autres sources, mais elles doivent être formatées de sorte à
être utilisées par les fonctions de la librairies
{epidemics}.
Normalisation
Dans le cadre de {epidemics} la normalisation de la
matrice de contact se fait durant l’appel de la fonction, nous n’avons
donc pas besoin de normaliser la matrice de contact avant de la passer à
la fonction epidemics::population() (voir section 3.
Structure de la population). Pour plus de détails sur la normalisation,
consultez le tutoriel sur les matrices
de contact .
Make a pause.
Use slides to introduce the topics of:
- Initial conditions and
- Population structure.
Then continue with the livecoding.
2. Conditions initiales
Les conditions initiales sont la proportion d’individus dans chaque état pathologique \(S\), \(E\), \(I\) et \(R\) pour chaque groupe d’âge au temps 0. Dans cet exemple, nous avons trois groupes d’âge : âge entre 0 et 20 ans, âge entre 20 et 40 ans et plus. Supposons que dans la catégorie d’âge la plus jeune, un individu sur un million soit infectieux, et que les autres catégories d’âge soient exemptes d’infection.
Les conditions initiales dans la première catégorie d’âge sont les suivantes \(S(0)=1-\frac{1}{1,000,000}\), \(E(0) =0\), \(I(0)=\frac{1}{1,000,000}\), \(R(0)=0\). Il est spécifié sous la forme d’un vecteur comme suit :
R
# 1 in 1,000,000 is equivalent to 1e-6
initial_i <- 1e-6
initial_conditions_inf <- c(
S = 1 - initial_i, E = 0, I = initial_i, R = 0, V = 0
)
Notez que R utilise la notation scientifique e, où
e vous indique de multiplier le nombre de base par 10 élevé
à la puissance indiquée (DataKwery,
2020). L’expression \(1 \times
10^{-6}\) équivaut à 1e-6.
Pour les catégories d’âge exemptes d’infection, les conditions initiales sont les suivantes \(S(0)=1\), \(E(0) =0\), \(I(0)=0\), \(R(0)=0\). Nous spécifions ceci comme suit,
R
initial_conditions_free <- c(
S = 1, E = 0, I = 0, R = 0, V = 0
)
Nous combinons les trois vecteurs de conditions initiales en une seule matrice,
R
# combiner les conditions initiales dans un objet de classe matricielle
initial_conditions <- rbind(
initial_conditions_inf, # groupe d'age 1 (seul groupe infectieux)
initial_conditions_free, # groupe d'age 2
initial_conditions_free # groupe d'age 3
)
# utiliser la matrice de contact pour renommer les noms de lignes de la matrice
# des conditions initiales
rownames(initial_conditions) <- rownames(socialcontact_matrix)
initial_conditions
SORTIE
S E I R V
[0,20) 0.999999 0 1e-06 0 0
[20,40) 1.000000 0 0e+00 0 0
40+ 1.000000 0 0e+00 0 03. Structure de la population
L’objet de la classe contact_data
que nous avons obtenu à l’aide de la librairie
socialmixr.
R
# extraire le vecteur démographique
demography_vector <- contact_data$demography$population
# utiliser la matrice de contact pour renommer les noms
# des lignes du vecteur démographique
names(demography_vector) <- rownames(socialcontact_matrix)
demography_vector
SORTIE
[0,20) [20,40) 40+
14799290 16526302 28961159 Pour créer notre objet de classe {epidemics}, nous utiliserons la fonction
epidemics::population() en spécifiant le nom du pays, la
matrice de contact, le vecteur démographique et les conditions
initiales.
R
library(epidemics)
uk_population <- epidemics::population(
name = "UK",
contact_matrix = socialcontact_matrix,
demography_vector = demography_vector,
initial_conditions = initial_conditions
)
Make a pause.
Use slides to introduce the topics of:
- Model parameters and
- New infections.
Then continue with the livecoding.
4. Paramètres du modèle
Pour exécuter notre modèle, nous devons spécifier les paramètres :
- le taux de transmission \(\beta\),
- taux d’infectiosité \(\alpha\) (période préinfectieuse=\(1/\alpha\)),
- taux de guérison \(\gamma\) (période infectieuse=\(1/\gamma\)).
Dans {epidemics} nous spécifions les paramètres du
modèle comme étant :
-
transmission_rate\(\beta = R_0 \gamma\), -
infectiousness_rate= \(\alpha\), -
recovery_rate= \(\gamma\),
Nous simulerons une souche de grippe à potentiel pandémique ayant les caractéristiques suivantes \(R_0=1.46\) avec une période pré-infectieuse de 3 jours et une période infectieuse de 7 jours. Nos données d’entrée seront donc les suivantes
R
# les délais
preinfectious_period <- 3.0
infectious_period <- 7.0
basic_reproduction <- 1.46
R
# les taux
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
transmission_rate <- basic_reproduction / infectious_period
Le nombre de reproduction de base \(R_0\)
Le nombre de reproduction de base, \(R_0\) pour le modèle SEIR est le suivant :
\[ R_0 = \frac{\beta}{\gamma}.\]
Par conséquent, nous pouvons réécrire le taux de transmission \(\beta\) comme suit :
\[ \beta = R_0 \gamma.\]
Exécution du modèle
Exécution (résolution) du modèle
Pour les modèles décrits par les équations différentielles, “exécuter” le modèle signifie en fait prendre le système d’équations différentielles et le “résoudre” pour découvrir comment le nombre de personnes dans les compartiments sous-jacents évolue dans le temps. Étant donné que les équations différentielles décrivent le taux de changement des états pathologiques en fonction du temps, plutôt que le nombre d’individus dans chacun de ces états, nous devons généralement utiliser des méthodes numériques pour résoudre les équations.
Un solveur ODE est le logiciel utilisé pour trouver des
solutions numériques aux équations différentielles. Si vous souhaitez
savoir comment un système d’équations différentielles est résolu dans
{epidemics} nous vous suggérons de lire la section sur Systèmes
et modèles d’EDO de la vignette “Design principles”.
Nous sommes maintenant prêts à exécuter notre modèle en utilisant
epidemics::model_default() de la librairies
{epidemics}.
Précisons time_end=600 pour exécuter le modèle pendant
600 jours.
R
output <- epidemics::model_default(
# population
population = uk_population,
# les taux
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# duree de l'épidémie
time_end = 600,
increment = 1.0
)
head(output)
SORTIE
time demography_group compartment value
<num> <char> <char> <num>
1: 0 [0,20) susceptible 14799275
2: 0 [20,40) susceptible 16526302
3: 0 40+ susceptible 28961159
4: 0 [0,20) exposed 0
5: 0 [20,40) exposed 0
6: 0 40+ exposed 0Remarque : ce modèle permet également d’inclure la vaccination et de suivre le nombre d’individus vaccinés au fil du temps. Même si nous n’avons pas spécifié de vaccination, il y a toujours un compartiment vacciné dans le résultat (ne contenant aucun individu). Nous aborderons l’utilisation de la vaccination dans le prochain tutoriel.
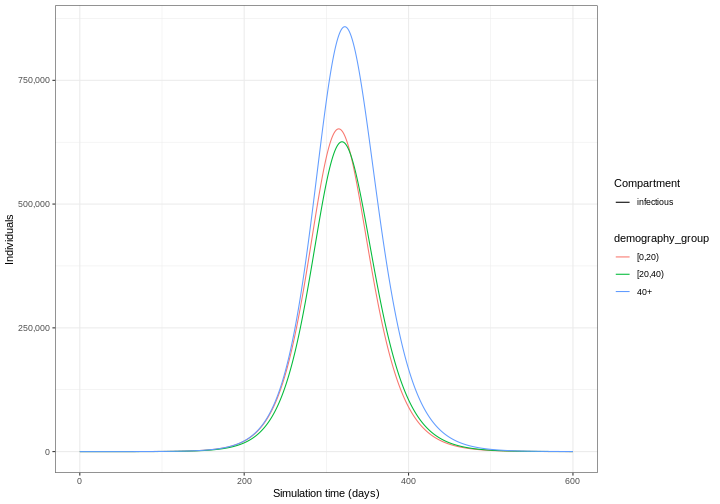
Le résultat de notre modèle est le nombre d’individus dans chaque compartiment de chaque groupe d’âge au cours du temps. Nous pouvons visualiser uniquement les individus infectieux (ceux qui se trouvent dans le compartiment \(I\)) au cours du temps.
R
library(tidyverse)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
geom_line(
aes(
x = time,
y = value,
colour = demography_group
)
) +
scale_y_continuous(
labels = scales::comma
) +
theme_bw() +
labs(
x = "Durée de la simulation (en jours)",
linetype = "Compartiment",
y = "nombre d'invidus"
)
Incréments de temps
Notez qu’il existe une valeur par défaut de l’argument
increment = 1. Il s’agit du pas de temps du solveur ODE.
Lorsque les paramètres sont spécifiés sur une échelle de temps
quotidienne et la limite de temps (time_end) est de jours,
le pas de temps par défaut du solveur ODE est d’un jour.
Le choix de l’incrément dépend de l’échelle de temps des paramètres et de la vitesse à laquelle les événements peuvent se produire. En général, l’incrément doit être plus petit que l’événement le plus rapide qui puisse se produire. Par exemple, l’incrément doit être plus petit que l’événement le plus rapide qui peut se produire :
- si les paramètres se situent sur une échelle de temps quotidienne et que tous les événements sont signalés quotidiennement, l’incrément doit être égal à un jour ;
- si les paramètres se situent sur une échelle de temps mensuelle, mais que certains événements se produisent au cours d’un mois, l’incrément doit être inférieur à un mois.
Témoignage
Deux fonctions d’aide dans
{epidemics}
Utilisez epidemics::epidemic_peak() pour obtenir l’heure
et la taille du pic le plus élevé d’un compartiment pour tous les
groupes démographiques. Par défaut, cela calculera pour le compartiment
infectieux.
R
epidemics::epidemic_peak(data = output)
SORTIE
demography_group compartment time value
<char> <char> <num> <num>
1: [0,20) infectious 315 651944.3
2: [20,40) infectious 319 625863.8
3: 40+ infectious 322 858259.1Utilisez epidemics::epidemic_size() pour obtenir la
taille de l’épidémie à n’importe quel stade entre le début et la fin.
Celle-ci est calculée comme le nombre d’individus guéris de
l’infection à ce stade de l’épidémie.
R
epidemics::epidemic_size(data = output)
SORTIE
[1] 9285873 9040679 12540088Ces fonctions de synthèse peuvent vous aider à obtenir des résultats pertinents pour comparer des scénarios ou pour toute autre analyse en aval.
La figure ci-dessus montre le nombre total ou le nombre cumulé
d’individus dans le compartiment infectieux à chaque instant. Si vous
souhaitez montrer la charge totale de la maladie, le
compartiment infectious est le plus approprié. En revanche,
si vous souhaitez montrer la charge quotidienne, vous pouvez
utiliser epidemics::new_infections() pour obtenir
l’incidence quotidienne.
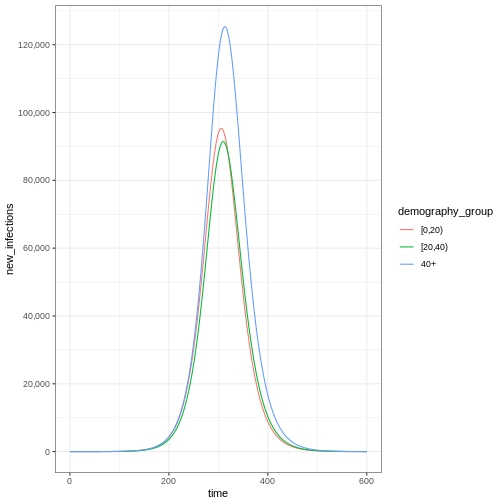
Notez que le nombre de nouveaux cas infectés à chaque instant (comme dans la figure ci-dessous) est inférieur au nombre cumulé de personnes infectieuses à chaque instant (comme dans la figure ci-dessus).
R
# New infections
newinfections_bygroup <- epidemics::new_infections(data = output)
# Visualise the spread of the epidemic in terms of new infections
newinfections_bygroup %>%
ggplot(aes(x = time, y = new_infections, colour = demography_group)) +
geom_line() +
scale_y_continuous(
breaks = scales::breaks_pretty(n = 5),
labels = scales::comma
) +
theme_bw()
Stop the livecoding.
Suggest learners to read the rest of the episode.
Return to slides.
Prise en compte de l’incertitude
Le modèle épidémique est déterministe, c’est-à-dire qu’il fonctionne comme une horloge : les mêmes paramètres conduiront toujours à la même trajectoire. Un modèle déterministe est un modèle dont le résultat est entièrement déterminé par les conditions et les paramètres initiaux, sans aucune variation aléatoire. Cependant, la réalité n’est pas aussi prévisible à cause de ces deux raisons principales : le processus de transmission peut être aléatoire et nous pouvons ne pas connaître les caractéristiques épidémiologiques exactes de l’agent pathogène qui nous intéresse. Dans le prochain épisode, nous examinerons les modèles “stochastiques” (c’est-à-dire les modèles dans lesquels nous pouvons définir le processus qui crée un caractère aléatoire dans la transmission). Entre-temps, nous pouvons inclure l’incertitude dans la valeur des paramètres qui entrent dans le modèle déterministe. Pour tenir compte de cette incertitude, nous devons exécuter notre modèle pour différentes combinaisons de paramètres.
Nous avons exécuté notre modèle avec \(R_0 = 1.5\). Cependant, nous pensons que \(R_0\) suit une distribution normale avec une moyenne de 1,5 et un écart-type de 0,05. Pour tenir compte de l’incertitude, nous exécuterons le modèle pour différentes valeurs de \(R_0\). Les étapes à suivre pour ce faire sont les suivantes :
- Obtenir 100 valeurs aléatoires de \(R_0\) à partir d’une distribution normale.
R
# spécifier la moyenne et l'écart-type de R0
r_estimate_mean <- 1.5
r_estimate_sd <- 0.05
# Générer 100 R0 de façon aléatoire
r_samples <- withr::with_seed(
seed = 1,
rnorm(
n = 100, mean = r_estimate_mean, sd = r_estimate_sd
)
)
infectious_period <- 7
beta <- r_samples / infectious_period
- Exécutez le modèle 100 fois en variant \(R_0\) à chaque itération
R
output_samples <- epidemics::model_default(
population = uk_population,
transmission_rate = beta,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 600,
increment = 1
)
- Calculez la moyenne et les quantiles à 95 % du nombre d’individus infectieux pour chaque simulation du modèle et visualisez les résultats.
R
output_samples %>%
mutate(r_value = r_samples) %>%
unnest(data) %>%
filter(compartment == "infectious") %>%
ggplot() +
geom_line(
aes(time, value, color = r_value, group = param_set),
alpha = 3
) +
scale_color_fermenter(
palette = "RdBu",
name = "R"
) +
scale_y_continuous(
labels = scales::comma
) +
facet_grid(
cols = vars(demography_group)
) +
theme_bw() +
labs(
x = "Durée de simulation (en jours)",
y = "Nombre d'individus"
)
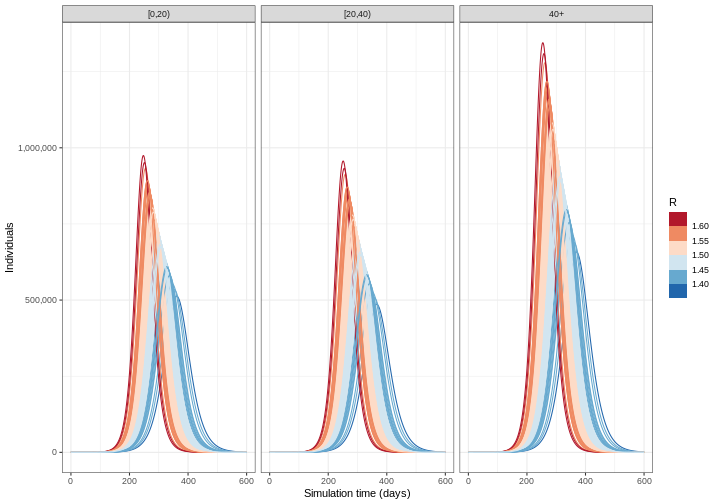
Le choix des paramètres dans lesquels inclure l’incertitude dépend de plusieurs facteurs : le degré d’information sur la valeur d’un paramètre, par exemple la cohérence des estimations tirées de la littérature ; la sensibilité des résultats du modèle aux changements de valeur des paramètres ; et l’objectif de la tâche de modélisation. Voir aussi McCabe et al. 2021 pour en savoir plus sur les différents types d’incertitude dans la modélisation des maladies infectieuses.
Résumé
Dans ce tutoriel, nous avons appris à simuler la propagation d’une maladie à l’aide d’un modèle mathématique. Une fois qu’un modèle a été choisi, les paramètres et autres données d’entrées doivent être spécifiés de manière correcte pour effectuer les simulations du modèle. Dans le prochain tutoriel, nous verrons comment choisir le modèle approprié pour différentes tâches.
Points clés
- Les trajectoires de la maladie peuvent être générées à l’aide du
package
{epidemics}de R. - L’incertitude devrait être incluse dans les trajectoires du modèle en utilisant une gamme de valeurs des paramètres du modèle.
