Construction d'un modèle déterministe simple

Dernière mise à jour le 2025-07-29 | Modifier cette page

Durée estimée : 128 minutes

Vue d'ensemble

Questions

  • Comment construire un modèle simplifié de Zika ?

Objectifs

A la fin de cet atelier, vous serez capable de :

  • Reconnaître comment un modèle déterministe simple est construit en. des équations différentielles ordinaires.
  • Identifier les paramètres pertinents pour la modélisation des épidémies de MTEV.
  • Schématiser l’interaction entre les différents compartiments de l’organisme. système à l’aide des paramètres.
  • Traduire les équations mathématiques du modèle déterministe en code. Code en langage R.
  • Étudier l’utilisation des simulations du modèle pour projeter les résultats de l’étude. scénarios de transmission et l’impact potentiel des interventions

Pré-requis

Cette unité a comme prérequis

  • Introduction à R et RStudio
  • Introduction à la théorie des épidémies
  • Histoire des épidémies et des pandémies
  • Visualisation des données en R avec ggplot

Table des matières

Thème 1 : Maladies à transmission vectorielle → Biologie de la maladie, biologie des vecteurs → Virus Zika, diagnostics et interventions

Sujet 2 : Qu’est-ce qu’un modèle déterministe simple ?

Sujet 3 : Modèle SIR simple pour Zika

Sujet 4 : Développement de diagrammes et équations du modèle Zika |

Sujet 5 : Table des paramètres du modèle simple pour Zika → Description du modèle simple Zika

Sujet 6 : Implémentation du modèle Zika en R

Thème 7 : Paramétrage des interventions de contrôle pour Zika

Introduction

Dans cette unité, nous aborderons la construction d’un modèle déterministe simple, en particulier pour le virus Zika, une maladie qui a déclenché une épidémie majeure en Amérique latine et dans les Caraïbes, et qui a été déclarée urgence de santé publique de portée internationale. En utilisant des connaissances préalables sur la théorie des épidémies, nous construirons un modèle déterministe de type SIR qui incorpore des aspects démographiques.

Pour construire ce modèle, nous apprendrons la dynamique de l’interaction entre l’homme et les vecteurs, ainsi que les paramètres fondamentaux qui régissent ces processus biologiques. En construisant un diagramme, nous examinerons ces relations et formulerons des équations qui décrivent le comportement du système. Ces équations serviront de base à la simulation du modèle dans le langage de programmation R. À notre tour, nous proposerons et modéliserons des stratégies d’intervention.

Grâce à l’analyse du modèle, nous évaluerons l’impact potentiel de cette épidémie sur la société, en contextualisant certaines de ces interventions en Amérique latine. En outre, nous renforcerons et appliquerons des thèmes clés tels que : Le modèle SIR, l’immunité du troupeau, les paramètres et les interventions de contrôle (pulvérisation, moustiquaires et vaccination) pour une maladie à transmission vectorielle (VBD).

Thème 6 : Modèle Zika en R

Dans cette section, nous allons utiliser les connaissances acquises sur Zika, les mécanismes impliqués dans la transmission et les équations du modèle. L’objectif est de le construire en R.

Le seul package nécessaire à la modélisation est deSolve, qui permet de résoudre les équations différentielles. En outre, pour le traitement des données et la représentation graphique des résultats, nous vous recommandons d’utiliser tidyverse et cowplot.

6.1 Démarrage pratique avec R

Pour commencer notre pratique en R veuillez ouvrir un projet de Ret créez un nouveau document. Dans ce document, nous devons charger les fonctions que nous venons d’expliquer. Si vous rencontrez des difficultés avec ce processus, veuillez consulter la section Introduction à R.

install.packages(deSolve) # deSolve package pour la résolution d’équations différentielles

Une fois que vous avez installé le paquet deSolve, chargez les paquets avec les lignes de code suivantes, copiez-les dans votre script R et exécutez-les.

R 

library(deSolve)

library(tidyverse)

library(cowplot)

Rappelons que pour créer un modèle, nous avons besoin de compartiments, de conditions initiales, de paramètres et d’équations.

Pour ce modèle en R, nous commencerons par définir les paramètres, c’est-à-dire toutes les valeurs qui ont été collectées par la recherche et qui font partie du comportement de la maladie. Dans la section précédente, nous avons parlé de ces paramètres et les avons complétés dans un tableau. Il est maintenant temps de les entrer dans R.

Instruction Reprenez le tableau sur lequel vous avez travaillé précédemment et indiquez la valeur de chacun de ces paramètres.

NOTE : VEUILLEZ INDIQUER LA VALEUR DE CHACUN DE CES PARAMÈTRES :

Il est important de rappeler qu’en R, vous pouvez utiliser des objets précédemment créés pour effectuer des calculs. Par exemple, le paramètre muv est l’inverse du paramètre Lv, c’est-à-dire muv = 1/Lv. Par conséquent, dans R, vous pouvez assigner cette valeur directement avec muv <- 1/Lv. Il n’est pas nécessaire d’effectuer la division et d’affecter le résultat manuellement.

Défi 1

Instruction : Reprenez le tableau sur lequel vous avez travaillé précédemment et entrez la valeur de chacun de ces paramètres.

R 

# Liste des paramètres
 Lv <-                   # Espérance de vie des moustiques (en jours)

 Lh <-                   # Espérance de vie des humains (en jours)

 PIh <-                  # Période infectieuse chez les humains (en jours)

 PIv <-                  # Période infectieuse chez les moustiques (en jours)

 PIE <-                  # Période d'incubation extrinsèque chez les moustiques adultes (en jours)

 muv <-                  # Taux de mortalité par habitant de la population de moustiques (1/Lv)

 muh <-                  # Taux de mortalité par habitant de la population humaine (1/Lh)

 alphav <-               # Taux de natalité par habitant de la population de moustiques. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

 alphah <-               # Taux de natalité par habitant de la population humaine. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

 gamma <-                # Taux de rétablissement chez les humains (1/PIh)

 delta <-                # Taux d'incubation extrinsèque (1/PIE)

 Nh <-                   # Nombre d'humains. Pour cet exercice, nous suggérons 100 000 humains. Vous pouvez le modifier selon la ville que vous avez choisie pour la modélisation.

 m <-                    # Densité de moustiques femelles par humain

 Nv <-                   # Nombre de moustiques (m * Nh)

 R0 <-                 # Nombre de reproduction de base

 ph <-                 # Probabilité de transmission d'un moustique infecté à un humain susceptible après une piqûre.

 pv <-                 # Probabilité de transmission d'un humain infecté à un moustique susceptible après une piqûre.

 b <- sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
 (m * ph * pv * delta)) # Taux de piqûre

 betah <-              # Coefficient de transmission d'un moustique infecté à un humain susceptible après une piqûre (ph*b)

 betav <-              # Coefficient de transmission d'un humain infecté à un moustique susceptible après une piqûre (pv*b)

 TEMP <- 1             # Nombre d'années à simuler. Pour cet exercice, nous commencerons avec la première année de l’épidémie.

R 

# Liste des paramètres
Lv <- 10                # Espérance de vie des moustiques (en jours)

Lh <- 50 * 365          # Espérance de vie des humains (en jours)

PIh <- 7                # Période infectieuse chez les humains (en jours)

PIv <- 6                # Période infectieuse chez les moustiques (en jours)

PIE <- 8.4              # Période d'incubation extrinsèque chez les moustiques adultes (en jours)

muv <- 1 / Lv           # Taux de mortalité par habitant de la population de moustiques (1/Lv)

muh <- 1 / Lh           # Taux de mortalité par habitant de la population humaine (1/Lh)

alphav <- muv           # Taux de natalité par habitant de la population de moustiques. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

alphah <- muh           # Taux de natalité par habitant de la population humaine. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

gamma <- 1 / PIh        # Taux de rétablissement chez les humains (1/PIh)

delta <- 1 / PIE        # Taux d'incubation extrinsèque (1/PIE)

Nh <- 100000            # Nombre d'humains. Pour cet exercice, nous suggérons 100 000 humains. Vous pouvez le modifier selon la ville que vous avez choisie pour la modélisation.

m <- 2                  # Densité de moustiques femelles par humain

Nv <- m * Nh            # Nombre de moustiques (m * Nh)

R0 <- 3              # Nombre de reproduction de base

ph <- 0.7               # Probabilité de transmission d'un moustique infecté à un humain susceptible après une piqûre.

pv <- 0.7               # Probabilité de transmission d'un humain infecté à un moustique susceptible après une piqûre.

b <- sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
         (m * ph * pv * delta)) # Taux de piqûre

betah <- ph * b         # Coefficient de transmission d'un moustique infecté à un humain susceptible après une piqûre (ph*b)

betav <- pv * b         # Coefficient de transmission d'un humain infecté à un moustique susceptible après une piqûre (pv*b)

TEMP <- 1               # Nombre d'années à simuler. Pour cet exercice, nous commencerons avec la première année de l’épidémie.

6.2 Équations du modèle

Maintenant que nous avons introduit les paramètres dans le script, il est temps d’utiliser les équations écrites précédemment, qui nous permettent de connaître le nombre d’individus dans chacun des six compartiments en fonction du temps. Trois compartiments pour les humains et trois compartiments pour les moustiques, qui sont identifiés par un h (pour l’homme) et un v(pour les moustiques). Pour les humains, nous avons les compartiments : sensible, infecté et guéri (d’où le mot SIR) et pour les moustiques, les compartiments sont les suivants : sensible, exposé et infectieux (SEI).

Compartiments

  • \(S_h\) Homme sensible

  • \(I_h\) Humains infectieux

  • \(R_h\) Humains infectieux : Humains guéris d’une infection (immunisés contre la maladie). nouvelle infection)

  • \(S_v\) Vecteurs sensibles

  • \(E_v\) Vecteurs à risque : Vecteurs exposés

  • \(I_v\) Vecteurs infectieux

Pour ce modèle, nous utiliserons les équations différentielles suivantes :

6.2.1 Humain

\[\ \frac{dSh}{dt} = \alpha_h N_h - \beta_h \frac {I_v}{N_h}S_h - \mu_h S_h \]

\[\ \frac{dIh}{dt} = \beta_h \frac {I_v}{N_h}S_h - (\gamma + \mu_h) I_h \]

\[\ \frac{dRh}{dt} = \gamma I_h - \mu_h R_h\]

6.2.2 Vecteurs

\[\ \frac{dSv}{dt} = \alpha_v N_v - \beta_v \frac{ I_h} {N_h}S_v - \mu_v Sv\]

\[\ \frac{dE_v}{dt} = \beta_v \frac{I_h} {N_h}S_v- (\delta + \mu_v) Ev\]

\[\ \frac{dI_v}{dt} = \delta Ev - \mu_v I_v\]

6.3 Formule de calcul \(R_0\) (Nombre de base de la reproduction)

Formule nécessaire pour estimer \(R_0\):

\[ R_0 = \frac{mb^2 p_h p_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma)} \]

Défi

Instruction Traduire les équations en R

R 

# Humains
         dSh   <-  alphah * Nh - betah * (Iv/Nh) * Sh - muh * Sh
         dIh   <-______ * (Iv/Nh) * Sh - (____ + _____) * Ih
         dRh   <-  ______ * Ih  - ______ * Rh

 # Moustiques
         dSv  <-  alphav * Nv - _____ * (Ih/Nh) * Sv - _____ * Sv
         dEv  <-  _____ * (Ih/Nh) * Sv - (____ + _____)* Ev
         dIv  <-  _____ * Ev - _____ * Iv

Une fois que nous savons comment traduire les équations en code, nous procédons à l’exécution du modèle. Pour ce faire, nous utiliserons la fonction ode du paquetage deSolve.

Vous commencez par créer la fonction (qui sera ensuite utilisée dans l’argument fun). Pour ce faire, il faut traduire les équations du modèle Zika en R. Vous trouverez ci-dessous la fonction déjà construite modelo_zika pour remplacer les équations que vous avez déjà remplies ci-dessus.

Défi 3

Instruction Instruction : Remplacez les équations incomplètes du code suivant par les équations complètes du modèle Zika sur lequel vous avez travaillé dans l’instruction précédente.

R 

# Modèle déterministe simple (FUN)
modele_zika <- function(temp, variable_detat, parametres) {
  
  with(as.list(c(variable_detat, parametres)), # environnement local pour évaluer les dérivées
       {
         # Humains
         dSh <- ____ * Nh - ____ * (Iv/Nh) * Sh - ____ * Sh   
         dIh <- ____ * (Iv/Nh) * Sh - (____ + ____) * Ih
         dRh <- ____ * Ih - ____ * Rh
         
         # Moustiques
         dSv <- alphav * Nv - ____ * (Ih/Nh) * Sv - ____ * Sv 
         dEv <- ____ * (Ih/Nh) * Sv - (____ + ____)* Ev
         dIv <- ____ * Ev - ____ * Iv
         
         list(c(dSh, dIh, dRh, dSv, dEv, dIv))
       }
  )
}

R 

# Modèle déterministe simple (FUN)
modele_zika <- function(temp, variable_detat, parametres) {
  
  with(as.list(c(variable_detat, parametres)), # environnement local pour évaluer les dérivées
       {
         # Humains
         dSh   <-  alphah * Nh - betah * (Iv/Nh) * Sh - muh * Sh
         dIh   <-  betah * (Iv/Nh) * Sh  - (gamma + muh) * Ih
         dRh   <-  gamma * Ih  - muh * Rh
         
         # Moustiques
         dSv   <-  alphav * Nv - betav * (Ih/Nh) * Sv - muv * Sv 
         dEv   <-  betav * (Ih/Nh) * Sv - (delta + muv)* Ev
         dIv   <-  delta * Ev - muv * Iv
         
         list(c(dSh, dIh, dRh, dSv, dEv, dIv))
       }
  )
}

6.4 Résolution du système

Pour résoudre le système, il est nécessaire de créer les trois arguments manquants (temps, parms y y) pour utiliser la fonction ode.

Défi 4

Instruction : Pour times y parms copiez le code ci-dessous et exécutez-le.

R 

# Séquence de temps (times)

temps <- seq(1, 365 * TEMP , by = 1)


# Parametres (parms)

parametres <- c(
  muv = muv,     
  muh = muh, 
  alphav = alphav,
  alphah = alphah,
  gamma = gamma,   
  delta = delta,   
  betav = betav,       
  betah = betah,   
  Nh = Nh,      
  Nv = Nv
)

Dans le code qui s’est exécuté, le temps a été créé (times) et des paramètres (params). Nous devons encore créer l’argument y que nous développerons dans la section suivante.

6.4.1. Conditions initiales du système (y)

Afin de définir les conditions initiales, rappelez-vous que le scénario à modéliser dans cet exercice est celui d’une date avant le rapport de la premier cas. Ces valeurs doivent donc refléter ce contexte.

Discussion

Réflexion : Quelles seraient les conditions initiales de chacun des compartiments ?

Défi 5

Instruction : Remplissez les cases comme vous l’avez appris dans le didacticiel.

R 

# Conditions initiales du système (y)
initiales <- c(
            Sh = _______ ,        # Compléter et commenter
            Ih = _______ ,        # Compléter et commenter
            Rh = _______ ,        # Compléter et commenter
            Sv = _______ ,        # Compléter et commenter
            Ev = _______ ,        # Compléter et commenter
            Iv = _______ )        # Compléter et commenter

R 

initiales <- c(Sh = Nh,        # Population d'humains susceptibles avant le début de l'épidémie
           Ih = 0,        # Population d'humains infectés  avant le début de l'épidémie
           Rh = 0,        # Population d'humains rétablis avant le début de l'épidémie
           Sv = Nv,        # Population de moustiques susceptibles avant le début de l'épidémie
           Ev = 0,        # Population de moustiques exposés avant le début de l'épidémie
           Iv = 0)        # Population de moustiques infectés  avant le début de l'épidémie

6.4.2 Code de fonction

Une fois que tous les arguments nécessaires ont été créés, il est temps de les entrer dans ode. Rappelons les quatre arguments de ode et a qui correspondent à :

  • y:maison. Vecteur créé avec les conditions initiales du six compartiments.

  • temps:temps. Vecteur avec séquence de temps

  • fun:zika_model. Fonction contenant les équations nécessaires pour simuler le modèle.

  • parms:paramètres. Vecteur dans lequel les paramètres nécessaires à la simulation du modèle ont été collectés.

Défi 6

Instruction Remplissez les cases en fonction de ce que vous avez appris jusqu’à présent.

R 

# Résoudre les équations
sortie <- ode(y = _______ , # Compléter et commenter
              times = _______ ,   # Compléter et commenter
              fun = _______ ,   # Compléter et commenter
              parms = _______  # Compléter et commenter
) %>%
  as.data.frame() # Conversion en data frame

R 

# Solution
sortie <- ode(y = initiales , 
              times = temps  ,   
              fun = modele_zika   ,   
              parms = parametres  
) %>%
  as.data.frame() # Conversion en data frame

6.4.3 Introduction du premier cas

Maintenant que tous les compartiments sont définis, il est temps d’introduire un individu infectieux dans le modèle pour lancer l’épidémie.

Discussion

Réflexion : Selon vous, quelle est la probabilité la plus élevée : un être humain infectieux ou un moustique infectieux pénétrant dans une population (dans un autre pays) ?

Pour notre cas hypothétique, supposons qu’une personne ait été infectée au Brésil lors d’un voyage touristique et qu’elle soit ensuite retournée dans la ville ______________ (la ville que vous avez définie au début de l’exercice) et qu’elle ait été le premier sujet infectieux dans cette population. Dans ce contexte, le compartiment des humains infectieux comptera alors un individu, Ih = 1 et le compartiment des humains sensibles aura un individu de moins, Sh = Nh - 1.

Défi

Piste : Modifier dans R les conditions initiales (de départ) de sorte que Ih = 1 et Sh = Nh - 1.

R 

# Conditions initiales au début de l'épidémie
initiales <- c(Sh = Nh-1, # Population initiale d'humains susceptibles
               Ih = 1, # Premier cas humain infecté au début de l'épidémie
               Rh = 0, # Aucun humain rétabli au départ
               Sv = Nv, # Population initiale de moustiques susceptibles
               Ev = 0, # Aucun moustique exposé au début de l'épidémie
               Iv = 0) # Aucun moustique infecté au début de l'épidémie

R 

sortie <- ode(y = initiales , 
              times = temps  ,   
              fun = modele_zika   ,   
              parms = parametres  
) %>%
  as.data.frame() # Conversion en data frame

6.5 Exécutons maintenant le modèle !

À ce stade, vous avez complété toutes les informations manquantes dans la rubrique le script afin de pouvoir exécuter le modèle.

À noter

Instruction : Exécutez chaque ensemble de lignes de script vues ci-dessus, c’est-à-dire exécutez les sections : Liste des paramètres, la section Modèle déterministe simple (où vous avez construit le modèle), les sections Séquence temporelle (temps (times)), Les paramètres (parameters (parms)), la section Conditions initiales du système (start (y)) et la section finale Résoudre les équations.

Instruction : Vérifiez qu’aucune erreur n’est affichée. En cas d’erreur, veuillez vérifier l’orthographe du code et qu’il ne reste pas d’autres caractères dans le code qui ne correspondent pas, par exemple “_____”, les traits d’union dans les espaces à remplir.

6.6 Visualisation des résultats

Dans notre cours, nous utiliserons ggplot pour la visualisation des données. Il s’agit de important de revoir l’unité 4. Visualisation de données avec ggplot

Il convient de rappeler que l’unité de temps du modèle Zika est déjà définie à partir des paramètres comme suit jours.

Toutefois, si vous souhaitez visualiser les résultats en semaines, mois ou années, vous pouvez le faire à partir des résultats du modèle (salida$time). Pour ce faire, vous pouvez utiliser le code suivant.

Défi 7

Pour une visualisation plus significative des résultats, convertissez les unités de temps de jours a ans et un semaines.

R 

# Convertir les temps de jours en années et en semaines, respectivement
sortie$annees <- sortie$time/365
sortie$semaines <- sortie$time/7

6.7 Visualiser et analyser la première épidémie

Commençons par une visualisation de la première épidémie. Comme il s’agit d’une période d’un an, visualisons les graphiques en semaines.

Instructions : Exécutez le code ci-dessous et analysez les graphiques obtenus.

R 

# Passez en revue la première épidémie
p1e <- ggplot(data = sortie, aes(y = Ih, x = semaines)) +  
  geom_line(color='firebrick', linewidth=1) +  
  labs(title = "Population humaine infectieuse", x = "Semaines", y = "Nombre") +  
  theme_bw() # Graphique de la population humaine infectieuse  
p2e <- ggplot(data = sortie, aes(y = Rh, x = semaines)) +  
  geom_line(color='olivedrab', linewidth=1) +  
  labs(title = "Population humaine rétablis", x = "Semaines", y = "Nombre") +  
  theme_bw() # Graphique de la population humaine rétablis  


plot_grid(p1e, p2e) # Graphique comparatif de la population humaine infectieuse et de la population humaine rétablis

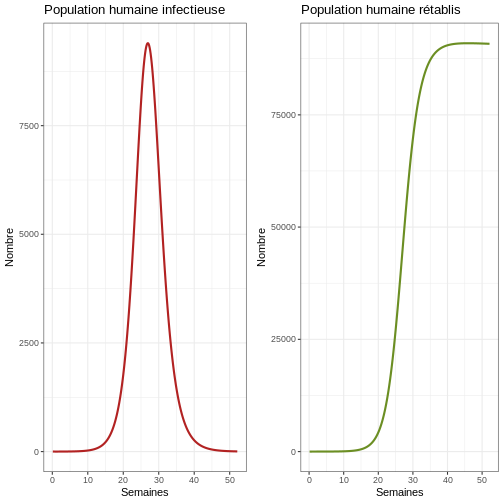
Discussion

Réflexion : Que voyez-vous dans le graphique ? Observez attentivement l’axe des ordonnées. Quelle proportion d’humains est infectieuse en même temps ?

Pour y voir plus clair, nous pouvons créer des graphiques des proportions :

R 

# Passez en revue la première épidémie avec proportions
p1p <- ggplot(data = sortie, aes(y = Ih/(Sh+Ih+Rh), x = semaines)) +  
  geom_line(color = 'firebrick', linewidth = 1) +  
  ggtitle("Population humaine infectieuse") +  
  theme_bw() + ylab("Proportion") + xlab("Semaines") +  
  coord_cartesian(ylim = c(0,1)) # Graphique de la population humaine infectieuse  

p2p <- ggplot(data = sortie, aes(y = Rh/(Sh+Ih+Rh), x = semaines)) +  
  geom_line(color = 'olivedrab', linewidth = 1) +  
  ggtitle("Population humaine rétablie") +  
  theme_bw() + ylab("Proportion") + xlab("Semaines") +  
  coord_cartesian(ylim = c(0,1))  # Graphique de la population humaine rétablie  

plot_grid(p1p, p2p) # Graphique comparatif de la population humaine infectieuse et rétablie

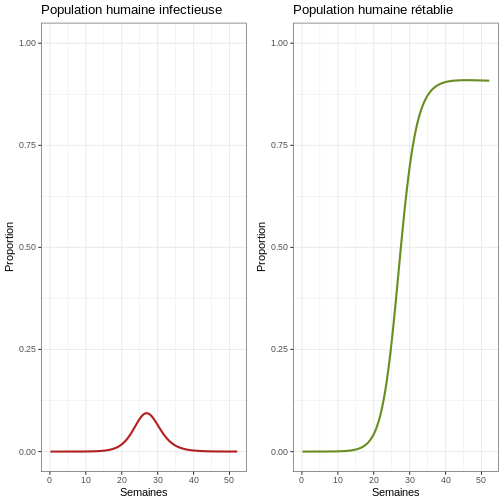
Comportement général (population humaine)

Après avoir observé la première épidémie, il est maintenant temps de projeter l’épidémie à plus long terme.

Instruction : Revenez aux paramètres et changez le paramètre TEMP en 100 ans. Exécutez le bloc de code suivant et observez le nombre d’épidémies qui se produisent dans la population humaine et la taille de chaque épidémie.

R 

#Examiner le comportement du modèle sur 100 ans  


p1h <- ggplot(data = sortie, aes(y = (Rh + Ih + Sh), x = annees)) +  
  geom_line(color='grey68', linewidth=1) +  
  labs(title = "Population humaine totale", x = "Années", y = "Nombre") +  
  theme_bw()  


p2h <- ggplot(data = sortie, aes(y = Sh, x = annees)) +  
  geom_line(color='royalblue', linewidth=1) +  
  labs(title = "Population humaine susceptible", x = "Années", y = "Nombre") +  
  theme_bw()  


p3h <- ggplot(data = sortie, aes(y = Ih, x = annees)) +  
  geom_line(color='firebrick', linewidth=1) +  
  labs(title = "Population humaine infectés", x = "Années", y = "Nombre") +  
  theme_bw()  


p4h <- ggplot(data = sortie, aes(y = Rh, x = annees)) +  
  geom_line(color='olivedrab', linewidth=1) +  
  labs(title = "Population humaine rétablis", x = "Années", y = "Nombre") +  
  theme_bw() 


plot_grid(p1h, p2h, p3h, p4h, ncol = 2)

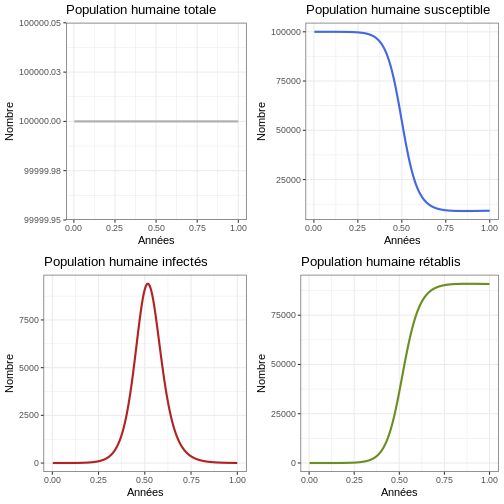
Comportement général (population de moustiques)

Instruction : Exécutez le bloc de code suivant et observez le nombre d’épidémies qui se produisent dans la population de moustiques et la taille de chaque épidémie. Comparez les graphiques avec ceux de la population humaine.

R 

# Examiner le comportement du modèle
p1v <- ggplot(data = sortie, aes(y = (Sv + Ev + Iv), x = annees)) +  
  geom_line(color='grey68', linewidth=1) +  
  labs(title = "Population totale de moustiques", x = "Années", y = "Nombre") +  
  theme_bw()  


p2v <- ggplot(data = sortie, aes(y = Sv, x = annees)) +  
  geom_line(color='royalblue', linewidth=1) +  
  labs(title = "Population de moustiques susceptibles", x = "Années", y = "Nombre") +  
  theme_bw()  


p3v <- ggplot(data = sortie, aes(y = Ev, x = annees)) +  
  geom_line(color='orchid', linewidth=1) +  
  labs(title = "Population de moustiques exposés", x = "Années", y = "Nombre") +  
  theme_bw()  


p4v <- ggplot(data = sortie, aes(y = Iv, x = annees)) +  
  geom_line(color='firebrick', linewidth=1) +  
  labs(title = "Population de moustiques infectés", x = "Années", y = "Nombre") +  
  theme_bw() 


plot_grid(p1v, p2v, p3v, p4v, ncol = 2)

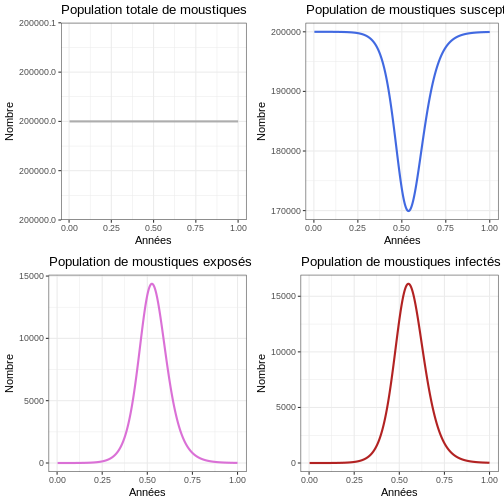
Proportion

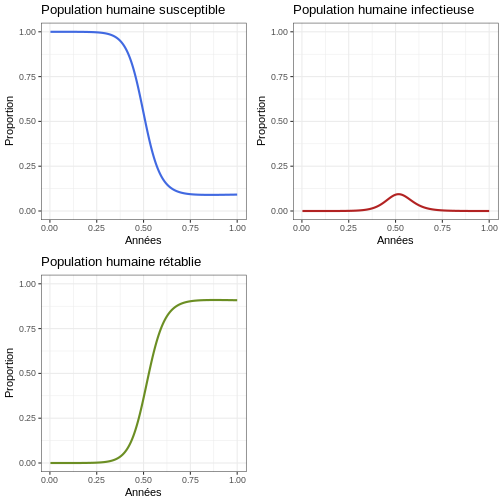
Instruction : Exécutez le bloc de code suivant et comparez-le aux graphiques générés pour la population humaine.

R 

#Proportions

p1 <- ggplot(data = sortie, aes(y = Sh/(Sh+Ih+Rh), x = annees)) +
  geom_line(color='royalblue', linewidth=1) +
  ggtitle('Population humaine susceptible') +
  theme_bw() + ylab('Proportion') + xlab('Années') +
  coord_cartesian(ylim = c(0,1))

p2 <- ggplot(data = sortie, aes(y = Ih/(Sh+Ih+Rh), x = annees)) +
  geom_line(color='firebrick', linewidth=1) +
  ggtitle('Population humaine infectieuse') +
  theme_bw() + ylab('Proportion') + xlab('Années') +
  coord_cartesian(ylim = c(0,1))

p3 <- ggplot(data = sortie, aes(y = Rh/(Sh+Ih+Rh), x = annees)) +
  geom_line(color='olivedrab', linewidth=1) +
  ggtitle('Population humaine rétablie') +
  theme_bw() + ylab('Proportion') + xlab('Années') +
  coord_cartesian(ylim = c(0,1))

plot_grid(p1, p2, p3, ncol = 2)

Points clés

Vérifiez si vous avez acquis ces compétences à la fin de cette leçon :

  • Appliquer des concepts tels que les paramètres, \(R_0\) et l’immunité de groupe, appris lors de la session A de l’atelier
  • Traduire les formules mathématiques des interactions entre le virus et le virus de l’immunité. paramètres du modèle en code R
  • Réaliser un modèle simple en R pour une maladie transmise par maladie vectorielle
  • Discuter des modifications apportées aux projections du modèle lorsqu’elles sont mises en œuvre différentes stratégies de contrôle des infections

Contributions

  • Zulma Cucunuba & Pierre Nouvellet : Version initiale
  • Kelly Charinga & Zhian N. Kamvar : Edition
  • José M. Velasco-Espagne : Traduction de l’anglais vers l’espagnol et édition
  • Andree Valle-Campos : éditions mineures
  • Hugo Gruson: Traduction en français

Affaires juridiques

Droit d’auteur Copyright : Zulma Cucunuba & Pierre Nouvellet, 2017

Références

de Carvalho, S. S., Rodovalho, C. M., Gaviraghi, A., Mota, M. B. S., Jablonka, W., Rocha-Santos, C., Nunes, R. D., Sá-Guimarães, T. da E., Oliveira, D. S., Melo, A. C. A., Moreira, M. F., Fampa, P., Oliveira, M. F., da Silva-Neto, M. A. C., Mesquita, R. D. et Atella, G. C. (2021). Aedes aegypti post-emergence transcriptome : Unveiling the molecular basis for the hematophagic and gonotrophic capacitation. PLoS Neglected Tropical Diseases, 15(1), 1–32. https://doi.org/10.1371/journal.pntd.0008915

Chang, C., Ortiz, K., Ansari, A. et Gershwin, M. E. (2016). The Zika outbreak of the 21st century”, Journal of Autoimmunity, 68, 1–13. https://doi.org/10.1016/j.jaut.2016.02.006

Cori, A., Ferguson, N. M., Fraser, C. et Cauchemez, S. (2013). A new framework and software to estimate time-varying reproduction numbers. during epidemics. American Journal of Epidemiology, 178(9), 1505–1512. https://doi.org/10.1093/aje/kwt133

Duffy, M. R., Chen, T.-H., Hancock, W. T., Powers, A. M., Kool, J. L., Lanciotti, R. S., Pretrick, M., Marfel, M., Holzbauer, S., Dubray, C., Guillaumot, L., Griggs, A., Bel, M., Lambert, A. J., Laven, J., Kosoy, O., Panella, A., Biggerstaff, B. J., Fischer, M. et Hayes, E. B. (2009). Épidémie de virus Zika sur l’île de Yap, États fédérés de Micronésie. Nouveau New England Journal of Medicine, 360(24), 2536–2543. https://doi.org/10.1056/nejmoa0805715

Ferguson, N. M., Cucunubá, Z. M., Dorigatti, I., Nedjati-Gilani, G. L., Donnelly, C. A., Basáñez, M. G., Nouvellet, P. et Lessler, J. (2016). Lutter contre l’épidémie de Zika en Amérique latine. Science, 353(6297). https://doi.org/10.1126/science.aag0219

Heesterbeek, J. A. P. (2002). Une brève histoire du R0 et une recette pour son développement. calcul. Acta Biotheoretica, 50(3). https://doi.org/10.1023/A:1016599411804

Lee, E. K., Liu, Y. et Pietz, F. H. (2016). A Compartmental Model for Zika Virus avec des populations humaines et vectorielles dynamiques. AMIA … Annual Symposium Proceedings. Symposium de l’AMIA, 2016, 743–752.

Pettersson, J. H. O., Eldholm, V., Seligman, S. J., Lundkvist, Å.., Falconar, A. K., Gaunt, M. W., Musso, D., Nougairède, A., Charrel, R., Gould, E. A., & de Lamballerie, X. (2016). Comment le virus zika a-t-il émergé en les îles du Pacifique et l’Amérique latine ? MBio, 7(5). https://doi.org/10.1128/mBio.01239-16