Matériel du kit de formation Epi pour le cours d´introduction à la modélisation des maladies infectieuses pour les cours de santé publique: Tout sur une seule page

Content from Unité de statistiques et de probabilités

Dernière mise à jour le 2025-07-24 | Modifier cette page

Durée estimée : 44 minutes

Vue d'ensemble

Questions

Comment les statistiques et les probabilités peuvent-elles être utilisées pour répondre aux questions en matière d’épidémiologie des maladies infectieuses ?

Objectifs

A la fin de cet atelier, vous serez capable de :

Comprendre le rôle des statistiques dans l’étude des maladies infectieuses.
Comprendre et utiliser des mesures statistiques pour résumer et analyser des informations.
Se familiariser avec le concept de variable aléatoire et reconnaître les distributions de probabilité courantes.
Apprendre à aborder un problème statistique comme un problème d’inférence à partir d’un échantillon.
Comprendre le concept d’intervalles de confiance pour l’estimation des paramètres épidémiologiques.

Pré-requis

Cette unité est un complément à l’unité Introduction à la modélisation des maladies infectieuses pour les cours de santé publique

Table des matières

Thème 1 : Introduction à la pensée statistique (Voir dans plateforme de cours)

Thème 2 : Statistiques descriptives (Voir le complément dans la plate-forme de cours)

Thème 3 : Probabilité (Voir plateforme de cours complémentaire)

Thème 4 : Principales distributions de probabilités (Voir le module complémentaire de la plate-forme de cours)

Thème 5 : Introduction à l’inférence statistique (Voir le supplément sur la plateforme de cours)

Avant de commencer

Veuillez vérifier que vous avez installé les bibliothèques suivantes tidyverse, pak, epiparameter e infer si ce n’est pas le cas, exécutez le code ci-dessous en fonction de vos besoins :

R

# Pour installer le package tidyverse si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if(!require("tidyverse")) install.packages("tidyverse")

# Pour installer le package epiparameter si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if (!require("epiparameter")) install.packages("epiparameter")

# Pour installer le package epitools si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if (!require(epitools)) install.packages("epitools")

# Pour installer le package infer si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if(!require("infer")) install.packages("infer")

# Pour installer le package cfr si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if (!require("cfr")) install.packages("cfr")


# Avant de commencer et à chaque fois que vous démarrez une session R, chargez ces bibliothèques
library(ggplot2)
library(dplyr)
library(epiparameter)
library(epitools)
library(infer)
library(cfr)

Thème 2 : Statistiques descriptives

Exercice : Visualiser et analyser des données avec R

Il existe de nombreux graphiques en fonction du type d’échelle de la variable que vous souhaitez analyser. Voici quelques exemples pour vous aider à comprendre ces concepts.

Veuillez tenir compte du fait que vous avez déjà suivi l’unité d’introduction sur R et l’unité sur la visualisation des données. Le tableau de données pour cette se trouve dans : https://raw.githubusercontent.com/epiverse-trace/translation-EpiTKit-FR/refs/heads/main/data/donnees_echantillon.RDS
Une fois que vous avez téléchargé les données sur votre ordinateur et qu’elles se trouvent dans l’application de votre projet, vous pouvez exécuter la commande suivante :

R

 echantillon_covid <-  readRDS("data/echantillon_covid.RDS")

Histogramme et Boxplot

Les deux types de graphiques les plus courants pour visualiser la distribution de variables quantitatives sont les histogrammes et les boxplots.

L’histogramme histogrammes vous permettent de décrire visuellement la distribution des données en regroupant les données en intervalles sur l’axe des x, qui sont généralement de taille égale, puis en décrivant pour chaque intervalle la fréquence absolue, la fréquence relative ou la densité sur l’axe des y. Un histogramme de densité ajuste la fréquence relative de chaque intervalle en fonction de la largeur de l’intervalle. Dans R, il peut être construit comme suit :

R

# Histogramme avec fréquence absolue

ggplot(data = echantillon_covid, aes(x = age)) +   
  geom_histogram(color="darkblue", fill="lightblue") +  
  labs(y = "Fréquence absolue", x = "Âge en années",
     title = "Répartition par âge")

ERREUR

Error in ggplot(data = echantillon_covid, aes(x = age)): could not find function "ggplot"

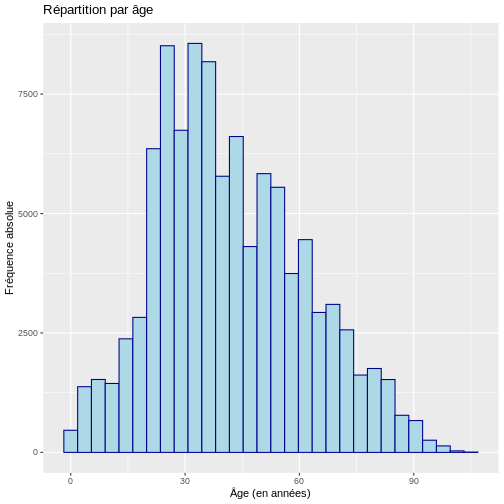
R

# Histogramme avec densité

ggplot(data = echantillon_covid, aes(x = age)) +   
  geom_histogram(aes(y = after_stat(density)), 
                 color = "darkblue", fill = "lightblue") +  
  labs(y = "Density", x = "Âge en années", 
       title = "Age Distribution")

ERREUR

Error in ggplot(data = echantillon_covid, aes(x = age)): could not find function "ggplot"

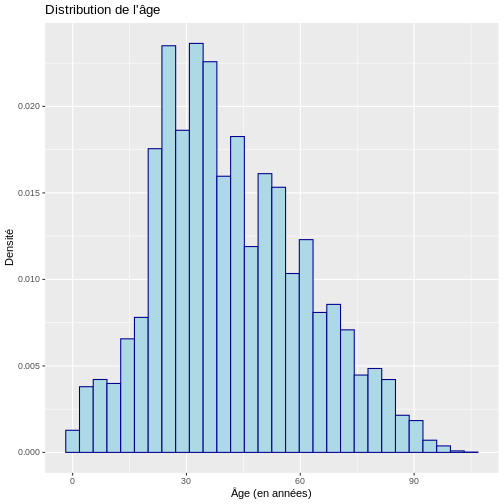
Ensuite, nous allons visualiser l’âge des cas COVID-19 à l’aide d’un diagramme en boîte.

R

# Boxplot

ggplot(echantillon_covid, aes(x = " ", y = age)) +
  geom_boxplot(outlier.shape = NA) +
  ylab("Âge (en années)") + xlab(" ")

ERREUR

Error in ggplot(echantillon_covid, aes(x = " ", y = age)): could not find function "ggplot"

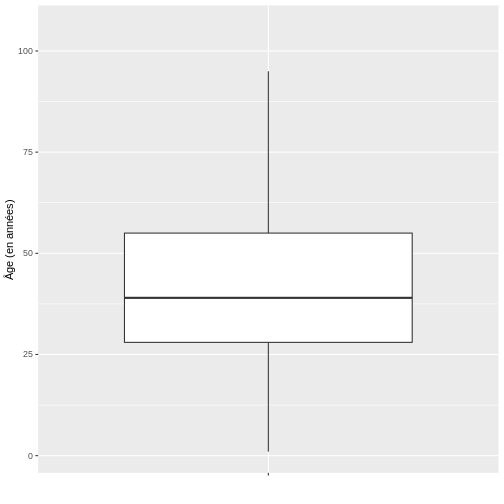
D’après le diagramme en boîte de l’âge de l’échantillon de cas COVID-19, il est possible de conclure que la distribution des données est positivement asymétrique, étant donné qu’il y a une plus grande proximité entre les valeurs de Q1 et la médiane, il est donc conseillé de décrire le comportement de cette dernière au moyen de la médiane et de l’intervalle interquartile, ce qui, dans R, peut être trouvé de la manière suivante en utilisant les fonctions surlignées en bleu :

R

# Statistiques Descriptives Variables Quantitatives    

echantillon_covid %>% dplyr::summarise(
  n = n (), # Nombre d'observations
  moyenne = mean(age), # Moyenne
  et = sd(age), # Écart-type
  mediane = quantile(age, 0.50), # Médiane - 50e percentile
  p25 = quantile(age, 0.25), # 25e percentile
  p75 = quantile(age, 0.75)) # 75e percentile

ERREUR

Error in echantillon_covid %>% dplyr::summarise(n = n(), moyenne = mean(age), : could not find function "%>%"

Enfin, pour la variable âge, on peut conclure que la moitié des patients atteints de covid-19 sont âgés de 27 à 52 ans (“RIQ”) avec une médiane de 38 ans, ce qui indique que la moitié des cas sont âgés de moins de cette valeur. Il est important de noter qu’en raison de l’asymétrie de la distribution, la moyenne et la médiane ne coïncident pas, ce qui est normal dans les distributions asymétriques.

Graphiques en barres et tableaux de fréquence

Il est recommandé de représenter les variables qualitatives par des diagrammes en barres. Généralement, ceux-ci sont construits en indiquant sur l’axe X les catégories des variables et sur l’axe Y la valeur des fréquences absolues, relatives ou en pourcentage selon les besoins, c’est-à-dire qu’il est toujours nécessaire d’évaluer d’abord le tableau de fréquence de la variable. Supposons que nous voulions connaître le type d’infection de COVID-19. Cela peut être fait dans R à l’aide de la commande suivante :

R

# Tableaux de fréquences

tableau <- echantillon_covid %>% # Tableau de fréquence créé
  dplyr::count(type_de_contagion) %>% # Comptage de fréquence pour la variable d'état
  dplyr::mutate(prop = base::prop.table(n), # Proportion
       perc = base::prop.table(n)*100) # Pourcentage

ERREUR

Error in echantillon_covid %>% dplyr::count(type_de_contagion) %>% dplyr::mutate(prop = base::prop.table(n), : could not find function "%>%"

R

tableau

ERREUR

Error: object 'tableau' not found

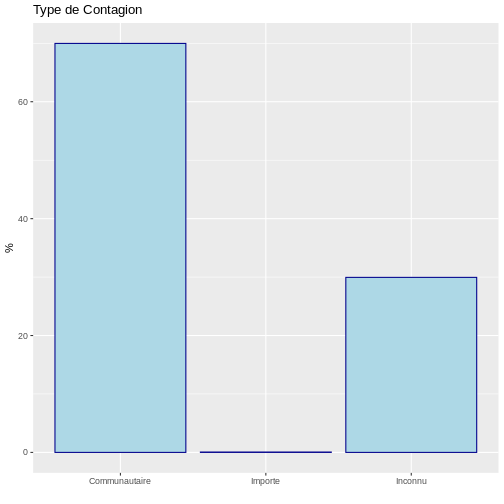
Ces informations permettent de conclure que 70 % des cas de COVID-19 provenaient de la communauté et que seulement 0,06 % étaient importés d’ailleurs. Ce résultat peut être visualisé à l’aide d’un diagramme à barres :

R

# Graphiques à barres
ggplot(data = tableau, aes(x = type_de_contagion, y = perc)) +
  geom_bar(stat="identity", color="darkblue", fill="lightblue")+
  labs(y = "%", x = " ", title = "Type de Contagion")

ERREUR

Error in ggplot(data = tableau, aes(x = type_de_contagion, y = perc)): could not find function "ggplot"

Thème 3 : Probabilité

Dans une étude publiée dans le NEJM en 2014 et intitulée “Ebola Virus Disease in West Africa- The First 9 Months of the Epidemic and Forward Projections” (La maladie à virus Ebola en Afrique de l’Ouest - Les 9 premiers mois de l’épidémie et les projections futures) (DOI : 10.1056/NEJMoa1411100), a décrit les caractéristiques cliniques et épidémiologiques des cas d’Ebola signalés au cours de l’épidémie qui a touché les pays de Guinée, du Liberia, du Nigeria et de la Sierra Leone depuis décembre 2013. L’étude a révélé que les personnes âgées de plus de 44 ans étaient plus susceptibles de mourir de la maladie. Comme dans l’article cité en référence, une conclusion comparable est obtenue si l’on effectue un calcul équivalent en utilisant des mesures d’association vues dans l’unité d’épidémiologie générale appliquées aux maladies infectieuses, telles que les risques relatifs (RR) du rapport de risque ou le risque relatif (RR). Pour ce faire, un tableau 2x2 peut être reconstruit, où le RR peut être mesuré par le rapport entre le CFR d’un groupe A (par exemple, les cas âgés de 45 ans ou plus) et d’un groupe B (par exemple, les cas âgés de 44 ans ou moins), où le CFR est le risque de létalité (CFR).

Ainsi, nous obtenons que le risque de décès chez les cas âgés de 45 ans ou plus est 1,20 fois le risque de décès chez les cas âgés de 44 ans ou moins, avec un intervalle de confiance à 95 % de 1,13 à 1,27, et une valeur p inférieure à 0,01. Pour reproduire ce calcul, vous pouvez utiliser la fonctionepitools comme indiqué ci-dessous.

R

library(epitools)

tableau2x2 <- matrix(c(311, 51, 768, 299),nrow = 2, ncol = 2)

epitools::riskratio(tableau2x2)

SORTIE

$data
          Outcome
Predictor  Disease1 Disease2 Total
  Exposed1      311      768  1079
  Exposed2       51      299   350
  Total         362     1067  1429

$measure
          risk ratio with 95% C.I.
Predictor  estimate    lower    upper
  Exposed1 1.000000       NA       NA
  Exposed2 1.200227 1.133086 1.271346

$p.value
          two-sided
Predictor    midp.exact fisher.exact   chi.square
  Exposed1           NA           NA           NA
  Exposed2 3.179312e-08 4.200177e-08 9.982161e-08

$correction
[1] FALSE

attr(,"method")
[1] "Unconditional MLE & normal approximation (Wald) CI"

Vous trouverez une introduction à l’inférence statistique et aux intervalles de confiance dans le thème 5 de cette unité.

Thème 4 : Principales distributions de probabilité

Comme décrit dans le thème 3, les probabilités étudient le comportement des phénomènes aléatoires, les “événements”. Dans ce processus, on observe les variables aléatoires (v.a), généralement désignées par X qui visent à attribuer un nombre réel à chaque événement susceptible de se produire dans l’espace d’échantillonnage.

Pour l’explication et les exemples des principales distributions, il est important que vous installiez et chargiez les paquets epiparameter d’Epiverse.

R

# vérifier si {epiparameter} est installé
if(!require("epiparameter")) install.packages("epiparameter")

SORTIE

Loading required package: epiparameter

R

# chargez la bibliothèque epiparameter
library(epiparameter)

Modèles discrets

La distribution binomiale permet de décrire la probabilité d’occurrence d’un événement ayant deux issues possibles, le succès (p) ou l’échec (1-p), dans un nombre donné d’essais indépendants n avec une probabilité constante de succès p. La variable aléatoire étudiée correspond à :

X : Nombre de succès en n essais

Le modèle binomial peut être utile pour connaître la probabilité d’observer un nombre donné d’événements (par exemple, des cas, des décès, des réinfections) dans une population de taille n, en supposant que la probabilité de l’événement est constante. La distribution binomiale dépend de deux paramètres : la probabilité de succès p et le nombre d’essais indépendants n.

Si X a une distribution binomiale, il est représenté comme suit : X~Bin(n,p)

Et sa fonction de densité, sa moyenne, son espérance et sa variance correspondent à :

$f(x)=P(X=x)=(n x )$

$p^x (1-p)^{(n-x)}$

$E(x)=np$

$Var(x)=np(1-p)$

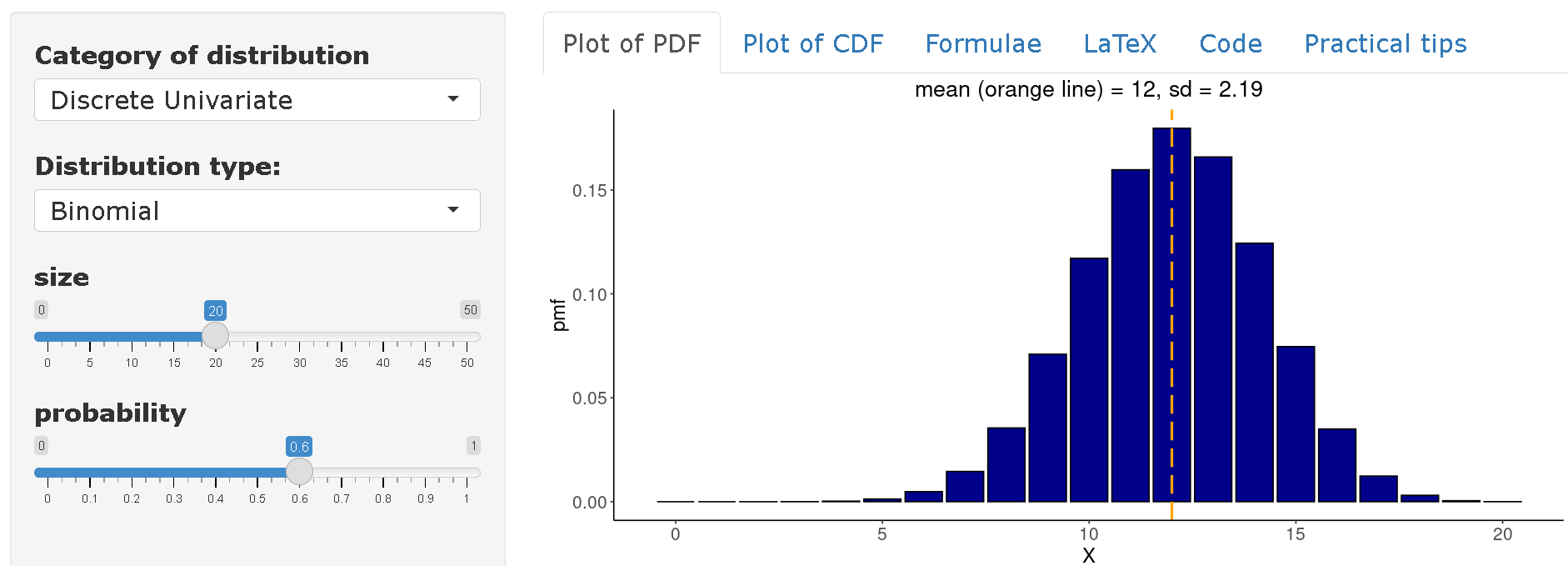
Exemple : Si un virus ayant un taux d’attaque de 60 % est introduit dans une communauté de 20 individus, quelle est la probabilité que 10 individus ou moins soient infectés dans cette communauté ?

Be $X~Bin(n=20,p=0.60)$ il faut alors calculer l’expression suivante :

$P(X≤10)=∑_(x=0)^10 (20 x ) 〖0.60〗^x (1-0.60)^(20-x)$

Dans R, cette expression peut être calculée comme suit :

R

p <- 0.60
n <- 20
x <- 10

pbinom(x,n,p, lower.tail = TRUE)

SORTIE

[1] 0.2446628

Par conséquent, la probabilité qu’un maximum de 10 personnes soient infectées est de 24,5 %.

Sur distribution-zoo vous pouvez consulter la distribution complète de la variable

$X~Bin(n=20,p=0.60)$. On peut donc conclure qu’en moyenne, on peut s’attendre à trouver 12 personnes infectées dans une communauté de 20 individus, sur la base d’un taux d’attaque de 60 %.

Distribution de Poisson

La distribution de Distribution de Poisson modélise le comportement des variables aléatoires décrivant le nombre d’événements, de “comptes”, survenant dans un intervalle d’observation fixe, par exemple le temps (nombre d’infections survenant dans une heure, un jour, une semaine, une année, etc.) ou la zone (nombre d’infections survenant dans une municipalité, un hôpital, etc.)

Cette distribution possède un paramètre appelé lambda ($λ$), $λ>0$ qui décrit le nombre moyen d’événements survenant dans l’intervalle d’observation fixé. Si $X$ a une distribution de Poisson, elle est représentée comme suit :

$X$~$Poisson(λ)$

Sa fonction de densité, d’espérance, de moyenne et de variance correspond à :

$fx=P(X=x)=\frac{e^{-λ}λ^x}{x!}, x=0,1,2,..,$

$E(x)=λ Var(x)=λ$

Dans le domaine des maladies infectieuses, la distribution de Poisson peut être utilisée pour modéliser le nombre de cas secondaires générés par un cas primaire. Dans ce contexte, le paramètre est fonction du nombre effectif de réplications R qui représente le nombre moyen d’infections secondaires causées par chaque cas primaire au fil du temps dans une population composée d’individus sensibles et non sensibles.

::: challenge \[**Exemple**\]{.underline}

Supposons que l’on souhaite étudier la propagation d’une épidémie basée sur un modèle de Poisson au fur et à mesure que les jours (t) s’écoulent. La variable aléatoire d’intérêt est :

$X_{(t )}$ le nombre de cas secondaires causés par chaque cas primaire le jour t

Il s’agit d’un modèle de Poisson puisqu’il y a un intervalle d’observation fixe “chaque cas primaire” et que l’on souhaite étudier le nombre de cas secondaires observés “événements”. On peut donc construire le modèle suivant :

$X_{(t )}∼Poisson (λ= R X_{(t-1)})$

Le modèle ci-dessus exprime que le nombre moyen de cas secondaires au jour t dépend du nombre de reproductions. $R$ et du nombre de cas observés $X$ le jour précédent $(t-1)$. Cependant, R est difficile à connaître dans la réalité et il peut être intéressant d’approximer sa valeur sur la base des données observées au cours de l’épidémie afin d’élaborer des stratégies de lutte.

Supposons qu’au premier jour de l’épidémie $(t=1)$ un total de 5 nouveaux cas sont apparus le premier jour de l’épidémie et que le jour suivant $(t=2)$ 10 nouveaux cas sont apparus le jour suivant. Avec les informations ci-dessus, nous sommes intéressés par l’étude du nombre de cas secondaires au jour 2, ce qui équivaut à :

$X_{(2 )}$ Nombre de cas secondaires causés par chaque cas primaire au jour 2.

Il est réparti de la manière suivante :

$X_{(2 )}∼Poisson (λ= R *5)$

A partir de là, nous pouvons estimer la valeur de $R$ en recherchant la valeur qui maximise la probabilité d’observer ce nombre spécifique de cas secondaires le jour 2, c’est-à-dire

$P(X_{(2 )}=10)=\frac{e^{-(R *5)} (R *5)^{10}}{10!}$

Dans R, nous pourrions découvrir cela en faisant varier différentes valeurs du nombre de nombre de reproduction (R) comme suit :

R

# Fonction de calcul de la probabilité de Poisson
probabilite_poisson <- function(valeur1, valeur2, taux_reproduction) {
  dpois(valeur2, taux_reproduction * valeur1)
}


# Valeurs d'entrée
valeur1 <- 5
valeur2 <- 10
nombres_reproduction <- seq(0, 5, 0.01)


# Calcul des probabilités
resultats_poisson <- probabilite_poisson(valeur1, valeur2, nombres_reproduction)


# Création du dataframe pour ggplot
donnees_resultats <- data.frame(nombres_reproduction, resultats_poisson)


# Trouver le nombre de reproduction le plus probable
nombre_reproduction_probable <- donnees_resultats %>%
  filter(resultats_poisson == max(resultats_poisson)) %>%
  pull(nombres_reproduction)

ERREUR

Error in donnees_resultats %>% filter(resultats_poisson == max(resultats_poisson)) %>% : could not find function "%>%"

R

# Créer le graphique avec ggplot2
ggplot(donnees_resultats, aes(x = nombres_reproduction, y = resultats_poisson)) +
  geom_line() +
  geom_vline(xintercept = nombre_reproduction_probable, color = "red", size = 1) +
  labs(y = "Probabilité", x = "Nombre de reproduction (R)", title = "Modèle de Poisson")

ERREUR

Error in ggplot(donnees_resultats, aes(x = nombres_reproduction, y = resultats_poisson)): could not find function "ggplot"

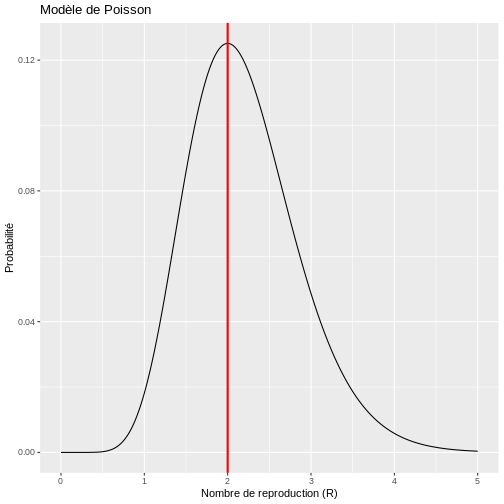
Par conséquent, si le nombre de cas secondaires se comporte selon une distribution de Poisson, il y a une forte probabilité que le nombre de nouveaux cas observés le jour 2 ait été généré avec un nombre de reproduction de R=2. Cela implique que le nombre moyen de cas secondaires par cas primaire est de 2. Toutefois, ce modèle simple suppose que le nombre de cas secondaires générés par chaque cas primaire a une moyenne et une variance égales, ce qui implique que tous les cas primaires génèrent en moyenne un nombre similaire de cas secondaires. Cette hypothèse peut être difficile à formuler pour certaines maladies infectieuses, en particulier lorsqu’elles suivent un modèle de surdispersion (20 % des cas sont à l’origine de 80 % de la transmission), de sorte que le modèle de Poisson présente des limites dans son application. :::

Distribution binomiale négative

Comme la distribution de Poisson, la distribution binomiale négative permet de modéliser le nombre d’événements qui se produisent. Si $X$ a une distribution binomiale négative, il est représenté comme suit.

$X $~$ BN(μ,k)$

Où ? $μ$ représente la moyenne de la distribution et $k$ est le paramètre de dispersion qui permet à la moyenne et à la variance des événements de ne pas être égales. Ce paramètre $k$ permet d’introduire dans le modèle le degré de dispersion dans la façon dont les événements sont générés. Ainsi, $k$ mesure inversement le degré de variation des événements qui se produisent, étant donné que la moyenne et la variance de la distribution correspondent à :

$E(x)=μ$

$Var(x)=μ(1+\frac{μ}{k})$

Avec la fonction de densité :

$f(x)=\frac{Γ(x+k)}{Γ(k)Γ(x+1)} (\frac{μ}{μ+k})^x (\frac{k}{μ+k})^k,x=0,1,2...$

Défi

\[**Exemple**\]{.underline}

Dans l’étude des maladies infectieuses, la distribution binomiale négative joue un rôle important puisqu’elle permet de modéliser la distribution du nombre de cas secondaires générés par un cas primaire, c’est-à-dire qu’elle permet de connaître la distribution du nombre de reproduction de base R_0. Dans ce contexte, la moyenne de la distribution correspond à $R_0$(nombre de cas secondaires dans une population totalement sensible) et le paramètre $k$ contrôle la variation entre les cas primaires. Ainsi, de petites valeurs de k suggèrent que les cas secondaires sont générés par un petit groupe de cas primaires, tandis que de grandes valeurs suggèrent que la propagation du virus est élevée. Ainsi, le fait d’être $X$ le nombre de cas secondaires, alors

$X \sim Bn(R_0,k)$

$E(x)=R_0$

$Var(x)=R_0 (\frac{1+R_0}{k})$

L’article de Lloyd-Smith et al. montre comment la distribution binomiale négative permet de modéliser la distribution des cas secondaires de divers pathogènes. Sur la base des cas signalés lors de l’épidémie de SRAS à Singapour en 2023, ils ont estimé les paramètres de la distribution binomiale négative et ont trouvé une valeur de $R_0=1.630$ y $k=0.160$. Ces estimations sont disponibles dans le epiparameter qui est un paquet disponible à l’adresse R qui compile les principales estimations de plusieurs paramètres épidémiologiques d’intérêt pour l’étude des maladies infectieuses.

R

# Récupérer les données des paramètres épidémiologiques pour le SARS
SARS_R <- epiparameter::epiparameter_db(
  disease = "SARS",  # Spécifier la maladie comme étant le SARS
  epi_name = "offspring distribution", # Sélectionner le paramètre épidémiologique : distribution de descendance
  single_epiparameter = TRUE# Demander un seul paramètre épidémiologique
)

SORTIE

Using Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>..
To retrieve the citation use the 'get_citation' function

R

# Afficher les données récupérées
SARS_R

SORTIE

Disease: SARS
Pathogen: SARS-Cov-1
Epi Parameter: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom (No units)
Parameters:
  mean: 1.630
  dispersion: 0.160

Grâce à ces résultats, il serait possible de tracer la distribution du nombre de cas secondaires de SRAS afin de suggérer des mesures de contrôle. Cette information est également disponible dans la base de données epiparameter avec la fonction plot.

R

plot(SARS_R)

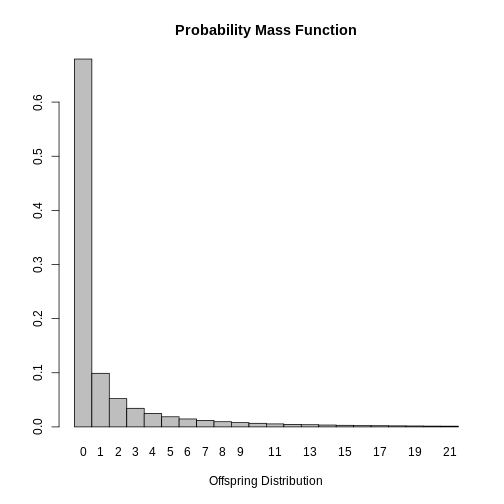
Enfin, il est possible de conclure que la plupart des cas infectés par le SRAS ne propagent pas la maladie puisque le mode de la distribution est $0$. Ce résultat est attendu étant donné que $k<1$ indiquant que les cas secondaires sont générés par un petit groupe de personnes infectées et que la valeur estimée de $R_0$ varie selon les cas.

Distribution géométrique

La distribution géométrique est une autre distribution discrète intéressante qui peut être utilisée pour modéliser les comptages ou le nombre d’événements. Dans le domaine des maladies infectieuses, elle est principalement utilisée lorsque le paramètre de dispersion de la distribution négative est égal à 1. Cette distribution dépend de la probabilité d’occurrence de l’événement en question et est représentée comme suit.

$X \sim Geom(p)$

où p représente la probabilité de succès ou la probabilité d’occurrence de l’événement d’intérêt avec une moyenne égale à :

$E(x)=\frac{1}{p}$

Défi

Exemple

Si, dans le cas d’une épidémie de SRAS à Singapour en 2023, la valeur estimée de $k$ aurait été de $1$ alors la distribution des cas secondaires pourrait être modélisée par une distribution géométrique telle que sa moyenne soit égale à la valeur de $R_0$ c’est-à-dire qu’il doit être satisfait que :

$E(x)=\frac{1}{p}=1.630$ et donc, $p=\frac{1}{1.630}$

La distribution du nombre de contacts secondaires peut donc s’écrire comme suit :

$X \sim Geom(p=0.613)$

Dans R, nous pourrions simuler le comportement du nombre de cas secondaires avec le code suivant :

R

# Distribution géométrique
# Créer une séquence de valeurs de 0 à 20 représentant différents valeurs de R
x <- seq(0, 20, 1)


# Définir le paramètre de probabilité pour la distribution géométrique  
probabilite <- 1/(1.630)


# Créer un data frame avec les valeurs de x et leurs probabilités géométriques correspondantes
donnees_geom <- data.frame(x, prob_geom = dgeom(x, probabilite))


# Création du graphique avec ggplot2
ggplot(data = donnees_geom, aes(x = x, y = prob_geom)) +
  geom_bar(stat = "identity") +
  labs(y = "Probabilité", x = "Cas secondaires", title = "Distribution géométrique")

ERREUR

Error in ggplot(data = donnees_geom, aes(x = x, y = prob_geom)): could not find function "ggplot"

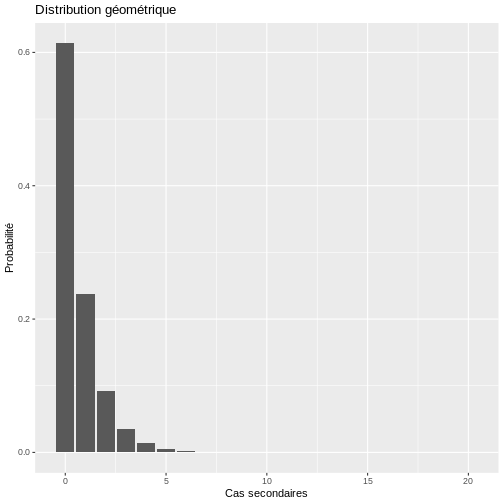
Dans le cadre de la distribution géométrique, la probabilité qu’un cas primaire transmette le virus est plus élevée puisque la probabilité qu’un cas primaire génère 1, 2 ou plus de cas secondaires est plus élevée avec ce modèle qu’elle ne l’est avec le modèle binomial négatif.

Modèles continus

Distribution uniforme

La distribution uniforme modélise une variable continue dont les valeurs sont comprises dans un intervalle. $ [a,b] $ avec la même probabilité. Cette distribution est souvent utilisée dans la simulation de nombres aléatoires. Si $X$ suit une distribution uniforme, elle peut être représentée par :

$X ∼U(a,b)$

Ses paramètres a et b représentent respectivement la valeur minimale et maximale que peut prendre la variable. Sa fonction de densité est déterminée par :

$f(x)=\frac{1}{b-a}$,avec $a<x<b$

La moyenne et la variance sont déterminées par :

$E(x)=\frac{a+b}{2}$ y $V(x)=\frac{(b-a)^2}{12}$

Défi

Exemple

Un chercheur souhaite simuler le comportement de COVID-19 et doit générer de manière aléatoire la valeur que peut prendre le numéro de reproduction de base. $R_0$ et l’utiliser ensuite dans son modèle de propagation. Pour ce faire, il suppose que le $R_0$ de COVID-19 suit une distribution uniforme entre 2 et 5 :

$R0∼U [2,5] $

Pour votre simulation, vous devez générer cinq valeurs possibles de $R_0$ avec la même probabilité, c’est-à-dire en R est résolu à l’aide du code suivant :

R

# Génération de nombres aléatoires avec une distribution uniforme
# Définir le nombre de valeurs aléatoires à générer
n <- 5  
# Définir les bornes inférieure et supérieure de la distribution uniforme
a <- 2  
b <- 5  
# Générer 'n' nombres aléatoires distribués uniformément entre 'a' et 'b'
runif(n, a, b)

SORTIE

[1] 3.164584 2.087320 2.242914 4.394300 4.563492

Distribution normale

La distribution normale est sans aucun doute le modèle probabiliste le plus important de la théorie statistique en raison de sa capacité à modéliser de nombreux problèmes de la vie réelle et de son rôle important dans le domaine de l’inférence. Cette distribution tente de modéliser des variables aléatoires qui peuvent être influencées par de multiples facteurs, dont les effets additionnés font tendre les valeurs de la distribution vers le centre (la moyenne). Par exemple, la température corporelle peut suivre une distribution normale puisqu’elle est influencée par de multiples facteurs biologiques et environnementaux qui, additionnés, font que la plupart des individus se situent autour d’une valeur centrale.

Pour exprimer mathématiquement qu’une variable continue a une distribution normale, nous écrivons :

$X ∼N(μ,σ)$

à laquelle sera associée la fonction de densité de probabilité suivante :

$f(x)=exp [-frac{1}{2 σ^2}(x-u)2] $

Où $μ$ y $σ$ sont les paramètres de la distribution et représentent respectivement la moyenne et l’écart-type de la variable aléatoire, c’est-à-dire la valeur centrale et la dispersion des données par rapport à celle-ci. Ces paramètres correspondent aux valeurs que l’on obtiendrait si l’on étudiait l’ensemble de la population plutôt qu’un échantillon de celle-ci.

Lorsque $μ=0$ y $σ=1$ est appelé distribution normale normale. Cependant, il existe de nombreuses distributions normales en fonction des valeurs prises par leurs paramètres, mais quelle que soit la valeur des paramètres, la forme de la distribution est toujours symétrique et peut toujours être transformée en une distribution normale standard au moyen d’une procédure de normalisation appliquant la formule suivante :

$Z=\frac{X-μ}{σ}∼N(0,1)$

Défi

Exemple,

Si l’on sait que dans une communauté, l’âge des personnes décédées du COVID-19 a une distribution normale avec une moyenne de 67,8 ans et un écart-type de 15,4 ans. Quelle est la probabilité qu’une personne décédée ait moins de 40 ans ?

Tout d’abord, nous définissons la variable à étudier, qui a une distribution normale.

$X∼N(67.8,15.4)$

$X$ Il s’agit de l’âge des cas décédés de COVID-19.

Dans R, nous pouvons utiliser la fonction pnorm() comme suit pour trouver :

$P(X<40)=?$

R

# Définir la moyenne de la distribution normale
mu <- 67.8
# Définir l'écart-type de la distribution normale
sigma <- 15.4
# Définir la valeur pour laquelle nous voulons calculer la probabilité cumulative
x <- 40
# Calculer la probabilité cumulative
pnorm(x, mean = mu, sd = sigma)

SORTIE

[1] 0.0355221

Par conséquent, la probabilité qu’un accidenté COVID-19 soit âgé de moins de 40 ans est de 3,5 %.

Distribution log-normale

La distribution log-normale apparaît lorsque l’on considère des variables aléatoires continues qui ne prennent pas la valeur de zéro ou de nombres négatifs, dont la distribution a une forme asymétrique et dont la variation est générée par de multiples facteurs dont les effets ne sont pas symétriques. Si une variable aléatoire suit une distribution log-normale, sa transformation par l’application de la fonction logarithme générera une variable normale, d’où son nom. Dans le domaine des maladies infectieuses, la distribution log-normale est très utile pour modéliser les périodes d’incubation (temps écoulé entre l’infection et l’apparition des symptômes).

Si $X ∼LogN(μ,σ)$ alors on peut dire que $Y=log (X) ∼N(μ,σ)$ et la fonction de densité de $X$ est donnée par :

$f(x)=\frac{1}{ xσ\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{ln(x)-u}{σ})^2}$

Contrairement à la distribution normale, dans la distribution log-normale, le paramètre μ joue le rôle d’un paramètre d’échelle puisqu’il augmente la dispersion des données en augmentant leur degré d’amplitude et le paramètre σ contrôle la forme, c’est-à-dire le degré d’asymétrie.

Défi

Exemple

Dans l’article de 2009 de Lessler et al., les périodes d’incubation de plusieurs agents pathogènes ont été modélisées sur la base d’une distribution log-normale. L’intérêt principal était d’estimer les paramètres de $(μ,σ)$. Par exemple, dans le cas du SRAS, on a trouvé une estimation de $μ=0.660$, y $σ=1.205$ ce qui implique qu’en moyenne, un cas infecté développe des symptômes en 0,7 jour. Cette information peut être obtenue dans le paquet epiparameter avec la commande suivante :

R

# Récupérer les données des paramètres épidémiologiques pour la période d'incubation du SARS
SARS_incubation <- epiparameter::epiparameter_db(  
  disease = "SARS",  # Spécifier la maladie comme étant le SARS
  epi_name = "incubation period",  # Sélectionner le paramètre épidémiologique : période d'incubation
  single_epiparameter = TRUE  # Demander un seul paramètre épidémiologique
)

SORTIE

Using Lessler J, Reich N, Brookmeyer R, Perl T, Nelson K, Cummings D (2009).
"Incubation periods of acute respiratory viral infections: a systematic
review." _The Lancet Infectious Diseases_.
doi:10.1016/S1473-3099(09)70069-8
<https://doi.org/10.1016/S1473-3099%2809%2970069-8>..
To retrieve the citation use the 'get_citation' function

R

# Afficher les données récupérées sur la période d'incubation
SARS_incubation

SORTIE

Disease: SARS
Pathogen: SARS-Cov-1
Epi Parameter: incubation period
Study: Lessler J, Reich N, Brookmeyer R, Perl T, Nelson K, Cummings D (2009).
"Incubation periods of acute respiratory viral infections: a systematic
review." _The Lancet Infectious Diseases_.
doi:10.1016/S1473-3099(09)70069-8
<https://doi.org/10.1016/S1473-3099%2809%2970069-8>.
Distribution: lnorm (days)
Parameters:
  meanlog: 1.386
  sdlog: 0.593

La distribution complète de la période d’incubation pour le SRAS peut être tracée au moyen de :

R

plot(SARS_incubacion)

ERREUR

Error: object 'SARS_incubacion' not found

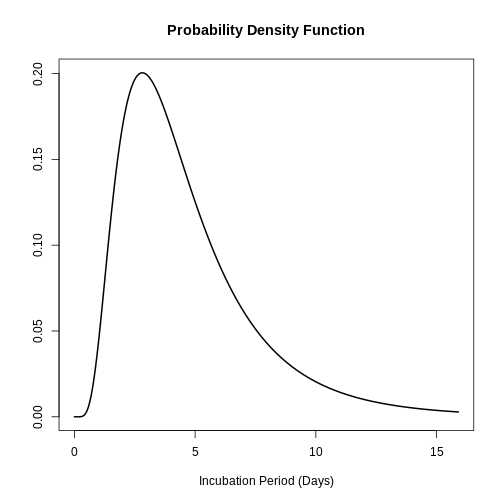
Les données ci-dessus sont utiles pour répondre à des questions telles que : Quelle est la probabilité qu’un cas de SRAS développe des symptômes deux jours après l’infection ?

R

# Calculer la probabilité cumulative complémentaire (P(X > 2)) pour une distribution lognormale

stats::plnorm(2, meanlog = 0.660, sdlog = 1.205, lower.tail = FALSE)

SORTIE

[1] 0.4890273

Distribution Gamma

Lorsque nous étudions des variables aléatoires de Poisson, nous nous intéressons généralement au nombre d’événements qui se produisent avec une moyenne de $λ$ pour un intervalle de temps donné. La distribution Gamma se concentre sur l’étude de la v.a $X$ La distribution Gamma se concentre sur l’étude de la v.a. : le temps nécessaire pour qu’un nombre donné d’événements se produisent. $α^th$. Par exemple, si nous évaluons le nombre d’infections par heure et que nous voulons étudier combien de temps peut s’écouler jusqu’à ce que nous trouvions α infections, alors graphiquement $X$ correspond à :

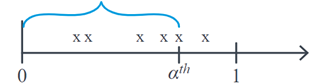
La distribution Gamma est largement utilisée dans l’analyse de survie en raison de sa flexibilité due à ses paramètres de forme. $α$ et l’échelle $θ$ qui déterminent sa fonction de densité, laquelle a un comportement asymétrique. Ici, $θ$ représente le temps d’attente moyen jusqu’à ce que le premier événement se produise, et $α$ est le nombre d’événements attendus. Cette distribution est représentée comme suit :

$X ∼Gamma(α,θ)$

$f(x)=\frac{1}{(α-1)!θ^α}e^{\frac{-x}{θ}} x^{α-1}$

$E(x)=αθ$

$Var(x)=αθ^2$

Lorsque $θ$ augmente, la concentration de la probabilité se déplace vers la droite, il en va de même lorsque l’on s’attend à un plus grand nombre d’événements. $α$ Étant donné que le temps d’attente $X$ peut être plus long.

::: challenge Exemple

Une application possible de la distribution Gamma est la modélisation de l’intervalle sériel des maladies infectieuses. L’intervalle sériel (s) est défini comme le temps écoulé entre l’apparition des symptômes du cas primaire et l’apparition des symptômes du cas secondaire. Dans l’étude de Ghani et al., la distribution de l’intervalle sériel de la grippe a été décrite comme suit Grippe-A-H1N1Pdm au moyen de la distribution gamma et a trouvé les paramètres suivants :

$s ∼Gamma( α=2.622,θ=0.957)$

Ces informations peuvent également être obtenues dans le paquet epiparameter avec la commande suivante :

R

# Récupérer les données des paramètres épidémiologiques pour l'intervalle sériel de la grippe
influenza_s <- epiparameter::epiparameter_db(  
  disease = "Influenza",  # Spécifier la maladie comme étant la grippe
  epi_name = "serial_interval",  # Sélectionner le paramètre épidémiologique : intervalle sériel
  single_epiparameter = TRUE  # Demander un seul paramètre épidémiologique
)

SORTIE

Using Ghani A, Baguelin M, Griffin J, Flasche S, van Hoek A, Cauchemez S,
Donnelly C, Robertson C, White M, Truscott J, Fraser C, Garske T, White
P, Leach S, Hall I, Jenkins H, Ferguson N, Cooper B (2009). "The Early
Transmission Dynamics of H1N1pdm Influenza in the United Kingdom."
_PLoS Currents_. doi:10.1371/currents.RRN1130
<https://doi.org/10.1371/currents.RRN1130>..
To retrieve the citation use the 'get_citation' function

R

# Afficher les données récupérées sur l'intervalle sériel
influenza_s

SORTIE

Disease: Influenza
Pathogen: Influenza-A-H1N1Pdm
Epi Parameter: serial interval
Study: Ghani A, Baguelin M, Griffin J, Flasche S, van Hoek A, Cauchemez S,
Donnelly C, Robertson C, White M, Truscott J, Fraser C, Garske T, White
P, Leach S, Hall I, Jenkins H, Ferguson N, Cooper B (2009). "The Early
Transmission Dynamics of H1N1pdm Influenza in the United Kingdom."
_PLoS Currents_. doi:10.1371/currents.RRN1130
<https://doi.org/10.1371/currents.RRN1130>.
Distribution: gamma (days)
Parameters:
  shape: 2.622
  scale: 0.957

R

plot(influenza_s)

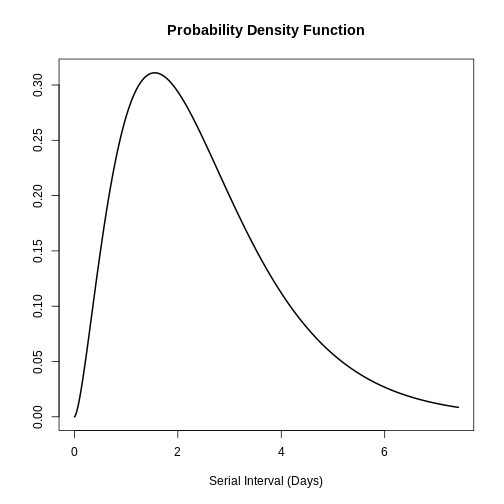
Avec ces informations, la moyenne et l’écart-type de la distribution peuvent être trouvés sur la base de l’application de la distribution gamma :

R

# Definir les parametres de forme et d'echelle
forme <- 2.622
echelle <- 0.957


# Calculer la moyenne de la distribution
moyenne <- forme * echelle  


# Calculer l'ecart-type de la distribution
ecart_type <- sqrt(forme * echelle^2)  


# Afficher la moyenne et l'ecart-type calcules
print(c(moyenne, ecart_type))

SORTIE

[1] 2.509254 1.549631

Par conséquent, la moyenne de l’intervalle sériel de la grippe est de 5,51 jours avec un écart-type de 1,55 jours. :::

Distribution de Weibull

Comme la distribution Gamma, la distribution de Weibull est utile dans l’analyse des v.a.s représentant les temps d’attente jusqu’à l’observation d’un événement particulier. La distribution de Weibull a deux paramètres et sa fonction de densité est définie par :

$f(x)= \frac{β}{η}(\frac{x}{η})^{β-1}{e^{-(x/η)}}^β$

Ici, $η$ est le paramètre d’échelle et $β$ le paramètre de forme. Le paramètre de forme $β$ est également appelé pente et tente de modéliser la relation entre la probabilité et les délais. Ainsi, lorsque $β>1$ le taux d’occurrence des événements augmente avec le temps, tandis que si $β<1$ décrit que le risque de l’événement diminue avec le temps. Le paramètre d’échelle gère le degré de variabilité de la distribution et se trouve dans les mêmes unités de $X$.

::: challenge Exemple

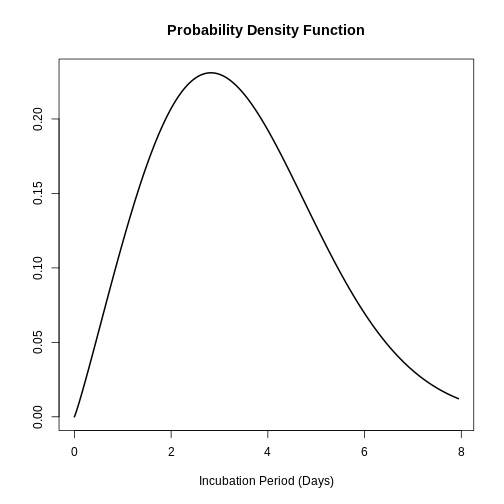
L’étude de Virlogeux et al. a décrit la distribution du temps d’incubation de la grippe à l’aide de la distribution de Weibull et a trouvé les paramètres suivants :

$x∼Gamma( β=2.101,η=3.839)$

Cette information peut également être obtenue dans le package epiparameter avec la commande suivante :

R

# Récupérer les données des paramètres épidémiologiques pour la période d'incubation de la grippe
influenza_incubation <- epiparameter::epiparameter_db(  
  disease = "Influenza",  # Spécifier la maladie comme étant la grippe
  epi_name = "incubation period",  # Sélectionner le paramètre épidémiologique : période d'incubation
  single_epiparameter = TRUE  # Demander un seul paramètre épidémiologique
)

SORTIE

Using Virlogeux V, Li M, Tsang T, Feng L, Fang V, Jiang H, Wu P, Zheng J, Lau
E, Cao Y, Qin Y, Liao Q, Yu H, Cowling B (2015). "Estimating the
Distribution of the Incubation Periods of Human Avian Influenza A(H7N9)
Virus Infections." _American Journal of Epidemiology_.
doi:10.1093/aje/kwv115 <https://doi.org/10.1093/aje/kwv115>..
To retrieve the citation use the 'get_citation' function

R

influenza_incubacion

ERREUR

Error: object 'influenza_incubacion' not found

R

# Tracer les données récupérées sur la période d'incubation

plot(influenza_incubation)

:::

Thème 5 : Introduction à l’inférence statistique

Les statistiques peuvent être divisées en deux branches principales : descriptive et inférentielle. Comme nous l’avons vu dans les unités précédentes, la première cherche généralement à résumer et à explorer les données qui ont été collectées à partir d’un échantillon sélectionné d’une population. En revanche, les secondes visent à généraliser et à tirer des conclusions sur l’ensemble de la population sur la base des informations ou des données provenant d’un échantillon.

De par la nature du processus déductif, qui repose sur le prélèvement d’échantillons aléatoires dans la population, un estimateur peut prendre plusieurs valeurs puisqu’il dépend des unités qui ont été sélectionnées dans l’échantillon. Cette variation due au hasard, appeléevariation variation d’échantillonnage doit être impliquée dans le processus d’inférence, comme nous le verrons plus loin.

Il est important de souligner que la variation d’échantillonnage dépend de la taille de l’échantillon. Par exemple, si nous prenons des échantillons de taille 10 et que nous calculons le CFR dans chacun d’entre eux, ces estimations seront plus proches les unes des autres que celles obtenues lorsque seulement 5 individus par échantillon sont sélectionnés. Vous pouvez le vérifier en effectuant une simulation dans R et en sélectionnant 1000 échantillons de taille 5 et 10, respectivement. Comme le montre la figure ci-dessous, les CFR estimés lorsque la taille de l’échantillon passe de 5 à 10 sont plus similaires avec un RIQ plus faible.

R

library(infer)

SORTIE


Attaching package: 'infer'

SORTIE

The following object is masked from 'package:epiparameter':

    generate

R

# Définir la graine aléatoire pour la reproductibilité
set.seed(200)  


# Créer le cadre de données de la population avec des indicateurs de décès (1 = décédé, 0 = vivant)
population <- data.frame(dead = c(rep(1, 40), rep(0, 160)))  


# Échantillon de taille 5 : Tirer 100 échantillons aléatoires de taille 5 (sans remplacement)
samples_n5 <- population %>%  
  rep_sample_n(size = 5, reps = 100, replace = FALSE)  


# Calculer le taux de létalité (CFR) pour chaque réplique dans l'échantillon de taille 5
cfr_n5 <- samples_n5 %>%  
  group_by(replicate) %>%  
  summarise(cfr = mean(dead))

ERREUR

Error in summarise(., cfr = mean(dead)): could not find function "summarise"

R

# Échantillon de taille 10 : Tirer 100 échantillons aléatoires de taille 10 (sans remplacement)
samples_n10 <- population %>%  
  rep_sample_n(size = 10, reps = 100, replace = FALSE)  


# Calculer le taux de létalité (CFR) pour chaque réplique dans l'échantillon de taille 10
cfr_n10 <- samples_n10 %>%  
  group_by(replicate) %>%  
  summarise(cfr = mean(dead))

ERREUR

Error in summarise(., cfr = mean(dead)): could not find function "summarise"

R

# Combiner les résultats des deux tailles d'échantillons (5 et 10)
cfr <- bind_rows(cfr_n5, cfr_n10) %>%  
  mutate(size = factor(c(rep(5, 100), rep(10, 100))))

ERREUR

Error in mutate(., size = factor(c(rep(5, 100), rep(10, 100)))): could not find function "mutate"

R

# Tracer la distribution d'échantillonnage des estimations du CFR en utilisant un boxplot
ggplot(cfr, aes(x = size, y = cfr, fill = size)) +  
  geom_boxplot(show.legend = FALSE) +  # Créer un boxplot sans légende
  labs(x = "Taille de l'échantillon", y = "Estimation du CFR",  
     title = "Distribution d'échantillonnage des estimations du CFR") +  # Ajouter des étiquettes et un titre
  scale_fill_brewer(palette = "Blues")  # Utiliser une palette de couleurs bleues pour la visualisation

ERREUR

Error in ggplot(cfr, aes(x = size, y = cfr, fill = size)): could not find function "ggplot"

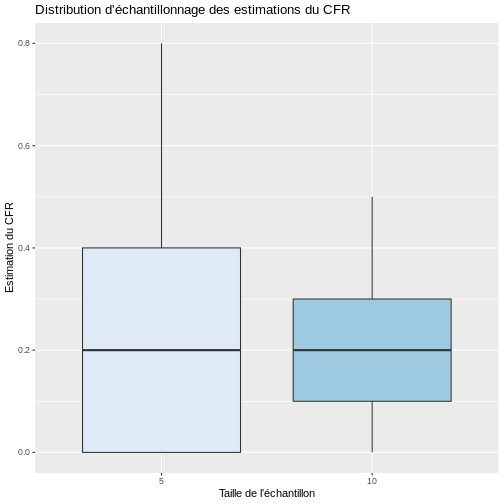
Si nous calculons la moyenne et l’écart-type des valeurs estimées du CFR avec les échantillons de taille 5 et 10, nous constatons que l’écart-type des estimations est effectivement plus petit avec l’augmentation de la taille de l’échantillon, mais dans les deux cas, en moyenne, les échantillons étaient plus proches de la vraie valeur du paramètre de 0,20.

R

# Résumer les estimations du CFR par taille d'échantillon


cfr %>%  
  group_by(size) %>%  # Regrouper les données par taille d'échantillon  
  summarise(  
  moyenne = mean(cfr),  # Moyenne du CFR  
  et = sd(cfr),  # Écart-type du CFR  
  médiane = median(cfr),  # Médiane du CFR  
  p25 = quantile(cfr, 0.25),  # 25e centile (quartile inférieur)  
  p75 = quantile(cfr, 0.75)  # 75e centile (quartile supérieur)  
  )

ERREUR

Error in summarise(., moyenne = mean(cfr), et = sd(cfr), médiane = median(cfr), : could not find function "summarise"

Mais si, dans la réalité, nous ne pouvons prendre qu’un seul échantillon aléatoire, cela signifie que nous n’aurons qu’une seule chance de calculer une statistique qui sera la estimateur ponctueldu paramètre. Toutefois, cette valeur unique ne pourra pas fournir d’informations sur la variabilité inhérente à la sélection aléatoire de l’échantillon. En outre, comme nous l’avons vu dans l’exemple précédent, il est fort probable que de nombreuses configurations possibles de l’échantillon donnent des estimations éloignées de la valeur réelle du paramètre. Par conséquent, nous devons essayer d’intégrer la variabilité de l’échantillonnage dans le processus d’estimation.

Estimation par intervalles de confiance

L’objectif de l’estimation de l’intervalle de confiance est de fournir une plage de valeurs, une limite inférieure et une limite supérieure (a ; b), qui, avec une forte probabilité, “…”.confiance”contient la vraie valeur du paramètre à estimer. Bien que chaque échantillon aléatoire qui peut être sélectionné produise des bornes différentes, cette procédure garantit qu’un échantillon de confiance “contient la vraie valeur du paramètre à estimer”. $(1-α) %$ des intervalles construits contiendra la vraie valeur du paramètre. Cela implique également que a $α%$ des intervalles ne contiendra pas la valeur réelle. Le symbole α est appelé niveau de signification.

En général, un intervalle de confiance est construit avec les ingrédients suivants :

$\text{Estimateur} ±(\text{coefficient de fiabilité})*(\text{erreur standard})$

Défi

Exemple

Dans le paquet CFR de l’initiative Epiverse-TRACE, des informations sont disponibles sur une épidémie d’Ebola qui s’est produite en 1976 au Zaïre, aujourd’hui appelé République du Congo, documentant le nombre de cas et de décès sur une période de 73 jours. En fin de compte, 245 cas d’Ebola ont été signalés, dont 234 cas mortels. Si l’intérêt est d’effectuer une estimation de l’intervalle CFR à 95 %. Quelle doit être la procédure ?

● \[**Étape 1-Estimateur**\]{.underline}: il faut commencer par trouver l’estimation dans l’échantillon observé :

$\hat{p} = \widehat{\text{CFR}} = \frac{234}{245}= 0.955$

Le CFR estimé est donc de 95,5 %.

● \[**Étape 2 - Coefficient de fiabilité**\]{.underline} basé sur la distribution normale pour un niveau de confiance de 95% correspondrait à 1,96

● \[**Étape 3 - Erreur standard :**\]{.underline}

$\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}=\sqrt{\frac{0.955 (1-0.955)}{245}}$

● \[**Étape 4 - Rassembler les ingrédients**\]{.underline}

Comme vous l’avez remarqué jusqu’à présent, ce pas-à-pas peut devenir lourd à cause des calculs, mais en R, nous pouvons tout obtenir de manière plus rapide et plus efficace comme suit :

$ = $

Comme vous l’avez remarqué jusqu’à présent, ce pas-à-pas peut devenir lourd à cause des calculs, mais en R, nous pouvons obtenir tout cela d’une manière plus rapide et plus efficace de la façon suivante :

R

# Télécharger les données sur l'épidémie d'Ebola de 1976
data(ebola1976)

AVERTISSEMENT

Warning in data(ebola1976): data set 'ebola1976' not found

R

# Calculer les statistiques clés liées au taux de létalité (CFR)
cfr_summary <- ebola1976 %>%  
  summarise(  
  n = sum(cases),  # Nombre total de cas  
  deces = sum(deaths),  # Nombre total de décès  
  cfr_est = deces / n,  # Estimation du taux de létalité (CFR)  
  error = sqrt((cfr_est * (1 - cfr_est)) / n),  # Calcul de l'erreur standard  
  lim_inf = cfr_est - 1.96 * error,  # Limite inférieure de l'intervalle de confiance à 95 %  
  lim_sup = cfr_est + 1.96 * error  # Limite supérieure de l'intervalle de confiance à 95 %  
  )

ERREUR

Error in summarise(., n = sum(cases), deces = sum(deaths), cfr_est = deces/n, : could not find function "summarise"

R

# Afficher le résultat
print(cfr_summary)

ERREUR

Error: object 'cfr_summary' not found

Enfin, nous pouvons conclure qu’avec un niveau de confiance de 95 %, le TFC d’Ebola lors de l’épidémie de 1976 en République démocratique du Congo est contenu dans l’intervalle entre 92,9 % et 98,1 %.

Le progiciel CFR dispose également d’une fonction intégrée permettant d’estimer automatiquement le CFR au cours d’une épidémie, avec son intervalle de confiance respectif de 95 %, au moyen de la fonction :

R

# Calculer un taux de létalité statique (CFR) en utilisant le package cfr

cfr::cfr_static(data = ebola1976)

ERREUR

Error: object 'ebola1976' not found

Comme vous pouvez le constater, il existe de légères différences entre l’IC construit pas à pas et celui rapporté par la fonction cfr_static. Cela s’explique par le fait que le progiciel CFR construit l’IC par la méthode basée sur le maximum de vraisemblance et différentes distributions statistiques en fonction du nombre total de cas, mais l’interprétation ne change pas.

Points clés

À la fin de la session, vérifiez si vous avez atteint les objectifs :

Comprendre le rôle des statistiques dans l’étude de l’environnement. maladies infectieuses.
Comprendre les mesures statistiques permettant de résumer et d’analyser les données sur les maladies infectieuses. l’information.
Se familiariser avec le concept de variable aléatoire et reconnaître les principales distributions de probabilité.
Identifier et comprendre le processus du problème statistique en tant que problème d’inférence à partir d’un échantillon.
Comprendre le concept d’intervalle de confiance et la procédure. de test d’hypothèse.

Les contributions

Erika Cantor : Version initiale
Zulma M. Cucunuba : Edition
Laura Gómez-Bermeo : Montage
Andree Valle-Campo : Modifications mineures
José M. Velasco-España : Editions mineures
Hugo Gruson: Traduction en français

Content from Construction d'un modèle déterministe simple

Dernière mise à jour le 2025-07-29 | Modifier cette page

Durée estimée : 128 minutes

Vue d'ensemble

Questions

Comment construire un modèle simplifié de Zika ?

Objectifs

A la fin de cet atelier, vous serez capable de :

Reconnaître comment un modèle déterministe simple est construit en. des équations différentielles ordinaires.
Identifier les paramètres pertinents pour la modélisation des épidémies de MTEV.
Schématiser l’interaction entre les différents compartiments de l’organisme. système à l’aide des paramètres.
Traduire les équations mathématiques du modèle déterministe en code. Code en langage R.
Étudier l’utilisation des simulations du modèle pour projeter les résultats de l’étude. scénarios de transmission et l’impact potentiel des interventions

Pré-requis

Cette unité a comme prérequis

Introduction à R et RStudio
Introduction à la théorie des épidémies
Histoire des épidémies et des pandémies
Visualisation des données en R avec ggplot

Table des matières

Thème 1 : Maladies à transmission vectorielle → Biologie de la maladie, biologie des vecteurs → Virus Zika, diagnostics et interventions

Sujet 2 : Qu’est-ce qu’un modèle déterministe simple ?

Sujet 3 : Modèle SIR simple pour Zika

Sujet 4 : Développement de diagrammes et équations du modèle Zika |

Sujet 5 : Table des paramètres du modèle simple pour Zika → Description du modèle simple Zika

Sujet 6 : Implémentation du modèle Zika en R

Thème 7 : Paramétrage des interventions de contrôle pour Zika

Introduction

Dans cette unité, nous aborderons la construction d’un modèle déterministe simple, en particulier pour le virus Zika, une maladie qui a déclenché une épidémie majeure en Amérique latine et dans les Caraïbes, et qui a été déclarée urgence de santé publique de portée internationale. En utilisant des connaissances préalables sur la théorie des épidémies, nous construirons un modèle déterministe de type SIR qui incorpore des aspects démographiques.

Pour construire ce modèle, nous apprendrons la dynamique de l’interaction entre l’homme et les vecteurs, ainsi que les paramètres fondamentaux qui régissent ces processus biologiques. En construisant un diagramme, nous examinerons ces relations et formulerons des équations qui décrivent le comportement du système. Ces équations serviront de base à la simulation du modèle dans le langage de programmation R. À notre tour, nous proposerons et modéliserons des stratégies d’intervention.

Grâce à l’analyse du modèle, nous évaluerons l’impact potentiel de cette épidémie sur la société, en contextualisant certaines de ces interventions en Amérique latine. En outre, nous renforcerons et appliquerons des thèmes clés tels que : Le modèle SIR, l’immunité du troupeau, les paramètres et les interventions de contrôle (pulvérisation, moustiquaires et vaccination) pour une maladie à transmission vectorielle (VBD).

Thème 6 : Modèle Zika en R

Dans cette section, nous allons utiliser les connaissances acquises sur Zika, les mécanismes impliqués dans la transmission et les équations du modèle. L’objectif est de le construire en R.

Le seul package nécessaire à la modélisation est deSolve, qui permet de résoudre les équations différentielles. En outre, pour le traitement des données et la représentation graphique des résultats, nous vous recommandons d’utiliser tidyverse et cowplot.

6.1 Démarrage pratique avec R

Pour commencer notre pratique en R veuillez ouvrir un projet de Ret créez un nouveau document. Dans ce document, nous devons charger les fonctions que nous venons d’expliquer. Si vous rencontrez des difficultés avec ce processus, veuillez consulter la section Introduction à R.

install.packages(deSolve) # deSolve package pour la résolution d’équations différentielles

Une fois que vous avez installé le paquet deSolve, chargez les paquets avec les lignes de code suivantes, copiez-les dans votre script R et exécutez-les.

R

library(deSolve)

library(tidyverse)

library(cowplot)

Rappelons que pour créer un modèle, nous avons besoin de compartiments, de conditions initiales, de paramètres et d’équations.

Pour ce modèle en R, nous commencerons par définir les paramètres, c’est-à-dire toutes les valeurs qui ont été collectées par la recherche et qui font partie du comportement de la maladie. Dans la section précédente, nous avons parlé de ces paramètres et les avons complétés dans un tableau. Il est maintenant temps de les entrer dans R.

Instruction Reprenez le tableau sur lequel vous avez travaillé précédemment et indiquez la valeur de chacun de ces paramètres.

NOTE : VEUILLEZ INDIQUER LA VALEUR DE CHACUN DE CES PARAMÈTRES :

Il est important de rappeler qu’en R, vous pouvez utiliser des objets précédemment créés pour effectuer des calculs. Par exemple, le paramètre muv est l’inverse du paramètre Lv, c’est-à-dire muv = 1/Lv. Par conséquent, dans R, vous pouvez assigner cette valeur directement avec muv <- 1/Lv. Il n’est pas nécessaire d’effectuer la division et d’affecter le résultat manuellement.

Défi 1

Instruction : Reprenez le tableau sur lequel vous avez travaillé précédemment et entrez la valeur de chacun de ces paramètres.

R

# Liste des paramètres
 Lv <-                   # Espérance de vie des moustiques (en jours)

 Lh <-                   # Espérance de vie des humains (en jours)

 PIh <-                  # Période infectieuse chez les humains (en jours)

 PIv <-                  # Période infectieuse chez les moustiques (en jours)

 PIE <-                  # Période d'incubation extrinsèque chez les moustiques adultes (en jours)

 muv <-                  # Taux de mortalité par habitant de la population de moustiques (1/Lv)

 muh <-                  # Taux de mortalité par habitant de la population humaine (1/Lh)

 alphav <-               # Taux de natalité par habitant de la population de moustiques. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

 alphah <-               # Taux de natalité par habitant de la population humaine. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

 gamma <-                # Taux de rétablissement chez les humains (1/PIh)

 delta <-                # Taux d'incubation extrinsèque (1/PIE)

 Nh <-                   # Nombre d'humains. Pour cet exercice, nous suggérons 100 000 humains. Vous pouvez le modifier selon la ville que vous avez choisie pour la modélisation.

 m <-                    # Densité de moustiques femelles par humain

 Nv <-                   # Nombre de moustiques (m * Nh)

 R0 <-                 # Nombre de reproduction de base

 ph <-                 # Probabilité de transmission d'un moustique infecté à un humain susceptible après une piqûre.

 pv <-                 # Probabilité de transmission d'un humain infecté à un moustique susceptible après une piqûre.

 b <- sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
 (m * ph * pv * delta)) # Taux de piqûre

 betah <-              # Coefficient de transmission d'un moustique infecté à un humain susceptible après une piqûre (ph*b)

 betav <-              # Coefficient de transmission d'un humain infecté à un moustique susceptible après une piqûre (pv*b)

 TEMP <- 1             # Nombre d'années à simuler. Pour cet exercice, nous commencerons avec la première année de l’épidémie.

Solution 1

R

# Liste des paramètres
Lv <- 10                # Espérance de vie des moustiques (en jours)

Lh <- 50 * 365          # Espérance de vie des humains (en jours)

PIh <- 7                # Période infectieuse chez les humains (en jours)

PIv <- 6                # Période infectieuse chez les moustiques (en jours)

PIE <- 8.4              # Période d'incubation extrinsèque chez les moustiques adultes (en jours)

muv <- 1 / Lv           # Taux de mortalité par habitant de la population de moustiques (1/Lv)

muh <- 1 / Lh           # Taux de mortalité par habitant de la population humaine (1/Lh)

alphav <- muv           # Taux de natalité par habitant de la population de moustiques. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

alphah <- muh           # Taux de natalité par habitant de la population humaine. Pour l’instant, nous supposerons qu’il est égal au taux de mortalité.

gamma <- 1 / PIh        # Taux de rétablissement chez les humains (1/PIh)

delta <- 1 / PIE        # Taux d'incubation extrinsèque (1/PIE)

Nh <- 100000            # Nombre d'humains. Pour cet exercice, nous suggérons 100 000 humains. Vous pouvez le modifier selon la ville que vous avez choisie pour la modélisation.

m <- 2                  # Densité de moustiques femelles par humain

Nv <- m * Nh            # Nombre de moustiques (m * Nh)

R0 <- 3              # Nombre de reproduction de base

ph <- 0.7               # Probabilité de transmission d'un moustique infecté à un humain susceptible après une piqûre.

pv <- 0.7               # Probabilité de transmission d'un humain infecté à un moustique susceptible après une piqûre.

b <- sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
         (m * ph * pv * delta)) # Taux de piqûre

betah <- ph * b         # Coefficient de transmission d'un moustique infecté à un humain susceptible après une piqûre (ph*b)

betav <- pv * b         # Coefficient de transmission d'un humain infecté à un moustique susceptible après une piqûre (pv*b)

TEMP <- 1               # Nombre d'années à simuler. Pour cet exercice, nous commencerons avec la première année de l’épidémie.

6.2 Équations du modèle

Maintenant que nous avons introduit les paramètres dans le script, il est temps d’utiliser les équations écrites précédemment, qui nous permettent de connaître le nombre d’individus dans chacun des six compartiments en fonction du temps. Trois compartiments pour les humains et trois compartiments pour les moustiques, qui sont identifiés par un h (pour l’homme) et un v(pour les moustiques). Pour les humains, nous avons les compartiments : sensible, infecté et guéri (d’où le mot SIR) et pour les moustiques, les compartiments sont les suivants : sensible, exposé et infectieux (SEI).

Compartiments

$S_h$ Homme sensible
$I_h$ Humains infectieux
$R_h$ Humains infectieux : Humains guéris d’une infection (immunisés contre la maladie). nouvelle infection)
$S_v$ Vecteurs sensibles
$E_v$ Vecteurs à risque : Vecteurs exposés
$I_v$ Vecteurs infectieux

Pour ce modèle, nous utiliserons les équations différentielles suivantes :

6.2.1 Humain

\[\ \frac{dSh}{dt} = \alpha_h N_h - \beta_h \frac {I_v}{N_h}S_h - \mu_h S_h \]

\[\ \frac{dIh}{dt} = \beta_h \frac {I_v}{N_h}S_h - (\gamma + \mu_h) I_h \]

\[\ \frac{dRh}{dt} = \gamma I_h - \mu_h R_h\]

6.2.2 Vecteurs

\[\ \frac{dSv}{dt} = \alpha_v N_v - \beta_v \frac{ I_h} {N_h}S_v - \mu_v Sv\]

\[\ \frac{dE_v}{dt} = \beta_v \frac{I_h} {N_h}S_v- (\delta + \mu_v) Ev\]

\[\ \frac{dI_v}{dt} = \delta Ev - \mu_v I_v\]

6.3 Formule de calcul $R_0$ (Nombre de base de la reproduction)

Formule nécessaire pour estimer $R_0$:

\[ R_0 = \frac{mb^2 p_h p_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma)} \]

Défi

Instruction Traduire les équations en R

R

# Humains
         dSh   <-  alphah * Nh - betah * (Iv/Nh) * Sh - muh * Sh
         dIh   <-______ * (Iv/Nh) * Sh - (____ + _____) * Ih
         dRh   <-  ______ * Ih  - ______ * Rh

 # Moustiques
         dSv  <-  alphav * Nv - _____ * (Ih/Nh) * Sv - _____ * Sv
         dEv  <-  _____ * (Ih/Nh) * Sv - (____ + _____)* Ev
         dIv  <-  _____ * Ev - _____ * Iv

Une fois que nous savons comment traduire les équations en code, nous procédons à l’exécution du modèle. Pour ce faire, nous utiliserons la fonction ode du paquetage deSolve.

Vous commencez par créer la fonction (qui sera ensuite utilisée dans l’argument fun). Pour ce faire, il faut traduire les équations du modèle Zika en R. Vous trouverez ci-dessous la fonction déjà construite modelo_zika pour remplacer les équations que vous avez déjà remplies ci-dessus.

Défi 3

Instruction Instruction : Remplacez les équations incomplètes du code suivant par les équations complètes du modèle Zika sur lequel vous avez travaillé dans l’instruction précédente.

R

# Modèle déterministe simple (FUN)
modele_zika <- function(temp, variable_detat, parametres) {
  
  with(as.list(c(variable_detat, parametres)), # environnement local pour évaluer les dérivées
       {
         # Humains
         dSh <- ____ * Nh - ____ * (Iv/Nh) * Sh - ____ * Sh   
         dIh <- ____ * (Iv/Nh) * Sh - (____ + ____) * Ih
         dRh <- ____ * Ih - ____ * Rh
         
         # Moustiques
         dSv <- alphav * Nv - ____ * (Ih/Nh) * Sv - ____ * Sv 
         dEv <- ____ * (Ih/Nh) * Sv - (____ + ____)* Ev
         dIv <- ____ * Ev - ____ * Iv
         
         list(c(dSh, dIh, dRh, dSv, dEv, dIv))
       }
  )
}

Solution 3

R

# Modèle déterministe simple (FUN)
modele_zika <- function(temp, variable_detat, parametres) {
  
  with(as.list(c(variable_detat, parametres)), # environnement local pour évaluer les dérivées
       {
         # Humains
         dSh   <-  alphah * Nh - betah * (Iv/Nh) * Sh - muh * Sh
         dIh   <-  betah * (Iv/Nh) * Sh  - (gamma + muh) * Ih
         dRh   <-  gamma * Ih  - muh * Rh
         
         # Moustiques
         dSv   <-  alphav * Nv - betav * (Ih/Nh) * Sv - muv * Sv 
         dEv   <-  betav * (Ih/Nh) * Sv - (delta + muv)* Ev
         dIv   <-  delta * Ev - muv * Iv
         
         list(c(dSh, dIh, dRh, dSv, dEv, dIv))
       }
  )
}

6.4 Résolution du système

Pour résoudre le système, il est nécessaire de créer les trois arguments manquants (temps, parms y y) pour utiliser la fonction ode.

Défi 4

Instruction : Pour times y parms copiez le code ci-dessous et exécutez-le.

R

# Séquence de temps (times)

temps <- seq(1, 365 * TEMP , by = 1)


# Parametres (parms)

parametres <- c(
  muv = muv,     
  muh = muh, 
  alphav = alphav,
  alphah = alphah,
  gamma = gamma,   
  delta = delta,   
  betav = betav,       
  betah = betah,   
  Nh = Nh,      
  Nv = Nv
)

Dans le code qui s’est exécuté, le temps a été créé (times) et des paramètres (params). Nous devons encore créer l’argument y que nous développerons dans la section suivante.

6.4.1. Conditions initiales du système (y)

Afin de définir les conditions initiales, rappelez-vous que le scénario à modéliser dans cet exercice est celui d’une date avant le rapport de la premier cas. Ces valeurs doivent donc refléter ce contexte.

Discussion

Réflexion : Quelles seraient les conditions initiales de chacun des compartiments ?

Défi 5

Instruction : Remplissez les cases comme vous l’avez appris dans le didacticiel.

R

# Conditions initiales du système (y)
initiales <- c(
            Sh = _______ ,        # Compléter et commenter
            Ih = _______ ,        # Compléter et commenter
            Rh = _______ ,        # Compléter et commenter
            Sv = _______ ,        # Compléter et commenter
            Ev = _______ ,        # Compléter et commenter
            Iv = _______ )        # Compléter et commenter

Solution 5

R

initiales <- c(Sh = Nh,        # Population d'humains susceptibles avant le début de l'épidémie
           Ih = 0,        # Population d'humains infectés  avant le début de l'épidémie
           Rh = 0,        # Population d'humains rétablis avant le début de l'épidémie
           Sv = Nv,        # Population de moustiques susceptibles avant le début de l'épidémie
           Ev = 0,        # Population de moustiques exposés avant le début de l'épidémie
           Iv = 0)        # Population de moustiques infectés  avant le début de l'épidémie

6.4.2 Code de fonction

Une fois que tous les arguments nécessaires ont été créés, il est temps de les entrer dans ode. Rappelons les quatre arguments de ode et a qui correspondent à :

y:maison. Vecteur créé avec les conditions initiales du six compartiments.
temps:temps. Vecteur avec séquence de temps
fun:zika_model. Fonction contenant les équations nécessaires pour simuler le modèle.
parms:paramètres. Vecteur dans lequel les paramètres nécessaires à la simulation du modèle ont été collectés.

Défi 6

Instruction Remplissez les cases en fonction de ce que vous avez appris jusqu’à présent.

R

# Résoudre les équations
sortie <- ode(y = _______ , # Compléter et commenter
              times = _______ ,   # Compléter et commenter
              fun = _______ ,   # Compléter et commenter
              parms = _______  # Compléter et commenter
) %>%
  as.data.frame() # Conversion en data frame

Solution 6

R

# Solution
sortie <- ode(y = initiales , 
              times = temps  ,   
              fun = modele_zika   ,   
              parms = parametres  
) %>%
  as.data.frame() # Conversion en data frame

6.4.3 Introduction du premier cas

Maintenant que tous les compartiments sont définis, il est temps d’introduire un individu infectieux dans le modèle pour lancer l’épidémie.

Discussion

Réflexion : Selon vous, quelle est la probabilité la plus élevée : un être humain infectieux ou un moustique infectieux pénétrant dans une population (dans un autre pays) ?

Pour notre cas hypothétique, supposons qu’une personne ait été infectée au Brésil lors d’un voyage touristique et qu’elle soit ensuite retournée dans la ville ______________ (la ville que vous avez définie au début de l’exercice) et qu’elle ait été le premier sujet infectieux dans cette population. Dans ce contexte, le compartiment des humains infectieux comptera alors un individu, Ih = 1 et le compartiment des humains sensibles aura un individu de moins, Sh = Nh - 1.

Défi

Piste : Modifier dans R les conditions initiales (de départ) de sorte que Ih = 1 et Sh = Nh - 1.

Solution

R

# Conditions initiales au début de l'épidémie
initiales <- c(Sh = Nh-1, # Population initiale d'humains susceptibles
               Ih = 1, # Premier cas humain infecté au début de l'épidémie
               Rh = 0, # Aucun humain rétabli au départ
               Sv = Nv, # Population initiale de moustiques susceptibles
               Ev = 0, # Aucun moustique exposé au début de l'épidémie
               Iv = 0) # Aucun moustique infecté au début de l'épidémie

R

sortie <- ode(y = initiales , 
              times = temps  ,   
              fun = modele_zika   ,   
              parms = parametres  
) %>%
  as.data.frame() # Conversion en data frame

6.5 Exécutons maintenant le modèle !

À ce stade, vous avez complété toutes les informations manquantes dans la rubrique le script afin de pouvoir exécuter le modèle.

À noter

Instruction : Exécutez chaque ensemble de lignes de script vues ci-dessus, c’est-à-dire exécutez les sections : Liste des paramètres, la section Modèle déterministe simple (où vous avez construit le modèle), les sections Séquence temporelle (temps (times)), Les paramètres (parameters (parms)), la section Conditions initiales du système (start (y)) et la section finale Résoudre les équations.

Instruction : Vérifiez qu’aucune erreur n’est affichée. En cas d’erreur, veuillez vérifier l’orthographe du code et qu’il ne reste pas d’autres caractères dans le code qui ne correspondent pas, par exemple “_____”, les traits d’union dans les espaces à remplir.

6.6 Visualisation des résultats

Dans notre cours, nous utiliserons ggplot pour la visualisation des données. Il s’agit de important de revoir l’unité 4. Visualisation de données avec ggplot

Il convient de rappeler que l’unité de temps du modèle Zika est déjà définie à partir des paramètres comme suit jours.

Toutefois, si vous souhaitez visualiser les résultats en semaines, mois ou années, vous pouvez le faire à partir des résultats du modèle (salida$time). Pour ce faire, vous pouvez utiliser le code suivant.

Défi 7

Pour une visualisation plus significative des résultats, convertissez les unités de temps de jours a ans et un semaines.

R

# Convertir les temps de jours en années et en semaines, respectivement
sortie$annees <- sortie$time/365
sortie$semaines <- sortie$time/7

6.7 Visualiser et analyser la première épidémie

Commençons par une visualisation de la première épidémie. Comme il s’agit d’une période d’un an, visualisons les graphiques en semaines.

Instructions : Exécutez le code ci-dessous et analysez les graphiques obtenus.

R

# Passez en revue la première épidémie
p1e <- ggplot(data = sortie, aes(y = Ih, x = semaines)) +  
  geom_line(color='firebrick', linewidth=1) +  
  labs(title = "Population humaine infectieuse", x = "Semaines", y = "Nombre") +  
  theme_bw() # Graphique de la population humaine infectieuse  
p2e <- ggplot(data = sortie, aes(y = Rh, x = semaines)) +  
  geom_line(color='olivedrab', linewidth=1) +  
  labs(title = "Population humaine rétablis", x = "Semaines", y = "Nombre") +  
  theme_bw() # Graphique de la population humaine rétablis  


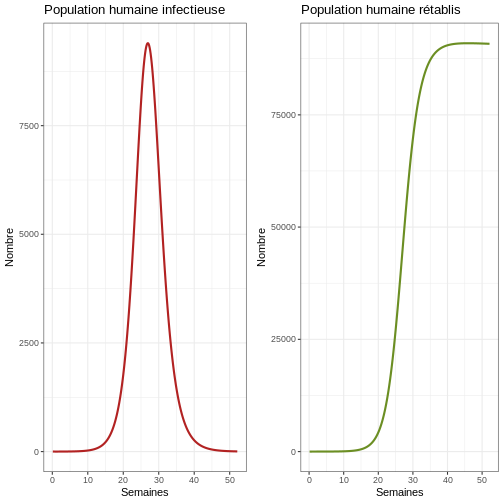
plot_grid(p1e, p2e) # Graphique comparatif de la population humaine infectieuse et de la population humaine rétablis

Discussion

Réflexion : Que voyez-vous dans le graphique ? Observez attentivement l’axe des ordonnées. Quelle proportion d’humains est infectieuse en même temps ?

Pour y voir plus clair, nous pouvons créer des graphiques des proportions :

R

# Passez en revue la première épidémie avec proportions
p1p <- ggplot(data = sortie, aes(y = Ih/(Sh+Ih+Rh), x = semaines)) +  
  geom_line(color = 'firebrick', linewidth = 1) +  
  ggtitle("Population humaine infectieuse") +  
  theme_bw() + ylab("Proportion") + xlab("Semaines") +  
  coord_cartesian(ylim = c(0,1)) # Graphique de la population humaine infectieuse  

p2p <- ggplot(data = sortie, aes(y = Rh/(Sh+Ih+Rh), x = semaines)) +  
  geom_line(color = 'olivedrab', linewidth = 1) +  
  ggtitle("Population humaine rétablie") +  
  theme_bw() + ylab("Proportion") + xlab("Semaines") +  
  coord_cartesian(ylim = c(0,1))  # Graphique de la population humaine rétablie  

plot_grid(p1p, p2p) # Graphique comparatif de la population humaine infectieuse et rétablie

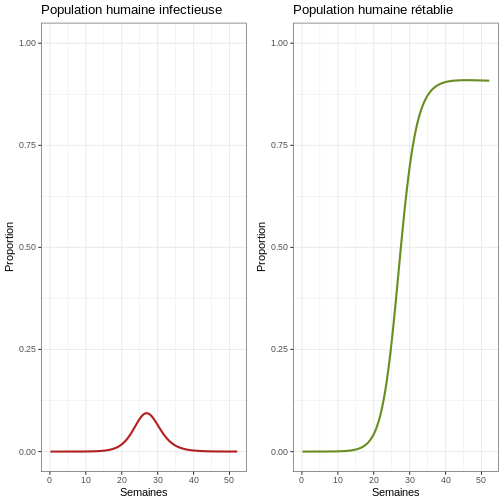
Comportement général (population humaine)

Après avoir observé la première épidémie, il est maintenant temps de projeter l’épidémie à plus long terme.

Instruction : Revenez aux paramètres et changez le paramètre TEMP en 100 ans. Exécutez le bloc de code suivant et observez le nombre d’épidémies qui se produisent dans la population humaine et la taille de chaque épidémie.

R

#Examiner le comportement du modèle sur 100 ans  


p1h <- ggplot(data = sortie, aes(y = (Rh + Ih + Sh), x = annees)) +  
  geom_line(color='grey68', linewidth=1) +  
  labs(title = "Population humaine totale", x = "Années", y = "Nombre") +  
  theme_bw()  


p2h <- ggplot(data = sortie, aes(y = Sh, x = annees)) +  
  geom_line(color='royalblue', linewidth=1) +  
  labs(title = "Population humaine susceptible", x = "Années", y = "Nombre") +  
  theme_bw()  


p3h <- ggplot(data = sortie, aes(y = Ih, x = annees)) +  
  geom_line(color='firebrick', linewidth=1) +  
  labs(title = "Population humaine infectés", x = "Années", y = "Nombre") +  
  theme_bw()  


p4h <- ggplot(data = sortie, aes(y = Rh, x = annees)) +  
  geom_line(color='olivedrab', linewidth=1) +  
  labs(title = "Population humaine rétablis", x = "Années", y = "Nombre") +  
  theme_bw() 


plot_grid(p1h, p2h, p3h, p4h, ncol = 2)

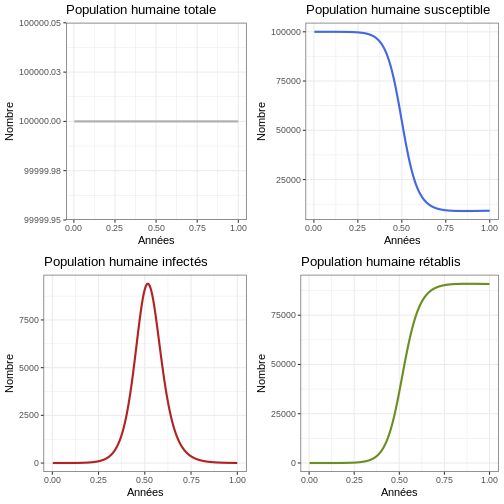
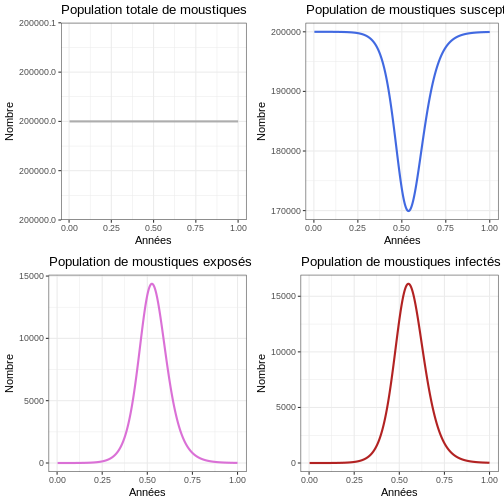
Comportement général (population de moustiques)

Instruction : Exécutez le bloc de code suivant et observez le nombre d’épidémies qui se produisent dans la population de moustiques et la taille de chaque épidémie. Comparez les graphiques avec ceux de la population humaine.

R

# Examiner le comportement du modèle
p1v <- ggplot(data = sortie, aes(y = (Sv + Ev + Iv), x = annees)) +  
  geom_line(color='grey68', linewidth=1) +  
  labs(title = "Population totale de moustiques", x = "Années", y = "Nombre") +  
  theme_bw()  


p2v <- ggplot(data = sortie, aes(y = Sv, x = annees)) +  
  geom_line(color='royalblue', linewidth=1) +  
  labs(title = "Population de moustiques susceptibles", x = "Années", y = "Nombre") +  
  theme_bw()  


p3v <- ggplot(data = sortie, aes(y = Ev, x = annees)) +  
  geom_line(color='orchid', linewidth=1) +  
  labs(title = "Population de moustiques exposés", x = "Années", y = "Nombre") +  
  theme_bw()  


p4v <- ggplot(data = sortie, aes(y = Iv, x = annees)) +  
  geom_line(color='firebrick', linewidth=1) +  
  labs(title = "Population de moustiques infectés", x = "Années", y = "Nombre") +  
  theme_bw() 


plot_grid(p1v, p2v, p3v, p4v, ncol = 2)

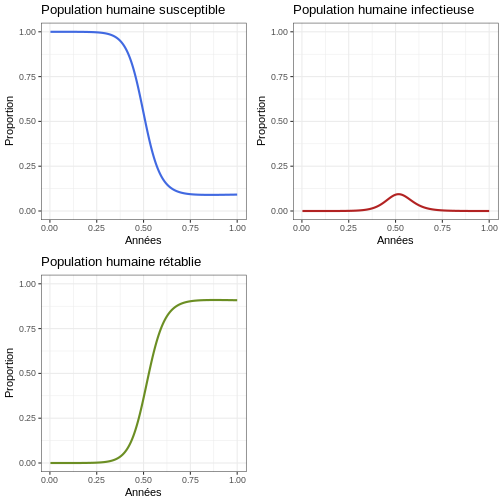
Proportion

Instruction : Exécutez le bloc de code suivant et comparez-le aux graphiques générés pour la population humaine.

R

#Proportions

p1 <- ggplot(data = sortie, aes(y = Sh/(Sh+Ih+Rh), x = annees)) +
  geom_line(color='royalblue', linewidth=1) +
  ggtitle('Population humaine susceptible') +
  theme_bw() + ylab('Proportion') + xlab('Années') +
  coord_cartesian(ylim = c(0,1))

p2 <- ggplot(data = sortie, aes(y = Ih/(Sh+Ih+Rh), x = annees)) +
  geom_line(color='firebrick', linewidth=1) +
  ggtitle('Population humaine infectieuse') +
  theme_bw() + ylab('Proportion') + xlab('Années') +
  coord_cartesian(ylim = c(0,1))

p3 <- ggplot(data = sortie, aes(y = Rh/(Sh+Ih+Rh), x = annees)) +
  geom_line(color='olivedrab', linewidth=1) +
  ggtitle('Population humaine rétablie') +
  theme_bw() + ylab('Proportion') + xlab('Années') +
  coord_cartesian(ylim = c(0,1))

plot_grid(p1, p2, p3, ncol = 2)

Points clés

Vérifiez si vous avez acquis ces compétences à la fin de cette leçon :

Appliquer des concepts tels que les paramètres, $R_0$ et l’immunité de groupe, appris lors de la session A de l’atelier
Traduire les formules mathématiques des interactions entre le virus et le virus de l’immunité. paramètres du modèle en code R
Réaliser un modèle simple en R pour une maladie transmise par maladie vectorielle
Discuter des modifications apportées aux projections du modèle lorsqu’elles sont mises en œuvre différentes stratégies de contrôle des infections

Contributions

Zulma Cucunuba & Pierre Nouvellet : Version initiale
Kelly Charinga & Zhian N. Kamvar : Edition
José M. Velasco-Espagne : Traduction de l’anglais vers l’espagnol et édition
Andree Valle-Campos : éditions mineures
Hugo Gruson: Traduction en français

Affaires juridiques

Références

de Carvalho, S. S., Rodovalho, C. M., Gaviraghi, A., Mota, M. B. S., Jablonka, W., Rocha-Santos, C., Nunes, R. D., Sá-Guimarães, T. da E., Oliveira, D. S., Melo, A. C. A., Moreira, M. F., Fampa, P., Oliveira, M. F., da Silva-Neto, M. A. C., Mesquita, R. D. et Atella, G. C. (2021). Aedes aegypti post-emergence transcriptome : Unveiling the molecular basis for the hematophagic and gonotrophic capacitation. PLoS Neglected Tropical Diseases, 15(1), 1–32. https://doi.org/10.1371/journal.pntd.0008915

Chang, C., Ortiz, K., Ansari, A. et Gershwin, M. E. (2016). The Zika outbreak of the 21st century”, Journal of Autoimmunity, 68, 1–13. https://doi.org/10.1016/j.jaut.2016.02.006

Cori, A., Ferguson, N. M., Fraser, C. et Cauchemez, S. (2013). A new framework and software to estimate time-varying reproduction numbers. during epidemics. American Journal of Epidemiology, 178(9), 1505–1512. https://doi.org/10.1093/aje/kwt133

Duffy, M. R., Chen, T.-H., Hancock, W. T., Powers, A. M., Kool, J. L., Lanciotti, R. S., Pretrick, M., Marfel, M., Holzbauer, S., Dubray, C., Guillaumot, L., Griggs, A., Bel, M., Lambert, A. J., Laven, J., Kosoy, O., Panella, A., Biggerstaff, B. J., Fischer, M. et Hayes, E. B. (2009). Épidémie de virus Zika sur l’île de Yap, États fédérés de Micronésie. Nouveau New England Journal of Medicine, 360(24), 2536–2543. https://doi.org/10.1056/nejmoa0805715

Ferguson, N. M., Cucunubá, Z. M., Dorigatti, I., Nedjati-Gilani, G. L., Donnelly, C. A., Basáñez, M. G., Nouvellet, P. et Lessler, J. (2016). Lutter contre l’épidémie de Zika en Amérique latine. Science, 353(6297). https://doi.org/10.1126/science.aag0219

Heesterbeek, J. A. P. (2002). Une brève histoire du R0 et une recette pour son développement. calcul. Acta Biotheoretica, 50(3). https://doi.org/10.1023/A:1016599411804

Lee, E. K., Liu, Y. et Pietz, F. H. (2016). A Compartmental Model for Zika Virus avec des populations humaines et vectorielles dynamiques. AMIA … Annual Symposium Proceedings. Symposium de l’AMIA, 2016, 743–752.

Pettersson, J. H. O., Eldholm, V., Seligman, S. J., Lundkvist, Å.., Falconar, A. K., Gaunt, M. W., Musso, D., Nougairède, A., Charrel, R., Gould, E. A., & de Lamballerie, X. (2016). Comment le virus zika a-t-il émergé en les îles du Pacifique et l’Amérique latine ? MBio, 7(5). https://doi.org/10.1128/mBio.01239-16

Content from Banque de questions fréquemment posées et d'erreurs

Dernière mise à jour le 2025-07-24 | Modifier cette page

Durée estimée : 88 minutes

Vue d'ensemble

Questions

Avez-vous des difficultés avec le code dans R ?

Objectifs

Dans ce document, vous trouverez quelques-unes des questions fréquemment posées et des erreurs dans l’exécution du code R.

Banque de questions

RTools est-il nécessaire ?

Il existe plusieurs problèmes courants dans R qui peuvent nécessiter l’installation de Rtools.

Installation de paquets nécessitant une compilation : certains paquets R doivent être compilés à partir du code source, ce qui nécessite des outils de compilation fournis par Rtools.
Dépendances C, C++ ou Fortran : Si vous souhaitez installer des paquets qui dépendent d’un code écrit en C, C++ ou Fortran, vous aurez besoin de Rtools pour compiler ces composants.
Erreurs de compilation : Si vous rencontrez des erreurs lors de l’installation de paquets mentionnant des problèmes de compilation, Rtools peut résoudre ces problèmes en fournissant les outils nécessaires.
Développement de paquets personnalisés : si vous développez votre propre paquetage R et que vous devez compiler le code source, Rtools est essentiel pour ce processus.

Comment installer RTools ?

Avant de commencer, vérifiez que vous disposez des droits d’administrateur sur l’ordinateur ou le portable.

Installation de Rtools

L’installation de Rtools dépend du système d’exploitation que vous utilisez.

Windows

Vérifiez la version de R dont vous disposez :

Dans la console R, tapez et exécutez cette commande :

R

sessionInfo()

SORTIE

R version 4.5.1 (2025-06-13)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 22.04.5 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.10.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.10.0  LAPACK version 3.10.0

locale:
 [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8
 [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8
 [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C
[10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C

time zone: UTC
tzcode source: system (glibc)

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base

loaded via a namespace (and not attached):
[1] compiler_4.5.1 tools_4.5.1    yaml_2.3.10    knitr_1.49     xfun_0.51
[6] renv_1.1.4     evaluate_1.0.3

Vous obtiendrez des informations similaires à celles-ci.

Visitez la page RTools sur le CRAN dans le navigateur de votre choix : https://cran.r-project.org/bin/windows/Rtools/et sélectionnez la version de Rtools qui correspond à la version actuelle de R que vous avez sur votre machine et à l’architecture de votre ordinateur. Vous pouvez également cliquer sur l’un des liens suivants pour télécharger le programme d’installation :

Pour les versions de R…	Installez :
À partir de la version 4.5.0	RTools 4.5
À partir de la version 4.4.0	RTools 4.4
À partir de la version 4.3.0	RTools 4.3
À partir de la version 4.2.	RTools 4.2
Entre 4.0.0 et 4.1.3	RTools 4.0
Avant la version 4.0.0	anciennes versions de RTools

Sur la page de téléchargement, recherchez la phrase : “peut être installé à partir du site”et cliquez sur Installateur Rtools44 ou dans la version que vous avez sélectionnée ci-dessus Installateur RtoolsXX.

Attendez la fin du téléchargement et exécutez le fichier.
Cliquez sur “Suivant” o “Suivant” pour toutes les options affichées à l’écran.

Mac

Sur Mac, il vous suffit d’installer Xcode Command Line Tools.

Cliquez sur Spotlight Search en haut à droite de l’écran, puis recherchez “Terminal”.
Ouvrez un terminal ou une ligne de commande sur votre machine.
Dans le terminal, copiez et collez la commande suivante : xcode-select –install
Vous devrez probablement fournir votre mot de passe pour installer le logiciel.
Suivez les instructions du terminal et attendez la fin de l’installation.

Vous pouvez également le faire directement à partir de R comme expliqué dans cette vidéo : Installation à l’aide de R

Comment installer un package ou une “bibliothèque” dans R ?

Pour installer un paquetage dans R, vous pouvez le faire via :

Nous vous recommandons de le faire par le biais de la fonction :

R

install.packages("package")

Certains paquets qui sont en phase de développement peuvent être installés à partir de la dernière version sur github ou d’autres emplacements en utilisant des remotes ou des paquets pak.

Une autre option consiste à utiliser la fonction require :

R

if (!require("package")) {
  install.packages("package")
}

Cette option est utile car elle installe le paquet s’il n’est pas déjà installé. Elle peut être combinée avec remotes ou pak

Utilisez l’interface RStudio :
1. Cliquez sur le bouton Packages
2. Cliquez sur le bouton Install
3. Saisissez le nom du (des) paquet(s) à installer.
4. Appuyez sur le bouton Install.

Comment utiliser une fonction ?

Si la fonction appartient à un paquetage R, vous pouvez procéder de deux manières :

Appelez le nom du paquetage R et mettez deux fois deux points. (::) puis appelez le nom de la fonction. Vous devez maintenant remplir les arguments

R

package::nom_de_la_fonction(arguments)

Chargez le paquetage R avec library:

R

library("package")

et une fois chargé. Appelez le nom de la fonction et remplissez les arguments.

R

nom_de_la_fonction(arguments)

Il est important que le paquetage ait été installé au préalable. En cas de doute, rendez-vous sur Comment installer un paquetage dans R ?

Si la fonction a été créée par vous et se trouve dans l’environnement global :

Appelez simplement la fonction par son nom et fournissez les arguments nécessaires :

R

nom_de_la_fonction(arguments)

Comment charger un paquet ou une “bibliothèque” ?

Voici quelques options pour télécharger un paquet :

Il est recommandé d’utiliser la fonction library :

R

library("package")

Utiliser l’interface RStudio :
1. Allez dans la section en bas à droite de l’interface RStudio. Packages
2. Cliquez sur la case devant chaque fonction, ce qui activera la fonction. library.

Si je charge les bibliothèques, dois-je les charger chaque fois que j’utilise la fonction ?

Non, vous ne devez les charger qu’une seule fois par session R. Cependant, si vous fermez votre RStudio ou ouvrez un nouveau projet, cela compte comme une nouvelle session et vous devez donc les charger à nouveau pour qu’elles fonctionnent.

Puis-je désactiver une bibliothèque que j’ai déjà chargée sans redémarrer R ?

Oui, c’est possible grâce à deux options :

Utiliser la fonction detach

R

detach("package", unload = TRUE)

Utiliser l’interface RStudio :
1. Allez dans la section en bas à droite de l’interface RStudio. Packages
2. Cliquez sur la case devant chaque fonction (si la case est cochée, le paquet est chargé ; si la case est vide, le paquet n’est pas chargé), ce qui activera la fonction. detach. Avertissement En appuyant sur le symbole x à côté du paquet, vous le désinstallez.

L’objet ou la fonction n’a pas été créé

Cela peut se produire pour plusieurs raisons :

Exécution incomplète du code La raison la plus fréquente est que le code n’a pas été exécuté partiellement ou complètement. Veillez à exécuter l’intégralité du script afin que toutes les lignes de code soient exécutées dans le bon ordre. Pour créer l’objet, assurez-vous d’avoir effectué l’une de ces deux actions :

écrire le code dans la console et l’exécuter (en appuyant sur Enter)
ou dans le script RMarkdown ou Chunck, appuyez sur Control + Enter sous Windows ou Command + Enter sur Mac.

Si l’objet ou la fonction a été créé correctement, il apparaîtra dans l’environnement global (Environnement) situé dans la zone supérieure droite.

Un paquetage requis est manquant : vérifiez que tous les paquetages ou bibliothèques requis sont chargés au début du script.
Erreurs dans le code : vérifiez qu’aucune erreur n’empêche le code de s’exécuter correctement. Lors de l’exécution du code dans la console, certaines alertes d’erreur apparaîtront.

Recommandation

Regardez toujours la console pour vérifier si :

Le code a été exécuté avec succès. S’il ne s’est pas exécuté, vous pouvez le relancer.
Si une commande est toujours en cours d’exécution et que vous voyez le symbole rouge arrêt. Dans ce cas, attendez que R termine le processus avant d’exécuter d’autres commandes.
Si une erreur s’est produite. Examinez les erreurs ou les avertissements, car ils peuvent vous donner des indications sur la manière de résoudre le problème.

Je ne vois pas le résultat de mon code

Cela peut arriver pour plusieurs raisons :

Si j’enregistre le résultat en utilisant le symbole d’allocation (c’est-à-dire nombre <- "Laura"). Celui-ci apparaîtra dans l’environnement global (zone en haut à droite) et ne sera pas exécuté sur la console à moins que l’objet ne soit appelé, c’est-à-dire
1. le nom de l’objet est affiché dans la console et exécuté (en appuyant sur la touche Enter)
2. ou que dans le script RMarkdown ou Chunck, vous appuyez sur Control + Enter sous Windows ou Command + Enter sur Mac.
Une bibliothèque requise est manquante. Vérifiez que toutes les bibliothèques requises sont chargées au début du script.
Le code contient des erreurs. Vérifiez qu’il n’y a pas d’erreurs qui empêchent le code de s’exécuter correctement. Lorsque vous exécutez le code dans la console, vous verrez des alertes d’erreur que le code peut avoir.
Le script ne s’est pas exécuté complètement. Veillez à exécuter l’intégralité du script afin que toutes les lignes de code soient exécutées dans le bon ordre.

Erreurs courantes lors de l’utilisation de `ggplot`

Syntaxe incorrecte :
1. Utilisez ++ au lieu de + pour concaténer des fonctions.
2. Il peut également arriver que la fonction + se trouve sur la ligne inférieure, il est important de noter que pour concaténer des fonctions, il doit se trouver à la fin de la ligne précédant celle que vous voulez concaténer.
Ne spécifiez pas l’esthétique :
1. Ne pas inclure aes().
2. Ne pas définir aes() correctement, par exemple en n’indiquant pas x ou y.
3. Bien que l’aes puisse dans certains cas se trouver dans la partie initiale, la géométrie ou être divisée en sections, il est essentiel qu’elle soit toujours présente.
Données non présentes :

La colonne mentionnée dans aes() n’existe pas dans le jeu de données. Utilisez le mauvais nom, n’oubliez pas que R est sensible à la casse.VariableX est différent de variableX ou variablex.

Manque de librairies :

Avant de travailler avec ggplot n’oubliez pas de charger la bibliothèque avec library:

R

library(ggplot2)

Erreurs dans geom:

Sélectionner la mauvaise géométrie pour le type de données à représenter.

`filter` ne fonctionne pas

Cela peut se produire pour plusieurs raisons :

Le paquet dplyr n’est pas chargé. Veillez à inclure library(dplyr) o library(tidyverse) dans votre script et de l’exécuter à chaque nouvelle session.
Il existe des conflits de noms de fonctions avec d’autres paquets. Utilisez dplyr::filter() pour spécifier la fonction que vous souhaitez utiliser filter fonction de dplyr.
Il se peut que les données ne soient pas dans le format attendu. Vérifiez que la colonne que vous filtrez existe et qu’elle possède les valeurs appropriées.

filter Acceptez des conditions logiques pour la sélection des lignes. Voyons quelques exemples :

- Valeurs spécifiques :

R

covid19 %>% filter(eta_du_cas == "deces")

Plages de valeurs :

R

covid19 %>% filter(date >= "2020-01-01" & date <= "2020-12-31")

- Conditions multiples :

R

covid19 %>% filter(eta_du_cas == "deces" & pays == "Kenya")

- Affections avec fonctions :

R

covid19 %>% filter(grepl("Kenya", pays))

Pour plus d’informations sur le filtrage, reportez-vous à la section documentation.

Où se trouve l’objet que vous créez ?

Lorsqu’un objet est créé, il est stocké dans l’environnement global. Vous pouvez voir l’environnement global dans l’interface R située en haut à droite.

Le tuyau ne fonctionne pas `%>%`

Rappelez-vous les points suivants :

Il est important de précharger une bibliothèque contenant le tuyau. Par exemple : magrittr, dplyr, tidyr o purrr.
Le tuyau doit être placé à l’extrémité de la ligne à raccorder. Pas au début de la ligne raccordée :

Comment éviter les accidents ?

Lorsque vous allez enregistrer des modifications dans l’objet où est stocké le dataframe, il est conseillé de prendre quelques précautions pour éviter de perdre des informations :

Créez une sauvegarde des données dans les objets :

o Faites des sauvegardes régulières pendant le processus. Il est recommandé de faire une première copie pour éviter de recharger la base de données. Après avoir effectué certains traitements, en particulier ceux qui prennent du temps, il est recommandé de créer des sauvegardes. Vous pouvez en créer autant que vous le souhaitez. Il est recommandé de créer des notes pour identifier chaque processus

Créez une sauvegarde des données dans les fichiers :

o Comme pour l’enregistrement des objets, il est judicieux de sauvegarder sur le disque de l’ordinateur des données qui ont déjà fait l’objet d’un certain nombre de traitements. Cela permet d’éviter que les données traitées ne soient sauvegardées en cas de plantage de la session ou d’arrêt de l’ordinateur. La fréquence de stockage dépend de la personne qui effectue le traitement.

Test avant stockage :

o Effectuez des tests sur les changements souhaités avant le stockage final.

o Exemple : si vous voulez transformer une variable en une variable numérique, avant de la stocker, et que vous obtenez en fin de compte NAs des changements non désirés dans les données, il est conseillé d’effectuer un test avant de les stocker, afin de voir si ces changements seront générés. NAs

Créez des variables de sauvegarde :

o Parfois, lorsque nous allons transformer une variable, il est préférable d’en créer une nouvelle qui stocke le contenu de la transformation. Cela évite le risque de perdre des informations lors de la transformation d’une variable.

Attention au stockage :

o Ne stockez pas de tableaux ou d’objets transformés accidentellement.

o Par exemple, si nous créons un tableau pour voir si la variable a changé comme souhaité, puis réutilisons le code et ajoutons l’affectation vers l’avant, nous stockons le tableau et perdons l’information que l’objet contenait.

Mon cadre de données a changé de façon inattendue

Lorsque nous avons des accidents avec nos données, certaines options sont possibles :

Vérifier les dommages et voir s’ils sont réparables. Par exemple, le mauvais caractère a été modifié dans une chaîne de texte.
Chargez les données à partir d’une sauvegarde. Si nous avons créé des sauvegardes du processus, nous pouvons éviter des temps de traitement trop longs. Parmi ces sauvegardes, on trouve les variables de sauvegarde ou les objets de sauvegarde (voir Comment éviter les crashs ?).

Utilisation de la fonction `rename`

Appeler la base de données

R

donees

Utiliser le tuyau%>% pour établir un lien avec la fonction de renommage
Appelez la fonctionrename et tapez d’abord le nom de la nouvelle colonne, puis le nom de la colonne préexistante que vous voulez renommer

R

donees <- donees %>% rename(nouvelle = préexistante)

Sélectionner quelques lignes d’un groupe de données

Appeler la base de données

R

donees

Utiliser le tuyau%>% pour établir un lien avec la base de données group_by

R

datos %>% group_by(variable_grupo)

La fonction group_by crée des groupes de données en fonction d’une variable donnée, dans lesquels vous pouvez effectuer d’autres actions telles que la sélection des données dans l’en-tête de chaque groupe.

Utilisez ensuite la fonction comme dans cet exemple, nous pourrions utiliserhead uniquement pour les données de l’en-tête de chaque groupe.

R

donees <- donees %>% group_by(variable) %>% head()

Comment utiliser `summarise`?

Appelez la base de données

R

donees

Utiliser le tuyau%>%pour établir un lien avec le summarise

R

donees %>% summarise()

La fonction “summarise” ne peut pas être utilisée directement, elle doit donc être utilisée en conjonction avec un argument à l’intérieur, par exemple :

Obtenir la moyenne

R

donees %>%
  summarise(mean = mean(variable))

Obtenir l’écart-type

R

donees %>%
  summarise(sd = sd(variable))

Cette fonction peut être utilisée avec le pré-clustering (group_by) pour obtenir ces valeurs pour chaque groupe, par exemple,

R

donees %>%  group_by(pays) %>%
  summarise(
    mean = mean(variable),
    sd = sd(variable))

Erreurs liées au groupe (`group_by` y `ungroup`)

Une erreur très fréquente est que l’objet groupé est stocké (group_by), car l’action de dégroupage n’a pas été effectuée à la fin. Cela peut entraîner des erreurs telles que des calculs incorrects, des résumés par groupe au lieu de l’ensemble des données, ainsi que des problèmes lors d’opérations ultérieures sur l’ensemble de données. C’est pourquoi nous vous recommandons de toujours utiliser (ungroup) avant de stocker. Pour utiliser ungroup() il suffit de le mettre à la fin.

R

donnees <- donnees %>%
  group_by(categorie) %>%
  traitement_des_donnees(...) %>%
  ungroup()

Examinons un exemple d’erreur qui peut se produire si l’on ne procède pas au dégroupage :

R

library("tidyverse")
set.seed(123) # Pour la reproductibilité
# Exemple de dataframe
type_sanguin <- c("A", "B", "O", "AB")
rh <- sample(c("+", "-"), 10, replace = TRUE)
jour <- c(1:5)
f_battements <- sample(60:100, 200, replace = TRUE)
f_respiratoire <- sample(12:20, 200, replace = TRUE)
df <- data.frame(type_sanguin, rh, jour, f_battements, f_respiratoire)

# Résumé par colonnes
par_jour <- df %>%
  group_by(type_sanguin, rh, jour) %>%
  summarize(
    f_b = mean(f_battements),
    f_r = mean(f_respiratoire)
  )

Créons une variable contenant des identifiants uniques pour chaque ligne.

R

par_jour %>% mutate(id = row_number())

SORTIE

# A tibble: 20 × 6
# Groups:   type_sanguin, rh [8]
   type_sanguin rh     jour   f_b   f_r    id
   <chr>        <chr> <int> <dbl> <dbl> <int>
 1 A            +         1  76.3  15.2     1
 2 A            +         3  81.5  16.6     2
 3 A            +         4  81.2  15.6     3
 4 A            +         5  81    15.9     4
 5 A            -         2  78.3  16.2     1
 6 AB           +         2  79.3  16       1
 7 AB           +         5  73.1  17.4     2
 8 AB           -         1  83    16.6     1
 9 AB           -         3  79.8  15       2
10 AB           -         4  84.8  17.4     3
11 B            +         2  77.8  16.4     1
12 B            +         5  83.8  14.6     2
13 B            -         1  74.5  14.9     1
14 B            -         3  85.1  16.2     2
15 B            -         4  83.3  16.6     3
16 O            +         1  80.3  15       1
17 O            +         3  78.9  14.8     2
18 O            +         4  81.2  14.9     3
19 O            +         5  84.9  15       4
20 O            -         2  80.7  16.1     1

Comme vous pouvez le voir dans la colonne id, au lieu d’identifiants uniques, nous avons des identifiants répétitifs. Pourquoi cela se produit-il si chaque ligne est différente ?

La raison de ce problème réside dans le fait que les données sont toujours regroupées. Même si nous n’appliquons pas directement la méthodeungroup comme expliqué ci-dessus, nous pouvons tout de même le résoudre.

Voyons d’abord comment il ne serait pas résolu. Une erreur fréquente lors de la résolution de ce problème est d’appliquer la fonction de dégroupement sans enregistrer le résultat.

R

# mauvaise application de ungroup
par_jour %>% ungroup()

SORTIE

# A tibble: 20 × 5
   type_sanguin rh     jour   f_b   f_r
   <chr>        <chr> <int> <dbl> <dbl>
 1 A            +         1  76.3  15.2
 2 A            +         3  81.5  16.6
 3 A            +         4  81.2  15.6
 4 A            +         5  81    15.9
 5 A            -         2  78.3  16.2
 6 AB           +         2  79.3  16
 7 AB           +         5  73.1  17.4
 8 AB           -         1  83    16.6
 9 AB           -         3  79.8  15
10 AB           -         4  84.8  17.4
11 B            +         2  77.8  16.4
12 B            +         5  83.8  14.6
13 B            -         1  74.5  14.9
14 B            -         3  85.1  16.2
15 B            -         4  83.3  16.6
16 O            +         1  80.3  15
17 O            +         3  78.9  14.8
18 O            +         4  81.2  14.9
19 O            +         5  84.9  15
20 O            -         2  80.7  16.1

R

# bien que cela désagrège l'objet pour l'affichage,
# tant que l'objet n'est pas stocké, il restera groupé
par_jour %>% mutate(id = row_number())

SORTIE

# A tibble: 20 × 6
# Groups:   type_sanguin, rh [8]
   type_sanguin rh     jour   f_b   f_r    id
   <chr>        <chr> <int> <dbl> <dbl> <int>
 1 A            +         1  76.3  15.2     1
 2 A            +         3  81.5  16.6     2
 3 A            +         4  81.2  15.6     3
 4 A            +         5  81    15.9     4
 5 A            -         2  78.3  16.2     1
 6 AB           +         2  79.3  16       1
 7 AB           +         5  73.1  17.4     2
 8 AB           -         1  83    16.6     1
 9 AB           -         3  79.8  15       2
10 AB           -         4  84.8  17.4     3
11 B            +         2  77.8  16.4     1
12 B            +         5  83.8  14.6     2
13 B            -         1  74.5  14.9     1
14 B            -         3  85.1  16.2     2
15 B            -         4  83.3  16.6     3
16 O            +         1  80.3  15       1
17 O            +         3  78.9  14.8     2
18 O            +         4  81.2  14.9     3
19 O            +         5  84.9  15       4
20 O            -         2  80.7  16.1     1

Comme vous pouvez le constater, le problème n’a pas été corrigé.

Pour le corriger, nous pouvons soit inclure le ungroup dès le début lorsque nous créons l’objet por_dia soit appliquer la modification et l’enregistrer dans l’objet :

R

# nous stockons maintenant le désagrégement
par_jour_sans_groupe <- par_jour %>% ungroup()

par_jour_sans_groupe %>% mutate(id = row_number())

SORTIE

# A tibble: 20 × 6
   type_sanguin rh     jour   f_b   f_r    id
   <chr>        <chr> <int> <dbl> <dbl> <int>
 1 A            +         1  76.3  15.2     1
 2 A            +         3  81.5  16.6     2
 3 A            +         4  81.2  15.6     3
 4 A            +         5  81    15.9     4
 5 A            -         2  78.3  16.2     5
 6 AB           +         2  79.3  16       6
 7 AB           +         5  73.1  17.4     7
 8 AB           -         1  83    16.6     8
 9 AB           -         3  79.8  15       9
10 AB           -         4  84.8  17.4    10
11 B            +         2  77.8  16.4    11
12 B            +         5  83.8  14.6    12
13 B            -         1  74.5  14.9    13
14 B            -         3  85.1  16.2    14
15 B            -         4  83.3  16.6    15
16 O            +         1  80.3  15      16
17 O            +         3  78.9  14.8    17
18 O            +         4  81.2  14.9    18
19 O            +         5  84.9  15      19
20 O            -         2  80.7  16.1    20

Comme vous pouvez le voir maintenant, si nous avons chaque ligne avec son propre identifiant.

Remarque : il est important de préciser que, dans les scénarios précédents, le dégroupage est effectué après l’opération, alors que, dans le cas présent, il est effectué avant l’opération.

Lorsque j’essaie de créer un pdf dans RMarkdown, j’obtiens l’erreur suivante

Si le fichier sort correctement dans d’autres formats que le pdf. L’une des situations les plus fréquentes est que l’installation de LaTeX est manquante : RMarkdown a besoin de LaTeX pour générer des PDF. Assurez-vous que LaTeX est installé sur votre système.

Pour installer LaTeX à partir de RStudio, vous pouvez utiliser le paquetage TinyTeX :

R

install.packages("tinytex")

tinytex::install_tinytex()

Configurez RStudio :

Allez dans Outils > Options globales > Sweave.

Assurez-vous que l’option “Typeset PDF” est réglée pour utiliser TinyTeX.

Contributions

José M. Velasco-España : Version initiale
Andree Valle-Campos : Éditions mineures
Laura Gómez-Bermeo : Éditions mineures
Geraldine Gomez : Éditions mineures
Hugo Gruson: Traduction en français