Unité de statistiques et de probabilités

Dernière mise à jour le 2025-07-24 | Modifier cette page

Durée estimée : 44 minutes

Vue d'ensemble

Questions

Comment les statistiques et les probabilités peuvent-elles être utilisées pour répondre aux questions en matière d’épidémiologie des maladies infectieuses ?

Objectifs

A la fin de cet atelier, vous serez capable de :

Comprendre le rôle des statistiques dans l’étude des maladies infectieuses.
Comprendre et utiliser des mesures statistiques pour résumer et analyser des informations.
Se familiariser avec le concept de variable aléatoire et reconnaître les distributions de probabilité courantes.
Apprendre à aborder un problème statistique comme un problème d’inférence à partir d’un échantillon.
Comprendre le concept d’intervalles de confiance pour l’estimation des paramètres épidémiologiques.

Pré-requis

Cette unité est un complément à l’unité Introduction à la modélisation des maladies infectieuses pour les cours de santé publique

Table des matières

Thème 1 : Introduction à la pensée statistique (Voir dans plateforme de cours)

Thème 2 : Statistiques descriptives (Voir le complément dans la plate-forme de cours)

Thème 3 : Probabilité (Voir plateforme de cours complémentaire)

Thème 4 : Principales distributions de probabilités (Voir le module complémentaire de la plate-forme de cours)

Thème 5 : Introduction à l’inférence statistique (Voir le supplément sur la plateforme de cours)

Avant de commencer

Veuillez vérifier que vous avez installé les bibliothèques suivantes tidyverse, pak, epiparameter e infer si ce n’est pas le cas, exécutez le code ci-dessous en fonction de vos besoins :

R

# Pour installer le package tidyverse si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if(!require("tidyverse")) install.packages("tidyverse")

# Pour installer le package epiparameter si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if (!require("epiparameter")) install.packages("epiparameter")

# Pour installer le package epitools si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if (!require(epitools)) install.packages("epitools")

# Pour installer le package infer si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if(!require("infer")) install.packages("infer")

# Pour installer le package cfr si vous ne l'avez pas (ou si vous n'êtes pas sûr de l'avoir), exécutez le code suivant

if (!require("cfr")) install.packages("cfr")


# Avant de commencer et à chaque fois que vous démarrez une session R, chargez ces bibliothèques
library(ggplot2)
library(dplyr)
library(epiparameter)
library(epitools)
library(infer)
library(cfr)

Thème 2 : Statistiques descriptives

Exercice : Visualiser et analyser des données avec R

Il existe de nombreux graphiques en fonction du type d’échelle de la variable que vous souhaitez analyser. Voici quelques exemples pour vous aider à comprendre ces concepts.

Veuillez tenir compte du fait que vous avez déjà suivi l’unité d’introduction sur R et l’unité sur la visualisation des données. Le tableau de données pour cette se trouve dans : https://raw.githubusercontent.com/epiverse-trace/translation-EpiTKit-FR/refs/heads/main/data/donnees_echantillon.RDS
Une fois que vous avez téléchargé les données sur votre ordinateur et qu’elles se trouvent dans l’application de votre projet, vous pouvez exécuter la commande suivante :

R

 echantillon_covid <-  readRDS("data/echantillon_covid.RDS")

Histogramme et Boxplot

Les deux types de graphiques les plus courants pour visualiser la distribution de variables quantitatives sont les histogrammes et les boxplots.

L’histogramme histogrammes vous permettent de décrire visuellement la distribution des données en regroupant les données en intervalles sur l’axe des x, qui sont généralement de taille égale, puis en décrivant pour chaque intervalle la fréquence absolue, la fréquence relative ou la densité sur l’axe des y. Un histogramme de densité ajuste la fréquence relative de chaque intervalle en fonction de la largeur de l’intervalle. Dans R, il peut être construit comme suit :

R

# Histogramme avec fréquence absolue

ggplot(data = echantillon_covid, aes(x = age)) +   
  geom_histogram(color="darkblue", fill="lightblue") +  
  labs(y = "Fréquence absolue", x = "Âge en années",
     title = "Répartition par âge")

ERREUR

Error in ggplot(data = echantillon_covid, aes(x = age)): could not find function "ggplot"

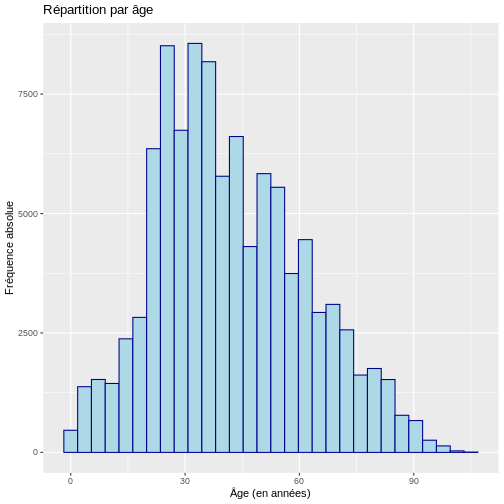
R

# Histogramme avec densité

ggplot(data = echantillon_covid, aes(x = age)) +   
  geom_histogram(aes(y = after_stat(density)), 
                 color = "darkblue", fill = "lightblue") +  
  labs(y = "Density", x = "Âge en années", 
       title = "Age Distribution")

ERREUR

Error in ggplot(data = echantillon_covid, aes(x = age)): could not find function "ggplot"

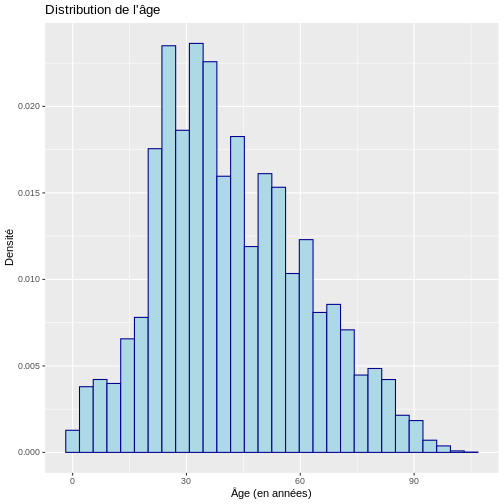
Ensuite, nous allons visualiser l’âge des cas COVID-19 à l’aide d’un diagramme en boîte.

R

# Boxplot

ggplot(echantillon_covid, aes(x = " ", y = age)) +
  geom_boxplot(outlier.shape = NA) +
  ylab("Âge (en années)") + xlab(" ")

ERREUR

Error in ggplot(echantillon_covid, aes(x = " ", y = age)): could not find function "ggplot"

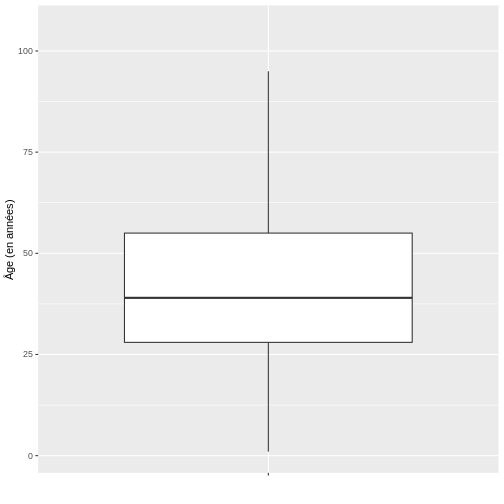
D’après le diagramme en boîte de l’âge de l’échantillon de cas COVID-19, il est possible de conclure que la distribution des données est positivement asymétrique, étant donné qu’il y a une plus grande proximité entre les valeurs de Q1 et la médiane, il est donc conseillé de décrire le comportement de cette dernière au moyen de la médiane et de l’intervalle interquartile, ce qui, dans R, peut être trouvé de la manière suivante en utilisant les fonctions surlignées en bleu :

R

# Statistiques Descriptives Variables Quantitatives    

echantillon_covid %>% dplyr::summarise(
  n = n (), # Nombre d'observations
  moyenne = mean(age), # Moyenne
  et = sd(age), # Écart-type
  mediane = quantile(age, 0.50), # Médiane - 50e percentile
  p25 = quantile(age, 0.25), # 25e percentile
  p75 = quantile(age, 0.75)) # 75e percentile

ERREUR

Error in echantillon_covid %>% dplyr::summarise(n = n(), moyenne = mean(age), : could not find function "%>%"

Enfin, pour la variable âge, on peut conclure que la moitié des patients atteints de covid-19 sont âgés de 27 à 52 ans (“RIQ”) avec une médiane de 38 ans, ce qui indique que la moitié des cas sont âgés de moins de cette valeur. Il est important de noter qu’en raison de l’asymétrie de la distribution, la moyenne et la médiane ne coïncident pas, ce qui est normal dans les distributions asymétriques.

Graphiques en barres et tableaux de fréquence

Il est recommandé de représenter les variables qualitatives par des diagrammes en barres. Généralement, ceux-ci sont construits en indiquant sur l’axe X les catégories des variables et sur l’axe Y la valeur des fréquences absolues, relatives ou en pourcentage selon les besoins, c’est-à-dire qu’il est toujours nécessaire d’évaluer d’abord le tableau de fréquence de la variable. Supposons que nous voulions connaître le type d’infection de COVID-19. Cela peut être fait dans R à l’aide de la commande suivante :

R

# Tableaux de fréquences

tableau <- echantillon_covid %>% # Tableau de fréquence créé
  dplyr::count(type_de_contagion) %>% # Comptage de fréquence pour la variable d'état
  dplyr::mutate(prop = base::prop.table(n), # Proportion
       perc = base::prop.table(n)*100) # Pourcentage

ERREUR

Error in echantillon_covid %>% dplyr::count(type_de_contagion) %>% dplyr::mutate(prop = base::prop.table(n), : could not find function "%>%"

R

tableau

ERREUR

Error: object 'tableau' not found

Ces informations permettent de conclure que 70 % des cas de COVID-19 provenaient de la communauté et que seulement 0,06 % étaient importés d’ailleurs. Ce résultat peut être visualisé à l’aide d’un diagramme à barres :

R

# Graphiques à barres
ggplot(data = tableau, aes(x = type_de_contagion, y = perc)) +
  geom_bar(stat="identity", color="darkblue", fill="lightblue")+
  labs(y = "%", x = " ", title = "Type de Contagion")

ERREUR

Error in ggplot(data = tableau, aes(x = type_de_contagion, y = perc)): could not find function "ggplot"

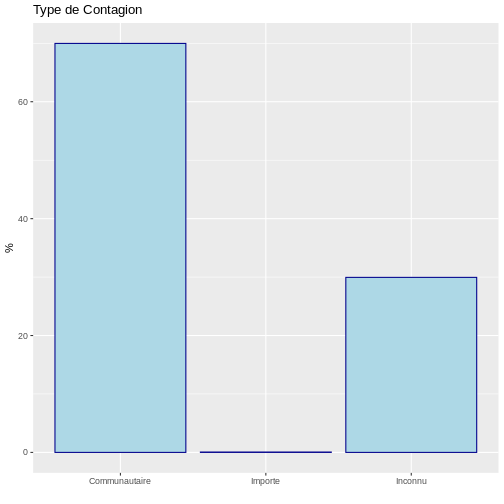
Thème 3 : Probabilité

Dans une étude publiée dans le NEJM en 2014 et intitulée “Ebola Virus Disease in West Africa- The First 9 Months of the Epidemic and Forward Projections” (La maladie à virus Ebola en Afrique de l’Ouest - Les 9 premiers mois de l’épidémie et les projections futures) (DOI : 10.1056/NEJMoa1411100), a décrit les caractéristiques cliniques et épidémiologiques des cas d’Ebola signalés au cours de l’épidémie qui a touché les pays de Guinée, du Liberia, du Nigeria et de la Sierra Leone depuis décembre 2013. L’étude a révélé que les personnes âgées de plus de 44 ans étaient plus susceptibles de mourir de la maladie. Comme dans l’article cité en référence, une conclusion comparable est obtenue si l’on effectue un calcul équivalent en utilisant des mesures d’association vues dans l’unité d’épidémiologie générale appliquées aux maladies infectieuses, telles que les risques relatifs (RR) du rapport de risque ou le risque relatif (RR). Pour ce faire, un tableau 2x2 peut être reconstruit, où le RR peut être mesuré par le rapport entre le CFR d’un groupe A (par exemple, les cas âgés de 45 ans ou plus) et d’un groupe B (par exemple, les cas âgés de 44 ans ou moins), où le CFR est le risque de létalité (CFR).

Ainsi, nous obtenons que le risque de décès chez les cas âgés de 45 ans ou plus est 1,20 fois le risque de décès chez les cas âgés de 44 ans ou moins, avec un intervalle de confiance à 95 % de 1,13 à 1,27, et une valeur p inférieure à 0,01. Pour reproduire ce calcul, vous pouvez utiliser la fonctionepitools comme indiqué ci-dessous.

R

library(epitools)

tableau2x2 <- matrix(c(311, 51, 768, 299),nrow = 2, ncol = 2)

epitools::riskratio(tableau2x2)

SORTIE

$data
          Outcome
Predictor  Disease1 Disease2 Total
  Exposed1      311      768  1079
  Exposed2       51      299   350
  Total         362     1067  1429

$measure
          risk ratio with 95% C.I.
Predictor  estimate    lower    upper
  Exposed1 1.000000       NA       NA
  Exposed2 1.200227 1.133086 1.271346

$p.value
          two-sided
Predictor    midp.exact fisher.exact   chi.square
  Exposed1           NA           NA           NA
  Exposed2 3.179312e-08 4.200177e-08 9.982161e-08

$correction
[1] FALSE

attr(,"method")
[1] "Unconditional MLE & normal approximation (Wald) CI"

Vous trouverez une introduction à l’inférence statistique et aux intervalles de confiance dans le thème 5 de cette unité.

Thème 4 : Principales distributions de probabilité

Comme décrit dans le thème 3, les probabilités étudient le comportement des phénomènes aléatoires, les “événements”. Dans ce processus, on observe les variables aléatoires (v.a), généralement désignées par X qui visent à attribuer un nombre réel à chaque événement susceptible de se produire dans l’espace d’échantillonnage.

Pour l’explication et les exemples des principales distributions, il est important que vous installiez et chargiez les paquets epiparameter d’Epiverse.

R

# vérifier si {epiparameter} est installé
if(!require("epiparameter")) install.packages("epiparameter")

SORTIE

Loading required package: epiparameter

R

# chargez la bibliothèque epiparameter
library(epiparameter)

Modèles discrets

La distribution binomiale permet de décrire la probabilité d’occurrence d’un événement ayant deux issues possibles, le succès (p) ou l’échec (1-p), dans un nombre donné d’essais indépendants n avec une probabilité constante de succès p. La variable aléatoire étudiée correspond à :

X : Nombre de succès en n essais

Le modèle binomial peut être utile pour connaître la probabilité d’observer un nombre donné d’événements (par exemple, des cas, des décès, des réinfections) dans une population de taille n, en supposant que la probabilité de l’événement est constante. La distribution binomiale dépend de deux paramètres : la probabilité de succès p et le nombre d’essais indépendants n.

Si X a une distribution binomiale, il est représenté comme suit : X~Bin(n,p)

Et sa fonction de densité, sa moyenne, son espérance et sa variance correspondent à :

$f(x)=P(X=x)=(n x )$

$p^x (1-p)^{(n-x)}$

$E(x)=np$

$Var(x)=np(1-p)$

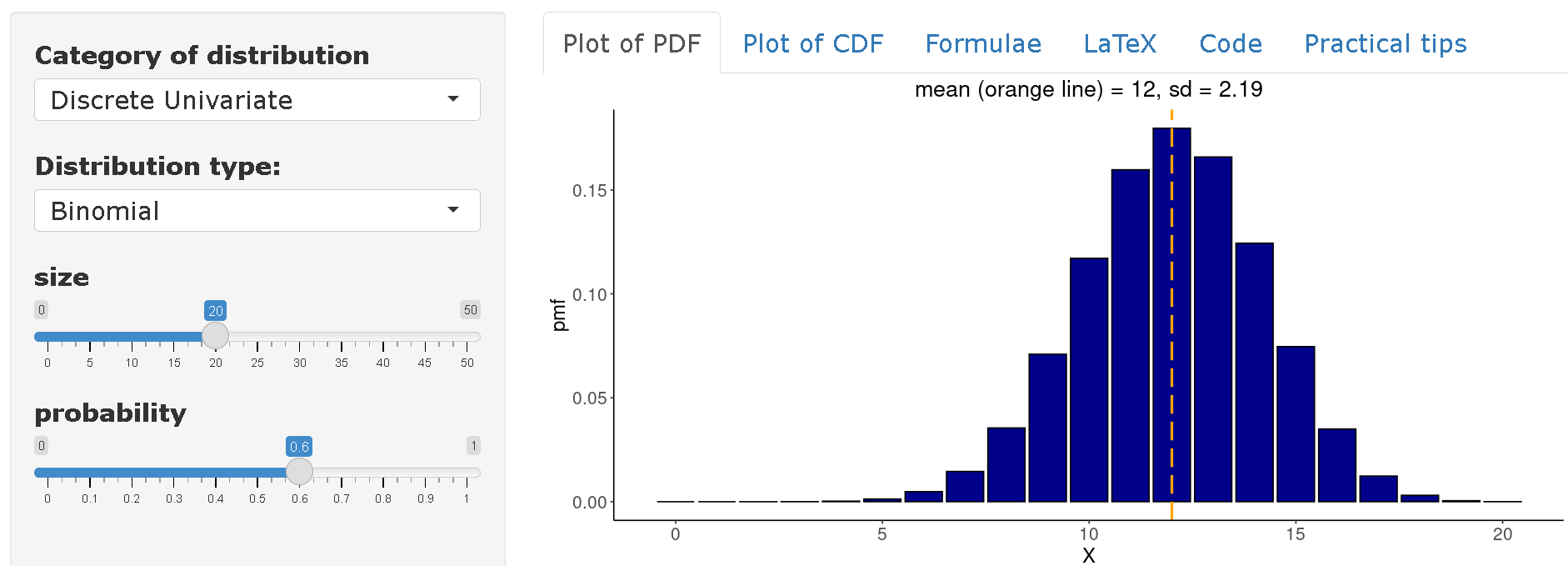
Exemple : Si un virus ayant un taux d’attaque de 60 % est introduit dans une communauté de 20 individus, quelle est la probabilité que 10 individus ou moins soient infectés dans cette communauté ?

Be $X~Bin(n=20,p=0.60)$ il faut alors calculer l’expression suivante :

$P(X≤10)=∑_(x=0)^10 (20 x ) 〖0.60〗^x (1-0.60)^(20-x)$

Dans R, cette expression peut être calculée comme suit :

R

p <- 0.60
n <- 20
x <- 10

pbinom(x,n,p, lower.tail = TRUE)

SORTIE

[1] 0.2446628

Par conséquent, la probabilité qu’un maximum de 10 personnes soient infectées est de 24,5 %.

Sur distribution-zoo vous pouvez consulter la distribution complète de la variable

$X~Bin(n=20,p=0.60)$. On peut donc conclure qu’en moyenne, on peut s’attendre à trouver 12 personnes infectées dans une communauté de 20 individus, sur la base d’un taux d’attaque de 60 %.

Distribution de Poisson

La distribution de Distribution de Poisson modélise le comportement des variables aléatoires décrivant le nombre d’événements, de “comptes”, survenant dans un intervalle d’observation fixe, par exemple le temps (nombre d’infections survenant dans une heure, un jour, une semaine, une année, etc.) ou la zone (nombre d’infections survenant dans une municipalité, un hôpital, etc.)

Cette distribution possède un paramètre appelé lambda ($λ$), $λ>0$ qui décrit le nombre moyen d’événements survenant dans l’intervalle d’observation fixé. Si $X$ a une distribution de Poisson, elle est représentée comme suit :

$X$~$Poisson(λ)$

Sa fonction de densité, d’espérance, de moyenne et de variance correspond à :

$fx=P(X=x)=\frac{e^{-λ}λ^x}{x!}, x=0,1,2,..,$

$E(x)=λ Var(x)=λ$

Dans le domaine des maladies infectieuses, la distribution de Poisson peut être utilisée pour modéliser le nombre de cas secondaires générés par un cas primaire. Dans ce contexte, le paramètre est fonction du nombre effectif de réplications R qui représente le nombre moyen d’infections secondaires causées par chaque cas primaire au fil du temps dans une population composée d’individus sensibles et non sensibles.

::: challenge \[**Exemple**\]{.underline}

Supposons que l’on souhaite étudier la propagation d’une épidémie basée sur un modèle de Poisson au fur et à mesure que les jours (t) s’écoulent. La variable aléatoire d’intérêt est :

$X_{(t )}$ le nombre de cas secondaires causés par chaque cas primaire le jour t

Il s’agit d’un modèle de Poisson puisqu’il y a un intervalle d’observation fixe “chaque cas primaire” et que l’on souhaite étudier le nombre de cas secondaires observés “événements”. On peut donc construire le modèle suivant :

$X_{(t )}∼Poisson (λ= R X_{(t-1)})$

Le modèle ci-dessus exprime que le nombre moyen de cas secondaires au jour t dépend du nombre de reproductions. $R$ et du nombre de cas observés $X$ le jour précédent $(t-1)$. Cependant, R est difficile à connaître dans la réalité et il peut être intéressant d’approximer sa valeur sur la base des données observées au cours de l’épidémie afin d’élaborer des stratégies de lutte.

Supposons qu’au premier jour de l’épidémie $(t=1)$ un total de 5 nouveaux cas sont apparus le premier jour de l’épidémie et que le jour suivant $(t=2)$ 10 nouveaux cas sont apparus le jour suivant. Avec les informations ci-dessus, nous sommes intéressés par l’étude du nombre de cas secondaires au jour 2, ce qui équivaut à :

$X_{(2 )}$ Nombre de cas secondaires causés par chaque cas primaire au jour 2.

Il est réparti de la manière suivante :

$X_{(2 )}∼Poisson (λ= R *5)$

A partir de là, nous pouvons estimer la valeur de $R$ en recherchant la valeur qui maximise la probabilité d’observer ce nombre spécifique de cas secondaires le jour 2, c’est-à-dire

$P(X_{(2 )}=10)=\frac{e^{-(R *5)} (R *5)^{10}}{10!}$

Dans R, nous pourrions découvrir cela en faisant varier différentes valeurs du nombre de nombre de reproduction (R) comme suit :

R

# Fonction de calcul de la probabilité de Poisson
probabilite_poisson <- function(valeur1, valeur2, taux_reproduction) {
  dpois(valeur2, taux_reproduction * valeur1)
}


# Valeurs d'entrée
valeur1 <- 5
valeur2 <- 10
nombres_reproduction <- seq(0, 5, 0.01)


# Calcul des probabilités
resultats_poisson <- probabilite_poisson(valeur1, valeur2, nombres_reproduction)


# Création du dataframe pour ggplot
donnees_resultats <- data.frame(nombres_reproduction, resultats_poisson)


# Trouver le nombre de reproduction le plus probable
nombre_reproduction_probable <- donnees_resultats %>%
  filter(resultats_poisson == max(resultats_poisson)) %>%
  pull(nombres_reproduction)

ERREUR

Error in donnees_resultats %>% filter(resultats_poisson == max(resultats_poisson)) %>% : could not find function "%>%"

R

# Créer le graphique avec ggplot2
ggplot(donnees_resultats, aes(x = nombres_reproduction, y = resultats_poisson)) +
  geom_line() +
  geom_vline(xintercept = nombre_reproduction_probable, color = "red", size = 1) +
  labs(y = "Probabilité", x = "Nombre de reproduction (R)", title = "Modèle de Poisson")

ERREUR

Error in ggplot(donnees_resultats, aes(x = nombres_reproduction, y = resultats_poisson)): could not find function "ggplot"

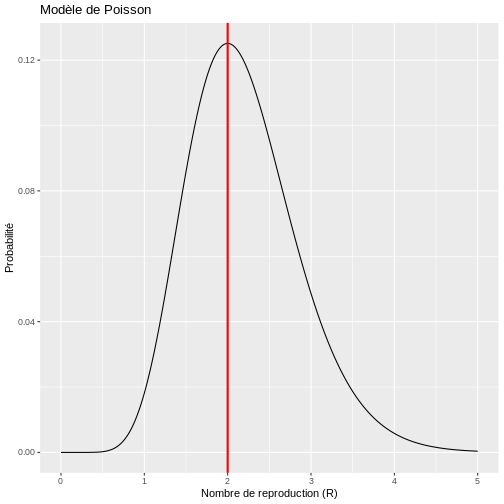
Par conséquent, si le nombre de cas secondaires se comporte selon une distribution de Poisson, il y a une forte probabilité que le nombre de nouveaux cas observés le jour 2 ait été généré avec un nombre de reproduction de R=2. Cela implique que le nombre moyen de cas secondaires par cas primaire est de 2. Toutefois, ce modèle simple suppose que le nombre de cas secondaires générés par chaque cas primaire a une moyenne et une variance égales, ce qui implique que tous les cas primaires génèrent en moyenne un nombre similaire de cas secondaires. Cette hypothèse peut être difficile à formuler pour certaines maladies infectieuses, en particulier lorsqu’elles suivent un modèle de surdispersion (20 % des cas sont à l’origine de 80 % de la transmission), de sorte que le modèle de Poisson présente des limites dans son application. :::

Distribution binomiale négative

Comme la distribution de Poisson, la distribution binomiale négative permet de modéliser le nombre d’événements qui se produisent. Si $X$ a une distribution binomiale négative, il est représenté comme suit.

$X $~$ BN(μ,k)$

Où ? $μ$ représente la moyenne de la distribution et $k$ est le paramètre de dispersion qui permet à la moyenne et à la variance des événements de ne pas être égales. Ce paramètre $k$ permet d’introduire dans le modèle le degré de dispersion dans la façon dont les événements sont générés. Ainsi, $k$ mesure inversement le degré de variation des événements qui se produisent, étant donné que la moyenne et la variance de la distribution correspondent à :

$E(x)=μ$

$Var(x)=μ(1+\frac{μ}{k})$

Avec la fonction de densité :

$f(x)=\frac{Γ(x+k)}{Γ(k)Γ(x+1)} (\frac{μ}{μ+k})^x (\frac{k}{μ+k})^k,x=0,1,2...$

Défi

\[**Exemple**\]{.underline}

Dans l’étude des maladies infectieuses, la distribution binomiale négative joue un rôle important puisqu’elle permet de modéliser la distribution du nombre de cas secondaires générés par un cas primaire, c’est-à-dire qu’elle permet de connaître la distribution du nombre de reproduction de base R_0. Dans ce contexte, la moyenne de la distribution correspond à $R_0$(nombre de cas secondaires dans une population totalement sensible) et le paramètre $k$ contrôle la variation entre les cas primaires. Ainsi, de petites valeurs de k suggèrent que les cas secondaires sont générés par un petit groupe de cas primaires, tandis que de grandes valeurs suggèrent que la propagation du virus est élevée. Ainsi, le fait d’être $X$ le nombre de cas secondaires, alors

$X \sim Bn(R_0,k)$

$E(x)=R_0$

$Var(x)=R_0 (\frac{1+R_0}{k})$

L’article de Lloyd-Smith et al. montre comment la distribution binomiale négative permet de modéliser la distribution des cas secondaires de divers pathogènes. Sur la base des cas signalés lors de l’épidémie de SRAS à Singapour en 2023, ils ont estimé les paramètres de la distribution binomiale négative et ont trouvé une valeur de $R_0=1.630$ y $k=0.160$. Ces estimations sont disponibles dans le epiparameter qui est un paquet disponible à l’adresse R qui compile les principales estimations de plusieurs paramètres épidémiologiques d’intérêt pour l’étude des maladies infectieuses.

R

# Récupérer les données des paramètres épidémiologiques pour le SARS
SARS_R <- epiparameter::epiparameter_db(
  disease = "SARS",  # Spécifier la maladie comme étant le SARS
  epi_name = "offspring distribution", # Sélectionner le paramètre épidémiologique : distribution de descendance
  single_epiparameter = TRUE# Demander un seul paramètre épidémiologique
)

SORTIE

Using Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>..
To retrieve the citation use the 'get_citation' function

R

# Afficher les données récupérées
SARS_R

SORTIE

Disease: SARS
Pathogen: SARS-Cov-1
Epi Parameter: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom (No units)
Parameters:
  mean: 1.630
  dispersion: 0.160

Grâce à ces résultats, il serait possible de tracer la distribution du nombre de cas secondaires de SRAS afin de suggérer des mesures de contrôle. Cette information est également disponible dans la base de données epiparameter avec la fonction plot.

R

plot(SARS_R)

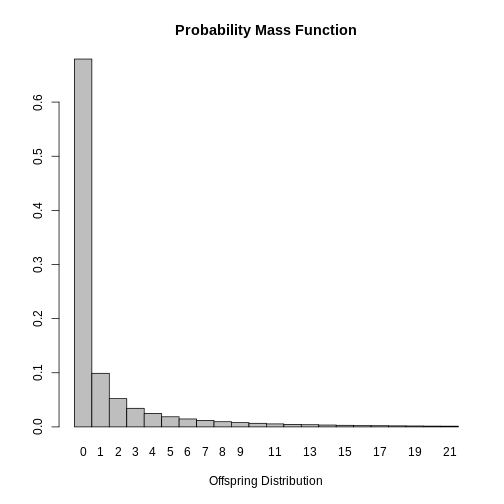
Enfin, il est possible de conclure que la plupart des cas infectés par le SRAS ne propagent pas la maladie puisque le mode de la distribution est $0$. Ce résultat est attendu étant donné que $k<1$ indiquant que les cas secondaires sont générés par un petit groupe de personnes infectées et que la valeur estimée de $R_0$ varie selon les cas.

Distribution géométrique

La distribution géométrique est une autre distribution discrète intéressante qui peut être utilisée pour modéliser les comptages ou le nombre d’événements. Dans le domaine des maladies infectieuses, elle est principalement utilisée lorsque le paramètre de dispersion de la distribution négative est égal à 1. Cette distribution dépend de la probabilité d’occurrence de l’événement en question et est représentée comme suit.

$X \sim Geom(p)$

où p représente la probabilité de succès ou la probabilité d’occurrence de l’événement d’intérêt avec une moyenne égale à :

$E(x)=\frac{1}{p}$

Défi

Exemple

Si, dans le cas d’une épidémie de SRAS à Singapour en 2023, la valeur estimée de $k$ aurait été de $1$ alors la distribution des cas secondaires pourrait être modélisée par une distribution géométrique telle que sa moyenne soit égale à la valeur de $R_0$ c’est-à-dire qu’il doit être satisfait que :

$E(x)=\frac{1}{p}=1.630$ et donc, $p=\frac{1}{1.630}$

La distribution du nombre de contacts secondaires peut donc s’écrire comme suit :

$X \sim Geom(p=0.613)$

Dans R, nous pourrions simuler le comportement du nombre de cas secondaires avec le code suivant :

R

# Distribution géométrique
# Créer une séquence de valeurs de 0 à 20 représentant différents valeurs de R
x <- seq(0, 20, 1)


# Définir le paramètre de probabilité pour la distribution géométrique  
probabilite <- 1/(1.630)


# Créer un data frame avec les valeurs de x et leurs probabilités géométriques correspondantes
donnees_geom <- data.frame(x, prob_geom = dgeom(x, probabilite))


# Création du graphique avec ggplot2
ggplot(data = donnees_geom, aes(x = x, y = prob_geom)) +
  geom_bar(stat = "identity") +
  labs(y = "Probabilité", x = "Cas secondaires", title = "Distribution géométrique")

ERREUR

Error in ggplot(data = donnees_geom, aes(x = x, y = prob_geom)): could not find function "ggplot"

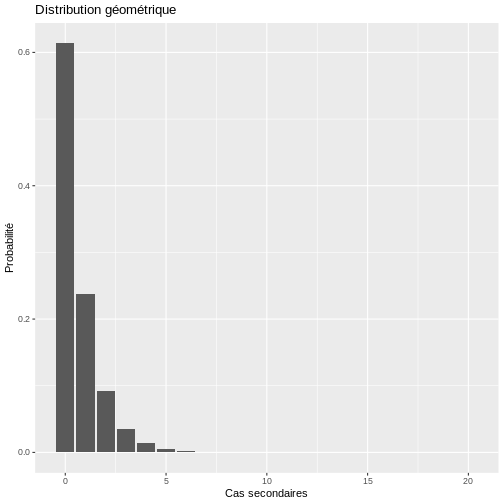
Dans le cadre de la distribution géométrique, la probabilité qu’un cas primaire transmette le virus est plus élevée puisque la probabilité qu’un cas primaire génère 1, 2 ou plus de cas secondaires est plus élevée avec ce modèle qu’elle ne l’est avec le modèle binomial négatif.

Modèles continus

Distribution uniforme

La distribution uniforme modélise une variable continue dont les valeurs sont comprises dans un intervalle. $ [a,b] $ avec la même probabilité. Cette distribution est souvent utilisée dans la simulation de nombres aléatoires. Si $X$ suit une distribution uniforme, elle peut être représentée par :

$X ∼U(a,b)$

Ses paramètres a et b représentent respectivement la valeur minimale et maximale que peut prendre la variable. Sa fonction de densité est déterminée par :

$f(x)=\frac{1}{b-a}$,avec $a<x<b$

La moyenne et la variance sont déterminées par :

$E(x)=\frac{a+b}{2}$ y $V(x)=\frac{(b-a)^2}{12}$

Défi

Exemple

Un chercheur souhaite simuler le comportement de COVID-19 et doit générer de manière aléatoire la valeur que peut prendre le numéro de reproduction de base. $R_0$ et l’utiliser ensuite dans son modèle de propagation. Pour ce faire, il suppose que le $R_0$ de COVID-19 suit une distribution uniforme entre 2 et 5 :

$R0∼U [2,5] $

Pour votre simulation, vous devez générer cinq valeurs possibles de $R_0$ avec la même probabilité, c’est-à-dire en R est résolu à l’aide du code suivant :

R

# Génération de nombres aléatoires avec une distribution uniforme
# Définir le nombre de valeurs aléatoires à générer
n <- 5  
# Définir les bornes inférieure et supérieure de la distribution uniforme
a <- 2  
b <- 5  
# Générer 'n' nombres aléatoires distribués uniformément entre 'a' et 'b'
runif(n, a, b)

SORTIE

[1] 3.164584 2.087320 2.242914 4.394300 4.563492

Distribution normale

La distribution normale est sans aucun doute le modèle probabiliste le plus important de la théorie statistique en raison de sa capacité à modéliser de nombreux problèmes de la vie réelle et de son rôle important dans le domaine de l’inférence. Cette distribution tente de modéliser des variables aléatoires qui peuvent être influencées par de multiples facteurs, dont les effets additionnés font tendre les valeurs de la distribution vers le centre (la moyenne). Par exemple, la température corporelle peut suivre une distribution normale puisqu’elle est influencée par de multiples facteurs biologiques et environnementaux qui, additionnés, font que la plupart des individus se situent autour d’une valeur centrale.

Pour exprimer mathématiquement qu’une variable continue a une distribution normale, nous écrivons :

$X ∼N(μ,σ)$

à laquelle sera associée la fonction de densité de probabilité suivante :

$f(x)=exp [-frac{1}{2 σ^2}(x-u)2] $

Où $μ$ y $σ$ sont les paramètres de la distribution et représentent respectivement la moyenne et l’écart-type de la variable aléatoire, c’est-à-dire la valeur centrale et la dispersion des données par rapport à celle-ci. Ces paramètres correspondent aux valeurs que l’on obtiendrait si l’on étudiait l’ensemble de la population plutôt qu’un échantillon de celle-ci.

Lorsque $μ=0$ y $σ=1$ est appelé distribution normale normale. Cependant, il existe de nombreuses distributions normales en fonction des valeurs prises par leurs paramètres, mais quelle que soit la valeur des paramètres, la forme de la distribution est toujours symétrique et peut toujours être transformée en une distribution normale standard au moyen d’une procédure de normalisation appliquant la formule suivante :

$Z=\frac{X-μ}{σ}∼N(0,1)$

Défi

Exemple,

Si l’on sait que dans une communauté, l’âge des personnes décédées du COVID-19 a une distribution normale avec une moyenne de 67,8 ans et un écart-type de 15,4 ans. Quelle est la probabilité qu’une personne décédée ait moins de 40 ans ?

Tout d’abord, nous définissons la variable à étudier, qui a une distribution normale.

$X∼N(67.8,15.4)$

$X$ Il s’agit de l’âge des cas décédés de COVID-19.

Dans R, nous pouvons utiliser la fonction pnorm() comme suit pour trouver :

$P(X<40)=?$

R

# Définir la moyenne de la distribution normale
mu <- 67.8
# Définir l'écart-type de la distribution normale
sigma <- 15.4
# Définir la valeur pour laquelle nous voulons calculer la probabilité cumulative
x <- 40
# Calculer la probabilité cumulative
pnorm(x, mean = mu, sd = sigma)

SORTIE

[1] 0.0355221

Par conséquent, la probabilité qu’un accidenté COVID-19 soit âgé de moins de 40 ans est de 3,5 %.

Distribution log-normale

La distribution log-normale apparaît lorsque l’on considère des variables aléatoires continues qui ne prennent pas la valeur de zéro ou de nombres négatifs, dont la distribution a une forme asymétrique et dont la variation est générée par de multiples facteurs dont les effets ne sont pas symétriques. Si une variable aléatoire suit une distribution log-normale, sa transformation par l’application de la fonction logarithme générera une variable normale, d’où son nom. Dans le domaine des maladies infectieuses, la distribution log-normale est très utile pour modéliser les périodes d’incubation (temps écoulé entre l’infection et l’apparition des symptômes).

Si $X ∼LogN(μ,σ)$ alors on peut dire que $Y=log (X) ∼N(μ,σ)$ et la fonction de densité de $X$ est donnée par :

$f(x)=\frac{1}{ xσ\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{ln(x)-u}{σ})^2}$

Contrairement à la distribution normale, dans la distribution log-normale, le paramètre μ joue le rôle d’un paramètre d’échelle puisqu’il augmente la dispersion des données en augmentant leur degré d’amplitude et le paramètre σ contrôle la forme, c’est-à-dire le degré d’asymétrie.

Défi

Exemple

Dans l’article de 2009 de Lessler et al., les périodes d’incubation de plusieurs agents pathogènes ont été modélisées sur la base d’une distribution log-normale. L’intérêt principal était d’estimer les paramètres de $(μ,σ)$. Par exemple, dans le cas du SRAS, on a trouvé une estimation de $μ=0.660$, y $σ=1.205$ ce qui implique qu’en moyenne, un cas infecté développe des symptômes en 0,7 jour. Cette information peut être obtenue dans le paquet epiparameter avec la commande suivante :

R

# Récupérer les données des paramètres épidémiologiques pour la période d'incubation du SARS
SARS_incubation <- epiparameter::epiparameter_db(  
  disease = "SARS",  # Spécifier la maladie comme étant le SARS
  epi_name = "incubation period",  # Sélectionner le paramètre épidémiologique : période d'incubation
  single_epiparameter = TRUE  # Demander un seul paramètre épidémiologique
)

SORTIE

Using Lessler J, Reich N, Brookmeyer R, Perl T, Nelson K, Cummings D (2009).
"Incubation periods of acute respiratory viral infections: a systematic
review." _The Lancet Infectious Diseases_.
doi:10.1016/S1473-3099(09)70069-8
<https://doi.org/10.1016/S1473-3099%2809%2970069-8>..
To retrieve the citation use the 'get_citation' function

R

# Afficher les données récupérées sur la période d'incubation
SARS_incubation

SORTIE

Disease: SARS
Pathogen: SARS-Cov-1
Epi Parameter: incubation period
Study: Lessler J, Reich N, Brookmeyer R, Perl T, Nelson K, Cummings D (2009).
"Incubation periods of acute respiratory viral infections: a systematic
review." _The Lancet Infectious Diseases_.
doi:10.1016/S1473-3099(09)70069-8
<https://doi.org/10.1016/S1473-3099%2809%2970069-8>.
Distribution: lnorm (days)
Parameters:
  meanlog: 1.386
  sdlog: 0.593

La distribution complète de la période d’incubation pour le SRAS peut être tracée au moyen de :

R

plot(SARS_incubacion)

ERREUR

Error: object 'SARS_incubacion' not found

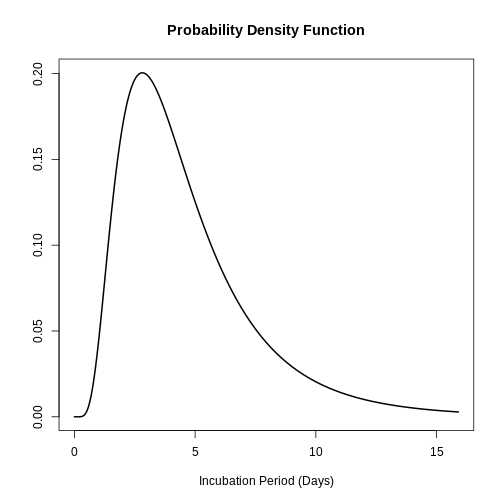
Les données ci-dessus sont utiles pour répondre à des questions telles que : Quelle est la probabilité qu’un cas de SRAS développe des symptômes deux jours après l’infection ?

R

# Calculer la probabilité cumulative complémentaire (P(X > 2)) pour une distribution lognormale

stats::plnorm(2, meanlog = 0.660, sdlog = 1.205, lower.tail = FALSE)

SORTIE

[1] 0.4890273

Distribution Gamma

Lorsque nous étudions des variables aléatoires de Poisson, nous nous intéressons généralement au nombre d’événements qui se produisent avec une moyenne de $λ$ pour un intervalle de temps donné. La distribution Gamma se concentre sur l’étude de la v.a $X$ La distribution Gamma se concentre sur l’étude de la v.a. : le temps nécessaire pour qu’un nombre donné d’événements se produisent. $α^th$. Par exemple, si nous évaluons le nombre d’infections par heure et que nous voulons étudier combien de temps peut s’écouler jusqu’à ce que nous trouvions α infections, alors graphiquement $X$ correspond à :

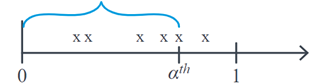
La distribution Gamma est largement utilisée dans l’analyse de survie en raison de sa flexibilité due à ses paramètres de forme. $α$ et l’échelle $θ$ qui déterminent sa fonction de densité, laquelle a un comportement asymétrique. Ici, $θ$ représente le temps d’attente moyen jusqu’à ce que le premier événement se produise, et $α$ est le nombre d’événements attendus. Cette distribution est représentée comme suit :

$X ∼Gamma(α,θ)$

$f(x)=\frac{1}{(α-1)!θ^α}e^{\frac{-x}{θ}} x^{α-1}$

$E(x)=αθ$

$Var(x)=αθ^2$

Lorsque $θ$ augmente, la concentration de la probabilité se déplace vers la droite, il en va de même lorsque l’on s’attend à un plus grand nombre d’événements. $α$ Étant donné que le temps d’attente $X$ peut être plus long.

::: challenge Exemple

Une application possible de la distribution Gamma est la modélisation de l’intervalle sériel des maladies infectieuses. L’intervalle sériel (s) est défini comme le temps écoulé entre l’apparition des symptômes du cas primaire et l’apparition des symptômes du cas secondaire. Dans l’étude de Ghani et al., la distribution de l’intervalle sériel de la grippe a été décrite comme suit Grippe-A-H1N1Pdm au moyen de la distribution gamma et a trouvé les paramètres suivants :

$s ∼Gamma( α=2.622,θ=0.957)$

Ces informations peuvent également être obtenues dans le paquet epiparameter avec la commande suivante :

R

# Récupérer les données des paramètres épidémiologiques pour l'intervalle sériel de la grippe
influenza_s <- epiparameter::epiparameter_db(  
  disease = "Influenza",  # Spécifier la maladie comme étant la grippe
  epi_name = "serial_interval",  # Sélectionner le paramètre épidémiologique : intervalle sériel
  single_epiparameter = TRUE  # Demander un seul paramètre épidémiologique
)

SORTIE

Using Ghani A, Baguelin M, Griffin J, Flasche S, van Hoek A, Cauchemez S,
Donnelly C, Robertson C, White M, Truscott J, Fraser C, Garske T, White
P, Leach S, Hall I, Jenkins H, Ferguson N, Cooper B (2009). "The Early
Transmission Dynamics of H1N1pdm Influenza in the United Kingdom."
_PLoS Currents_. doi:10.1371/currents.RRN1130
<https://doi.org/10.1371/currents.RRN1130>..
To retrieve the citation use the 'get_citation' function

R

# Afficher les données récupérées sur l'intervalle sériel
influenza_s

SORTIE

Disease: Influenza
Pathogen: Influenza-A-H1N1Pdm
Epi Parameter: serial interval
Study: Ghani A, Baguelin M, Griffin J, Flasche S, van Hoek A, Cauchemez S,
Donnelly C, Robertson C, White M, Truscott J, Fraser C, Garske T, White
P, Leach S, Hall I, Jenkins H, Ferguson N, Cooper B (2009). "The Early
Transmission Dynamics of H1N1pdm Influenza in the United Kingdom."
_PLoS Currents_. doi:10.1371/currents.RRN1130
<https://doi.org/10.1371/currents.RRN1130>.
Distribution: gamma (days)
Parameters:
  shape: 2.622
  scale: 0.957

R

plot(influenza_s)

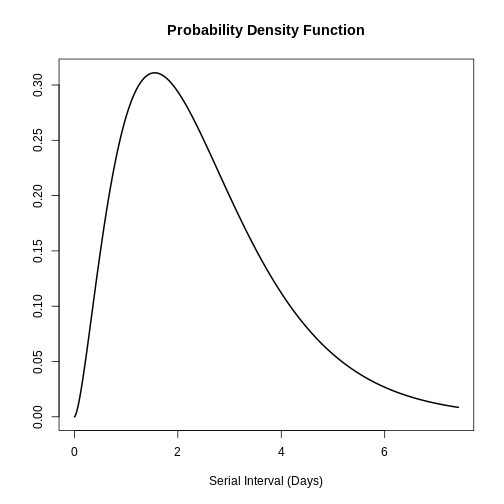
Avec ces informations, la moyenne et l’écart-type de la distribution peuvent être trouvés sur la base de l’application de la distribution gamma :

R

# Definir les parametres de forme et d'echelle
forme <- 2.622
echelle <- 0.957


# Calculer la moyenne de la distribution
moyenne <- forme * echelle  


# Calculer l'ecart-type de la distribution
ecart_type <- sqrt(forme * echelle^2)  


# Afficher la moyenne et l'ecart-type calcules
print(c(moyenne, ecart_type))

SORTIE

[1] 2.509254 1.549631

Par conséquent, la moyenne de l’intervalle sériel de la grippe est de 5,51 jours avec un écart-type de 1,55 jours. :::

Distribution de Weibull

Comme la distribution Gamma, la distribution de Weibull est utile dans l’analyse des v.a.s représentant les temps d’attente jusqu’à l’observation d’un événement particulier. La distribution de Weibull a deux paramètres et sa fonction de densité est définie par :

$f(x)= \frac{β}{η}(\frac{x}{η})^{β-1}{e^{-(x/η)}}^β$

Ici, $η$ est le paramètre d’échelle et $β$ le paramètre de forme. Le paramètre de forme $β$ est également appelé pente et tente de modéliser la relation entre la probabilité et les délais. Ainsi, lorsque $β>1$ le taux d’occurrence des événements augmente avec le temps, tandis que si $β<1$ décrit que le risque de l’événement diminue avec le temps. Le paramètre d’échelle gère le degré de variabilité de la distribution et se trouve dans les mêmes unités de $X$.

::: challenge Exemple

L’étude de Virlogeux et al. a décrit la distribution du temps d’incubation de la grippe à l’aide de la distribution de Weibull et a trouvé les paramètres suivants :

$x∼Gamma( β=2.101,η=3.839)$

Cette information peut également être obtenue dans le package epiparameter avec la commande suivante :

R

# Récupérer les données des paramètres épidémiologiques pour la période d'incubation de la grippe
influenza_incubation <- epiparameter::epiparameter_db(  
  disease = "Influenza",  # Spécifier la maladie comme étant la grippe
  epi_name = "incubation period",  # Sélectionner le paramètre épidémiologique : période d'incubation
  single_epiparameter = TRUE  # Demander un seul paramètre épidémiologique
)

SORTIE

Using Virlogeux V, Li M, Tsang T, Feng L, Fang V, Jiang H, Wu P, Zheng J, Lau
E, Cao Y, Qin Y, Liao Q, Yu H, Cowling B (2015). "Estimating the
Distribution of the Incubation Periods of Human Avian Influenza A(H7N9)
Virus Infections." _American Journal of Epidemiology_.
doi:10.1093/aje/kwv115 <https://doi.org/10.1093/aje/kwv115>..
To retrieve the citation use the 'get_citation' function

R

influenza_incubacion

ERREUR

Error: object 'influenza_incubacion' not found

R

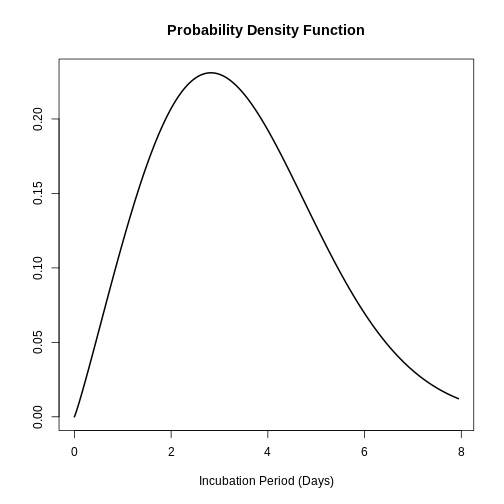
# Tracer les données récupérées sur la période d'incubation

plot(influenza_incubation)

:::

Thème 5 : Introduction à l’inférence statistique

Les statistiques peuvent être divisées en deux branches principales : descriptive et inférentielle. Comme nous l’avons vu dans les unités précédentes, la première cherche généralement à résumer et à explorer les données qui ont été collectées à partir d’un échantillon sélectionné d’une population. En revanche, les secondes visent à généraliser et à tirer des conclusions sur l’ensemble de la population sur la base des informations ou des données provenant d’un échantillon.

De par la nature du processus déductif, qui repose sur le prélèvement d’échantillons aléatoires dans la population, un estimateur peut prendre plusieurs valeurs puisqu’il dépend des unités qui ont été sélectionnées dans l’échantillon. Cette variation due au hasard, appeléevariation variation d’échantillonnage doit être impliquée dans le processus d’inférence, comme nous le verrons plus loin.

Il est important de souligner que la variation d’échantillonnage dépend de la taille de l’échantillon. Par exemple, si nous prenons des échantillons de taille 10 et que nous calculons le CFR dans chacun d’entre eux, ces estimations seront plus proches les unes des autres que celles obtenues lorsque seulement 5 individus par échantillon sont sélectionnés. Vous pouvez le vérifier en effectuant une simulation dans R et en sélectionnant 1000 échantillons de taille 5 et 10, respectivement. Comme le montre la figure ci-dessous, les CFR estimés lorsque la taille de l’échantillon passe de 5 à 10 sont plus similaires avec un RIQ plus faible.

R

library(infer)

SORTIE


Attaching package: 'infer'

SORTIE

The following object is masked from 'package:epiparameter':

    generate

R

# Définir la graine aléatoire pour la reproductibilité
set.seed(200)  


# Créer le cadre de données de la population avec des indicateurs de décès (1 = décédé, 0 = vivant)
population <- data.frame(dead = c(rep(1, 40), rep(0, 160)))  


# Échantillon de taille 5 : Tirer 100 échantillons aléatoires de taille 5 (sans remplacement)
samples_n5 <- population %>%  
  rep_sample_n(size = 5, reps = 100, replace = FALSE)  


# Calculer le taux de létalité (CFR) pour chaque réplique dans l'échantillon de taille 5
cfr_n5 <- samples_n5 %>%  
  group_by(replicate) %>%  
  summarise(cfr = mean(dead))

ERREUR

Error in summarise(., cfr = mean(dead)): could not find function "summarise"

R

# Échantillon de taille 10 : Tirer 100 échantillons aléatoires de taille 10 (sans remplacement)
samples_n10 <- population %>%  
  rep_sample_n(size = 10, reps = 100, replace = FALSE)  


# Calculer le taux de létalité (CFR) pour chaque réplique dans l'échantillon de taille 10
cfr_n10 <- samples_n10 %>%  
  group_by(replicate) %>%  
  summarise(cfr = mean(dead))

ERREUR

Error in summarise(., cfr = mean(dead)): could not find function "summarise"

R

# Combiner les résultats des deux tailles d'échantillons (5 et 10)
cfr <- bind_rows(cfr_n5, cfr_n10) %>%  
  mutate(size = factor(c(rep(5, 100), rep(10, 100))))

ERREUR

Error in mutate(., size = factor(c(rep(5, 100), rep(10, 100)))): could not find function "mutate"

R

# Tracer la distribution d'échantillonnage des estimations du CFR en utilisant un boxplot
ggplot(cfr, aes(x = size, y = cfr, fill = size)) +  
  geom_boxplot(show.legend = FALSE) +  # Créer un boxplot sans légende
  labs(x = "Taille de l'échantillon", y = "Estimation du CFR",  
     title = "Distribution d'échantillonnage des estimations du CFR") +  # Ajouter des étiquettes et un titre
  scale_fill_brewer(palette = "Blues")  # Utiliser une palette de couleurs bleues pour la visualisation

ERREUR

Error in ggplot(cfr, aes(x = size, y = cfr, fill = size)): could not find function "ggplot"

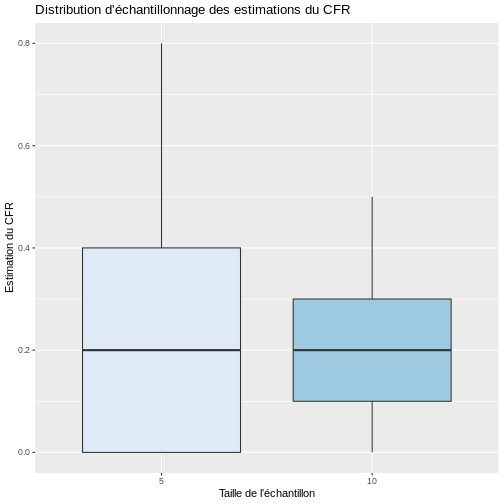
Si nous calculons la moyenne et l’écart-type des valeurs estimées du CFR avec les échantillons de taille 5 et 10, nous constatons que l’écart-type des estimations est effectivement plus petit avec l’augmentation de la taille de l’échantillon, mais dans les deux cas, en moyenne, les échantillons étaient plus proches de la vraie valeur du paramètre de 0,20.

R

# Résumer les estimations du CFR par taille d'échantillon


cfr %>%  
  group_by(size) %>%  # Regrouper les données par taille d'échantillon  
  summarise(  
  moyenne = mean(cfr),  # Moyenne du CFR  
  et = sd(cfr),  # Écart-type du CFR  
  médiane = median(cfr),  # Médiane du CFR  
  p25 = quantile(cfr, 0.25),  # 25e centile (quartile inférieur)  
  p75 = quantile(cfr, 0.75)  # 75e centile (quartile supérieur)  
  )

ERREUR

Error in summarise(., moyenne = mean(cfr), et = sd(cfr), médiane = median(cfr), : could not find function "summarise"

Mais si, dans la réalité, nous ne pouvons prendre qu’un seul échantillon aléatoire, cela signifie que nous n’aurons qu’une seule chance de calculer une statistique qui sera la estimateur ponctueldu paramètre. Toutefois, cette valeur unique ne pourra pas fournir d’informations sur la variabilité inhérente à la sélection aléatoire de l’échantillon. En outre, comme nous l’avons vu dans l’exemple précédent, il est fort probable que de nombreuses configurations possibles de l’échantillon donnent des estimations éloignées de la valeur réelle du paramètre. Par conséquent, nous devons essayer d’intégrer la variabilité de l’échantillonnage dans le processus d’estimation.

Estimation par intervalles de confiance

L’objectif de l’estimation de l’intervalle de confiance est de fournir une plage de valeurs, une limite inférieure et une limite supérieure (a ; b), qui, avec une forte probabilité, “…”.confiance”contient la vraie valeur du paramètre à estimer. Bien que chaque échantillon aléatoire qui peut être sélectionné produise des bornes différentes, cette procédure garantit qu’un échantillon de confiance “contient la vraie valeur du paramètre à estimer”. $(1-α) %$ des intervalles construits contiendra la vraie valeur du paramètre. Cela implique également que a $α%$ des intervalles ne contiendra pas la valeur réelle. Le symbole α est appelé niveau de signification.

En général, un intervalle de confiance est construit avec les ingrédients suivants :

$\text{Estimateur} ±(\text{coefficient de fiabilité})*(\text{erreur standard})$

Défi

Exemple

Dans le paquet CFR de l’initiative Epiverse-TRACE, des informations sont disponibles sur une épidémie d’Ebola qui s’est produite en 1976 au Zaïre, aujourd’hui appelé République du Congo, documentant le nombre de cas et de décès sur une période de 73 jours. En fin de compte, 245 cas d’Ebola ont été signalés, dont 234 cas mortels. Si l’intérêt est d’effectuer une estimation de l’intervalle CFR à 95 %. Quelle doit être la procédure ?

● \[**Étape 1-Estimateur**\]{.underline}: il faut commencer par trouver l’estimation dans l’échantillon observé :

$\hat{p} = \widehat{\text{CFR}} = \frac{234}{245}= 0.955$

Le CFR estimé est donc de 95,5 %.

● \[**Étape 2 - Coefficient de fiabilité**\]{.underline} basé sur la distribution normale pour un niveau de confiance de 95% correspondrait à 1,96

● \[**Étape 3 - Erreur standard :**\]{.underline}

$\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}=\sqrt{\frac{0.955 (1-0.955)}{245}}$

● \[**Étape 4 - Rassembler les ingrédients**\]{.underline}

Comme vous l’avez remarqué jusqu’à présent, ce pas-à-pas peut devenir lourd à cause des calculs, mais en R, nous pouvons tout obtenir de manière plus rapide et plus efficace comme suit :

$ = $

Comme vous l’avez remarqué jusqu’à présent, ce pas-à-pas peut devenir lourd à cause des calculs, mais en R, nous pouvons obtenir tout cela d’une manière plus rapide et plus efficace de la façon suivante :

R

# Télécharger les données sur l'épidémie d'Ebola de 1976
data(ebola1976)

AVERTISSEMENT

Warning in data(ebola1976): data set 'ebola1976' not found

R

# Calculer les statistiques clés liées au taux de létalité (CFR)
cfr_summary <- ebola1976 %>%  
  summarise(  
  n = sum(cases),  # Nombre total de cas  
  deces = sum(deaths),  # Nombre total de décès  
  cfr_est = deces / n,  # Estimation du taux de létalité (CFR)  
  error = sqrt((cfr_est * (1 - cfr_est)) / n),  # Calcul de l'erreur standard  
  lim_inf = cfr_est - 1.96 * error,  # Limite inférieure de l'intervalle de confiance à 95 %  
  lim_sup = cfr_est + 1.96 * error  # Limite supérieure de l'intervalle de confiance à 95 %  
  )

ERREUR

Error in summarise(., n = sum(cases), deces = sum(deaths), cfr_est = deces/n, : could not find function "summarise"

R

# Afficher le résultat
print(cfr_summary)

ERREUR

Error: object 'cfr_summary' not found

Enfin, nous pouvons conclure qu’avec un niveau de confiance de 95 %, le TFC d’Ebola lors de l’épidémie de 1976 en République démocratique du Congo est contenu dans l’intervalle entre 92,9 % et 98,1 %.

Le progiciel CFR dispose également d’une fonction intégrée permettant d’estimer automatiquement le CFR au cours d’une épidémie, avec son intervalle de confiance respectif de 95 %, au moyen de la fonction :

R

# Calculer un taux de létalité statique (CFR) en utilisant le package cfr

cfr::cfr_static(data = ebola1976)

ERREUR

Error: object 'ebola1976' not found

Comme vous pouvez le constater, il existe de légères différences entre l’IC construit pas à pas et celui rapporté par la fonction cfr_static. Cela s’explique par le fait que le progiciel CFR construit l’IC par la méthode basée sur le maximum de vraisemblance et différentes distributions statistiques en fonction du nombre total de cas, mais l’interprétation ne change pas.

Points clés

À la fin de la session, vérifiez si vous avez atteint les objectifs :

Comprendre le rôle des statistiques dans l’étude de l’environnement. maladies infectieuses.
Comprendre les mesures statistiques permettant de résumer et d’analyser les données sur les maladies infectieuses. l’information.
Se familiariser avec le concept de variable aléatoire et reconnaître les principales distributions de probabilité.
Identifier et comprendre le processus du problème statistique en tant que problème d’inférence à partir d’un échantillon.
Comprendre le concept d’intervalle de confiance et la procédure. de test d’hypothèse.

Les contributions

Erika Cantor : Version initiale
Zulma M. Cucunuba : Edition
Laura Gómez-Bermeo : Montage
Andree Valle-Campo : Modifications mineures
José M. Velasco-España : Editions mineures
Hugo Gruson: Traduction en français