An Introduction To Force-of-Infection Models

The current version of serofoi supports three different types of serocatalytic models for estimating the Force-of-Infection (FoI): constant, age-varying, and time-varying FoI. To estimate relevant parameters we employ a suit of Bayesian models using age-disaggregated population-based cross-sectional serological surveys as input data.

What is the FoI

The FoI, also known as the hazard rate or the infection pressure, is a key concept in mathematical modelling of infectious diseases. It represents the rate at which susceptible individuals become infected given their exposure to a pathogen. In simple terms, the FoI quantifies the risk of a susceptible individual becoming infected over a period of time. It is usually expressed as a rate per unit of time (e.g., per day or per year).

To illustrate this, consider a simple SIR model: $$\begin{aligned} \frac{dS}{dt} &= -\beta S I,\\ \frac{dI}{dt} &= \beta S I - \gamma I,\\ \frac{dR}{dt} &= \gamma I, \end{aligned}$$

In this case, the FoI is defined as $\lambda(t) = \beta I(t)$ (Note that the FoI is time dependent by definition). To solve this system of equations we need to know the transmission rate $\beta>0$, and the rate of recovery from infection $\gamma>0$, as well as some initial conditions.

Serocatalytic models offer a simpler perspective. Here we are interested in estimating how the risk of historical exposure to a pathogen varies depending on the time of birth of the individuals in the sample. For this, we put together the $I$ and $R$ compartments into a single seropositives compartment $P(t)$ and consider that the dynamics of each birth cohort separately

$$\begin{aligned} &\frac{dN^{\tau}(t)}{dt} = -\lambda(t) N^{\tau}(t),\\ &\frac{dP^{\tau}(t)}{dt} = \lambda(t) N^{\tau}(t), \\ &N^{\tau}(t)+P^{\tau}(t)=1; \quad t<\tau \end{aligned}$$ where $0 \leq N^\tau(t)\leq 1$ is the proportion of individuals born in year $\tau$ who are seronegative at time $t$. Assuming lack of maternal antibodies, the initial condition for each cohort can be specified as $N^{\tau}(\tau) = 1$. Depending on whether the FoI is constant, time dependent, or age dependent, this system of equations yields the different solutions on which serofoi is based on.

Constant vs Time-varying FoI

The FoI is often incorrectly assumed to be constant over time. Identifying whether the FoI follows a constant, an age-varying or a time-varying trend can be important in the identification and characterization of the spread of disease. serofoi offers tools to implement and compare a wide variety of Bayesian models to estimate the FoI according to the aforementioned serocatalytic models.

In the idealised situation where the FoI is constant $\lambda(t) = \lambda$:

$$\frac{dP^{\tau}(t)}{dt} = \lambda (1 - P^{\tau}(t)).$$ Applying the integrating factor method and using the initial conditions $X^\tau(\tau) = 0$ yields to the solution:

$$P^{\tau}(t) = 1 - \exp(-\bar \lambda t),$$

meaning that, in the long run, the seropositivity converges to 1.

In more realistic applications, the FoI is assumed to be piecewise-constant on discrete intervals of 1-year length. The solution for each year is then: $$P^{\tau}(t) = 1 + (P_0 - 1) \exp(-\lambda_t t)$$ where $P_0$ corresponds to the seropositivity at the end of the previous year and $\lambda_t$ is the constant value assumed for the FoI at time $t$. From the resulting recursive equation, it is possible to obtain analytical solutions for the seropositivity $P^\tau(t)$ along each 1-year length chunk.

Considering seroreversion

Since it is possible for seropositive individuals to lose immunity over time, we consider the rate at which infected individuals become seronegative $\mu$. The system of equations is now:

$$\begin{aligned} \frac{dP^{\tau}(t)}{dt} &= \lambda(t) (1 - P^{\tau}(t)) - \mu P^{\tau}(t),\\ P^{\tau}(\tau) &= 0, \end{aligned}$$

Similarly, this yields to a iterative solution for the seropositivity $P^\tau (t)$ when piece-wise constant FoI is considered:

$$P^{\tau}(t) = \frac{\lambda_t}{\lambda_t + \mu} + \left(P_0 - \frac{\lambda_t}{\lambda_t + \mu}\right) \exp(-(\lambda_t + \mu)),$$

where, again, $P_0$ corresponds to the proportion of seropositive individuals of cohort $\tau$ by the end of the previous year. Correct indexation and simplification of this equation allows the description of age-dependent FoIs.

Estimating the FoI - Bayesian modelling

Now that we can describe the proportion of seropositive individuals $P(t)$ by means of the serocatalytic models for constant, time-varying, and age-varying FoIs, what we want is to obtain estimates of the FoI ($\lambda$) and the seroreversion rate ($\mu$) by sampling bye means of Bayesian methods taking a cross-sectional serological survey as data. For this, we can use serofoi’s fit_seromodel(), which relies on the statistical programming language Stan to perform this task. The current available options for modelling are summarised in table 1:

model_type	scale (is_log_foi)	$\lambda_1$	$\lambda_i$, $i>1$	$\mu$	$\sigma$
"constant"	FALSE	$\sim\mathcal{N}(\bar{\lambda},\sigma)$ or $\sim\mathcal{U(\lambda_{min},\lambda_{max})}$	-	$\sim\mathcal{N}(\bar{\mu},\sigma_\mu)$ or $\sim\mathcal{U(\mu_{min},\mu_{max})}$	$\mathcal{C}(\sigma_0, \gamma)$
"age"	FALSE	$\sim\mathcal{N}(\bar{\lambda}_1,\sigma)$ or $\sim\mathcal{U(\lambda_{1,min},\lambda_{1,max})}$	$\sim\mathcal{N}(\lambda_{i-1},\sigma)$	$\sim\mathcal{N}(\bar{\mu},\sigma_\mu)$ or $\sim\mathcal{U(\mu_{min},\mu_{max})}$	$\mathcal{C}(\sigma_0, \gamma)$
"time"	FALSE	$\sim\mathcal{N}(\bar{\lambda}_1,\sigma)$ or $\sim\mathcal{U(\lambda_{1,min},\lambda_{1,max})}$	$\sim\mathcal{N}(\lambda_{i-1},\sigma)$	$\sim\mathcal{N}(\bar{\mu},\sigma_\mu)$ or $\sim\mathcal{U(\mu_{min},\mu_{max})}$	$\mathcal{C}(\sigma_0, \gamma)$
"time"	TRUE	$\sim\mathcal{N}(\bar{\lambda}_1,\sigma)$ or $\sim\mathcal{U(\lambda_{1,min},\lambda_{1,max})}$	$\sim\mathcal{N}(\lambda_{i-1},\sigma)$	$\sim\mathcal{N}(\bar{\mu},\sigma_\mu)$ or $\sim\mathcal{U(\mu_{min},\mu_{max})}$	$\mathcal{C}(\sigma_0, \gamma)$

Table 1. Available options. Here, $\mathcal{N}$ corresponds to the normal distribution, $\mathcal{U}$ to the uniform distribution, and $\mathcal{C}$ to the Cauchy distribution.

The number of seropositives at the time of the survey $X(a)$, corresponding to n_seropositive in the data, follows a binomial distribution:

$$X(a) \sim Binom\left(n(a), P^{T - a} (T)\right)$$

where $n(a)$ corresponds to the sample size for age group $a$ (n_sample) and $T$ is the time when the serosurvey was conducted. Note that $T-a$ correspond to the birth year of the cohort with age $a$ at the time of the survey.

The prior distributions for each parameter can be selected in fit_seromodel(). This is done by means of the helper functions sf_normal(), `sf_uniform() and sf_cauchy(). For example:

fit_seromodel(
  serosurvey,
  model_type = "time",
  foi_prior = sf_uniform(0.5, 1),
  foi_sigma_rw = sf_cauchy(0.01, 0.005),
  is_seroreversion = TRUE,
  seroreversion_prior = sf_normal(0.02, 0.01)
)

Corresponds to the model: $$\begin{align} \lambda_1 &\sim \mathcal{U}(0.5, 1) \\ \sigma &\sim \mathcal{C}(0.01, 0.005) \\ \mu &\sim \mathcal{N}(0.02, 0.01) \end{align}$$ The available options for each parameter are shown in table 1. Note that, in the case of the age- and time-varying models, the FoI prior that can be specified is that of the first FoI value to be estimated (i.e. the birth year of the oldest age-group in the time-varying case and the youngest age-group in the age-varying case), such that the means for subsequent ages/years are selected iteratively as the FoI value estimated for the previous index.

Model 1. Constant Force-of-Infection (endemic model)

The endemic constant model is a simple mathematical model used in epidemiology to describe the seroprevalence of an infectious disease within a population, as a product of a long-term transmission. In this case, the rate of infection acquisition $\lambda$ is constant over time, and the seroprevalence $P(A)$ behaves as a cumulative process increasing monotonically with age.

To test the constant model we simulate a serosurvey following a stepwise decreasing FoI (red line in Fig. 1) using the data simulation functions of serofoi:

# how the disease circulates
foi_df <- data.frame(
    year = seq(2000, 2049, 1),
    foi = rep(0.02, 50)
)

# specify 5-year age bins for observations
survey_features <- data.frame(
    age_min = seq(1, 50, 5),
    age_max = seq(5, 50, 5),
    n_sample = rep(25, 10)
)

serosurvey_constant <- simulate_serosurvey(
  "time",
  foi_df,
  survey_features
) |>
mutate(survey_year = 2050)

The simulated dataset serosurvey_constant contains information about 250 samples of individuals between 1 and 50 years old (5 samples per age) with age groups of 5 years length. The following code shows how to implement the constant model to this simulated serosurvey:

seromodel_constant <- fit_seromodel(
  serosurvey = serosurvey_constant,
  model_type = "constant",
  iter = 800
)
plot_seromodel(
  seromodel_constant,
  serosurvey = serosurvey_constant,
  foi_df = foi_df,
  size_text = 6
)

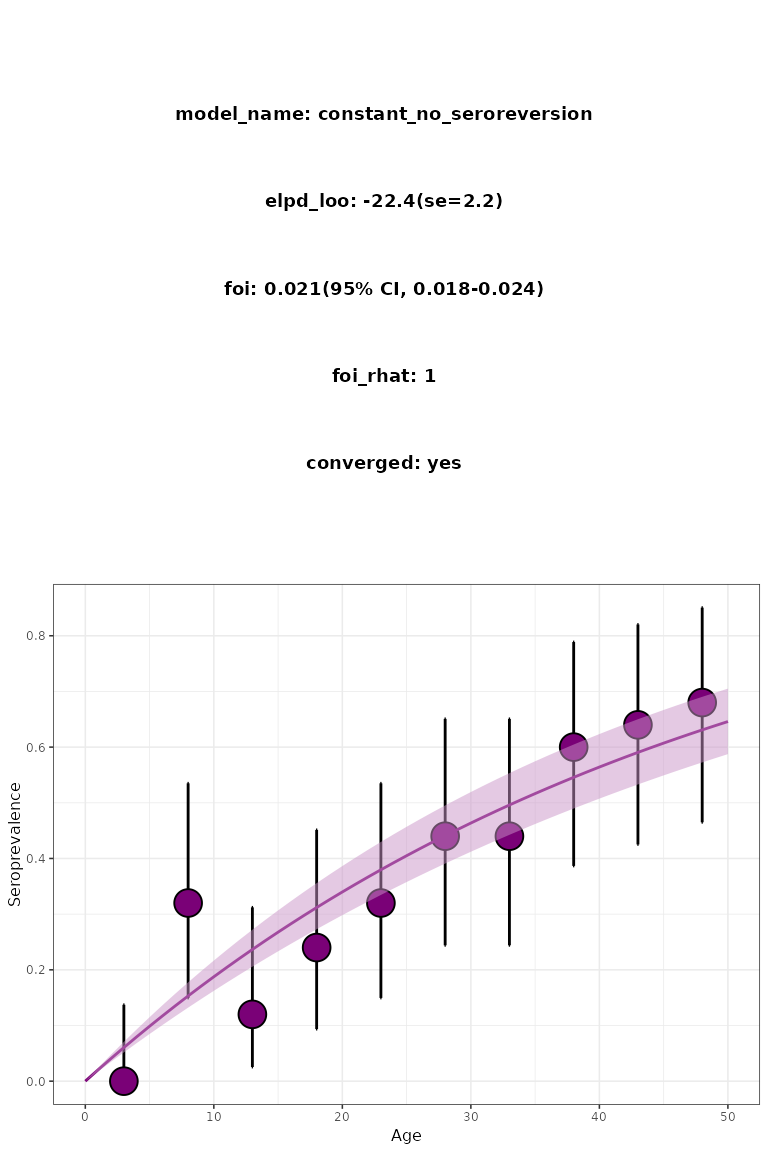
Figure 1. Constant serofoi model plot. Simulated (red) vs modelled (blue) FoI.

In this case, 800 iterations are enough to ensure convergence. plot_seromodel() returns a visualisation of the results including a summary where the expected log pointwise predictive density (elpd) and its standard error (se) are shown. We say that a model converges if all the R-hat estimates are below 1.01.

Time-varying FoI models

For the time-varying FoI models, the probability for a case to be positive at age a at time $t$ also follows a binomial distribution, as described above. However, the seroprevalence is obtained from a cumulative of the yearly-varying values of the FoI over time:

$$P^{\tau}(t) = \frac{\lambda_t}{\lambda_t + \mu} + \left(P_0 - \frac{\lambda_t}{\lambda_t + \mu}\right) \exp(-(\lambda_t + \mu)),$$

Model 2. Time-varying FoI - Slow Time-Varying FoI

The time-varying model (model_type = "time") uses a forward random walk algorithm where the prior of the first chronological FoI value in the time-span of the serological survey can be either a normal distribution (foi_prior = sf_normal()) or a uniform distribution (foi_prior = sf_uniform()). Subsequent values of the FoI are sampled from the normal distribution as $\lambda_i \sim \mathcal{N}(\lambda_{i-1}, \sigma)$, where $\sigma \sim \mathcal{C}(0, 1)$. The prior distribution for the seroreversion rate can also be either normal or uniform, and is specified by setting is_seroreversion = TRUE and by means of the parameter seroreversion_prior.

To test the "time" using a normal prior in the FoI, we simulate a serosurvey following a stepwise decreasing FoI (red line in Fig. 2) using the data simulation functions of serofoi:

foi_df <- data.frame(
    year = seq(2000, 2049, 1),
    foi = c(
      rep(0.2, 25),
      rep(0.1, 10),
      rep(0.00001, 15)
    )
)

survey_features <- data.frame(
    age_min = seq(1, 50, 5),
    age_max = seq(5, 50, 5),
    n_sample = rep(25, 10)
)

serosurvey_sw_dec <- simulate_serosurvey(
  "time",
  foi_df,
  survey_features
) |>
mutate(survey_year = 2050)

The simulated dataset serosurvey_sw_dec contains information 250 samples of individuals between 1 and 50 years old (5 samples per age) with age groups of 5 years length. The following code shows how to implement the slow time-varying normal model to this simulated serological survey:

foi_index <- data.frame(
  year = seq(2000, 2049),
  foi_index = rep(c(1, 2, 3), c(25, 10, 15))
)
seromodel_time_normal <- fit_seromodel(
  serosurvey = serosurvey_sw_dec,
  model_type = "time",
  foi_index = foi_index,
  iter = 1500
)
plot_seromodel(
  seromodel_time_normal,
  serosurvey = serosurvey_sw_dec,
  foi_df = foi_df,
  size_text = 6
)

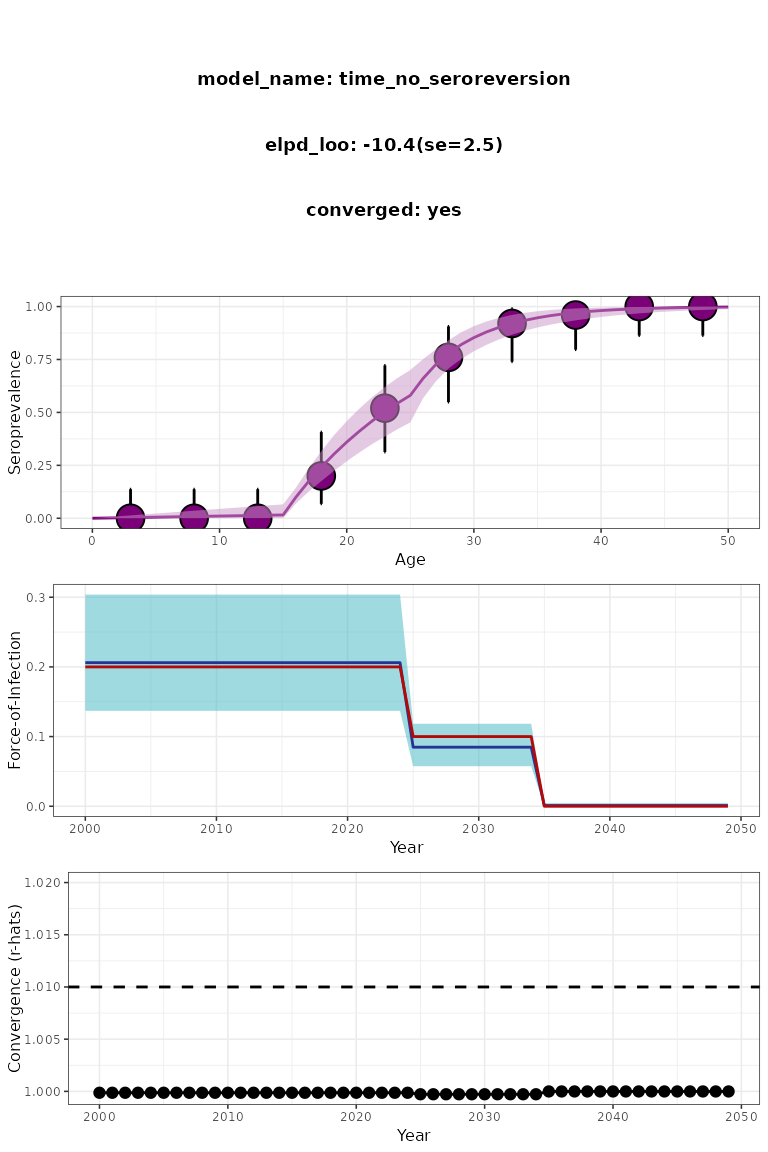
Figure 2. Slow time-varying serofoi model plot. Simulated (red) vs modelled (blue) FoI.

The number of iterations required may depend on the number of years, reflected by the difference between the year of the serosurvey and the maximum age-class sampled.

Model 3. Time-varying FoI - Fast Epidemic Model

The time-varying fast epidemic model is parametrized in such a way that the initial FoI value in the forward random walk is sampled in the logarithmic scale. In this case, the priors for subsequent FoIs are:

$$\begin{aligned} \log\left(\lambda_t\right) &\sim \mathcal{N}(\log(\lambda_{t-1}), \sigma) \\ \sigma &\sim \mathcal{N} (0, 1) \end{aligned}$$

This is done in order to capture fast changes in the FoI trend.

To test the log_time model we simulate a serosurvey conducted in 2050 emulating a hypothetical situation where a three-year epidemic occurred between 2030 and 2035:

foi_df <- data.frame(
    year = seq(2000, 2049, 1),
    foi = c(
      rep(0, 30),
      rep(0.7, 3),
      rep(0, 17)
    )
)

survey_features <- data.frame(
    age_min = seq(1, 50, 5),
    age_max = seq(5, 50, 5),
    n_sample = rep(25, 10)
)

serosurvey_large_epi <- simulate_serosurvey(
  survey_features = survey_features,
  foi_df,
  model = "time"
) |>
mutate(survey_year = 2050)

The simulated serosurvey tests 250 individuals between 1 and 50 years old by the year 2050. The implementation of the fast epidemic model can be obtained running the following:

foi_index <- data.frame(
  year = seq(2000, 2049),
  foi_index = rep(c(1, 2, 3), c(30, 3, 17))
)
seromodel_log_time_normal <- fit_seromodel(
  serosurvey = serosurvey_large_epi,
  model_type = "time",
  is_log_foi = TRUE,
  foi_index = foi_index,
  iter = 2000
)

plot_log_time_normal <- plot_seromodel(
  seromodel_log_time_normal,
  serosurvey = serosurvey_large_epi,
  foi_df = foi_df,
  size_text = 5,
  foi_max = 0.7
)
plot(plot_log_time_normal)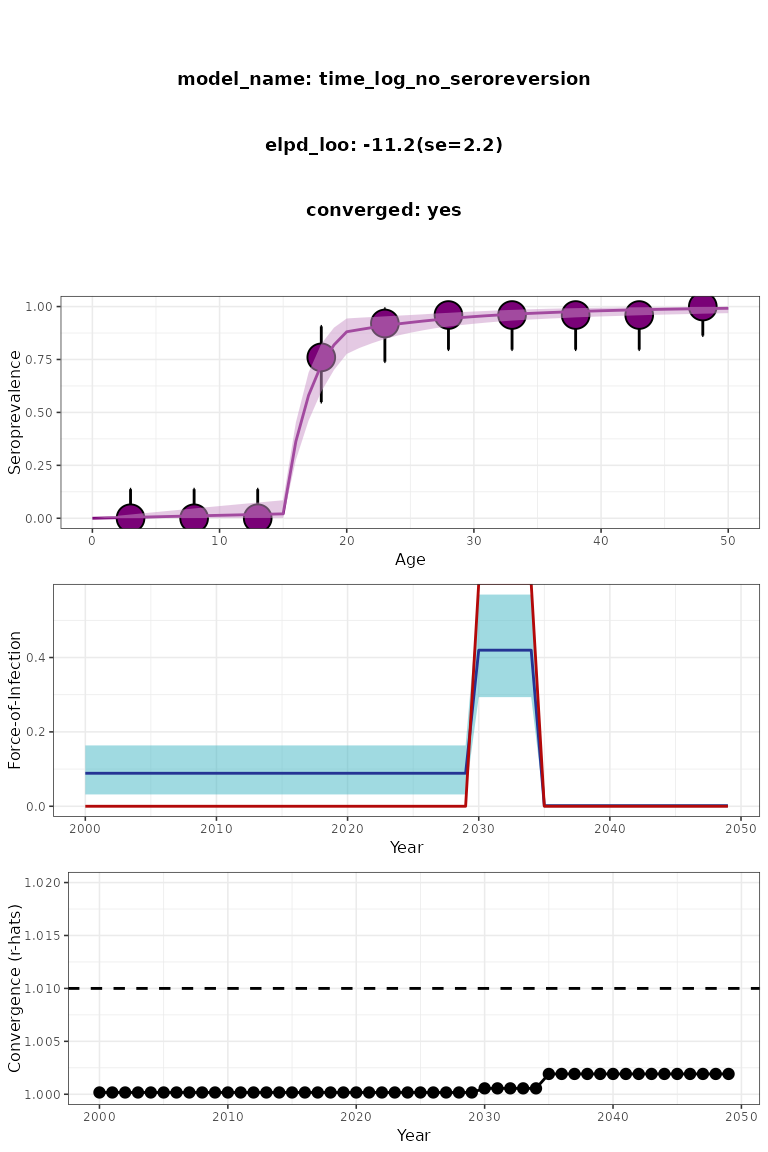

Figure 3. Time-varying fast epidemic serofoi model plot. Simulated (red) vs modelled (blue) FoI.

In Fig 3 we can see that the fast epidemic serofoi model is able to identify the large epidemic simulated on the simdata_large_epi dataset.

Models Comparison

Above we showed that the fast epidemic model (specified by model_type = "time" and is_log = TRUE in fit_seromodel()) is able to identify the large epidemic outbreak described by the dataset simulated according to a step-wise decreasing FoI (red line in Fig 3).

Now, we would like to know whether this model actually fits this dataset better than the other available models in serofoi. For this, we also implement both the endemic model (model_type = "constant") and the slow time-varying normal model (model_type="time", is_log = FALSE):

Using the function cowplot::plot_grid we can visualise the results of the three models simultaneously:

cowplot::plot_grid(
  plot_constant, plot_time_normal, plot_log_time_normal,
  nrow = 1, ncol = 3, labels = "AUTO"
)

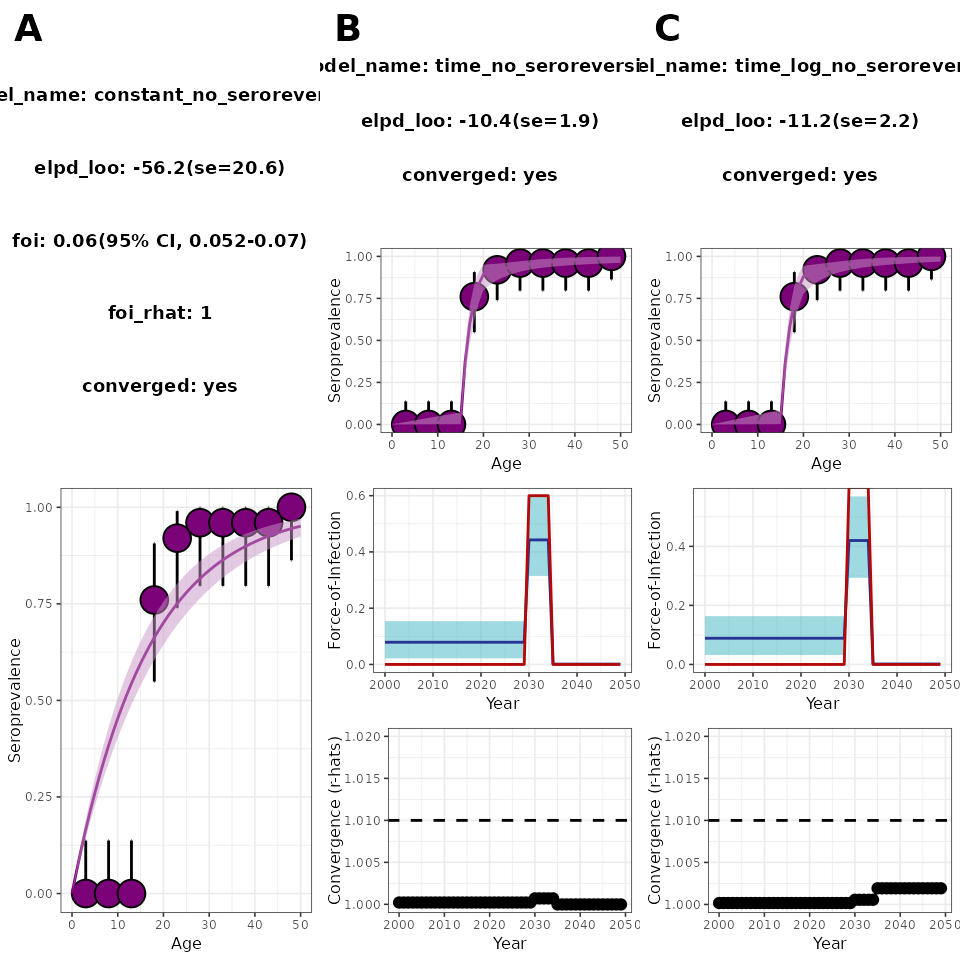
Figure 4. Model comparison between the three serofoi models for a large-epidemic simulated dataset.

A common criterion to decide what model fits the data the best is to choose the one with the larger elpd. According to this criterion, in this case the epidemic and fast-epidemic models perform similarly (see the second row of panels B and C in Figure 4).

NOTE: Running the serofoi models for the first time on your local computer may take a few minutes for the rstan code to compile locally. However, once the initial compilation is complete, there is no further need for local compilation.

References