Modélisation des interventions

Dernière mise à jour le 2025-11-23 | Modifier cette page

Vue d'ensemble

Questions

Comment étudier l’effet des interventions sur les trajectoires des maladies ?

Objectifs

Ajoutez les interventions pharmaceutiques et non pharmaceutiques à la liste des interventions d’un modèle crée avec le package {epidemics}

Pré-requis

Compléter le tutoriel sur La simulation de la transmission.

Les apprenants doivent également se familiariser avec les dépendances des concepts suivants avant de travailler sur ce tutoriel :

Réponse à l’épidémie : Types d’intervention.

R packages installés: {epidemics}, socialmixr, scales, tidyverse.

Afficher les détails

Installer les packages si elles ne le sont pas déjà:

R

if (!base::require("pak")) install.packages("pak")
pak::pak(c("epiverse-trace/epidemics", "socialmixr", "scales", "tidyverse"))

Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.

Introduction

Les modèles mathématiques peuvent être utilisés pour générer des trajectoires de propagation de maladies dans le cadre de la mise en œuvre d’interventions à différents stades d’une épidémie. Ces trajectoires peuvent être utilisées pour prendre des décisions sur les interventions à mettre en place pour ralentir la propagation des maladies.

Les interventions sont généralement incorporées dans les modèles mathématiques en manipulant les valeurs des paramètres pertinents, par exemple la réduction de la transmission, ou en introduisant un nouvel état de la maladie, par exemple la classe vaccinée, où nous supposons que les individus qui appartiennent à cette classe ne sont plus susceptibles d’être infectés.

Dans ce tutoriel, nous apprendrons à utiliser le package {epidemics} pour modéliser les interventions et l’accès aux données de contact social avec socialmixr. Nous utiliserons dplyr, ggplot2 et le tuyau %>% pour relier certaines de leurs fonctions, alors appelons aussi tidyverse:

R

library(epidemics)
library(socialmixr)
library(tidyverse)

Modèle de référence

Nous étudierons l’effet des interventions sur une épidémie de COVID-19 à l’aide d’un modèle SEIR (model_default() dans le paquetage R {epidemics}). Pour être en mesure de voir l’effet de notre intervention, nous exécutons également une variante de base du modèle, c’est-à-dire sans intervention.

Le modèle SEIR divise la population en quatre compartiments : Susceptible (S), Exposé (E), Infectieux (I) et Rétabli (R). Nous définirons les paramètres suivants pour notre modèle : \(R_0 = 2.7\) (nombre de reproduction de base), période de latence ou période pré-infectieuse \(= 4\) jours, et la période infectieuse \(= 5.5\) jours (paramètres adaptés de Davies et al. (2020)). Nous adoptons une matrice de contact avec des tranches d’âge 0-18, 18-65, 65 ans et plus en utilisant socialmixr et supposons qu’un individu sur un million dans chaque groupe d’âge est contagieux au début de l’épidémie.

R

# charger les données de l'enquête
survey_data <- socialmixr::polymod

# générer une matrice de contacts
cm_results <- socialmixr::contact_matrix(
  survey = survey_data,
  countries = "United Kingdom",
  age.limits = c(0, 15, 65),
  symmetric = TRUE
)

# prépare la matrice de contact
cm_matrix <- t(cm_results$matrix)

# prépare le vecteur de la démographie
demography_vector <- cm_results$demography$population
names(demography_vector) <- rownames(cm_matrix)

# conditions initiales: une personne sur un million est infecté
initial_i <- 1e-6
initial_conditions <- c(
  S = 1 - initial_i,
  E = 0,
  I = initial_i,
  R = 0,
  V = 0
)

# crée la matrice de conditions initiales pour chaque tranche d'âge
initial_conditions <- base::rbind(
  initial_conditions,
  initial_conditions,
  initial_conditions
)
rownames(initial_conditions) <- rownames(cm_matrix)

# prépare la population à modéliser comme étant touchée par l'épidémie
uk_population <- epidemics::population(
  name = "UK",
  contact_matrix = cm_matrix,
  demography_vector = demography_vector,
  initial_conditions = initial_conditions
)

En utilisant le taux d’infectiosité \(= 1/4\), le taux de guérison \(= 1/5.5\) et le taux de transmission \(= 2.7/5.5\) (rappelez-vous que taux de transmission = \(R_0\)* taux de guérison) comme suit :

R

# périodes de temp
preinfectious_period <- 4.0
infectious_period <- 5.5
basic_reproduction <- 2.7

# taux
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
transmission_rate <- basic_reproduction * recovery_rate

# exécuter une variante de base du modèle sans intervention
output_baseline <- epidemics::model_default(
  population = uk_population,
  transmission_rate = transmission_rate,
  infectiousness_rate = infectiousness_rate,
  recovery_rate = recovery_rate,
  time_end = 300, increment = 1.0
)

Interventions non-pharmaceutiques

Interventions non-pharmaceutiques Les interventions non pharmaceutiques (INP) sont des mesures mises en place pour réduire la transmission qui n’incluent pas l’administration de médicaments ou de vaccins. Les IPN visent à réduire les contacts entre les personnes infectieuses et les personnes sensibles en fermant les écoles et les lieux de travail et en prenant d’autres mesures pour empêcher la propagation de la maladie, par exemple en se lavant les mains et en portant des masques.

Effet des fermetures d’écoles sur la propagation de COVID-19

Le premier IPN que nous examinerons est l’effet des fermetures d’écoles sur la réduction du nombre de personnes infectées par le COVID-19 au fil du temps. Nous supposons qu’une fermeture d’école réduit la fréquence des contacts au sein des différents groupes d’âge et entre eux. Sur la base d’études empiriques, nous supposons que les fermetures d’écoles réduiront de 50 % les contacts entre enfants d’âge scolaire (0-15 ans) et entraîneront une faible réduction (1 %) des contacts entre adultes (15 ans et plus).

Pour inclure une intervention dans notre modèle, nous devons créer un objet intervention. Les données d’entrée sont le nom de l’intervention (name), le type d’intervention (contacts ou rate), l’heure de début (time_begin), l’heure de fin (time_end) et la réduction (reduction). Les valeurs de la matrice de réduction sont spécifiées dans le même ordre que les groupes d’âge dans la matrice de contact.

R

rownames(cm_matrix)

SORTIE

[1] "[0,15)"  "[15,65)" "65+"

Par conséquent, nous spécifions reduction = matrix(c(0.5, 0.01, 0.01)). Nous supposons que les fermetures d’écoles commencent le 50e jour et se poursuivent pendant 100 jours supplémentaires. Notre objet d’intervention est donc :

R

close_schools <- epidemics::intervention(
  name = "School closure",
  type = "contacts",
  time_begin = 50,
  time_end = 50 + 100,
  reduction = matrix(c(0.5, 0.01, 0.01))
)

Effet des interventions sur les contacts

Dans le cadre de {epidemics} la matrice des contacts est réduite par des proportions pour la période pendant laquelle l’intervention est en place. Pour comprendre comment la réduction est calculée dans les fonctions du modèle, considérons une matrice de contacts pour deux groupes d’âge avec un nombre égal de contacts :

SORTIE

     [,1] [,2]
[1,]    1    1
[2,]    1    1

Si la réduction est de 50 % dans le groupe 1 et de 10 % dans le groupe 2, la matrice des contacts pendant l’intervention sera la suivante :

SORTIE

     [,1] [,2]
[1,] 0.25 0.45
[2,] 0.45 0.81

Les contacts au sein du groupe 1 sont réduits de 50 % deux fois pour tenir compte d’une réduction de 50 % des contacts sortants et entrants (\(1\times 0.5 \times 0.5 = 0.25\)). De même, les contacts au sein du groupe 2 sont réduits deux fois de 10 %. Les contacts entre le groupe 1 et le groupe 2 sont réduits de 50 %, puis de 10 % (\(1 \times 0.5 \times 0.9= 0.45\)).

Nous exécutons le modèle avec intervention = list(contacts = close_schools) comme suit :

R

output_school <- epidemics::model_default(
  # population
  population = uk_population,
  # taux
  transmission_rate = transmission_rate,
  infectiousness_rate = infectiousness_rate,
  recovery_rate = recovery_rate,
  # intervention
  intervention = list(contacts = close_schools),
  # temps
  time_end = 300, increment = 1.0
)

Pour observer l’effet de notre intervention, nous combinerons les sorties du modèle de référence et celles de l’intervention dans un seul tableau de données, puis nous tracerons les résultats. Ici, nous représentons le nombre total d’individus infectieux dans tous les groupes d’âge en utilisant les données suivantes ggplot2::stat_summary() fonction :

R

# créer une colonne intervention_type pour le graphique
output_school$intervention_type <- "school closure"
output_baseline$intervention_type <- "baseline"
output <- base::rbind(output_school, output_baseline)

output %>%
  filter(compartment == "infectious") %>%
  ggplot() +
  aes(
    x = time,
    y = value,
    color = intervention_type,
    linetype = intervention_type
  ) +
  stat_summary(
    fun = "sum",
    geom = "line",
    linewidth = 1
  ) +
  scale_y_continuous(
    labels = scales::comma
  ) +
  geom_vline(
    xintercept = c(
      close_schools$time_begin,
      close_schools$time_end
    ),
    linetype = 2
  ) +
  theme_bw() +
  labs(
    x = "Simulation time (days)",
    y = "Individuals"
  )

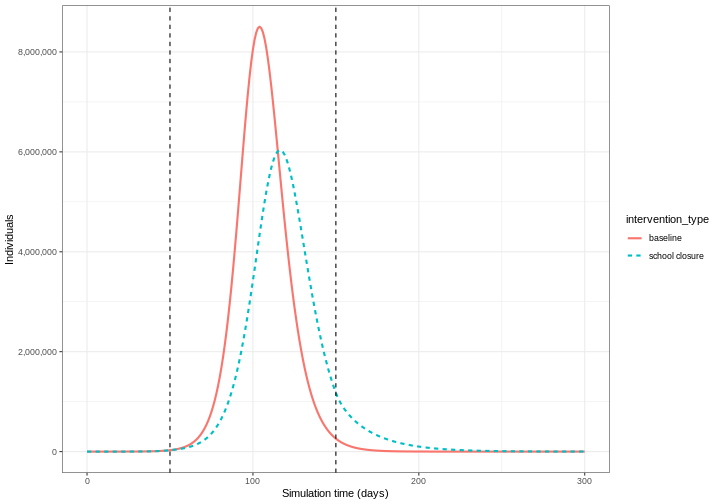
Nous pouvons constater qu’avec l’intervention en place, l’infection se propage toujours dans la population et que l’accumulation de l’immunité contribue à l’éventuel pic et déclin. Toutefois, le nombre maximal de personnes infectées est inférieur (ligne pointillée verte) à la ligne de base sans intervention (ligne continue rouge), ce qui montre une réduction du nombre absolu de cas.

Effet du port du masque sur la propagation de COVID-19

Nous pouvons également modéliser l’effet d’autres IPN en réduisant la valeur des paramètres pertinents. Par exemple, étudier l’effet du port du masque sur le nombre de personnes infectées par COVID-19 au fil du temps.

Nous nous attendons à ce que le port du masque réduise la contagiosité d’un individu, sur la base de nombreuses études montrant l’efficacité des masques dans la réduction de la transmission. Comme nous utilisons un modèle basé sur la population, nous ne pouvons pas modifier les comportements individuels et nous supposons donc que le taux de transmission \(\beta\) est réduit par une proportion due au port du masque dans la population. Nous spécifions cette proportion, \(\theta\) comme le produit de la proportion de personnes portant un masque multiplié par la proportion de réduction du taux de transmission (adapté de Li et al. 2020).

Nous créons un objet d’intervention avec type = "rate" et reduction = 0.161. En utilisant des paramètres adaptés de Li et al. 2020 nous avons la proportion de personnes portant des masques = couverture \(\times\) disponibilité = \(0.54 \times 0.525 = 0.2835\) et la proportion de réduction du taux de transmission = \(0.575\). Par conséquent, \(\theta = 0.2835 \times 0.575 = 0.163\). Nous supposons que l’obligation de porter un masque commence au 40e jour et reste en vigueur pendant 200 jours.

R

mask_mandate <- epidemics::intervention(
  name = "mask mandate",
  type = "rate",
  time_begin = 40,
  time_end = 40 + 200,
  reduction = 0.163
)

Pour mettre en œuvre cette intervention sur le taux de transmission \(\beta\) nous spécifions intervention = list(transmission_rate = mask_mandate).

R

output_masks <- epidemics::model_default(
  # population
  population = uk_population,
  # taux
  transmission_rate = transmission_rate,
  infectiousness_rate = infectiousness_rate,
  recovery_rate = recovery_rate,
  # intervention
  intervention = list(transmission_rate = mask_mandate),
  # temps
  time_end = 300, increment = 1.0
)

R

# créer une colonne intervention_type pour le graphique
output_masks$intervention_type <- "mask mandate"
output_baseline$intervention_type <- "baseline"
output <- base::rbind(output_masks, output_baseline)

output %>%
  filter(compartment == "infectious") %>%
  ggplot() +
  aes(
    x = time,
    y = value,
    color = intervention_type,
    linetype = intervention_type
  ) +
  stat_summary(
    fun = "sum",
    geom = "line",
    linewidth = 1
  ) +
  scale_y_continuous(
    labels = scales::comma
  ) +
  geom_vline(
    xintercept = c(
      mask_mandate$time_begin,
      mask_mandate$time_end
    ),
    linetype = 2
  ) +
  theme_bw() +
  labs(
    x = "Simulation time (days)",
    y = "Individuals"
  )

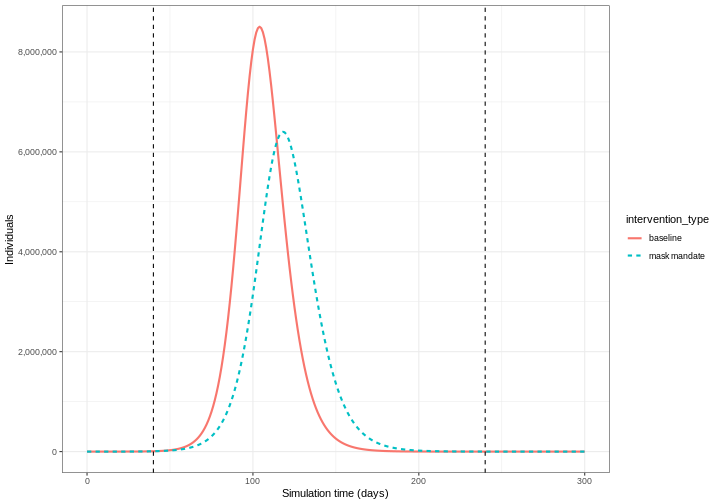
Types d’intervention

Il existe deux types d’intervention pour model_default(). Interventions sur les paramètres du modèle (transmission_rate \(\beta\), infectiousness_rate \(\sigma\) et recovery_rate \(\gamma\)) et les réductions des matrices de contact (contacts).

Pour mettre en œuvre les interventions sur les contacts et les taux dans la même simulation, elles doivent être transmises sous la forme d’une liste, par exemple, intervention = list(transmission_rate = mask_mandate, contacts = close_schools). Toutefois, si plusieurs interventions ciblent les taux de contact, elles doivent être transmises sous la forme d’une seule entrée du modèle contacts. Voir la vignette sur la modélisation des interventions qui se chevauchent pour plus de détails.

Interventions pharmaceutiques

Les interventions pharmaceutiques (IP) sont des mesures telles que les programmes de vaccination et de traitement de masse. Dans la section précédente, nous avons intégré les interventions dans le modèle en réduisant les valeurs des paramètres pendant une période spécifique de la fenêtre temporelle au cours de laquelle ces interventions doivent avoir lieu. Dans le cas de la vaccination, nous supposons qu’après l’intervention, les individus ne sont plus sensibles et doivent être classés dans un état pathologique différent. Par conséquent, nous spécifions le taux auquel les individus sont vaccinés et suivons le nombre d’individus vaccinés au fil du temps.

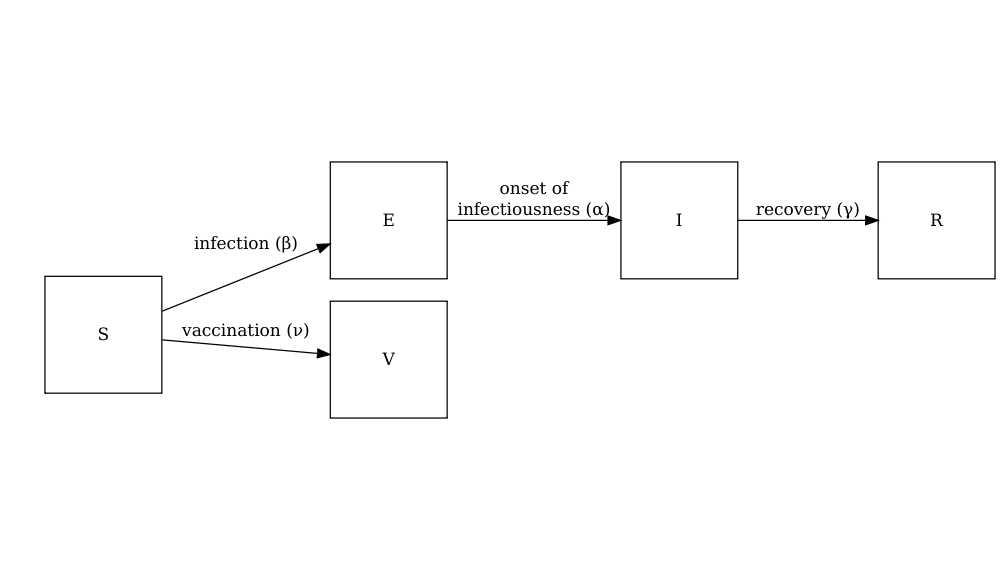
Le diagramme ci-dessous montre le modèle SEIRV mis en œuvre à l’aide de model_default() où les individus sensibles sont vaccinés et passent ensuite à l’étape de la vaccination. \(V\) classe.

Les équations décrivant ce modèle sont les suivantes :

\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j -\nu_{t} S_i \\ \frac{dE_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \alpha E_i \\ \frac{dI_i}{dt} &= \alpha E_i - \gamma I_i \\ \frac{dR_i}{dt} &=\gamma I_i \\ \frac{dV_i}{dt} & =\nu_{i,t} S_i\\ \end{aligned} \]

Les individus de la tranche d’âge (\(i\)) à un moment spécifique (\(t\)) sont vaccinés à un taux (\(\nu_{i,t}\)). Les autres composantes SEIR de ces équations sont décrites dans le tutoriel simuler la transmission.

Pour étudier l’effet de la vaccination, nous devons créer un objet de vaccination que nous transmettrons en tant qu’entrée à la fonction model_default() qui comprend le taux de vaccination pour chaque tranche d’âge nu et les dates de début et de fin du programme de vaccination pour chaque tranche d’âge (time_begin et time_end).

Nous supposerons ici que tous les groupes d’âge sont vaccinés au même taux (0,01) et que le programme de vaccination commence au 40e jour et se poursuit pendant 150 jours.

R

# prépare un object de vaccination
vaccinate <- epidemics::vaccination(
  name = "vaccinate all",
  time_begin = matrix(40, nrow(cm_matrix)),
  time_end = matrix(40 + 150, nrow(cm_matrix)),
  nu = matrix(c(0.01, 0.01, 0.01))
)

Nous passons notre objet de vaccination dans le modèle en utilisant l’argument vaccination = vaccinate:

R

output_vaccinate <- epidemics::model_default(
  # population
  population = uk_population,
  # rate
  transmission_rate = transmission_rate,
  infectiousness_rate = infectiousness_rate,
  recovery_rate = recovery_rate,
  # intervention
  vaccination = vaccinate,
  # time
  time_end = 300, increment = 1.0
)

Comparez les interventions

Représentez sur un même graphique les trois interventions (vaccination, fermeture des écoles et obligation de porter un masque) et la simulation de référence sans intervention. Quelle intervention réduit le plus le nombre maximal de personnes infectieuses ?

Montrer la solution

R

# create intervention_type column for plotting
output_vaccinate$intervention_type <- "vaccination"
output <- base::rbind(
  output_school,
  output_masks,
  output_vaccinate,
  output_baseline
)

output %>%
  filter(compartment == "infectious") %>%
  ggplot() +
  aes(
    x = time,
    y = value,
    color = intervention_type,
    linetype = intervention_type
  ) +
  stat_summary(
    fun = "sum",
    geom = "line",
    linewidth = 1
  ) +
  scale_y_continuous(
    labels = scales::comma
  ) +
  theme_bw() +
  labs(
    x = "Simulation time (days)",
    y = "Individuals"
  )

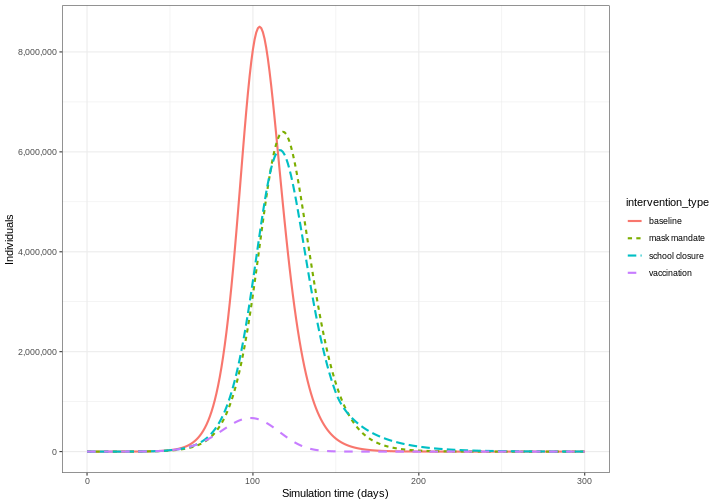
Le graphique montre que le pic du nombre total d’individus infectieux en cas de vaccination est beaucoup plus faible que lors des fermetures d’écoles et des interventions avec port du masque.

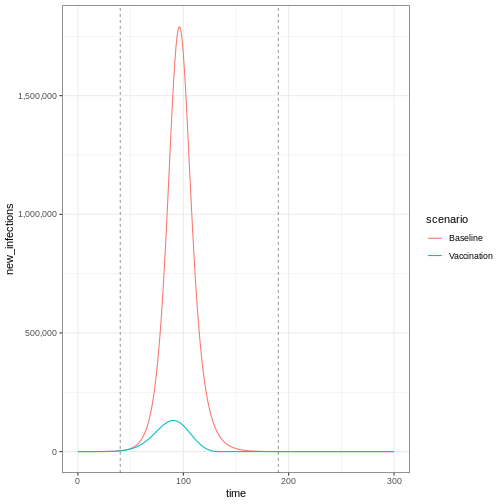
Enfin, si vous souhaitez représenter graphiquement les nouvelles infections à partir d’un object de epidemics::model_default() qui inclut la vaccination, vous devez ajouter un argument à epidemics::new_infections() : définissez exclude_compartments = "vaccinated" pour indiquer à la fonction que les personnes passant de « susceptibles » à « vaccinées » ne sont pas infectées. Cela garantit que les personnes vaccinées ne seront pas comptées comme des infections.

Afficher les détails

Notez que si nous ajoutons by_group = FALSE dans epidemics::new_infections(), nous obtenons un résumé des nouvelles infections dans la population.

R

infections_baseline <- epidemics::new_infections(
  data = output_baseline,
  exclude_compartments = "vaccinated", # if vaccination
  by_group = FALSE
)

infections_intervention <- epidemics::new_infections(
  data = output_vaccinate,
  exclude_compartments = "vaccinated", # if vaccination
  by_group = FALSE
)

# Assigner les noms des scénarios
infections_baseline$scenario <- "Baseline"
infections_intervention$scenario <- "Vaccination"

# Combiner les données des deux scénarios
infections_baseline_interv <- dplyr::bind_rows(
  infections_baseline,
  infections_intervention
)

infections_baseline_interv %>%
  ggplot(aes(x = time, y = new_infections, colour = scenario)) +
  geom_line() +
  geom_vline(
    xintercept = c(vaccinate$time_begin, vaccinate$time_end),
    linetype = "dashed",
    linewidth = 0.2
  ) +
  scale_y_continuous(labels = scales::comma) +
  theme_bw()

Pour obtenir un graphique stratifié par âge, conservez la valeur par défaut by_group = TRUE, puis ajoutez linetype = demography_group lors de la déclaration des variables dans ggplot(aes(...)).

Résumé

Différents types d’intervention peuvent être mis en œuvre à l’aide de la modélisation mathématique. La modélisation des interventions nécessite des hypothèses sur les paramètres du modèle qui sont affectés (par exemple, les matrices de contact, le taux de transmission), ainsi que sur l’ampleur et le moment de la simulation d’une épidémie.

L’étape suivante consiste à quantifier l’effet d’une intervention. Si vous souhaitez apprendre à comparer les interventions, veuillez suivre le tutoriel suivant Comparer les résultats des interventions en matière de santé publique.

Points clés

L’effet des NPI peut être modélisé comme une réduction des taux de contact entre les groupes d’âge ou une réduction du taux de transmission de l’infection.
La vaccination peut être modélisée en supposant que les individus passent à un état pathologique différent \(V\).

Références

Davies, N. G., Klepac, P., Liu, Y., Prem, K., Jit, M. et Eggo, R. M. (2020). Age-dependent effects in the transmission and control of COVID-19 epidemics (Effets dépendants de l’âge dans la transmission et le contrôle des épidémies de COVID-19). Nature Medicine, 26(8), 1205-1211. https://doi.org/10.1016/S2468-2667\(20\)30133-X
Li, Y., Liang, M., Gao, L., Ahmed, M. A., Uy, J. P., Cheng, C., … & Sun, C. (2020). Masques de protection pour prévenir la transmission du COVID-19 : A systematic review and meta-analysis. American Journal of Infection Control, 49(7), 900-906. https://doi.org/10.1371/journal.pone.0237691
Mossong, J., Hens, N., Jit, M., Beutels, P., Auranen, K., Mikolajczyk, R., … & Edmunds, W. J. (2008). Social contacts and mixing patterns relevant to the spread of infectious diseases (contacts sociaux et modèles de mélange pertinents pour la propagation des maladies infectieuses). PLoS medicine, 5(3), e74. https://doi.org/10.1371/journal.pmed.0050074