Comparer les résultats des interventions de santé publique
Dernière mise à jour le 2025-11-23 | Modifier cette page
Vue d'ensemble
Questions
- Comment puis-je quantifier l’effet d’une intervention ?
Objectifs
- Comparez les scénarios d’intervention
Pré-requis
- Compléter les tutoriels Simuler la transmission et Modélisation des interventions
Les apprenants doivent se familiariser avec les dépendances conceptuelles suivantes avant de travailler sur ce didacticiel :
Réponse à l’épidémie : Types d’intervention.
Introduction
Dans ce tutoriel, nous allons comparer des scénarios d’intervention les uns par rapport aux autres. Pour quantifier l’effet d’une intervention, nous devons comparer notre scénario d’intervention à un scénario contrefactuel (de référence). Le scénario contrefactuel est le scénario dans lequel rien ne change, souvent appelé “scénario du statu quo”. Le scénario contrefactuel peut consister de :
- Aucune intervention, ou
- Interventions existantes (si nous étudions l’impact potentiel d’une intervention supplémentaire)
Nous devons également définir nos résultat d’intérêt afin d’établir des comparaisons entre les scénarios d’intervention et les scénarios contrefactuels. Le résultat d’intérêt peut être :
- Les résultats directs du modèle (par exemple, le nombre d’infections, d’hospitalisations)
- Mesures épidémiologiques (par exemple, période de pic de l’épidémie, sa taille finale)
- Mesures de l’impact sur la santé (par exemple, années de vie ajustée par la qualité [AVAQs] ou les années de vie corrigées de l’incapacité [AVCI] )
- Mesures économiques (par exemple, coûts des soins de santé, pertes de productivité)
Dans ce tutoriel, nous allons apprendre à utiliser le package
{epidemics} dans R pour comparer l’effet de différentes
interventions sur des trajectoires d’épidémies simulées. Nous
utiliserons socialmixr pour les données sur les contacts
sociaux et tidyverse (y compris dplyr,
ggplot2 et le tuyau %>%) pour la
manipulation et la visualisation des données.
R
library(epidemics)
library(socialmixr)
library(tidyverse)
Visualiser l’effet des interventions
Pour comparer le scénario de base aux scénarios d’intervention, nous pouvons visualiser le résultat qui nous intéresse. Ce résultat peut être simplement la sortie du modèle ou une mesure agrégée de la sortie du modèle.
Si nous voulons étudier le changementdu pic épidémique après l’application d’une intervention, nous pouvons tracer les trajectoires du modèle dans le temps :
R
output_baseline <- epidemics::model_default(
population = uk_population,
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0
)
output_school <- epidemics::model_default(
# population
population = uk_population,
# rate
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
intervention = list(contacts = close_schools),
# time
time_end = 300, increment = 1.0
)
# create intervention_type column for plotting
output_school$intervention_type <- "school closure"
output_baseline$intervention_type <- "baseline"
output <- rbind(output_school, output_baseline)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
close_schools$time_begin,
close_schools$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
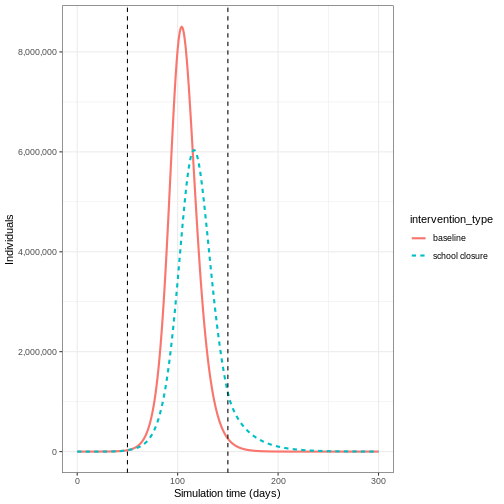
Si nous voulons quantifier l’impact de l’intervention sur les résultats du modèle dans le temps, nous pouvons considérer le nombre cumulé de personnes infectieuses dans le scénario de base par rapport au scénario d’intervention :
R
output %>%
filter(compartment == "infectious") %>%
group_by(time, intervention_type) %>%
summarise(value_total = sum(value)) %>%
group_by(intervention_type) %>%
mutate(cum_value = cumsum(value_total)) %>%
ggplot() +
geom_line(
aes(
x = time,
y = cum_value,
color = intervention_type,
linetype = intervention_type
),
linewidth = 1.2
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
close_schools$time_begin,
close_schools$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Cumulative number of infectious individuals"
)
SORTIE
`summarise()` has grouped output by 'time'. You can override using the
`.groups` argument.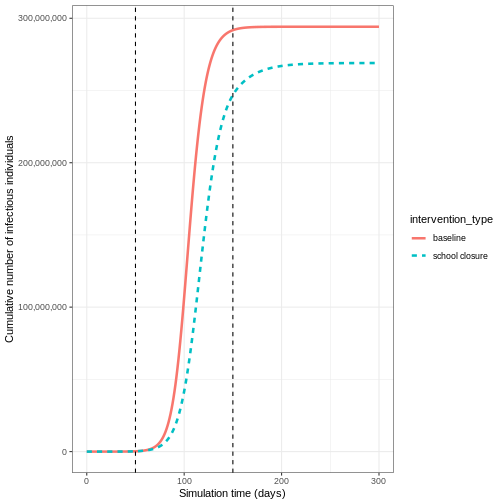
Modèle Vacamole
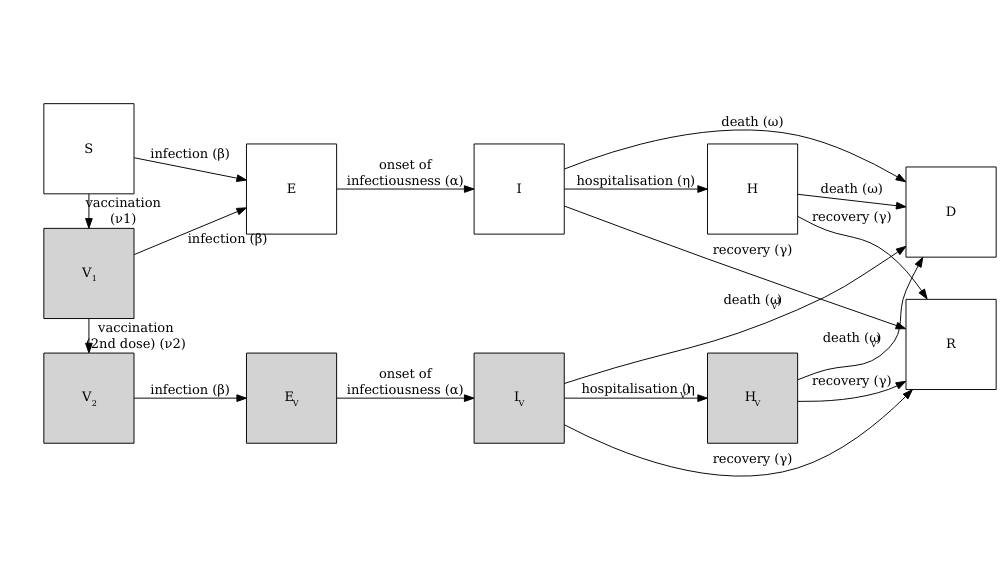
Le modèle Vacamole est un modèle déterministe basé sur un système d’équations différentielles ordinaires (ODE) développé par Ainslie et al. (2022) pour décrire l’effet de la vaccination sur la dynamique de COVID-19. Le modèle se compose de 11 compartiments, dans lesquels les individus sont classés comme suit :
- Susceptibles (\(S\))
- Partiellement vacciné (\(V_1\))
- Totalement vacciné (\(V_2\))
- Exposé (\(E\)) et exposé alors qu’ils sontvacciné (\(E_V\))
- Infectieux (\(I\)) et infectieux en cas de vaccination (\(I_V\))
- Hospitalisé (\(H\)) et hospitalisé alors qu’ils étaient vacciné (\(H_V\))
- Mort (\(D\))
- Récupéré (\(R\))
Le schéma ci-dessous décrit le flux d’individus à travers les différents compartiments.
Exécution d’un scénario contrefactuel à l’aide du modèle Vacamole
- Exécutez le modèle avec les valeurs par défaut de paramètres pour la population britannique en supposant que :
- un individu sur un million (0,0001 %) est contagieux (et non vacciné) au début de la simulation.
- La matrice des contacts pour le Royaume-Uni comporte les tranches
d’âge suivantes :
- 0-20 ans
- 20-40 ans
- 40 ans et plus
Pour les scénarios suivants :
- Scénario de base : Programme de vaccination à deux doses
- La dose 1 (taux de vaccination 0,01) commence à partir du jour 30.
- La dose 2 (taux de vaccination 0,01) est administrée à partir du 60e jour.
- Les deux programmes durent 300 jours
- Intervention : Mandat de masque
- Commence à partir du jour 60
- Durée de 100 jours
- Réduit le taux de transmission de 16,3 % (d’après des études empiriques sur l’efficacité des masques)
Il n’y a pas de programme de vaccination en place
- À l’aide du résultat, tracez le nombre cumulé de décès au fil du temps.
Nous pouvons exécuter le modèle Vacamole avec les valeurs par défaut de paramètres en spécifiant simplement l’objet de la population et le nombre de pas de temps pour lesquels le modèle doit être exécuté :
R
output <- epidemics::model_vacamole(
population = uk_population,
time_end = 300
)
- Exécutez le modèle
R
polymod <- socialmixr::polymod
contact_data <- socialmixr::contact_matrix(
survey = polymod,
countries = "United Kingdom",
age.limits = c(0, 20, 40),
symmetric = TRUE
)
SORTIE
Removing participants that have contacts without age information. To change this behaviour, set the 'missing.contact.age' optionR
# prepare contact matrix
contact_matrix <- t(contact_data$matrix)
# extract demography vector
demography_vector <- contact_data$demography$population
names(demography_vector) <- rownames(contact_matrix)
# prepare initial conditions
initial_i <- 1e-6
initial_conditions_vacamole <- c(
S = 1 - initial_i,
V1 = 0, V2 = 0,
E = 0, EV = 0,
I = initial_i, IV = 0,
H = 0, HV = 0, D = 0, R = 0
)
initial_conditions_vacamole <- rbind(
initial_conditions_vacamole,
initial_conditions_vacamole,
initial_conditions_vacamole
)
rownames(initial_conditions_vacamole) <- rownames(contact_matrix)
# prepare population object
uk_population_vacamole <- epidemics::population(
name = "UK",
contact_matrix = contact_matrix,
demography_vector = demography_vector,
initial_conditions = initial_conditions_vacamole
)
# prepare two vaccination objects
# dose 1 vaccination
dose_1 <- epidemics::vaccination(
name = "two-dose vaccination", # name given to first dose
nu = matrix(0.01, nrow = 3),
time_begin = matrix(30, nrow = 3),
time_end = matrix(300, nrow = 3)
)
# prepare the second dose with a 30 day interval in start date
dose_2 <- epidemics::vaccination(
name = "two-dose vaccination", # name given to first dose
nu = matrix(0.01, nrow = 3),
time_begin = matrix(30 + 30, nrow = 3),
time_end = matrix(300, nrow = 3)
)
# use `c()` to combine the two doses
double_vaccination <- c(dose_1, dose_2)
# run baseline model
output_baseline_vc <- epidemics::model_vacamole(
population = uk_population_vacamole,
vaccination = double_vaccination,
time_end = 300
)
# create mask intervention
mask_mandate <- epidemics::intervention(
name = "mask mandate",
type = "rate",
time_begin = 60,
time_end = 60 + 100,
reduction = 0.163
)
# run intervention model
output_intervention_vc <- epidemics::model_vacamole(
population = uk_population_vacamole,
vaccination = double_vaccination,
intervention = list(
transmission_rate = mask_mandate
),
time_end = 300
)
- Tracez le nombre cumulé de décès au fil du temps
R
# create intervention_type column for plotting
output_intervention_vc$intervention_type <- "mask mandate"
output_baseline_vc$intervention_type <- "baseline"
output_vacamole <- rbind(output_intervention_vc, output_baseline_vc)
output_vacamole %>%
filter(compartment == "dead") %>%
group_by(time, intervention_type) %>%
summarise(value_total = sum(value)) %>%
group_by(intervention_type) %>%
mutate(cum_value = cumsum(value_total)) %>%
ggplot() +
geom_line(
aes(
x = time,
y = cum_value,
color = intervention_type,
linetype = intervention_type
),
linewidth = 1.2
) +
scale_y_continuous(
labels = scales::comma
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Cumulative number of deaths"
)
SORTIE
`summarise()` has grouped output by 'time'. You can override using the
`.groups` argument.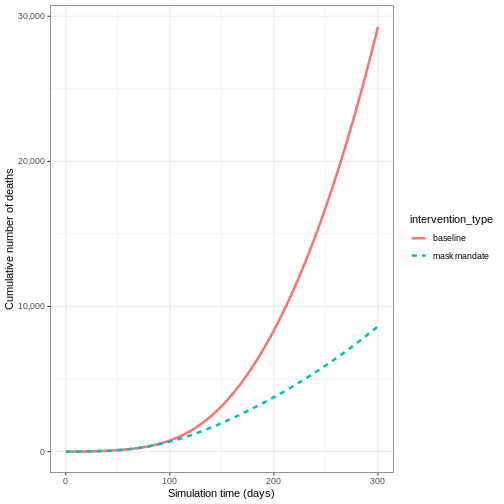
Calcul des résultats évités
Si les visualisations sont utiles pour comparer les scénarios d’intervention dans le temps, nous avons également besoin des mesures pour quantifier l’impact de l’intervention. Une de ces mesures est le nombre d’infections évitées, qui nous aide à comprendre la différence entre les scénarios d’intervention.
Le package {epidemics} de R fournit l’outil
outcomes_averted() pour calculer les infections évitées en
tenant compte de l’incertitude des paramètres. Étendons notre exemple
COVID-19 de Modélisation des
interventions pour tenir compte de l’incertitude concernant le
nombre de reproduction de base (\(R_0\)).
R
# time periods
preinfectious_period <- 4.0
infectious_period <- 5.5
# specify the mean and standard deviation of R0
r_estimate_mean <- 2.7
r_estimate_sd <- 0.05
# generate 100 R samples
r_samples <- withr::with_seed(
seed = 1,
rnorm(
n = 100, mean = r_estimate_mean, sd = r_estimate_sd
)
)
beta <- r_samples / infectious_period
# rates
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
Nous utilisons ces valeurs de paramètres en même temps que la structure de la population et la matrice de contact utilisées dans le Modélisation des interventions afin d’exécuter le modèle pour le scénario de base :
R
output_baseline <- epidemics::model_default(
population = uk_population,
transmission_rate = beta,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0
)
Ensuite, nous créons une liste de toutes les interventions que nous voulons inclure dans notre comparaison. Nous définissons nos scénarios comme suit :
- scénario 1 : fermer les écoles
- scénario 2 : mandat de masque
- scénario 3 : fermeture des écoles et mandat de masque.
Dans R, nous spécifions ceci comme :
R
intervention_scenarios <- list(
scenario_1 = list(
contacts = close_schools
),
scenario_2 = list(
transmission_rate = mask_mandate
),
scenario_3 = list(
contacts = close_schools,
transmission_rate = mask_mandate
)
)
Nous utilisons cette liste comme entrée pour
intervention dans model_default
R
output <- epidemics::model_default(
uk_population,
transmission_rate = beta,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0,
intervention = intervention_scenarios
)
head(output)
SORTIE
transmission_rate infectiousness_rate recovery_rate time_end param_set
<num> <num> <num> <num> <int>
1: 0.4852141 0.25 0.1818182 300 1
2: 0.4852141 0.25 0.1818182 300 1
3: 0.4852141 0.25 0.1818182 300 1
4: 0.4925786 0.25 0.1818182 300 2
5: 0.4925786 0.25 0.1818182 300 2
6: 0.4925786 0.25 0.1818182 300 2
population intervention vaccination time_dependence increment scenario
<list> <list> <list> <list> <num> <int>
1: <population[4]> <list[1]> [NULL] <list[1]> 1 1
2: <population[4]> <list[1]> [NULL] <list[1]> 1 2
3: <population[4]> <list[2]> [NULL] <list[1]> 1 3
4: <population[4]> <list[1]> [NULL] <list[1]> 1 1
5: <population[4]> <list[1]> [NULL] <list[1]> 1 2
6: <population[4]> <list[2]> [NULL] <list[1]> 1 3
data
<list>
1: <data.table[4515x4]>
2: <data.table[4515x4]>
3: <data.table[4515x4]>
4: <data.table[4515x4]>
5: <data.table[4515x4]>
6: <data.table[4515x4]>Maintenant que nous avons des résultats de notre modèle pour tous nos scénarios, nous voulons comparer les résultats des interventions à notre base de référence.
Nous pouvons le faire en utilisant outcomes_averted()
dans {epidemics}. Cette fonction calcule la taille finale
de l’épidémie pour chaque scénario, puis le nombre d’infections évitées
dans chaque scénario par rapport à la ligne de base. Pour utiliser cette
fonction, il faut spécifier :
- le résultat du scénario de base
- les résultats des scénario(s) d’intervention.
R
intervention_effect <- epidemics::outcomes_averted(
baseline = output_baseline, scenarios = output
)
intervention_effect
SORTIE
scenario demography_group averted_median averted_lower averted_upper
<int> <char> <num> <num> <num>
1: 1 65+ 405810.5 383340.3 414044.8
2: 1 [0,15) 2890964.4 2577490.7 3082420.9
3: 1 [15,65) 1288482.1 1257862.4 1290841.4
4: 2 65+ 900819.9 882242.1 912790.7
5: 2 [0,15) 517742.8 478431.1 558631.8
6: 2 [15,65) 2413423.7 2259624.9 2566010.9
7: 3 65+ 1004123.7 864726.7 1100018.0
8: 3 [0,15) 1974788.9 1494800.2 2415088.5
9: 3 [15,65) 2908140.6 2546313.2 3129329.3Le résultat nous donne le nombre d’infections évitées dans chaque
scénario par rapport à la ligne de base. Pour obtenir le nombre total
d’infections évitées, nous spécifions by_group = FALSE:
R
intervention_effect <- epidemics::outcomes_averted(
baseline = output_baseline, scenarios = output,
by_group = FALSE
)
intervention_effect
SORTIE
scenario averted_median averted_lower averted_upper
<int> <num> <num> <num>
1: 1 4587505 4220698 4770734
2: 2 3831986 3620298 4037433
3: 3 5887053 4905840 6644436Vignettes de paquets
Nous vous recommandons de lire la vignette sur Modélisation des réponses à une épidémie stochastique de virus Ebola pour utiliser un modèle compartimental stochastique à temps discret d’Ebola utilisé lors de l’épidémie de MVE de 2014 en Afrique de l’Ouest.
Défi : Analyse de l’épidémie d’Ebola
Vous avez été chargé d’étudier l’impact potentiel d’une intervention
sur une épidémie d’Ebola en Guinée (par exemple, une réduction des
contacts à haute risque avec les cas). En utilisant
model_ebola() et les informations détaillées ci-dessous,
trouvez le nombre d’infections évitées lorsque :
- une intervention est appliquée pour réduire le taux de transmission de 50 % à partir du jour 60 et,
- une intervention est appliquée pour réduire la transmission de 10 % à partir du jour 30.
Pour les deux interventions, nous supposons qu’il existe une certaine incertitude quant au taux de transmission de base. Nous capturons cette incertitude en la tirant d’une distribution normale avec une moyenne = 1,1 / 12 (c.-à-d. \(R_0=1.1\) et la période infectieuse = 12 jours) et un écart-type = 0,01.
Remarque : selon le nombre de réplicats utilisés, l’exécution de cette simulation peut prendre plusieurs minutes.
- Taille de la population : 14 millions
- Nombre initial d’individus exposés : 10
- Nombre initial d’individus infectieuses : 5
- Durée de la simulation : 120 jours
- Valeurs des paramètres :
-
\(R_0\) (
r0) = 1.1, -
\(p^I\)
(
infectious_period) = 12, -
\(p^E\)
(
preinfectious_period) = 5, - \(k^E=k^I = 2\),
-
\(1-p_{hosp}\)
(
prop_community) = 0.9, -
\(p_{ETU}\) (
etu_risk) = 0.7, -
\(p_{funeral}\)
(
funeral_risk) = 0.5
-
\(R_0\) (
R
population_size <- 14e6
E0 <- 10
I0 <- 5
# prepare initial conditions as proportions
initial_conditions <- c(
S = population_size - (E0 + I0), E = E0, I = I0, H = 0, F = 0, R = 0
) / population_size
# set up population object
guinea_population <- population(
name = "Guinea",
contact_matrix = matrix(1), # note dummy value
demography_vector = population_size, # 14 million, no age groups
initial_conditions = matrix(
initial_conditions,
nrow = 1
)
)
# generate 100 beta samples
beta <- withr::with_seed(
seed = 1,
rnorm(
n = 100, mean = 1.1 / 12, sd = 0.01
)
)
# run the baseline
output_baseline <- epidemics::model_ebola(
population = guinea_population,
transmission_rate = beta,
infectiousness_rate = 2.0 / 5,
removal_rate = 2.0 / 12,
prop_community = 0.9,
etu_risk = 0.7,
funeral_risk = 0.5,
time_end = 100,
replicates = 100 # replicates argument
)
# create intervention objects
reduce_transmission_1 <- epidemics::intervention(
type = "rate",
time_begin = 60, time_end = 100, reduction = 0.5
)
reduce_transmission_2 <- epidemics::intervention(
type = "rate",
time_begin = 30, time_end = 100, reduction = 0.1
)
# create intervention list
intervention_scenarios <- list(
scenario_1 = list(
transmission_rate = reduce_transmission_1
),
scenario_2 = list(
transmission_rate = reduce_transmission_2
)
)
# run model
output_intervention <- epidemics::model_ebola(
population = guinea_population,
transmission_rate = beta,
infectiousness_rate = 2.0 / 5,
removal_rate = 2.0 / 12,
prop_community = 0.9,
etu_risk = 0.7,
funeral_risk = 0.5,
time_end = 100,
replicates = 100, # replicates argument,
intervention = intervention_scenarios
)
AVERTISSEMENT
Warning: Running 2 scenarios and 100 parameter sets with 100 replicates each, for a
total of 20000 model runs.R
# calculate outcomes averted
intervention_effect <- epidemics::outcomes_averted(
baseline = output_baseline, scenarios = output_intervention,
by_group = FALSE
)
intervention_effect
SORTIE
scenario averted_median averted_lower averted_upper
<int> <num> <num> <num>
1: 1 31 1 112
2: 2 20 -22 105Note : Le nombre d’infections évitées peut être négatif. Cela est dû à la variation stochastique des trajectoires de la maladie pour un taux de transmission donné, qui peut entraîner une épidémie de taille différente.
Points clés
- Un scénario contrefactuel (de référence) doit être clairement défini pour permettre des comparaisons significatives.
- Les scénarios peuvent être comparés à l’aide de visualisations et de mesures quantitatives.
- La fonction outcomes_averted() permet de quantifier les effets des interventions.
- L’incertitude des paramètres doit être prise en compte dans l’analyse des interventions.
