Modelling interventions
Last updated on 2026-02-05 | Edit this page
Overview
Questions
- How do I investigate the effect of interventions on disease trajectories?
Objectives
- Add pharmaceutical and non-pharmaceutical interventions to
{epidemics}model
Prerequisite
- Complete tutorial on Simulating transmission.
Learners should also familiarise themselves with following concept dependencies before working through this tutorial:
Outbreak response : Intervention types.
R packages installed: {epidemics},
socialmixr, scales,
tidyverse.
Install packages if their are not already installed
R
if (!base::require("pak")) install.packages("pak")
pak::pak(c("epiverse-trace/epidemics", "socialmixr", "scales", "tidyverse"))
If you have any error message, go to the main setup page.
Introduction
Mathematical models can be used to generate trajectories of disease spread under the implementation of interventions at different stages of an outbreak. These trajectories can be used to make decisions on what interventions could be implemented to slow down the spread of diseases.
Interventions are usually incorporated into mathematical models via manipulating values of relevant parameters, e.g., reduce transmission, or via introducing a new disease state, e.g., vaccinated class where we assume that individuals who belong to this class are no longer susceptible to infection.
In this tutorial, we will learn how to use {epidemics}
to model interventions and access to social contact data with
socialmixr. We’ll use dplyr,
ggplot2 and the pipe %>% to connect some
of their functions, so let’s also call tidyverse:
R
library(epidemics)
library(socialmixr)
library(tidyverse)
Baseline model
We will investigate the effect of interventions on a COVID-19
outbreak using an SEIR model (model_default() in the R
package {epidemics}). To be able to see the effect of our
intervention, we will run a baseline variant of the model, i.e, without
intervention.
The SEIR model divides the population into four compartments: Susceptible (S), Exposed (E), Infectious (I), and Recovered (R). We will set the following parameters for our model: \(R_0 = 2.7\) (basic reproduction number), latent period or pre-infectious period \(= 4\) days, and the infectious period \(= 5.5\) days (parameters adapted from Davies et al. (2020)). We adopt a contact matrix with age bins 0-18, 18-65, 65 years and older using socialmixr, and assume that one in every 1 million individuals in each age group is infectious at the start of the epidemic.
R
# load survey data
survey_data <- socialmixr::polymod
# generate contact matrix
cm_results <- socialmixr::contact_matrix(
survey = survey_data,
countries = "United Kingdom",
age_limits = c(0, 15, 65),
symmetric = TRUE
)
# transpose contact matrix
cm_matrix <- t(cm_results$matrix)
# prepare the demography vector
demography_vector <- cm_results$demography$population
names(demography_vector) <- rownames(cm_matrix)
# initial conditions: one in every 1 million is infected
initial_i <- 1e-6
initial_conditions <- c(
S = 1 - initial_i,
E = 0,
I = initial_i,
R = 0,
V = 0
)
# build for all age groups
initial_conditions <- base::rbind(
initial_conditions,
initial_conditions,
initial_conditions
)
rownames(initial_conditions) <- rownames(cm_matrix)
# prepare the population to model as affected by the epidemic
uk_population <- epidemics::population(
name = "UK",
contact_matrix = cm_matrix,
demography_vector = demography_vector,
initial_conditions = initial_conditions
)
We run the model with an infectiousness rate \(= 1/4\), a recovery rate \(= 1/5.5\), and a transmission rate \(= 2.7/5.5\) (remember that transmission rate = \(R_0\)* recovery rate) as follows:
R
# time periods
preinfectious_period <- 4.0
infectious_period <- 5.5
basic_reproduction <- 2.7
# rates
infectiousness_rate <- 1.0 / preinfectious_period
recovery_rate <- 1.0 / infectious_period
transmission_rate <- basic_reproduction * recovery_rate
# run baseline simulation with no intervention
output_baseline <- epidemics::model_default(
population = uk_population,
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
time_end = 300, increment = 1.0
)
Non-pharmaceutical interventions
Non-pharmaceutical interventions (NPIs) are measures put in place to reduce transmission that do not include the administration of drugs or vaccinations. NPIs aim at reducing contacts between infectious and susceptible individuals by closure of schools and workplaces, and other measures to prevent the spread of the disease, for example, washing hands and wearing masks.
Effect of school closures on COVID-19 spread
The first NPI we will consider is the effect of school closures on reducing the number of individuals infected with COVID-19 over time. We assume that a school closure will reduce the frequency of contacts within and between different age groups. Based on empirical studies, we assume that school closures will reduce the contacts between school-aged children (aged 0-15) by 50%, and will cause a small reduction (1%) in the contacts between adults (aged 15 and over).
To include an intervention in our model we must create an
intervention object. The inputs are the name of the
intervention (name), the type of intervention
(contacts or rate), the start time
(time_begin), the end time (time_end) and the
reduction (reduction). The values of the reduction matrix
are specified in the same order as the age groups in the contact
matrix.
R
rownames(cm_matrix)
OUTPUT
[1] "[0,15)" "[15,65)" "65+" Therefore, we specify
reduction = matrix(c(0.5, 0.01, 0.01)). We assume that the
school closures start on day 50 and continue to be in place for a
further 100 days. Therefore our intervention object is:
R
close_schools <- epidemics::intervention(
name = "School closure",
type = "contacts",
time_begin = 50,
time_end = 50 + 100,
reduction = matrix(c(0.5, 0.01, 0.01))
)
Effect of interventions on contacts
In {epidemics}, the contact matrix is scaled down by
proportions for the period in which the intervention is in place. To
understand how the reduction is calculated within the model functions,
consider a contact matrix for two age groups with equal number of
contacts:
OUTPUT
[,1] [,2]
[1,] 1 1
[2,] 1 1If the reduction is 50% in group 1 and 10% in group 2, the contact matrix during the intervention will be:
OUTPUT
[,1] [,2]
[1,] 0.25 0.45
[2,] 0.45 0.81The contacts within group 1 are reduced by 50% twice to accommodate for a 50% reduction in outgoing and incoming contacts (\(1\times 0.5 \times 0.5 = 0.25\)). Similarly, the contacts within group 2 are reduced by 10% twice. The contacts between group 1 and group 2 are reduced by 50% and then by 10% (\(1 \times 0.5 \times 0.9= 0.45\)).
We run the model with
intervention = list(contacts = close_schools) as
follows:
R
output_school <- epidemics::model_default(
# population
population = uk_population,
# rate
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
intervention = list(contacts = close_schools),
# time
time_end = 300, increment = 1.0
)
To observe the effect of our intervention, we will combine the
baseline and intervention outputs into a single data frame and then plot
the results. Here we plot the total number of infectious individuals in
all age groups using ggplot2::stat_summary() function:
R
# create intervention_type column for plotting
output_school$intervention_type <- "school closure"
output_baseline$intervention_type <- "baseline"
output <- base::rbind(output_school, output_baseline)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
close_schools$time_begin,
close_schools$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)

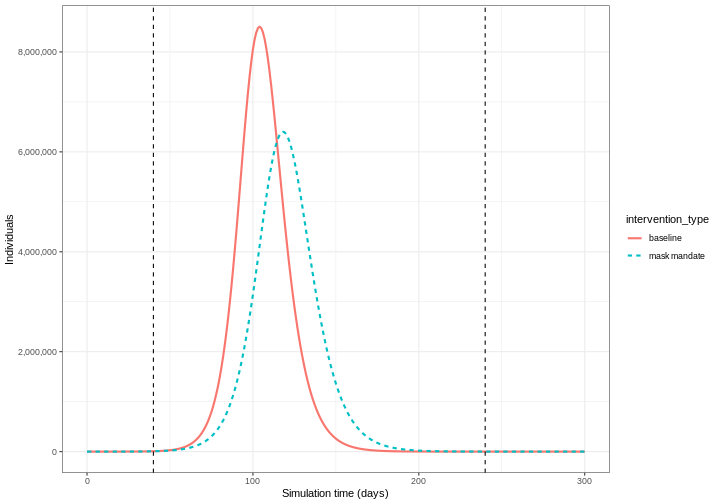
We can see that with the intervention in place, the infection still spreads through the population and hence accumulation of immunity contributes to the eventual peak-and-decline. However, the peak number of infectious individuals is smaller (green dashed line) than the baseline with no intervention in place (red solid line), showing a reduction in the absolute number of cases.
Effect of mask wearing on COVID-19 spread
We can also model the effect of other NPIs by reducing the value of the relevant parameters. For example, investigating the effect of mask wearing on the number of individuals infected with COVID-19 over time.
We expect that mask wearing will reduce an individual’s infectiousness, based on multiple studies showing the effectiveness of masks in reducing transmission. As we are using a population-based model, we cannot make changes to individual behavior and so assume that the transmission rate \(\beta\) is reduced by a proportion due to mask wearing in the population. We specify this proportion, \(\theta\) as product of the proportion wearing masks multiplied by the proportion reduction in transmission rate (adapted from Li et al. 2020).
We create an intervention object with type = "rate" and
reduction = 0.161. Using parameters adapted from Li et al. 2020
we have proportion wearing masks = coverage \(\times\) availability = \(0.54 \times 0.525 = 0.2835\) and proportion
reduction in transmission rate = \(0.575\). Therefore, \(\theta = 0.2835 \times 0.575 = 0.163\). We
assume that the mask wearing mandate starts at day 40 and continue to be
in place for 200 days.
R
mask_mandate <- epidemics::intervention(
name = "mask mandate",
type = "rate",
time_begin = 40,
time_end = 40 + 200,
reduction = 0.163
)
To implement this intervention on the transmission rate \(\beta\), we specify
intervention = list(transmission_rate = mask_mandate).
R
output_masks <- epidemics::model_default(
# population
population = uk_population,
# rate
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
intervention = list(transmission_rate = mask_mandate),
# time
time_end = 300, increment = 1.0
)
R
# create intervention_type column for plotting
output_masks$intervention_type <- "mask mandate"
output_baseline$intervention_type <- "baseline"
output <- base::rbind(output_masks, output_baseline)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
geom_vline(
xintercept = c(
mask_mandate$time_begin,
mask_mandate$time_end
),
linetype = 2
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
Intervention types
There are two intervention types for model_default().
Rate interventions on model parameters (transmission_rate
\(\beta\),
infectiousness_rate \(\sigma\) and recovery_rate
\(\gamma\)) and contact matrix
reductions (contacts).
To implement both contact and rate interventions in the same
simulation they must be passed as a list, e.g.,
intervention = list(transmission_rate = mask_mandate, contacts = close_schools).
But if there are multiple interventions that target contact rates, these
must be passed as one contacts input. See the vignette
on modelling overlapping interventions for more detail.
Pharmaceutical interventions
Pharmaceutical interventions (PIs) are measures such as vaccination and mass treatment programs. In the previous section, we integrated the interventions into the model by reducing parameter values during specific period of time window in which these intervention set to take place. In the case of vaccination, we assume that after the intervention, individuals are no longer susceptible and should be classified into a different disease state. Therefore, we specify the rate at which individuals are vaccinated and track the number of vaccinated individuals over time.
The diagram below shows the SEIRV model implemented using
model_default() where susceptible individuals are
vaccinated and then move to the \(V\)
class.
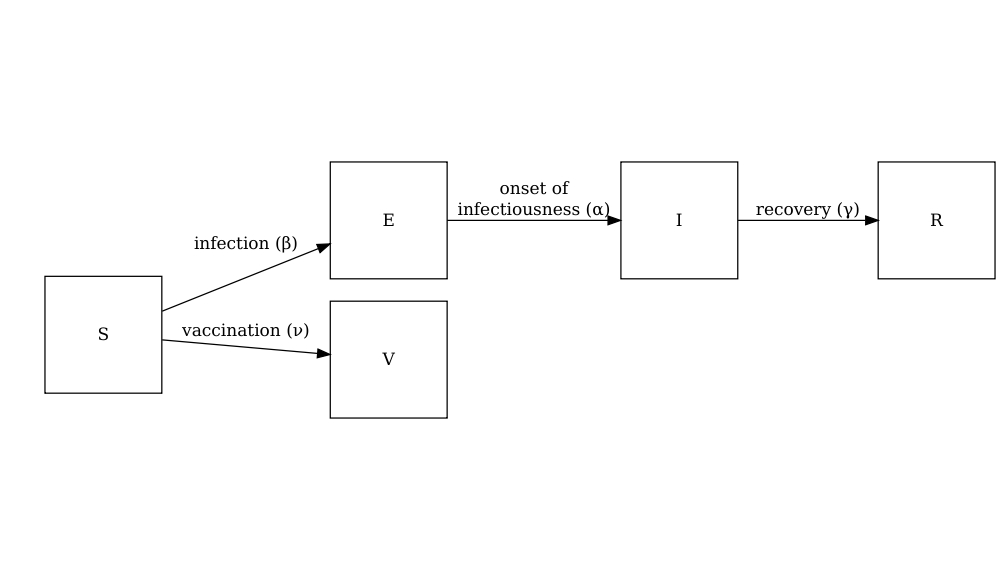
The equations describing this model are as follows:
\[ \begin{aligned} \frac{dS_i}{dt} & = - \beta S_i \sum_j C_{i,j} I_j/N_j -\nu_{t} S_i \\ \frac{dE_i}{dt} &= \beta S_i\sum_j C_{i,j} I_j/N_j - \alpha E_i \\ \frac{dI_i}{dt} &= \alpha E_i - \gamma I_i \\ \frac{dR_i}{dt} &=\gamma I_i \\ \frac{dV_i}{dt} & =\nu_{i,t} S_i\\ \end{aligned} \]
Individuals in age group (\(i\)) at specific time dependent (\(t\)) are vaccinated at rate (\(\nu_{i,t}\)). The other SEIR components of these equations are described in the tutorial simulating transmission.
To explore the effect of vaccination we need to create a vaccination
object to pass as an input into model_default() that
includes age groups specific vaccination rate nu and age
groups specific start and end times of the vaccination program
(time_begin and time_end).
Here we will assume all age groups are vaccinated at the same rate 0.01 and that the vaccination program starts on day 40 and continue to be in place for 150 days.
R
# prepare a vaccination object
vaccinate <- epidemics::vaccination(
name = "vaccinate all",
time_begin = matrix(40, nrow(cm_matrix)),
time_end = matrix(40 + 150, nrow(cm_matrix)),
nu = matrix(c(0.01, 0.01, 0.01))
)
We pass our vaccination object into the model using the argument
vaccination = vaccinate:
R
output_vaccinate <- epidemics::model_default(
# population
population = uk_population,
# rate
transmission_rate = transmission_rate,
infectiousness_rate = infectiousness_rate,
recovery_rate = recovery_rate,
# intervention
vaccination = vaccinate,
# time
time_end = 300, increment = 1.0
)
Compare interventions
Plot the three interventions vaccination, school closure and mask mandate and the baseline simulation on one plot. Which intervention reduces the peak number of infectious individuals the most?
R
# create intervention_type column for plotting
output_vaccinate$intervention_type <- "vaccination"
output <- base::rbind(
output_school,
output_masks,
output_vaccinate,
output_baseline
)
output %>%
filter(compartment == "infectious") %>%
ggplot() +
aes(
x = time,
y = value,
color = intervention_type,
linetype = intervention_type
) +
stat_summary(
fun = "sum",
geom = "line",
linewidth = 1
) +
scale_y_continuous(
labels = scales::comma
) +
theme_bw() +
labs(
x = "Simulation time (days)",
y = "Individuals"
)
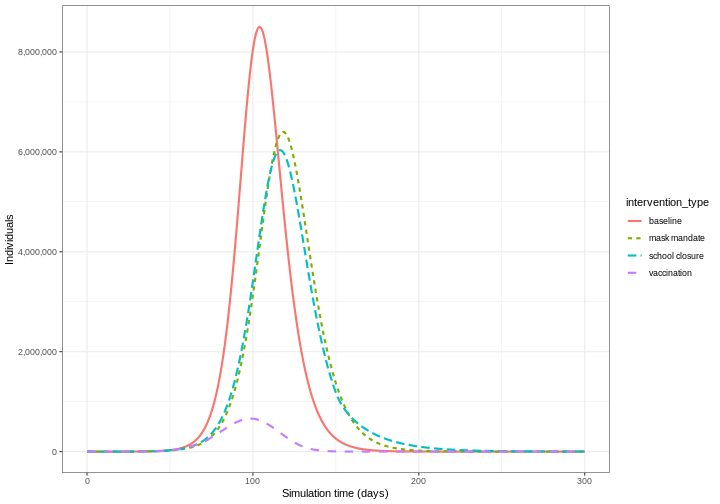
From the plot, we see that the peak number of total number of infectious individuals when vaccination is in place is much lower compared to school closures and mask-wearing interventions.
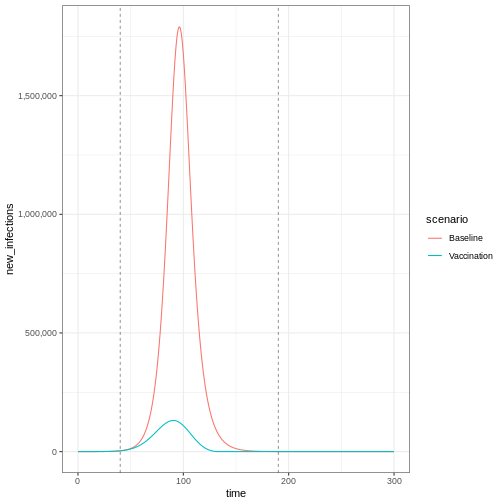
Lastly, if you want to plot new infections from an
epidemics::model_default() that includes a
vaccination intervention, you need to add one argument to
epidemics::new_infections(): Set
exclude_compartments = "vaccinated" to tell the function
that people moving from “susceptible” to “vaccinated” are not becoming
infected. This ensures vaccinated individuals aren’t counted as
infections.
Note that if we add by_group = FALSE in
epidemics::new_infections(), we get a summary of the new
infections in the population.
R
infections_baseline <- epidemics::new_infections(
data = output_baseline,
exclude_compartments = "vaccinated", # if vaccination
by_group = FALSE
)
infections_intervention <- epidemics::new_infections(
data = output_vaccinate,
exclude_compartments = "vaccinated", # if vaccination
by_group = FALSE
)
# Assign scenario names
infections_baseline$scenario <- "Baseline"
infections_intervention$scenario <- "Vaccination"
# Combine the data from both scenarios
infections_baseline_interv <- dplyr::bind_rows(
infections_baseline,
infections_intervention
)
infections_baseline_interv %>%
ggplot(aes(x = time, y = new_infections, colour = scenario)) +
geom_line() +
geom_vline(
xintercept = c(vaccinate$time_begin, vaccinate$time_end),
linetype = "dashed",
linewidth = 0.2
) +
scale_y_continuous(labels = scales::comma) +
theme_bw()
To get an age-stratified plot, keep the default
by_group = TRUE and then add
linetype = demography_group when declaring variables in
ggplot(aes(...)).
Summary
Different types of intervention can be implemented using mathematical modelling. Modelling interventions requires assumptions of which model parameters are affected (e.g. contact matrices, transmission rate), and by what magnitude and what times in the simulation of an outbreak.
The next step is to quantify the effect of an interventions. If you are interested in learning how to compare interventions, please complete the tutorial Comparing public health outcomes of interventions.
Key Points
- The effect of NPIs can be modelled as reducing contact rates between age groups or reducing the transmission rate of infection
- Vaccination can be modelled by assuming individuals move to a different disease state \(V\)
References
Davies, N. G., Klepac, P., Liu, Y., Prem, K., Jit, M., & Eggo, R. M. (2020). Age-dependent effects in the transmission and control of COVID-19 epidemics. Nature Medicine, 26(8), 1205-1211. https://doi.org/10.1016/S2468-2667(20)30133-X
Li, Y., Liang, M., Gao, L., Ahmed, M. A., Uy, J. P., Cheng, C., … & Sun, C. (2020). Face masks to prevent transmission of COVID-19: A systematic review and meta-analysis. American Journal of Infection Control, 49(7), 900-906. https://doi.org/10.1371/journal.pone.0237691
Mossong, J., Hens, N., Jit, M., Beutels, P., Auranen, K., Mikolajczyk, R., … & Edmunds, W. J. (2008). Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS medicine, 5(3), e74. https://doi.org/10.1371/journal.pmed.0050074
