Simulate transmission chains
Última actualización: 2024-11-19 | Mejora esta página
Hoja de ruta
Preguntas
- How can we simulate transmission chains based on infection characteristics?
Objetivos
- Create a short term projection using a branching process with epichains.
Prerequisites
Learners should familiarise themselves with the following concept dependencies before working through this tutorial:
Statistics: Common probability distributions, including Poisson and negative binomial.
Epidemic theory: The reproduction number, \(R\).
Introduction
Individual variation in transmission can affect both the potential for an epidemic to establish in a population and the ease of control (Cori et al., 2017).
Greater variation reduces the overall probably of a single new case causing a large local outbreak, because most cases infect few others and individuals that generate a large number of secondary cases are relatively rare.
However, if a ‘superspreading event’ does occur and the outbreak gets established, this variation can make an outbreak harder to control using mass interventions (i.e. blanket interventions that implicitly assume everyone contributes equally to transmission), because some cases contribute disproportionality: a single uncontrolled case may generate a large number of secondary cases.
Conversely, variation in transmission may provide opportunities for targeted interventions if the individuals who contribute more to transmission (due to biological or behavioural factors), or the settings in which ‘superspreading events’ occur, share socio-demographic, environmental or geographical characteristics that can be defined.
How can we quantify the potential of a new infection to cause a large outbreak based on its reproduction number \(R\) and the dispersion \(k\) of its offspring distribution?

In this episode, we will use the epichains package to
simulate transmission chains and estimate the potential for large
outbreaks following the introduction of a new case. We are going to use
it with functions from {epiparameter}, dplyr
and purrr, so also loading the tidyverse
package:
R
library(epichains)
library(epiparameter)
library(tidyverse)
The double-colon
The double-colon :: in R let you call a specific
function from a package without loading the entire package into the
current environment.
For example, dplyr::filter(data, condition) uses
filter() from the dplyr package.
This help us remember package functions and avoid namespace conflicts.
Simulation of uncontrolled outbreaks
Infectious disease epidemics spread through populations when a chain of infected individuals transmit the infection to others. Branching processes can be used to model this transmission. A branching process is a stochastic process (i.e. a random process that can be described by a known probability distribution), where each infectious individual gives rise to a random number of individuals in the next generation of infection, starting with the index case in generation 1. The distribution of the number of secondary cases each individual generates is called the offspring distribution (Azam & Funk, 2024).
epichains provides methods to analyse and simulate the size and length of branching processes with an given offspring distribution. epichains implements a rapid and simple model to simulate transmission chains to assess epidemic risk, project cases into the future, and evaluate interventions that change \(R\).
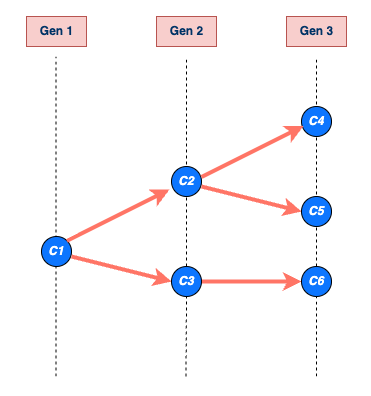
chain size and length
The size of the transmission chain is defined as the total number of individuals infected across all generations of infection, and
the length of the transmission chain is the number of generations from the first case to the last case in the outbreak before the chain ended.
The size calculation includes the first case, and the length calculation contains the first generation when the first case starts the chain (See figure below).
To use epichains, we need to know (or assume) two key epidemiological values: the offspring distribution and the generation time.
Get the offspring distribution
Here we assume the MERS offspring distribution follows a negative
binomial distribution, with mean (reproduction number \(R\)) and dispersion \(k\) values estimated from the linelist and
contact data of mers_korea_2015 in the
outbreaks R package in the previous episode.
R
mers_offspring <- c(mean = 0.60, dispersion = 0.02)
offspring distribution for epichains
We input an offspring distribution to epichains by
referring to the R function that generates random values from the
distribution we want. For a negative binomial distribution, we use
rnbinom with its corresponding mu and
size arguments:
The reference manual in ?rnbinom tells us our required
specific arguments.
epichains can accept any R function that generates random numbers, so the specified arguments will change depending on the R function used. For more details on the range of possible options, see the function reference manual.
For example, let’s say we want to use a Poisson distribution for the
offspring distribution. First, read the argument required in the
?rpois reference manual. Second, specify the
lambda argument parameter, also known as rate or mean in
the literature. In epichains, this can look like
this:
In this example, we can specify
lambda = mers_offspring["mean"] because the mean number of
secondary cases generated (i.e. \(R\))
should be the same regardless of the distribution we assume. What
changes is the variance of the distribution, and hence the level of
individual-level variation in transmission. When the dispersion
parameter \(k\) approaches infinity
(\(k \rightarrow \infty\)) in a
negative binomial distribution, the variance equals the mean. This makes
the conventional Poisson distribution a special case of the negative
binomial distribution.
Get generation time
The serial interval distribution is often used to approximate the generation time distribution. This approximation is commonly used because it is easier to observe and measure the onset of symptoms in each case than the precise time of infection.

However, using the serial interval as an approximation of the generation time is primarily valid for diseases in which infectiousness starts after symptom onset (Chung Lau et al., 2021). In cases where infectiousness starts before symptom onset, the serial intervals can have negative values, which is the case for diseases with pre-symptomatic transmission (Nishiura et al., 2020).
Let’s use the {epiparameter} package to access and use
the available serial interval for MERS disease:
R
serial_interval <- epidist_db(
disease = "mers",
epi_dist = "serial",
single_epidist = TRUE
)
plot(serial_interval, day_range = 0:25)

The serial interval for MERS has a mean of 12.6 days and a standard deviation of 2.8 days.
generation time for epichains
In epichains, we need to specify the generation time
as a function that generates random numbers. Using
{epiparameter} has the advantage of using the distribution
function epiparameter::generate() for this input. This will
look like this:
R
function(x) generate(x = serial_interval, times = x)
This interface is similar to the one cfr uses to link
with {epiparameter}. Read the work
with delay distributions vignette for further context.
Simulate a single chain
Now we are prepared to use the simulate_chains()
function from epichains to create one
transmission chain:
R
epichains::simulate_chains(
# simulation controls
n_chains = 5,
statistic = "size",
# offspring
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
# generation
generation_time = function(x) generate(x = serial_interval, times = x)
)
simulate_chains() requires three sets of arguments as a
minimum:
- simulation controls,
- offspring distribution, and
- generation time.
In the lines above, we described how to specify the offspring distribution and generation time. The simulation controls include at least two arguments:
-
index_case, which defines the number of index cases to simulate transmission chains for and -
statistic, which defines a chain statistic to track (either"size"or"length") as the stopping criteria for each chain being simulated.
Stopping criteria
This is an customisable feature of epichains. By
default, branching process simulations end when they have gone extinct.
For long-lasting transmission chains, in simulate_chains()
you can add the stat_max argument.
For example, if we set an stopping criteria for
statistic = "size" of stat_max = 500, no more
offspring will be produced after a chain of size 500.
The simulate_chains() output creates a
<epichains> class object, which we can then analyse
further in R.
Simulate multiple chains
We can use simulate_chains() to create multiple chains
and increase the probability of simulating uncontrolled outbreak
projections given an overdispersed offspring distribution.
We need to specify three additional elements:
-
set.seed(<integer>), which is a random number generator function with a specified seed value, the<integer>number, to ensure consistent results across different runs of the code. -
number_simulations, which defines the number of simulations to run. -
initial_casesdefines the number of initial cases to input to then_chainsargument explained in the lines above.
R
# Set seed for random number generator
set.seed(33)
# Number of simulation runs
number_simulations <- 1000
# Number of initial cases
initial_cases <- 1
number_simulations and initial_cases are
conveniently stored in objects to facilitate downstream reuse in the
workflow.
Iteration using purrr
Iteration aims to perform the same action on different objects repeatedly.
Learn how to use the core purrr functions like
map() from the YouTube tutorial on How to purrr by
Equitable Equations.
Or, if you previously used the *apply family of
functions, visit the package vignette on purrr base R,
which shares key differences, direct translations, and examples.
To get multiple chains, we must apply the
simulate_chains() function to each chain defined by a
sequence of numbers from 1 to 1000.
purrr and epichains
First, let’s sketch how we use purrr::map() with
epichains::simulate_chains(). The map()
function requires two arguments:
-
.x, with a vector of numbers, and -
.f, a function to iterate to each vector value.
R
map(
# vector of numbers (simulation IDs)
.x = seq_len(number_simulations),
# function to iterate to each simulation ID number
.f = function(sim) {
simulate_chains(...) %>%
# creates a column with the simulation ID number
mutate(simulation_id = sim)
}
) %>%
# combine list outputs (for each simulation ID) into a single data frame
list_rbind()
The sim element is placed to register the iteration
number (simulation ID) as a new column in the
<epichains> output. The
purrr::list_rbind() function aims to combine all the list
outputs from map().
Why a dot (.) as a prefix? In the tidy design
principles book we have a chapter on the dot prefix!
Now, we are prepared to use map() to repeatedly simulate
from simulate_chains() and store in a vector from 1 to
1000:
R
simulated_chains_map <-
# iterate one function across multiple numbers (simulation IDs)
purrr::map(
# vector of numbers (simulation IDs)
.x = seq_len(number_simulations),
# function to iterate to each simulation ID number
.f = function(sim) {
epichains::simulate_chains(
# simulation controls
n_chains = initial_cases,
statistic = "size",
# offspring
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
# generation
generation_time = function(x) generate(x = serial_interval, times = x)
) %>%
# creates a column with the simulation ID number
dplyr::mutate(simulation_id = sim)
}
) %>%
# combine list outputs (for each simulation ID) into a single data frame
purrr::list_rbind()
Read the epichains output
To explore the output format of the <epichains>
class object of name simulated_chains_map, let’s look at
the simulated simulation_id number 806.
Let’s use dplyr::filter() for this:
R
chain_to_observe <- 806
R
#### get epichain summary ----------------------------------------------------
simulated_chains_map %>%
dplyr::filter(simulation_id == chain_to_observe)
SALIDA
`<epichains>` object
< epichains head (from first known infector) >
chain infector infectee generation time simulation_id
2 1 1 2 2 16.38623 806
3 1 1 3 2 11.79430 806
4 1 1 4 2 10.77252 806
5 1 1 5 2 11.39945 806
6 1 1 6 2 10.23130 806
7 1 2 7 3 26.01046 806
Number of infectors (known): 3
Number of generations: 3
Use `as.data.frame(<object_name>)` to view the full output in the console.Key elements from this output are in the footer, the piece of text that appears at the bottom:
SALIDA
Number of infectors (known): 3
Number of generations: 3The simulated simulation_id number 806 has three known
infectors and three generations. These numbers are more visible when
reading the <epichains> objects as a data frame.
R
#### infector-infectee data frame --------------------------------------------
simulated_chains_map %>%
dplyr::filter(simulation_id == chain_to_observe) %>%
dplyr::as_tibble()
SALIDA
# A tibble: 9 × 6
chain infector infectee generation time simulation_id
<int> <dbl> <dbl> <int> <dbl> <int>
1 1 NA 1 1 0 806
2 1 1 2 2 16.4 806
3 1 1 3 2 11.8 806
4 1 1 4 2 10.8 806
5 1 1 5 2 11.4 806
6 1 1 6 2 10.2 806
7 1 2 7 3 26.0 806
8 1 2 8 3 29.8 806
9 1 2 9 3 26.6 806Chain 806 tells us a story: “In the first
transmission generation at time = 0, one index case
infected the first case with sim_id = 1. Then, in the
second transmission generation (between time 10 to 16),
sim_id = 1 infected five cases. Later, in the third
transmission generation (between time 26 to 30),
sim_id = 2 infected three new cases.”
The output data frame collects infectees as the observation unit:
- Each infectee has a
sim_id. - Each infectee that behaved as an infector is
registered in the
infectorcolumn usingsim_idof that infectee. - Each infectee got infected in a specific
generationand (continuous)time. - The simulation number is registered under the
simulation_idcolumn.
Note: The Number of infectors (known)
includes the NA observation under the infector
column. This refers to the infector specified as index case (in the
n_chains argument), which started the transmission chain to
the infectee of sim_id = 1, at generation = 1,
and time = 0.
Visualize multiple chains
To visualize the simulated chains, we need some pre-processing:
- Let’s use dplyr to get round time numbers to resemble surveillance days.
- Count the daily cases in each simulation (by
simulation_id). - Calculate the cumulative number of cases within a simulation.
R
# daily aggregate of cases
simulated_chains_day <- simulated_chains_map %>%
# use data.frame output from <epichains> object
dplyr::as_tibble() %>%
# transform simulation ID column to factor (categorical variable)
dplyr::mutate(simulation_id = as_factor(simulation_id)) %>%
# get the round number (day) of infection times
dplyr::mutate(day = ceiling(time)) %>%
# count the daily number of cases in each simulation (simulation ID)
dplyr::count(simulation_id, day, name = "cases") %>%
# calculate the cumulative number of cases for each simulation (simulation ID)
dplyr::group_by(simulation_id) %>%
dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
dplyr::ungroup()
Before the plot, let’s create a summary table with the total time
duration and size of each chain. We can use the dplyr
“combo” of group_by(), summarise() and
ungroup():
R
# Summarise the chain duration and size
sim_chains_max <-
simulated_chains_day %>%
dplyr::group_by(simulation_id) %>%
dplyr::summarise(
# duration
day_max = max(day),
# size
cases_total = max(cases_cumsum)
) %>%
dplyr::ungroup()
sim_chains_max
SALIDA
# A tibble: 1,000 × 3
simulation_id day_max cases_total
<fct> <dbl> <int>
1 1 0 1
2 2 0 1
3 3 0 1
4 4 0 1
5 5 0 1
6 6 0 1
7 7 0 1
8 8 0 1
9 9 0 1
10 10 0 1
# ℹ 990 more rowsNow, we are prepared for using the ggplot2 package:
R
# Visualize transmission chains by cumulative cases
ggplot() +
# create grouped chain trajectories
geom_line(
data = simulated_chains_day,
mapping = aes(
x = day,
y = cases_cumsum,
group = simulation_id
),
color = "black",
alpha = 0.25,
show.legend = FALSE
) +
# create points to visualize the chain endpoint
geom_point(
data = sim_chains_max,
mapping = aes(
x = day_max,
y = cases_total,
group = simulation_id,
color = simulation_id
),
show.legend = FALSE
) +
# define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2) +
labs(
x = "Day",
y = "Cumulative cases"
)

Although most introductions of 1 index case do not generate secondary cases (N = 940) or most outbreaks rapidly become extinct (median duration of 17.5 and median size of 9), only 2 epidemic trajectories among 1000 simulations (0.2%) can reach to more than 100 infected cases. This finding is particularly remarkable because the reproduction number \(R\) is less than 1 (offspring distribution mean of 0.6), but, given an offspring distribution dispersion parameter of 0.02, it shows the potential for explosive outbreaks of MERS disease.
We can count how many chains reached the 100-case threshold using dplyr functions:
R
# number of chains that reached the 100-case threshold
sim_chains_max %>%
dplyr::arrange(desc(day_max)) %>%
dplyr::filter(cases_total > 100)
SALIDA
# A tibble: 2 × 3
simulation_id day_max cases_total
<fct> <dbl> <int>
1 666 88 110
2 23 45 113Let’s overlap the cumulative number of observed cases using the
linelist object from the mers_korea_2015 dataset of the
outbreaks R package. To prepare the dataset so we can
plot daily total cases over time, we use incidence2 to
convert the linelist to an <incidence2> object,
complete the missing dates of the time series with
complete_dates()
R
library(outbreaks)
mers_cumcases <- mers_korea_2015$linelist %>%
# incidence2 workflow
incidence2::incidence(date_index = "dt_onset") %>%
incidence2::complete_dates() %>%
# wrangling using {dplyr}
dplyr::mutate(count_cumsum = cumsum(count)) %>%
tibble::rownames_to_column(var = "day") %>%
dplyr::mutate(day = as.numeric(day))
Use plot() to make an incidence plot:
R
# plot the incidence2 object
plot(mers_cumcases)

When plotting the observed number of cumulative cases from the Middle East respiratory syndrome (MERS) outbreak in South Korea in 2015 alongside the previously simulated chains, we see that the observed cases followed a trajectory that is consistent with the simulated explosive outbreak dynamics (which makes sense, given the simulation uses parameters based on this specific outbreak).

When we increase the dispersion parameter from \(k = 0.01\) to \(k = \infty\) - and hence reduce individual-level variation in transmission - and assume a fixed reproduction number \(R = 1.5\), the proportion of simulated outbreaks that reached the 100-case threshold increases. This is because the simulated outbreaks now have more of a consistent, clockwise dynamic, rather than the high level of variability seen previously.

Early spread projections
In the epidemic’s initial phase, you can use epichains to apply a branching process model to project the number of future cases. Even though the model accounts for randomness in transmission and variation in the number of secondary cases, there may be additional local features we have not considered. Analysis of early forecasts made for COVID in different countries using this model structure found that predictions were often overconfident (Pearson et al., 2020). This is likely because the real-time model did not include all the changes in the offspring distribution that were happening at the local level as a result of behaviour change and control measures. You can read more about the importance of local context in COVID-19 models in Eggo et al. (2020).
We invite you to read the vignette on Projecting infectious disease incidence: a COVID-19 example! for more on making predictions using epichains.
Challenges
Monkeypox large outbreak potential
Evaluate the potential for a new Monkey pox (Mpox) case to generate an explosive large outbreak.
- Simulate 1000 transmission chains with 1 initial case each.
- Use the appropriate package to access delay data from previous outbreaks.
- How many simulated trajectories reach more than 100 infected cases?
With {epiparameter}, you can access and use offspring
and delay distributions from previous Ebola outbreaks.
R
library(epiparameter)
library(tidyverse)
epiparameter::epidist_db(epi_dist = "offspring") %>%
epiparameter::parameter_tbl() %>%
dplyr::count(disease, epi_distribution)
SALIDA
# Parameter table:
# A data frame: 6 × 3
disease epi_distribution n
<chr> <chr> <int>
1 Ebola Virus Disease offspring distribution 1
2 Hantavirus Pulmonary Syndrome offspring distribution 1
3 Mpox offspring distribution 1
4 Pneumonic Plague offspring distribution 1
5 SARS offspring distribution 2
6 Smallpox offspring distribution 4R
epiparameter::epidist_db(epi_dist = "serial interval") %>%
epiparameter::parameter_tbl() %>%
dplyr::count(disease, epi_distribution)
SALIDA
# Parameter table:
# A data frame: 6 × 3
disease epi_distribution n
<chr> <chr> <int>
1 COVID-19 serial interval 4
2 Ebola Virus Disease serial interval 4
3 Influenza serial interval 1
4 MERS serial interval 2
5 Marburg Virus Disease serial interval 2
6 Mpox serial interval 5R
# load packages -----------------------------------------------------------
library(epiparameter)
library(tidyverse)
# delays ------------------------------------------------------------------
mpox_offspring_epidist <- epiparameter::epidist_db(
disease = "mpox",
epi_dist = "offspring",
single_epidist = TRUE
)
mpox_offspring <- epiparameter::get_parameters(mpox_offspring_epidist)
mpox_serialint <- epiparameter::epidist_db(
disease = "mpox",
epi_dist = "serial interval",
single_epidist = TRUE
)
# iterate -----------------------------------------------------------------
# Set seed for random number generator
set.seed(33)
# Number of simulation runs
number_simulations <- 1000
# Number of initial cases
initial_cases <- 1
simulated_chains_mpox <-
# iterate one function across multiple numbers (simulation IDs)
purrr::map(
# vector of numbers (simulation IDs)
.x = seq_len(number_simulations),
# function to iterate to each simulation ID number
.f = function(sim) {
epichains::simulate_chains(
# simulation controls
n_chains = initial_cases,
statistic = "size",
# offspring
offspring_dist = rnbinom,
mu = mpox_offspring["mean"],
size = mpox_offspring["dispersion"],
# generation
generation_time = function(x) generate(x = mpox_serialint, times = x)
) %>%
# creates a column with the simulation ID number
dplyr::mutate(simulation_id = sim)
}
) %>%
# combine list outputs (for each simulation ID) into a single data frame
purrr::list_rbind()
# visualize ---------------------------------------------------------------
# daily aggregate of cases
simulated_chains_mpox_day <- simulated_chains_mpox %>%
# use data.frame output from <epichains> object
dplyr::as_tibble() %>%
# transform simulation ID column to factor (categorical variable)
dplyr::mutate(simulation_id = as_factor(simulation_id)) %>%
# get the round number (day) of infection times
dplyr::mutate(day = ceiling(time)) %>%
# count the daily number of cases in each simulation (simulation ID)
dplyr::count(simulation_id, day, name = "cases") %>%
# calculate the cumulative number of cases for each simulation (simulation ID)
dplyr::group_by(simulation_id) %>%
dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
dplyr::ungroup()
# Visualize transmission chains by cumulative cases
ggplot() +
# create grouped chain trajectories
geom_line(
data = simulated_chains_mpox_day,
mapping = aes(
x = day,
y = cases_cumsum,
group = simulation_id
),
color = "black",
alpha = 0.25,
show.legend = FALSE
) +
# define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2) +
labs(
x = "Day",
y = "Cumulative cases"
)

Assuming a Monkey pox outbreak with \(R\) = 0.32 and \(k\) = 0.58, there is no trajectory among 1000 simulations that reach more than 100 infected cases. Compared to MERS (\(R\) = 0.6 and \(k\) = 0.02).
With {superspreading}, you can get numerical solutions
to processes that epichains solve using branching
processes. We invite you to read the {superspreading}
vignette on Epidemic
risk and respond to:
- What is the probability that a newly introduced pathogen will cause a large outbreak?
- What is the probability that an infection will, by chance, fail to establish following initial introduction(s)?
- What is the probability the outbreak will be contained?
Check how these estimates vary non-linearly with respect to the mean reproduction number \(R\) and dispersion \(k\) of a given disease.
R
library(superspreading)
R
library(superspreading)
From a distribution of secondary cases
Christian Althaus, 2015 reused data published by Faye et al., 2015 (Figure 2) on the transmission tree on Ebola virus disease in Conakry, Guinea, 2014.
Using the data under the hint tab, estimate the offspring distribution from the distribution of secondary cases. Then estimate the large outbreak potential from this data.
Code with the transmission tree data written by Christian Althaus, 2015:
R
# Number of individuals in the trees
n <- 152
# Number of secondary cases for all individuals
c1 <- c(1, 2, 2, 5, 14, 1, 4, 4, 1, 3, 3, 8, 2, 1, 1,
4, 9, 9, 1, 1, 17, 2, 1, 1, 1, 4, 3, 3, 4, 2,
5, 1, 2, 2, 1, 9, 1, 3, 1, 2, 1, 1, 2)
c0 <- c(c1, rep(0, n - length(c1)))
c0 %>%
enframe() %>%
ggplot(aes(value)) +
geom_histogram()

R
# load packages ---------------------------
library(epichains)
library(epiparameter)
library(fitdistrplus)
library(tidyverse)
R
# fit a negative binomial distribution ------------------------------------
# Fitting a negative binomial distribution to the number of secondary cases
fit.cases <- fitdistrplus::fitdist(c0, "nbinom")
fit.cases
SALIDA
Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
estimate Std. Error
size 0.1814260 0.03990278
mu 0.9537995 0.19812301R
# serial interval parameters ----------------------------------------------
ebola_serialinter <- epiparameter::epidist_db(
disease = "ebola",
epi_dist = "serial interval",
single_epidist = TRUE
)
# simulate outbreak trajectories ------------------------------------------
# Set seed for random number generator
set.seed(645)
# Number of simulation runs
number_simulations <- 1e2
# Number of initial cases
initial_cases <- 1
sim_multiple_chains <-
purrr::map(
.x = seq_len(number_simulations),
.f = function(sim) {
epichains::simulate_chains(
n_chains = initial_cases,
# stopping
statistic = "size",
# offspring
offspring_dist = rnbinom,
mu = fit.cases$estimate["mu"],
size = fit.cases$estimate["size"],
# generation
generation_time = function(x) generate(x = ebola_serialinter, times = x)
) %>%
dplyr::mutate(simulation_n = sim)
}
) %>%
# combine list outputs (for each simulation ID) into a single data frame
purrr::list_rbind()
# visualize ----------------------------------------
sim_chains_aggregate <-
sim_multiple_chains %>%
dplyr::as_tibble() %>%
dplyr::mutate(simulation_n = as_factor(simulation_n)) %>%
dplyr::mutate(day = ceiling(time)) %>%
dplyr::count(simulation_n, day, name = "cases") %>%
dplyr::group_by(simulation_n) %>%
dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
dplyr::ungroup()
ggplot() +
geom_line(
data = sim_chains_aggregate,
mapping = aes(
x = day,
y = cases_cumsum,
group = simulation_n
),
show.legend = FALSE
) +
# define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2)

Remarkably, even with R0 less than 1 (R = 0.95) we can have potentially explosive outbreaks. The observed variation in individual infectiousness in Ebola means that although the probability of extinction is high, new index cases also have the potential for explosive regrowth of the epidemic.
Puntos Clave
- Use epichains to simulate the large outbreak potential of diseases with overdispersed offspring distributions.
