Estimación de la severidad del brote
Última actualización: 2024-11-19 | Mejora esta página
Hoja de ruta
Preguntas
¿Por qué estimamos la gravedad clínica de una epidemia?
¿Cómo se puede estimar la probabilidad de muerte (CFR por sus siglas en inglés: Case Fatality Risk) al principio de una epidemia en curso?
Objetivos
Estimar la probabilidad de muerte a partir de datos de casos agregados utilizando el paquete cfr, case fatality risk en inglés (riesgo de fatalidad de casos).
Estima la probabilidad de muerte, ajustando este cálculo teniendo en cuenta el intervalo entre la aparición de síntomas y la muerte del paciente utilizando los paquetes
{epiparameter}y cfr.Estima la probabilidad de muerte de una enfermedad durante la fase de crecimiento exponencial de una epidemia en expansión utilizando cfr.
Requisitos previos
Este episodio requiere que estés familiarizado con
Ciencia de datos Programación básica con R
Teoría epidémica: Distribuciones temporales.
Introducción
Entre las preguntas más comunes en la fase inicial de una epidemia se incluyen:
- ¿Cuál es el impacto probable del brote en la salud pública en términos de gravedad clínica?
- ¿Cuáles son los grupos más gravemente afectados?
- ¿Tiene el brote potencial para causar una epidemia de grandes dimensiones o incluso una pandemia?
Podemos evaluar el potencial pandémico de una epidemia con dos medidas críticas: la transmisibilidad y la gravedad clínica (Fraser et al., 2009, CDC, 2016).
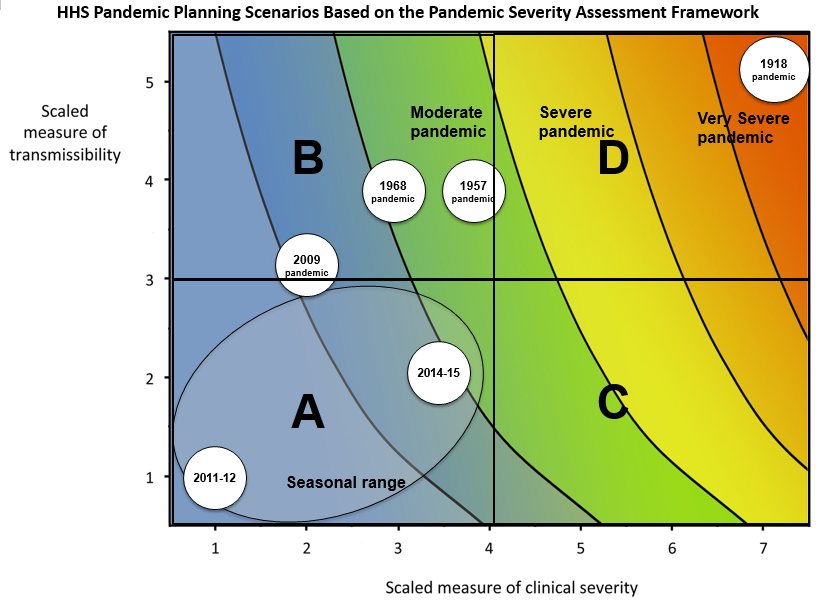
Un enfoque epidemiológico para estimar la gravedad clínica consiste en cuantificar la probabilidad de muerte (CFR). CFR es la probabilidad condicional de muerte una vez confirmado el diagnóstico de la enfermedad, calculada como el número acumulado de muertes por una enfermedad infecciosa dividido por el número de casos diagnosticados confirmados. Sin embargo, calcularlo directamente durante el curso de una epidemia tiende a dar como resultado un CFR sesgado, dado el intervalo temporal que ocurre desde el inicio de lo síntomas hasta la muerte. Este retraso temporal varía sustancialmente a medida que avanza la epidemia y se estabiliza en las últimas fases del brote (Ghani et al., 2005).
En términos más generales, estimar la gravedad puede ser útil incluso fuera de un escenario de planificación pandémica y en el contexto de la salud pública rutinaria. Saber si un brote tiene o tuvo una gravedad diferente a la del registro histórico puede motivar investigaciones causales, que podrían ser intrínsecas al agente infeccioso (por ejemplo, una nueva cepa más grave) o debidas a factores subyacentes en la población (por ejemplo, inmunidad reducida o factores de morbilidad) (Lipsitch et al., 2015).
En este tutorial vamos a aprender a utilizar la función
cfr para calcular y ajustar una estimación de la
probabilidad de muerte utilizando distribuciones temporales
provenientes de {epiparameter} o de otras fuentes,
basándose en los métodos desarrollados por Nishiura
et al., 2009 además, aprenderemos como reimplementar las funciones
de cfr para realizar otras mediciones de la gravedad de
la enfermedad, por ejemplo, el riesgo de fatalidad hospitalaria.
Utilizaremos el operador %>% para conectar funciones,
por lo que es necesario también acceder al
paquetetidyverse:
R
library(cfr)
library(epiparameter)
library(tidyverse)
library(outbreaks)
El doble punto
El doble punto :: en R te permite llamar a una función
específica de un paquete sin cargar todo el paquete en el entorno
actual.
Por ejemplo dplyr::filter(data, condition) utiliza
filter() del paquete dplyr.
Esto nos ayuda a recordar las funciones requeridas y evitar usar funciones que fueron creadas con el mismo nombre pero provienen de otros paquetes.
Fuentes de datos para la gravedad clínica
¿Qué fuentes de datos podemos utilizar para estimar la gravedad clínica de un brote epidémico? Verity et al., 2020 resume el espectro de casos de COVID-19:
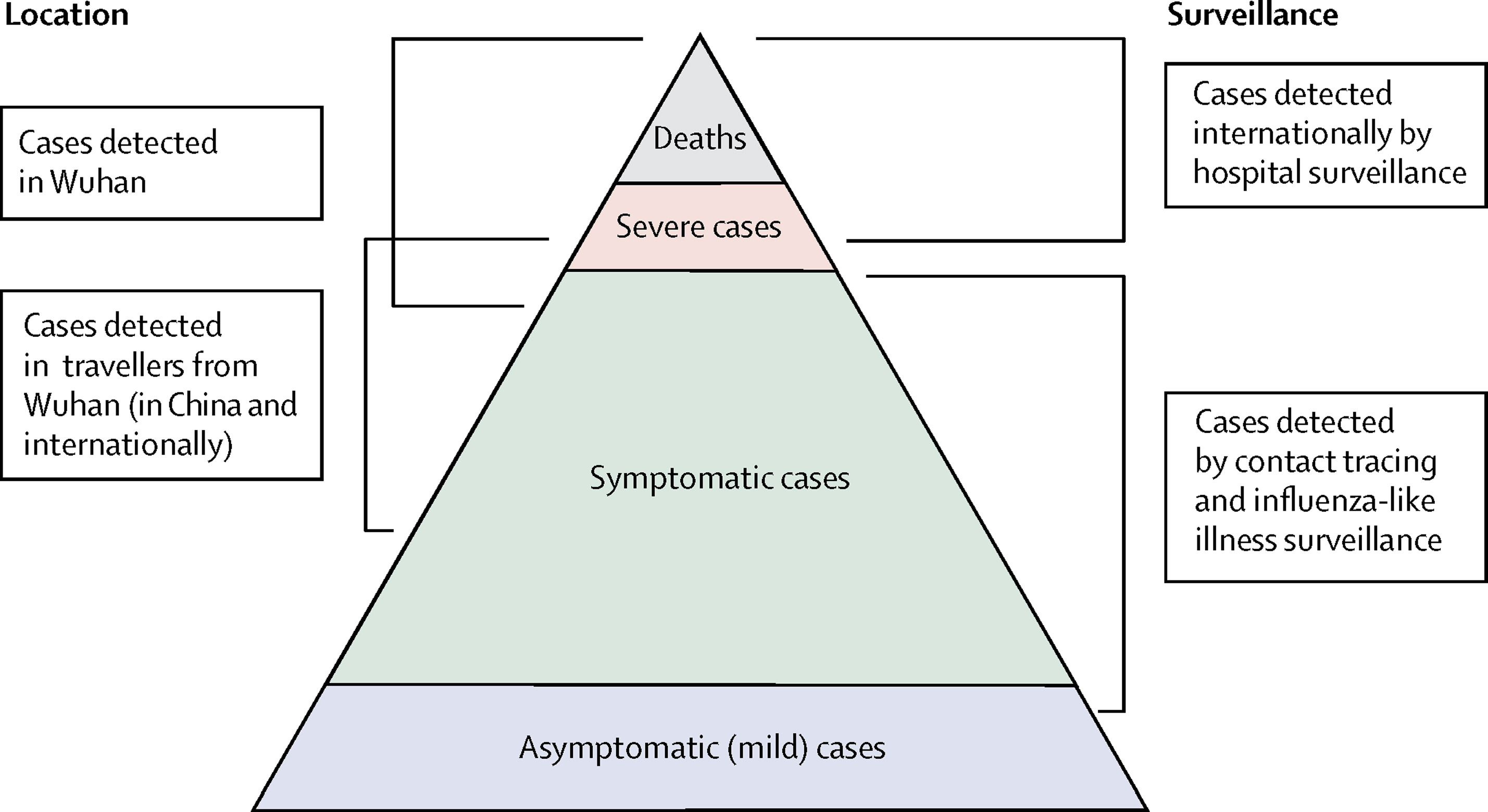
- En la cúspide de la pirámide, los que cumplían los criterios de caso de la OMS para grave o críticos, identificados en el ámbito hospitalario, presentando una neumonía vírica atípica. Estos casos se habrían identificado en China continental y entre los categorizados internacionalmente como de transmisión local.
- Es probable que haya muchos más casos sintomáticos (es decir, con fiebre, tos o mialgia) pero no requiriesen hospitalización. Estos casos se habrían identificado mediante el rastro de casos potenciales en vuelos internacionales a zonas de alto riesgo y mediante el rastreo de los contactos de los casos confirmados, o a través de vigilancia pasiva de otras enfermedades infecciosas respiratorias en la población.
- La parte inferior de la pirámide representa enfermedad leve (y posiblemente asintomática). Estos casos podrían identificarse mediante el rastreo de contactos, mediante pruebas serológicas.
CFR no ajustado
Medimos la gravedad de la enfermedad en términos de riesgo/probabilidad de muerte (CFR). CFR se interpreta como la probabilidad condicional de muerte dado un diagnóstico confirmado, calculada como el número acumulado de muertes \(D_{t}\) sobre el número acumulado de casos confirmados \(C_{t}\) en un momento determinado \(t\). Podemos referirnos al CFR sesgado (\(b_{t}\)):
\[ b_{t} = \frac{D_{t}}{C_{t}} \]
Este cálculo es sesgado porque genera una subestimación del CFR real, debido al retraso temporal desde el inicio de los síntomas hasta la muerte, que sólo se estabiliza en las últimas fases del brote.
Para calcular el CFR de forma directa y sin ajustar el retraso temporal entre la aparición de síntomas y la muerte del paciente (conocida como probabilidad de muerte “naive”), el paquete cfr requiere un una base de datos (dataframe) que contenga las siguientes tres columnas:
datecasesdeaths
Exploremos la base de datos ebola1976 incluido en {cfr}
que procede del primer brote de ébola en lo que entonces se llamaba
Zaire (ahora República Democrática del Congo) en 1976, analizado por
Camacho et al. (2014).
R
# Cargamos la base de datos Ebola 1976, incluida en el paquete {cfr}
data("ebola1976")
# Asumiendo que solo tenemos datos para los primeros 30 días del brote
ebola1976 %>%
slice_head(n = 30) %>%
as_tibble()
SALIDA
# A tibble: 30 × 3
date cases deaths
<date> <int> <int>
1 1976-08-25 1 0
2 1976-08-26 0 0
3 1976-08-27 0 0
4 1976-08-28 0 0
5 1976-08-29 0 0
6 1976-08-30 0 0
7 1976-08-31 0 0
8 1976-09-01 1 0
9 1976-09-02 1 0
10 1976-09-03 1 0
# ℹ 20 more rowsNecesitamos datos de incidencia agregados
cfr lee datos de incidencia agregados por día
Estos deben ser agregados por día, es decir, cada fila de la base de datos contiene el número diario de casos y muertes notificadas. También deben incluirse aquellos días que tengan valores nulos o ausentes, de forma similar a los datos de series temporales.
cfr requiere datos diarios y no puede considerar otras unidades temporales de agregación, como semanas o meses.
Utilizando la función cfr_static() directamente,
calculamos la probabilidad de muerte sin ajustar:
R
# Cálculo de la probabilidad de muerte sin ajustar durante los primeros 30 días
cfr::cfr_static(data = ebola1976 %>% slice_head(n = 30))
SALIDA
severity_estimate severity_low severity_high
1 0.4740741 0.3875497 0.5617606Desafío
Descarga el archivo sarscov2_casos_defunciones.csv y léelo en R.
Estima la probabilidad de muerte sin ajustar.
Comprueba el formato de los datos introducidos.
- ¿Contiene datos diarios?
- ¿Los nombres de las columnas son los requeridos por
cfr_static()? - ¿Cómo se cambian los nombres de las columnas de una base de datos (dataframe) en R?
Leemos los datos introducidos mediante
readr::read_csv(). Esta función reconoce que la columna
date tiene el formato correcto,<date>,
que corresponde a fechas.
R
# lee la base de datos
# por ejemplo, si la ruta al archivo es data/raw-data/ebola_cases.csv :
sarscov2_input <-
readr::read_csv(here::here("data", "raw-data", "sarscov2_cases_deaths.csv"))
R
# Inspect data
sarscov2_input
SALIDA
# A tibble: 93 × 3
date cases_jpn deaths_jpn
<date> <dbl> <dbl>
1 2020-01-20 1 0
2 2020-01-21 1 0
3 2020-01-22 0 0
4 2020-01-23 1 0
5 2020-01-24 1 0
6 2020-01-25 3 0
7 2020-01-26 3 0
8 2020-01-27 4 0
9 2020-01-28 6 0
10 2020-01-29 7 0
# ℹ 83 more rowsPodemos utilizar dplyr::rename() para cambiar los
nombres de las columnas de este archivo y adaptarlos a los requeridos
por cfr_static().
R
# Cambio de nombre de las columnas en base al formato requerido por `cfr_static`
sarscov2_input %>%
dplyr::rename(
cases = cases_jpn,
deaths = deaths_jpn
) %>%
cfr::cfr_static()
SALIDA
severity_estimate severity_low severity_high
1 0.01895208 0.01828832 0.01963342Sesgos que afectan a la estimación del CFR
Dos sesgos que afectan a la estimación del CFR
Lipsitch et al., 2015 describen dos posibles sesgos que pueden afectar a la estimación de la probabilidad de muerte (y sus posibles soluciones):
Para enfermedades con un espectro de presentaciones clínicas, es más probable que los casos de mayor gravedad sean reconocidos y notificados a las autoridades de salud pública y se registran en las bases de datos de vigilancia, ya que las personas con síntomas graves son las que suelen buscar atención médica y acuden al centro de salud/hospital.
Por lo tanto, el CFR será normalmente más elevada entre los casos detectados que entre toda la población de casos, dado que esta última puede incluir individuos con presentaciones leves, subclínicas, y (según algunas definiciones de “caso”) asintomáticas.
En tiempo real durante una epidemia, suele haber un retraso temporal entre el momento en que alguien muere y el momento en que se notifica su muerte a la autoridad correspondiente. Por lo tanto, la lista de casos en tiempo real incluye a personas que morirán a causa de la enfermedad en el futuro, pero que aún siguen vivas, o que han muerto, pero cuya muerte no se ha notificado aún. Así pues, dividir el número acumulado de muertes notificadas por el número acumulado de casos notificados en un momento concreto durante un brote epidémico subestimará el CFR verdadera.
Los determinantes clave de la magnitud del sesgo son la tasa de crecimiento de la epidemia y la distribución del intervalo de tiempo desde la notificación del caso hasta la notificación de la defunción. Cuanto más largos sea este intervalo de tiempo y mayor sea la tasa de crecimiento, mayor será el sesgo.
En este episodio del tutorial, vamos a centrarnos en las soluciones para hacer frente a este sesgo utilizando el paquete de Rcfr ¡!
Mejorar la estimación de la probabilidad de muerte, ajustando su cálculo al retraso temporal entre notificación de casos y muerte es crucial para determinar la gravedad de la enfermedad, adaptar la intensidad y el tipo de intervenciones de salud pública y asesorar a la población.
En 2009, durante el virus de la gripe porcina, Gripe A (H1N1) en México, la estimación temprana de la probabilidad de muerte fue sesgada. Los informes iniciales del gobierno de México sugerían una infección virulenta, mientras que, en otros países, el mismo virus se percibía como leve (TIME, 2009).
En EE.UU. y Canadá, no se atribuyó ninguna muerte al virus en los diez primeros días tras la declaración de emergencia de salud pública por parte de la Organización Mundial de la Salud.
Fraser et al., 2009 reinterpretó los datos evaluando los sesgos y obteniendo una gravedad clínica inferior a la de la pandemia de gripe de 1918, pero comparable a la observada en la pandemia de 1957.
CFR ajustado al retraso temporal
Nishiura et al, 2009 desarrollaron un método que tiene en cuenta la distribución temporal desde el inicio de los síntomas hasta la muerte.
Los brotes en tiempo real pueden tener un número de muertes
insuficiente para determinar la distribución temporal entre el inicio de
síntomas y la muerte. Por tanto, podemos estimar la distribución
temporal en brotes históricos o utilizar las distribuciones
incluidas en paquetes de R como {epiparameter} o
{epireview} que los recogen de la literatura científica
publicada. Para una guía paso a paso, lee el episodio tutorial sobre
cómo acceder
a distribuciones temporales epidemiológicas.
Utilicemos {epiparameter}:
R
# Get delay distribution
onset_to_death_ebola <-
epiparameter::epidist_db(
disease = "Ebola",
epi_dist = "onset_to_death",
single_epidist = TRUE
)
# Plot <epidist> object
plot(onset_to_death_ebola, day_range = 0:40)
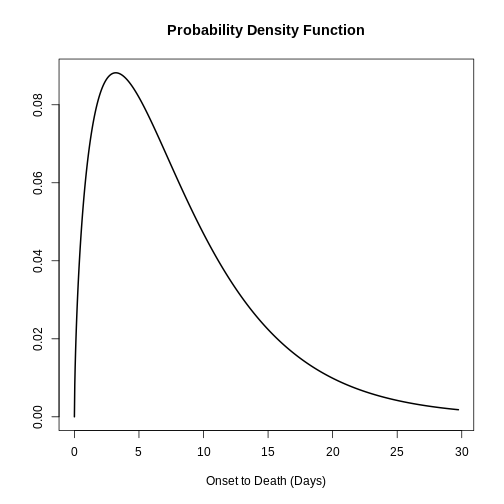
Para calcular el CFR ajustado, podemos utilizar la función
cfr_static(), a través del argumento
delay_density.
R
# Calculate the delay-adjusted CFR
# for the first 30 days
cfr::cfr_static(
data = ebola1976 %>% slice_head(n = 30),
delay_density = function(x) density(onset_to_death_ebola, x)
)
SALIDA
Total cases = 135 and p = 0.955: using Normal approximation to binomial likelihood.SALIDA
severity_estimate severity_low severity_high
1 0.9717 0.8201 0.9866SALIDA
Total cases = 135 and p = 0.955: using Normal approximation to binomial likelihood.La probabilidad de muerte ajustada indicó que la gravedad de la enfermedad al final del brote o con el últimos datos disponibles en ese momento es 0.9717 con un intervalo de confianza del 95% entre 0.8201 y 0.9866, con un valor superior al obtenido a través del cálculo directo sin ajustar.
Utiliza la clase epidist
Cuando utilices una clase <epidist> puedes
utilizar esta expresión como plantilla:
function(x) density(<EPIDIST_OBJECT>, x)
Para distribuciones cuyos parámetros no estén disponibles en
{epiparameter}, te proponemos dos alternativas:
Crear un objeto
<epidist>, que puede ser utilizado con otros paquetes de R para análisis de brotes. Lee la documentación de referencia deepiparameter::epidist()oLee la viñeta para una introducción al trabajo con distribuciones temporales.
Desafío
Utiliza el mismo archivo del reto anterior (sarscov2_casos_muertes.csv).
Estima el CFR ajustado al retraso temporal utilizando la distribución apropiada y
- ¡Compara los valores del CFR ajustado y sin ajuste temporal!
- Encuentra el
<epidist>¡apropiado!
Utilizamos {epiparameter} para acceder a una
distribución temporal para los datos de incidencia agregados del
SARS-CoV-2:
R
library(epiparameter)
sarscov2_delay <-
epidist_db(
disease = "covid",
epi_dist = "onset to death",
single_epidist = TRUE
)
Leemos el archivo de datos mediante readr::read_csv().
Esta función reconoce que la columna date es de la clase
<date>, es decir, una fecha.
R
# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
sarscov2_input <-
readr::read_csv(here::here("data", "raw-data", "sarscov2_cases_deaths.csv"))
R
# Inspect data
sarscov2_input
SALIDA
# A tibble: 93 × 3
date cases_jpn deaths_jpn
<date> <dbl> <dbl>
1 2020-01-20 1 0
2 2020-01-21 1 0
3 2020-01-22 0 0
4 2020-01-23 1 0
5 2020-01-24 1 0
6 2020-01-25 3 0
7 2020-01-26 3 0
8 2020-01-27 4 0
9 2020-01-28 6 0
10 2020-01-29 7 0
# ℹ 83 more rowsPodemos utilizar dplyr::rename() para cambiar los
nombres de las columnas del archivo a los requeridos
porcfr_static().
R
# Rename before Estimate naive CFR
sarscov2_input %>%
dplyr::rename(
cases = cases_jpn,
deaths = deaths_jpn
) %>%
cfr::cfr_static(delay_density = function(x) density(sarscov2_delay, x))
SALIDA
Total cases = 159402 and p = 0.0734: using Normal approximation to binomial likelihood.SALIDA
severity_estimate severity_low severity_high
1 0.047 0.0221 0.2931Interpreta las diferencias entre las estimaciones de la probabilidad de muerte sin ajustar y con ajuste temporal al intervalo entre la aparición inicial de síntomas en los casos y su muerte.
En cfr_static() y toda la familia de funciones en
cfr_*(), la opción más adecuada son las distribuciones
discretas. Esto se debe a que trabajaremos con datos
diarios de casos y defunciones.
Podemos suponer que la función de densidad de probabilidad (PDF) de una distribución continua es equivalente a la función de masa de probabilidad (PMF) de la distribución discreta correspondiente.
Sin embargo, esta suposición puede no ser adecuada en el caso de
distribuciones con picos pronunciados y baja varianza, en las que los
valores se concentran alrededor de la tendencia central. En tales casos,
se espera que la disparidad media entre la PDF y la PMF sea más
pronunciada en comparación con las distribuciones más dispersas. Una
forma de abordar esto es discretizar la distribución continua. Esto lo
podemos hacer en R, si discretizamos los objetos
<epidist>, utilizando la función
epiparameter::discretise().
Para ajustar la probabilidad de muerte, Nishiura et al., 2009 utilizan los datos de incidencia de casos y muertes para estimar el número de casos con resultados conocidos:
\[ u_t = \dfrac{\sum_{i = 0}^t \sum_{j = 0}^\infty c_{i - j} f_{j}}{\sum_{i = 0} c_i}, \]
donde
- \(c_{t}\) es la incidencia diaria de casos en el momento \(t\),
- \(f_{t}\) es el valor de la función de masa de probabilidad (PMF) de la distribución temporal entre el inicio de síntomas y la muerte, y
- \(u_{t}\) representa el factor de subestimación de los resultados conocidos.
\(u_{t}\) se utiliza para
escalar el valor del número acumulado de casos en el
denominador en el cálculo del CFR. Se calcula internamente con la
función estimate_outcomes()
El estimador para la probabilidad de muerte puede expresarse como:
\[p_{t} = \frac{b_{t}}{u_{t}}\]
donde \(p_{t}\) es la proporción realizada de casos confirmados que morirán a causa de la infección (o el CFR real), y \(b_{t}\) es la estimación cruda y sesgada del CFR.
A partir de esta última ecuación, observamos que el CFR no sesgada \(p_{t}\) es mayor que el CFR sesgada \(b_{t}\) porque en \(u_{t}\) el numerador es menor que el denominador (observa que \(f_{t}\) es la distribución de probabilidad del retraso temporal entre síntomas y muerte). Por tanto, nos referimos a \(b_{t}\) como el estimador sesgado de la probabilidad de muerte.
Cuando observamos todo el curso de una epidemia (desde \(t \rightarrow \infty\)), \(u_{t}\) tiende a 1, lo que hace que \(b_{t}\) tiende a \(p_{t}\) y se convierta en un estimador no sesgado (Nishiura et al., 2009).
Estimación temprana del CFR
En el reto anterior, descubrimos que el valor de la probabilidad de muerte ajustada y no ajustada son diferentes.
La CFR sin ajustar es útil para obtener una estimación global de la gravedad del brote. Una vez que el brote haya finalizado o haya progresado de forma que se notifiquen más muertes, el CFR estimada es entonces más cercana a el CFR “verdadera” o no sesgada.
Por otra parte, el CFR ajustada puede ser utilizada para estimar la gravedad de una enfermedad infecciosa emergente de una forma más temprana durante una epidemia.
Podemos explorar la CFR ajustado al retraso temporal de
forma temprana utilizando la función cfr_rolling()
Aviso
cfr_rolling() es una función que calcula automáticamente
el CFR en cada día del brote con los datos disponibles hasta ese día, lo
que ahorra tiempo al usuario, ya que no hace falta calcular este
parámetro manualmente para cada momento.
R
# Calculate the rolling daily naive CFR
# for all the 73 days in the Ebola dataset
rolling_cfr_naive <- cfr::cfr_rolling(data = ebola1976)
SALIDA
`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.R
utils::tail(rolling_cfr_naive)
SALIDA
date severity_estimate severity_low severity_high
68 1976-10-31 0.9510204 0.9160061 0.9744387
69 1976-11-01 0.9510204 0.9160061 0.9744387
70 1976-11-02 0.9510204 0.9160061 0.9744387
71 1976-11-03 0.9510204 0.9160061 0.9744387
72 1976-11-04 0.9510204 0.9160061 0.9744387
73 1976-11-05 0.9551020 0.9210866 0.9773771R
# Calculate the rolling daily delay-adjusted CFR
# for all the 73 days in the Ebola dataset
rolling_cfr_adjusted <- cfr::cfr_rolling(
data = ebola1976,
delay_density = function(x) density(onset_to_death_ebola, x)
)
SALIDA
`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.SALIDA
Some daily ratios of total deaths to total cases with known outcome are below 0.01%: some CFR estimates may be unreliable.FALSER
utils::tail(rolling_cfr_adjusted)
SALIDA
date severity_estimate severity_low severity_high
68 1976-10-31 0.9843 0.9003 0.9925
69 1976-11-01 0.9843 0.9003 0.9925
70 1976-11-02 0.9817 0.8838 0.9913
71 1976-11-03 0.9817 0.8838 0.9913
72 1976-11-04 0.9817 0.8838 0.9913
73 1976-11-05 0.9818 0.8843 0.9913Con utils::tail() mostramos como los últimos valores
estimados del CFR ajustado y sin ajustar tienen rangos superpuestos de
intervalos de confianza del 95%.
Ahora, visualicemos ambos resultados en una serie temporal. ¿Cómo se comportarían en tiempo real las estimaciones de CFR ajustados y sin ajustar?
R
# get the latest delay-adjusted CFR
rolling_cfr_adjusted_end <-
rolling_cfr_adjusted %>%
dplyr::slice_tail()
# bind by rows both output data frames
bind_rows(
rolling_cfr_naive %>%
mutate(method = "naive"),
rolling_cfr_adjusted %>%
mutate(method = "adjusted")
) %>%
# visualise both adjusted and unadjusted rolling estimates
ggplot() +
geom_ribbon(
aes(
date,
ymin = severity_low,
ymax = severity_high,
fill = method
),
alpha = 0.2, show.legend = FALSE
) +
geom_line(
aes(date, severity_estimate, colour = method)
) +
geom_hline(
data = rolling_cfr_adjusted_end,
aes(yintercept = severity_estimate)
) +
geom_hline(
data = rolling_cfr_adjusted_end,
aes(yintercept = severity_low),
lty = 2
) +
geom_hline(
data = rolling_cfr_adjusted_end,
aes(yintercept = severity_high),
lty = 2
)
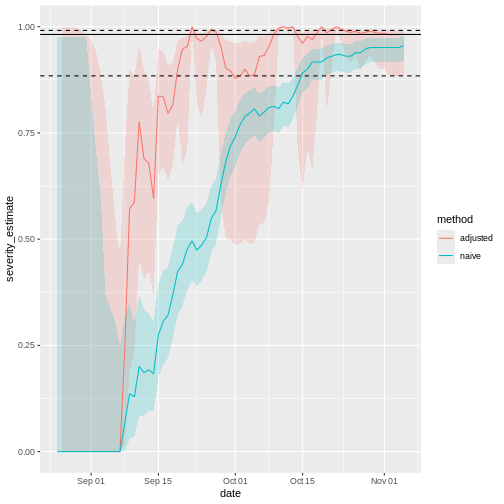
La línea horizontal representa el CFR ajustado al retraso temporal, estimada al final del brote. La línea punteada significa que la estimación tiene un intervalo de confianza del 95% (IC 95%).
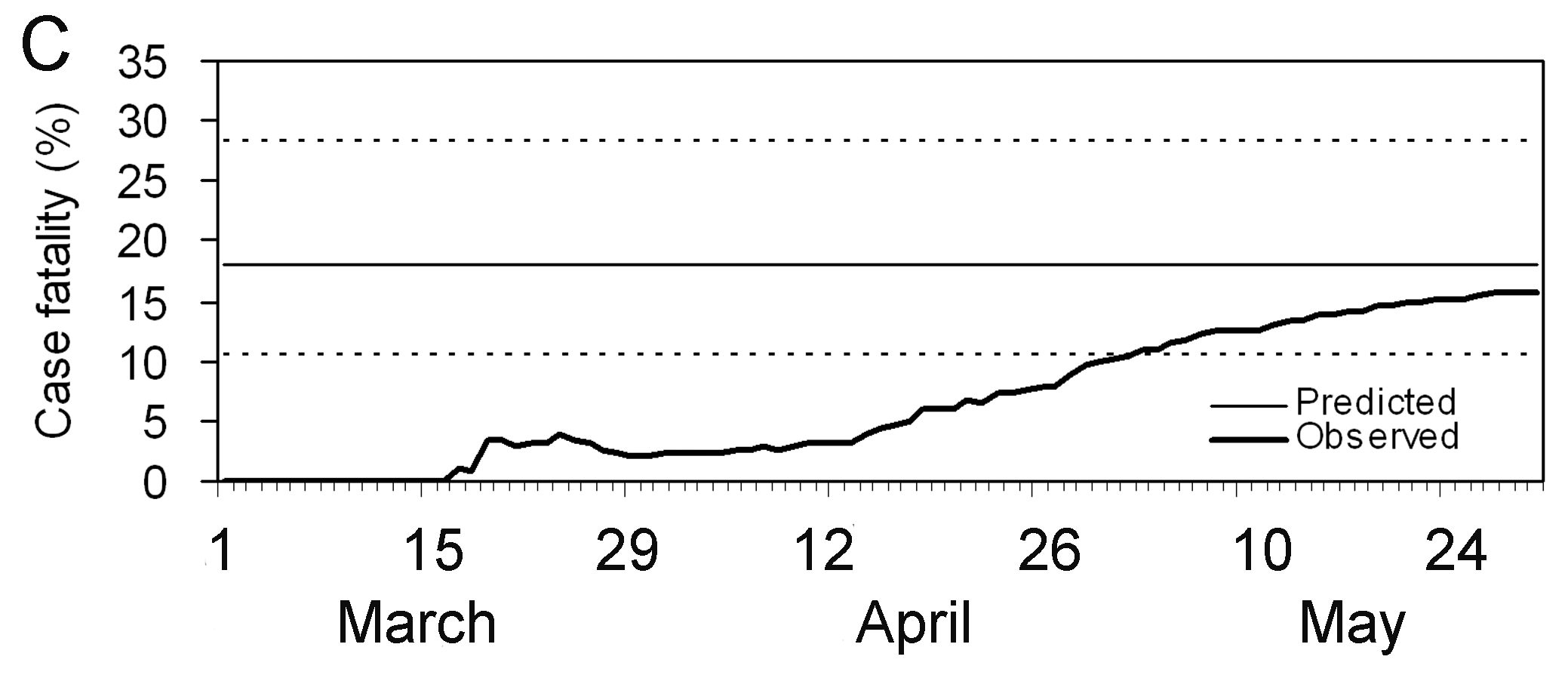
Observa que este cálculo ajustado al retraso temporal entre síntomas y muerte es especialmente útil cuando los únicos datos disponibles son curvas epidémica de casos confirmados (es decir, cuando no se dispone de datos individuales, especialmente durante la fase inicial de la epidemia). Cuando hay pocas muertes o ninguna, hay que hacer una suposición para la distribución temporal desde la aparición de síntomas hasta la muerte, por ejemplo, a partir de la literatura basada en brotes anteriores. Nishiura et al., 2009 representan esto en las figuras con datos del brote de SARS en Hong Kong, 2003.
Las figuras A y B muestran el número acumulado de casos y muertes por SRAS, y la figura C muestra las estimaciones observadas (sesgadas) del CFR en función del tiempo, es decir, el número acumulado de muertes sobre casos en el momento \(t\). Debido al retraso temporal desde el inicio de los síntomas hasta la muerte, la estimación sesgada de la probabilidad de muerte en el tiempo \(t\) subestima el valor en las etapas finales del brote (es decir, 302/1755 = 17,2%).
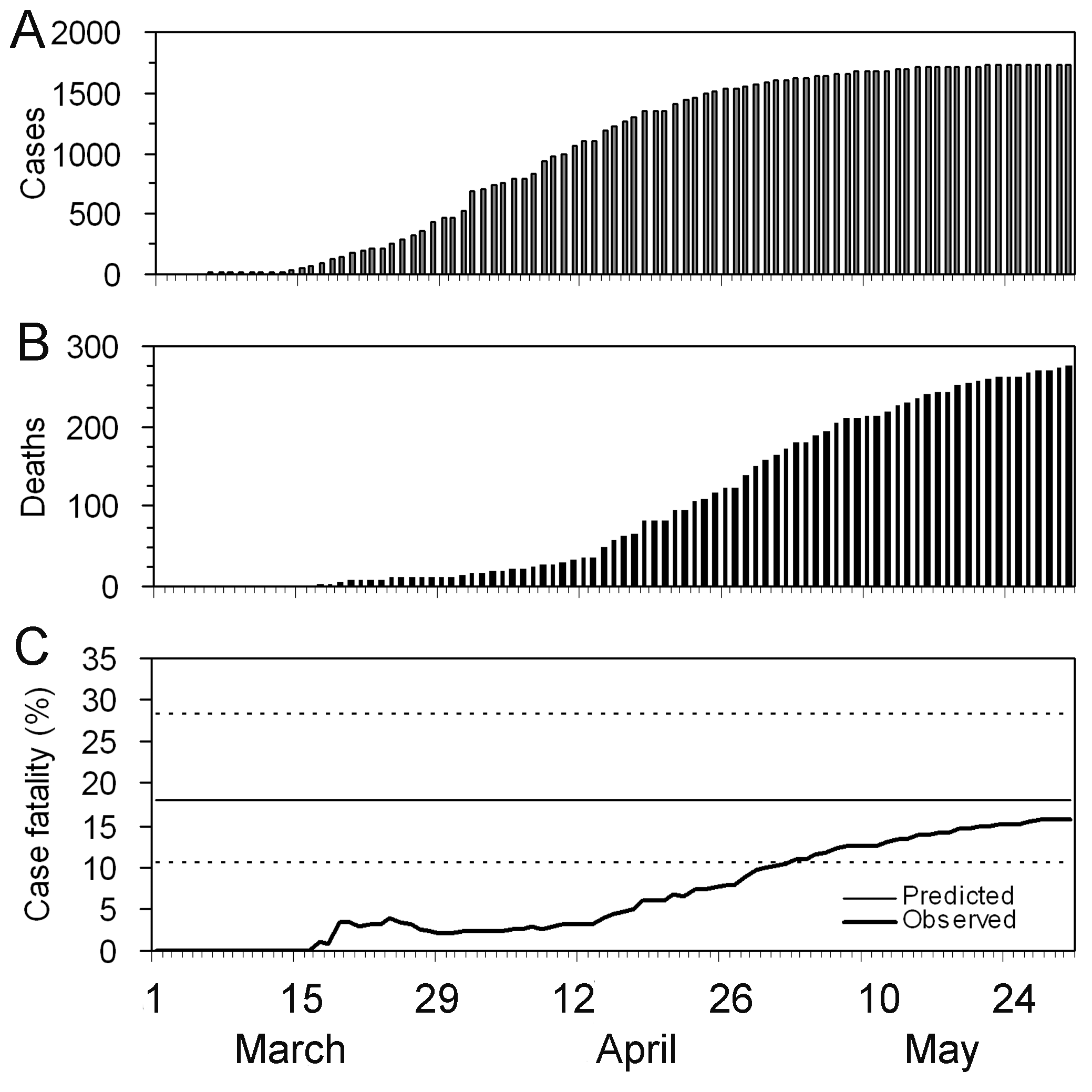
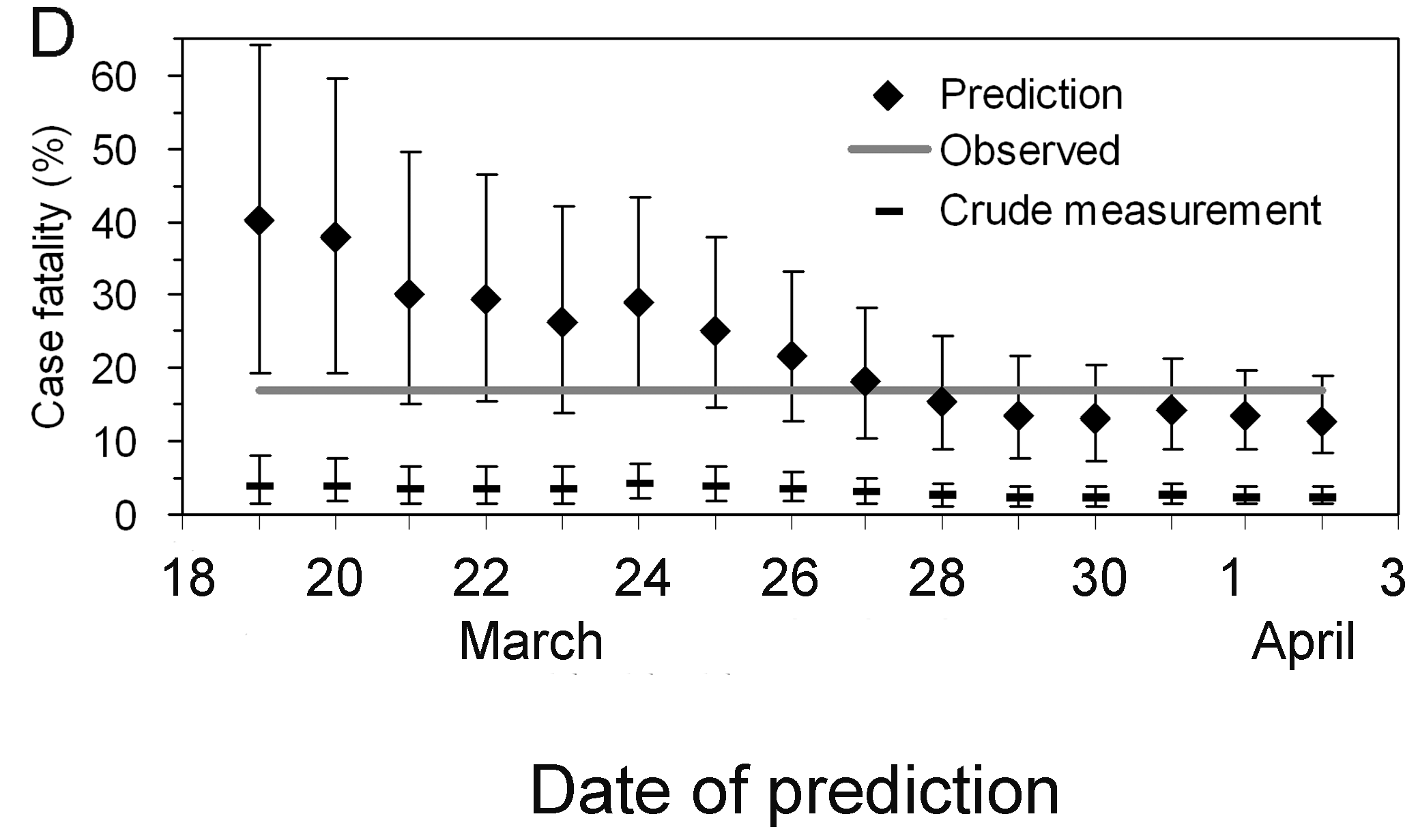
No obstante, incluso utilizando únicamente los datos observados para
el periodo comprendido entre el 19 de marzo y el 2 de abril,
cfr_static() puede obtener una predicción adecuada (Figura
D), por ejemplo, el CFR ajustado al retraso en el 27 de marzo es del
18,1% (IC del 95%: 10,5, 28,1). Se observa una sobreestimación en las
fases muy tempranas de la epidemia, pero los límites de confianza del
95% en las fases posteriores incluyen el CFR realizado (es decir, 17,2
%).
Interpretar la estimación del CFR en la fase inicial del brote
Basándote en la figura anterior:
- ¿Cuántos días hay entre el inicio del brote y la fecha en la que el intervalo de confianza de la CFR ajustado se cruza con el intervalo de confianza de la CFR sin ajustar? ¿Los intervalos se cruzan con el CFR estimada al final del brote?
Discusión:
- ¿Cuáles son las implicaciones para la política de salud pública de tener una CFR ajustado por retraso temporal?
Podemos utilizar la inspección visual o el análisis de los marcos de datos de salida.
Hay casi un mes de diferencia.
Nótese que la estimación tiene una incertidumbre considerable al principio de la serie temporal. Al cabo de dos semanas, el CFR ajustado se aproxima a la estimación global del CFR al final del brote.
¿Es este patrón similar al de otros brotes? Podemos utilizar los conjuntos de datos de los retos de este episodio. ¡Te invitamos a averiguarlo!
Lista de verificación
Con cfr estimamos el CFR como la proporción de muertes entre confirmadas confirmados.
Utilizando sólo el número de casos confirmados está claro que se pasarán por alto todos los casos que no busquen tratamiento médico o no sean notificados, así como todos los casos asintomáticos. Esto significa que la estimación del CFR es superior a la proporción de muertes entre los infectados.
cfr tiene como objetivo obtener un estimador insesgado “mucho antes” de observar el curso completo del brote. Para ello cfr utiliza el factor de subestimación \(u_{t}\) para estimar el CFR sin sesgo \(p_{t}\) , utilizando métodos de máxima verosimilitud, dado el proceso de muestreo definido por Nishiura et al., 2009.

En datos agregados de incidencia en el momento \(t\) conocemos el número acumulado de casos confirmados y muertes, \(C_{t}\) y \(D_{t}\) y deseamos estimar el CFR sin sesgo \(\pi\) mediante el factor de subestimación \(u_{t}\).
Si conociéramos el factor de subestimación \(u_{t}\) podríamos especificar el tamaño de la población de casos confirmados que ya no corren riesgo (\(u_{t}C_{t}\), sombreado), aunque no sabemos qué individuos supervivientes pertenecen a este grupo. Una proporción \(\pi\) de los del grupo de casos aún en riesgo (tamaño \((1- u_{t})C_{t}\), sin sombrear) se espera que muera.
Ya que cada caso que deja de estar en riesgo tiene una probabilidad independiente de morir, \(\pi\) el número de muertes, \(D_{t}\) es una muestra de una distribución binomial con tamaño de muestra \(u_{t}C_{t}\) y probabilidad de morir \(p_{t}\) = \(\pi\).
Esto se representa mediante la siguiente función de verosimilitud para obtener la estimación de máxima verosimilitud del CFR sin sesgo \(p_{t}\) = \(\pi\):
\[ {\sf L}(\pi | C_{t},D_{t},u_{t}) = \log{\dbinom{u_{t}C_{t}}{D_{t}}} + D_{t} \log{\pi} + (u_{t}C_{t} - D_{t})\log{(1 - \pi)}, \]
Esta estimación la realiza la función interna
?cfr:::estimate_severity().
- La CFR ajustado al retraso temporal no aborda todas las fuentes de error en los datos, como el infradiagnóstico de individuos infectados.
Desafíos
Los datos agregados difieren de los listados de casos individuales
Los datos de incidencia agregados difieren de lista en los que cada observación contiene datos a nivel individual.
R
outbreaks::ebola_sierraleone_2014 %>% as_tibble()
SALIDA
# A tibble: 11,903 × 8
id age sex status date_of_onset date_of_sample district chiefdom
<int> <dbl> <fct> <fct> <date> <date> <fct> <fct>
1 1 20 F confirmed 2014-05-18 2014-05-23 Kailahun Kissi Teng
2 2 42 F confirmed 2014-05-20 2014-05-25 Kailahun Kissi Teng
3 3 45 F confirmed 2014-05-20 2014-05-25 Kailahun Kissi Tonge
4 4 15 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
5 5 19 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
6 6 55 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
7 7 50 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
8 8 8 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
9 9 54 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
10 10 57 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
# ℹ 11,893 more rowsUtiliza el paquete incidence2 para reordenar tus datos
¿Cómo reorganizar mis datos de entrada?
Reorganizar los datos de entrada para el análisis de datos puede llevarte la mayor parte del tiempo. Para estar listo para el análisis con datos de incidencia agregados te animamos a utilizar incidence2 ¡!
Primero, en la viñeta Inicio
de incidence2 explora cómo utilizar
date_index al leer un listado de casos con fechas en varias
columnas.
A continuación, consulta la viñeta Manejo
de datos de {incidence2} del paquete
cfr, sobre cómo utilizar la función
cfr::prepare_data() con los objetos incidence2.
R
# Carga los paquetes
library(cfr)
library(epiparameter)
library(incidence2)
library(outbreaks)
library(tidyverse)
# Accede a la distribución de retrasos temporales
mers_delay <-
epidist_db(
disease = "mers",
epi_dist = "onset to death",
single_epidist = TRUE
)
# Lee el listado de casos
mers_korea_2015$linelist %>%
as_tibble() %>%
select(starts_with("dt_"))
SALIDA
# A tibble: 162 × 6
dt_onset dt_report dt_start_exp dt_end_exp dt_diag dt_death
<date> <date> <date> <date> <date> <date>
1 2015-05-11 2015-05-19 2015-04-18 2015-05-04 2015-05-20 NA
2 2015-05-18 2015-05-20 2015-05-15 2015-05-20 2015-05-20 NA
3 2015-05-20 2015-05-20 2015-05-16 2015-05-16 2015-05-21 2015-06-04
4 2015-05-25 2015-05-26 2015-05-16 2015-05-20 2015-05-26 NA
5 2015-05-25 2015-05-27 2015-05-17 2015-05-17 2015-05-26 NA
6 2015-05-24 2015-05-28 2015-05-15 2015-05-17 2015-05-28 2015-06-01
7 2015-05-21 2015-05-28 2015-05-16 2015-05-17 2015-05-28 NA
8 2015-05-26 2015-05-29 2015-05-15 2015-05-15 2015-05-29 NA
9 NA 2015-05-29 2015-05-15 2015-05-17 2015-05-29 NA
10 2015-05-21 2015-05-29 2015-05-16 2015-05-16 2015-05-29 NA
# ℹ 152 more rowsR
# Usa {incidence2} para contabilizar la incidencia diaria
mers_incidence <- mers_korea_2015$linelist %>%
# convertir a un objeto incidence2
incidence(date_index = c("dt_onset", "dt_death")) %>%
# completa las fechas de la primera a la última
incidence2::complete_dates()
# Explora los resultados de incidence2
mers_incidence
SALIDA
# incidence: 72 x 3
# count vars: dt_death, dt_onset
date_index count_variable count
<date> <chr> <int>
1 2015-05-11 dt_death 0
2 2015-05-11 dt_onset 1
3 2015-05-12 dt_death 0
4 2015-05-12 dt_onset 0
5 2015-05-13 dt_death 0
6 2015-05-13 dt_onset 0
7 2015-05-14 dt_death 0
8 2015-05-14 dt_onset 0
9 2015-05-15 dt_death 0
10 2015-05-15 dt_onset 0
# ℹ 62 more rowsR
# Prepara los datos {incidence2} para usarlos en {cfr}
mers_incidence %>%
prepare_data(
cases_variable = "dt_onset",
deaths_variable = "dt_death"
)
SALIDA
date deaths cases
1 2015-05-11 0 1
2 2015-05-12 0 0
3 2015-05-13 0 0
4 2015-05-14 0 0
5 2015-05-15 0 0
6 2015-05-16 0 0
7 2015-05-17 0 1
8 2015-05-18 0 1
9 2015-05-19 0 0
10 2015-05-20 0 5
11 2015-05-21 0 6
12 2015-05-22 0 2
13 2015-05-23 0 4
14 2015-05-24 0 2
15 2015-05-25 0 3
16 2015-05-26 0 1
17 2015-05-27 0 2
18 2015-05-28 0 1
19 2015-05-29 0 3
20 2015-05-30 0 5
21 2015-05-31 0 10
22 2015-06-01 2 16
23 2015-06-02 0 11
24 2015-06-03 1 7
25 2015-06-04 1 12
26 2015-06-05 1 9
27 2015-06-06 0 7
28 2015-06-07 0 7
29 2015-06-08 2 6
30 2015-06-09 0 1
31 2015-06-10 2 6
32 2015-06-11 1 3
33 2015-06-12 0 0
34 2015-06-13 0 2
35 2015-06-14 0 0
36 2015-06-15 0 1R
# Estima el CFR ajustado a retrasos temporales
mers_incidence %>%
cfr::prepare_data(
cases_variable = "dt_onset",
deaths_variable = "dt_death"
) %>%
cfr::cfr_static(delay_density = function(x) density(mers_delay, x))
SALIDA
severity_estimate severity_low severity_high
1 0.0907 0.042 0.4847Heterogeneidad de la gravedad
La CFR puede diferir entre poblaciones (por ejemplo, edad, espacio, tratamiento); cuantificar estas heterogeneidades puede ayudar a dirigir los recursos adecuadamente y a comparar distintos regímenes asistenciales (Cori et al., 2017).
Utiliza la base de datos cfr::covid_data para estimar
una CFR ajustado al retraso temporal estratificada por países.
Una forma de hacer un análisis estratificado es aplicar un
modelo a datos anidados. Esta viñeta
{tidyr} te muestra cómo aplicar la función
group_by() + nest() a los datos anidados, y
luego mutate() + map() para aplicar el
modelo.
R
library(cfr)
library(epiparameter)
library(tidyverse)
covid_data %>% glimpse()
SALIDA
Rows: 20,786
Columns: 4
$ date <date> 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2…
$ country <chr> "Argentina", "Brazil", "Colombia", "France", "Germany", "India…
$ cases <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ deaths <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…R
delay_onset_death <-
epidist_db(
disease = "covid",
epi_dist = "onset to death",
single_epidist = TRUE
)
covid_data %>%
group_by(country) %>%
nest() %>%
mutate(
temp =
map(
.x = data,
.f = cfr::cfr_static,
delay_density = function(x) density(delay_onset_death, x)
)
) %>%
unnest(cols = temp)
SALIDA
# A tibble: 19 × 5
# Groups: country [19]
country data severity_estimate severity_low severity_high
<chr> <list> <dbl> <dbl> <dbl>
1 Argentina <tibble> 0.0133 0.0133 0.0133
2 Brazil <tibble> 0.0195 0.0195 0.0195
3 Colombia <tibble> 0.0225 0.0224 0.0226
4 France <tibble> 0.0044 0.0044 0.0044
5 Germany <tibble> 0.0045 0.0045 0.0045
6 India <tibble> 0.0119 0.0119 0.0119
7 Indonesia <tibble> 0.024 0.0239 0.0241
8 Iran <tibble> 0.0191 0.0191 0.0192
9 Italy <tibble> 0.0075 0.0075 0.0075
10 Mexico <tibble> 0.0461 0.046 0.0462
11 Peru <tibble> 0.0318 0.0151 0.202
12 Poland <tibble> 0.0186 0.0186 0.0187
13 Russia <tibble> 0.0182 0.0182 0.0182
14 South Africa <tibble> 0.0254 0.0253 0.0255
15 Spain <tibble> 0.0087 0.0087 0.0087
16 Turkey <tibble> 0.006 0.006 0.006
17 Ukraine <tibble> 0.0204 0.0203 0.0205
18 United Kingdom <tibble> 0.009 0.009 0.009
19 United States <tibble> 0.0111 0.0111 0.0111¡Estupendo! Ahora puedes utilizar un código similar para cualquier otro análisis estratificado, como la edad, las regiones u otros.
Pero, ¿cómo podemos interpretar que existe una variabilidad de gravedad por países a partir del mismo patógeno diagnosticado?
Factores locales como la capacidad de análisis, la definición de caso y el régimen de muestreo pueden afectar a la notificación de casos y muertes, afectando así a la comprobación de los casos. Echa un vistazo a la viñeta Estimar la proporción de casos que se determinan durante un brote del paquete cfr para más información ¡!
Apéndice
El paquete cfr tiene una función llamada
cfr_time_varying() con una funcionalidad distinta de
cfr_rolling().
¿Cuándo utilizar cfr_rolling()?
cfr_rolling() muestra el CFR estimada en cada día del brote, dado que los datos futuros sobre casos y muertes no están disponibles en ese momento. El valor final de cfr_rolling() estimado es idéntico al de cfr_static() con los mismos datos.
Recuerda, como se muestra arriba cfr_rolling() es útil para obtener estimaciones del CFR en las primeras fases y comprobar si la estimación del CFR de un brote se ha estabilizado. Así, cfr_rolling() no es sensible a la duración ni al tamaño de la epidemia.
¿Cuándo utilizar cfr_time_varying()?
Por otra parte, cfr_time_varying() calcula el CFR a lo largo de una ventana móvil y ayuda a comprender los cambios en el CFR debidos a cambios en la epidemia, por ejemplo, debidos a una nueva variante o a una mayor inmunidad por vacunación.
Sin embargo, cfr_time_variying() es sensible a la incertidumbre del muestreo. Por tanto, es sensible al tamaño del brote. Cuanto mayor sea el número de casos con resultados esperados en un día determinado, más estimaciones razonables del CFR variable en el tiempo obtendremos.
Por ejemplo, con 100 casos, la estimación del riesgo de mortalidad tendrá, a grandes rasgos, un intervalo de confianza del 95% ±10% de la estimación media (IC binomial). Por tanto, si tenemos >100 casos con resultados esperados en un día determinado podemos obtener estimaciones razonables del CFR variable en el tiempo. Pero si sólo tenemos >100 casos a lo largo de toda la epidemia probablemente tengamos que basarnos en cfr_rolling() que utiliza los datos acumulados.
Te invitamos a leer esta viñeta
sobre cfr_time_varying().
Más medidas de gravedad
Supongamos que necesitamos evaluar la gravedad clínica de la epidemia en un contexto distinto al de los datos de vigilancia, como la gravedad entre los casos que llegan a los hospitales o los casos que recogiste en una encuesta serológica representativa.
Utilizando cfr podemos cambiar las entradas para el
numerador casos (cases) y el denominador
muertes (deaths) para estimar más medidas
de gravedad, como el Riesgo de Fatalidad por Infección (RFI) o el Riesgo
de Fatalidad por Hospitalización (RFH). Podemos seguir esta
analogía:
Si para la una probabilidad de muerte (CFR o CFR en inglés), exigimos:
- Incidencia de casos y muertes, con una:
- Distribución de retraso temporal entre casos y muertes (o una aproximación cercana, como el tiempo entre inicio de los síntomas y la muerte).
Entonces, el Riesgo de Fatalidad por Infección (IFR, por sus siglas en inglés) requiere:
- Incidencia de infecciones y muertes, con una:
- Distribución de retraso temporal desde la infección hasta la muerte (o una aproximación cercana).
Del mismo modo, el Riesgo de Fatalidad por Hospitalización (HFR) requiere:
- Incidencia de hospitalizaciones y muertes, y una:
- Distribución del retraso temporal entre la hospitalización y la muerte.
Yang et al., 2020 resume diferentes definiciones y fuentes de datos:
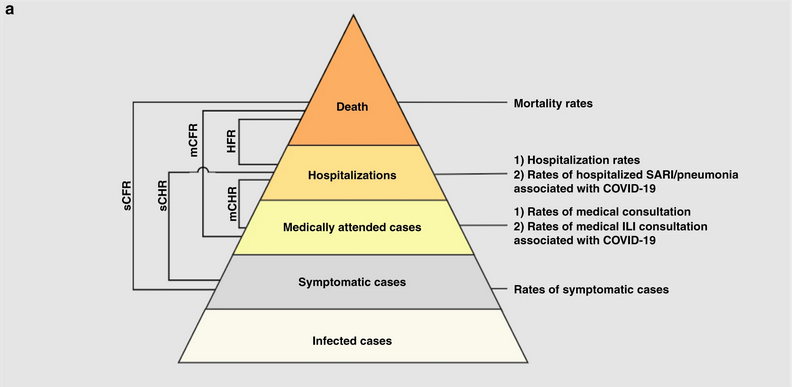
- sCFR riesgo sintomático de muerte,
- sCHR riesgo sintomático de hospitalización,
- mCFR riesgo de caso-fatalidad médicamente atendido,
- mCHR riesgo de hospitalización de casos atendidos médicamente,
- HFR riesgo de hospitalización-fatalidad.
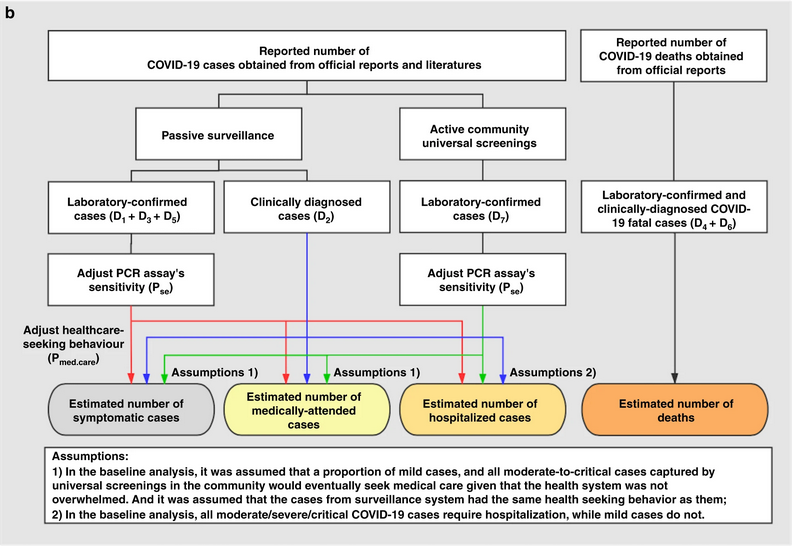
Discusión
Basándote en tu experiencia:
- Comparte algún brote anterior en el que hayas participado en su respuesta.
Responde a estas preguntas:
- ¿Cómo evaluaste la gravedad clínica del brote?
- ¿Cuáles fueron las principales fuentes de sesgo?
- ¿Qué hiciste para tener en cuenta el sesgo identificado?
- ¿Qué análisis complementario harías para resolver el sesgo?
Puntos Clave
Utiliza cfr para estimar la gravedad
Utiliza
cfr_static()para estimar el CFR global con los últimos datos disponibles.Utiliza
cfr_rolling()para mostrar cuál sería el CFR estimada en cada día del brote.Utiliza la
delay_densitypara ajustar el CFR según la distribución de retrasos correspondiente.
