Real-time analysis and forecasting for outbreak analytics with R: Todo en una sola página

Content from Acceder a las distribuciones de retrasos epidemiológicos

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

¿Cómo acceder a las distribuciones de retraso de la enfermedad desde una base de datos preestablecida para su uso en el análisis?

Objetivos

Obtener retrasos de una base de datos de búsqueda bibliográfica con {epiparameter}.
Obtén parámetros de distribución y estadísticas resumidas de distribuciones de retrasos.

Requisitos previos

Este episodio requiere que estés familiarizado con

Ciencia de datos Programación básica con R

Teoría epidémica : Pparámetros epidemiológicos, periodos de tiempo de la enfermedad, como el periodo de incubación, el tiempo de generación y el intervalo serial.

Introducción

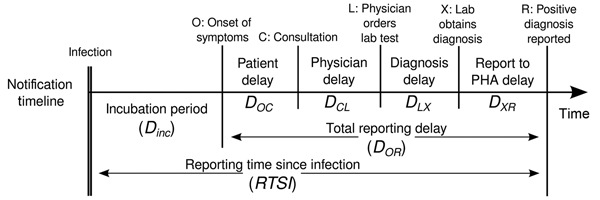
Las enfermedades infecciosas siguen un ciclo de infección, que generalmente incluye las siguientes fases: periodo presintomático, periodo sintomático y periodo de recuperación, tal y como se describe en su historia natural. Estos periodos de tiempo pueden utilizarse para comprender la dinámica de transmisión e informar sobre las intervenciones de prevención y control de enfermedades.

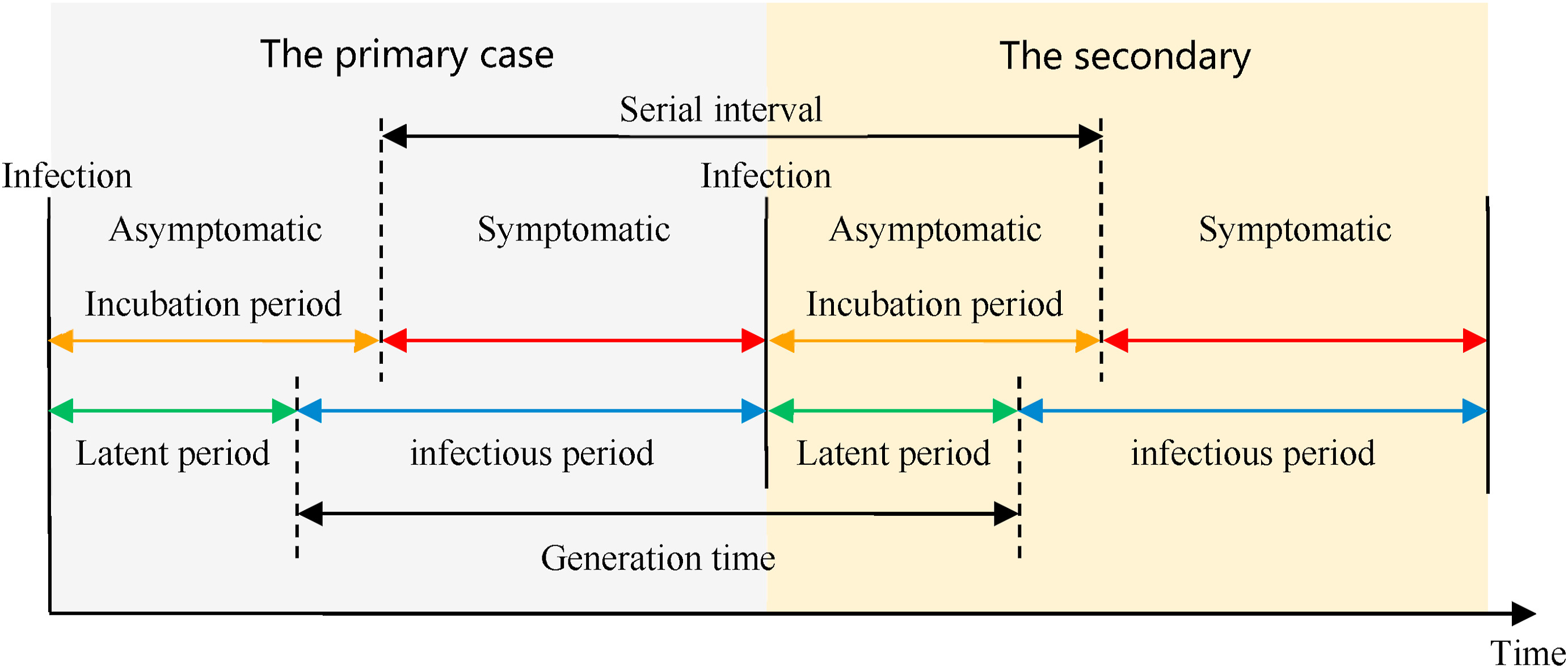
Definición de los periodos de tiempo clave. En Xiang et al, 2021

Definiciones

Mira el glosario ¡para ver las definiciones de todos los periodos de tiempo de la figura anterior!

Sin embargo, al inicio de una epidemia, los esfuerzos de modelamiento pueden verse retrasados por la falta de un recurso centralizado que resuma los parámetros de entrada para la enfermedad de interés (Nash et al., 2023). Proyectos como {epiparameter} y {epireview} están construyendo catálogos en línea siguiendo protocolos de síntesis de literatura que pueden ayudar a parametrizar modelos accediendo fácilmente a una extensa biblioteca de parámetros epidemiológicos previamente estimados de brotes pasados.

Para ejemplificar cómo utilizar el {epiparameter} R en tu canal de análisis, nuestro objetivo en este episodio será acceder a un conjunto específico de parámetros epidemiológicos de la literatura, en lugar de copiarlos y pegarlos manualmente, para integrarlos en un flujo de trabajo de análisis con EpiNow2

Empecemos cargando el paquete {epiparameter}. Utilizaremos la tubería %>% para conectar algunas de sus funciones, algunas funciones detibble y dplyr, así que llamaremos también al paquetetidyverse:

R

library(epiparameter)
library(tidyverse)

El doble punto

El doble punto :: en R te permite llamar a una función específica de un paquete sin cargar todo el paquete en el entorno actual.

Por ejemplo dplyr::filter(data, condition) utiliza filter() del paquetedplyr.

Esto nos ayuda a recordar las funciones del paquete y a evitar conflictos de espacio de nombres.

El problema

Si queremos estimar la transmisibilidad de una infección, es común utilizar un paquete como EpiEstim o EpiNow2. Sin embargo, ambos requieren cierta información epidemiológica como entrada. Por ejemplo, en EpiNow2 utilizamos EpiNow2::Gamma() para especificar un tiempo de generación como una distribución de probabilidad añadiendo su media mean desviación estándar (sd) y el valor máximo (max).

Para especificar un tiempo de generación generation_time que sigue a un Gamma con media $\mu = 4$ y desviación estándar $\sigma = 2$ y un valor máximo de 20, escribimos

R

generation_time <-
  EpiNow2::Gamma(
  mean = 4,
  sd = 2,
  max = 20
  )

Es una práctica común para analistas, buscar manualmente en la literatura disponible y copiar y pegar el resumen estadístico o los parámetros de distribución de las publicaciones científicas. Un reto frecuente al que nos enfrentamos a menudo es que la información sobre las distintas distribuciones estadísticas no es coherente en toda la literatura. El objetivo de {epiparameter} es facilitar el acceso a estimaciones confiables de los parámetros de distribución para una serie de enfermedades infecciosas, de modo que puedan implementarse fácilmente en las líneas de análisis de brotes.

En este episodio acceder a a las estadísticas resumidas del tiempo de generación de COVID-19 desde la biblioteca de parámetros epidemiológicos proporcionada por {epiparameter}. Estos parámetros pueden utilizarse para estimar la transmisibilidad de esta enfermedad utilizando EpiNow2 en episodios posteriores.

Empecemos por ver cuántas entradas hay disponibles en el base de datos de distribuciones epidemiológicas en {epiparameter} utilizando epidist_db() para la distribución epidemiológica epi_dist llamada tiempo de generación con la cadena "generation":

R

epiparameter::epidist_db(
  epi_dist = "generation"
)

SALIDA

Returning 1 results that match the criteria (1 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SALIDA

Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Distribution: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull
Parameters:
  shape: 2.360
  scale: 3.180

Actualmente, en la biblioteca de parámetros epidemiológicos, tenemos una entrada de tiempo generación "generation" para Influenza. En su lugar, podemos consultar intervalos seriales "serial" para COVID-19. ¡Veamos qué debemos tener en cuenta para ello!

Tiempo de generación vs intervalo serial

El tiempo de generación, junto con el número reproductivo ($R$), proporcionan información valiosa sobre la fuerza de transmisión e informan la implementación de medidas de control. Dado un $R>1$, cuanto más corto sea el tiempo de generación, más rápidamente aumentará la incidencia de casos de enfermedad.

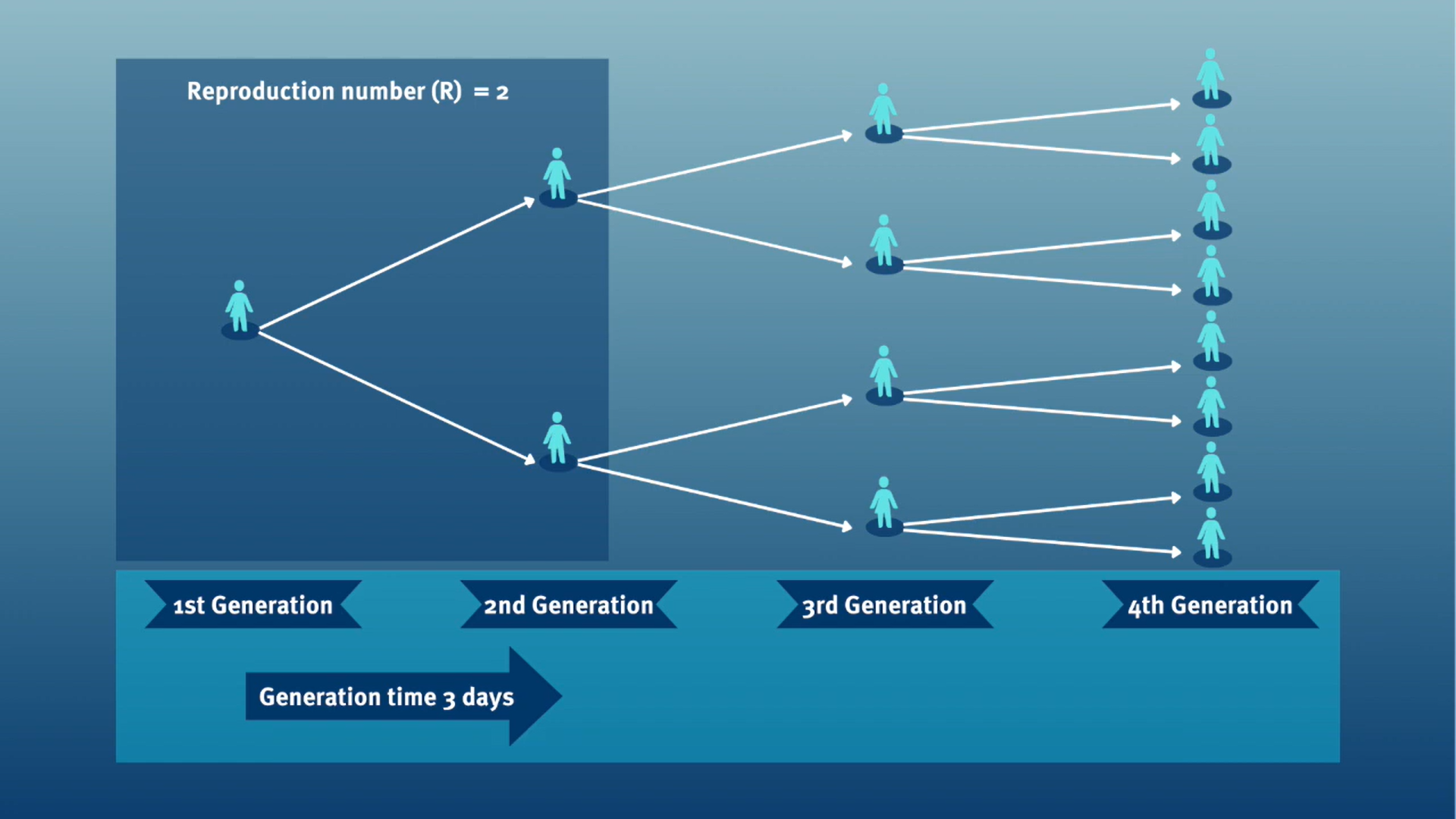
Vídeo del Centro MRC para el Análisis Global de las Enfermedades Infecciosas, Ep 76. Ciencia en Contexto - Grupo de Revisión de Parámetros Epi con la Dra. Anne Cori (27-07-2023) en https://youtu.be/VvpYHhFDIjI?si=XiUyjmSV1gKNdrrL

Al calcular el número de reproducción efectivo ($R_{t}$), el tiempo de generación suele aproximarse mediante el intervalo serial serial. Esta aproximación frecuente se debe a que es más fácil observar y medir el inicio de los síntomas que el inicio de la infección.

Un Esquema de la relación de los distintos periodos de tiempo de transmisión entre un infector y un infectado en un par de transmisión. La ventana de exposición se define como el intervalo de tiempo que tiene la exposición viral, y la ventana de transmisión se define como el intervalo de tiempo para la transmisión posterior con respecto al tiempo de infección (Chung Lau et al., 2021).

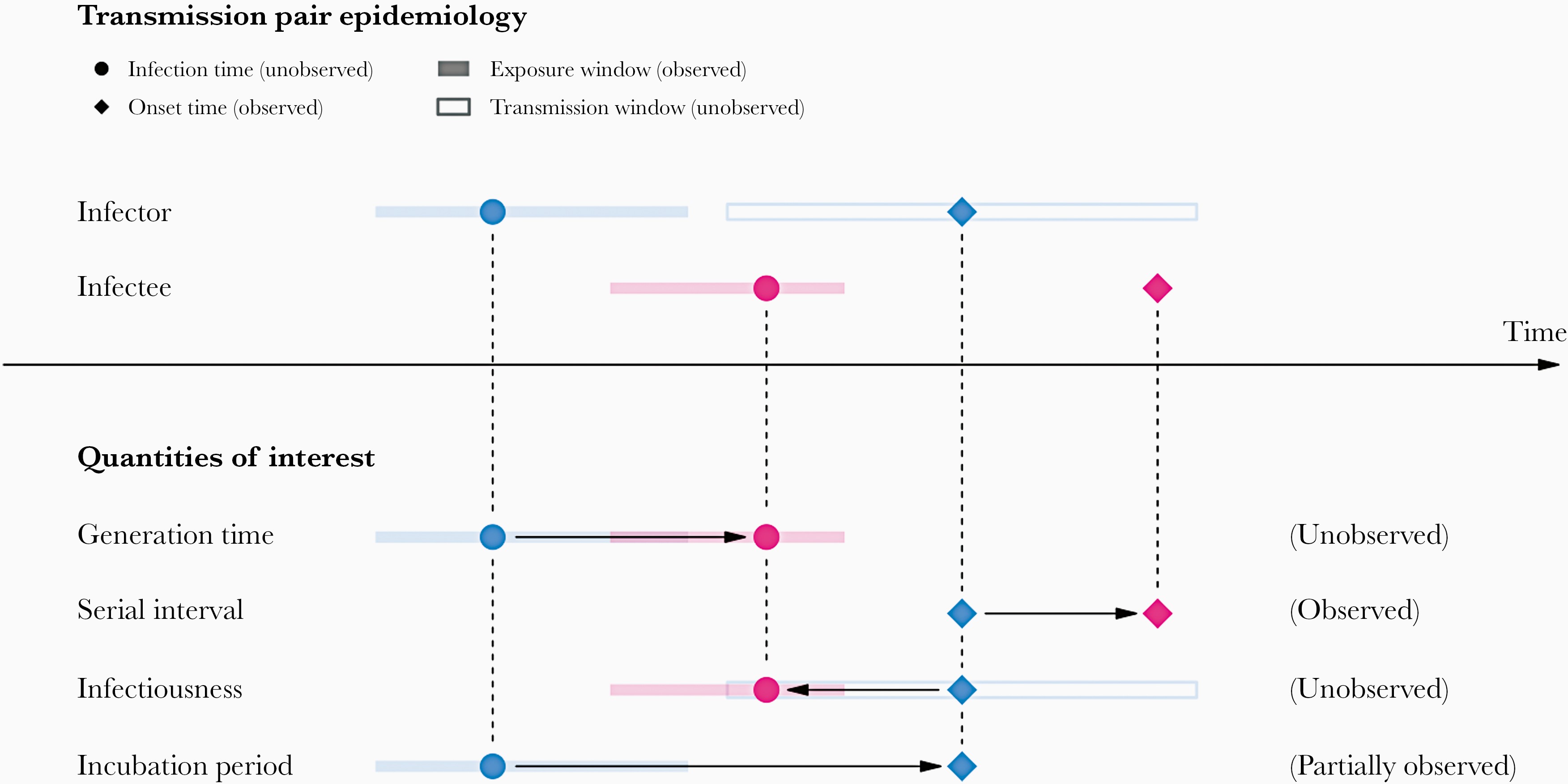
Sin embargo, usar elintervalo serial como una aproximación del tiempo de generación es válido principalmente para las enfermedades en las que la infecciosidad comienza después de la aparición de los síntomas (Chung Lau et al., 2021). En los casos en que la infecciosidad comienza antes de la aparición de los síntomas, los intervalos seriales pueden tener valores negativos, como ocurre en las enfermedades con transmisión presintomática (Nishiura et al., 2020).

De los periodos de tiempo a las distribuciones de probabilidad.

Cuando calculamos el intervalo serial vemos que no todos los pares de casos tienen la misma duración temporal. Observaremos esta variabilidad para cualquier par de casos y periodo de tiempo individual, incluido el periodo de incubación y periodo infeccioso.

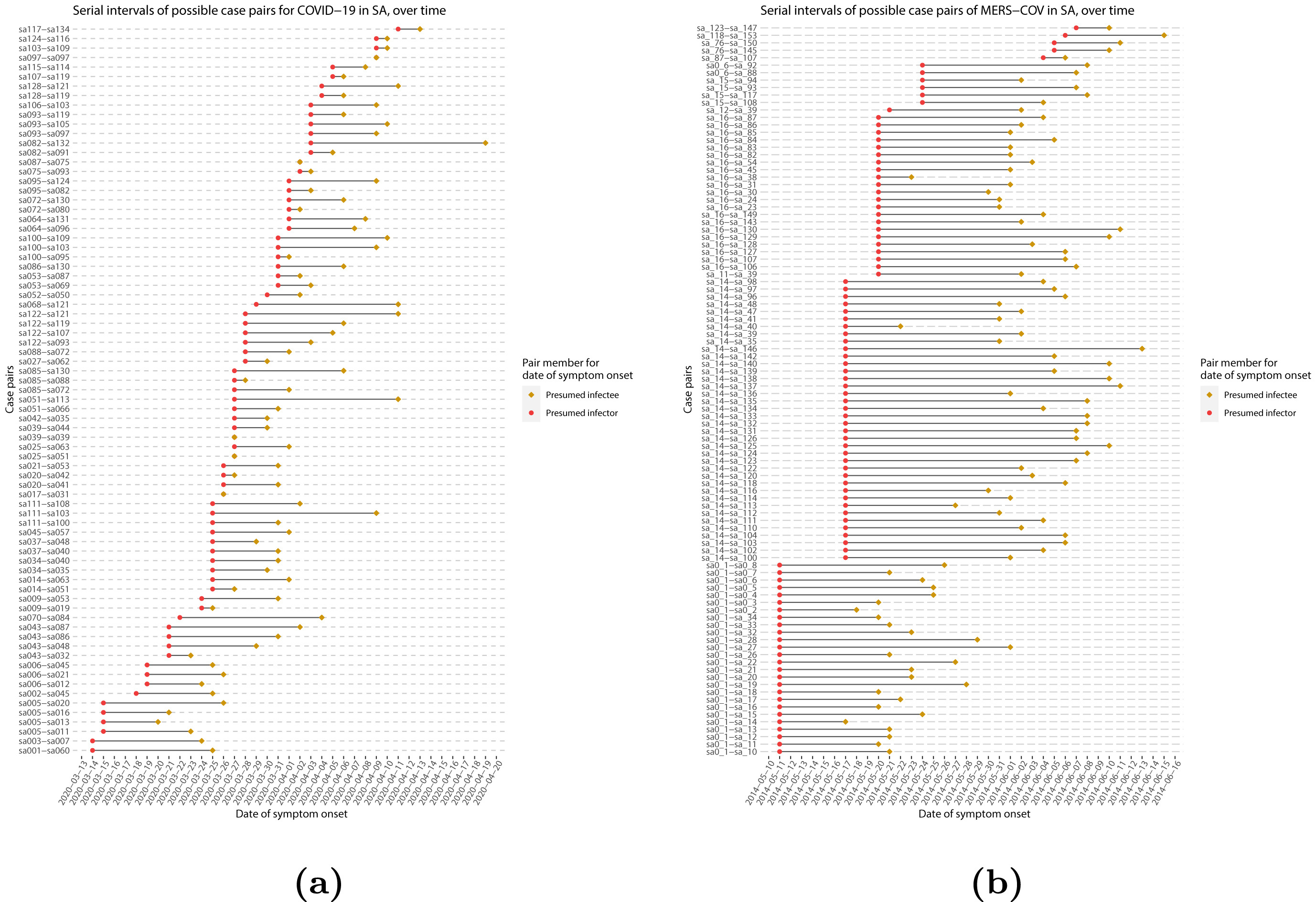
Intervalos seriales de posibles parejas de casos en (a) COVID-19 y (b) MERS-CoV. Los pares representan un supuesto infector y su presunto infectado trazados por fecha de inicio de los síntomas (Althobaity et al., 2022).

Para resumir estos datos de periodos de tiempo individuales y de pares, podemos encontrar las distribuciones estadísticas que mejor se ajusten a los datos (McFarland et al., 2023).

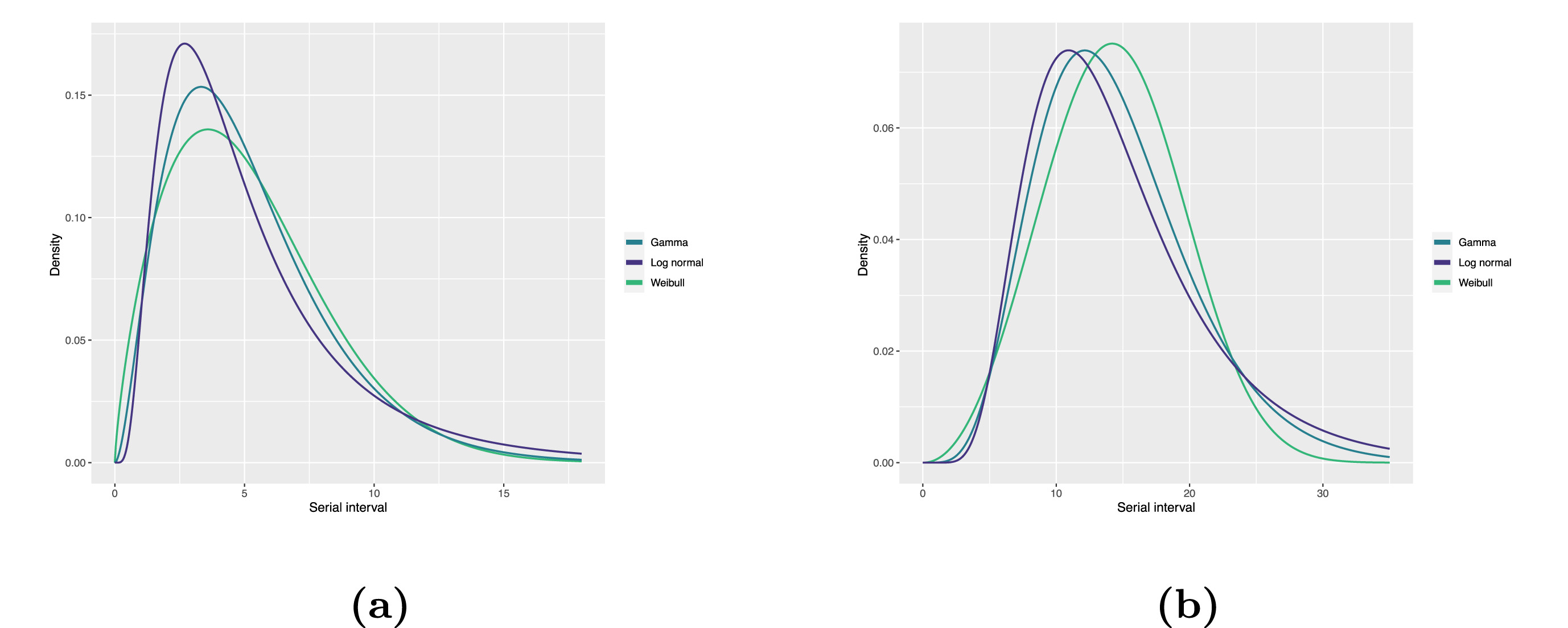
Distribución ajustada del intervalo serial para (a) COVID-19 y (b) MERS-CoV basada en pares de transmisión notificados en Arabia Saudí. Ajustamos tres distribuciones comunmente usadas, Log normal, Gamma y Weibull, respectivamente (Althobaity et al., 2022).

Las distribuciones estadísticas se resumen en función de sus estadísticas de resumen como la ubicación (media y percentiles) y dispersión (varianza o desviación estándar) de la distribución, o con su parámetros de distribución que informan sobre la forma (shape y rate/scale) de la distribución. Estos valores estimados pueden reportarse con su incertidumbre (intervalos de confianza del 95%).

Gamma	media	forma	velocidad/escala
MERS-CoV	14.13(13.9-14.7)	6.31(4.88-8.52)	0.43(0.33-0.60)
COVID-19	5.1(5.0-5.5)	2.77(2.09-3.88)	0.53(0.38-0.76)

Weibull	media	forma	velocidad/escala
MERS-CoV	14.2(13.3-15.2)	3.07(2.64-3.63)	16.1(15.0-17.1)
COVID-19	5.2(4.6-5.9)	1.74(1.46-2.11)	5.83(5.08-6.67)

Log normal	media	mean-log	sd-log
MERS-CoV	14.08(13.1-15.2)	2.58(2.50-2.68)	0.44(0.39-0.5)
COVID-19	5.2(4.2-6.5)	1.45(1.31-1.61)	0.63(0.54-0.74)

Tabla: Estimaciones del intervalo serial utilizando las distribuciones Gamma, Weibull y Log Normal. Los intervalos de confianza del 95% para los parámetros de forma y escala (shape y rate, en inglés) para Gamma (meanlog y sdlog para Log Normal) se muestran entre paréntesis (Althobaity et al., 2022).

Intervalo serial

Supongamos que COVID-19 y SARS tienen valores similares de número de reproducción y que el intervalo serial se aproxima al tiempo de generación.

Dado el intervalo serial de ambas infecciones en la siguiente gráfica

¿Cuál sería más difícil de controlar?
¿Por qué llegas a esa conclusión?

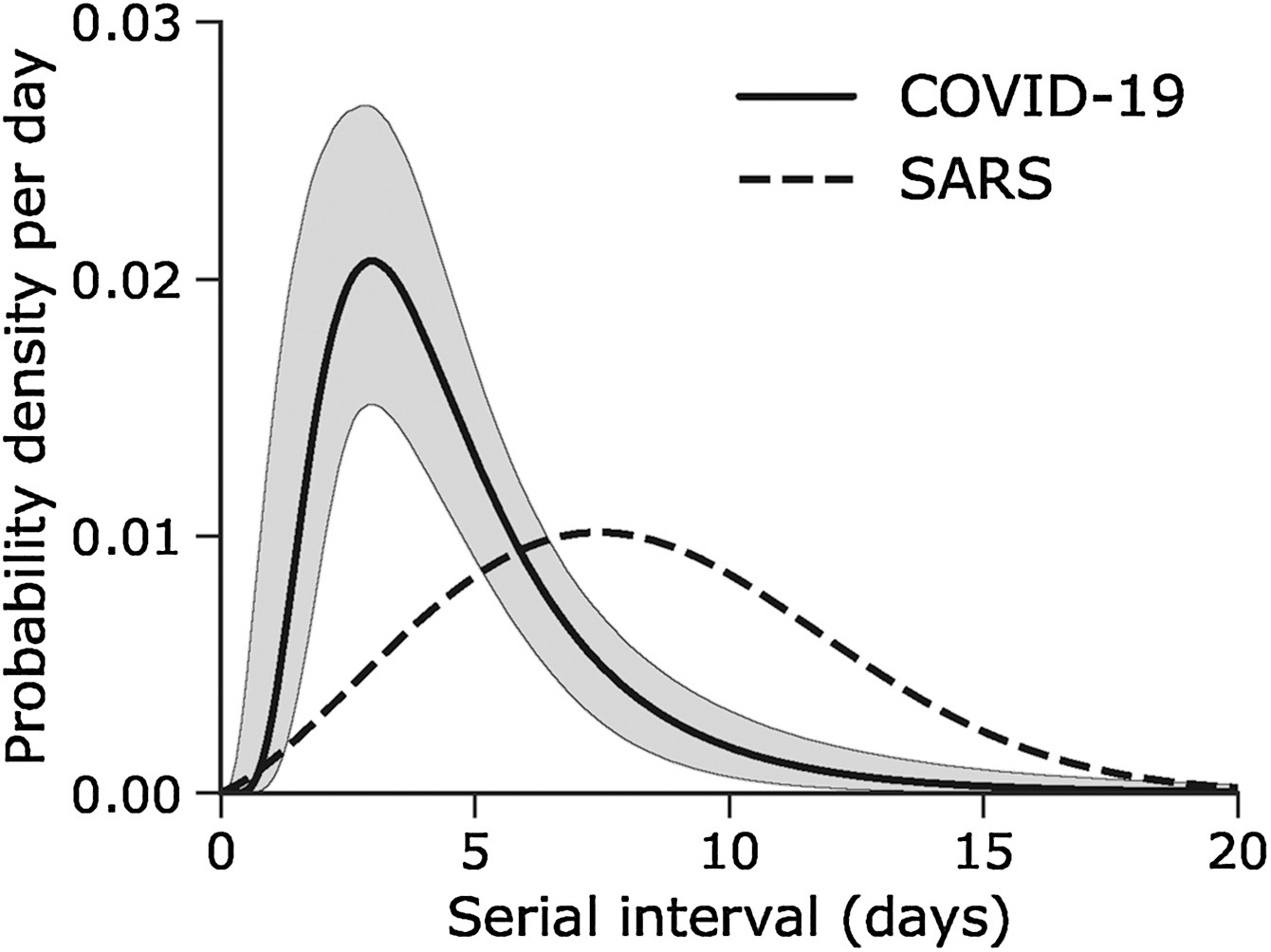
El Intervalo serial de nuevas infecciones por coronavirus (COVID-19) superpuesto a una distribución publicada del SRAS. (Nishiura et al., 2020)

Dar una pista

El pico de cada curva puede informarte sobre la ubicación de la media de cada distribución. Cuanto mayor sea la media, mayor será el intervalo serial.

Mostrar la solución

¿Cuál sería más difícil de controlar?

COVID-19

¿Por qué concluyes eso?

COVID-19 tiene el intervalo serial promedioo más bajo. El valor promedio aproximado del intervalo serial de COVID-19 es de unos cuatro días, mientras que del SARS es de aproximadamentesiete días. Por lo tanto, es probable que COVID-19 tenga nuevas generaciones en menos tiempo que el SARS, asumiendo valores de número de reproducción similares.

Elección de parámetros epidemiológicos

En esta sección, utilizaremos {epiparameter} para obtener el intervalo serial de COVID-19, como una alternativa al tiempo de generación.

Preguntémonos ahora cuántos parámetros tenemos en la base de datos de distribuciones epidemiológicas (epidist_db()) con la enfermedaddisease denominada covid-19. ¡Ejecútalo localmente!

R

epiparameter::epidist_db(
  disease = "covid"
)

Desde el paquete {epiparameter} podemos utilizar la función epidist_db() para consultar cualquier enfermedad disease y también para una distribución epidemiológica concreta (epi_dist). Ejecútalo en tu consola:

R

epiparameter::epidist_db(
  disease = "COVID",
  epi_dist = "serial"
)

Con esta combinación de consultas, obtenemos más de una distribución de retraso. Esta salida es un <epidist> objeto de clase.

INSENSIBLE A MAYÚSCULAS Y MINÚSCULAS

epidist_db es insensible a mayúsculas y minúsculas. Esto significa que puedes utilizar cadenas con letras en mayúsculas o minúsculas indistintamente. Cadenas como "serial", "serial interval" o "serial_interval" también son válidos.

Como se sugiere en los resultados, para resumir una <epidist> y obtener los nombres de las columnas de la base de datos de parámetros subyacente, podemos añadir la función epiparameter::parameter_tbl() al código anterior utilizando la tubería %>%:

R

epiparameter::epidist_db(
  disease = "covid",
  epi_dist = "serial"
) %>%
  epiparameter::parameter_tbl()

SALIDA

Returning 4 results that match the criteria (3 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SALIDA

# Parameter table:
# A data frame:    4 × 7
  disease  pathogen  epi_distribution prob_distribution author  year sample_size
  <chr>    <chr>     <chr>            <chr>             <chr>  <dbl>       <dbl>
1 COVID-19 SARS-CoV… serial interval  <NA>              Alene…  2021        3924
2 COVID-19 SARS-CoV… serial interval  lnorm             Nishi…  2020          28
3 COVID-19 SARS-CoV… serial interval  weibull           Nishi…  2020          18
4 COVID-19 SARS-CoV… serial interval  norm              Yang …  2020         131

En el epiparameter::parameter_tbl() salida, también podemos encontrar distintos tipos de distribuciones de probabilidad (por ejemplo, Log-normal, Weibull, Normal).

{epiparameter} utiliza la base R para las distribuciones. Por eso Normal logarítmica se llama lnorm.

¿Por qué tenemos una entrada “NA”?

Las entradas con un valor faltante (<NA>) en la columna prob_distribution son entradas no parametrizada. Tienen estadísticas de resumen, pero no una distribución de probabilidad. Compara estos dos resultados:

R

# get an <epidist> object
distribution <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "serial"
  )

distribution %>%
  # pluck the first entry in the object class <list>
  pluck(1) %>%
  # check if <epidist> object have distribution parameters
  is_parameterised()

# check if the second <epidist> object
# have distribution parameters
distribution %>%
  pluck(2) %>%
  is_parameterised()

Las entradas parametrizadas tienen un método de Inferencia

Como se detalla en ?is_parameterised una distribución parametrizada es la entrada que tiene una distribución de probabilidad asociada proporcionada por un método inference_method como se muestra en los metadatosmetadata:

R

distribution[[1]]$metadata$inference_method
distribution[[2]]$metadata$inference_method
distribution[[4]]$metadata$inference_method

¡Encuentra tus distribuciones de retraso!

Tómate 2 minutos para explorar el paquete {epiparameter}.

Elige una enfermedad de interés (por ejemplo, Influenza estacional, sarampión, etc.) y una distribución de retrasos (por ejemplo, el periodo de incubación, desde el inicio hasta la muerte, etc.).

Encuéntra:

¿Cuántas distribuciones de retraso hay para esa enfermedad?
¿Cuántos tipos de distribución de probabilidad (por ejemplo, gamma, log normal) hay para un retraso determinado en esa enfermedad?

Pregunta:

¿Reconoces los artículos?
¿Debería la revisión de literatura de{epiparameter} considerar otro artículo?

Dar una pista

La función epidist_db() con disease sólo con la enfermedad cuenta el número de entradas como

estudios, y
distribuciones de retrasos.

La función epidist_db() función con la enfermedad disease y epi_dist obtiene una lista de todas las entradas con:

la cita completa,
en tipo de distribución de probabilidad, y
valores de los parámetros de la distribución.

La combinación de epidist_db() y parameter_tbl() obtiene un marco de datos de todas las entradas con columnas como

el tipo de la distribución de probabilidad por cada fila, y
autor y año del estudio.

Mostrar la solución

Elegimos explorar las distribuciones de retraso del Ébola:

R

# we expect 16 delays distributions for ebola
epiparameter::epidist_db(
  disease = "ebola"
)

SALIDA

Returning 17 results that match the criteria (17 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SALIDA

# List of 17 <epidist> objects
Number of diseases: 1
❯ Ebola Virus Disease
Number of epi distributions: 9
❯ hospitalisation to death ❯ hospitalisation to discharge ❯ incubation period ❯ notification to death ❯ notification to discharge ❯ offspring distribution ❯ onset to death ❯ onset to discharge ❯ serial interval
[[1]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Distribution: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom
Parameters:
  mean: 1.500
  dispersion: 5.100

[[2]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Distribution: incubation period
Study: Eichner M, Dowell S, Firese N (2011). "Incubation period of ebola
hemorrhagic virus subtype zaire." _Osong Public Health and Research
Perspectives_. doi:10.1016/j.phrp.2011.04.001
<https://doi.org/10.1016/j.phrp.2011.04.001>.
Distribution: lnorm
Parameters:
  meanlog: 2.487
  sdlog: 0.330

[[3]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Distribution: onset to death
Study: The Ebola Outbreak Epidemiology Team, Barry A, Ahuka-Mundeke S, Ali
Ahmed Y, Allarangar Y, Anoko J, Archer B, Abedi A, Bagaria J, Belizaire
M, Bhatia S, Bokenge T, Bruni E, Cori A, Dabire E, Diallo A, Diallo B,
Donnelly C, Dorigatti I, Dorji T, Waeber A, Fall I, Ferguson N,
FitzJohn R, Tengomo G, Formenty P, Forna A, Fortin A, Garske T,
Gaythorpe K, Gurry C, Hamblion E, Djingarey M, Haskew C, Hugonnet S,
Imai N, Impouma B, Kabongo G, Kalenga O, Kibangou E, Lee T, Lukoya C,
Ly O, Makiala-Mandanda S, Mamba A, Mbala-Kingebeni P, Mboussou F,
Mlanda T, Makuma V, Morgan O, Mulumba A, Kakoni P, Mukadi-Bamuleka D,
Muyembe J, Bathé N, Ndumbi Ngamala P, Ngom R, Ngoy G, Nouvellet P, Nsio
J, Ousman K, Peron E, Polonsky J, Ryan M, Touré A, Towner R, Tshapenda
G, Van De Weerdt R, Van Kerkhove M, Wendland A, Yao N, Yoti Z, Yuma E,
Kalambayi Kabamba G, Mwati J, Mbuy G, Lubula L, Mutombo A, Mavila O,
Lay Y, Kitenge E (2018). "Outbreak of Ebola virus disease in the
Democratic Republic of the Congo, April–May, 2018: an epidemiological
study." _The Lancet_. doi:10.1016/S0140-6736(18)31387-4
<https://doi.org/10.1016/S0140-6736%2818%2931387-4>.
Distribution: gamma
Parameters:
  shape: 2.400
  scale: 3.333

# ℹ 14 more elements
# ℹ Use `print(n = ...)` to see more elements.
# ℹ Use `parameter_tbl()` to see a summary table of the parameters.
# ℹ Explore database online at: https://epiverse-trace.github.io/epiparameter/dev/articles/database.html

Ahora, a partir de la salida de epiparameter::epidist_db() ¿Qué es un distribución de la descendencia?

Elegimos encontrar los periodos de incubación del ébola. Esta salida lista todos los documentos y parámetros encontrados. Ejecútalo localmente si es necesario:

R

epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "incubation"
)

Utilizamos parameter_tbl() para obtener una visualización resumida de todo:

R

# we expect 2 different types of delay distributions
# for ebola incubation period
epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "incubation"
) %>%
  parameter_tbl()

SALIDA

Returning 5 results that match the criteria (5 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SALIDA

# Parameter table:
# A data frame:    5 × 7
  disease   pathogen epi_distribution prob_distribution author  year sample_size
  <chr>     <chr>    <chr>            <chr>             <chr>  <dbl>       <dbl>
1 Ebola Vi… Ebola V… incubation peri… lnorm             Eichn…  2011         196
2 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015        1798
3 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015          49
4 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015         957
5 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015         792

Encontramos dos tipos de distribuciones de probabilidad para esta consulta: log normal y gamma.

¿Cómo realiza {epiparameter} la recopilación y revisión de la literatura revisada por pares? ¡Te invitamos a leer la viñeta sobre “Protocolo de Recopilación y Síntesis de Datos” !

Selecciona una única distribución

En epiparameter::epidist_db() funciona como una función de filtrado o subconjunto. Utilicemos el argumento author para filtrar los parámetros Hiroshi Nishiura:

R

epiparameter::epidist_db(
  disease = "covid",
  epi_dist = "serial",
  author = "Hiroshi"
) %>%
  epiparameter::parameter_tbl()

SALIDA

Returning 2 results that match the criteria (2 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SALIDA

# Parameter table:
# A data frame:    2 × 7
  disease  pathogen  epi_distribution prob_distribution author  year sample_size
  <chr>    <chr>     <chr>            <chr>             <chr>  <dbl>       <dbl>
1 COVID-19 SARS-CoV… serial interval  lnorm             Nishi…  2020          28
2 COVID-19 SARS-CoV… serial interval  weibull           Nishi…  2020          18

Seguimos obteniendo más de un parámetro epidemiológico. Podemos establecer el argumento single_epidist en TRUE para obtener sólo uno:

R

epiparameter::epidist_db(
  disease = "covid",
  epi_dist = "serial",
  single_epidist = TRUE
)

SALIDA

Using Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>..
To retrieve the citation use the 'get_citation' function

SALIDA

Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Distribution: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: lnorm
Parameters:
  meanlog: 1.386
  sdlog: 0.568

¿Cómo funciona ‘single_epidist’?

Consultando la documentación de ayuda de ?epiparameter::epidist_db():

Si varias entradas coinciden con los argumentos suministrados y single_epidist = TRUE entonces devolverá el <epidist> parametrizado con el mayor tamaño de muestra
Si varias entradas son iguales después de esta clasificación, se devolverá la primera entrada.

¿Qué es un <epidist>parametrizado ? Mira ?is_parameterised.

Asignemos este objeto de clase <epidist> al objetocovid_serialint.

R

covid_serialint <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "serial",
    single_epidist = TRUE
  )

Puedes utilizar plot() para objetos <epidist> para visualizarlos:

la Función de densidad de probabilidad (PDF, por sus siglas en inglés) y
la Función de distribución acumulativa (CDF, por sus siglas en inglés).

R

# plot <epidist> object
plot(covid_serialint)

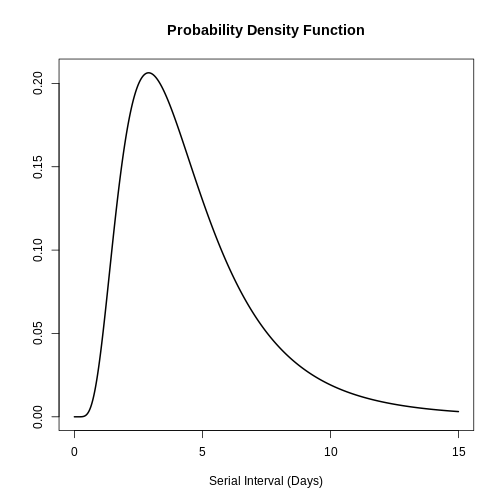
Con el argumento day_range, puedes cambiar la duración o el número de días del x eje. Explora cómo se ve esto:

R

# plot <epidist> object
plot(covid_serialint, day_range = 0:20)

Extrae las estadísticas de resumen

Podemos obtener la media o primediomean y la desviación estándar(sd) a partir de <epidist> accediendo al objetosummary_stats:

R

# get the mean
covid_serialint$summary_stats$mean

SALIDA

[1] 4.7

¡Ahora tenemos un parámetro epidemiológico que podemos reutilizar! Dado que el covid_serialint es una distribución log normal lnorm o, podemos reemplazar las estadísticas de resumen que introducimos en la función EpiNow2::LogNormal()

R

generation_time <-
  EpiNow2::LogNormal(
  mean = covid_serialint$summary_stats$mean, # replaced!
  sd = covid_serialint$summary_stats$sd, # replaced!
  max = 20
  )

En el próximo episodio aprenderemos a utilizar EpiNow2 para especificar correctamente las distribuciones y estimar la transmisibilidad. Después, cómo utilizar funciones de distribución para obtener un valor máximo (max) para EpiNow2::LogNormal() y utilizar {epiparameter} en tu análisis.

Distribuciones logarítmicas normales

Si necesitas los parámetros de la distribución log normal log normales en lugar de las estadísticas de resumen, podemos utilizar epiparameter::get_parameters():

R

covid_serialint_parameters <-
  epiparameter::get_parameters(covid_serialint)

covid_serialint_parameters

SALIDA

  meanlog     sdlog
1.3862617 0.5679803

Se obtiene un vector de clase <numeric> ¡listo para usar como entrada para cualquier otro paquete!

Desafíos

Intervalo serial del ébola

Tómate 1 minuto para

Obtener acceso al intervalo serial de ébola con el mayor tamaño de muestra.

Responde:

¿Qué es el sd de la distribución epidemiológica?
¿Cuál es el tamaño de muestra sample_size utilizado en ese estudio?

Dar una pista

Utiliza el $ más el operador tab o ↹ para explorarlos como una lista desplegable:

R

covid_serialint$

Utiliza el str() para mostrar la estructura del objeto de R <epidist>.

Mostrar la solución

R

# ebola serial interval
ebola_serial <-
  epiparameter::epidist_db(
    disease = "ebola",
    epi_dist = "serial",
    single_epidist = TRUE
  )

SALIDA

Using WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>..
To retrieve the citation use the 'get_citation' function

R

ebola_serial

SALIDA

Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Distribution: serial interval
Study: WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>.
Distribution: gamma
Parameters:
  shape: 2.188
  scale: 6.490

R

# get the sd
ebola_serial$summary_stats$sd

SALIDA

[1] 9.6

R

# get the sample_size
ebola_serial$metadata$sample_size

SALIDA

[1] 305

Intenta visualizar esta distribución utilizando plot().

Explora también todos los demás elementos anidados dentro del objecto <epidist> .

Comparte sobre:

¿Qué elementos encuentras útiles para tu análisis?
¿Qué otros elementos te gustaría ver en este objeto? ¿Cómo?

Parámetro de severidad del ébola

Un parámetro de severidad como la duración de la hospitalización podría añadir información necesaria sobre la capacidad de camas en respuesta a un brote (Cori et al., 2017).

Para el ébola:

¿Cuál es la estimación puntual reportada de la duración media de la asistencia sanitaria y el aislamiento de casos?

Dar una pista

Un retraso informativo debe medir el tiempo transcurrido desde el inicio de los síntomas hasta la recuperación o la muerte.

Encuentra una forma de acceder a toda la base de datos {epiparameter} y averigua cómo se puede almacenar ese retraso. La salida de parameter_tbl() es un dataframe o tabla de datos.

Mostrar la solución

R

# one way to get the list of all the available parameters
epidist_db(disease = "all") %>%
  parameter_tbl() %>%
  as_tibble() %>%
  distinct(epi_distribution)

SALIDA

Returning 122 results that match the criteria (99 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SALIDA

# A tibble: 12 × 1
   epi_distribution
   <chr>
 1 incubation period
 2 serial interval
 3 generation time
 4 onset to death
 5 offspring distribution
 6 hospitalisation to death
 7 hospitalisation to discharge
 8 notification to death
 9 notification to discharge
10 onset to discharge
11 onset to hospitalisation
12 onset to ventilation

R

ebola_severity <- epidist_db(
  disease = "ebola",
  epi_dist = "onset to discharge"
)

SALIDA

Returning 1 results that match the criteria (1 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' function

R

# point estimate
ebola_severity$summary_stats$mean

SALIDA

[1] 15.1

Comprueba que para algunas entradas de {epiparameter} también tendrás la incertidumbre en torno a las estimación puntual de cada estadística de síntesis:

R

# 95% confidence intervals
ebola_severity$summary_stats$mean_ci

SALIDA

[1] 95

R

# limits of the confidence intervals
ebola_severity$summary_stats$mean_ci_limits

SALIDA

[1] 14.6 15.6

Un zoológico de distribuciones

¡Explora esta shinyapp llamada The distribution zoo !

Sigue estos pasos para reproducir la forma de la distribución de intervalo serial COVID desde {epiparameter} (covid_serialint objeto):

Accede al sitio web de shiny app https://ben18785.shinyapps.io/distribution-zoo/,
Ve al panel izquierdo,
Mantén pulsado el botón Categoría de distribución: Continuous Univariate,
Selecciona un nuevo Tipo de distribución: Log-Normal,
Mueve los controles deslizantes es decir, el elemento de control gráfico que te permite ajustar un valor moviendo una barra horizontal hacia la posición covid_serialint parámetros.

Reprodúcelos con el botón distribution y todos sus elementos de lista: [[2]], [[3]] y [[4]]. Explora cómo cambia la forma de una distribución cuando cambian sus parámetros.

Comparte sobre:

¿Qué otras funciones del sitio web te parecen útiles?

Puntos Clave

Utiliza {epiparameter} para acceder al catálogo de literatura sobre distribuciones epidemiológicas de retraso.
Utiliza epidist_db() para seleccionar distribuciones de retraso individuales.
Utiliza parameter_tbl() para obtener una visión general de las distribuciones de retardo múltiples.
Reutiliza las estimaciones conocidas para una enfermedad desconocida en la fase inicial de un brote cuando no se disponga de datos de rastreo de contactos.

Content from Cuantificar la transmisión

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

¿Cómo puedo estimar el número de reproducción variable en el tiempo ($Rt$) y la tasa de crecimiento a partir de una serie temporal de datos de casos?
¿Cómo puedo cuantificar la heterogeneidad geográfica a partir de estas métricas de transmisión?

Objetivos

Aprender a estimar las métricas de transmisión a partir de una serie temporal de datos de casos utilizando el paquete R EpiNow2

Requisitos previos

Los alumnos deben familiarizarse con los siguientes conceptos antes de trabajar con este tutorial:

Estadística Distribuciones de probabilidad y principio del análisis bayesiano.

Teoría epidémica Número de reproducción efectiva.

Ciencia de los datos Transformación y visualización de datos. Puedes revisar el episodio en Agregar y visualizar datos de incidencia.

Recordatorio: el Número de Reproducción Efectiva, $R_t$

El número básico de reproducción, $R_0$ es el número medio de casos causados por un individuo infeccioso en una población totalmente susceptible.

Pero en un brote en curso, la población no permanece totalmente susceptible, ya que los que se recuperan de la infección suelen ser inmunes. Además, puede haber cambios de comportamiento u otros factores que afecten la transmisión. Por lo tanto, cuando nos interesa controlar los cambios en la transmisión, es más importante tener en cuenta el valor del número de reproducción efectiva, $R_t$ y el número medio de casos causados por un individuo infeccioso en la población en el momento $t$.

Introducción

La intensidad de la transmisión de un brote se cuantifica mediante dos métricas clave: el número de reproducción, que informa sobre la fuerza de la transmisión indicando cuántos casos nuevos se esperan de cada caso existente; y la tasa de crecimiento que informa sobre la velocidad de la transmisión, indicando la rapidez con que el brote se propaga o disminuye (tiempo de duplicación/desaparición) dentro de una población. Para más detalles sobre la distinción entre velocidad y fuerza de transmisión y las implicaciones para el control, revisa Dushoff y Park, 2021.

Para estimar estas métricas clave utilizando datos de casos, debemos tener en cuenta los retrasos entre la fecha de las infecciones y la fecha de los casos notificados. En una situación de brote, normalmente sólo se dispone de datos sobre las fechas notificadas, por lo que debemos utilizar métodos de estimación para tener en cuenta estos retrasos cuando intentemos comprender los cambios en la transmisión a lo largo del tiempo.

En los próximos tutoriales nos centraremos en cómo utilizar las funciones de EpiNow2 para estimar las métricas de transmisión de los datos de casos. No cubriremos el trasfondo teórico de los modelos ni el marco de inferencia; para más detalles sobre estos conceptos, consulta la viñeta.

En este tutorial vamos a aprender a utilizar el paquete EpiNow2 para estimar el número de reproducción variable en el tiempo. Obtendremos los datos de entrada de incidence2. Utilizaremos el paquete tidyr y dplyr para ordenar algunas de sus salidas, ggplot2 para visualizar la distribución de casos, y el operador tubería %>% para conectar algunas de sus funciones, así que también llamaremos al paquete tidyverse:

R

library(EpiNow2)
library(incidence2)
library(tidyverse)

El doble punto

El doble punto :: en R te permite llamar a una función específica de un paquete sin cargar todo el paquete en el entorno actual.

Por ejemplo dplyr::filter(data, condition) utiliza la función filter() del paquete dplyr.

Esto nos ayuda a recordar las funciones del paquete y a evitar conflictos de espacio de nombres.

Inferencia bayesiana

El paquete R EpiNow2 utiliza inferencia bayesiana para estimar las cifras de reproducción y los tiempos de infección basándose en las fechas de notificación.

En la inferencia bayesiana, utilizamos el conocimiento previo (distribuciones previas) con los datos (en una función de verosimilitud) para hallar la probabilidad posterior.

Probabilidad posterior $\propto$ verosimilitud $\times$ probabilidad previa

Distribuciones de retrasos y datos de casos

Datos de casos

Para explorar las funciones de EpiNow2 utilizaremos los datos del brote del inicio de la pandemia COVID-19 del Reino Unido. Los datos están disponibles en el paquete R incidence2.

R

dplyr::as_tibble(incidence2::covidregionaldataUK)

SALIDA

# A tibble: 6,370 × 13
   date       region   region_code cases_new cases_total deaths_new deaths_total
   <date>     <chr>    <chr>           <dbl>       <dbl>      <dbl>        <dbl>
 1 2020-01-30 East Mi… E12000004          NA          NA         NA           NA
 2 2020-01-30 East of… E12000006          NA          NA         NA           NA
 3 2020-01-30 England  E92000001           2           2         NA           NA
 4 2020-01-30 London   E12000007          NA          NA         NA           NA
 5 2020-01-30 North E… E12000001          NA          NA         NA           NA
 6 2020-01-30 North W… E12000002          NA          NA         NA           NA
 7 2020-01-30 Norther… N92000002          NA          NA         NA           NA
 8 2020-01-30 Scotland S92000003          NA          NA         NA           NA
 9 2020-01-30 South E… E12000008          NA          NA         NA           NA
10 2020-01-30 South W… E12000009          NA          NA         NA           NA
# ℹ 6,360 more rows
# ℹ 6 more variables: recovered_new <dbl>, recovered_total <dbl>,
#   hosp_new <dbl>, hosp_total <dbl>, tested_new <dbl>, tested_total <dbl>

Para utilizar los datos, debemos darles formato para que tengan dos columnas:

date: la fecha (para validar si un objeto es de tipo fecha ver ?is.Date()),
confirm número de casos confirmados en esa fecha.

Utilicemos tidyr y incidence2 para ello:

R

cases <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = "cases_new",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable)

Con incidence2::incidence() agregamos casos en distintos tiempos intervalos (es decir, días, semanas o meses) o por grupo categorías. También podemos tener fechas completas para todo el rango de fechas por categoría de grupo utilizando complete_dates = TRUE Explora más adelante la incidence2::incidence() manual de referencia

¿Podemos replicar {incidence2} con {dplyr}?

Podemos obtener un objeto similar a cases de la tabla de datos (data.frame) incidence2::covidregionaldataUK utilizando las siguientes funciones del paquete dplyr:

R

incidence2::covidregionaldataUK %>%
  dplyr::select(date, cases_new) %>%
  dplyr::group_by(date) %>%
  dplyr::summarise(confirm = sum(cases_new, na.rm = TRUE)) %>%
  dplyr::ungroup()

Sin embargo, la función incidence2::incidence() contiene argumentos prácticos como complete_dates que facilitan la obtención de un objeto de incidencia con el mismo rango de fechas para cada agrupación sin necesidad de líneas de código adicionales ni de un paquete de series temporales.

Hay datos de casos disponibles para 490 días, pero en una situación de brote es probable que sólo tuviéramos acceso al principio de este conjunto de datos. Por lo tanto, suponemos que sólo disponemos de los primeros 90 días de estos datos.

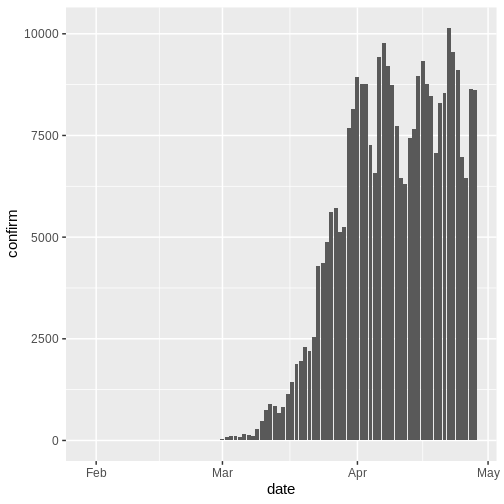
Distribuciones de retraso

Suponemos que hay retrasos desde el momento de la infección hasta el momento en que se notifica un caso. Especificamos estos retrasos como distribuciones para tener en cuenta la incertidumbre en las diferencias a nivel individual. El retraso puede consistir en múltiples tipos de retrasos/procesos. Un retraso típico desde el momento de la infección hasta la notificación del caso puede consistir en:

tiempo desde la infección hasta la aparición de los síntomas (el período de incubación) + tiempo desde el inicio de los síntomas hasta la notificación del caso (el tiempo de notificación).

La distribución del retraso para cada uno de estos procesos puede estimarse a partir de los datos u obtenerse de la bibliografía. Podemos expresar la incertidumbre sobre cuáles son los parámetros correctos de las distribuciones, suponiendo que las distribuciones tienen parámetros fijos (_fixed) o si tienen parámetros variables (_variable). Para entender la diferencia entre distribuciones fijas y variables, consideremos el periodo de incubación.

Retrasos y datos

El número de retrasos y su tipo son una entrada flexible que depende de los datos. Los siguientes ejemplos muestran cómo se pueden especificar los retrasos para distintas fuentes de datos:

Fuente de datos	Retraso(s)
Hora de inicio de los síntomas	Periodo de incubación
Hora del informe del caso	Periodo de incubación + tiempo desde el inicio de los síntomas hasta la notificación del caso
Tiempo de hospitalización	Periodo de incubación + tiempo desde el inicio de los síntomas hasta la hospitalización

Distribución del periodo de incubación

La distribución del periodo de incubación de muchas enfermedades suele obtenerse de la bibliografía. El paquete {epiparameter} contiene una biblioteca de parámetros epidemiológicos de distintas enfermedades obtenidos de la literatura.

Especificamos una distribución gamma (fija) con media $\mu = 4$ y desviación estándar $\sigma= 2$ (forma = $4$, escala = $1$) mediante la función Gamma() de la siguiente manera:

R

incubation_period_fixed <- EpiNow2::Gamma(
  mean = 4,
  sd = 2,
  max = 20
)

incubation_period_fixed

SALIDA

- gamma distribution (max: 20):
  shape:
    4
  rate:
    1

El argumento max es el valor máximo que puede tomar la distribución, en este ejemplo 20 días.

¿Por qué una distribución gamma?

El periodo de incubación debe tener un valor positivo. Por lo tanto, tenemos que especificar una distribución en EpiNow2 que sea sólo para valores positivos.

Gamma() admite distribuciones Gamma y LogNormal() Distribuciones logarítmicas normales, que son distribuciones sólo para valores positivos.

Para todos los tipos de retraso, tendremos que utilizar distribuciones sólo para valores positivos: ¡no queremos incluir retrasos de días negativos en nuestro análisis!

Incluyendo la incertidumbre de distribución

Para especificar una distribución variable, incluimos la incertidumbre en torno a la media $\mu$ y la desviación estándar $\sigma$ de nuestra distribución gamma. Si nuestra distribución del periodo de incubación tiene una media $\mu$ y una desviación estándar $\sigma$ entonces suponemos que la media ($\mu$) sigue una distribución Normal con desviación estándar $\sigma_{\mu}$:

\[\mbox{Normal}(\mu,\sigma_{\mu}^2)\]

y una desviación estándar ($\sigma$) sigue una distribución Normal con desviación estándar $\sigma_{\sigma}$:

\[\mbox{Normal}(\sigma,\sigma_{\sigma}^2).\]

Lo especificamos utilizando Normal() para cada argumento: la media ($\mu=4$ con $\sigma_{\mu}=0.5$) y la desviación estándar ($\sigma=2$ con $\sigma_{\sigma}=0.5$).

R

incubation_period_variable <- EpiNow2::Gamma(
  mean = EpiNow2::Normal(mean = 4, sd = 0.5),
  sd = EpiNow2::Normal(mean = 2, sd = 0.5),
  max = 20
)

incubation_period_variable

SALIDA

- gamma distribution (max: 20):
  shape:
    - normal distribution:
      mean:
        4
      sd:
        0.61
  rate:
    - normal distribution:
      mean:
        1
      sd:
        0.31

Retrasos en los informes

Tras el periodo de incubación, habrá un retraso adicional desde el inicio de los síntomas hasta la notificación del caso: el retraso de notificación. Podemos especificarlo como una distribución fija o variable, o estimar una distribución a partir de los datos.

Al especificar una distribución, es útil visualizar la densidad de probabilidad para ver el pico y la dispersión de la distribución, en este caso utilizaremos una log normal logarítmica normal.

Si queremos suponer que la media del retraso en la notificación es de 2 días (con una desviación estándar de 1 día), escribimos:

Utilizando la media y la desviación estándar de la distribución log normal, podemos especificar una distribución fija o variable utilizando LogNormal() como antes:

R

reporting_delay_variable <- EpiNow2::LogNormal(
  mean = EpiNow2::Normal(mean = 2, sd = 0.5),
  sd = EpiNow2::Normal(mean = 1, sd = 0.5),
  max = 10
)

Visualiza una distribución log Normal utilizando {epiparameter}

Utilizando epiparameter::epidist() podemos crear una distribución personalizada. La distribución log normal tendrá el siguiente aspecto:

R

library(epiparameter)

R

epiparameter::epidist(
  disease = "covid",
  epi_dist = "reporting delay", # retraso del reporte
  prob_distribution = "lnorm",
  summary_stats = epiparameter::create_epidist_summary_stats(
    mean = 2,
    sd = 1
  )
) %>%
  plot()

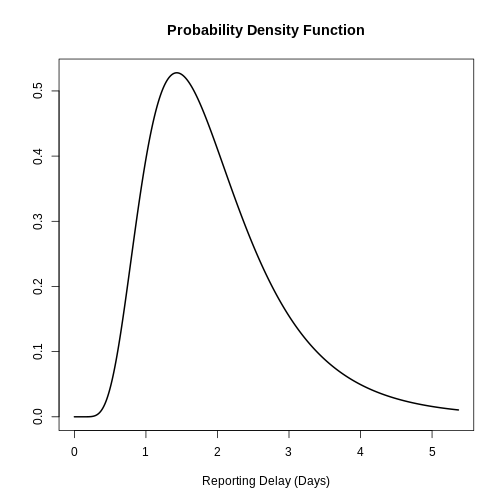
Podemos trazar distribuciones simples y combinadas generadas por EpiNow2 utilizando plot(). Combinemos en un gráfico el retraso desde la infección hasta la notificación, que incluye el periodo de incubación y el retraso en la notificación:

R

plot(incubation_period_variable + reporting_delay_variable)

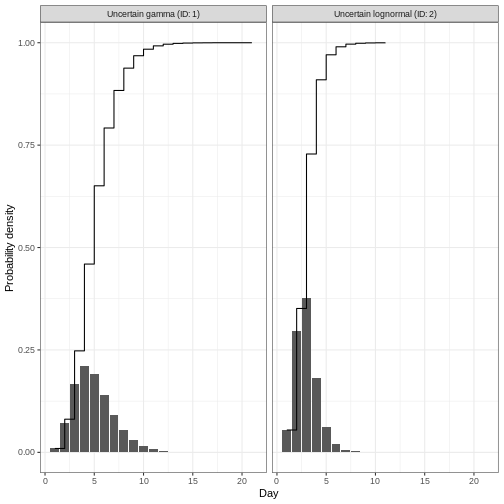
Aviso

Si disponemos de datos sobre el tiempo transcurrido entre el inicio de los síntomas y la notificación, podemos utilizar la función estimate_delay() para estimar una distribución log normal a partir de un vector de retrasos. El siguiente código muestra cómo utilizar estimate_delay() con datos sintéticos de retrasos.

R

delay_data <- rlnorm(500, log(5), 1) # datos de retraso sintéticos

reporting_delay <- EpiNow2::estimate_delay(
  delay_data,
  samples = 1000,
  bootstraps = 10
)

Tiempo de generación

También debemos especificar una distribución para el tiempo de generación. Aquí utilizaremos una distribución log normal con media 3.6 y desviación estándar 3.1 (Ganyani et al. 2020).

R

generation_time_variable <- EpiNow2::LogNormal(
  mean = EpiNow2::Normal(mean = 3.6, sd = 0.5),
  sd = EpiNow2::Normal(mean = 3.1, sd = 0.5),
  max = 20
)

Estimaciones de hallazgos

La función epinow() es una envoltura de la función estimate_infections() utilizada para estimar los casos por fecha de infección. La distribución del tiempo de generación y las distribuciones del retraso deben pasarse utilizando las funciones generation_time_opts() y delay_opts() respectivamente.

Hay muchas otras entradas que se pueden pasar a epinow() ver ?EpiNow2::epinow() para más detalles. Una entrada opcional es especificar una log normal para el número de reproducción efectivo $R_t$ al inicio del brote. Especificamos una media de 2 días y una desviación estándar de 2 días como argumentos de prior dentro de rt_opts():

R

# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = base::list(mean = 2, sd = 2))

Inferencia bayesiana con Stan

La inferencia bayesiana se realiza utilizando métodos MCMC con el programa Stan. Hay una serie de entradas por defecto para las funciones Stan, incluido el número de cadenas y el número de muestras por cadena (ver ?EpiNow2::stan_opts()).

Para reducir el tiempo de cálculo, podemos ejecutar las cadenas en paralelo. Para ello, debemos establecer el número de núcleos que se van a utilizar. Por defecto, se ejecutan 4 cadenas MCMC (ver stan_opts()$chains), por lo que podemos establecer un número igual de núcleos para que se utilicen en paralelo de la siguiente manera:

R

withr::local_options(base::list(mc.cores = 4))

Para averiguar el número máximo de núcleos disponibles en tu máquina, utiliza parallel::detectCores().

Lista de verificación

Nota: En el siguiente código _fixed se utilizan distribuciones en lugar de _variable (distribuciones de retraso con incertidumbre). Esto se hace para acelerar el tiempo de cálculo. En general, se recomienda utilizar distribuciones variables que tengan en cuenta la incertidumbre adicional.

R

# alternativas: distribuciones con parámetros fijos
generation_time_fixed <- EpiNow2::LogNormal(
  mean = 3.6,
  sd = 3.1,
  max = 20
)

reporting_delay_fixed <- EpiNow2::LogNormal(
  mean = 2,
  sd = 1,
  max = 10
)

Ahora estás listo para ejecutar EpiNow2::epinow() para estimar el número de reproducción variable en el tiempo durante los primeros 90 días:

R

reported_cases <- cases %>%
  dplyr::slice_head(n = 90)

R

estimates <- EpiNow2::epinow(
  # casos
  data = reported_cases,
  # retrasos
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  # prior
  rt = rt_prior
)

No esperes a que esto continúe

Para efectos de este tutorial, podemos utilizar opcionalmente EpiNow2::stan_opts() para reducir el tiempo de cálculo. Podemos especificar un número fijo de samples = 1000 y chains = 3 al argumento stan de la función EpiNow2::epinow(). Esperamos que esto lleve aproximadamente 3 minutos.

R

# puedes adicionar el argumento `stan`
EpiNow2::epinow(
  ...,
  stan = EpiNow2::stan_opts(samples = 1000, chains = 3)
)

Recuerda: Utilizar un número adecuado de muestras y cadenas es crucial para garantizar la convergencia y obtener estimaciones fiables en los cálculos bayesianos con Stan. Los resultados más precisos se obtienen a costa de la velocidad.

Resultados

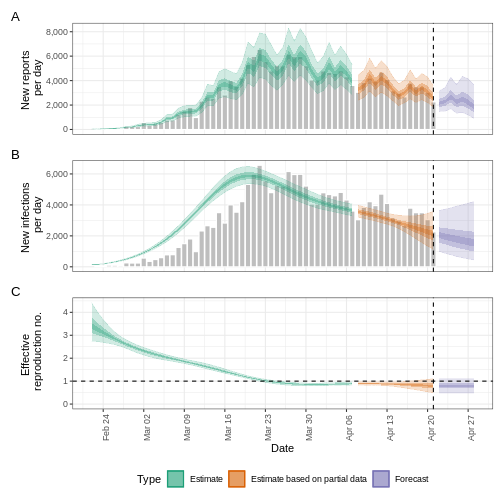
Podemos extraer y visualizar estimaciones del número de reproducción efectivo a lo largo del tiempo:

R

estimates$plots$R

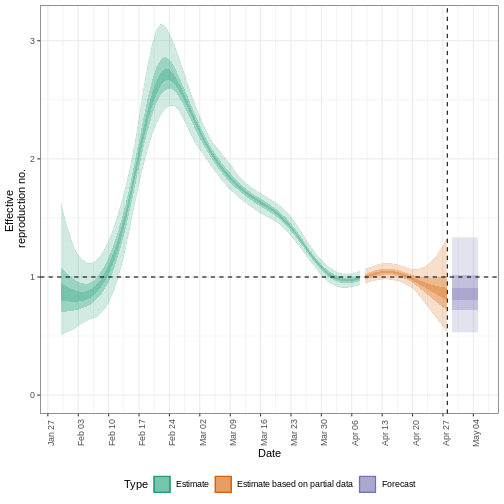
La incertidumbre de las estimaciones aumenta con el tiempo. Esto se debe a que las estimaciones se basan en datos del pasado, dentro de los periodos de retraso. Esta diferencia de incertidumbre se clasifica en Estimación (verde) utiliza todos los datos y Estimación basada en datos parciales (naranja) estimaciones que se basan en menos datos (porque es más probable que las infecciones que se produjeron en su momento no se hayan observado todavía), por este motivo, tienen intervalos cada vez más amplios hacia la fecha del último punto de datos. Por último, el Pronóstico (morado) es una proyección a futuro.

También podemos visualizar la estimación de la tasa de crecimiento a lo largo del tiempo:

R

estimates$plots$growth_rate

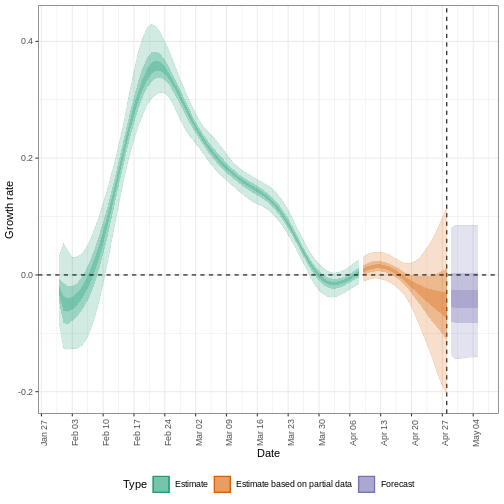
Para extraer un resumen de las métricas clave de transmisión en la última fecha de los datos:

R

summary(estimates)

SALIDA

                            measure               estimate
                             <char>                 <char>
1:           New infections per day   6476 (2738 -- 13517)
2: Expected change in daily reports      Likely decreasing
3:       Effective reproduction no.     0.87 (0.51 -- 1.3)
4:                   Rate of growth -0.046 (-0.22 -- 0.11)
5:     Doubling/halving time (days)      -15 (6.4 -- -3.2)

Como estas estimaciones se basan en datos parciales, tienen un amplio intervalo de incertidumbre.

Del resumen de nuestro análisis se desprende que el cambio esperado en los casos diarios es de con la estimación de nuevos casos confirmados .
El número de reproducción efectivo $R_t$ estimado (en la última fecha de los datos) es 0.87 (0.51 – 1.3).
La tasa de crecimiento exponencial del número de casos es -0.046 (-0.22 – 0.11).
El tiempo de duplicación (el tiempo que tarda en duplicarse el número de casos) es -15 (6.4 – -3.2).

`Expected change in daily cases`

Un factor que describe el cambio esperado en los casos diarios, basado en la probabilidad posterior de que $R_t < 1$.

Probabilidad ($p$)	Cambio esperado
$p < 0,05$	Aumentando
$0,05 \leq p< 0,4$	Probable aumento
$0,4 \leq p< 0,6$	Estable
$0,6 \leq p < 0,95$	Probable disminución
$0,95 \leq p \leq 1$	En disminución

Cuantificar la heterogeneidad geográfica

Los datos del brote del inicio de la pandemia COVID-19 del Reino Unido del paquete R incidence2 incluyen la región en la que se registraron los casos. Para encontrar estimaciones regionales del número de reproducción efectiva y de casos, debemos dar formato a los datos para que tengan tres columnas:

date: la fecha.
region: la región.
confirm: número de casos confirmados para una región en una fecha determinada.

R

regional_cases <- incidence2::covidregionaldataUK %>%
  # usar {tidyr} para pre-procesar los valores faltantes
  tidyr::replace_na(base::list(cases_new = 0)) %>%
  # usar {incidence2} para convertir datos agregados en datos de incidencia
  incidence2::incidence(
    date_index = "date",
    groups = "region",
    counts = "cases_new",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable)

# mantener las primeras 90 fechas para todas las regiones

# obtener el vector de las primeras 90 fechas
date_range <- regional_cases %>%
  dplyr::distinct(date) %>%
  # desde {incidence2}, las fechas ya están ordenadas en orden ascendente
  dplyr::slice_head(n = 90) %>%
  dplyr::pull(date)

# filtrar las fechas en la variable date_range
regional_cases <- regional_cases %>%
  dplyr::filter(magrittr::is_in(x = date, table = date_range))

dplyr::as_tibble(regional_cases)

SALIDA

# A tibble: 1,170 × 3
   date       region           confirm
   <date>     <chr>              <dbl>
 1 2020-01-30 East Midlands          0
 2 2020-01-30 East of England        0
 3 2020-01-30 England                2
 4 2020-01-30 London                 0
 5 2020-01-30 North East             0
 6 2020-01-30 North West             0
 7 2020-01-30 Northern Ireland       0
 8 2020-01-30 Scotland               0
 9 2020-01-30 South East             0
10 2020-01-30 South West             0
# ℹ 1,160 more rows

Para hallar las estimaciones regionales, utilizamos los mismos datos que epinow() para la función regional_epinow():

R

estimates_regional <- EpiNow2::regional_epinow(
  # casos
  data = regional_cases,
  # retrasos
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  # prior
  rt = rt_prior
)

SALIDA

INFO [2024-11-19 01:34:09] Producing following optional outputs: regions, summary, samples, plots, latest
INFO [2024-11-19 01:34:09] Reporting estimates using data up to: 2020-04-28
INFO [2024-11-19 01:34:09] No target directory specified so returning output
INFO [2024-11-19 01:34:09] Producing estimates for: East Midlands, East of England, England, London, North East, North West, Northern Ireland, Scotland, South East, South West, Wales, West Midlands, Yorkshire and The Humber
INFO [2024-11-19 01:34:09] Regions excluded: none
INFO [2024-11-19 02:31:34] Completed regional estimates
INFO [2024-11-19 02:31:34] Regions with estimates: 13
INFO [2024-11-19 02:31:34] Regions with runtime errors: 0
INFO [2024-11-19 02:31:34] Producing summary
INFO [2024-11-19 02:31:34] No summary directory specified so returning summary output
INFO [2024-11-19 02:31:34] No target directory specified so returning timings

R

estimates_regional$summary$summarised_results$table

SALIDA

                      Region New infections per day
                      <char>                 <char>
 1:            East Midlands       346 (185 -- 618)
 2:          East of England       483 (258 -- 857)
 3:                  England    3163 (1598 -- 5887)
 4:                   London       291 (167 -- 486)
 5:               North East       239 (108 -- 493)
 6:               North West       515 (256 -- 938)
 7:         Northern Ireland         37 (15 -- 101)
 8:                 Scotland       272 (108 -- 769)
 9:               South East      588 (300 -- 1099)
10:               South West       469 (304 -- 726)
11:                    Wales         81 (46 -- 133)
12:            West Midlands        202 (83 -- 451)
13: Yorkshire and The Humber       444 (224 -- 816)
    Expected change in daily reports Effective reproduction no.
                              <fctr>                     <char>
 1:                Likely increasing          1.1 (0.77 -- 1.4)
 2:                           Stable            1 (0.69 -- 1.3)
 3:                Likely decreasing         0.87 (0.58 -- 1.2)
 4:                Likely decreasing         0.89 (0.66 -- 1.2)
 5:                Likely decreasing         0.91 (0.59 -- 1.3)
 6:                Likely decreasing         0.87 (0.58 -- 1.2)
 7:                Likely decreasing         0.75 (0.43 -- 1.3)
 8:                           Stable         0.95 (0.55 -- 1.7)
 9:                           Stable         0.98 (0.65 -- 1.4)
10:                       Increasing             1.3 (1 -- 1.6)
11:                       Decreasing         0.7 (0.49 -- 0.94)
12:                Likely decreasing         0.68 (0.38 -- 1.1)
13:                Likely decreasing         0.93 (0.63 -- 1.3)
             Rate of growth Doubling/halving time (days)
                     <char>                       <char>
 1:  0.022 (-0.099 -- 0.12)               31 (5.6 -- -7)
 2:  -0.0081 (-0.14 -- 0.1)            -86 (6.9 -- -5.1)
 3: -0.046 (-0.18 -- 0.084)            -15 (8.3 -- -3.8)
 4: -0.029 (-0.13 -- 0.069)             -24 (10 -- -5.2)
 5:  -0.027 (-0.17 -- 0.11)              -26 (6.5 -- -4)
 6: -0.043 (-0.17 -- 0.064)             -16 (11 -- -4.1)
 7:  -0.071 (-0.24 -- 0.13)           -9.7 (5.5 -- -2.9)
 8: -0.0099 (-0.18 -- 0.21)            -70 (3.2 -- -3.9)
 9: -0.0096 (-0.15 -- 0.12)            -73 (5.8 -- -4.6)
10: 0.079 (-0.0084 -- 0.17)               8.8 (4 -- -82)
11: -0.093 (-0.2 -- 0.0083)            -7.5 (83 -- -3.5)
12:  -0.11 (-0.28 -- 0.074)           -6.1 (9.3 -- -2.5)
13: -0.028 (-0.17 -- 0.092)            -24 (7.5 -- -4.2)

R

estimates_regional$summary$plots$R

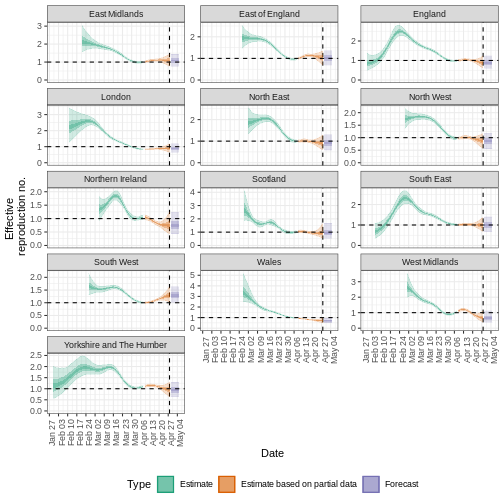
Resumen

EpiNow2 puede utilizarse para estimar las métricas de transmisión a partir de los datos de casos en cualquier momento del curso de un brote. La fiabilidad de estas estimaciones depende de la calidad de los datos y de la elección adecuada de las distribuciones de retraso. En el siguiente tutorial aprenderemos a hacer previsiones e investigaremos algunas de las opciones adicionales de inferencia disponibles en EpiNow2.

Puntos Clave

Las métricas de transmisión pueden estimarse a partir de los datos del caso tras tener en cuenta los retrasos
La incertidumbre puede tenerse en cuenta en las distribuciones de retrasos

Content from Utilizar distribuciones de retraso en el análisis

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

¿Cómo reutilizar los retrasos almacenados en el paquete {epiparameter} con mi flujo de análisis existente?

Objetivos

Utilizar funciones de distribución para distribuciones continuas y discretas almacenadas como objetos <epidist>.
Convertir una distribución continua en discreta con {epiparameter}.
Conectar las salidas de {epiparameter} con entradas de EpiNow2.

Requisitos previos

Completar el tutorial Cuantificar la transmisión

Este episodio requiere que estés familiarizado con:

Ciencia de datos : Programación básica con R.

Estadística : Distribuciones de probabilidad.

Teoría epidémica Parámetros epidemiológicos, periodos de tiempo, número reproductivo efectivo.

Introducción

{epiparameter} nos ayuda a elegir un conjunto específico de parámetros epidemiológicos de la bibliografía, en lugar de copiarlos/pegarlos a mano:

R

covid_serialint <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "serial",
    author = "Nishiura",
    single_epidist = TRUE
  )

¡Ahora tenemos un parámetro epidemiológico que podemos utilizar en nuestro análisis! En el bloque de abajo hemos sustituido uno de los parámetros de estadísticas de resumen por EpiNow2::LogNormal()

R

generation_time <- 
  EpiNow2::LogNormal(
    mean = covid_serialint$summary_stats$mean, # replaced!
    sd = covid_serialint$summary_stats$sd, # replaced!
    max = 20
  )

En este episodio, utilizaremos las funciones de distribución que {epiparameter} proporciona para obtener un valor máximo (max) para este y cualquier otro paquete aguas abajo en tu flujo de análisis.

Carguemos los paquetes {epiparameter} y EpiNow2. En EpiNow2 estableceremos 4 núcleos para utilizarlos en cálculos paralelos. Utilizaremos el operador pipe %>%, algunos verbos de dplyr y ggplot2, así que llamemos también al paquete tidyverse:

R

library(epiparameter)
library(EpiNow2)
library(tidyverse)

withr::local_options(list(mc.cores = 4))

El doble punto

El doble punto :: en R te permite llamar a una función específica de un paquete sin cargar todo el paquete en el entorno actual.

Por ejemplo dplyr::filter(data, condition) utiliza filter() del paquete dplyr.

Esto nos ayuda a recordar las funciones del paquete y a evitar conflictos con los nombres de las funciones.

Funciones de distribución

En R, todas las distribuciones estadísticas tienen funciones para acceder a lo siguiente:

density(): Función de densidad de probabilidad (PDF, por sus siglas en inglés),
cdf(): Función de distribución acumulada (CDF, por sus siglas en inglés),
quantile(): Cuantil y
generate(): Generar valores aleatorios de la distribución dada.

Funciones para la distribución Normal

Si lo necesitas, ¡lee en detalle acerca de las funciones de probabilidad de R para la distribución normal, cada una de sus definiciones e identifica en qué parte de una distribución se encuentran!

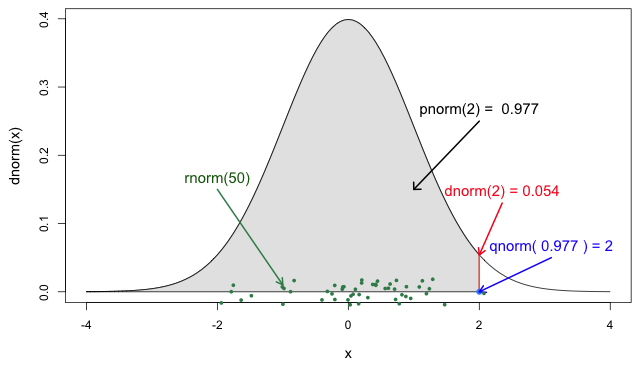
Las cuatro funciones de probabilidad de la distribución normal (Jack Weiss, 2012)

Si consultas ?stats::Distributions, cada tipo de distribución tiene un conjunto único de funciones. Sin embargo, ¡{epiparameter} te ofrece las mismas cuatro funciones para acceder a cada uno de los valores anteriores para cualquier objeto <epidist> que quieras!

R

# Grafica esto para tener una imagen de referencia
plot(covid_serialint, day_range = 0:20)

R

# El valor de densidad cuando el cuantil tiene un valor de 10 (días)
density(covid_serialint, at = 10)

SALIDA

[1] 0.01911607

R

# La probabilidad acumulada cuando el cuantil tiene un valor de 10 (días)
cdf(covid_serialint, q = 10)

SALIDA

[1] 0.9466605

R

# El valor del cuantil (día) cuando la probabilidad acumulada es 60%
quantile(covid_serialint, p = 0.6)

SALIDA

[1] 4.618906

R

# Generar 10 valores aleatorios (días) dada una familia de distribuciones y
# sus parámetros
generate(covid_serialint, times = 10)

SALIDA

 [1]  5.702350  8.846805  4.247009 10.232628  7.698895  4.088730 12.172251
 [8]  4.556690  5.119388  2.796879

Ventana para el rastreo de contactos y el intervalo en serie

El intervalo serial es importante en la optimización del rastreo de contactos, ya que proporciona una ventana temporal para la contención de la propagación de una enfermedad (Fine, 2003). A partir del intervalo serial, podemos evaluar la necesidad de ampliar el número de días previos a tener en cuenta para iniciar el rastreo de contactos e incluir más contactos retrospectivos (Davis et al., 2020).

Con el intervalo de serie COVID-19 (covid_serialint) calcula:

¿Cuántos más casos atrasados se podrían captar si el método de rastreo de contactos considerara los contactos de hasta 6 días antes del inicio en comparación con los de 2 días antes del inicio?

Dar una pista

En la Figura 5 de las funciones de probabilidad de R para la distribución normal, la sección sombreada representa una probabilidad acumulada de 0.997 para el valor del cuantil en x = 2.

Mostrar la solución

R

plot(covid_serialint)

R

cdf(covid_serialint, q = 2)

SALIDA

[1] 0.1111729

R

cdf(covid_serialint, q = 6)

SALIDA

[1] 0.7623645

Dado el intervalo de serie COVID-19:

Un método de rastreo de contactos que considere los contactos hasta 2 días antes del inicio captará alrededor del 11,1% de los casos retrospectivos.
Si este periodo se amplía a 6 días antes del inicio, se podría incluir el 76,2% de los contactos retrospectivos.

¿Y si

intercambiamos la pregunta entre días y probabilidad acumulada a:

Al considerar los casos secundarios, ¿cuántos días después del inicio de los síntomas de los casos primarios podemos esperar que se produzca un 55% de inicio de los síntomas?

R

quantile(covid_serialint, p = 0.55)

Una interpretación podría ser

El 55% del inicio de los síntomas de los casos secundarios ocurrirá después de 4,2 días del inicio de los síntomas de los casos primarios.

Discretizar una distribución continua

¡Nos acercamos al final! EpiNow2::LogNormal() todavía necesita un valor máximo (max).

Una forma de hacerlo es obtener el valor del cuantil del percentil 99 de la distribución o la probabilidad acumulada de 0.99 . Para ello, necesitamos acceder al conjunto de funciones de distribución de nuestro objeto <epidist>.

Podemos utilizar el conjunto de funciones de distribución de una distribución continua (como arriba). Sin embargo, estos valores serán continuos. Podemos discretizar la distribución continua almacenada en nuestro objeto <epidist> para obtener valores discretos a partir de una distribución continua.

Cuando usamos epiparameter::discretise() sobre la distribución continua, obtenemos una distribución discreta (o discretizada):

R

covid_serialint_discrete <-
  epiparameter::discretise(covid_serialint)

covid_serialint_discrete

SALIDA

Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Distribution: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: discrete lnorm
Parameters:
  meanlog: 1.386
  sdlog: 0.568

Identificamos este cambio en la línea de salida Distribution: del objeto <epidist>. Comprueba de nuevo esta línea:

Distribution: discrete lnorm

Mientras que para una distribución continua trazamos la Función de densidad de probabilidad (PDF) para una distribución discreta, trazamos la función de masa de probabilidad (PMF):

R

# continua
plot(covid_serialint)

# discreta
plot(covid_serialint_discrete)

Para obtener finalmente un valor máximo (max), accedamos al valor del cuantil del percentil 99 o cuando la probabilidad acumulada es 0.99 usando prob_dist$q de forma similar a como accedemos a los valores de estadísticas de resumen (summary_stats).

R

covid_serialint_discrete_max <-
  quantile(covid_serialint_discrete, p = 0.99)

Duración del periodo de cuarentena e incubación

El periodo de incubación es un retraso útil para evaluar la duración de la vigilancia activa o la cuarentena (Lauer et al., 2020). Del mismo modo, los retrasos desde la aparición de los síntomas hasta la recuperación (o la muerte) determinarán la duración necesaria de la asistencia sanitaria y el aislamiento del caso (Cori et al., 2017).

Calcula:

¿En qué plazo exacto de tiempo el 99% de las personas que presentan síntomas de COVID-19 después de la infección los presentan?

Dar una pista

¿Qué distribución del retraso mide el tiempo entre la infección y la aparición de los síntomas?

¡Las funciones de probabilidad discretas para <epidist> son las mismas que utilizamos para las continuas!

R

# Grafica esto para tener una imagen de referencia
plot(covid_serialint_discrete, day_range = 0:20)

# El valor de la densidad cuando el cuantil tiene un valor de 10 (días)
density(covid_serialint_discrete, at = 10)

# La probabilidad acumulada cuando el cuantil tiene un valor de 10 (días)
cdf(covid_serialint_discrete, q = 10)

# El valor del cuantil (días) cuando la probabilidad acumulada es 60%
quantile(covid_serialint_discrete, p = 0.6)

# Generar valores aleatorios
generate(covid_serialint_discrete, times = 10)

Mostrar la solución

R

covid_incubation <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "incubation",
    single_epidist = TRUE
  )

SALIDA

Using Linton N, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov A, Jung S, Yuan
B, Kinoshita R, Nishiura H (2020). "Incubation Period and Other
Epidemiological Characteristics of 2019 Novel Coronavirus Infections
with Right Truncation: A Statistical Analysis of Publicly Available
Case Data." _Journal of Clinical Medicine_. doi:10.3390/jcm9020538
<https://doi.org/10.3390/jcm9020538>..
To retrieve the citation use the 'get_citation' function

R

covid_incubation_discrete <- epiparameter::discretise(covid_incubation)

quantile(covid_incubation_discrete, p = 0.99)

SALIDA

[1] 19

El 99% de los que desarrollan síntomas de COVID-19 lo harán en los 16 días posteriores a la infección.

Ahora, ¿es esperable este resultado en términos epidemiológicos?

¿Cómo crear un gráfico de distribución?

A partir de un valor máximo con quantile() podemos crear una secuencia de valores de cuantiles como un vector numérico y calcular density() para cada uno:

R

# Crear la visualización para una distribución discreta
# a partir de un valor máximo de la distribución
quantile(covid_serialint_discrete, p = 0.99) %>%
  # Generar un vector de cuantiles
  # como una secuencia para cada número natural
  seq(1L, to = ., by = 1L) %>%
  # Convertir el vector numérico en un data.frame (tibble)
  as_tibble_col(column_name = "quantile_values") %>%
  mutate(
    # Calcular los valores de densidad
    # para cada cuantul en la función de densidad
    density_values =
      density(
        x = covid_serialint_discrete,
        at = quantile_values
      )
  ) %>%
  # Graficar
  ggplot(
    aes(
      x = quantile_values,
      y = density_values
    )
  ) +
  geom_col()

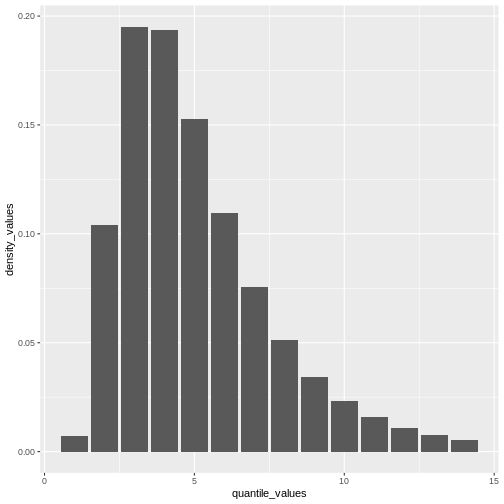
Recuerda: En las infecciones con transmisión presintomática, los intervalos seriales pueden tener valores negativos (Nishiura et al., 2020). ¡Cuando utilizamos el intervalo serial para aproximar el tiempo de generación necesitamos hacer esta distribución sólo con valores positivos!

Plug-in `{epiparameter}` a `{EpiNow2}`

¡Ahora podemos introducirlo todo en la función EpiNow2::LogNormal()!

Las estadísticas de resumen: media (mean) y desviación estándar (sd) de la distribución,
un valor máximo (max),
el nombre de la distribución (distribution).

Cuando utilices EpiNow2::LogNormal() para definir una distribución log normal como la del intervalo serial del COVID-19 (covid_serialint) podemos especificar la media (mean) y la desviación estándar (sd) como parámetros. Alternativamente, para obtener los parámetros “naturales” de una distribución log normal podemos convertir sus estadísticos de resumen en parámetros de distribución denominados meanlog y sdlog. Con {epiparameter} podemos obtener directamente los parámetros de la distribución utilizando epiparameter::get_parameters():

R

covid_serialint_parameters <-
  epiparameter::get_parameters(covid_serialint)

Entonces, tenemos:

R

serial_interval_covid <-
  EpiNow2::LogNormal(
    meanlog = covid_serialint_parameters["meanlog"],
    sdlog = covid_serialint_parameters["sdlog"],
    max = covid_serialint_discrete_max
  )

serial_interval_covid

SALIDA

- lognormal distribution (max: 14):
  meanlog:
    1.4
  sdlog:
    0.57

Suponiendo un escenario con COVID-19, utilicemos los primeros 60 días del conjunto de datos example_confirmed del paquete EpiNow2 como casos reportados(reported_cases) y el recientemente creado intervalo serial COVID (serial_interval_covid) como entradas para estimar el número reproductivo variable en el tiempo utilizando EpiNow2::epinow().

R

epinow_estimates_cg <- epinow(
  # casos
  data = example_confirmed[1:60],
  # retrasos
  generation_time = generation_time_opts(serial_interval_covid)
)

SALIDA

WARN [2024-11-19 02:33:14] epinow: There were 2 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:33:14] epinow: Examine the pairs() plot to diagnose sampling problems
 -

R

base::plot(epinow_estimates_cg)

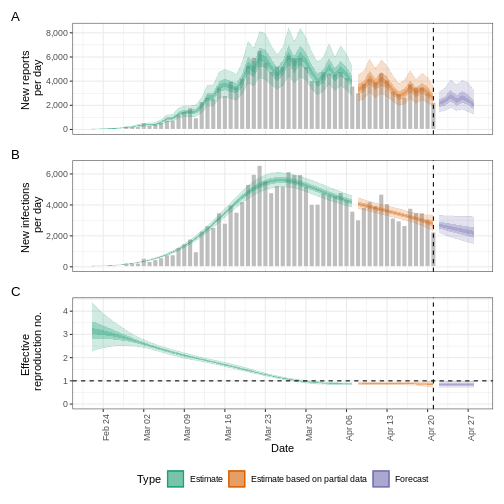
plot() incluye los casos estimados por fecha de infección, que se reconstruyen a partir de los casos notificados y los retrasos.

Advertencia

Utilizar el intervalo serial en lugar del tiempo de generación es una alternativa que puede propagar sesgos en tus estimaciones, más aún en enfermedades con transmisión presintomática reportada. (Chung Lau et al., 2021)

Ajuste por retrasos en la notificación

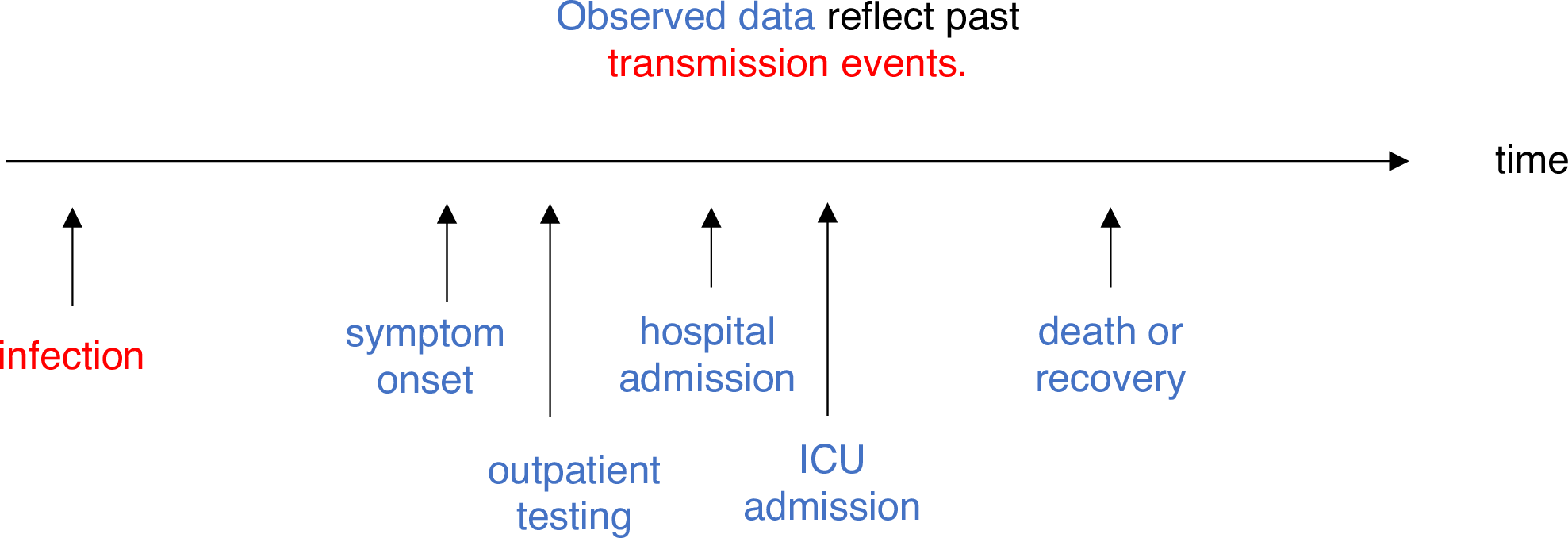
Estimar $R_t$ requiere datos sobre el número diario de nuevas infecciones. Debido a los retrasos en el desarrollo de cargas víricas detectables, la aparición de síntomas, la búsqueda de atención sanitaria y la notificación, estas cifras no están fácilmente disponibles. Todas las observaciones reflejan eventos de transmisión de algún momento del pasado. En otras palabras, si $d$ es el tiempo transcurrido desde la infección hasta la observación, las observaciones en el momento $t$ informan a $R_{t−d}$ no $R_t$. (Gostic et al., 2020)

Calendario de notificación de la cadena de enfermedades, Países Bajos. Lab, laboratorio; PHA, autoridad sanitaria pública. En Marinović y otros, 2015

La distribución del retraso podría inferirse conjuntamente con los tiempos de infección subyacentes o estimarse como la suma del periodo de incubación y la distribución de los retrasos desde el inicio de los síntomas hasta la observación a partir de los datos (retraso en la notificación). En EpiNow2 podemos especificar estas dos distribuciones de retraso complementarias con el argumento delays.

R_{t} es una medida de la transmisión en el momento t. Observaciones después del tiempo t deben ajustarse. UCI, unidad de cuidados intensivos. En Gostic et al., 2020

Utiliza un periodo de incubación de COVID-19 para estimar Rt

Estima el número reproductivo variable en el tiempo para los primeros 60 días del conjunto de datos example_confirmed de EpiNow2. Accede a un periodo de incubación para COVID-19 a partir de {epiparameter} para utilizarlo como retraso de notificación.

Utiliza el último cálculo de epinow() usando el argumento delays y la función auxiliar delay_opts().

El argumento delays y la función auxiliar delay_opts() son análogos al argumento generation_time y la función auxiliar generation_time_opts().

R

epinow_estimates <- epinow(
  # casos
  reported_cases = example_confirmed[1:60],
  # retrasos
  generation_time = generation_time_opts(covid_serial_interval),
  delays = delay_opts(covid_incubation_time)
)

Mostrar la solución

R

# Tiempo de generación ---------------------------------------------------------

# Intervalo serial covid
covid_serialint <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "serial",
    author = "Nishiura",
    single_epidist = TRUE
  )

# adaptar epidist para epinow2
covid_serialint_discrete_max <- covid_serialint %>%
  epiparameter::discretise() %>%
  quantile(p = 0.99)

covid_serialint_parameters <-
  epiparameter::get_parameters(covid_serialint)

covid_serial_interval <-
  EpiNow2::LogNormal(
    meanlog = covid_serialint_parameters["meanlog"],
    sdlog = covid_serialint_parameters["sdlog"],
    max = covid_serialint_discrete_max
  )

# Periodo de incubación -------------------------------------------------------

# Periodo de incubación
covid_incubation <- epiparameter::epidist_db(
  disease = "covid",
  epi_dist = "incubation",
  author = "Natalie",
  single_epidist = TRUE
)

# Adaptar epiparameter para epinow2
covid_incubation_discrete_max <- covid_incubation %>%
  epiparameter::discretise() %>%
  quantile(p = 0.99)

covid_incubation_parameters <-
  epiparameter::get_parameters(covid_incubation)

covid_incubation_time <-
  EpiNow2::LogNormal(
    meanlog = covid_incubation_parameters["meanlog"],
    sdlog = covid_incubation_parameters["sdlog"],
    max = covid_incubation_discrete_max
  )

# epinow ------------------------------------------------------------------

# usar epinow
epinow_estimates_cgi <- epinow(
  # casos
  data = example_confirmed[1:60],
  # retrasos
  generation_time = generation_time_opts(covid_serial_interval),
  delays = delay_opts(covid_incubation_time)
)

SALIDA

WARN [2024-11-19 02:34:51] epinow: There were 11 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:34:51] epinow: Examine the pairs() plot to diagnose sampling problems
 -

R

base::plot(epinow_estimates_cgi)

Intenta complementar el argumento delays con un retraso de notificación como el objeto reporting_delay_fixed del episodio anterior.

¿Cuánto ha cambiado?

Tras añadir el periodo de incubación, debata acerca de:

¿Cambia la tendencia del ajuste del modelo en la sección estimación (“Estimate”)?
¿Ha cambiado la incertidumbre?
¿Cómo explicaría o interpretaría estos cambios?

Compara todas las figuras generadas con EpiNow2 anteriormente.

Desafíos

Un consejo para completar código

Si escribimos el [ ] luego del objeto covid_serialint_parameters[ ], dentro de [ ] podemos utilizar el la tecla Tab en el teclado ↹ para usar la función de completado de código

Usar esto permite acceder rápidamente a covid_serialint_parameters["meanlog"] y covid_serialint_parameters["sdlog"].

¡Te invitamos a probarlo en otros bloques de código y en la consola de R!

Número de reproducción efectiva del ébola ajustado por retrasos en la notificación

Descarga y lee el conjunto de datos de ébola:

Estime el número reproductivo efectivo utilizando EpiNow2
Ajuste la estimación según los retrasos de notificación disponibles en {epiparameter}
¿Por qué eligió ese parámetro?

Para calcular el $R_t$ utilizando EpiNow2 necesitamos

Los datos de incidencia agregada con los casos confirmados por día, y
La distribución del tiempo de generación.
Opcionalmente, informar las distribuciones de retrasos cuando estén disponibles (por ejemplo, el periodo de incubación).

Para obtener las distribuciones de retrasos utilizando {epiparameter} podemos utilizar funciones como:

epiparameter::epidist_db()
epiparameter::parameter_tbl()
discretise()
quantile()

Mostrar la solución

R

# Leer datos
# e.j.: Si la ruta al archivo es data/raw-data/ebola_cases.csv entonces:
ebola_confirmed <-
  read_csv(here::here("data", "raw-data", "ebola_cases.csv"))

# Listar las distribuciones
epiparameter::epidist_db(disease = "ebola") %>%
  epiparameter::parameter_tbl()

R

# Tiempo de generación ---------------------------------------------------------

# Filtrar una distribución para el tiempo de generación
ebola_serial <- epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "serial",
  single_epidist = TRUE
)

# adaptar epiparameter para epinow2
ebola_serial_discrete <- epiparameter::discretise(ebola_serial)

serial_interval_ebola <-
  EpiNow2::Gamma(
    mean = ebola_serial$summary_stats$mean,
    sd = ebola_serial$summary_stats$sd,
    max = quantile(ebola_serial_discrete, p = 0.99)
  )

# Tiempo de incubación  -------------------------------------------------------

# Filtrar una distribución para el retraso del periodo de incubación
ebola_incubation <- epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "incubation",
  single_epidist = TRUE
)

# adaptar epiparameter para epinow2
ebola_incubation_discrete <- epiparameter::discretise(ebola_incubation)

incubation_period_ebola <-
  EpiNow2::Gamma(
    mean = ebola_incubation$summary_stats$mean,
    sd = ebola_incubation$summary_stats$sd,
    max = quantile(ebola_serial_discrete, p = 0.99)
  )

# epinow ------------------------------------------------------------------

# Usar epinow
epinow_estimates_egi <- epinow(
  # casos
  data = ebola_confirmed,
  # retrasos
  generation_time = generation_time_opts(serial_interval_ebola),
  delays = delay_opts(incubation_period_ebola)
)

SALIDA

WARN [2024-11-19 02:37:24] epinow: There were 181 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:37:24] epinow: Examine the pairs() plot to diagnose sampling problems
 -
WARN [2024-11-19 02:37:26] epinow: The largest R-hat is NA, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2024-11-19 02:37:27] epinow: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2024-11-19 02:37:28] epinow: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -

R

plot(epinow_estimates_egi)

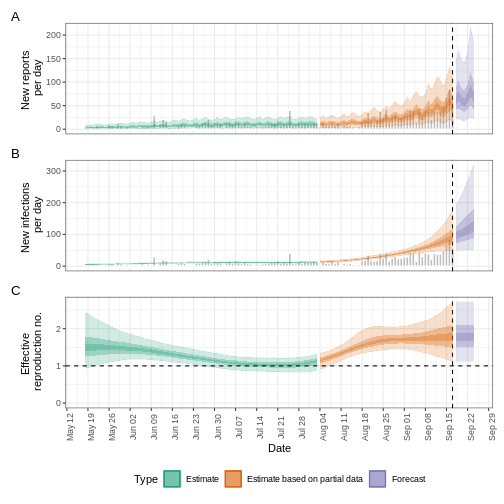
¿Qué hacer con las distribuciones de Weibull?

Utiliza el conjunto de datos influenza_england_1978_school del paquete outbreaks para calcular el número reproductivo efectivo mediante EpiNow2, ajustando por los retrasos de notificación disponibles en {epiparameter}.

EpiNow2::NonParametric() acepta Funciones de Masa de Probabilidad (PMF) de cualquier familia de distribuciones. Lee la guía de referencia sobre Distribuciones de probabilidad.

Mostrar la solución

R

# ¿Qué parámetros hay disponibles para Influenza?
epiparameter::epidist_db(disease = "influenza") %>%
  epiparameter::parameter_tbl() %>%
  count(epi_distribution)

SALIDA

# Parameter table:
# A data frame:    3 × 2
  epi_distribution      n
  <chr>             <int>
1 generation time       1
2 incubation period    15
3 serial interval       1

R

# Tiempo de generación  -------------------------------------------------------

# Leer tiempo de generación
influenza_generation <-
  epiparameter::epidist_db(
    disease = "influenza",
    epi_dist = "generation"
  )

influenza_generation

SALIDA

Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Distribution: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull
Parameters:
  shape: 2.360
  scale: 3.180

R

# EpiNow2 permite usar distribuciones Gamma o LogNormal
# Se puede introducir una PMF

influenza_generation_discrete <-
  epiparameter::discretise(influenza_generation)

influenza_generation_max <-
  quantile(influenza_generation_discrete, p = 0.99)

influenza_generation_pmf <-
  density(
    influenza_generation_discrete,
    at = 1:influenza_generation_max
  )

influenza_generation_pmf

SALIDA

[1] 0.06312336 0.22134988 0.29721220 0.23896828 0.12485164 0.04309454

R

# EpiNow2::NonParametric() también puede recibir valores de PMF
generation_time_influenza <-
  EpiNow2::NonParametric(
    pmf = influenza_generation_pmf
  )

# Periodo de incubación  -------------------------------------------------------

# Leer el periodo de incubación
influenza_incubation <-
  epiparameter::epidist_db(
    disease = "influenza",
    epi_dist = "incubation",
    single_epidist = TRUE
  )

# Discretizar el periodo de incubación
influenza_incubation_discrete <-
  epiparameter::discretise(influenza_incubation)

influenza_incubation_max <-
  quantile(influenza_incubation_discrete, p = 0.99)

influenza_incubation_pmf <-
  density(
    influenza_incubation_discrete,
    at = 1:influenza_incubation_max
  )

influenza_incubation_pmf

SALIDA

[1] 0.05749151 0.16687705 0.22443092 0.21507632 0.16104546 0.09746609 0.04841928

R

# EpiNow2::NonParametric() también puede recibit valores de PMF
incubation_time_influenza <-
  EpiNow2::NonParametric(
    pmf = influenza_incubation_pmf
  )

# epinow ------------------------------------------------------------------

# Leer datos
influenza_cleaned <-
  outbreaks::influenza_england_1978_school %>%
  select(date, confirm = in_bed)

# Usar epinow
epinow_estimates_igi <- epinow(
  # casos
  data = influenza_cleaned,
  # retrasos
  generation_time = generation_time_opts(generation_time_influenza),
  delays = delay_opts(incubation_time_influenza)
)

plot(epinow_estimates_igi)

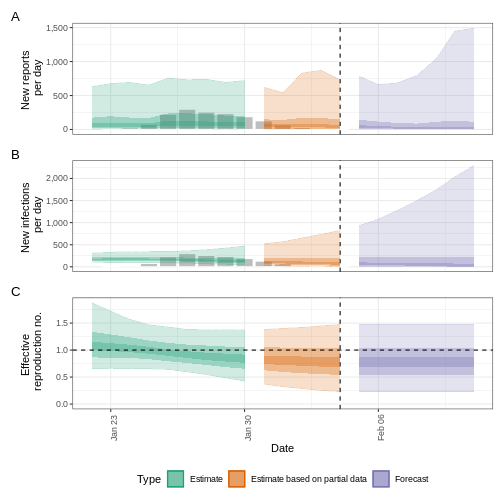
Próximos pasos

¿Cómo obtener parámetros de distribución a partir de distribuciones estadísticas?

¿Cómo obtener la media y la desviación típica de un tiempo de generación con sólo parámetros de distribución pero sin estadísticas de resumen como mean o sd para EpiNow2::Gamma() o EpiNow2::LogNormal()?

¡Mira en {epiparameter} la viñeta extracción y conversión de parámetros y sus casos de uso !

¿Cómo estimar las distribuciones de retraso de la Enfermedad X?

Consulta este excelente tutorial sobre la estimación del intervalo serial y el período de incubación de la Enfermedad X, teniendo en cuenta la censura por medio de inferencia bayesiana con paquetes como rstan y coarseDataTools.

Tutorial en Inglés: https://rpubs.com/tracelac/diseaseX
Tutorial en Español: https://epiverse-trace.github.io/epimodelac/EnfermedadX.html

Luego, después de obtener tus valores estimados, ¡puedes crear manualmente tus propios objetos con clase <epidist> por medio de epiparameter::epidist()! Echa un vistazo a su guía de referencia sobre “Crear un objeto <epidist>” ¡!

Por último, echa un vistazo al último paquete de R {epidist} que proporciona métodos para abordar los principales retos de la estimación de distribuciones, como el truncamiento, la censura por intervalos y los sesgos dinámicos.

Puntos Clave

Utilizar funciones de distribución con <epidist> para obtener estadísticas de resumen y parámetros informativos de las intervenciones de salud pública, como la Ventana de rastreo de contactos y la Duración de la cuarentena.
Utilizar discretise() para convertir distribuciones de retraso continuas en discretas.
Utilizar {epiparameter} para obtener los retrasos de información necesarios en las estimaciones de transmisibilidad.

Content from Crear una previsión a corto plazo

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

¿Cómo puedo crear previsiones a corto plazo a partir de datos de casos?
¿Cómo tengo en cuenta los informes incompletos en las previsiones?

Objetivos

Aprender a hacer previsiones de casos utilizando el paquete R EpiNow2
Aprende a incluir un proceso de observación en la estimación

Requisitos previos

Tutorial completo Cuantificar la transmisión

Los alumnos deben familiarizarse con las siguientes dependencias conceptuales antes de trabajar en este tutorial:

Estadísticas Distribuciones de probabilidad, principio del análisis bayesiano.

Teoría epidémica Número de reproducción efectiva.

Introducción

Dados los datos de casos de una epidemia, podemos crear estimaciones del número actual y futuro de casos teniendo en cuenta tanto los retrasos en la notificación y la infranotificación. Para hacer afirmaciones sobre el futuro de la epidemia, tenemos que hacer una suposición sobre cómo las observaciones hasta el presente están relacionadas con lo que esperamos que ocurra en el futuro. La forma más sencilla de hacerlo es suponer que “no hay cambios”, es decir, que el número de reproducciones sigue siendo el mismo en el futuro que el último observado. En este tutorial crearemos previsiones suponiendo que el número de reproducción seguirá siendo el mismo que el estimado en la última fecha para la que se disponía de datos.

En este tutorial vamos a aprender a utilizar la función EpiNow2 para prever los casos teniendo en cuenta las observaciones incompletas y prever las observaciones secundarias, como las defunciones.

Utilizaremos la tubería %>% para conectar funciones, así que vamos a llamar también a la función tidyverse paquete:

R

library(EpiNow2)
library(tidyverse)

El doble punto

El doble punto :: en R te permite llamar a una función específica de un paquete sin cargar todo el paquete en el entorno actual.

Por ejemplo dplyr::filter(data, condition) utiliza filter() del dplyr paquete.

Esto nos ayuda a recordar las funciones del paquete y a evitar conflictos de espacio de nombres.

Crear una previsión a corto plazo

La función epinow() descrita en el cuantificación de la transmisión es una envoltura de las funciones:

estimate_infections() utilizadas para estimar los casos por fecha de infección.
forecast_infections() Se utiliza para simular infecciones utilizando un ajuste existente (estimación) a los casos observados.

Utilicemos el mismo código utilizado en cuantificar la transmisi para obtener los datos de entrada, los retardos y las priors:

R

# Read cases dataset
cases <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = "cases_new",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable)

# Incubation period
incubation_period_fixed <- EpiNow2::Gamma(
  mean = 4,
  sd = 2,
  max = 20
)

# Log-tranformed mean
log_mean <- EpiNow2::convert_to_logmean(mean = 2, sd = 1)

# Log-transformed std
log_sd <- EpiNow2::convert_to_logsd(mean = 2, sd = 1)

# Reporting dalay
reporting_delay_fixed <- EpiNow2::LogNormal(
  mean = log_mean,
  sd = log_sd,
  max = 10
)

# Generation time
generation_time_fixed <- EpiNow2::LogNormal(
  mean = 3.6,
  sd = 3.1,
  max = 20
)

# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = base::list(mean = 2, sd = 2))

Ahora podemos extraer la previsión a corto plazo utilizando:

R

# Assume we only have the first 90 days of this data
reported_cases <- cases %>%
  dplyr::slice(1:90)

# Estimate and forecast
estimates <- EpiNow2::epinow(
  data = reported_cases,
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  rt = rt_prior
)

SALIDA

WARN [2024-11-19 02:45:04] epinow: There were 4 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:45:04] epinow: Examine the pairs() plot to diagnose sampling problems
 -

¡No esperes a que se complete!

Esta última parte puede tardar 10 minutos en ejecutarse. Sigue leyendo este episodio del tutorial mientras esto se ejecuta en segundo plano. Para más información sobre el tiempo de computación, lee la sección “Inferencia Bayesiana con Stan” dentro del tutorial cuantificar la transmisi de la transmisión.

Podemos visualizar las estimaciones del número de reproducciones efectivas y del número estimado de casos utilizando plot(). Las estimaciones se dividen en tres categorías:

Estimación (verde): utiliza todos los datos,
Estimación basada en datos parciales (naranja): contiene un mayor grado de incertidumbre porque dichas estimaciones se basan en menos datos,
Previsión (morado): previsiones hacia el futuro.

R

plot(estimates)

Previsión con observaciones incompletas

En la cuantificación de la transmisión tuvimos en cuenta los retrasos en la notificación. EpiNow2 también podemos tener en cuenta las observaciones incompletas, ya que, en realidad, el 100% de los casos no se notifican. Pasaremos otro argumento a epinow() función llamada obs para definir un modelo de observación. El formato de obs se define mediante la función obs_opt() (véase ?EpiNow2::obs_opts para más detalles).

Supongamos que creemos que los datos del brote COVID-19 del cases objeto no incluyen todos los casos notificados. Creemos que sólo observamos el 40% de los casos. Para especificar esto en el modelo de observación, debemos pasar un factor de escala con una media y una desviación típica. Si suponemos que el 40% de los casos están en los datos de casos (con una desviación típica del 1%), entonces especificamos el factor scale de entrada a obs_opts() como sigue:

R

obs_scale <- base::list(mean = 0.4, sd = 0.01)

Para ejecutar el marco de inferencia con este proceso de observación, añadimos obs = obs_opts(scale = obs_scale) a los argumentos de entrada de epinow():

R

# Define observation model
obs_scale <- base::list(mean = 0.4, sd = 0.01)

# Assume we only have the first 90 days of this data
reported_cases <- cases %>%
  dplyr::slice(1:90)

# Estimate and forecast
estimates <- EpiNow2::epinow(
  data = reported_cases,
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  rt = rt_prior,
  # Add observation model
  obs = EpiNow2::obs_opts(scale = obs_scale)
)

SALIDA

WARN [2024-11-19 02:53:55] epinow: There were 4 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:53:55] epinow: Examine the pairs() plot to diagnose sampling problems
 -
WARN [2024-11-19 02:53:56] epinow: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -

R

base::summary(estimates)

SALIDA

                            measure                estimate
                             <char>                  <char>
1:           New infections per day   17028 (9273 -- 30703)
2: Expected change in daily reports       Likely decreasing
3:       Effective reproduction no.      0.88 (0.59 -- 1.2)
4:                   Rate of growth -0.043 (-0.18 -- 0.096)
5:     Doubling/halving time (days)       -16 (7.2 -- -3.8)

Las estimaciones de las medidas de transmisión, como el número de reproducción efectivo y la tasa de crecimiento, son similares (o tienen el mismo valor) que cuando no tuvimos en cuenta las observaciones incompletas (ver cuantificar el episodio de trans en la sección “Encontrar estimaciones”). Sin embargo, el número de nuevos casos confirmados por fecha de infección ha cambiado sustancialmente de magnitud para reflejar la suposición de que sólo el 40% de los casos están en el conjunto de datos.

También podemos cambiar la distribución por defecto de Binomial Negativa a Poisson, eliminar el efecto de semana por defecto y más. Consulta ?EpiNow2::obs_opts para más detalles.

¿Cuáles son las implicaciones de este cambio?

Comparar diferentes porcentajes de observaciones %
¿En qué se diferencian en el número de infecciones estimadas?
¿Qué implicaciones tiene este cambio para la salud pública?

Previsión de observaciones secundarias

EpiNow2 también tiene la capacidad de estimar y pronosticar observaciones secundarias, por ejemplo, muertes y hospitalizaciones, a partir de una observación primaria, por ejemplo, casos. Aquí ilustraremos cómo prever el número de muertes derivadas de los casos observados de COVID-19 en las primeras fases del brote del Reino Unido.

En primer lugar, debemos formatear nuestros datos para que tengan las siguientes columnas:

date: la fecha (como objeto de fecha ver ?is.Date()),
primary: número de observaciones primarias en esa fecha, en este ejemplo casos,
secondary: número de observaciones secundarias fecha, en este ejemplo defunciones.

R

reported_cases_deaths <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0, deaths_new = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = c(primary = "cases_new", secondary = "deaths_new"),
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  # rearrange to wide format for {EpiNow2}
  pivot_wider(names_from = count_variable, values_from = count)

Distribution of secondary cases (deaths). We will drop the first 30 days with no observed deaths. We will use the deaths between day 31 and day 60 to estimate the secondary observations. We will forecast deaths from day 61 to day 90.

Utilizando los datos sobre casos y muertes entre el día 31 y el día 60, estimaremos la relación entre las observaciones primarias y secundarias utilizando estimate_secondary() y, a continuación, pronosticaremos las muertes futuras mediante forecast_secondary(). Para más detalles sobre el modelo, consulta el documentación del.

Debemos especificar el tipo de observación mediante type en secondary_opts(), las opciones incluyen:

“incidencia”: las observaciones secundarias surgen de las observaciones primarias previas, es decir, de las muertes que surgen de los casos registrados.
“Prevalencia”: las observaciones secundarias surgen de una combinación de observaciones primarias actuales y observaciones secundarias anteriores, es decir, el uso de camas hospitalarias que surge de los ingresos hospitalarios actuales y del uso de camas hospitalarias anteriores.

En este ejemplo especificamos secondary_opts(type = "incidence"). Consulta ?EpiNow2::secondary_opts para más detalles.

La última entrada clave es la distribución del retraso entre las observaciones primaria y secundaria. Aquí se trata del retraso entre la notificación del caso y la muerte, suponemos que sigue una distribución gamma con una media de 14 días y una desviación típica de 5 días (Alternativamente, podemos utilizar {epiparameter} para acceder a los retrasos epidemiológicos). Utilizando Gamma() especificamos una distribución gamma fija.

Hay más entradas de función para estimate_secondary() que se pueden especificar, incluida la adición de un proceso de observación, véase ?EpiNow2::estimate_secondary para más detalles sobre estas opciones.

Encontrar el ajuste del modelo entre casos y muertes:

R

# Estimate from day 31 to day 60 of this data
cases_to_estimate <- reported_cases_deaths %>%
  slice(31:60)

# Delay distribution between case report and deaths
delay_report_to_death <- EpiNow2::Gamma(
  mean = EpiNow2::Normal(mean = 14, sd = 0.5),
  sd = EpiNow2::Normal(mean = 5, sd = 0.5),
  max = 30
)

# Estimate secondary cases
estimate_cases_to_deaths <- EpiNow2::estimate_secondary(
  data = cases_to_estimate,
  secondary = EpiNow2::secondary_opts(type = "incidence"),
  delays = EpiNow2::delay_opts(delay_report_to_death)
)

Ten cuidado con la escala de tiempo

En las primeras fases de un brote puede haber cambios sustanciales en las pruebas y la notificación. Si hay cambios en las pruebas de un mes a otro, habrá un sesgo en el ajuste del modelo. Por tanto, debes tener cuidado con la escala temporal de los datos utilizados en el ajuste y la previsión del modelo.

Trazamos el ajuste del modelo (cintas sombreadas) con las observaciones secundarias (diagrama de barras) y las observaciones primarias (línea de puntos) de la siguiente manera:

R

plot(estimate_cases_to_deaths, primary = TRUE)

Para utilizar este ajuste del modelo para pronosticar las muertes, pasamos un marco de datos consistente en la observación primaria (casos) para las fechas no utilizadas en el ajuste del modelo.

Nota : en este episodio estamos utilizando datos en los que conocemos las muertes y los casos, por lo que creamos un marco de datos extrayendo los casos. Pero, en la práctica, se trataría de otro conjunto de datos formado sólo por los casos.

R

# Forecast from day 61 to day 90
cases_to_forecast <- reported_cases_deaths %>%
  dplyr::slice(61:90) %>%
  dplyr::mutate(value = primary)

Para pronosticar, utilizamos el ajuste del modelo estimate_cases_to_deaths:

R

# Forecast secondary cases
deaths_forecast <- EpiNow2::forecast_secondary(
  estimate = estimate_cases_to_deaths,
  primary = cases_to_forecast
)

plot(deaths_forecast)

haz una trama de previsión

R

deaths_forecast %>%
  purrr::pluck("predictions") %>%
  ggplot(aes(x = date, y = secondary)) +
  geom_col(
    fill = "grey", col = "white",
    show.legend = FALSE, na.rm = TRUE
  ) +
  geom_ribbon(aes(ymin = lower_90, ymax = upper_90),
              alpha = 0.2, linewidth = 1) +
  geom_ribbon(aes(ymin = lower_50, ymax = upper_50),
              alpha = 0.4, linewidth = 1) +
  geom_ribbon(aes(ymin = lower_20, ymax = upper_20),
              alpha = 0.6, linewidth = 1) +
  theme_bw() +
  labs(y = "Reports per day", x = "Date") +
  scale_x_date(date_breaks = "week", date_labels = "%b %d") +
  scale_y_continuous(labels = scales::comma) +
  theme(axis.text.x = ggplot2::element_text(angle = 90))

El gráfico muestra la previsión de observaciones secundarias (defunciones) en las fechas para las que hemos registrado casos. También es posible prever las defunciones mediante la previsión de casos, para lo que debes especificar primary como estimates salida de estimate_infections().

Intervalos creíbles

En todos EpiNow2 figuras de resultados, las regiones sombreadas reflejan los intervalos de credibilidad del 90%, 50% y 20% en orden de más claro a más oscuro.

Reto: Análisis del brote de ébola

Desafío

Descarga el archivo casos_ébola.csv y léelo en R. Los datos simulados consisten en la fecha de aparición de los síntomas y el número de casos confirmados de las primeras fases del brote de ébola en Sierra Leona en 2014.

Utiliza los 3 primeros meses (120 días) de datos:

Estima si los casos aumentan o disminuyen en el día 120 del brote
Contar con una capacidad de observación del 80% de los casos.
Crea una previsión de dos semanas del número de casos.

Puedes utilizar los siguientes valores de parámetro para la distribución o distribuciones del retraso y la distribución del tiempo de generación.

Periodo de incubación: Log normal$(2.487,0.330)$ (Eichner et al. 2011 a través de {epiparameter})
Tiempo de generación: Gamma$(15.3, 10.1)$ (Equipo de respuesta al ébola de la OMS 2014)

Puedes incluir cierta incertidumbre en torno a la media y la desviación típica de estas distribuciones.

Utilizamos el número de reproducción efectivo y la tasa de crecimiento para estimar si los casos aumentan o disminuyen.

Podemos utilizar el horizon argumento dentro del epinow() para ampliar el periodo de tiempo de la previsión. El valor por defecto es de siete días.

Asegúrate de que los datos tienen el formato correcto :

date: la fecha (como objeto de fecha ver ?is.Date()),
confirm número de casos confirmados en esa fecha.

SOLUCIÓN

Para estimar el número efectivo de reproducción y la tasa de crecimiento, utilizaremos la función epinow().

Como los datos consisten en la fecha de aparición de los síntomas, sólo necesitamos especificar una distribución de retardo para el periodo de incubación y el tiempo de generación.

Especificamos las distribuciones con cierta incertidumbre en torno a la media y la desviación típica de la distribución log normal para el periodo de incubación y la distribución Gamma para el tiempo de generación.

R

epiparameter::epidist_db(disease = "ebola", epi_dist = "incubation") %>%
  epiparameter::parameter_tbl()

SALIDA

# Parameter table:
# A data frame:    5 × 7
  disease   pathogen epi_distribution prob_distribution author  year sample_size
  <chr>     <chr>    <chr>            <chr>             <chr>  <dbl>       <dbl>
1 Ebola Vi… Ebola V… incubation peri… lnorm             Eichn…  2011         196
2 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015        1798
3 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015          49
4 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015         957
5 Ebola Vi… Ebola V… incubation peri… gamma             WHO E…  2015         792

R

ebola_eichner <- epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "incubation",
  author = "Eichner"
)

ebola_eichner_parameters <- epiparameter::get_parameters(ebola_eichner)

ebola_incubation_period <- EpiNow2::LogNormal(
  meanlog = EpiNow2::Normal(
    mean = ebola_eichner_parameters["meanlog"],
    sd = 0.5
  ),
  sdlog = EpiNow2::Normal(
    mean = ebola_eichner_parameters["sdlog"],
    sd = 0.5
  ),
  max = 20
)

ebola_generation_time <- EpiNow2::Gamma(
  mean = EpiNow2::Normal(mean = 15.3, sd = 0.5),
  sd = EpiNow2::Normal(mean = 10.1, sd = 0.5),
  max = 30
)

Leemos los datos de entrada utilizando readr::read_csv(). Esta función reconoce que la columna date es una <date> vector de clase.

R

# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
ebola_cases_raw <- readr::read_csv(
  here::here("data", "raw-data", "ebola_cases.csv")
)

Preprocesa y adapta los datos brutos para EpiNow2:

R

ebola_cases <- ebola_cases_raw %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(confirm = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = "confirm",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable)

dplyr::as_tibble(ebola_cases)

SALIDA

# A tibble: 123 × 2
   date       confirm
   <date>       <dbl>
 1 2014-05-18       1
 2 2014-05-19       0
 3 2014-05-20       2
 4 2014-05-21       4
 5 2014-05-22       6
 6 2014-05-23       1
 7 2014-05-24       2
 8 2014-05-25       0
 9 2014-05-26      10
10 2014-05-27       8
# ℹ 113 more rows

Definimos un modelo de observación para escalar el número estimado y previsto de nuevas infecciones:

R

# Define observation model
# mean of 80% and standard deviation of 1%
ebola_obs_scale <- base::list(mean = 0.8, sd = 0.01)

Como queremos crear también una previsión a dos semanas, especificamos horizon = 14 para prever 14 días en lugar de los 7 días por defecto.

R

ebola_estimates <- EpiNow2::epinow(
  data = ebola_cases %>% dplyr::slice(1:120), # first 3 months of data only
  generation_time = EpiNow2::generation_time_opts(ebola_generation_time),
  delays = EpiNow2::delay_opts(ebola_incubation_period),
  # Add observation model
  obs = EpiNow2::obs_opts(scale = ebola_obs_scale),
  # horizon needs to be 14 days to create two week forecast (default is 7 days)
  horizon = 14
)

SALIDA

WARN [2024-11-19 02:56:16] epinow: There were 6 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:56:16] epinow: Examine the pairs() plot to diagnose sampling problems
 -

R

summary(ebola_estimates)

SALIDA

                            measure              estimate
                             <char>                <char>
1:           New infections per day        83 (32 -- 207)
2: Expected change in daily reports     Likely increasing
3:       Effective reproduction no.      1.5 (0.8 -- 2.6)
4:                   Rate of growth 0.033 (-0.032 -- 0.1)
5:     Doubling/halving time (days)       21 (6.9 -- -21)

El número de reproducción efectivo $R_t$ estimado (en la última fecha de los datos) es 1.5 (0.8 – 2.6). La tasa de crecimiento exponencial del número de casos es 0.033 (-0.032 – 0.1).

Visualiza las estimaciones:

R

plot(ebola_estimates)

Previsión con estimaciones de $R_t$

Por defecto, las previsiones a corto plazo se crean utilizando la última estimación del número de reproducción $R_t$. Como esta estimación se basa en datos parciales, tiene una incertidumbre considerable.

El número de reproducciones que se proyecta en el futuro puede cambiarse por una estimación menos reciente basada en más datos utilizando rt_opts():

R

EpiNow2::rt_opts(future = "estimate")

El resultado serán previsiones menos inciertas (ya que se basan en $R_t$ con un intervalo de incertidumbre más estrecho), pero las previsiones se basarán en estimaciones menos recientes de $R_t$ y supondrán que no ha habido cambios desde entonces.

Además, existe la opción de proyectar el valor de $R_t$ en el futuro utilizando un modelo genérico fijando future = "project". Como esta opción utiliza un modelo para prever el valor de $R_t$ el resultado serán previsiones más inciertas que estimate por ejemplo ver aquí.

Resumen

EpiNow2 puede utilizarse para crear previsiones a corto plazo y estimar la relación entre distintos resultados. Hay una serie de opciones de modelo que pueden implementarse para diferentes análisis, incluida la adición de un proceso de observación para tener en cuenta los informes incompletos. Consulta la viñeta para más detalles sobre las distintas opciones de modelo en EpiNow2 que no se tratan en estos tutoriales.

Puntos Clave

Podemos crear previsiones a corto plazo haciendo suposiciones sobre el comportamiento futuro del número de reproducción
La notificación incompleta de casos puede tenerse en cuenta en las estimaciones

Content from Estimación de la severidad del brote

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

¿Por qué estimamos la gravedad clínica de una epidemia?
¿Cómo se puede estimar la probabilidad de muerte (CFR por sus siglas en inglés: Case Fatality Risk) al principio de una epidemia en curso?

Objetivos

Estimar la probabilidad de muerte a partir de datos de casos agregados utilizando el paquete cfr, case fatality risk en inglés (riesgo de fatalidad de casos).
Estima la probabilidad de muerte, ajustando este cálculo teniendo en cuenta el intervalo entre la aparición de síntomas y la muerte del paciente utilizando los paquetes {epiparameter} y cfr.
Estima la probabilidad de muerte de una enfermedad durante la fase de crecimiento exponencial de una epidemia en expansión utilizando cfr.

Requisitos previos

Este episodio requiere que estés familiarizado con

Ciencia de datos Programación básica con R

Teoría epidémica: Distribuciones temporales.

Introducción

Entre las preguntas más comunes en la fase inicial de una epidemia se incluyen:

¿Cuál es el impacto probable del brote en la salud pública en términos de gravedad clínica?
¿Cuáles son los grupos más gravemente afectados?
¿Tiene el brote potencial para causar una epidemia de grandes dimensiones o incluso una pandemia?

Podemos evaluar el potencial pandémico de una epidemia con dos medidas críticas: la transmisibilidad y la gravedad clínica (Fraser et al., 2009, CDC, 2016).

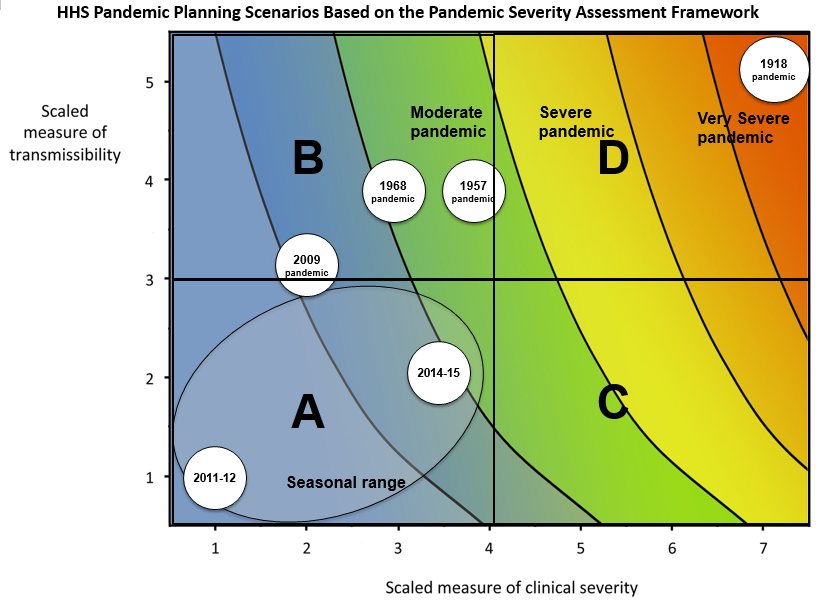
Escenarios de Planificación de Pandemias del HHS basados en el Marco de Evaluación de la Gravedad de la Pandemia. Éste utiliza una medida combinada de gravedad clínica y transmisibilidad para caracterizar los escenarios de pandemia de gripe. HHS: Departamento de Salud y Servicios Humanos de los Estados Unidos (CDC, 2016).

Un enfoque epidemiológico para estimar la gravedad clínica consiste en cuantificar la probabilidad de muerte (CFR). CFR es la probabilidad condicional de muerte una vez confirmado el diagnóstico de la enfermedad, calculada como el número acumulado de muertes por una enfermedad infecciosa dividido por el número de casos diagnosticados confirmados. Sin embargo, calcularlo directamente durante el curso de una epidemia tiende a dar como resultado un CFR sesgado, dado el intervalo temporal que ocurre desde el inicio de lo síntomas hasta la muerte. Este retraso temporal varía sustancialmente a medida que avanza la epidemia y se estabiliza en las últimas fases del brote (Ghani et al., 2005).

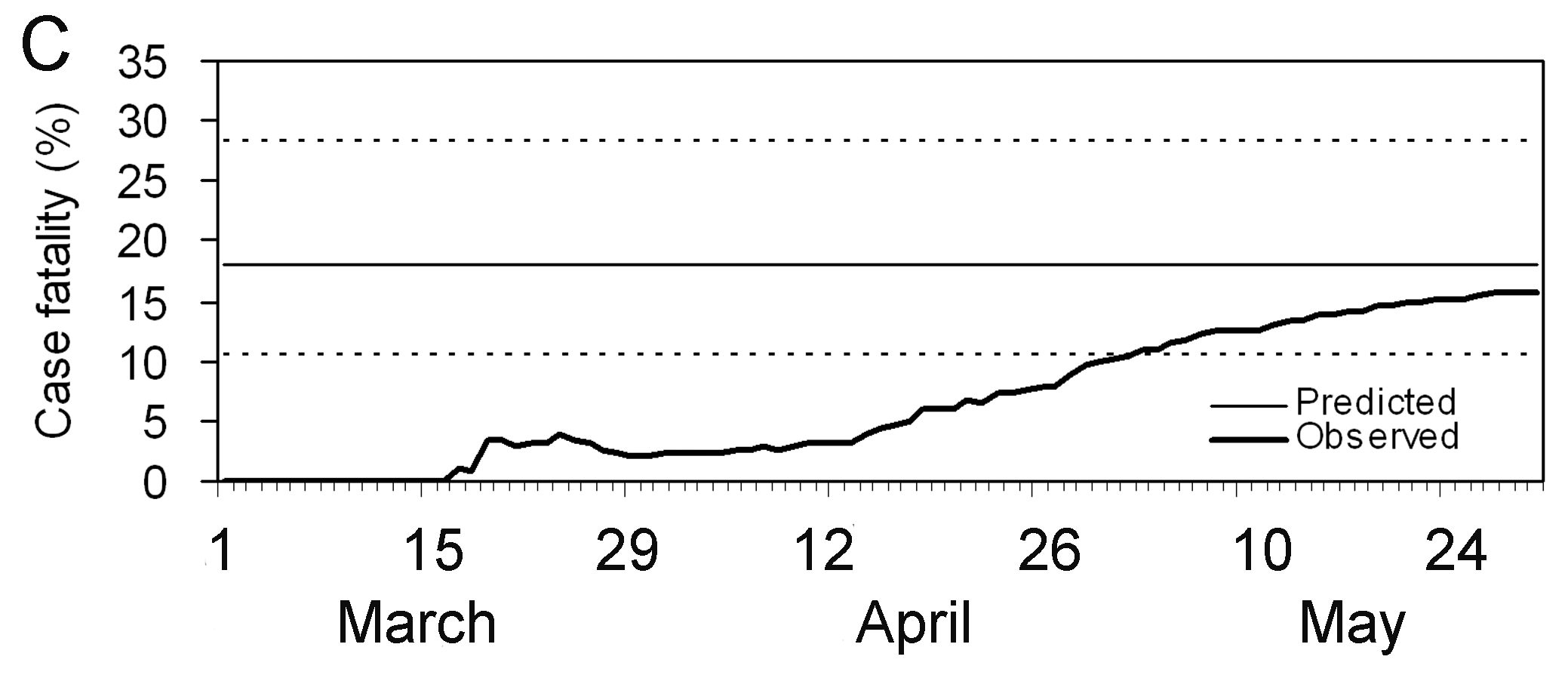
Estimaciones sesgadas de la probabilidad de muerte como función del tiempo (línea gruesa), calculado como el número acumulado de muertes dividido por el número de casos confirmados en el tiempo t. La estimación de la probabilidad de muerte al final de un brote (~30 de mayo) corresponde con la probabilidad de muerte verdadera. La línea continua horizontal y las líneas de puntos muestran el valor esperado y los intervalos de confianza del 95% (95% IC) de la predicción de la probabilidad de muerte ajustada al retraso temporal entre el periodo inicial de síntomas y muerte , utilizando los datos observados hasta el 27 de Marzo de 2003 (Nishiura et al., 2009)

En términos más generales, estimar la gravedad puede ser útil incluso fuera de un escenario de planificación pandémica y en el contexto de la salud pública rutinaria. Saber si un brote tiene o tuvo una gravedad diferente a la del registro histórico puede motivar investigaciones causales, que podrían ser intrínsecas al agente infeccioso (por ejemplo, una nueva cepa más grave) o debidas a factores subyacentes en la población (por ejemplo, inmunidad reducida o factores de morbilidad) (Lipsitch et al., 2015).

En este tutorial vamos a aprender a utilizar la función cfr para calcular y ajustar una estimación de la probabilidad de muerte utilizando distribuciones temporales provenientes de {epiparameter} o de otras fuentes, basándose en los métodos desarrollados por Nishiura et al., 2009 además, aprenderemos como reimplementar las funciones de cfr para realizar otras mediciones de la gravedad de la enfermedad, por ejemplo, el riesgo de fatalidad hospitalaria.

Utilizaremos el operador %>% para conectar funciones, por lo que es necesario también acceder al paquetetidyverse:

R

library(cfr)
library(epiparameter)
library(tidyverse)
library(outbreaks)

El doble punto

El doble punto :: en R te permite llamar a una función específica de un paquete sin cargar todo el paquete en el entorno actual.

Por ejemplo dplyr::filter(data, condition) utiliza filter() del paquete dplyr.

Esto nos ayuda a recordar las funciones requeridas y evitar usar funciones que fueron creadas con el mismo nombre pero provienen de otros paquetes.

Fuentes de datos para la gravedad clínica

¿Qué fuentes de datos podemos utilizar para estimar la gravedad clínica de un brote epidémico? Verity et al., 2020 resume el espectro de casos de COVID-19:

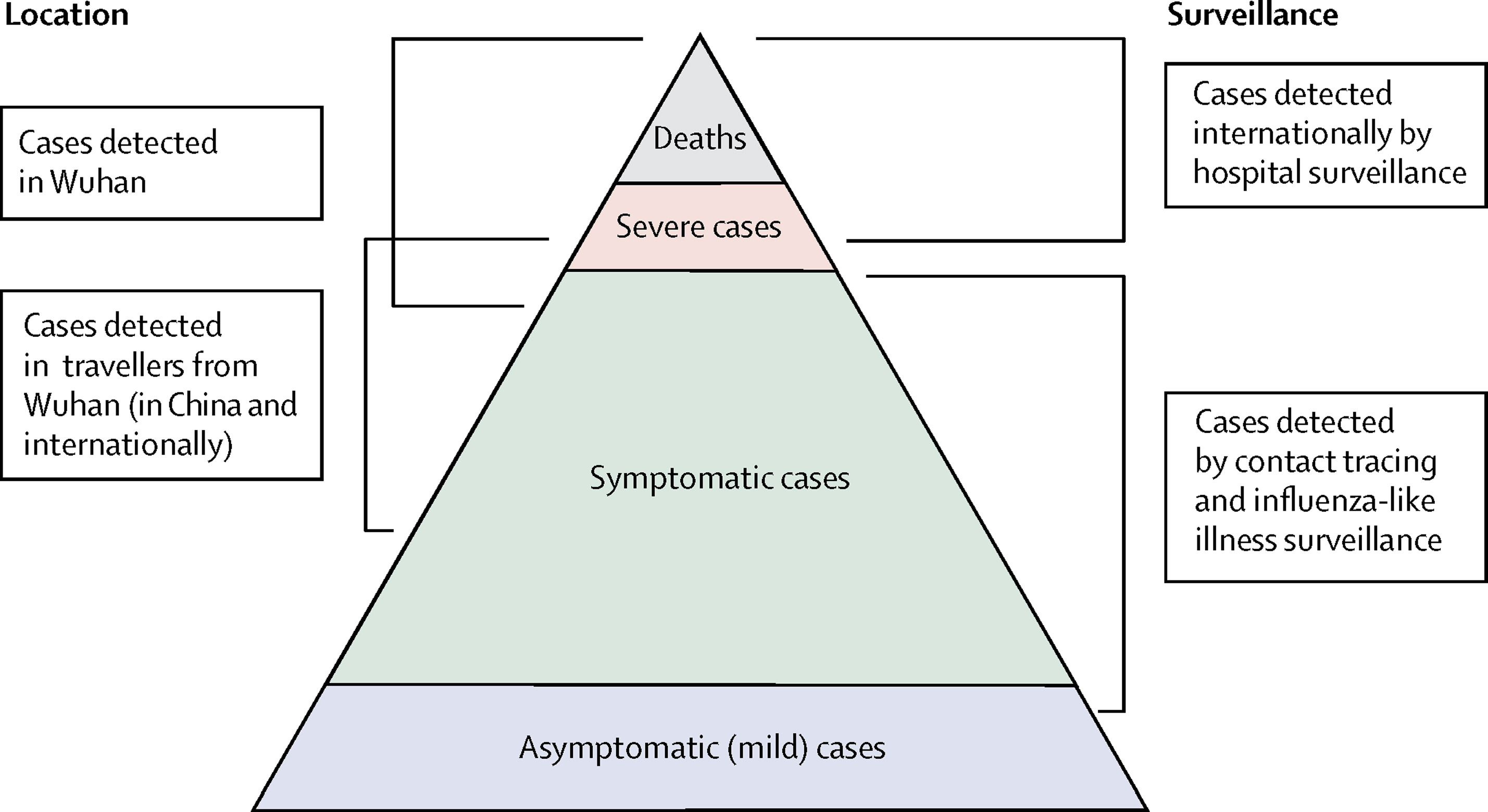
Espectro de casos de COVID-19. La probabilidad de muerte pretende estimar la proporción de muertes entre los casos confirmados en una epidemia. (Verity et al., 2020)

En la cúspide de la pirámide, los que cumplían los criterios de caso de la OMS para grave o críticos, identificados en el ámbito hospitalario, presentando una neumonía vírica atípica. Estos casos se habrían identificado en China continental y entre los categorizados internacionalmente como de transmisión local.
Es probable que haya muchos más casos sintomáticos (es decir, con fiebre, tos o mialgia) pero no requiriesen hospitalización. Estos casos se habrían identificado mediante el rastro de casos potenciales en vuelos internacionales a zonas de alto riesgo y mediante el rastreo de los contactos de los casos confirmados, o a través de vigilancia pasiva de otras enfermedades infecciosas respiratorias en la población.
La parte inferior de la pirámide representa enfermedad leve (y posiblemente asintomática). Estos casos podrían identificarse mediante el rastreo de contactos, mediante pruebas serológicas.

CFR no ajustado

Medimos la gravedad de la enfermedad en términos de riesgo/probabilidad de muerte (CFR). CFR se interpreta como la probabilidad condicional de muerte dado un diagnóstico confirmado, calculada como el número acumulado de muertes $D_{t}$ sobre el número acumulado de casos confirmados $C_{t}$ en un momento determinado $t$. Podemos referirnos al CFR sesgado ($b_{t}$):

\[ b_{t} = \frac{D_{t}}{C_{t}} \]

Este cálculo es sesgado porque genera una subestimación del CFR real, debido al retraso temporal desde el inicio de los síntomas hasta la muerte, que sólo se estabiliza en las últimas fases del brote.

Para calcular el CFR de forma directa y sin ajustar el retraso temporal entre la aparición de síntomas y la muerte del paciente (conocida como probabilidad de muerte “naive”), el paquete cfr requiere un una base de datos (dataframe) que contenga las siguientes tres columnas:

date
cases
deaths

Exploremos la base de datos ebola1976 incluido en {cfr} que procede del primer brote de ébola en lo que entonces se llamaba Zaire (ahora República Democrática del Congo) en 1976, analizado por Camacho et al. (2014).

R

# Cargamos la base de datos Ebola 1976, incluida en el paquete {cfr}
data("ebola1976")

# Asumiendo que solo tenemos datos para los primeros 30 días del brote
ebola1976 %>%
  slice_head(n = 30) %>%
  as_tibble()

SALIDA

# A tibble: 30 × 3
   date       cases deaths
   <date>     <int>  <int>
 1 1976-08-25     1      0
 2 1976-08-26     0      0
 3 1976-08-27     0      0
 4 1976-08-28     0      0
 5 1976-08-29     0      0
 6 1976-08-30     0      0
 7 1976-08-31     0      0
 8 1976-09-01     1      0
 9 1976-09-02     1      0
10 1976-09-03     1      0
# ℹ 20 more rows

Necesitamos datos de incidencia agregados

cfr lee datos de incidencia agregados por día

Estos deben ser agregados por día, es decir, cada fila de la base de datos contiene el número diario de casos y muertes notificadas. También deben incluirse aquellos días que tengan valores nulos o ausentes, de forma similar a los datos de series temporales.

cfr requiere datos diarios y no puede considerar otras unidades temporales de agregación, como semanas o meses.

Utilizando la función cfr_static() directamente, calculamos la probabilidad de muerte sin ajustar:

R

# Cálculo de la probabilidad de muerte sin ajustar durante los primeros 30 días
cfr::cfr_static(data = ebola1976 %>% slice_head(n = 30))

SALIDA

  severity_estimate severity_low severity_high
1         0.4740741    0.3875497     0.5617606

Desafío

Descarga el archivo sarscov2_casos_defunciones.csv y léelo en R.

Estima la probabilidad de muerte sin ajustar.

Dar una pista

Comprueba el formato de los datos introducidos.

¿Contiene datos diarios?
¿Los nombres de las columnas son los requeridos por cfr_static()?
¿Cómo se cambian los nombres de las columnas de una base de datos (dataframe) en R?

Mostrar la solución

Leemos los datos introducidos mediante readr::read_csv(). Esta función reconoce que la columna date tiene el formato correcto,<date>, que corresponde a fechas.

R

# lee la base de datos
# por ejemplo, si la ruta al archivo es data/raw-data/ebola_cases.csv :
sarscov2_input <-
  readr::read_csv(here::here("data", "raw-data", "sarscov2_cases_deaths.csv"))

R

# Inspect data
sarscov2_input

SALIDA

# A tibble: 93 × 3
   date       cases_jpn deaths_jpn
   <date>         <dbl>      <dbl>
 1 2020-01-20         1          0
 2 2020-01-21         1          0
 3 2020-01-22         0          0
 4 2020-01-23         1          0
 5 2020-01-24         1          0
 6 2020-01-25         3          0
 7 2020-01-26         3          0
 8 2020-01-27         4          0
 9 2020-01-28         6          0
10 2020-01-29         7          0
# ℹ 83 more rows

Podemos utilizar dplyr::rename() para cambiar los nombres de las columnas de este archivo y adaptarlos a los requeridos por cfr_static().

R

# Cambio de nombre de las columnas en base al formato requerido por `cfr_static`
sarscov2_input %>%
  dplyr::rename(
    cases = cases_jpn,
    deaths = deaths_jpn
  ) %>%
  cfr::cfr_static()

SALIDA

  severity_estimate severity_low severity_high
1        0.01895208   0.01828832    0.01963342

Sesgos que afectan a la estimación del CFR

Dos sesgos que afectan a la estimación del CFR

Lipsitch et al., 2015 describen dos posibles sesgos que pueden afectar a la estimación de la probabilidad de muerte (y sus posibles soluciones):

1. Sesgo por la identificación predominante de los casos más graves

Para enfermedades con un espectro de presentaciones clínicas, es más probable que los casos de mayor gravedad sean reconocidos y notificados a las autoridades de salud pública y se registran en las bases de datos de vigilancia, ya que las personas con síntomas graves son las que suelen buscar atención médica y acuden al centro de salud/hospital.

Por lo tanto, el CFR será normalmente más elevada entre los casos detectados que entre toda la población de casos, dado que esta última puede incluir individuos con presentaciones leves, subclínicas, y (según algunas definiciones de “caso”) asintomáticas.

2. Sesgo debido al retraso en la notificación de la defunción

En tiempo real durante una epidemia, suele haber un retraso temporal entre el momento en que alguien muere y el momento en que se notifica su muerte a la autoridad correspondiente. Por lo tanto, la lista de casos en tiempo real incluye a personas que morirán a causa de la enfermedad en el futuro, pero que aún siguen vivas, o que han muerto, pero cuya muerte no se ha notificado aún. Así pues, dividir el número acumulado de muertes notificadas por el número acumulado de casos notificados en un momento concreto durante un brote epidémico subestimará el CFR verdadera.

Los determinantes clave de la magnitud del sesgo son la tasa de crecimiento de la epidemia y la distribución del intervalo de tiempo desde la notificación del caso hasta la notificación de la defunción. Cuanto más largos sea este intervalo de tiempo y mayor sea la tasa de crecimiento, mayor será el sesgo.

En este episodio del tutorial, vamos a centrarnos en las soluciones para hacer frente a este sesgo utilizando el paquete de Rcfr ¡!

Caso de estudio: Gripe A (H1N1), México, 2009

Mejorar la estimación de la probabilidad de muerte, ajustando su cálculo al retraso temporal entre notificación de casos y muerte es crucial para determinar la gravedad de la enfermedad, adaptar la intensidad y el tipo de intervenciones de salud pública y asesorar a la población.

En 2009, durante el virus de la gripe porcina, Gripe A (H1N1) en México, la estimación temprana de la probabilidad de muerte fue sesgada. Los informes iniciales del gobierno de México sugerían una infección virulenta, mientras que, en otros países, el mismo virus se percibía como leve (TIME, 2009).

En EE.UU. y Canadá, no se atribuyó ninguna muerte al virus en los diez primeros días tras la declaración de emergencia de salud pública por parte de la Organización Mundial de la Salud.

Fraser et al., 2009 reinterpretó los datos evaluando los sesgos y obteniendo una gravedad clínica inferior a la de la pandemia de gripe de 1918, pero comparable a la observada en la pandemia de 1957.

CFR ajustado al retraso temporal

Nishiura et al, 2009 desarrollaron un método que tiene en cuenta la distribución temporal desde el inicio de los síntomas hasta la muerte.

Los brotes en tiempo real pueden tener un número de muertes insuficiente para determinar la distribución temporal entre el inicio de síntomas y la muerte. Por tanto, podemos estimar la distribución temporal en brotes históricos o utilizar las distribuciones incluidas en paquetes de R como {epiparameter} o {epireview} que los recogen de la literatura científica publicada. Para una guía paso a paso, lee el episodio tutorial sobre cómo acceder a distribuciones temporales epidemiológicas.

Utilicemos {epiparameter}:

R

# Get delay distribution
onset_to_death_ebola <-
  epiparameter::epidist_db(
    disease = "Ebola",
    epi_dist = "onset_to_death",
    single_epidist = TRUE
  )

# Plot <epidist> object
plot(onset_to_death_ebola, day_range = 0:40)

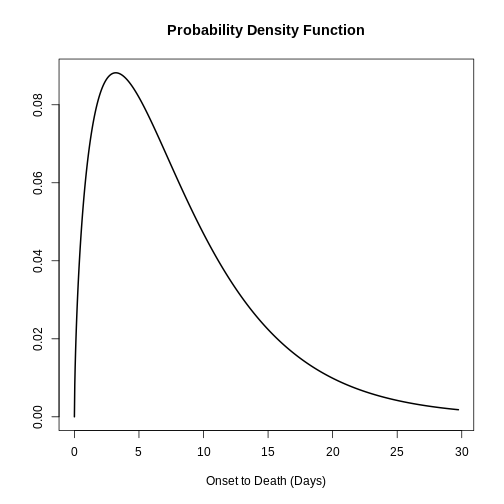
Para calcular el CFR ajustado, podemos utilizar la función cfr_static(), a través del argumento delay_density.

R

# Calculate the delay-adjusted CFR
# for the first 30 days
cfr::cfr_static(
  data = ebola1976 %>% slice_head(n = 30),
  delay_density = function(x) density(onset_to_death_ebola, x)
)

SALIDA

Total cases = 135 and p = 0.955: using Normal approximation to binomial likelihood.

SALIDA

  severity_estimate severity_low severity_high
1            0.9717       0.8201        0.9866

SALIDA

Total cases = 135 and p = 0.955: using Normal approximation to binomial likelihood.

La probabilidad de muerte ajustada indicó que la gravedad de la enfermedad al final del brote o con el últimos datos disponibles en ese momento es 0.9717 con un intervalo de confianza del 95% entre 0.8201 y 0.9866, con un valor superior al obtenido a través del cálculo directo sin ajustar.

Utiliza la clase epidist

Cuando utilices una clase <epidist> puedes utilizar esta expresión como plantilla:

function(x) density(<EPIDIST_OBJECT>, x)

Para distribuciones cuyos parámetros no estén disponibles en {epiparameter}, te proponemos dos alternativas:

Crear un objeto <epidist>, que puede ser utilizado con otros paquetes de R para análisis de brotes. Lee la documentación de referencia de epiparameter::epidist() o
Lee la viñeta para una introducción al trabajo con distribuciones temporales.

Desafío

Utiliza el mismo archivo del reto anterior (sarscov2_casos_muertes.csv).

Estima el CFR ajustado al retraso temporal utilizando la distribución apropiada y

¡Compara los valores del CFR ajustado y sin ajuste temporal!

Dar una pista

Encuentra el <epidist> ¡apropiado!

Mostrar la solución

Utilizamos {epiparameter} para acceder a una distribución temporal para los datos de incidencia agregados del SARS-CoV-2:

R

library(epiparameter)

sarscov2_delay <-
  epidist_db(
    disease = "covid",
    epi_dist = "onset to death",
    single_epidist = TRUE
  )

Leemos el archivo de datos mediante readr::read_csv(). Esta función reconoce que la columna date es de la clase <date>, es decir, una fecha.

R

# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
sarscov2_input <-
  readr::read_csv(here::here("data", "raw-data", "sarscov2_cases_deaths.csv"))

R

# Inspect data
sarscov2_input

SALIDA

# A tibble: 93 × 3
   date       cases_jpn deaths_jpn
   <date>         <dbl>      <dbl>
 1 2020-01-20         1          0
 2 2020-01-21         1          0
 3 2020-01-22         0          0
 4 2020-01-23         1          0
 5 2020-01-24         1          0
 6 2020-01-25         3          0
 7 2020-01-26         3          0
 8 2020-01-27         4          0
 9 2020-01-28         6          0
10 2020-01-29         7          0
# ℹ 83 more rows

Podemos utilizar dplyr::rename() para cambiar los nombres de las columnas del archivo a los requeridos porcfr_static().

R

# Rename before Estimate naive CFR
sarscov2_input %>%
  dplyr::rename(
    cases = cases_jpn,
    deaths = deaths_jpn
  ) %>%
  cfr::cfr_static(delay_density = function(x) density(sarscov2_delay, x))

SALIDA

Total cases = 159402 and p = 0.0734: using Normal approximation to binomial likelihood.

SALIDA

  severity_estimate severity_low severity_high
1             0.047       0.0221        0.2931

Interpreta las diferencias entre las estimaciones de la probabilidad de muerte sin ajustar y con ajuste temporal al intervalo entre la aparición inicial de síntomas en los casos y su muerte.

¿Cuándo utilizar distribuciones discretas?

En cfr_static() y toda la familia de funciones en cfr_*(), la opción más adecuada son las distribuciones discretas. Esto se debe a que trabajaremos con datos diarios de casos y defunciones.

Podemos suponer que la función de densidad de probabilidad (PDF) de una distribución continua es equivalente a la función de masa de probabilidad (PMF) de la distribución discreta correspondiente.

Sin embargo, esta suposición puede no ser adecuada en el caso de distribuciones con picos pronunciados y baja varianza, en las que los valores se concentran alrededor de la tendencia central. En tales casos, se espera que la disparidad media entre la PDF y la PMF sea más pronunciada en comparación con las distribuciones más dispersas. Una forma de abordar esto es discretizar la distribución continua. Esto lo podemos hacer en R, si discretizamos los objetos <epidist>, utilizando la función epiparameter::discretise().

¿Cómo funciona {cfr}?

Para ajustar la probabilidad de muerte, Nishiura et al., 2009 utilizan los datos de incidencia de casos y muertes para estimar el número de casos con resultados conocidos:

\[ u_t = \dfrac{\sum_{i = 0}^t \sum_{j = 0}^\infty c_{i - j} f_{j}}{\sum_{i = 0} c_i}, \]

donde

$c_{t}$ es la incidencia diaria de casos en el momento $t$,
$f_{t}$ es el valor de la función de masa de probabilidad (PMF) de la distribución temporal entre el inicio de síntomas y la muerte, y
$u_{t}$ representa el factor de subestimación de los resultados conocidos.

$u_{t}$ se utiliza para escalar el valor del número acumulado de casos en el denominador en el cálculo del CFR. Se calcula internamente con la función estimate_outcomes()

El estimador para la probabilidad de muerte puede expresarse como:

\[p_{t} = \frac{b_{t}}{u_{t}}\]

donde $p_{t}$ es la proporción realizada de casos confirmados que morirán a causa de la infección (o el CFR real), y $b_{t}$ es la estimación cruda y sesgada del CFR.

A partir de esta última ecuación, observamos que el CFR no sesgada $p_{t}$ es mayor que el CFR sesgada $b_{t}$ porque en $u_{t}$ el numerador es menor que el denominador (observa que $f_{t}$ es la distribución de probabilidad del retraso temporal entre síntomas y muerte). Por tanto, nos referimos a $b_{t}$ como el estimador sesgado de la probabilidad de muerte.

Cuando observamos todo el curso de una epidemia (desde $t \rightarrow \infty$), $u_{t}$ tiende a 1, lo que hace que $b_{t}$ tiende a $p_{t}$ y se convierta en un estimador no sesgado (Nishiura et al., 2009).

Estimación temprana del CFR

En el reto anterior, descubrimos que el valor de la probabilidad de muerte ajustada y no ajustada son diferentes.

La CFR sin ajustar es útil para obtener una estimación global de la gravedad del brote. Una vez que el brote haya finalizado o haya progresado de forma que se notifiquen más muertes, el CFR estimada es entonces más cercana a el CFR “verdadera” o no sesgada.

Por otra parte, el CFR ajustada puede ser utilizada para estimar la gravedad de una enfermedad infecciosa emergente de una forma más temprana durante una epidemia.

Podemos explorar la CFR ajustado al retraso temporal de forma temprana utilizando la función cfr_rolling()

Aviso

cfr_rolling() es una función que calcula automáticamente el CFR en cada día del brote con los datos disponibles hasta ese día, lo que ahorra tiempo al usuario, ya que no hace falta calcular este parámetro manualmente para cada momento.

R

# Calculate the rolling daily naive CFR
# for all the 73 days in the Ebola dataset
rolling_cfr_naive <- cfr::cfr_rolling(data = ebola1976)

SALIDA

`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.

R

utils::tail(rolling_cfr_naive)

SALIDA

         date severity_estimate severity_low severity_high
68 1976-10-31         0.9510204    0.9160061     0.9744387
69 1976-11-01         0.9510204    0.9160061     0.9744387
70 1976-11-02         0.9510204    0.9160061     0.9744387
71 1976-11-03         0.9510204    0.9160061     0.9744387
72 1976-11-04         0.9510204    0.9160061     0.9744387
73 1976-11-05         0.9551020    0.9210866     0.9773771

R

# Calculate the rolling daily delay-adjusted CFR
# for all the 73 days in the Ebola dataset
rolling_cfr_adjusted <- cfr::cfr_rolling(
  data = ebola1976,
  delay_density = function(x) density(onset_to_death_ebola, x)
)

SALIDA

`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.

SALIDA

Some daily ratios of total deaths to total cases with known outcome are below 0.01%: some CFR estimates may be unreliable.FALSE

R

utils::tail(rolling_cfr_adjusted)

SALIDA

         date severity_estimate severity_low severity_high
68 1976-10-31            0.9843       0.9003        0.9925
69 1976-11-01            0.9843       0.9003        0.9925
70 1976-11-02            0.9817       0.8838        0.9913
71 1976-11-03            0.9817       0.8838        0.9913
72 1976-11-04            0.9817       0.8838        0.9913
73 1976-11-05            0.9818       0.8843        0.9913

Con utils::tail() mostramos como los últimos valores estimados del CFR ajustado y sin ajustar tienen rangos superpuestos de intervalos de confianza del 95%.

Ahora, visualicemos ambos resultados en una serie temporal. ¿Cómo se comportarían en tiempo real las estimaciones de CFR ajustados y sin ajustar?

R

# get the latest delay-adjusted CFR
rolling_cfr_adjusted_end <-
  rolling_cfr_adjusted %>%
  dplyr::slice_tail()

# bind by rows both output data frames
bind_rows(
  rolling_cfr_naive %>%
    mutate(method = "naive"),
  rolling_cfr_adjusted %>%
    mutate(method = "adjusted")
) %>%
  # visualise both adjusted and unadjusted rolling estimates
  ggplot() +
  geom_ribbon(
    aes(
      date,
      ymin = severity_low,
      ymax = severity_high,
      fill = method
    ),
    alpha = 0.2, show.legend = FALSE
  ) +
  geom_line(
    aes(date, severity_estimate, colour = method)
  ) +
  geom_hline(
    data = rolling_cfr_adjusted_end,
    aes(yintercept = severity_estimate)
  ) +
  geom_hline(
    data = rolling_cfr_adjusted_end,
    aes(yintercept = severity_low),
    lty = 2
  ) +
  geom_hline(
    data = rolling_cfr_adjusted_end,
    aes(yintercept = severity_high),
    lty = 2
  )

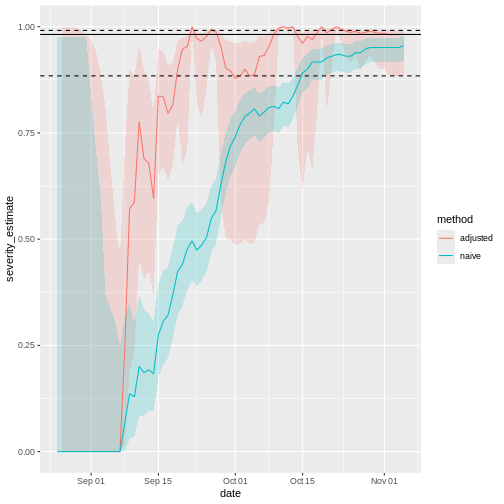
La línea horizontal representa el CFR ajustado al retraso temporal, estimada al final del brote. La línea punteada significa que la estimación tiene un intervalo de confianza del 95% (IC 95%).

Observa que este cálculo ajustado al retraso temporal entre síntomas y muerte es especialmente útil cuando los únicos datos disponibles son curvas epidémica de casos confirmados (es decir, cuando no se dispone de datos individuales, especialmente durante la fase inicial de la epidemia). Cuando hay pocas muertes o ninguna, hay que hacer una suposición para la distribución temporal desde la aparición de síntomas hasta la muerte, por ejemplo, a partir de la literatura basada en brotes anteriores. Nishiura et al., 2009 representan esto en las figuras con datos del brote de SARS en Hong Kong, 2003.

Caso de estudio: Brote de SARS, Hong Kong, 2003

Las figuras A y B muestran el número acumulado de casos y muertes por SRAS, y la figura C muestra las estimaciones observadas (sesgadas) del CFR en función del tiempo, es decir, el número acumulado de muertes sobre casos en el momento $t$. Debido al retraso temporal desde el inicio de los síntomas hasta la muerte, la estimación sesgada de la probabilidad de muerte en el tiempo $t$ subestima el valor en las etapas finales del brote (es decir, 302/1755 = 17,2%).

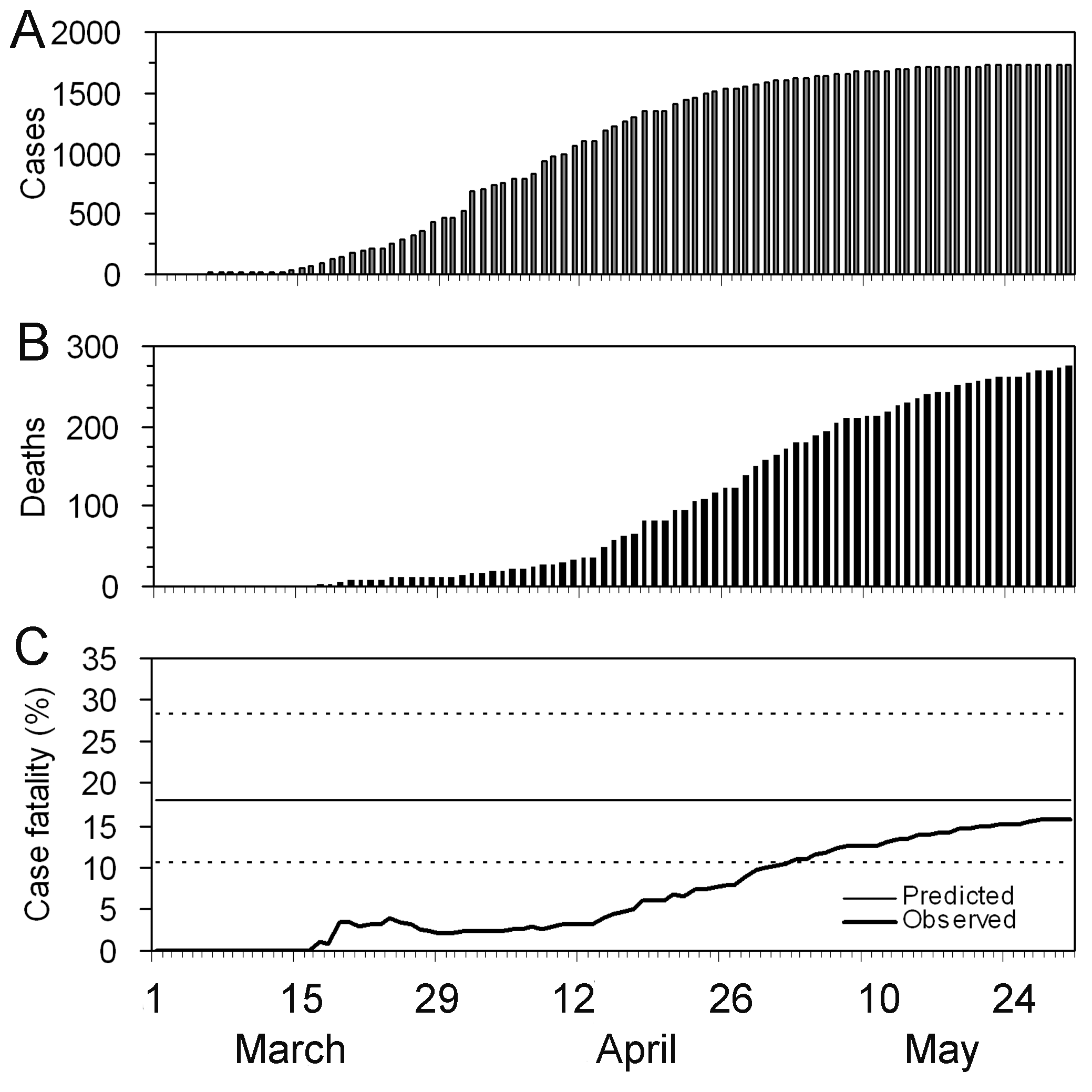
Riesgo observado (sesgado) de muerte confirmada del síndrome respiratorio agudo grave (SRAS) en Hong Kong, 2003. (Nishiura et al., 2009)

No obstante, incluso utilizando únicamente los datos observados para el periodo comprendido entre el 19 de marzo y el 2 de abril, cfr_static() puede obtener una predicción adecuada (Figura D), por ejemplo, el CFR ajustado al retraso en el 27 de marzo es del 18,1% (IC del 95%: 10,5, 28,1). Se observa una sobreestimación en las fases muy tempranas de la epidemia, pero los límites de confianza del 95% en las fases posteriores incluyen el CFR realizado (es decir, 17,2 %).

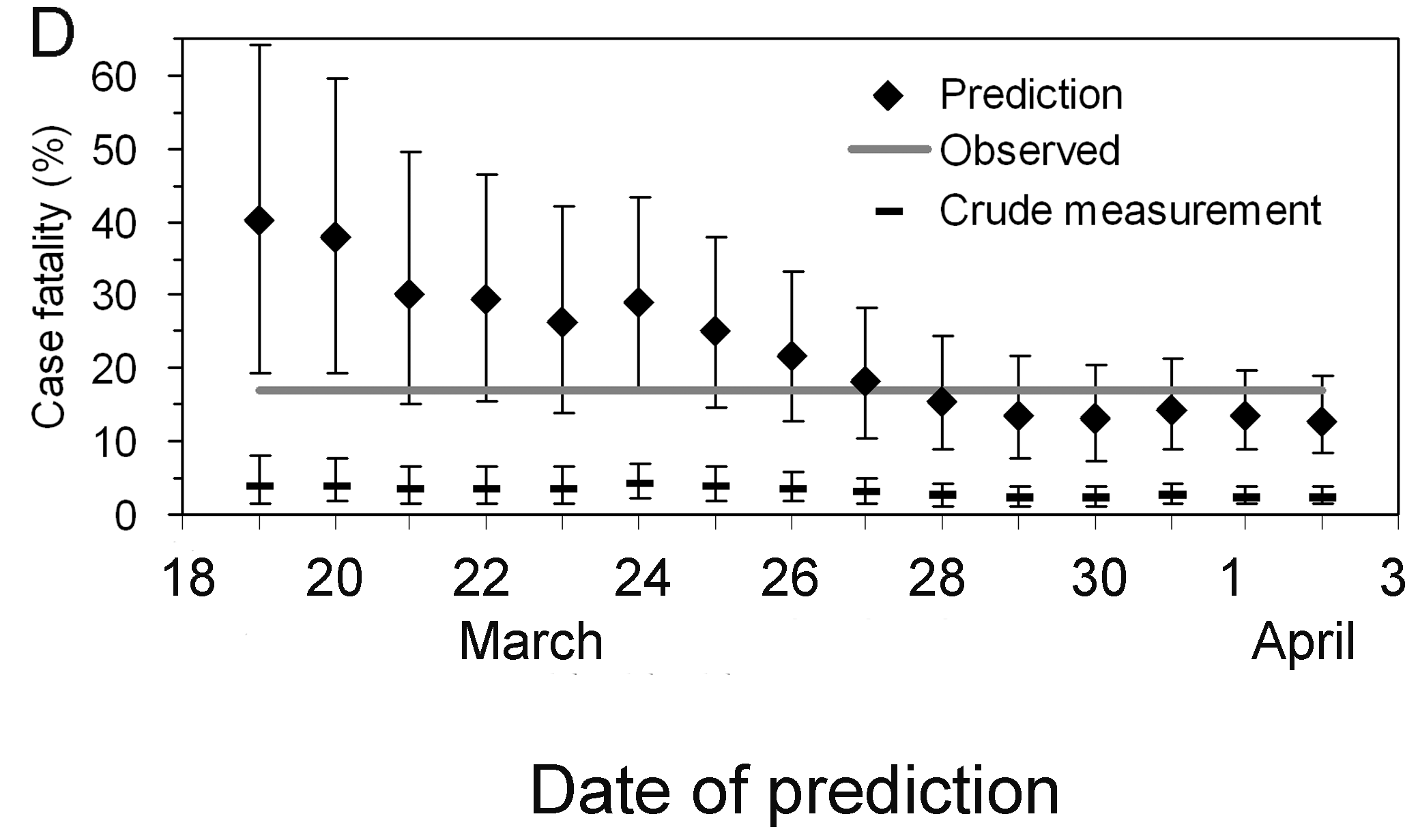
Determinación temprana del riesgo de muerte confirmada ajustado al retraso del síndrome respiratorio agudo grave (SRAS) en Hong Kong, 2003. (Nishiura et al., 2009)

Interpretar la estimación del CFR en la fase inicial del brote

Basándote en la figura anterior:

¿Cuántos días hay entre el inicio del brote y la fecha en la que el intervalo de confianza de la CFR ajustado se cruza con el intervalo de confianza de la CFR sin ajustar? ¿Los intervalos se cruzan con el CFR estimada al final del brote?

Discusión:

¿Cuáles son las implicaciones para la política de salud pública de tener una CFR ajustado por retraso temporal?

Dar una pista

Podemos utilizar la inspección visual o el análisis de los marcos de datos de salida.

Mostrar la solución

Hay casi un mes de diferencia.

Nótese que la estimación tiene una incertidumbre considerable al principio de la serie temporal. Al cabo de dos semanas, el CFR ajustado se aproxima a la estimación global del CFR al final del brote.

¿Es este patrón similar al de otros brotes? Podemos utilizar los conjuntos de datos de los retos de este episodio. ¡Te invitamos a averiguarlo!

Lista de verificación

Con cfr estimamos el CFR como la proporción de muertes entre confirmadas confirmados.

Utilizando sólo el número de casos confirmados está claro que se pasarán por alto todos los casos que no busquen tratamiento médico o no sean notificados, así como todos los casos asintomáticos. Esto significa que la estimación del CFR es superior a la proporción de muertes entre los infectados.

¿Por qué difieren el CFR sin ajustar y la ajustada al retraso temporal?

cfr tiene como objetivo obtener un estimador insesgado “mucho antes” de observar el curso completo del brote. Para ello cfr utiliza el factor de subestimación $u_{t}$ para estimar el CFR sin sesgo $p_{t}$ , utilizando métodos de máxima verosimilitud, dado el proceso de muestreo definido por Nishiura et al., 2009.

¿Qué es el proceso de muestreo?

La población de casos confirmados y el proceso de muestreo para estimar el CFR sin sesgo durante el transcurso de un brote. (Nishiura et al., 2009)

En datos agregados de incidencia en el momento $t$ conocemos el número acumulado de casos confirmados y muertes, $C_{t}$ y $D_{t}$ y deseamos estimar el CFR sin sesgo $\pi$ mediante el factor de subestimación $u_{t}$.

Si conociéramos el factor de subestimación $u_{t}$ podríamos especificar el tamaño de la población de casos confirmados que ya no corren riesgo ($u_{t}C_{t}$, sombreado), aunque no sabemos qué individuos supervivientes pertenecen a este grupo. Una proporción $\pi$ de los del grupo de casos aún en riesgo (tamaño $(1- u_{t})C_{t}$, sin sombrear) se espera que muera.

Ya que cada caso que deja de estar en riesgo tiene una probabilidad independiente de morir, $\pi$ el número de muertes, $D_{t}$ es una muestra de una distribución binomial con tamaño de muestra $u_{t}C_{t}$ y probabilidad de morir $p_{t}$ = $\pi$.

Esto se representa mediante la siguiente función de verosimilitud para obtener la estimación de máxima verosimilitud del CFR sin sesgo $p_{t}$ = $\pi$:

\[ {\sf L}(\pi | C_{t},D_{t},u_{t}) = \log{\dbinom{u_{t}C_{t}}{D_{t}}} + D_{t} \log{\pi} + (u_{t}C_{t} - D_{t})\log{(1 - \pi)}, \]

Esta estimación la realiza la función interna ?cfr:::estimate_severity().

Limitaciones

La CFR ajustado al retraso temporal no aborda todas las fuentes de error en los datos, como el infradiagnóstico de individuos infectados.

Desafíos

Los datos agregados difieren de los listados de casos individuales

Los datos de incidencia agregados difieren de lista en los que cada observación contiene datos a nivel individual.

R

outbreaks::ebola_sierraleone_2014 %>% as_tibble()

SALIDA

# A tibble: 11,903 × 8
      id   age sex   status    date_of_onset date_of_sample district chiefdom
   <int> <dbl> <fct> <fct>     <date>        <date>         <fct>    <fct>
 1     1    20 F     confirmed 2014-05-18    2014-05-23     Kailahun Kissi Teng
 2     2    42 F     confirmed 2014-05-20    2014-05-25     Kailahun Kissi Teng
 3     3    45 F     confirmed 2014-05-20    2014-05-25     Kailahun Kissi Tonge
 4     4    15 F     confirmed 2014-05-21    2014-05-26     Kailahun Kissi Teng
 5     5    19 F     confirmed 2014-05-21    2014-05-26     Kailahun Kissi Teng
 6     6    55 F     confirmed 2014-05-21    2014-05-26     Kailahun Kissi Teng
 7     7    50 F     confirmed 2014-05-21    2014-05-26     Kailahun Kissi Teng
 8     8     8 F     confirmed 2014-05-22    2014-05-27     Kailahun Kissi Teng
 9     9    54 F     confirmed 2014-05-22    2014-05-27     Kailahun Kissi Teng
10    10    57 F     confirmed 2014-05-22    2014-05-27     Kailahun Kissi Teng
# ℹ 11,893 more rows

Utiliza el paquete incidence2 para reordenar tus datos

Usando el paqueteoutbreaks, carga el listado de casos “MERS” incluido en el objeto mers_korea_2015.

Reordena el listado de casos para que tenga la estructura de entrada requerida por el paquete cfr.

Estima el HFR ajustado al retardo utilizando el retardo de distribución correspondiente.

Dar una pista

¿Cómo reorganizar mis datos de entrada?

Reorganizar los datos de entrada para el análisis de datos puede llevarte la mayor parte del tiempo. Para estar listo para el análisis con datos de incidencia agregados te animamos a utilizar incidence2 ¡!

Primero, en la viñeta Inicio de incidence2 explora cómo utilizar date_index al leer un listado de casos con fechas en varias columnas.

A continuación, consulta la viñeta Manejo de datos de {incidence2} del paquete cfr, sobre cómo utilizar la función cfr::prepare_data() con los objetos incidence2.

Mostrar la solución

R

# Carga los paquetes
library(cfr)
library(epiparameter)
library(incidence2)
library(outbreaks)
library(tidyverse)

# Accede a la distribución de retrasos temporales
mers_delay <-
  epidist_db(
    disease = "mers",
    epi_dist = "onset to death",
    single_epidist = TRUE
  )

# Lee el listado de casos
mers_korea_2015$linelist %>%
  as_tibble() %>%
  select(starts_with("dt_"))

SALIDA

# A tibble: 162 × 6
   dt_onset   dt_report  dt_start_exp dt_end_exp dt_diag    dt_death
   <date>     <date>     <date>       <date>     <date>     <date>
 1 2015-05-11 2015-05-19 2015-04-18   2015-05-04 2015-05-20 NA
 2 2015-05-18 2015-05-20 2015-05-15   2015-05-20 2015-05-20 NA
 3 2015-05-20 2015-05-20 2015-05-16   2015-05-16 2015-05-21 2015-06-04
 4 2015-05-25 2015-05-26 2015-05-16   2015-05-20 2015-05-26 NA
 5 2015-05-25 2015-05-27 2015-05-17   2015-05-17 2015-05-26 NA
 6 2015-05-24 2015-05-28 2015-05-15   2015-05-17 2015-05-28 2015-06-01
 7 2015-05-21 2015-05-28 2015-05-16   2015-05-17 2015-05-28 NA
 8 2015-05-26 2015-05-29 2015-05-15   2015-05-15 2015-05-29 NA
 9 NA         2015-05-29 2015-05-15   2015-05-17 2015-05-29 NA
10 2015-05-21 2015-05-29 2015-05-16   2015-05-16 2015-05-29 NA
# ℹ 152 more rows

R

# Usa {incidence2} para contabilizar la incidencia diaria
mers_incidence <- mers_korea_2015$linelist %>%
  # convertir a un objeto incidence2
  incidence(date_index = c("dt_onset", "dt_death")) %>%
  # completa las fechas de la primera a la última
  incidence2::complete_dates()

# Explora los resultados de incidence2
mers_incidence

SALIDA

# incidence:  72 x 3
# count vars: dt_death, dt_onset
   date_index count_variable count
   <date>     <chr>          <int>
 1 2015-05-11 dt_death           0
 2 2015-05-11 dt_onset           1
 3 2015-05-12 dt_death           0
 4 2015-05-12 dt_onset           0
 5 2015-05-13 dt_death           0
 6 2015-05-13 dt_onset           0
 7 2015-05-14 dt_death           0
 8 2015-05-14 dt_onset           0
 9 2015-05-15 dt_death           0
10 2015-05-15 dt_onset           0
# ℹ 62 more rows

R

# Prepara los datos {incidence2} para usarlos en {cfr}
mers_incidence %>%
  prepare_data(
    cases_variable = "dt_onset",
    deaths_variable = "dt_death"
  )

SALIDA

         date deaths cases
1  2015-05-11      0     1
2  2015-05-12      0     0
3  2015-05-13      0     0
4  2015-05-14      0     0
5  2015-05-15      0     0
6  2015-05-16      0     0
7  2015-05-17      0     1
8  2015-05-18      0     1
9  2015-05-19      0     0
10 2015-05-20      0     5
11 2015-05-21      0     6
12 2015-05-22      0     2
13 2015-05-23      0     4
14 2015-05-24      0     2
15 2015-05-25      0     3
16 2015-05-26      0     1
17 2015-05-27      0     2
18 2015-05-28      0     1
19 2015-05-29      0     3
20 2015-05-30      0     5
21 2015-05-31      0    10
22 2015-06-01      2    16
23 2015-06-02      0    11
24 2015-06-03      1     7
25 2015-06-04      1    12
26 2015-06-05      1     9
27 2015-06-06      0     7
28 2015-06-07      0     7
29 2015-06-08      2     6
30 2015-06-09      0     1
31 2015-06-10      2     6
32 2015-06-11      1     3
33 2015-06-12      0     0
34 2015-06-13      0     2
35 2015-06-14      0     0
36 2015-06-15      0     1

R

# Estima el CFR ajustado a retrasos temporales
mers_incidence %>%
  cfr::prepare_data(
    cases_variable = "dt_onset",
    deaths_variable = "dt_death"
  ) %>%
  cfr::cfr_static(delay_density = function(x) density(mers_delay, x))

SALIDA

  severity_estimate severity_low severity_high
1            0.0907        0.042        0.4847

Heterogeneidad de la gravedad

La CFR puede diferir entre poblaciones (por ejemplo, edad, espacio, tratamiento); cuantificar estas heterogeneidades puede ayudar a dirigir los recursos adecuadamente y a comparar distintos regímenes asistenciales (Cori et al., 2017).

Utiliza la base de datos cfr::covid_data para estimar una CFR ajustado al retraso temporal estratificada por países.

Dar una pista

Una forma de hacer un análisis estratificado es aplicar un modelo a datos anidados. Esta viñeta {tidyr} te muestra cómo aplicar la función group_by() + nest() a los datos anidados, y luego mutate() + map() para aplicar el modelo.

Mostrar la solución

R

library(cfr)
library(epiparameter)
library(tidyverse)

covid_data %>% glimpse()

SALIDA

Rows: 20,786
Columns: 4
$ date    <date> 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2…
$ country <chr> "Argentina", "Brazil", "Colombia", "France", "Germany", "India…
$ cases   <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ deaths  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…

R

delay_onset_death <-
  epidist_db(
    disease = "covid",
    epi_dist = "onset to death",
    single_epidist = TRUE
  )

covid_data %>%
  group_by(country) %>%
  nest() %>%
  mutate(
    temp =
      map(
        .x = data,
        .f = cfr::cfr_static,
        delay_density = function(x) density(delay_onset_death, x)
      )
  ) %>%
  unnest(cols = temp)

SALIDA

# A tibble: 19 × 5
# Groups:   country [19]
   country        data     severity_estimate severity_low severity_high
   <chr>          <list>               <dbl>        <dbl>         <dbl>
 1 Argentina      <tibble>            0.0133       0.0133        0.0133
 2 Brazil         <tibble>            0.0195       0.0195        0.0195
 3 Colombia       <tibble>            0.0225       0.0224        0.0226
 4 France         <tibble>            0.0044       0.0044        0.0044
 5 Germany        <tibble>            0.0045       0.0045        0.0045
 6 India          <tibble>            0.0119       0.0119        0.0119
 7 Indonesia      <tibble>            0.024        0.0239        0.0241
 8 Iran           <tibble>            0.0191       0.0191        0.0192
 9 Italy          <tibble>            0.0075       0.0075        0.0075
10 Mexico         <tibble>            0.0461       0.046         0.0462
11 Peru           <tibble>            0.0318       0.0151        0.202
12 Poland         <tibble>            0.0186       0.0186        0.0187
13 Russia         <tibble>            0.0182       0.0182        0.0182
14 South Africa   <tibble>            0.0254       0.0253        0.0255
15 Spain          <tibble>            0.0087       0.0087        0.0087
16 Turkey         <tibble>            0.006        0.006         0.006
17 Ukraine        <tibble>            0.0204       0.0203        0.0205
18 United Kingdom <tibble>            0.009        0.009         0.009
19 United States  <tibble>            0.0111       0.0111        0.0111

¡Estupendo! Ahora puedes utilizar un código similar para cualquier otro análisis estratificado, como la edad, las regiones u otros.

Pero, ¿cómo podemos interpretar que existe una variabilidad de gravedad por países a partir del mismo patógeno diagnosticado?

Factores locales como la capacidad de análisis, la definición de caso y el régimen de muestreo pueden afectar a la notificación de casos y muertes, afectando así a la comprobación de los casos. Echa un vistazo a la viñeta Estimar la proporción de casos que se determinan durante un brote del paquete cfr para más información ¡!

Apéndice

El paquete cfr tiene una función llamada cfr_time_varying() con una funcionalidad distinta de cfr_rolling().

¿Cuándo utilizar cfr_rolling()?

cfr_rolling() muestra el CFR estimada en cada día del brote, dado que los datos futuros sobre casos y muertes no están disponibles en ese momento. El valor final de cfr_rolling() estimado es idéntico al de cfr_static() con los mismos datos.

Recuerda, como se muestra arriba cfr_rolling() es útil para obtener estimaciones del CFR en las primeras fases y comprobar si la estimación del CFR de un brote se ha estabilizado. Así, cfr_rolling() no es sensible a la duración ni al tamaño de la epidemia.

¿Cuándo utilizar cfr_time_varying()?

Por otra parte, cfr_time_varying() calcula el CFR a lo largo de una ventana móvil y ayuda a comprender los cambios en el CFR debidos a cambios en la epidemia, por ejemplo, debidos a una nueva variante o a una mayor inmunidad por vacunación.

Sin embargo, cfr_time_variying() es sensible a la incertidumbre del muestreo. Por tanto, es sensible al tamaño del brote. Cuanto mayor sea el número de casos con resultados esperados en un día determinado, más estimaciones razonables del CFR variable en el tiempo obtendremos.

Por ejemplo, con 100 casos, la estimación del riesgo de mortalidad tendrá, a grandes rasgos, un intervalo de confianza del 95% ±10% de la estimación media (IC binomial). Por tanto, si tenemos >100 casos con resultados esperados en un día determinado podemos obtener estimaciones razonables del CFR variable en el tiempo. Pero si sólo tenemos >100 casos a lo largo de toda la epidemia probablemente tengamos que basarnos en cfr_rolling() que utiliza los datos acumulados.

Te invitamos a leer esta viñeta sobre cfr_time_varying().

Más medidas de gravedad

Supongamos que necesitamos evaluar la gravedad clínica de la epidemia en un contexto distinto al de los datos de vigilancia, como la gravedad entre los casos que llegan a los hospitales o los casos que recogiste en una encuesta serológica representativa.

Utilizando cfr podemos cambiar las entradas para el numerador casos (cases) y el denominador muertes (deaths) para estimar más medidas de gravedad, como el Riesgo de Fatalidad por Infección (RFI) o el Riesgo de Fatalidad por Hospitalización (RFH). Podemos seguir esta analogía:

Riesgo de mortalidad por infección y hospitalización

Si para la una probabilidad de muerte (CFR o CFR en inglés), exigimos:

Incidencia de casos y muertes, con una:
Distribución de retraso temporal entre casos y muertes (o una aproximación cercana, como el tiempo entre inicio de los síntomas y la muerte).

Entonces, el Riesgo de Fatalidad por Infección (IFR, por sus siglas en inglés) requiere:

Incidencia de infecciones y muertes, con una:
Distribución de retraso temporal desde la infección hasta la muerte (o una aproximación cercana).

Del mismo modo, el Riesgo de Fatalidad por Hospitalización (HFR) requiere:

Incidencia de hospitalizaciones y muertes, y una:
Distribución del retraso temporal entre la hospitalización y la muerte.

Fuentes de datos para más medidas de gravedad

Yang et al., 2020 resume diferentes definiciones y fuentes de datos:

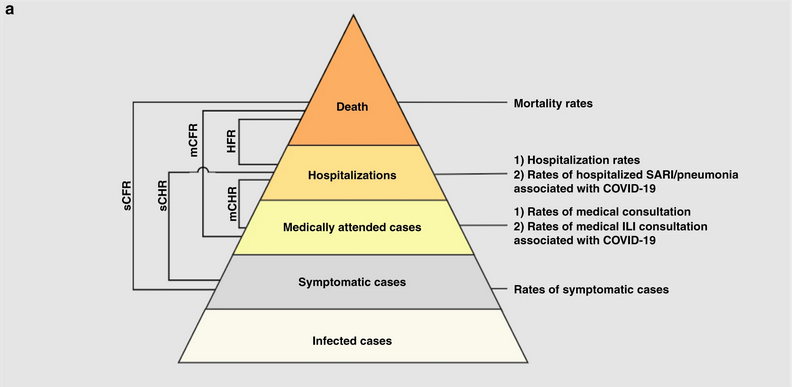
Niveles de gravedad de las infecciones por SRAS-CoV-2 y parámetros de interés. Se supone que cada nivel es un subconjunto del nivel inferior.

sCFR riesgo sintomático de muerte,
sCHR riesgo sintomático de hospitalización,
mCFR riesgo de caso-fatalidad médicamente atendido,
mCHR riesgo de hospitalización de casos atendidos médicamente,
HFR riesgo de hospitalización-fatalidad.

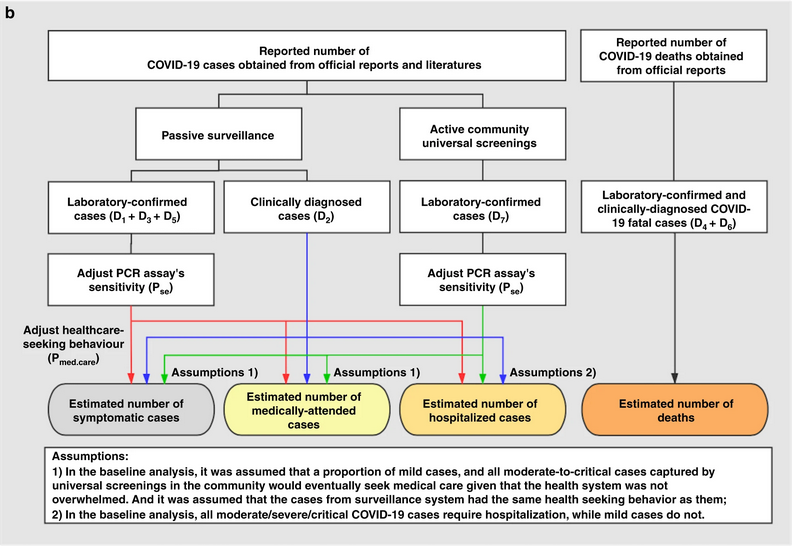
Diagrama esquemático de los análisis de referencia. Las flechas rojas, azules y verdes indican el flujo de datos desde los casos confirmados por laboratorio de la vigilancia pasiva, los casos diagnosticados clínicamente y los casos confirmados por laboratorio de los cribados activos.

Discusión

Basándote en tu experiencia:

Comparte algún brote anterior en el que hayas participado en su respuesta.

Responde a estas preguntas:

¿Cómo evaluaste la gravedad clínica del brote?
¿Cuáles fueron las principales fuentes de sesgo?
¿Qué hiciste para tener en cuenta el sesgo identificado?
¿Qué análisis complementario harías para resolver el sesgo?

Puntos Clave

Utiliza cfr para estimar la gravedad
Utiliza cfr_static() para estimar el CFR global con los últimos datos disponibles.
Utiliza cfr_rolling() para mostrar cuál sería el CFR estimada en cada día del brote.
Utiliza la delay_density para ajustar el CFR según la distribución de retrasos correspondiente.

Content from Account for superspreading

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

How can we estimate individual-level variation in transmission (i.e. superspreading potential) from contact tracing data?
What are the implications for variation in transmission for decision-making?

Objetivos

Estimate the distribution of onward transmission from infected individuals (i.e. offspring distribution) from outbreak data using epicontacts.
Estimate the extent of individual-level variation (i.e. the dispersion parameter) of the offspring distribution using fitdistrplus.
Estimate the proportion of transmission that is linked to ‘superspreading events’ using {superspreading}.

Prerequisites

Learners should familiarise themselves with following concept dependencies before working through this tutorial:

Statistics: common probability distributions, particularly Poisson and negative binomial.

Epidemic theory: The reproduction number, R.

Introduction

From smallpox to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), some infected individuals spread infection to more people than others. Disease transmission is the result of a combination of biological and social factors, and these factors average out to some extent at the population level during a large epidemic. Hence researchers often use population averages to assess the potential for disease to spread. However, in the earlier or later phases of an outbreak, individual differences in infectiousness can be more important. In particular, they increase the chance of superspreading events (SSEs), which can ignite explosive epidemics and also influence the chances of controlling transmission (Lloyd-Smith et al., 2005).

Chains of SARS-CoV-2 transmission in Hong Kong initiated by local or imported cases. (a), Transmission network of a cluster of cases traced back to a collection of four bars across Hong Kong (n = 106). (b), Transmission network associated with a wedding without clear infector–infectee pairs but linked back to a preceding social gathering and local source (n = 22). (c), Transmission network associated with a temple cluster of undetermined source (n = 19). (d), All other clusters of SARS-CoV-2 infections where the source and transmission chain could be determined (Adam et al., 2020).

The basic reproduction number, $R_{0}$, measures the average number of cases caused by one infectious individual in a entirely susceptible population. Estimates of $R_{0}$ are useful for understanding the average dynamics of an epidemic at the population-level, but can obscure considerable individual variation in infectiousness. This was highlighted during the global emergence of SARS-CoV-2 by numerous ‘superspreading events’ in which certain infectious individuals generated unusually large numbers of secondary cases (LeClerc et al, 2020).

In this tutorial, we are going to quantify individual variation in transmission, and hence estimate the potential for superspreading events. Then we are going to use these estimates to explore the implications of superspreading for contact tracing interventions.

We are going to use data from the outbreaks package, manage the linelist and contacts data using epicontacts, and estimate distribution parameters with fitdistrplus. Lastly, we are going to use {superspreading} to explore the implications of variation in transmission for decision-making.

We’ll use the pipe %>% to connect some of the functions from these packages, so let’s also call the tidyverse package.

R

library(outbreaks)
library(epicontacts)
library(fitdistrplus)
library(superspreading)
library(tidyverse)

The double-colon

The double-colon :: in R let you call a specific function from a package without loading the entire package into the current environment.

For example, dplyr::filter(data, condition) uses filter() from the dplyr package.

This help us remember package functions and avoid namespace conflicts.

The individual reprodution number

The individual reproduction number is defined as the number of secondary cases caused by a particular infected individual.

Early in an outbreak we can use contact data to reconstruct transmission chains (i.e. who infected whom) and calculate the number of secondary cases generated by each individual. This reconstruction of linked transmission events from contact data can provide an understanding about how different individuals have contributed to transmission during an epidemic (Cori et al., 2017).

Let’s practice this using the mers_korea_2015 linelist and contact data from the outbreaks package and integrate them with the epicontacts package to calculate the distribution of secondary cases during the 2015 MERS-CoV outbreak in South Korea (Campbell, 2022):

R

## first, make an epicontacts object
epi_contacts <-
  epicontacts::make_epicontacts(
    linelist = outbreaks::mers_korea_2015$linelist,
    contacts = outbreaks::mers_korea_2015$contacts
  )

R

# visualise contact network
epicontacts::vis_epicontacts(epi_contacts)

Is contact data tidy?

Contact data from a transmission chain can provide information on which infected individuals came into contact with others. We expect to have the infector (from) and the infectee (to) plus additional columns of variables related to their contact, such as location (exposure) and date of contact.

Following tidy data principles, the observation unit in our contact dataset is the infector-infectee pair. Although one infector can infect multiple infectees, from contact tracing investigations we may record contacts linked to more than one infector (e.g. within a household). But we should expect to have unique infector-infectee pairs, because typically each infected person will have acquired the infection from one other.

To ensure these unique pairs, we can check on replicates for infectees:

R

# no infector-infectee pairs are replicated
epi_contacts %>%
  purrr::pluck("contacts") %>%
  dplyr::group_by(to) %>%
  dplyr::filter(dplyr::n() > 1)

SALIDA

# A tibble: 5 × 4
# Groups:   to [2]
  from  to     exposure       diff_dt_onset
  <chr> <chr>  <fct>                  <int>
1 SK_16 SK_107 Emergency room            17
2 SK_87 SK_107 Emergency room             2
3 SK_14 SK_39  Hospital room             16
4 SK_11 SK_39  Hospital room             13
5 SK_12 SK_39  Hospital room             12

When each infector-infectee row is unique, the number of entries per infector corresponds to the number of secondary cases generated by that individual.

R

# count secondary cases per infector
infector_secondary <- epi_contacts %>%
  purrr::pluck("contacts") %>%
  dplyr::count(from, name = "secondary_cases")

But this output only contains number of secondary cases for reported infectors, not for each of the individuals in the whole epicontacts object.

To get this, first, we can use epicontacts::get_id() to get the full list of unique identifiers (“id”) from the epicontacts class object. Second, join it with the count secondary cases per infector stored in the infector_secondary object. Third, replace the missing values with 0 to express no report of secondary cases from them.

R

all_secondary <- epi_contacts %>%
  # extract ids in contact *and* linelist using "which" argument
  epicontacts::get_id(which = "all") %>%
  # transform vector to dataframe to use left_join()
  tibble::enframe(name = NULL, value = "from") %>%
  # join count secondary cases per infectee
  dplyr::left_join(infector_secondary) %>%
  # infectee with missing secondary cases are replaced with zero
  tidyr::replace_na(
    replace = list(secondary_cases = 0)
  )

From a histogram of the all_secondary object, we can identify the individual-level variation in the number of secondary cases. Three cases were related to more than 20 secondary cases, while the complementary cases with less than five or zero secondary cases.

R

## plot the distribution
all_secondary %>%
  ggplot(aes(secondary_cases)) +
  geom_histogram(binwidth = 1) +
  labs(
    x = "Number of secondary cases",
    y = "Frequency"
  )

The number of secondary cases can be used to empirically estimate the offspring distribution, which is the number of secondary infections caused by each case. One candidate statistical distribution used to model the offspring distribution is the negative binomial distribution with two parameters:

Mean, which represents the $R_{0}$, the average number of (secondary) cases produced by a single individual in an entirely susceptible population, and
Dispersion, expressed as $k$, which represents the individual-level variation in transmission by single individuals.

From the histogram and density plot, we can identify that the offspring distribution is highly skewed or overdispersed. In this framework, the superspreading events (SSEs) are not arbitrary or exceptional, but simply realizations from the right-hand tail of the offspring distribution, which we can quantify and analyse (Lloyd-Smith et al., 2005).

Terminology recap

From linelist and contact data, we calculate the number of secondary cases caused by the observed infected individuals.
Whereas $R_{0}$ captures the average transmission in the population, we can define the individual reproduction number as a random variable representing the expected number of secondary cases caused by a infected individual.
From the stochastic effects in transmission, the number of secondary infections caused by each case is described by an offspring distribution.
An empirical offspring distribution can be modeled by the negative-binomial distribution with mean $R_{0}$ and dispersion parameter $k$.

Poisson, overdispersion, and Negative Binomial

For occurrences of associated discrete events we can use Poisson or negative binomial discrete distributions.

In a Poisson distribution, mean is equal to variance. But when variance is higher than the mean, this is called overdispersion. In biological applications, overdispersion occurs and so a negative binomial may be worth considering as an alternative to Poisson distribution.

Negative binomial distribution is specially useful for discrete data over an unbounded positive range whose sample variance exceeds the sample mean. In such terms, the observations are overdispersed with respect to a Poisson distribution, for which the mean is equal to the variance.

In epidemiology, negative binomial have being used to model disease transmission for infectious diseases where the likely number of onward infections may vary considerably from individual to individual and from setting to setting, capturing all variation in infectious histories of individuals, including properties of the biological (i.e. degree of viral shedding) and environmental circumstances (e.g. type and location of contact).

Desafío

Calculate the distribution of secondary cases for Ebola using the ebola_sim_clean object from outbreaks package.

Is the offspring distribution of Ebola skewed or overdispersed?

Dar una pista

Note: This dataset has 5829 cases. Running epicontacts::vis_epicontacts() may overload your session!

Mostrar la solución

R

## first, make an epicontacts object
ebola_contacts <-
  epicontacts::make_epicontacts(
    linelist = ebola_sim_clean$linelist,
    contacts = ebola_sim_clean$contacts
  )

# count secondary cases

ebola_infector_secondary <- ebola_contacts %>%
  purrr::pluck("contacts") %>%
  dplyr::count(from, name = "secondary_cases")

ebola_secondary <- ebola_contacts %>%
  # extract ids in contact *and* linelist using "which" argument
  epicontacts::get_id(which = "all") %>%
  # transform vector to dataframe to use left_join()
  tibble::enframe(name = NULL, value = "from") %>%
  # join count secondary cases per infectee
  dplyr::left_join(ebola_infector_secondary) %>%
  # infectee with missing secondary cases are replaced with zero
  tidyr::replace_na(
    replace = list(secondary_cases = 0)
  )

## plot the distribution
ebola_secondary %>%
  ggplot(aes(secondary_cases)) +
  geom_histogram(binwidth = 1) +
  labs(
    x = "Number of secondary cases",
    y = "Frequency"
  )

From a visual inspection, the distribution of secondary cases for the Ebola data set in ebola_sim_clean shows an skewed distribution with secondary cases equal or lower than 6. We need to complement this observation with a statistical analysis to evaluate for overdispersion.

Estimate the dispersion parameter

To empirically estimate the dispersion parameter $k$, we could fit a negative binomial distribution to the number of secondary cases.

We can fit distributions to data using the fitdistrplus package, which provides maximum likelihood estimates.

R

library(fitdistrplus)

R

## fit distribution
offspring_fit <- all_secondary %>%
  dplyr::pull(secondary_cases) %>%
  fitdistrplus::fitdist(distr = "nbinom")

offspring_fit

SALIDA

Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
       estimate  Std. Error
size 0.02039807 0.007278299
mu   0.60452947 0.337893199

Name of parameters

From the fitdistrplus output:

The size object refers to the estimated dispersion parameter $k$, and
The mu object refers to the estimated mean, which represents the $R_{0}$,

From the number secondary cases distribution we estimated a dispersion parameter $k$ of 0.02, with a 95% Confidence Interval from 0.006 to 0.035. As the value of $k$ is significantly lower than one, we can conclude that there is considerable potential for superspreading events.

We can overlap the estimated density values of the fitted negative binomial distribution and the histogram of the number of secondary cases:

Individual-level variation in transmission

The individual-level variation in transmission is defined by the relationship between the mean ($R_{0}$), dispersion ($k$), and the variance of a negative binomial distribution.

The negative binomial model has $variance = R_{0}(1+\frac{R_{0}}{k})$, so smaller values of $k$ indicate greater variance and, consequently, greater individual-level variation in transmission.

\[\uparrow variance = R_{0}(1+\frac{R_{0}}{\downarrow k})\]

When $k$ approaches infinity ($k \rightarrow \infty$) the variance equals the mean (because $\frac{R_{0}}{\infty}=0$). This makes the conventional Poisson model an special case of the negative binomial model.

Desafío

Use the distribution of secondary cases from the ebola_sim_clean object from outbreaks package.

Fit a negative binomial distribution to estimate the mean and dispersion parameter of the offspring distribution.

Does the estimated dispersion parameter of Ebola provide evidence of an individual-level variation in transmission?

Dar una pista

Review how we fitted a negative binomial distribution using the fitdistrplus::fitdist() function.

Mostrar la solución

R

ebola_offspring <- ebola_secondary %>%
  dplyr::pull(secondary_cases) %>%
  fitdistrplus::fitdist(distr = "nbinom")

ebola_offspring

SALIDA

Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
     estimate  Std. Error
size 2.353899 0.250124611
mu   0.539300 0.009699219

R

## extract the "size" parameter
ebola_mid <- ebola_offspring$estimate[["size"]]

## calculate the 95% confidence intervals using the standard error estimate and
## the 0.025 and 0.975 quantiles of the normal distribution.

ebola_lower <- ebola_mid + ebola_offspring$sd[["size"]] * qnorm(0.025)

ebola_upper <- ebola_mid + ebola_offspring$sd[["size"]] * qnorm(0.975)

# ebola_mid
# ebola_lower
# ebola_upper

From the number secondary cases distribution we estimated a dispersion parameter $k$ of 2.354, with a 95% Confidence Interval from 1.864 to 2.844.

For dispersion parameter estimates higher than one we get low distribution variance, hence, low individual-level variation in transmission.

But does this mean that the secondary case distribution does not have superspreading events (SSEs)? You will later find one additional challenge: How do you define an SSE threshold for Ebola?

Select the best model

We can use the maximum likelihood estimates from fitdistrplus to compare different models and assess fit performance using estimators like the AIC and BIC. Read further in the vignette on Estimate individual-level transmission and use the {superspreading} helper function ic_tbl() for this!

The dispersion parameter across diseases

Research into sexually transmitted and vector-borne diseases has previously suggested a ‘20/80’ rule, with 20% of individuals contributing at least 80% of the transmission potential (Woolhouse et al).

On its own, the dispersion parameter $k$ is hard to interpret intuitively, and hence converting into proportional summary can enable easier comparison. When we consider a wider range of pathogens, we can see there is no hard and fast rule for the percentage that generates 80% of transmission, but variation does emerge as a common feature of infectious diseases

When the 20% most infectious cases contribute to the 80% of transmission (or more), there is a high individual-level variation in transmission, with a highly overdispersed offspring distribution ($k<0.1$), e.g., SARS-1.
When the 20% most infectious cases contribute to the ~50% of transmission, there is a low individual-level variation in transmission, with a moderately dispersed offspring distribution ($k > 0.1$), e.g. Pneumonic Plague.

Evidence for variation in individual reproductive number. (Left, c) Proportion of transmission expected from the most infectious 20% of cases, for 10 outbreak or surveillance data sets (triangles). Dashed lines show proportions expected under the 20/80 rule (top) and homogeneity (bottom). (Right, d), Reported superspreading events (SSEs; diamonds) relative to estimated reproductive number R (squares) for twelve directly transmitted infections. Crosses show the 99th-percentile proposed as threshold for SSEs. (More figure details in Lloyd-Smith et al., 2005)

Controlling superspreading with contact tracing

During an outbreak, it is common to try and reduce transmission by identifying people who have come into contact with an infected person, then quarantine them in case they subsequently turn out to be infected. Such contact tracing can be deployed in multiple ways. ‘Forward’ contact tracing targets downstream contacts who may have been infected by a newly identifed infection (i.e. the ‘index case’). ‘Backward’ tracing instead tracks the upstream primary case who infected the index case (or a setting or event at which the index case was infected), for example by retracing history of contact to the likely point of exposure. This makes it possible to identify others who were also potentially infected by this earlier primary case.

In the presence of individual-level variation in transmission, i.e., with an overdispersed offspring distribution, if this primary case is identified, a larger fraction of the transmission chain can be detected by forward tracing each of the contacts of this primary case (Endo et al., 2020).

Schematic representation of contact tracing strategies. Black arrows indicate the directions of transmission, blue and Orange arrows, a successful or failed contact tracing, respectivelly. When there is evidence of individual-level variation in transmission, often resulting in superspreading, backward contact tracing from the index case (blue circle) increase the probability to find the primary case (green circle) or clusters with a larger fraction of cases, potentially increasing the number of quarentined cases (yellow circles). Claire Blackmore, 2021

When there is evidence of individual-level variation (i.e. overdispersion), often resulting in so-called superspreading events, a large proportion of infections may be linked to a small proportion of original clusters. As a result, finding and targeting originating clusters in combination with reducing onwards infection may substantially enhance the effectiveness of tracing methods (Endo et al., 2020).

Empirical evidence focused on evaluating the efficiency of backward tracing lead to 42% more cases identified than forward tracing supporting its implementation when rigorous suppression of transmission is justified (Raymenants et al., 2022)

Probability of cases in a given cluster

Using {superspreading}, we can estimate the probability of having a cluster of secondary infections caused by a primary case identified by backward tracing of size $X$ or larger (Endo et al., 2020).

R

# Set seed for random number generator
set.seed(33)

# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
  R = offspring_fit$estimate["mu"],
  k = offspring_fit$estimate["size"],
  cluster_size = c(5, 10, 25)
)

SALIDA

          R          k prop_5 prop_10 prop_25
1 0.6045295 0.02039807  87.9%   74.6%   46.1%

Even though we have an $R<1$, a highly overdispersed offspring distribution ($k=0.02$) means that if we detect a new case, there is a 46.1% probability they originated from a cluster of 25 infections or more. Hence, by following a backwards strategy, contact tracing efforts will increase the probability of successfully contain and quarantining this large number of earlier infected individuals, rather than simply focusing on the new case, who is likely to have infected nobody (because $k$ is very small).

We can also use this number to prevent gathering of certain sized to reduce the epidemic by preventing potential superspreading events. Interventions can target to reduce the reproduction number in order to reduce the probability of having clusters of secondary cases.

Backward contact tracing for Ebola

Use the Ebola estimated parameters for ebola_sim_clean object from outbreaks package.

Calculate the probability of having a cluster of secondary infections caused by a primary case identified by backward tracing of size 5, 10, 15 or larger.

Would implementing a backward strategy at this stage of the Ebola outbreak increase the probability of containing and quarantining more onward cases?

Dar una pista

Review how we estimated the probability of having clusters of a fixed size, given an offspring distribution mean and dispersion parameters, using the superspreading::proportion_cluster_size() function.

Mostrar la solución

R

# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
  R = ebola_offspring$estimate["mu"],
  k = ebola_offspring$estimate["size"],
  cluster_size = c(5, 10, 25)
)

SALIDA

       R        k prop_5 prop_10 prop_25
1 0.5393 2.353899   1.8%      0%      0%

The probability of having clusters of five people is 1.8%. At this stage, given this offspring distribution parameters, a backward strategy may not increase the probability of contain and quarantine more onward cases.

Challenges

Does Ebola have any superspreading event?

‘Superspreading events’ can mean different things to different people, so Lloyd-Smith et al., 2005 proposed a general protocol for defining a superspreading event (SSE). If the number of secondary infections caused by each case, $Z$, follows a negative binomial distribution ($R, k$):

We define an SSE as any infected individual who infects more than $Z(n)$ others, where $Z(n)$ is the nth percentile of the $Poisson(R)$ distribution.
A 99th-percentile SSE is then any case causing more infections than would occur in 99% of infectious histories in a homogeneous population

Using the corresponding distribution function, estimate the SSE threshold to define a SSE for the Ebola offspring distribution estimates for the ebola_sim_clean object from outbreaks package.

Dar una pista

In a Poisson distribution, the lambda or rate parameter are equal to the estimated mean from a negative binomial distribution. You can explore this in The distribution zoo shiny app.

Mostrar la solución

To get the quantile value for the 99th-percentile we need to use the density function for the Poisson distribution dpois().

R

# get mean
ebola_mu_mid <- ebola_offspring$estimate["mu"]

# get 99th-percentile from poisson distribution
# with mean equal to mu
stats::qpois(
  p = 0.99,
  lambda = ebola_mu_mid
)

SALIDA

[1] 3

Compare this values with the ones reported by Lloyd-Smith et al., 2005. See figure below:

Reported superspreading events (SSEs; diamonds) relative to estimated reproduction number R (squares) for twelve directly transmitted infections. Lines show 5–95 percentile range of the number of secondary cases following a Poisson distribution with lambda equal to the reproduction number (Z∼Poisson(R)), and crosses show the 99th-percentile proposed as threshold for SSEs. Stars represent SSEs caused by more than one source case. ‘Other’ diseases are: 1, Streptococcus group A; 2, Lassa fever; 3, Mycoplasma pneumonia; 4, pneumonic plague; 5, tuberculosis. R is not shown for ‘other’ diseases, and is off-scale for monkeypox.

Expected proportion of transmission

What is the proportion of cases responsible for 80% of transmission?

Use {superspreading} and compare the estimates for MERS using the offspring distributions parameters from this tutorial episode, with SARS-1 and Ebola offspring distributions parameter accessible via the {epiparameter} R package.

Dar una pista

To use superspreading::proportion_transmission() we recommend to read the Estimate what proportion of cases cause a certain proportion of transmission reference manual.

Currently, {epiparameter} has offspring distributions for SARS, Smallpox, Mpox, Pneumonic Plague, Hantavirus Pulmonary Syndrome, Ebola Virus Disease. Let’s access the offspring distribution mean and dispersion parameters for SARS-1:

R

# Load parameters
sars <- epiparameter::epidist_db(
  disease = "SARS",
  epi_dist = "offspring distribution",
  single_epidist = TRUE
)
sars_params <- epiparameter::get_parameters(sars)
sars_params

SALIDA

      mean dispersion
      1.63       0.16

Mostrar la solución

R

#' estimate for ebola --------------

ebola_epiparameter <- epiparameter::epidist_db(
  disease = "Ebola",
  epi_dist = "offspring distribution",
  single_epidist = TRUE
)
ebola_params <- epiparameter::get_parameters(ebola_epiparameter)
ebola_params

SALIDA

      mean dispersion
       1.5        5.1

R

# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
  R = ebola_params[["mean"]],
  k = ebola_params[["dispersion"]],
  percent_transmission = 0.8
)

SALIDA

    R   k prop_80
1 1.5 5.1   43.2%

R

#' estimate for sars --------------

# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
  R = sars_params[["mean"]],
  k = sars_params[["dispersion"]],
  percent_transmission = 0.8
)

SALIDA

     R    k prop_80
1 1.63 0.16     13%

R

#' estimate for mers --------------

# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
  R = offspring_fit$estimate["mu"],
  k = offspring_fit$estimate["size"],
  percent_transmission = 0.8
)

SALIDA

          R          k prop_80
1 0.6045295 0.02039807    2.1%

MERS has the lowest percent of cases (2.1%) responsible of the 80% of the transmission, representative of highly overdispersed offspring distributions.

Ebola has the highest percent of cases (43%) responsible of the 80% of the transmission. This is representative of offspring distributions with high dispersion parameters.

inverse-dispersion?

The dispersion parameter $k$ can be expressed differently across the literature.

In the Wikipedia page for the negative binomial, this parameter is defined in its reciprocal form (refer to the variance equation).
In the distribution zoo shiny app, the dispersion parameter $k$ is named “Inverse-dispersion” but it is equal to parameter estimated in this episode. We invite you to explore this!

heterogeneity?

The individual-level variation in transmission is also referred as the heterogeneity in the transmission or degree of heterogeneity in Lloyd-Smith et al., 2005, heterogeneous infectiousness in Campbell et al., 2018 when introducing the {outbreaker2} package. Similarly, a contact network can store heterogeneous epidemiological contacts as in the documentation of the epicontacts package (Nagraj et al., 2018).

Read these blog posts

The Tracing monkeypox article from the JUNIPER consortium showcases the usefulness of network models on contact tracing.

The Going viral post from Adam Kucharski shares insides from YouTube virality, disease outbreaks, and marketing campaigns on the conditions that spark contagion online.

Puntos Clave

Use epicontacts to calculate the number of secondary cases cause by a particular individual from linelist and contact data.
Use fitdistrplus to empirically estimate the offspring distribution from the number of secondary cases distribution.
Use {superspreading} to estimate the probability of having clusters of a given size from primary cases and inform contact tracing efforts.

Content from Simulate transmission chains

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

How can we simulate transmission chains based on infection characteristics?

Objetivos

Create a short term projection using a branching process with epichains.

Prerequisites

Learners should familiarise themselves with the following concept dependencies before working through this tutorial:

Statistics: Common probability distributions, including Poisson and negative binomial.

Epidemic theory: The reproduction number, $R$.

Introduction

Individual variation in transmission can affect both the potential for an epidemic to establish in a population and the ease of control (Cori et al., 2017).

Greater variation reduces the overall probably of a single new case causing a large local outbreak, because most cases infect few others and individuals that generate a large number of secondary cases are relatively rare.
However, if a ‘superspreading event’ does occur and the outbreak gets established, this variation can make an outbreak harder to control using mass interventions (i.e. blanket interventions that implicitly assume everyone contributes equally to transmission), because some cases contribute disproportionality: a single uncontrolled case may generate a large number of secondary cases.
Conversely, variation in transmission may provide opportunities for targeted interventions if the individuals who contribute more to transmission (due to biological or behavioural factors), or the settings in which ‘superspreading events’ occur, share socio-demographic, environmental or geographical characteristics that can be defined.

How can we quantify the potential of a new infection to cause a large outbreak based on its reproduction number $R$ and the dispersion $k$ of its offspring distribution?

Observed number of cumulative cases from the Middle East respiratory syndrome (MERS) outbreak in South Korea, 2015, alongside with simulated transmission chains assuming an offspring distribution with $R=0.6$ and $k=0.02$.

In this episode, we will use the epichains package to simulate transmission chains and estimate the potential for large outbreaks following the introduction of a new case. We are going to use it with functions from {epiparameter}, dplyr and purrr, so also loading the tidyverse package:

R

library(epichains)
library(epiparameter)
library(tidyverse)

The double-colon

The double-colon :: in R let you call a specific function from a package without loading the entire package into the current environment.

For example, dplyr::filter(data, condition) uses filter() from the dplyr package.

This help us remember package functions and avoid namespace conflicts.

Simulation of uncontrolled outbreaks

Infectious disease epidemics spread through populations when a chain of infected individuals transmit the infection to others. Branching processes can be used to model this transmission. A branching process is a stochastic process (i.e. a random process that can be described by a known probability distribution), where each infectious individual gives rise to a random number of individuals in the next generation of infection, starting with the index case in generation 1. The distribution of the number of secondary cases each individual generates is called the offspring distribution (Azam & Funk, 2024).

epichains provides methods to analyse and simulate the size and length of branching processes with an given offspring distribution. epichains implements a rapid and simple model to simulate transmission chains to assess epidemic risk, project cases into the future, and evaluate interventions that change $R$.

chain size and length

The size of the transmission chain is defined as the total number of individuals infected across all generations of infection, and
the length of the transmission chain is the number of generations from the first case to the last case in the outbreak before the chain ended.

The size calculation includes the first case, and the length calculation contains the first generation when the first case starts the chain (See figure below).

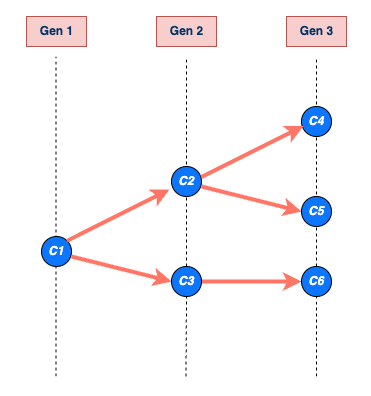
An example of a transmission chain starting with a single case C1. Cases are represented by blue circles and arrows indicating who infected whom. The chain grows through generations Gen 1, Gen 2, and Gen 3, producing cases C2, C3, C4, C5, and C6. The chain ends at generation Gen 3 with cases C4, C5, and C6. The size of C1’s chain is 6, including C1 (that is, the sum of all blue circles), and the length is 3, which includes Gen 1 (maximum number of generations reached by C1’s chain) (Azam & Funk, 2024).

To use epichains, we need to know (or assume) two key epidemiological values: the offspring distribution and the generation time.

Get the offspring distribution

Here we assume the MERS offspring distribution follows a negative binomial distribution, with mean (reproduction number $R$) and dispersion $k$ values estimated from the linelist and contact data of mers_korea_2015 in the outbreaks R package in the previous episode.

R

mers_offspring <- c(mean = 0.60, dispersion = 0.02)

offspring distribution for epichains

We input an offspring distribution to epichains by referring to the R function that generates random values from the distribution we want. For a negative binomial distribution, we use rnbinom with its corresponding mu and size arguments:

R

  offspring_dist = rnbinom,
  mu = mers_offspring["mean"],
  size = mers_offspring["dispersion"],

The reference manual in ?rnbinom tells us our required specific arguments.

Poisson and other distributions

epichains can accept any R function that generates random numbers, so the specified arguments will change depending on the R function used. For more details on the range of possible options, see the function reference manual.

For example, let’s say we want to use a Poisson distribution for the offspring distribution. First, read the argument required in the ?rpois reference manual. Second, specify the lambda argument parameter, also known as rate or mean in the literature. In epichains, this can look like this:

R

  offspring_dist = rpois,
  lambda = mers_offspring["mean"],

In this example, we can specify lambda = mers_offspring["mean"] because the mean number of secondary cases generated (i.e. $R$) should be the same regardless of the distribution we assume. What changes is the variance of the distribution, and hence the level of individual-level variation in transmission. When the dispersion parameter $k$ approaches infinity ($k \rightarrow \infty$) in a negative binomial distribution, the variance equals the mean. This makes the conventional Poisson distribution a special case of the negative binomial distribution.

Get generation time

The serial interval distribution is often used to approximate the generation time distribution. This approximation is commonly used because it is easier to observe and measure the onset of symptoms in each case than the precise time of infection.

generation time vs serial interval

A schematic of the relationship of different time periods of transmission between an infector and an infectee in a transmission pair. Exposure window is defined as the time interval having viral exposure, and transmission window is defined as the time interval for onward transmission with respect to the infection time (Chung Lau et al., 2021).

However, using the serial interval as an approximation of the generation time is primarily valid for diseases in which infectiousness starts after symptom onset (Chung Lau et al., 2021). In cases where infectiousness starts before symptom onset, the serial intervals can have negative values, which is the case for diseases with pre-symptomatic transmission (Nishiura et al., 2020).

Let’s use the {epiparameter} package to access and use the available serial interval for MERS disease:

R

serial_interval <- epidist_db(
  disease = "mers",
  epi_dist = "serial",
  single_epidist = TRUE
)

plot(serial_interval, day_range = 0:25)

The serial interval for MERS has a mean of 12.6 days and a standard deviation of 2.8 days.

generation time for epichains

In epichains, we need to specify the generation time as a function that generates random numbers. Using {epiparameter} has the advantage of using the distribution function epiparameter::generate() for this input. This will look like this:

R

function(x) generate(x = serial_interval, times = x)

This interface is similar to the one cfr uses to link with {epiparameter}. Read the work with delay distributions vignette for further context.

Simulate a single chain

Now we are prepared to use the simulate_chains() function from epichains to create one transmission chain:

R

epichains::simulate_chains(
  # simulation controls
  n_chains = 5,
  statistic = "size",
  # offspring
  offspring_dist = rnbinom,
  mu = mers_offspring["mean"],
  size = mers_offspring["dispersion"],
  # generation
  generation_time = function(x) generate(x = serial_interval, times = x)
)

simulate_chains() requires three sets of arguments as a minimum:

simulation controls,
offspring distribution, and
generation time.

In the lines above, we described how to specify the offspring distribution and generation time. The simulation controls include at least two arguments:

index_case, which defines the number of index cases to simulate transmission chains for and
statistic, which defines a chain statistic to track (either "size" or "length") as the stopping criteria for each chain being simulated.

Stopping criteria

This is an customisable feature of epichains. By default, branching process simulations end when they have gone extinct. For long-lasting transmission chains, in simulate_chains() you can add the stat_max argument.

For example, if we set an stopping criteria for statistic = "size" of stat_max = 500, no more offspring will be produced after a chain of size 500.

The simulate_chains() output creates a <epichains> class object, which we can then analyse further in R.

Simulate multiple chains

We can use simulate_chains() to create multiple chains and increase the probability of simulating uncontrolled outbreak projections given an overdispersed offspring distribution.

We need to specify three additional elements:

set.seed(<integer>), which is a random number generator function with a specified seed value, the <integer> number, to ensure consistent results across different runs of the code.
number_simulations, which defines the number of simulations to run.
initial_cases defines the number of initial cases to input to the n_chains argument explained in the lines above.

R

# Set seed for random number generator
set.seed(33)
# Number of simulation runs
number_simulations <- 1000
# Number of initial cases
initial_cases <- 1

number_simulations and initial_cases are conveniently stored in objects to facilitate downstream reuse in the workflow.

Iteration using purrr

Iteration aims to perform the same action on different objects repeatedly.

Learn how to use the core purrr functions like map() from the YouTube tutorial on How to purrr by Equitable Equations.

Or, if you previously used the *apply family of functions, visit the package vignette on purrr base R, which shares key differences, direct translations, and examples.

To get multiple chains, we must apply the simulate_chains() function to each chain defined by a sequence of numbers from 1 to 1000.

purrr and epichains

First, let’s sketch how we use purrr::map() with epichains::simulate_chains(). The map() function requires two arguments:

.x, with a vector of numbers, and
.f, a function to iterate to each vector value.

R

map(
  # vector of numbers (simulation IDs)
  .x = seq_len(number_simulations),
  # function to iterate to each simulation ID number
  .f = function(sim) {
    simulate_chains(...) %>%
      # creates a column with the simulation ID number
      mutate(simulation_id = sim)
  }
) %>%
  # combine list outputs (for each simulation ID) into a single data frame
  list_rbind()

The sim element is placed to register the iteration number (simulation ID) as a new column in the <epichains> output. The purrr::list_rbind() function aims to combine all the list outputs from map().

Why a dot (.) as a prefix? In the tidy design principles book we have a chapter on the dot prefix!

Now, we are prepared to use map() to repeatedly simulate from simulate_chains() and store in a vector from 1 to 1000:

R

simulated_chains_map <-
  # iterate one function across multiple numbers (simulation IDs)
  purrr::map(
    # vector of numbers (simulation IDs)
    .x = seq_len(number_simulations),
    # function to iterate to each simulation ID number
    .f = function(sim) {
      epichains::simulate_chains(
        # simulation controls
        n_chains = initial_cases,
        statistic = "size",
        # offspring
        offspring_dist = rnbinom,
        mu = mers_offspring["mean"],
        size = mers_offspring["dispersion"],
        # generation
        generation_time = function(x) generate(x = serial_interval, times = x)
      ) %>%
        # creates a column with the simulation ID number
        dplyr::mutate(simulation_id = sim)
    }
  ) %>%
  # combine list outputs (for each simulation ID) into a single data frame
  purrr::list_rbind()

Read the epichains output

To explore the output format of the <epichains> class object of name simulated_chains_map, let’s look at the simulated simulation_id number 806.

The epichains object

Let’s use dplyr::filter() for this:

R

chain_to_observe <- 806

R

#### get epichain summary ----------------------------------------------------

simulated_chains_map %>%
  dplyr::filter(simulation_id == chain_to_observe)

SALIDA

`<epichains>` object

< epichains head (from first known infector) >

  chain infector infectee generation     time simulation_id
2     1        1        2          2 16.38623           806
3     1        1        3          2 11.79430           806
4     1        1        4          2 10.77252           806
5     1        1        5          2 11.39945           806
6     1        1        6          2 10.23130           806
7     1        2        7          3 26.01046           806


Number of infectors (known): 3
Number of generations: 3
Use `as.data.frame(<object_name>)` to view the full output in the console.

Key elements from this output are in the footer, the piece of text that appears at the bottom:

SALIDA

Number of infectors (known): 3
Number of generations: 3

The simulated simulation_id number 806 has three known infectors and three generations. These numbers are more visible when reading the <epichains> objects as a data frame.

The epichains data frame

R

#### infector-infectee data frame --------------------------------------------

simulated_chains_map %>%
  dplyr::filter(simulation_id == chain_to_observe) %>%
  dplyr::as_tibble()

SALIDA

# A tibble: 9 × 6
  chain infector infectee generation  time simulation_id
  <int>    <dbl>    <dbl>      <int> <dbl>         <int>
1     1       NA        1          1   0             806
2     1        1        2          2  16.4           806
3     1        1        3          2  11.8           806
4     1        1        4          2  10.8           806
5     1        1        5          2  11.4           806
6     1        1        6          2  10.2           806
7     1        2        7          3  26.0           806
8     1        2        8          3  29.8           806
9     1        2        9          3  26.6           806

Chain 806 tells us a story: “In the first transmission generation at time = 0, one index case infected the first case with sim_id = 1. Then, in the second transmission generation (between time 10 to 16), sim_id = 1 infected five cases. Later, in the third transmission generation (between time 26 to 30), sim_id = 2 infected three new cases.”

An infectee data frame

The output data frame collects infectees as the observation unit:

Each infectee has a sim_id.
Each infectee that behaved as an infector is registered in the infector column using sim_id of that infectee.
Each infectee got infected in a specific generation and (continuous) time.
The simulation number is registered under the simulation_id column.

Note: The Number of infectors (known) includes the NA observation under the infector column. This refers to the infector specified as index case (in the n_chains argument), which started the transmission chain to the infectee of sim_id = 1, at generation = 1, and time = 0.

Visualize multiple chains

To visualize the simulated chains, we need some pre-processing:

Let’s use dplyr to get round time numbers to resemble surveillance days.
Count the daily cases in each simulation (by simulation_id).
Calculate the cumulative number of cases within a simulation.

R

# daily aggregate of cases
simulated_chains_day <- simulated_chains_map %>%
  # use data.frame output from <epichains> object
  dplyr::as_tibble() %>%
  # transform simulation ID column to factor (categorical variable)
  dplyr::mutate(simulation_id = as_factor(simulation_id)) %>%
  # get the round number (day) of infection times
  dplyr::mutate(day = ceiling(time)) %>%
  # count the daily number of cases in each simulation (simulation ID)
  dplyr::count(simulation_id, day, name = "cases") %>%
  # calculate the cumulative number of cases for each simulation (simulation ID)
  dplyr::group_by(simulation_id) %>%
  dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
  dplyr::ungroup()

Before the plot, let’s create a summary table with the total time duration and size of each chain. We can use the dplyr “combo” of group_by(), summarise() and ungroup():

R

# Summarise the chain duration and size
sim_chains_max <-
  simulated_chains_day %>%
  dplyr::group_by(simulation_id) %>%
  dplyr::summarise(
    # duration
    day_max = max(day),
    # size
    cases_total = max(cases_cumsum)
  ) %>%
  dplyr::ungroup()

sim_chains_max

SALIDA

# A tibble: 1,000 × 3
   simulation_id day_max cases_total
   <fct>           <dbl>       <int>
 1 1                   0           1
 2 2                   0           1
 3 3                   0           1
 4 4                   0           1
 5 5                   0           1
 6 6                   0           1
 7 7                   0           1
 8 8                   0           1
 9 9                   0           1
10 10                  0           1
# ℹ 990 more rows

Now, we are prepared for using the ggplot2 package:

R

# Visualize transmission chains by cumulative cases
ggplot() +
  # create grouped chain trajectories
  geom_line(
    data = simulated_chains_day,
    mapping = aes(
      x = day,
      y = cases_cumsum,
      group = simulation_id
    ),
    color = "black",
    alpha = 0.25,
    show.legend = FALSE
  ) +
  # create points to visualize the chain endpoint
  geom_point(
    data = sim_chains_max,
    mapping = aes(
      x = day_max,
      y = cases_total,
      group = simulation_id,
      color = simulation_id
    ),
    show.legend = FALSE
  ) +
  # define a 100-case threshold
  geom_hline(aes(yintercept = 100), lty = 2) +
  labs(
    x = "Day",
    y = "Cumulative cases"
  )

Although most introductions of 1 index case do not generate secondary cases (N = 940) or most outbreaks rapidly become extinct (median duration of 17.5 and median size of 9), only 2 epidemic trajectories among 1000 simulations (0.2%) can reach to more than 100 infected cases. This finding is particularly remarkable because the reproduction number $R$ is less than 1 (offspring distribution mean of 0.6), but, given an offspring distribution dispersion parameter of 0.02, it shows the potential for explosive outbreaks of MERS disease.

We can count how many chains reached the 100-case threshold using dplyr functions:

R

# number of chains that reached the 100-case threshold
sim_chains_max %>%
  dplyr::arrange(desc(day_max)) %>%
  dplyr::filter(cases_total > 100)

SALIDA

# A tibble: 2 × 3
  simulation_id day_max cases_total
  <fct>           <dbl>       <int>
1 666                88         110
2 23                 45         113

Observed cases vs simulated chains

Let’s overlap the cumulative number of observed cases using the linelist object from the mers_korea_2015 dataset of the outbreaks R package. To prepare the dataset so we can plot daily total cases over time, we use incidence2 to convert the linelist to an <incidence2> object, complete the missing dates of the time series with complete_dates()

R

library(outbreaks)

mers_cumcases <- mers_korea_2015$linelist %>%
  # incidence2 workflow
  incidence2::incidence(date_index = "dt_onset") %>%
  incidence2::complete_dates() %>%
  # wrangling using {dplyr}
  dplyr::mutate(count_cumsum = cumsum(count)) %>%
  tibble::rownames_to_column(var = "day") %>%
  dplyr::mutate(day = as.numeric(day))

Use plot() to make an incidence plot:

R

# plot the incidence2 object
plot(mers_cumcases)

When plotting the observed number of cumulative cases from the Middle East respiratory syndrome (MERS) outbreak in South Korea in 2015 alongside the previously simulated chains, we see that the observed cases followed a trajectory that is consistent with the simulated explosive outbreak dynamics (which makes sense, given the simulation uses parameters based on this specific outbreak).

When we increase the dispersion parameter from $k = 0.01$ to $k = \infty$ - and hence reduce individual-level variation in transmission - and assume a fixed reproduction number $R = 1.5$, the proportion of simulated outbreaks that reached the 100-case threshold increases. This is because the simulated outbreaks now have more of a consistent, clockwise dynamic, rather than the high level of variability seen previously.

Growth of simulated outbreaks with R = 1.5 and one initial case, conditional on non-extinction. Boxes show the median and interquartile range (IQR) of the first disease generation with 100 cases; whiskers show the most extreme values within 1.5 × IQR of the boxes, and crosses show outliers. Percentages show the proportion of 10,000 simulated outbreaks that reached the 100-case threshold (Lloyd-Smith et al., 2005).

Early spread projections

In the epidemic’s initial phase, you can use epichains to apply a branching process model to project the number of future cases. Even though the model accounts for randomness in transmission and variation in the number of secondary cases, there may be additional local features we have not considered. Analysis of early forecasts made for COVID in different countries using this model structure found that predictions were often overconfident (Pearson et al., 2020). This is likely because the real-time model did not include all the changes in the offspring distribution that were happening at the local level as a result of behaviour change and control measures. You can read more about the importance of local context in COVID-19 models in Eggo et al. (2020).

We invite you to read the vignette on Projecting infectious disease incidence: a COVID-19 example! for more on making predictions using epichains.

Challenges

Monkeypox large outbreak potential

Evaluate the potential for a new Monkey pox (Mpox) case to generate an explosive large outbreak.

Simulate 1000 transmission chains with 1 initial case each.
Use the appropriate package to access delay data from previous outbreaks.
How many simulated trajectories reach more than 100 infected cases?

Dar una pista

With {epiparameter}, you can access and use offspring and delay distributions from previous Ebola outbreaks.

R

library(epiparameter)
library(tidyverse)

epiparameter::epidist_db(epi_dist = "offspring") %>%
  epiparameter::parameter_tbl() %>%
  dplyr::count(disease, epi_distribution)

SALIDA

# Parameter table:
# A data frame:    6 × 3
  disease                       epi_distribution           n
  <chr>                         <chr>                  <int>
1 Ebola Virus Disease           offspring distribution     1
2 Hantavirus Pulmonary Syndrome offspring distribution     1
3 Mpox                          offspring distribution     1
4 Pneumonic Plague              offspring distribution     1
5 SARS                          offspring distribution     2
6 Smallpox                      offspring distribution     4

R

epiparameter::epidist_db(epi_dist = "serial interval") %>%
  epiparameter::parameter_tbl() %>%
  dplyr::count(disease, epi_distribution)

SALIDA

# Parameter table:
# A data frame:    6 × 3
  disease               epi_distribution     n
  <chr>                 <chr>            <int>
1 COVID-19              serial interval      4
2 Ebola Virus Disease   serial interval      4
3 Influenza             serial interval      1
4 MERS                  serial interval      2
5 Marburg Virus Disease serial interval      2
6 Mpox                  serial interval      5

Mostrar la solución

R

# load packages -----------------------------------------------------------

library(epiparameter)
library(tidyverse)

# delays ------------------------------------------------------------------

mpox_offspring_epidist <- epiparameter::epidist_db(
  disease = "mpox",
  epi_dist = "offspring",
  single_epidist = TRUE
)

mpox_offspring <- epiparameter::get_parameters(mpox_offspring_epidist)

mpox_serialint <- epiparameter::epidist_db(
  disease = "mpox",
  epi_dist = "serial interval",
  single_epidist = TRUE
)

# iterate -----------------------------------------------------------------

# Set seed for random number generator
set.seed(33)
# Number of simulation runs
number_simulations <- 1000
# Number of initial cases
initial_cases <- 1

simulated_chains_mpox <-
  # iterate one function across multiple numbers (simulation IDs)
  purrr::map(
    # vector of numbers (simulation IDs)
    .x = seq_len(number_simulations),
    # function to iterate to each simulation ID number
    .f = function(sim) {
      epichains::simulate_chains(
        # simulation controls
        n_chains = initial_cases,
        statistic = "size",
        # offspring
        offspring_dist = rnbinom,
        mu = mpox_offspring["mean"],
        size = mpox_offspring["dispersion"],
        # generation
        generation_time = function(x) generate(x = mpox_serialint, times = x)
      ) %>%
        # creates a column with the simulation ID number
        dplyr::mutate(simulation_id = sim)
    }
  ) %>%
  # combine list outputs (for each simulation ID) into a single data frame
  purrr::list_rbind()

# visualize ---------------------------------------------------------------

# daily aggregate of cases
simulated_chains_mpox_day <- simulated_chains_mpox %>%
  # use data.frame output from <epichains> object
  dplyr::as_tibble() %>%
  # transform simulation ID column to factor (categorical variable)
  dplyr::mutate(simulation_id = as_factor(simulation_id)) %>%
  # get the round number (day) of infection times
  dplyr::mutate(day = ceiling(time)) %>%
  # count the daily number of cases in each simulation (simulation ID)
  dplyr::count(simulation_id, day, name = "cases") %>%
  # calculate the cumulative number of cases for each simulation (simulation ID)
  dplyr::group_by(simulation_id) %>%
  dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
  dplyr::ungroup()

# Visualize transmission chains by cumulative cases
ggplot() +
  # create grouped chain trajectories
  geom_line(
    data = simulated_chains_mpox_day,
    mapping = aes(
      x = day,
      y = cases_cumsum,
      group = simulation_id
    ),
    color = "black",
    alpha = 0.25,
    show.legend = FALSE
  ) +
  # define a 100-case threshold
  geom_hline(aes(yintercept = 100), lty = 2) +
  labs(
    x = "Day",
    y = "Cumulative cases"
  )

Assuming a Monkey pox outbreak with $R$ = 0.32 and $k$ = 0.58, there is no trajectory among 1000 simulations that reach more than 100 infected cases. Compared to MERS ($R$ = 0.6 and $k$ = 0.02).

Epidemic Risk assessment accounting for superspreading

With {superspreading}, you can get numerical solutions to processes that epichains solve using branching processes. We invite you to read the {superspreading} vignette on Epidemic risk and respond to:

What is the probability that a newly introduced pathogen will cause a large outbreak?
What is the probability that an infection will, by chance, fail to establish following initial introduction(s)?
What is the probability the outbreak will be contained?

Check how these estimates vary non-linearly with respect to the mean reproduction number $R$ and dispersion $k$ of a given disease.

R

library(superspreading)

R

library(superspreading)

From a distribution of secondary cases

Christian Althaus, 2015 reused data published by Faye et al., 2015 (Figure 2) on the transmission tree on Ebola virus disease in Conakry, Guinea, 2014.

Using the data under the hint tab, estimate the offspring distribution from the distribution of secondary cases. Then estimate the large outbreak potential from this data.

Dar una pista

Code with the transmission tree data written by Christian Althaus, 2015:

R

# Number of individuals in the trees
n <- 152
# Number of secondary cases for all individuals
c1 <- c(1, 2, 2, 5, 14, 1, 4, 4, 1, 3, 3, 8, 2, 1, 1,
        4, 9, 9, 1, 1, 17, 2, 1, 1, 1, 4, 3, 3, 4, 2,
        5, 1, 2, 2, 1, 9, 1, 3, 1, 2, 1, 1, 2)
c0 <- c(c1, rep(0, n - length(c1)))

c0 %>%
  enframe() %>%
  ggplot(aes(value)) +
  geom_histogram()

Mostrar la solución

R

# load packages ---------------------------
library(epichains)
library(epiparameter)
library(fitdistrplus)
library(tidyverse)

R

# fit a negative binomial distribution ------------------------------------

# Fitting a negative binomial distribution to the number of secondary cases
fit.cases <- fitdistrplus::fitdist(c0, "nbinom")
fit.cases

SALIDA

Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
      estimate Std. Error
size 0.1814260 0.03990278
mu   0.9537995 0.19812301

R

# serial interval parameters ----------------------------------------------

ebola_serialinter <- epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "serial interval",
  single_epidist = TRUE
)

# simulate outbreak trajectories ------------------------------------------

# Set seed for random number generator
set.seed(645)
# Number of simulation runs
number_simulations <- 1e2
# Number of initial cases
initial_cases <- 1

sim_multiple_chains <-
  purrr::map(
    .x = seq_len(number_simulations),
    .f = function(sim) {
      epichains::simulate_chains(
        n_chains = initial_cases,
        # stopping
        statistic = "size",
        # offspring
        offspring_dist = rnbinom,
        mu = fit.cases$estimate["mu"],
        size = fit.cases$estimate["size"],
        # generation
        generation_time = function(x) generate(x = ebola_serialinter, times = x)
      ) %>%
        dplyr::mutate(simulation_n = sim)
    }
  ) %>%
  # combine list outputs (for each simulation ID) into a single data frame
  purrr::list_rbind()

# visualize ----------------------------------------

sim_chains_aggregate <-
  sim_multiple_chains %>%
  dplyr::as_tibble() %>%
  dplyr::mutate(simulation_n = as_factor(simulation_n)) %>%
  dplyr::mutate(day = ceiling(time)) %>%
  dplyr::count(simulation_n, day, name = "cases") %>%
  dplyr::group_by(simulation_n) %>%
  dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
  dplyr::ungroup()

ggplot() +
  geom_line(
    data = sim_chains_aggregate,
    mapping = aes(
      x = day,
      y = cases_cumsum,
      group = simulation_n
    ),
    show.legend = FALSE
  ) +
  # define a 100-case threshold
  geom_hline(aes(yintercept = 100), lty = 2)

Remarkably, even with R0 less than 1 (R = 0.95) we can have potentially explosive outbreaks. The observed variation in individual infectiousness in Ebola means that although the probability of extinction is high, new index cases also have the potential for explosive regrowth of the epidemic.

Puntos Clave

Use epichains to simulate the large outbreak potential of diseases with overdispersed offspring distributions.

Probabilidad (\(p\))	Cambio esperado
\(p < 0,05\)	Aumentando
\(0,05 \leq p< 0,4\)	Probable aumento
\(0,4 \leq p< 0,6\)	Estable
\(0,6 \leq p < 0,95\)	Probable disminución
\(0,95 \leq p \leq 1\)	En disminución