Simuler des chaînes de transmission
Dernière mise à jour le 2025-11-11 | Modifier cette page
Vue d'ensemble
Questions
- Comment simuler des chaînes de transmission basées sur les caractéristiques de l’infection ?
Objectifs
- Estimez le potentiel d’épidémies importantes suite à l’introduction d’un nouveau cas à l’aide d’un processus de ramification avec epichains.
Conditions préalables
Les apprenants devraient se familiariser avec les concepts suivants avant de suivre ce tutoriel :
Statistiques Les distributions de probabilités courantes, y compris les distributions de Poisson et binomiale négative.
Théorie des épidémies: Le nombre de reproduction, \(R\).
Introduction
La variation individuelle de la transmission peut affecter à la fois le potentiel d’établissement d’une épidémie dans une population et la facilité de sa contrôle (Cori et al., 2017).
Une plus grande variation réduit la probabilité globale qu’un nouveau cas unique soit à l’origine d’une épidémie locale de grande ampleur, car la plupart des cas infectent peu d’autres personnes et les individus qui génèrent un grand nombre de cas secondaires sont relativement rares.
Toutefois, si un “événement de super propagation” se produit et que l’épidémie s’installe, cette variation peut rendre l’épidémie plus difficile à contrôler en utilisant des interventions de masse (c’est-à-dire des interventions générales qui supposent implicitement que tout le monde contribue de manière égale à la transmission), car certains cas contribuent de manière disproportionnée : un seul cas non contrôlé peut générer un grand nombre de cas secondaires.
Inversement, la variation de la transmission peut offrir des possibilités des interventions ciblées si les individus qui contribuent le plus à la transmission (en raison de facteurs biologiques ou comportementaux), ou les environnements dans lesquels se produisent les “événements de super propagation”, partagent des caractéristiques sociodémographiques, environnementales ou géographiques qui peuvent être définies.
Comment peut-on quantifier le potentiel d’une nouvelle infection à provoquer une épidémie de grande ampleur sur la base de son nombre de reproduction \(R\) et de la dispersion \(k\) de la distribution de sa descendance ?
Dans cet épisode, nous utiliserons le package epichains pour simuler des chaînes de transmission et estimer le potentiel d’épidémies importantes suite à l’introduction d’un nouveau cas. Nous allons l’utiliser avec les fonctions de epiparameter, dplyr et purrrdonc il faut également charger le tidyverse package :
R
library(epichains)
library(epiparameter)
library(tidyverse)
Le double point-virgule
Le double point-virgule :: en R vous permet d’appeler
une fonction spécifique d’un package sans charger le package entier dans
l’environnement courant.
Par exemple, vous pouvez appeler une fonction spécifique d’un package
sans charger le package entier dans l’environnement actuel,
dplyr::filter(data, condition) utilise
filter() à partir de l’outil dplyr
package.
Cela nous permet de nous souvenir des fonctions du package et d’éviter les conflits d’espace de noms.
Simulation des épidémies incontrôlées
Les épidémies de maladies infectieuses se propagent dans les populations lorsqu’une chaîne d’individus infectés transmet l’infection à d’autres. Processus de ramification peuvent être utilisés pour modéliser cette transmission. Un processus de ramification est un processus stochastique (c’est-à-dire un processus aléatoire qui peut être décrit par une distribution de probabilité connue), dans lequel chaque individu infectieux donne naissance à un nombre aléatoire d’individus dans la génération suivante d’infection, en commençant par le cas index dans la génération 1. La distribution du nombre de cas secondaires générés par chaque individu est appelée distribution de la descendance (Azam & Funk, 2024).
epichains fournit des méthodes d’analyse et de simulation de la taille et longueur des processus de ramification pour une certaine distribution de la descendance. epichains met en œuvre un modèle simple et rapide pour simuler les chaînes de transmission afin d’évaluer le risque épidémique, de projeter les cas dans l’avenir et d’évaluer les interventions qui modifient \(R\).
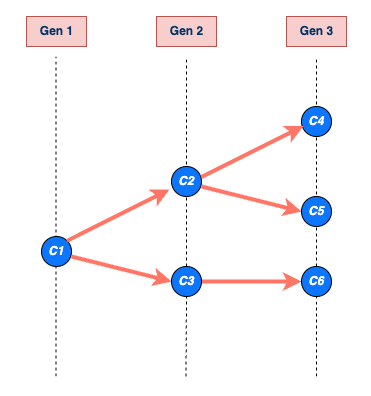
taille et longueur de la chaîne
La taille de la chaîne de transmission est définie comme le nombre total d’individus infectés sur toutes les générations d’infection, et
la longueur de la chaîne de transmission est le nombre de générations entre le premier et le dernier cas de l’épidémie avant que la chaîne se termine.
Le calcul de la taille inclut le premier cas, et le calcul de la longueur contient la première génération lorsque le premier cas commence la chaîne (voir figure ci-dessous).
Pour utiliser epichains nous devons connaître (ou supposer) deux valeurs épidémiologiques clés : la distribution de la descendance et le temps de génération.
Obtenez la distribution de la descendance
Nous supposons ici que la distribution de la descendance du MERS suit
une distribution binomiale négative, avec une moyenne (nombre de
reproduction \(R\)) et une dispersion
\(k\) estimées à partir de la liste et
des données de contact de mers_korea_2015 dans le package
outbreaks R de l’épisode précédent.
R
mers_offspring <- c(mean = 0.60, dispersion = 0.02)
Distribution de la descendance pour épichains
Nous entrons une distribution de descendance dans
epichains en faisant référence à la fonction R qui génère
des valeurs aléatoires à partir de la distribution souhaitée. Pour une
distribution binomiale négative, nous utilisons rnbinom
avec les arguments mu et size:
En interne, epichains tire une valeur aléatoire, compte tenu des paramètres, afin de simuler le nombre de nouvelles infections à partir d’un individu infecté (transmission ultérieure).
R
# generate one random number given the distribution family and its parameters
# (run this line many times to get different values)
rnbinom(n = 1, mu = mers_offspring["mean"], size = mers_offspring["dispersion"])
Le manuel de référence en ?rnbinom nous indique les
arguments spécifiques requis.
epichains peut accepter n’importe quelle fonction R qui génère des nombres aléatoires, de sorte que les arguments spécifiés changeront en fonction de la fonction R utilisée. Pour plus de détails sur les options possibles, consultez le manuel de référence de la fonction.
Par exemple, disons que nous voulons utiliser une distribution de
Poisson pour la distribution de la descendance. Tout d’abord, lisez
l’argument requis ?rpois dans le manuel de référence.
Ensuite, spécifiez l’argument lambda également connu sous
le nom de taux ou de moyenne dans la littérature. En
epichains cela peut ressembler à ceci :
Dans cet exemple, nous pouvons spécifier
lambda = mers_offspring["mean"] car le nombre moyen de cas
secondaires générés (c’est-à-dire \(R\)) devrait être le même quelle que soit
la distribution que nous supposons. Ce qui change, c’est la variance de
la distribution, et donc le niveau de variation de la transmission au
niveau individuel. Lorsque le paramètre de dispersion \(k\) s’approche l’infini (\(k \rightarrow \infty\)) dans une
distribution binomiale négative, la variance est égale à la moyenne.
Cela fait de la distribution de Poisson classique un cas particulier de
la distribution binomiale négative.
Obtenir le temps de génération
La distribution de l’intervalle de série est souvent utilisée pour approximer la distribution du temps de génération. Cette approximation est couramment utilisée parce qu’il est plus facile d’observer et de mesurer l’apparition des symptômes dans chaque cas que le moment précis de l’infection.
Cependant, l’utilisation de l’option intervalle de série comme approximation du temps de génération est principalement valable pour les maladies dans lesquelles l’infectiosité commence après l’apparition des symptômes (Chung Lau et al., 2021). Dans les cas où l’infectiosité commence avant l’apparition des symptômes, les intervalles sériels peuvent avoir des valeurs négatives, ce qui est le cas pour les maladies à transmission pré-symptomatique (Nishiura et al., 2020).
Utilisons le package epiparameter pour accéder à l’intervalle de série disponible pour la maladie MERS :
R
serial_interval <- epiparameter::epiparameter_db(
disease = "mers",
epi_name = "serial",
single_epiparameter = TRUE
)
plot(serial_interval, day_range = 0:25)
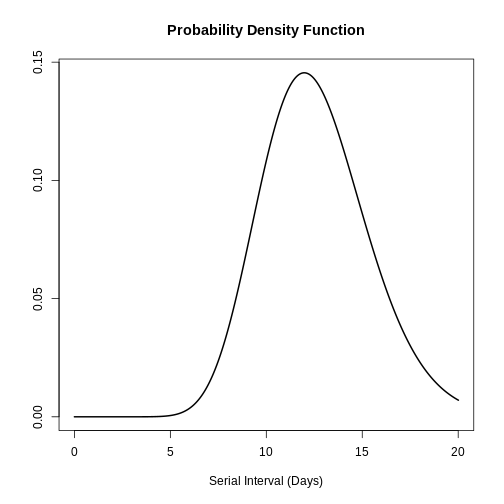
L’intervalle de série pour le MERS a une moyenne de 12.6 jours et un écart-type de 2.8 jours.
temps de génération pour epichains
Dans chaque étape de la simulation, epichains tire des
valeurs du temps de génération pour chaque nouvelle infection génèré de
la distribution de la descendance. Pour les objets de la classe
epiparameter::generate() pour cette entrée.:
R
# In step one, the number of new infections is 2, then:
# generate 2 random values given the serial interval distribution
generate(x = serial_interval, times = 2)
SORTIE
[1] 14.60507 15.06471R
# In step two, the number of new infections is 6, then:
# generate 6 random values given the serial interval distribution
generate(x = serial_interval, times = 6)
SORTIE
[1] 12.522027 16.109812 14.195049 6.875113 15.432142 12.349850Étant donné que le valeur de l’entrée pour le champ
times changera à chaque étape, nous devons intégrer
generate() dedans la fonction. epichains
tirera autant de valeurs aléatoires du temps de génération que le nombre
de nouvelles infections à cette étape. Le résultat sera le suivant :
R
function(x) generate(x = serial_interval, times = x)
Cette interface est similaire à celle que cfr utilise pour établir un lien avec epiparameter. Lisez le vignette travailler avec des distributions de retard pour plus de détails.
Simuler une chaîne unique
Nous sommes maintenant prêts à utiliser la fonction
simulate_chains() de epichains pour créer
un chaîne de transmission :
R
epichains::simulate_chains(
n_chains = 1,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
)
simulate_chains() nécessite au minimum trois séries
d’arguments :
-
les contrôles de simulation (
n_chainsetstatistic), -
la distribution des descendants
(
offspring_distet les paramètres de distributions requis), et - le temps de génération (
generation_time).
Dans les lignes ci-dessus, nous avons décrit comment spécifier la distribution des descendants et le temps de génération. Les contrôles la simulation comprend au moins deux arguments :
-
n_chains, qui définit le nombre de chaînes de transmission à simuler pour et -
statisticqui définit une statistique de chaîne à suivre (soit"size"ou"length") comme critère d’arrêt pour chaque chaîne simulée.
Critères d’arrêt
Il s’agit d’une fonction personnalisable de epichains.
Par défaut, les simulations de processus de ramification se terminent
lorsqu’elles se sont éteintes. Pour les chaînes de transmission de
longue durée, en simulate_chains() vous pouvez ajouter
l’argument stat_threshold
Par exemple, si on définit un critère d’arrêt pour
statistic = "size" de stat_threshold = 500 il
n’y aura plus de descendance après une chaîne de taille 500.
La sortie de simulate_chains() crée un objet de classe
<epichains> que nous pouvons ensuite analyser dans
R.
Simuler plusieurs chaînes
Nous pouvons utiliser simulate_chains() pour créer
plusieurs chaînes et augmenter la probabilité de simuler des projections
de épidémies incontrôlées en cas de distribution de la descendance trop
dispersée.
Nous devons spécifier un élément supplémentaire :
-
set.seed(<integer>), qui est une fonction de générateur de nombres aléatoires avec une valeur de semence spécifiée, le nombre<integer>afin de garantir des résultats cohérents entre les différentes exécutions de code.
Avec cette configuration, chaque chaîne représentera
un cas initial. Les cas de chaque chaîne sont
indépendants, isolés et sans interactions. Cela signifie que chaque
chaîne disposera de son propre pool de susceptibles, que tu peux
configurer à l’aide de l’option pop ou
percent_immune.
Maintenant, simulons 100 chaînes de transmission :
R
# Run all this chunk together to let set.seed() work!
# Set seed for random number generator
set.seed(33)
multiple_epichains <- epichains::simulate_chains(
n_chains = 100,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
)
Tu peux inspecter le taille total de chaque chaîne
simulée, ce qui équivaut au nombre cumulé de cas par chaîne, à l’aide de
la fonction summary() à l’objet de classe
<epichains>:
R
summary(multiple_epichains)
SORTIE
`epichains_summary` object
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[19] 7 1 1 1 1 1 1 1 1 1 1 14 1 2 1 1 2 1
[37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[55] 1 1 1 1 512 1 1 1 1 1 104 1 1 1 1 1 1 1
[73] 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1
[91] 1 1 1 1 1 1 1 1 1 1
Simulated sizes:
Max: 512
Min: 1Nous pouvons compter visuellement le nombre de chaînes qui atteignent plus de 100 cas d’infection, ainsi que les nombres maximum et minimum.
Défi
Utilise la dernière exécution de
epichains::simulate_chains() pour simuler plusieurs
chaînes. Modifie le statistic de "size" à
"length". Exécute le fonction summary().
- Pour quelle chaîne cette sortie compte-t-elle ?
Si tu as besoin d’aide, reviens à la boîte “Taille et longueur de la chaîne” depuis le début.
Lire la sortie d’épichains
Pour explorer le format de sortie de l’objet multiple_epichains du
classe <epichains>, examinons la simulation
chain nombre 30.
Utilisons dplyr::filter() pour cela :
R
chain_to_observe <- 30
R
#### get epichain summary ----------------------------------------------------
multiple_epichains %>%
dplyr::filter(chain == chain_to_observe)
SORTIE
`<epichains>` object
< epichains head (from first known infector) >
chain infector infectee generation time
2 30 1 2 2 14.100967
3 30 1 3 2 10.640301
4 30 1 4 2 15.608764
5 30 1 5 2 13.515424
6 30 1 6 2 9.967474
7 30 1 7 2 9.376222
Number of chains: 100
Number of infectors (known): 3
Number of generations: 3
Use `as.data.frame(<object_name>)` to view the full output in the console.Cette sortie contient deux parties :
- Un
head()des paires infecteur-infecté en commençant par le premier infecteur connu. - Un pied de page récapitulatif, le morceau de texte qui apparaît en bas :
SORTIE
Number of infectors (known): 3
Number of generations: 3Le chain nombre 30 simulé comporte trois infecteurs
connus et trois générations. Ces nombres sont plus visibles lorsque l’on
imprime les objets <epichains> sous la forme d’un
cadre de données (ou <tibble>).
R
#### infector-infectee data frame --------------------------------------------
multiple_epichains %>%
dplyr::filter(chain == chain_to_observe) %>%
dplyr::as_tibble()
SORTIE
# A tibble: 14 × 5
chain infector infectee generation time
<int> <dbl> <dbl> <int> <dbl>
1 30 NA 1 1 0
2 30 1 2 2 14.1
3 30 1 3 2 10.6
4 30 1 4 2 15.6
5 30 1 5 2 13.5
6 30 1 6 2 9.97
7 30 1 7 2 9.38
8 30 1 8 2 11.5
9 30 4 9 3 31.0
10 30 4 10 3 25.3
11 30 4 11 3 28.5
12 30 4 12 3 29.6
13 30 4 13 3 25.9
14 30 4 14 3 24.6 Chaîne 30 nous raconte une histoire:
“Dans la première génération de transmission à time = 0,
un sujet (ID = NA) a infecté le sujet avec
ID = 1. Sujet ID = 1 est le premier infecteur
connu.
“Ensuite, dans la deuxième génération de transmission, le sujet
ID = 1 a infecté sept sujets, de ID = 2 à
ID = 8. Ces infections se sont produites chez
time entre le 9e et le 15e jour, après la première
infection connue.
“Plus tard, lors de la troisième génération de transmission, le sujet
ID = 4 a infecté six nouveaux sujets, de
ID = 9 à ID = 14. Ces infections se sont
produites chez time entre le 24e et le 31e jour, après la
première infection connue.”
Le cadre de données de sortie recueille les infectés comme unité d’observation :
- Chaque personne infectée a un
infectee“ID”. - Chaque infecté qui se comporte comme un infecteur
est enregistré dans la base de données
infectorcolonne à l’aide deinfectee“id”. - Chaque personne infectée l’a été à un moment précis.
generationettime(continu). - Le numéro de simulation est enregistré sous le
chaincolonne.
Remarque : Le
Number of infectors (known) comprend le sujet
ID = NA sous le infector colonne. Il s’agit de
l’infecteur spécifié comme cas d’index (dans la colonne
n_chains ), qui a commencé la chaîne de transmission à
l’infecté de ID = 1 à generation = 1 et
time = 0.
Répéter les simulations
Comme précédemment, nous pouvons configurer la simulation de
plusieurs chaînes en augmentant simplement le nombre de chaînes (par ex.
n_chains = 1 à n_chains = 100). Cependant, si
nous devons supposer que chaque cas initial commence (à être infectieux)
à un moment différent, cela ne peut être configuré que dans une seule
fonction de simulation. Il faut donc itérer plusieurs
fois sur une configuration spécifique de simulation de chaîne pour
augmenter la probabilité de simuler des projections d’épidémies
incontrôlées. Le tableau suivant compare les alternatives :
| Simulations | Cas initiaux | Heure de début (t0) |
Utilise |
|---|---|---|---|
| Un | 1 | Idem |
epichains::simulate_chains() avec
n_chains = 1
|
| Multiple (100, par exemple) | 1 | Idem |
epichains::simulate_chains() avec
n_chains = 100
|
| Multiple (100, par exemple) | Plus d’un | Différents | Itère 100 fois en utilisant purrr::map() sur
epichains::simulate()
|
La différence essentielle de la troisième configuration est
l’argument t0 de epichains::simulate_chains().
L’argument t0 définit l’heure de début de chaque cas
initial par chaîne.
À noter
Un exemple d’utilisation de l’itération est disponible dans la vignette epichains sur Prévision de l’incidence des maladies infectieuses : un exemple de COVID-19. Il s’agit de simuler l’importation de 13 cas à différents moments.
R
epichains::covid19_sa[1:5, ] %>%
dplyr::mutate(start_time = date - min(date))
SORTIE
# A tibble: 5 × 3
date cases start_time
<date> <int> <drtn>
1 2020-03-05 1 0 days
2 2020-03-07 1 2 days
3 2020-03-08 1 3 days
4 2020-03-09 4 4 days
5 2020-03-11 6 6 days Au lieu d’avoir 100 chaînes commençant au même jour 0
(t0 = 0, par défaut), chaque simulation créera des chaînes
qui commenceront à un moment différent dans le temps. Elle considérera
le jour 2020-03-05 comme Jour 0. La première
chaîne commence au jour 0, une au jour 2, une au jour 3, quatre au jour
4 et six au jour 6. L’argument t0 aura cette structure
:
R
t0 <- c(0, 2, 3, rep(4, 4), rep(6, 6))
t0
SORTIE
[1] 0 2 3 4 4 4 4 6 6 6 6 6 6Pour augmenter la probabilité de simuler des projections d’épidémies incontrôlées, ce même scénario doit être itéré 100 fois. Cela nous aidera à fournir une projection avec de l’incertitude.
Dans cette section, nous allons te montrer comment construire le
itération sur epichains étape par étape.
Nous répliquerons la même simulation que précédemment : 100 chaînes de
transmission avec 1 cas initial chacune à partir du jour 0
(t0 = 0). Mais au lieu d’utiliser
n_chains = 100 nous allons itérer 100 fois sur la
simulation d’une chaîne de transmission avec un cas initial à partir du
jour 0 (n_chains = 1).
Nous devons spécifier deux éléments supplémentaires :
-
number_simulations, qui définit le nombre de simulations à effectuer. -
initial_casesdéfinit le nombre de cas initiaux à introduire dans l’argumentn_chainsexpliqué dans les lignes ci-dessus.
R
# Number of simulation runs
number_simulations <- 100
# Number of initial cases
initial_cases <- 1
number_simulations et initial_cases sont
commodément stockés dans des objets pour faciliter leur réutilisation en
aval dans le flux de travail.
Itération à l’aide de purrr
Itération vise à effectuer la même action sur différents objets de manière répétée.
Apprenez à utiliser les fonctions de base de purrr
comme map() à partir du tutoriel YouTube sur How to purrr par
Equitable Equations.
Ou, si vous avez déjà utilisé la famille de
fonctions*apply, visitez la vignette du package purrr base R
qui présente les principales différences, des traductions directes et
des exemples.
Pour obtenir plusieurs chaînes, nous devons appliquer la méthode
simulate_chains() à chaque chaîne définie par une séquence
de nombres allant de 1 à 100.
purrr et epichains
Tout d’abord, décrivons comment nous utilisons
purrr::map() avec
epichains::simulate_chains(). La fonction
map() nécessite deux arguments :
-
.x, un vecteur de nombres, et -
.fune fonction permettant d’itérer sur chaque valeur du vecteur.
R
# steps:
# - purrr::map() will run 100 times function(sim).
# - seq_len() creates a vector with sequence of numbers (simulation IDs from 1 to 100) and
# - function(sim) iterates {epichains} to each simulation ID number, then
# - dplyr::mutate() adds a column to the <epichains> output with the simulation ID number.
# - purrr::list_rbind() combines all the list class outputs (for each simulation ID) into a single data frame.
purrr::map(
.x = seq_len(number_simulations),
.f = function(sim) {
epichains::simulate_chains(...) %>% # <-- {epichains}
dplyr::mutate(simulation_id = sim)
}
) %>%
purrr::list_rbind()
# pseudo code: do not run.
L’élément sim est placé pour enregistrer le numéro
d’itération (ID de simulation) dans une nouvelle
colonne dans la sortie <epichains>. La fonction
purrr::list_rbind() a pour but de combiner toutes les
sorties de liste de map().
Pourquoi un point (.) comme préfixe ?
Dans le principes de
conception ordonnée nous avons un chapitre sur le préfixe point
!
Nous sommes maintenant prêts à utiliser purrr::map()
pour simuler de manière répétée de simulate_chains() et de
stocker dans un vecteur de 1 à 100:
R
set.seed(33)
simulated_chains_map <-
purrr::map(
.x = seq_len(number_simulations),
.f = function(sim) {
epichains::simulate_chains(
n_chains = initial_cases,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
) %>%
dplyr::mutate(simulation_id = sim)
}
) %>%
purrr::list_rbind()
Une limitation de la sortie itérative est que nous ne pouvons pas
utiliser la fonction summary(
R
simulated_chains_map %>%
dplyr::count(simulation_id) %>%
dplyr::pull(n)
SORTIE
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 9 1 1 1
[19] 1 1 1 1 113 1 1 1 1 1 1 1 1 1 19 1 1 1
[37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[55] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 22 1 1 1
[73] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[91] 1 1 1 1 1 1 1 1 1 1Visualiser plusieurs chaînes
Pour augmenter la probabilité de simuler des projections d’épidémies incontrôlées compte tenu d’une distribution surdispersée de la progéniture, simulons 1000 chaînes de transmission avec 1 cas initial pour chacune d’entre elles, à partir du jour 0.
Nous allons créer une simulation multiple sans itération pour cette section :
R
set.seed(33)
multiple_epichains <- epichains::simulate_chains(
n_chains = 1000,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
)
Pour visualiser les chaînes simulées, nous avons besoin d’un traitement préalable :
- Utilisons dplyr pour obtenir des nombres de temps ronds qui ressemblent à des journées de surveillance.
- Compte les cas quotidiens dans chaque simulation (par
chain). - Calcule le nombre cumulé de cas dans une simulation.
R
# daily aggregate of cases
aggregate_chains <- multiple_epichains %>%
# use data.frame output from <epichains> object
dplyr::as_tibble() %>%
# get the round number (day) of infection times
dplyr::mutate(day = ceiling(time)) %>%
# count the daily number of cases in each chain
dplyr::count(chain, day, name = "cases") %>%
# calculate the cumulative number of cases for each chain
dplyr::group_by(chain) %>%
dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
dplyr::ungroup()
Avant le graphique, créons un tableau de sommaire avec la durée
totale et la taille de chaque chaîne. Nous pouvons utiliser la “combo”
dplyr de group_by(),
summarise() et ungroup():
R
# Summarise the chain duration and size
summary_chains <-
aggregate_chains %>%
dplyr::group_by(chain) %>%
dplyr::summarise(
# duration
day_max = max(day),
# size
cases_total = max(cases_cumsum)
) %>%
dplyr::ungroup()
summary_chains
SORTIE
# A tibble: 1,000 × 3
chain day_max cases_total
<int> <dbl> <int>
1 1 0 1
2 2 0 1
3 3 0 1
4 4 0 1
5 5 0 1
6 6 0 1
7 7 0 1
8 8 0 1
9 9 0 1
10 10 0 1
# ℹ 990 more rowsMaintenant, nous sommes prêts à utiliser le package ggplot2 :
R
# Visualize transmission chains by cumulative cases
ggplot() +
# create grouped chain trajectories
geom_line(
data = aggregate_chains,
mapping = aes(
x = day,
y = cases_cumsum,
group = chain
),
color = "black",
alpha = 0.25,
show.legend = FALSE
) +
# define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2) +
labs(
x = "Day",
y = "Cumulative cases"
)
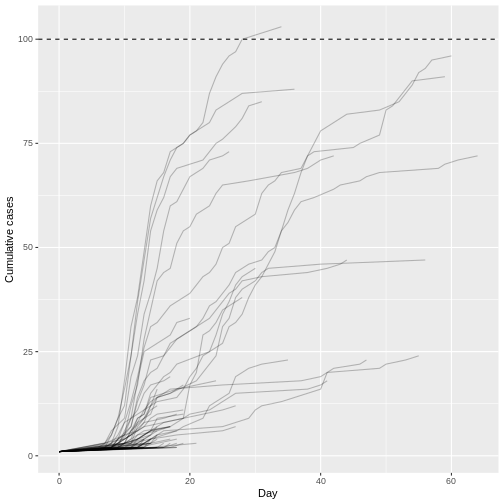
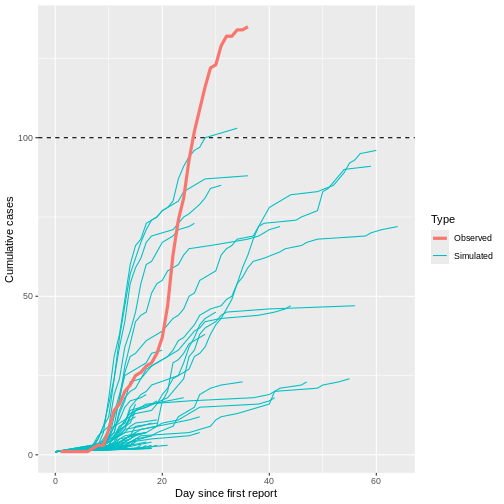
Bien que la plupart des présentations de 1 ne génèrent pas de cas secondaires (N = 934) ou que la plupart des épidémies s’éteignent rapidement (durée médiane de 17 et taille médiane de 5.5), seulement 1 trajectoires épidémiques parmi les 100 simulations (1%) peuvent atteindre plus de 100 cas infectés. Ce résultat est remarquable carle nombre de reproduction \(R\) est inférieur à 1 (moyenne de la distribution des descendants de 0.6), mais, compte tenu d’un paramètre de dispersion de la distribution de la progéniture de 0.02 il montre le potentiel de épidémies explosives de la maladie MERS.
Nous pouvons compter combien de chaînes ont atteint le seuil de 100 cas en utilisant les fonctionsdplyr. Cette sortie devrait nous donner des résultats équivalents à summary(multiple_epichains)`:
R
# number of chains that reached the 100-case threshold
summary_chains %>%
dplyr::arrange(desc(cases_total)) %>%
dplyr::filter(cases_total > 100)
SORTIE
# A tibble: 1 × 3
chain day_max cases_total
<int> <dbl> <int>
1 65 34 103Recouvrons le nombre cumulé de cas observés à l’aide de l’objet
linelist de l’ensemble de données mers_korea_2015 du
package R outbreaks. Pour préparer l’ensemble de données
afin de pouvoir tracer le nombre total de cas quotidiens au fil du
temps, nous utilisons incidence2 pour convertir la liste
de lignes en un objet <incidence2>, et compléte les
dates manquantes de la série temporelle à l’aide de
complete_dates()
R
library(outbreaks)
mers_cumcases <- mers_korea_2015$linelist %>%
# incidence2 workflow
incidence2::incidence(date_index = "dt_onset") %>%
incidence2::complete_dates() %>%
# wrangling using {dplyr}
dplyr::mutate(count_cumsum = cumsum(count)) %>%
tibble::rownames_to_column(var = "day") %>%
dplyr::mutate(day = as.numeric(day))
Utilise plot() pour faire un graphique d’incidence :
R
# plot the incidence2 object
plot(mers_cumcases)
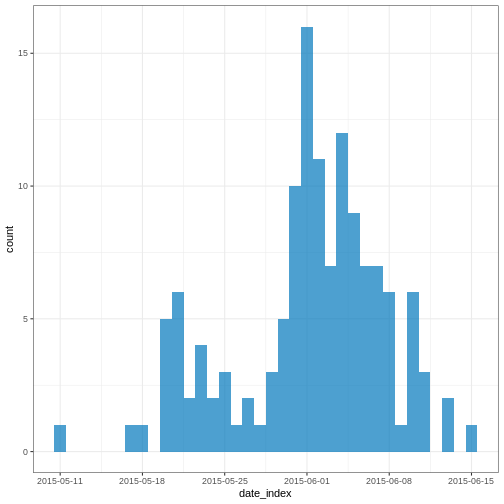
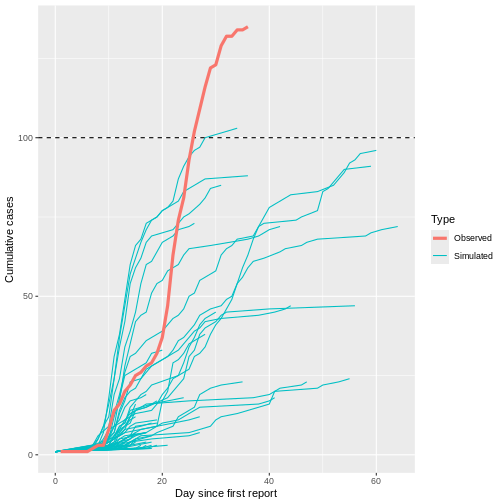
En traçant le nombre observé de cas cumulés de l’épidémie de syndrome respiratoire du Moyen-Orient (MERS) en Corée du Sud en 2015 à côté des chaînes simulées précédemment, on constate que les cas observés ont suivi une trajectoire conforme à la dynamique de l’épidémie explosive simulée (ce qui est logique, étant donné que la simulation utilise des paramètres basés sur cette épidémie spécifique).
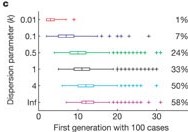
Lorsque nous augmentons le paramètre de dispersion de \(k = 0.01\) à \(k = \infty\) - et réduisons ainsi la variation de la transmission au niveau individuel - et supposons un nombre de reproduction fixe \(R = 1.5\) La proportion de épidémies simulés ayant atteint le seuil de 100 cas augmente. Cela s’explique par le fait que les épidémies simulées ont maintenant une dynamique plus cohérente, dans le sens des aiguilles d’une montre, plutôt que le niveau élevé de variabilité observé précédemment.
Les premières projections de propagation
Dans la phase initiale de l’épidémie, tu peux utiliser epichains pour appliquer un modèle de processus de ramification afin de prévoir le nombre de cas futurs. Même si le modèle tient compte du caractère aléatoire de la transmission et de la variation du nombre de cas secondaires, il peut y avoir des caractéristiques locales supplémentaires que nous n’avons pas prises en compte. L’analyse des premières prévisions faites pour le COVID dans différents pays à l’aide de cette structure de modèle a révélé que les prévisions étaient souvent trop confiantes (Pearson et al., 2020). Cela est probablement dû au fait que le modèle en temps réel n’incluait pas tous les changements dans la distribution de descendance qui se produisaient au niveau local à la suite des changements de comportement et des mesures de contrôle. Tu peux en savoir plus sur l’importance du contexte local dans les modèles COVID-19 dans . Eggo et al. (2020).
Nous t’invitons à lire la vignette sur Prévision de l’incidence des maladies infectieuses : un exemple de COVID-19! pour en savoir plus sur l’établissement de prévisions à l’aide de epichains.
Défis
Potentiel d’une épidémie importante de variole du singe
Évalue le potentiel d’un nouveau cas de variole du singe (Mpox) à générer une grande épidémie explosive.
- Simule 1000 chaînes de transmission avec 1 cas initial chacune à partir du jour 0.
- Utilise le paquet approprié pour accéder aux données de retard des épidémies précédentes.
- Combien de trajectoires simulées atteignent plus de 100 cas infectés ?
Avec epiparameter, tu peux accéder et utiliser les distributions des descendants et des retards des épidémies d’Ebola précédentes.
R
library(epiparameter)
library(tidyverse)
epiparameter::epiparameter_db(epi_name = "offspring") %>%
epiparameter::parameter_tbl() %>%
dplyr::count(disease, epi_name)
SORTIE
# Parameter table:
# A data frame: 6 × 3
disease epi_name n
<chr> <chr> <int>
1 Ebola Virus Disease offspring distribution 1
2 Hantavirus Pulmonary Syndrome offspring distribution 1
3 Mpox offspring distribution 1
4 Pneumonic Plague offspring distribution 1
5 SARS offspring distribution 2
6 Smallpox offspring distribution 4R
epiparameter::epiparameter_db(epi_name = "serial interval") %>%
epiparameter::parameter_tbl() %>%
dplyr::count(disease, epi_name)
SORTIE
# Parameter table:
# A data frame: 6 × 3
disease epi_name n
<chr> <chr> <int>
1 COVID-19 serial interval 4
2 Ebola Virus Disease serial interval 4
3 Influenza serial interval 1
4 MERS serial interval 2
5 Marburg Virus Disease serial interval 2
6 Mpox serial interval 5De plus, étant donné que tu n’as besoin que d’une seule chaîne par itération, commençant le même jour, il n’est peut-être pas nécessaire d’utiliser l’itération pour celle-ci.
Avec superspreading tu peux obtenir des solutions numériques à des processus qui epichains résoudre à l’aide de processus de branchement. Nous t’invitons à lire le vignette superspreading sur Le risque épidémique et répondre à :
- Quelle est la probabilité qu’un agent pathogène nouvellement introduit provoque une grande épidémie ?
- Quelle est la probabilité qu’une infection ne s’établisse pas, par hasard, après une ou plusieurs introductions initiales ?
- Quelle est la probabilité que l’épidémie soit contenue ?
Vérifie sices estimations varient de façon non linéaire en fonction du nombre moyen de reproduction. \(R\) et de la dispersion \(k\) d’une maladie donnée.
A partir d’une répartition des cas secondaires
Christian Althaus, 2015 a réutiliser des données publiées par Faye et al, 2015 (Figure 2) sur l’arbre de transmission de la maladie à virus Ebola à Conakry, en Guinée, en 2014.
En utilisant les données sous l’onglet “indice” :
- Estime la distribution de la descendance à partir de la distribution des cas secondaires.
- Estime ensuite le potentiel de grande épidémie à partir de ces données, en effectuant 100 simulations avec un cas initial.
- Imprime le résumé de l’objet de classe
<epichains>. Cela devrait nous aider à compter le nombre de chaînes qui atteignent unsizede plus de 100 cas infectés.
Pour des résultats reproductibles, utilise
set.seed(645).
Code avec les données de l’arbre de transmission écrites par Christian Althaus, 2015:
R
# Number of individuals in the trees
n <- 152
# Number of secondary cases for all individuals
c1 <- c(1, 2, 2, 5, 14, 1, 4, 4, 1, 3, 3, 8, 2, 1, 1,
4, 9, 9, 1, 1, 17, 2, 1, 1, 1, 4, 3, 3, 4, 2,
5, 1, 2, 2, 1, 9, 1, 3, 1, 2, 1, 1, 2)
c0 <- c(c1, rep(0, n - length(c1)))
c0 %>%
enframe() %>%
ggplot(aes(value)) +
geom_histogram(binwidth = 1)
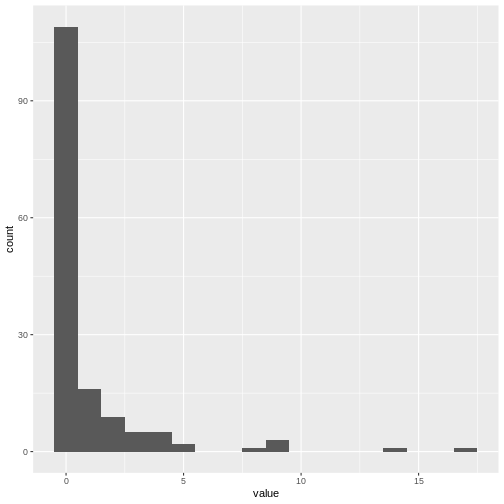
Défi facultatif :
- Reproduis la figure (B) de Christian Althaus, 2015 avec la sortie de la simulation.
Points clés
- Utilise epichains pour simuler le potentiel de grandes épidémies de maladies dont la distribution de la descendance est trop dispersée.
