Établir des prévisions à court terme

Dernière mise à jour le 2025-10-20 | Modifier cette page

Vue d'ensemble

Questions

  • Comment créer des prévisions à court terme à partir de données de cas ?
  • Comment tenir compte des rapports incomplets dans les prévisions ?

Objectifs

  • Apprendre à faire des prévisions de cas à l’aide du logiciel R EpiNow2
  • Apprendre à inclure un processus d’observation dans l’estimation

Conditions préalables

Les apprenants doivent se familiariser avec les dépendances conceptuelles suivantes avant de suivre ce tutoriel :

Statistiques: distributions de probabilités, principe d’ Analyse bayésienne.

Théorie des épidémies: Nombre de reproduction effectif.

Introduction

À partir des données relatives aux cas d’ épidémie, il est possible d’estimer le nombre actuel et futur de cas en tenant compte à la fois des délais de la déclaration et de la sous-déclaration. Pour faire des prévisions sur l’évolution future de l’épidémie, nous devons émettre une hypothèse sur la façon dont les observations faites jusqu’à présent sont liées à ce que nous attendons à l’avenir. La façon la plus simple de procéder est de supposer qu’il n’y a pas de changement, c’est-à-dire que le nombre de reproduction restera le même à l’avenir qu’au moment de la dernière observation. Dans ce tutoriel, nous établirons des prévisions en supposant que le nombre de reproductions restera le même que son estimation à la dernière date pour laquelle des données étaient disponibles.

Dans ce tutoriel, nous allons apprendre à utiliser la fonction EpiNow2 pour prévoir les cas en tenant compte des observations incomplètes et pour prévoir les observations secondaires telles que les décès.

Nous utiliserons le tuyau %>% pour connecter des fonctions, donc appelons aussi l’opérateur tidyverse au paquetage :

R 

library(EpiNow2)
library(tidyverse)

Le double point-virgule

Le double point-virgule :: dans R vous permet d’appeler une fonction spécifique d’un paquet sans charger l’intégralité du paquet dans l’environnement actuel.

Par exemple, vous pouvez appeler une fonction spécifique d’un paquet sans charger le paquet entier dans l’environnement actuel, dplyr::filter(data, condition) utilise filter() à partir de l’outil dplyr paquet.

Cela nous permet de nous souvenir des fonctions du paquet et d’éviter les conflits d’espace de noms.

Créez une prévision à court terme

La fonction epinow() décrite dans l’épisode quantifier la transmission est une enveloppe pour les fonctions :

  • estimate_infections() utilisée pour estimer le nombre de cas par date d’infection.
  • forecast_infections() utilisée pour simuler des infections à l’aide d’un ajustement existant (estimation) aux cas observés.

Utilisons le même code que celui utilisé dans l’épisode quantifier la transmission pour obtenir les données d’entrée, les délais et les priorités :

R 

# Read cases dataset
cases <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = "cases_new",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable)  # Drop count_variable as no longer needed

# Incubation period
incubation_period_fixed <- EpiNow2::Gamma(
  mean = 4,
  sd = 2,
  max = 20
)

# Log-tranformed mean
log_mean <- EpiNow2::convert_to_logmean(mean = 2, sd = 1)

# Log-transformed std
log_sd <- EpiNow2::convert_to_logsd(mean = 2, sd = 1)

# Reporting delay
reporting_delay_fixed <- EpiNow2::LogNormal(
  mean = log_mean,
  sd = log_sd,
  max = 10
)

# Generation time
generation_time_fixed <- EpiNow2::LogNormal(
  mean = 3.6,
  sd = 3.1,
  max = 20
)

# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = EpiNow2::LogNormal(mean = 2, sd = 2))

Nous pouvons maintenant extraire les prévisions à court terme à l’aide de :

R 

# Assume we only have the first 90 days of this data
reported_cases <- cases %>%
  dplyr::slice(1:90)

# Estimate and forecast
estimates <- EpiNow2::epinow(
  data = reported_cases,
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  rt = rt_prior
)

N’attendez pas que cela se termine !

Ce dernier morceau peut prendre 10 minutes à s’exécuter. Continuez à lire cet épisode du tutoriel pendant qu’il s’exécute en arrière-plan. Pour plus d’informations sur le temps de calcul, lisez la section “Inférence bayésienne à l’aide de Stan” dans la section quantification de la transmission.

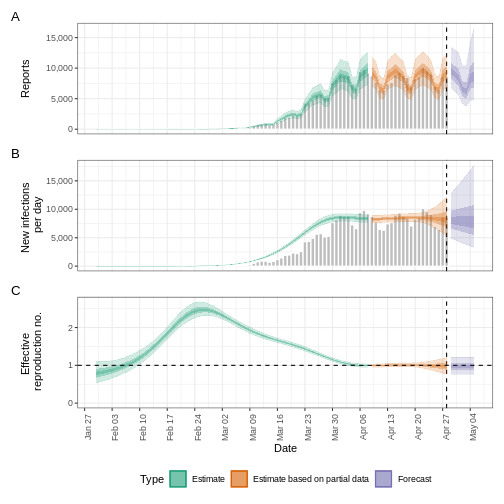
Nous pouvons visualiser les estimations du nombre de reproductions effectives et du nombre estimé de cas à l’aide de plot(). Les estimations sont réparties en trois catégories :

  • Estimation (vert) : utilise toutes les données,

  • Estimation basée sur des données partielles (orange) : contient un degré d’incertitude plus élevé car ces estimations sont basées sur moins de données,

  • Prévision (violet) : prévisions pour l’avenir.

R 

plot(estimates)

Prévision avec des observations incomplètes

Dans l’épisode de la quantification de la transmission nous avons tenu compte des délais de déclaration. Dans EpiNow2, nous pouvons également tenir compte des observations incomplètes, car dans la réalité, 100 % des cas ne sont pas déclarés. Nous passerons un argument supplémentaire appelé obs dans le epinow() pour définir un modèle d’observation. Le format de obs est défini par la fonction obs_opt() (voir ?EpiNow2::obs_opts pour plus de détails).

Supposons que nous estimions que les données de l’épidémie COVID-19 dans l’objet cases n’incluent pas tous les cas déclarés. Nous estimons que seuls 40 % des cas réels sont déclarés. Pour spécifier cela dans le modèle d’observation, nous devons passer un facteur d’échelle avec une moyenne et un écart type. Si nous supposons que 40 % des cas sont déclarés (avec un écart-type de 1 %), nous spécifions alors le facteur d’échelle scale à obs_opts() comme suit :

R 

obs_scale <- EpiNow2::Normal(mean = 0.4, sd = 0.01)

Pour exécuter le cadre d’inférence avec ce processus d’observation, nous ajoutons obs = obs_opts(scale = obs_scale) aux arguments d’entrée de epinow():

R 

# Define observation model
obs_scale <- EpiNow2::Normal(mean = 0.4, sd = 0.01)

# Assume we only have the first 90 days of this data
reported_cases <- cases %>%
  dplyr::slice(1:90)

# Estimate and forecast
estimates <- EpiNow2::epinow(
  data = reported_cases,
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  rt = rt_prior,
  # Add observation model
  obs = EpiNow2::obs_opts(scale = obs_scale)
)

SORTIE 

WARN [2025-10-20 14:21:43] epinow: There were 6 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2025-10-20 14:21:43] epinow: Examine the pairs() plot to diagnose sampling problems
 -

R 

base::summary(estimates)

SORTIE 

                        measure                 estimate
                         <char>                   <char>
1:       New infections per day   20281 (13237 -- 29973)
2:   Expected change in reports                   Stable
3:   Effective reproduction no.       0.97 (0.76 -- 1.2)
4:               Rate of growth -0.012 (-0.093 -- 0.068)
5: Doubling/halving time (days)         -58 (10 -- -7.4)

Les estimations des mesures de transmission telles que le nombre de reproduction efficace et le taux de croissance sont similaires (ou de même valeur) par rapport à la situation où nous n’avons pas tenu compte des observations incomplètes (voir l’épisode de quantification de la transmission dans la section “Recherche d’estimations”). Cependant, le nombre de nouveaux cas confirmés par date d’infection a considérablement changé d’ampleur pour refléter l’hypothèse selon laquelle seuls 40 % des cas sont déclarés.

Nous pouvons également changer la distribution par défaut de Binomiale négative à Poisson, supprimer l’effet de semaine par défaut (qui tient compte des schémas hebdomadaires de déclaration) et bien d’autres choses encore. Voir ?EpiNow2::obs_opts pour plus de détails.

Quelles sont les implications de ce changement ?

  • Comparer différents pourcentages d’observations %
  • En quoi diffèrent-ils en ce qui concerne le nombre d’infections estimées ?
  • Quelles sont les implications de ce changement pour la santé publique ?

Prévision des observations secondaires

L’outil EpiNow2 permet également d’estimer et de prévoir les observations secondaires, par exemple les décès et les hospitalisations, à partir d’une observation primaire, par exemple le nombre de cas. Nous illustrerons ici comment prévoir le nombre de décès découlant des cas observés de COVID-19 dans les premiers stades de l’épidémie au Royaume-Uni.

Tout d’abord, nous devons formater nos données de manière à ce qu’elles comportent les colonnes suivantes :

  • date: la date (en tant qu’objet date, voir ?is.Date()),
  • primary: nombre d’observations primaires à cette date, dans cet exemple cas,
  • secondary: nombre de dates d’observations secondaires, dans cet exemple décès.

R 

reported_cases_deaths <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0, deaths_new = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = c(primary = "cases_new", secondary = "deaths_new"),
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  # rearrange to wide format for {EpiNow2}
  pivot_wider(names_from = count_variable, values_from = count)
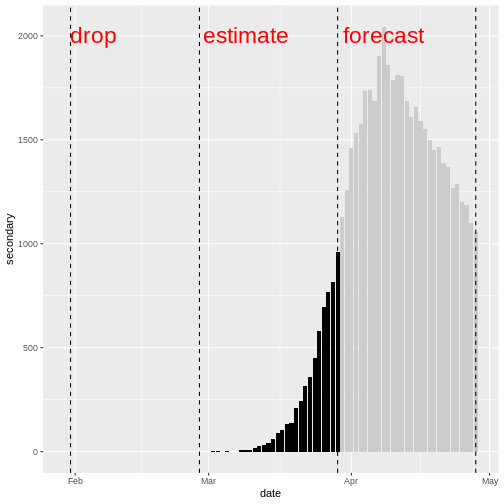
Distribution of secondary cases (deaths). We will drop the first 30 days with no observed deaths. We will use the deaths between day 31 and day 60 to estimate the secondary observations. We will forecast deaths from day 61 to day 90.
Distribution of secondary cases (deaths). We will drop the first 30 days with no observed deaths. We will use the deaths between day 31 and day 60 to estimate the secondary observations. We will forecast deaths from day 61 to day 90.

En utilisant les données sur les cas et les décès entre le 31e et le 60e jour, nous estimerons la relation entre les observations primaires et secondaires à l’aide de la méthode suivante estimate_secondary() puis nous prévoyons les décès futurs à l’aide de forecast_secondary(). Pour plus de détails sur le modèle, voir le documentation du modèle.

Nous devons spécifier le type d’observation en utilisant type en secondary_opts() Les options sont les suivantes :

  • “incidence” : les observations secondaires découlent d’observations primaires antérieures, c’est-à-dire de décès survenus à la suite de cas enregistrés.
  • “prévalence” : les observations secondaires résultent d’une combinaison d’observations primaires actuelles et d’observations secondaires antérieures, c’est-à-dire l’utilisation des lits d’hôpitaux à partir des admissions actuelles à l’hôpital et de l’utilisation passée des lits d’hôpitaux.

Dans cet exemple, nous spécifions secondary_opts(type = "incidence"). Voir ?EpiNow2::secondary_opts pour plus de détails.

La dernière donnée clé est la distribution des délais entre les observations primaires et secondaires. Il s’agit ici du délai entre le signalement du cas et le décès. Nous supposons que ce délai suit une distribution gamma avec une moyenne de 14 jours et un écart-type de 5 jours. Nous pouvons également utiser epiparameter, comme alternative, pour accéder aux délais épidémiologiques). Nous utilisons Gamma() pour spécifier une distribution gamma fixe.

Il existe d’autres fonctions d’entrée pour estimate_secondary() qui peuvent être spécifiées, y compris l’ajout d’un processus d’observation, voir ?EpiNow2::estimate_secondary pour plus de détails sur ces options.

Pour trouver l’ajustement du modèle entre les cas et les décès :

R 

# Estimate from day 31 to day 60 of this data
cases_to_estimate <- reported_cases_deaths %>%
  slice(31:60)

# Delay distribution between case report and deaths
delay_report_to_death <- EpiNow2::Gamma(
  mean = EpiNow2::Normal(mean = 14, sd = 0.5),
  sd = EpiNow2::Normal(mean = 5, sd = 0.5),
  max = 30
)

# Estimate secondary cases
estimate_cases_to_deaths <- EpiNow2::estimate_secondary(
  data = cases_to_estimate,
  secondary = EpiNow2::secondary_opts(type = "incidence"),
  delays = EpiNow2::delay_opts(delay_report_to_death)
)

SORTIE 

WARN [2025-10-20 14:21:50] estimate_secondary (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -

Soyez prudent avec l’échelle de temps

Au début d’une épidémie, il peut y avoir des changements substantiels dans les tests et les rapports. Si les tests changent d’un mois à l’autre, l’ajustement du modèle sera biaisé. Vous devez donc être prudent quant à l’échelle temporelle des données utilisées dans l’ajustement du modèle et les prévisions.

Nous représentons l’ajustement du modèle (rubans ombrés) avec les observations secondaires (diagramme à barres) et les observations primaires (ligne pointillée) comme suit :

R 

plot(estimate_cases_to_deaths, primary = TRUE)

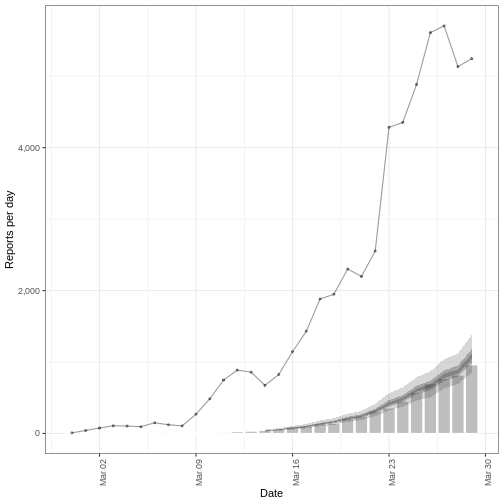
Pour utiliser cet ajustement de modèle afin de prévoir les décès, nous passons un cadre de données composé de l’observation primaire (cas) pour les dates non utilisées dans l’ajustement de modèle.

Remarque : dans cet épisode, nous utilisons des données dont nous connaissons les décès et les cas, nous créons donc une base de données en extrayant les cas. Mais dans la pratique, il s’agirait d’un ensemble de données différent composé uniquement de cas.

R 

# Forecast from day 61 to day 90
cases_to_forecast <- reported_cases_deaths %>%
  dplyr::slice(61:90) %>%
  dplyr::mutate(value = primary)

Pour faire des prévisions, nous utilisons l’ajustement du modèle estimate_cases_to_deaths:

R 

# Forecast secondary cases
deaths_forecast <- EpiNow2::forecast_secondary(
  estimate = estimate_cases_to_deaths,
  primary = cases_to_forecast
)

plot(deaths_forecast)

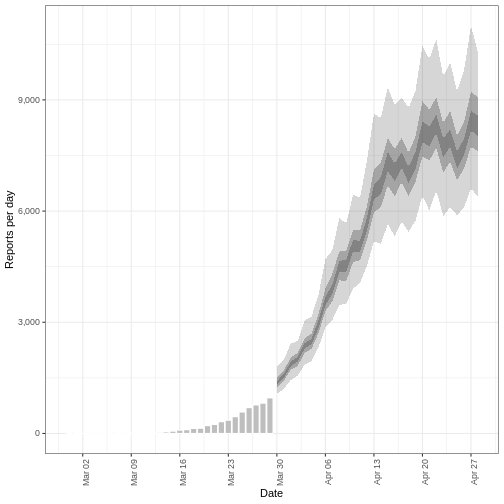
Le graphique montre les observations secondaires prévues (décès) pour les dates pour lesquelles nous avons enregistré des cas. Il est également possible de prévoir les décès à l’aide des cas prévus ; dans ce cas, vous devez spécifier primary comme estimates sortie de estimate_infections().

Intervalles crédibles

Dans tous les cas EpiNow2 les régions ombrées reflètent les intervalles de crédibilité de 90 %, 50 % et 20 %, dans l’ordre du plus clair au plus foncé.

Défi : Analyse de l’épidémie d’Ebola

Défi

Téléchargez le fichier ebola_cases.csv et lisez-le dans R. Les données simulées sont la date d’apparition des symptômes et le nombre de cas confirmés aux premiers stades de l’épidémie d’Ebola en Sierra Leone en 2014.

En utilisant les 3 premiers mois (120 jours) de données :

  1. Estimez si les cas augmentent ou diminuent au 120e jour de l’épidémie.
  2. Tenir compte d’une capacité d’observation de 80 % des cas.
  3. Établissez une prévision à deux semaines du nombre de cas.

Vous pouvez utiliser les valeurs de paramètres suivantes pour la (les) distribution(s) des délais et la distribution du temps de génération.

Vous pouvez inclure une certaine incertitude autour de la moyenne et de l’écart-type de ces distributions.

Nous utilisons le nombre de reproduction effectif et le taux de croissance pour estimer si les cas augmentent ou diminuent.

Nous pouvons utiliser le horizon à l’intérieur de la forecast_opts() fourni pour forecast argument dans epinow() pour étendre la durée de la prévision. La valeur par défaut est de sept jours.

Assurez-vous que les données sont au bon format :

  • date la date (en tant qu’objet de date, voir ?is.Date()),
  • confirm nombre de cas confirmés à cette date.

Pour estimer le nombre de reproductions effectives et le taux de croissance, nous utiliserons la fonction epinow().

Les données étant constituées de la date d’apparition des symptômes, il nous suffit de spécifier une distribution des délais pour la période d’incubation et le temps de génération.

Nous spécifions les distributions avec une certaine incertitude autour de la moyenne et de l’écart-type de la distribution log-normale pour la période d’incubation et de la distribution Gamma pour le temps de génération.

R 

epiparameter::epiparameter_db(
  disease = "ebola",
  epi_name = "incubation"
) %>%
  epiparameter::parameter_tbl()

SORTIE 

# Parameter table:
# A data frame:    5 × 7
  disease           pathogen epi_name prob_distribution author  year sample_size
  <chr>             <chr>    <chr>    <chr>             <chr>  <dbl>       <dbl>
1 Ebola Virus Dise… Ebola V… incubat… lnorm             Eichn…  2011         196
2 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015        1798
3 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015          49
4 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015         957
5 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015         792

R 

ebola_eichner <- epiparameter::epiparameter_db(
  disease = "ebola",
  epi_name = "incubation",
  author = "Eichner"
)

ebola_eichner_parameters <- epiparameter::get_parameters(ebola_eichner)

ebola_incubation_period <- EpiNow2::LogNormal(
  meanlog = EpiNow2::Normal(
    mean = ebola_eichner_parameters["meanlog"],
    sd = 0.5
  ),
  sdlog = EpiNow2::Normal(
    mean = ebola_eichner_parameters["sdlog"],
    sd = 0.5
  ),
  max = 20
)

ebola_generation_time <- EpiNow2::Gamma(
  mean = EpiNow2::Normal(mean = 15.3, sd = 0.5),
  sd = EpiNow2::Normal(mean = 10.1, sd = 0.5),
  max = 30
)

Nous lisons les données en utilisant readr::read_csv(). Cette fonction reconnaît que la colonne date est une <date> vecteur de classe.

R 

# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
ebola_cases_raw <- readr::read_csv(
  here::here("data", "raw-data", "ebola_cases.csv")
)

Prétraiter et adapter les données brutes pour EpiNow2:

R 

ebola_cases <- ebola_cases_raw %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(confirm = 0)) %>%
  # use {incidence2} to compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = "confirm",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable)

dplyr::as_tibble(ebola_cases)

SORTIE 

# A tibble: 123 × 2
   date       confirm
   <date>       <dbl>
 1 2014-05-18       1
 2 2014-05-19       0
 3 2014-05-20       2
 4 2014-05-21       4
 5 2014-05-22       6
 6 2014-05-23       1
 7 2014-05-24       2
 8 2014-05-25       0
 9 2014-05-26      10
10 2014-05-27       8
# ℹ 113 more rows

Nous définissons un modèle d’observation pour mettre à l’échelle le nombre estimé et prévu de nouvelles infections :

R 

# Define observation model
# mean of 80% and standard deviation of 1%
ebola_obs_scale <- EpiNow2::Normal(mean = 0.8, sd = 0.01)

Comme nous voulons également créer une prévision sur deux semaines, nous spécifions horizon = 14 pour prévoir 14 jours au lieu des 7 jours par défaut.

R 

ebola_estimates <- EpiNow2::epinow(
  data = ebola_cases %>% dplyr::slice(1:120), # first 3 months of data only
  generation_time = EpiNow2::generation_time_opts(ebola_generation_time),
  delays = EpiNow2::delay_opts(ebola_incubation_period),
  # Add observation model
  obs = EpiNow2::obs_opts(scale = ebola_obs_scale),
  # horizon needs to be 14 days to create two week forecast (default is 7 days)
  forecast = EpiNow2::forecast_opts(horizon = 14)
)

summary(ebola_estimates)

SORTIE 

                        measure               estimate
                         <char>                 <char>
1:       New infections per day         94 (50 -- 188)
2:   Expected change in reports             Increasing
3:   Effective reproduction no.       1.7 (1.2 -- 2.4)
4:               Rate of growth 0.042 (0.003 -- 0.088)
5: Doubling/halving time (days)        17 (7.9 -- 230)

Le numéro de reproduction effectif \(R_t\) (à la dernière date des données) est de 1.7 (1.2 – 2.4). Le taux de croissance exponentiel du nombre de cas est de 0.042 (0.003 – 0.088).

Visualisez les estimations :

R 

plot(ebola_estimates)

Prévision avec des estimations de \(R_t\)

Par défaut, les prévisions à court terme sont créées en utilisant la dernière estimation du nombre de reproductions \(R_t\). Cette estimation étant basée sur des données partielles, elle présente une grande incertitude.

Le nombre de reproductions projeté dans le futur peut être remplacé par une estimation moins récente, basée sur des données plus nombreuses, à l’aide de rt_opts():

R 

EpiNow2::rt_opts(future = "estimate")

Il en résultera des prévisions moins incertaines (puisqu’elles sont basées sur les données de l \(R_t\) avec un intervalle d’incertitude plus étroit), mais les prévisions seront basées sur des estimations moins récentes de \(R_t\) et supposeront qu’il n’y a pas eu de changement depuis lors.

En outre, il est possible de projeter la valeur de \(R_t\) dans le futur à l’aide d’un modèle générique en fixant future = "project". Comme cette option utilise un modèle pour prévoir la valeur de \(R_t\) il en résultera des prévisions plus incertaines que la valeur de estimate pour un exemple voir ici.

Résumé

EpiNow2 peut être utilisé pour créer des prévisions à court terme et pour estimer la relation entre différents résultats. Il existe une série d’options de modèle qui peuvent être mises en œuvre pour différentes analyses, y compris l’ajout d’un processus d’observation pour tenir compte des déclarations incomplètes. Voir le site web de l’Agence européenne pour la sécurité et la santé au travail. vignette pour plus de détails sur les différentes options de modèle dans EpiNow2 qui ne sont pas abordées dans ces tutoriels.

Points clés

  • Nous pouvons créer des prévisions à court terme en faisant des hypothèses sur le comportement futur du nombre de reproduction.
  • Les estimations peuvent tenir compte des déclarations de cas incomplètes.