Quantifier la transmission

Vue d'ensemble

Questions

• Comment puis-je estimer le nombre de reproduction variable dans le temps (\(Rt\)) et le taux de croissance à partir d’une série chronologique de données de cas ?
• Comment quantifier l’hétérogénéité géographique à partir de ces paramètres de transmission ?

Objectifs

• Apprenez à estimer les paramètres de transmission à partir d’une série chronologique de données sur les cas à l’aide du package EpiNow2.

Conditions préalables

Les étudiants doivent se familiariser avec les concepts suivants avant de suivre ce tutoriel :

Statistiques: distributions de probabilités, principe de l’analyse bayésienne.

Théorie des épidémies: Nombre de reproduction effectif.

Science des données: la transformation et la visualisation des données. Vous pouvez revoir l’épisode sur Agréger et visualiser les données d’incidence.

Rappel : le nombre de reproduction effectif, \(R_t\)

Le nombre de reproduction de base, \(R_0\) est le nombre moyen de cas causés par un individu infectieux dans une population entièrement susceptible.

Mais dans une épidémie en cours, la population ne reste pas entièrement susceptible, car les personnes qui se remettent de l’infection sont généralement immunisées. En outre, il peut y avoir des changements de comportement ou d’autres facteurs qui affectent la transmission. Lorsque nous voulons surveiller les changements dans la transmission, nous nous intéressons donc davantage à la valeur du nombre de reproduction effectif, \(R_t\) qui représente le nombre moyen de cas causés par un individu infectieux dans la population au temps \(t\) compte tenu de l’état actuel de la population (y compris les niveaux d’immunité et les mesures de contrôle).

Introduction

---

L’intensité de la transmission d’une épidémie est quantifiée à l’aide de deux paramètres clés : le nombre de reproduction, qui renseigne sur la force de la transmission en indiquant le nombre de nouveaux cas attendus pour chaque cas existant, et le nombre de décès. taux de croissance qui renseigne sur la vitesse de transmission en indiquant la rapidité avec laquelle l’épidémie se propage ou décline (temps de doublement/dédoublement) au sein d’une population. Pour plus de détails sur la distinction entre la vitesse et la force de la transmission et les implications pour la lutte, consultez le site Dushoff & Park, 2021.

Pour estimer ces paramètres clés à l’aide des données relatives aux cas, nous devons tenir compte des délais entre les dates d’infections et les dates de cas déclarés. Lors d’une épidémie, les données ne sont généralement disponibles qu’à partir des dates déclarées. Nous devons donc utiliser des méthodes d’estimation pour tenir compte de ces retards lorsque nous essayons de comprendre les changements dans la transmission au fil du temps.

Dans les prochains tutoriels, nous nous concentrerons sur la manière d’utiliser les fonctions de EpiNow2 pour estimer les paramètres de transmission des données de cas. Nous ne couvrirons pas le contexte théorique des modèles ou du cadre d’inférence, pour plus de détails sur ces concepts, consultez la vignette..

Dans ce tutoriel, nous allons apprendre à utiliser le package EpiNow2 pour estimer le nombre de reproduction variable dans le temps. Nous obtiendrons les données d’entrée de incidence2. Nous utiliserons le package tidyr et dplyr pour organiser certains de ses résultats, ggplot2 pour visualiser la distribution des cas, et le tuyau %>% pour relier certaines de leurs fonctions, alors appelons aussi le package tidyverse :

R

library(EpiNow2)
library(incidence2)
library(tidyverse)

Le double point-virgule

Le double deux-points :: dans R vous permet d’appeler une fonction spécifique d’un package sans charger l’ensemble du package dans l’environnement actuel.

Par exemple, vous pouvez appeler une fonction spécifique d’un package sans charger le package entier dans l’environnement actuel, dplyr::filter(data, condition) utilise filter() à partir du package dplyr.

Cela nous permet de nous souvenir des fonctions du package et d’éviter les conflits d’espace de noms.

Inférence bayésienne

Le package R EpiNow2 utilise une méthode d’inférence bayésienne inférence bayésienne pour estimer les nombres de reproduction et les durées d’infection sur la base des dates déclarées. En d’autres termes, il estime la transmission en fonction de la date à laquelle les personnes ont été effectivement infectées (plutôt que de l’apparition des symptômes), en tenant compte des retards dans les données observées. En revanche, l’approche EpiEstim permet une estimation en temps réel plus rapide et plus simple du nombre de reproductions en utilisant uniquement les données de cas au fil du temps, reflétant la façon dont la transmission change en fonction du moment où les symptômes apparaissent.

Dans l’inférence bayésienne, nous utilisons les connaissances a priori (distributions a priori) et les données (via une fonction de vraisemblance) pour obtenir la probabilité a posteriori :

\(\text{Probabilité a posteriori} \propto \text{vraisemblance} \times \text{probabilité a priori}\)

Distributions de délais et données de cas

---

Données de cas

Pour illustrer les fonctions des EpiNow2 nous utiliserons les données relatives au début de la pandémie de COVID-19 au Royaume-Uni, mais uniquement pour les 90 premiers jours observés. Les données sont disponibles dans le package R incidence2.

R

dplyr::as_tibble(incidence2::covidregionaldataUK)

SORTIE

# A tibble: 6,370 × 13
   date       region   region_code cases_new cases_total deaths_new deaths_total
   <date>     <chr>    <chr>           <dbl>       <dbl>      <dbl>        <dbl>
 1 2020-01-30 East Mi… E12000004          NA          NA         NA           NA
 2 2020-01-30 East of… E12000006          NA          NA         NA           NA
 3 2020-01-30 England  E92000001           2           2         NA           NA
 4 2020-01-30 London   E12000007          NA          NA         NA           NA
 5 2020-01-30 North E… E12000001          NA          NA         NA           NA
 6 2020-01-30 North W… E12000002          NA          NA         NA           NA
 7 2020-01-30 Norther… N92000002          NA          NA         NA           NA
 8 2020-01-30 Scotland S92000003          NA          NA         NA           NA
 9 2020-01-30 South E… E12000008          NA          NA         NA           NA
10 2020-01-30 South W… E12000009          NA          NA         NA           NA
# ℹ 6,360 more rows
# ℹ 6 more variables: recovered_new <dbl>, recovered_total <dbl>,
#   hosp_new <dbl>, hosp_total <dbl>, tested_new <dbl>, tested_total <dbl>

Pour utiliser les données, nous devons les formater de manière à ce qu’elles comportent deux colonnes :

• date la date (en tant qu’objet date, voir ?is.Date()),
• confirm: nombre de cas déclarés (confirmés) à cette date.

Utilisons tidyr et incidence2 pour cela :

R

cases_sliced <- incidence2::covidregionaldataUK %>%
  dplyr::as_tibble() %>%
  # Preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0)) %>%
  # Compute the daily incidence
  incidence2::incidence(
    date_index = "date",
    counts = "cases_new",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  # Keep the first 90 dates
  dplyr::slice_head(n = 90)

Avec incidence2::incidence() nous agrégeons des cas sur différentes périodes de temps (intervalles, c’est-à-dire des jours, des semaines ou des mois) ou par groupe. Nous pouvons également obtenir les dates complètes pour tous les intervalles de dates par catégorie de groupe à l’aide de la fonction complete_dates = TRUE Explorez plus tard les incidence2::incidence() manuel de référence

Afficher les détails

Pouvons-nous reproduire {incidence2} avec {dplyr}?

Nous pouvons obtenir un objet similaire à cases à partir de l’objet incidence2::covidregionaldataUK à l’aide du package dplyr.

R

incidence2::covidregionaldataUK %>%
  dplyr::select(date, cases_new) %>%
  dplyr::group_by(date) %>%
  dplyr::summarise(confirm = sum(cases_new, na.rm = TRUE)) %>%
  dplyr::ungroup() %>%
  dplyr::slice_head(n = 90)

Cependant, incidence2::incidence() contient des arguments pratiques comme complete_dates qui facilitent l’obtention d’un objet d’incidence avec le même intervalle de dates pour chaque groupe sans nécessiter de lignes de code supplémentaires ou un package de séries temporelles.

Dans une situation d’épidémie, il est probable que nous n’ayons accès qu’au début de l’ensemble des données d’entrée. Nous supposons donc que nous ne disposons que des 90 premiers jours de ces données.

R

plot(cases_sliced)

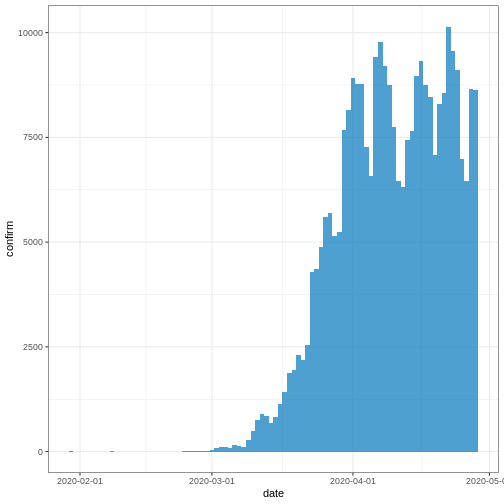
Pour transmettre les résultats de incidence2 à EpiNow2, nous devons supprimer une colonne de l’objet cases_filter :

R

# Drop column for {EpiNow2} input format
cases <- cases_sliced %>%
  dplyr::select(-count_variable)

cases

SORTIE

# A tibble: 90 × 2
   date       confirm
   <date>       <dbl>
 1 2020-01-30       3
 2 2020-01-31       0
 3 2020-02-01       0
 4 2020-02-02       0
 5 2020-02-03       0
 6 2020-02-04       0
 7 2020-02-05       2
 8 2020-02-06       0
 9 2020-02-07       0
10 2020-02-08       8
# ℹ 80 more rows

Distribution des délais

Nous supposons qu’il existe des délais entre le moment de l’infection et le moment où un cas est signalé. Nous spécifions ces délais sous forme de distributions pour tenir compte de l’incertitude des différences au niveau individuel. Le délai peut impliquer plusieurs types de processus. Un délai typique entre le moment de l’infection et la déclaration du cas peut consister en ce qui suit

le temps écoulé entre l’infection et l’apparition des symptômes (le période d’incubation) + délai entre l’apparition des symptômes et la notification du cas (délai de déclaration) .

La distribution des délais pour chacun de ces processus peut être estimée à partir de données ou obtenue à partir de la littérature. Nous pouvons exprimer l’incertitude quant aux paramètres corrects des distributions en supposant que les distributions ont fixe fixes ou qu’elles ont variables variables. Pour comprendre la différence entre fixe et variables considérons la période d’incubation.

Délais et données

Le nombre de retards et le type de retard sont des données flexibles qui dépendent des données. Les exemples ci-dessous montrent comment les délais peuvent être spécifiés pour différentes sources de données :

Source de données	Délai (s)
Heure d’apparition des symptômes	Période d’incubation
Date de la déclaration du cas	Période d’incubation + délai entre l’apparition des symptômes et la notification du cas
Durée de l’hospitalisation	Période d’incubation + temps écoulé entre l’apparition des symptômes et l’hospitalisation

Distribution de la période d’incubation

La distribution de la période d’incubation pour de nombreuses maladies peut généralement être obtenue à partir de la littérature. L’ensemble epiparameter contient une bibliothèque de paramètres épidémiologiques pour différentes maladies, obtenus à partir de la littérature.

Nous spécifions une distribution gamma (fixe) avec moyenne \(\mu = 4\) et un écart-type \(\sigma = 2\) (forme = \(4\), échelle = \(1\)) en utilisant la fonction Gamma() comme suit :

R

incubation_period_fixed <- EpiNow2::Gamma(
  mean = 4,
  sd = 2,
  max = 20
)

incubation_period_fixed

SORTIE

- gamma distribution (max: 20):
  shape:
    4
  rate:
    1

L’argument max est la valeur maximale que la distribution peut prendre ; dans cet exemple, 20 jours.

Nous pouvons tracer les distributions générées par EpiNow2 en utilisant plot().

R

plot(incubation_period_fixed)

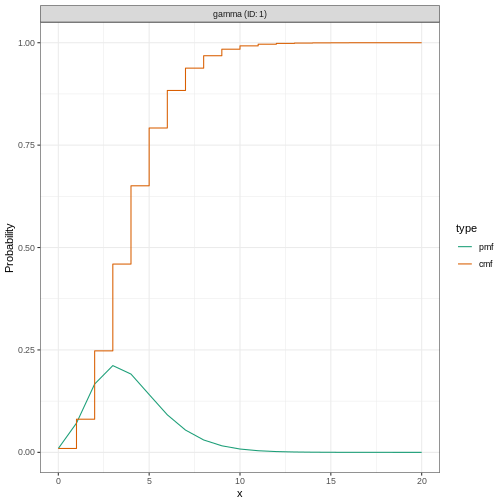
Pourquoi une distribution gamma ?

La période d’incubation doit être une valeur positive. Nous devons donc spécifier une distribution en EpiNow2 qui ne concerne que les valeurs positives.

Gamma() prend en charge les distributions Gamma et LogNormal() les distributions log-normales, qui sont des distributions pour les valeurs positives uniquement.

Pour tous les types de retard, nous devrons utiliser des distributions pour les valeurs positives uniquement - nous ne voulons pas inclure les retards de jours négatifs dans notre analyse !

Prise en compte de l’incertitude de la distribution

Pour spécifier une distribution variable nous incluons l’incertitude autour de la moyenne \(\mu\) et de l’écart-type \(\sigma\) de notre distribution gamma. Si notre distribution de la période d’incubation a une moyenne \(\mu\) et un écart-type \(\sigma\) nous supposons que la moyenne (\(\mu\)) suit une distribution normale avec un écart type \(\sigma_{\mu}\):

\[\mbox{Normal}(\mu,\sigma_{\mu}^2)\]

et un écart-type (\(\sigma\)) suit une distribution normale avec un écart type \(\sigma_{\sigma}\):

\[\mbox{Normal}(\sigma,\sigma_{\sigma}^2).\]

Nous spécifions ceci en utilisant Normal() pour chaque argument : la moyenne (\(\mu = 4\) avec \(\sigma_{\mu} = 0.5\)) et l’écart-type (\(\sigma = 2\) avec \(\sigma_{\sigma} = 0.5\)).

R

incubation_period_variable <- EpiNow2::Gamma(
  mean = EpiNow2::Normal(mean = 4, sd = 0.5),
  sd = EpiNow2::Normal(mean = 2, sd = 0.5),
  max = 20
)

incubation_period_variable

SORTIE

- gamma distribution (max: 20):
  shape:
    - normal distribution:
      mean:
        4
      sd:
        0.61
  rate:
    - normal distribution:
      mean:
        1
      sd:
        0.31

Traçons la distribution que nous venons de configurer :

R

plot(incubation_period_variable)

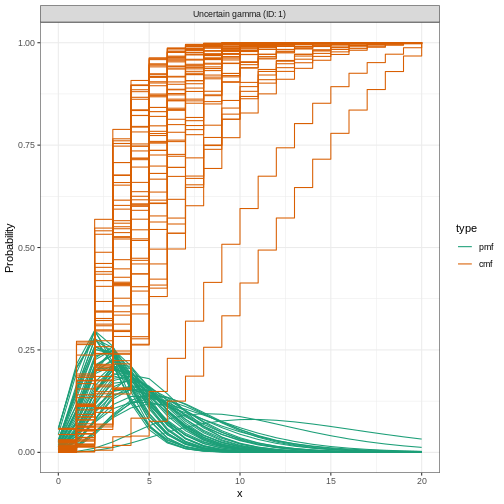
Retards dans l’établissement des rapports

Après la période d’incubation, il s’écoule un délai supplémentaire entre l’apparition des symptômes et la notification du cas : le délai de déclaration. Nous pouvons le spécifier comme une distribution fixe ou variable, ou estimer une distribution à partir de données.

Lorsque vous spécifiez une distribution, il est utile de visualiser la densité de probabilité pour voir le pic et l’étendue de la distribution. Dans cet example, nous allons utiliser une distribution log normale.

Si nous voulons supposer que le délai de déclaration moyen est de 2 jours (avec une incertitude de 0,5 jour) et que l’écart type est de 1 jour (avec une incertitude de 0,5 jour), nous pouvons spécifier une distribution variable à l’aide de la commande LogNormal() comme précédemment :

R

reporting_delay_variable <- EpiNow2::LogNormal(
  meanlog = EpiNow2::Normal(mean = 2, sd = 0.5),
  sdlog = EpiNow2::Normal(mean = 1, sd = 0.5),
  max = 10
)

Afficher les détails

Visualisez une distribution log-normale en utilisant {epiparameter}

En utilisant epiparameter::epiparameter() nous pouvons créer une distribution personnalisée. La distribution normale à logarithme fixe aura l’aspect suivant :

R

library(epiparameter)

R

epiparameter::epiparameter(
  disease = "covid",
  epi_name = "reporting delay",
  prob_distribution =
    epiparameter::create_prob_distribution(
      prob_distribution = "lnorm",
      prob_distribution_params = c(
        meanlog = 2,
        sdlog = 1
      )
    )
) %>%
  plot()

Afficher les détails

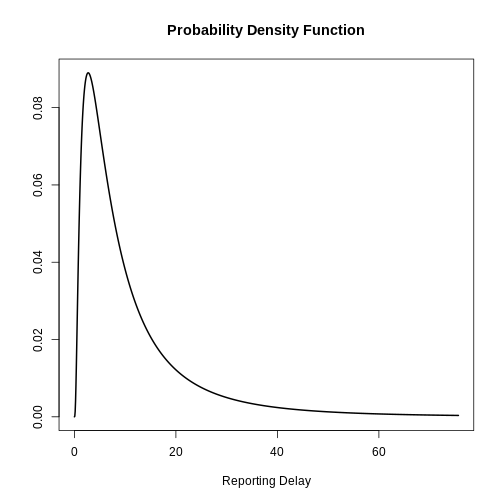
Comment obtenir le délai de reporting à partir des données ?

Si l’on dispose de données sur le délai entre l’apparition des symptômes et la déclaration, on peut utiliser la fonction estimate_delay() pour estimer une distribution log-normale à partir d’un vecteur de délais. Le code ci-dessous illustre comment utiliser la fonction estimate_delay() avec des données synthétiques sur les délais.

R

library(tidyverse)

# Steps:
# - get Ebola data from package {outbreaks}
# - keep a subset of columns for this example only
# - calculate the time difference between two dates in linelist
# - extract the time difference as a vector class object
# - estimate the delay parameters using {EpiNow2}

outbreaks::ebola_sim_clean$linelist %>%
  tibble::as_tibble() %>%
  dplyr::select(case_id, date_of_onset, date_of_hospitalisation) %>%
  dplyr::mutate(reporting_delay = date_of_hospitalisation - date_of_onset) %>%
  dplyr::pull(reporting_delay) %>%
  EpiNow2::estimate_delay(
    samples = 1000,
    bootstraps = 10
  )

SORTIE

WARN [2025-09-29 19:37:51] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:37:51] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:37:54] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:37:54] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:37:56] dist_fit (chain: 1): The largest R-hat is 1.08, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-09-29 19:37:56] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:37:56] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:37:58] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:37:58] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:38:00] dist_fit (chain: 1): The largest R-hat is 1.07, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-09-29 19:38:00] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:38:00] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:38:02] dist_fit (chain: 1): The largest R-hat is 1.11, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-09-29 19:38:02] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:38:02] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:38:04] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:38:04] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:38:06] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:38:06] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:38:08] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:38:08] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-09-29 19:38:11] dist_fit (chain: 1): The largest R-hat is 1.05, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-09-29 19:38:11] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-09-29 19:38:11] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess - 

SORTIE

- lognormal distribution (max: 22):
  meanlog:
    - normal distribution:
      mean:
        0.24
      sd:
        0.11
  sdlog:
    - normal distribution:
      mean:
        0.98
      sd:
        0.1

Temps de génération

Nous devons également spécifier une distribution pour le temps de génération. Nous utiliserons ici une distribution log-normale avec une moyenne de 3,6 et un écart-type de 3,1 (Ganyani et al. 2020).

R

generation_time_variable <- EpiNow2::LogNormal(
  mean = EpiNow2::Normal(mean = 3.6, sd = 0.5),
  sd = EpiNow2::Normal(mean = 3.1, sd = 0.5),
  max = 20
)

Trouver des estimations

---

La fonction epinow() est une “enveloppe” pour la fonction estimate_infections() utilisée pour estimer les cas par date d’infection. La distribution du temps de génération et la distribution des délais doivent être transmises à l’aide des fonctions generation_time_opts() et delay_opts() respectivement.

Il existe de nombreuses autres entrées qui peuvent être transmises à epinow() voir ?EpiNow2::epinow() pour plus de détails. Une entrée optionnelle consiste à spécifier un a priori log-normal pour le nombre de reproduction effectif \(R_t\) au début de l’épidémie. Nous spécifions une moyenne de 2 jours et un écart-type de 2 jours comme arguments de la commande prior dans rt_opts():

R

# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = EpiNow2::LogNormal(mean = 2, sd = 2))

Inférence bayésienne à l’aide de Stan

L’inférence bayésienne est réalisée à l’aide de méthodes MCMC avec le programme Stan. Les fonctions Stan disposent d’un certain nombre d’entrées par défaut, notamment le nombre de chaînes et le nombre d’échantillons par chaîne (voir ?EpiNow2::stan_opts()).

Pour réduire le temps de calcul, nous pouvons exécuter les chaînes en parallèle. Pour ce faire, nous devons définir le nombre de cœurs à utiliser. Par défaut, 4 chaînes MCMC sont exécutées (voir stan_opts()$chains), nous pouvons donc définir un nombre égal de cœurs à utiliser en parallèle comme suit :

R

withr::local_options(base::list(mc.cores = 4))

Pour connaître le nombre maximal de cœurs disponibles sur votre machine, utilisez la commande parallel::detectCores().

Liste de vérification

Note : Dans le code ci-dessous _fixed les distributions sont utilisées à la place de _variable (distributions de retard avec incertitude). Cela permet d’accélérer le temps de calcul. Il est généralement recommandé d’utiliser des distributions variables qui tiennent compte d’une incertitude supplémentaire.

R

# fixed alternatives
generation_time_fixed <- EpiNow2::LogNormal(
  mean = 3.6,
  sd = 3.1,
  max = 20
)

reporting_delay_fixed <- EpiNow2::LogNormal(
  mean = 2,
  sd = 1,
  max = 10
)

Vous êtes maintenant prêt à exécuter EpiNow2::epinow() pour estimer le nombre de reproduction variable dans le temps pour les 90 premiers jours :

R

estimates <- EpiNow2::epinow(
  # reported cases
  data = cases,
  # delays
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  # prior
  rt = rt_prior
)

SORTIE

WARN [2025-09-29 19:42:07] epinow: There were 1 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2025-09-29 19:42:07] epinow: Examine the pairs() plot to diagnose sampling problems
 - 

N’attendez pas que cela se poursuive

Pour les besoins de ce tutoriel, nous pouvons optionnellement utiliser EpiNow2::stan_opts() pour réduire le temps de calcul. Nous pouvons spécifier un nombre fixe de samples = 1000 et chains = 2 aux stan l’argument de la EpiNow2::epinow() de la fonction. Cette opération devrait prendre environ 3 minutes.

<Nous pouvons optionnellement définir stan = stan_opts(method = "vb") pour utiliser une méthode d’échantillonnage approximative. Cela devrait prendre moins d’une minute. –>

R

# you can add the `stan` argument
EpiNow2::epinow(
  ...,
  stan = EpiNow2::stan_opts(samples = 1000, chains = 3)
)

Rappelez-vous : En utilisant un nombre approprié d’ échantillons et de chaînes est cruciale pour garantir la convergence et obtenir des estimations fiables dans les calculs bayésiens utilisant Stan. L’obtention de résultats plus précis se fait au détriment de la vitesse.

Résultats

Nous pouvons extraire et visualiser des estimations du nombre de reproductions effectives au fil du temps :

R

estimates$plots$R

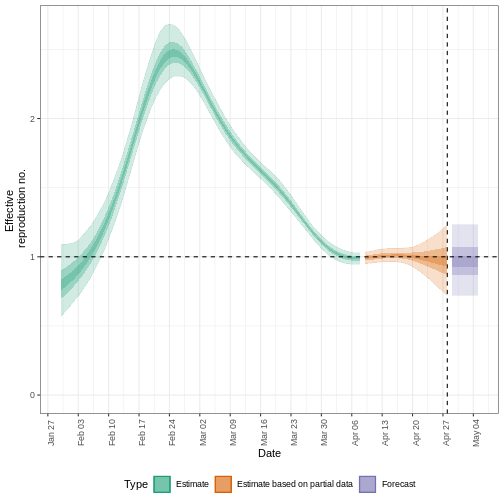
L’incertitude des estimations augmente avec le temps. Cela s’explique par le fait que les estimations sont fondées sur des données antérieures, c’est-à-dire sur les périodes de retard. Cette différence d’incertitude est classée dans les catégories suivantes Estimation (vert) utilise toutes les données et Estimation basée sur des données partielles (orange) des estimations basées sur moins de données (parce que les infections qui se sont produites à l’époque sont plus susceptibles de ne pas avoir encore été observées) et qui ont donc des intervalles de plus en plus larges vers la date du dernier point de données. Enfin, les Prévision (violet) est une projection dans le temps.

Nous pouvons également visualiser l’estimation du taux de croissance dans le temps :

R

estimates$plots$growth_rate

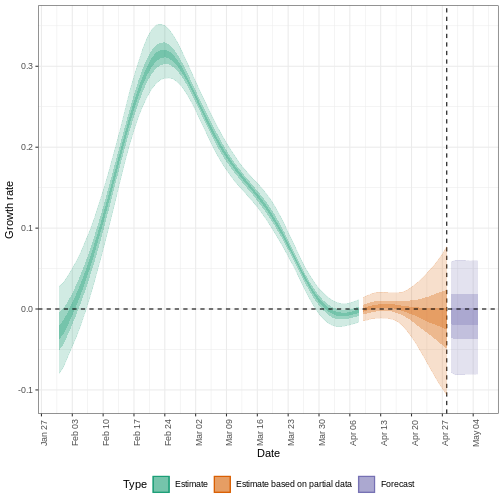
Pour extraire un résumé des principaux paramètres de transmission à dernière date* dans les données :

R

summary(estimates)

SORTIE

                        measure                estimate
                         <char>                  <char>
1:       New infections per day    7929 (4634 -- 13046)
2:   Expected change in reports                  Stable
3:   Effective reproduction no.      0.97 (0.72 -- 1.2)
4:               Rate of growth -0.012 (-0.11 -- 0.078)
5: Doubling/halving time (days)       -58 (8.9 -- -6.5)

Ces estimations étant basées sur des données partielles, elles présentent un large intervalle d’incertitude.

• Le résumé de notre analyse montre que le changement attendu dans les déclarations est de Stable avec l’estimation des nouvelles infections 7929 (4634 – 13046).

• Le nombre effectif de reproduction \(R_t\) (à la dernière date des données) est de 0.97 (0.72 – 1.2).

• Le taux de croissance exponentiel du nombre de cas est de -0.012 (-0.11 – 0.078).

• Le temps de doublement (le temps nécessaire pour que le nombre de cas double) est de -58 (8.9 – -6.5).

Expected change in reports

Un facteur décrivant l’évolution attendue des déclarations sur la base de la probabilité a posteriori que \(R_t < 1\).

Probabilité (\(p\))	Changement attendu (\(p\))
p < 0.05$	Augmentation
0,05$ p< 0,4$	Augmentation probable
0,4$ p< 0,6$	Stable
0,6$ p < 0,95$	Vraisemblablement décroissante
0,95$ p $	Décroissante

Intervalles crédibles

En tout EpiNow2 les régions ombrées reflètent les intervalles de crédibilité de 90 %, 50 % et 20 %, du plus clair au plus foncé.

Liste de vérification

EpiNow2 peut être utilisé pour estimer les paramètres de transmission à partir des données relatives aux cas, à tout moment de l’évolution d’une épidémie. La fiabilité de ces estimations dépend de la qualité des données et du choix approprié des distributions de délais. Dans le prochain tutoriel, nous apprendrons à faire des prévisions et nous étudierons certaines des options d’inférence supplémentaires disponibles dans le logiciel EpiNow2.

Défi

---

Défi

Quantifier l’hétérogénéité géographique

Les données relatives au début de la pandémie de COVID-19 au Royaume-Uni proviennent du package R incidence2 comprennent la région dans laquelle les cas ont été enregistrés. Pour obtenir des estimations régionales du nombre effectif de reproductions et de cas, nous devons formater les données de manière à ce qu’elles comportent trois colonnes :

• date la date,
• region: la région,
• confirm le nombre de déclarations de maladies (confirmées) pour une région à une date donnée.

Générer des estimations régionales de Rt à partir des incidence2::covidregionaldataUK à partir de la base de données :

• utiliser incidence2 pour convertir les données agrégées en données d’incidence par la variable region,
• conserver les 90 premières dates pour toutes les régions,
• estimer le Rt par région en utilisant le temps de génération défini et les retards dans cet épisode.

R

regional_cases <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0))

Donner un indice

Pour manipuler les données, vous pouvez

R

regional_cases <- incidence2::covidregionaldataUK %>%
  # use {tidyr} to preprocess missing values
  tidyr::replace_na(base::list(cases_new = 0)) %>%
  # use {incidence2} to convert aggregated data to incidence data
  incidence2::incidence(
    date_index = "date",
    groups = "region",
    counts = "cases_new",
    count_values_to = "confirm",
    date_names_to = "date",
    complete_dates = TRUE
  ) %>%
  dplyr::select(-count_variable) %>%
  dplyr::filter(date < ymd(20200301))

Pour apprendre à faire l’estimation régionale de Rt, lisez la section de la vignette “Get started” sur regional_epinow() à l’adresse https://epiforecasts.io/EpiNow2/articles/EpiNow2.html#regional_epinow

Montrer la solution

Pour obtenir des estimations régionales, nous utilisons les mêmes arguments de epinow() dans la fonction regional_epinow():

R

estimates_regional <- EpiNow2::regional_epinow(
  # cases
  data = regional_cases,
  # delays
  generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
  delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
  # prior
  rt = rt_prior
)

Visualisez les résultats avec :

R

estimates_regional$summary$summarised_results$table

estimates_regional$summary$plots$R

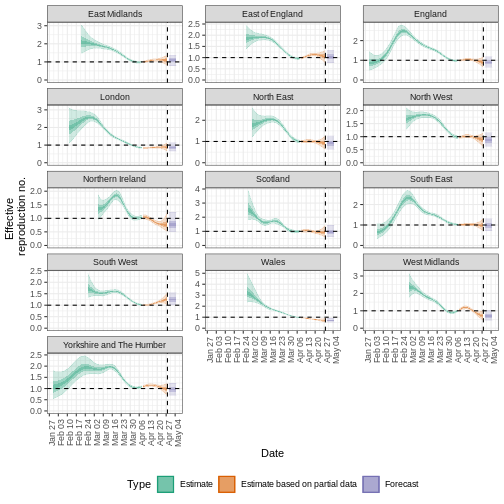
Points clés

• Les paramètres de transmission peuvent être estimés à partir des données du cas après prise en compte des retards.
• L’incertitude peut être prise en compte dans la distribution des retards.