Accéder aux distribution des délais épidémiologiques

Dernière mise à jour le 2025-10-13 | Modifier cette page

Vue d'ensemble

Questions

  • Comment accéder aux distributions des délais des maladies à partir d’une base de données préétablie pour les utiliser dans l’analyse ?

Objectifs

  • Obtenez les délais à partir d’une base de données de recherche documentaire avec epiparameter.
  • Obtenez les paramètres de distribution et les statistiques sommaires des distributions de délais.

Conditions préalables

Cet épisode nécessite que vous soyez familier avec :

la science des données Programmation de base avec R.

Théorie des épidémies La théorie des épidémies est basée sur les paramètres épidémiologiques, les périodes de la maladie, telles que la période d’incubation, le temps de génération et l’intervalle sériel.

Introduction

Les maladies infectieuses suivent un cycle infectieux qui comprend généralement les phases suivantes : période présymptomatique, période symptomatique et période de guérison, comme le décrivent leurs histoire naturelle. Ces périodes peuvent être utilisées pour comprendre la dynamique de la transmission et informer les interventions de prévention et de contrôle des maladies.

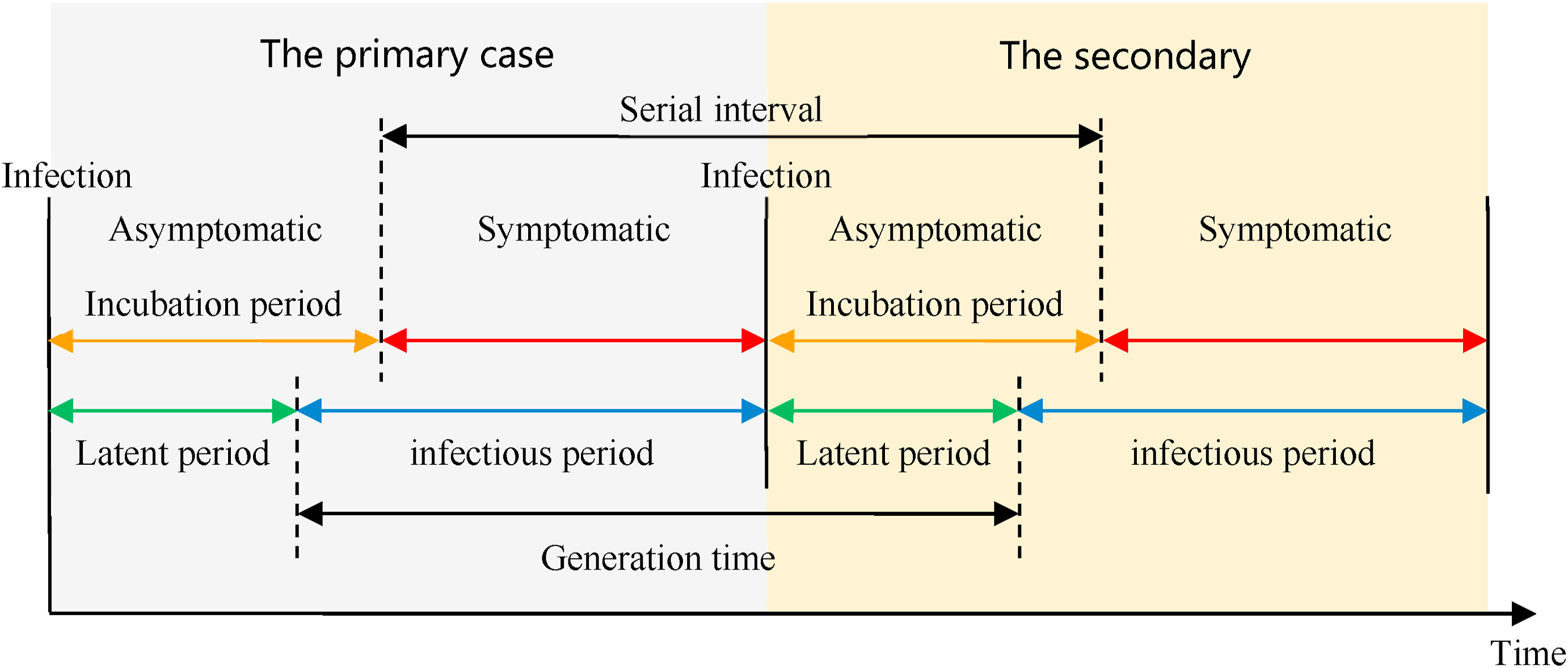
Définition des périodes clés. A partir de Xiang et al, 2021
Définition des périodes clés. A partir de Xiang et al, 2021

Définitions

Regardez le glossaire pour connaître les définitions de toutes les périodes de la figure ci-dessus !

Toutefois, au début d’une épidémie, les efforts visant à comprendre l’épidémie et les implications pour la lutte peuvent être retardés par l’absence d’un moyen facile d’accéder aux paramètres clés de la maladie en question (Nash et al., 2023). Des projets tels que epiparameter et {epireview} construisent des catalogues en ligne en suivant des protocoles de synthèse de la littérature qui peuvent aider à informer l’analyse et à paramétrer les modèles en fournissant une bibliothèque de paramètres épidémiologiques précédemment estimés à partir d’épidémies passées.

Pour illustrer l’utilisation de l’outil epiparameter R dans votre pipeline d’analyse, notre objectif dans cet épisode sera d’accéder à un ensemble spécifique de paramètres épidémiologiques de la littérature, au lieu d’extraire des articles et de les copier-coller à la main. Nous les insérerons ensuite dans un EpiNow2 flux de travail d’analyse.

Commençons par charger le fichier epiparameter paquetage. Nous utiliserons le tube %>% pour connecter certaines de ses fonctions, certaines tibble et dplyr donc appelons aussi à la fonction tidyverse paquetage :

R 

library(epiparameter)
library(tidyverse)

Le double point-virgule

Le double point-virgule :: dans R vous permet d’appeler une fonction spécifique d’un paquetage sans charger l’ensemble du paquetage dans l’environnement actuel.

Par exemple, vous pouvez appeler une fonction spécifique d’un package sans charger le package entier dans l’environnement actuel, dplyr::filter(data, condition) utilise filter() à partir de l’outil dplyr paquet.

Cela nous permet de nous souvenir des fonctions du paquet et d’éviter les conflits d’espace de noms.

Le problème

Si nous voulons estimer la transmissibilité d’une infection, il est courant d’utiliser un package tel que EpiEstim ou EpiNow2. Le paquet EpiEstim permet d’estimer en temps réel le nombre de reproductions à l’aide des données relatives aux cas dans le temps, reflétant ainsi l’évolution de la transmission en fonction de la date d’apparition des symptômes. Pour estimer la transmission en fonction du moment où les personnes ont été effectivement infectées (plutôt que de l’apparition des symptômes), le logiciel EpiNow2 étend cette idée en la combinant avec un modèle qui tient compte des délais dans les données observées. Les deux logiciels requièrent certaines informations épidémiologiques en entrée. Par exemple, dans EpiNow2 nous utilisons EpiNow2::Gamma() pour spécifier un temps de génération sous la forme d’une distribution de probabilité ajoutant son mean l’écart-type (sd) et sa valeur maximale (max).

Pour spécifier une valeur generation_time qui suit un Gamma avec une moyenne \(\mu = 4\) écart-type \(\sigma = 2\) et une valeur maximale de 20, nous écrivons :

R 

generation_time <- 
  EpiNow2::Gamma(
    mean = 4,
    sd = 2,
    max = 20
  )

Il est courant que les analystes recherchent manuellement la littérature disponible et copient et collent les résultats de la recherche. statistiques sommaires ou les paramètres de distribution des publications scientifiques. Une difficulté à laquelle on est souvent confronté est que la présentation des différentes distributions statistiques n’est pas cohérente dans la littérature (par exemple, un article peut ne présenter que la moyenne, plutôt que la distribution sous-jacente complète). epiparameter L’objectif du projet est de faciliter l’accès à des estimations fiables des paramètres de distribution pour une série de maladies infectieuses, afin qu’elles puissent être facilement mises en œuvre dans les pipelines d’analyse des épidémies.

Dans cet épisode, nous allons accéder les statistiques sommaires du temps de génération pour COVID-19 à partir de la bibliothèque de paramètres épidémiologiques fournie par l’Agence européenne pour la sécurité et la santé au travail (ESA). epiparameter. Ces paramètres peuvent être utilisés pour estimer la transmissibilité de cette maladie à l’aide de l’outil EpiNow2 dans les épisodes suivants.

Commençons par examiner le nombre d’entrées actuellement disponibles dans la base de données des base de données des distributions épidémiologiques en epiparameter en utilisant epiparameter_db() pour la distribution épidémiologique epi_name appelé temps de génération avec la chaîne "generation":

R 

epiparameter::epiparameter_db(
  epi_name = "generation"
)

SORTIE 

Returning 3 results that match the criteria (2 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SORTIE 

# List of 3 <epiparameter> objects
Number of diseases: 2
❯ Chikungunya ❯ Influenza
Number of epi parameters: 1
❯ generation time
[[1]]
Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Parameter: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull (days)
Parameters:
  shape: 2.360
  scale: 3.180

[[2]]
Disease: Chikungunya
Pathogen: Chikungunya Virus
Epi Parameter: generation time
Study: Salje H, Cauchemez S, Alera M, Rodriguez-Barraquer I, Thaisomboonsuk B,
Srikiatkhachorn A, Lago C, Villa D, Klungthong C, Tac-An I, Fernandez
S, Velasco J, Roque Jr V, Nisalak A, Macareo L, Levy J, Cummings D,
Yoon I (2015). "Reconstruction of 60 Years of Chikungunya Epidemiology
in the Philippines Demonstrates Episodic and Focal Transmission." _The
Journal of Infectious Diseases_. doi:10.1093/infdis/jiv470
<https://doi.org/10.1093/infdis/jiv470>.
Parameters: <no parameters>
Mean: 14 (days)

[[3]]
Disease: Chikungunya
Pathogen: Chikungunya Virus
Epi Parameter: generation time
Study: Guzzetta G, Vairo F, Mammone A, Lanini S, Poletti P, Manica M, Rosa R,
Caputo B, Solimini A, della Torre A, Scognamiglio P, Zumla A, Ippolito
G, Merler S (2020). "Spatial modes for transmission of chikungunya
virus during a large chikungunya outbreak in Italy: a modeling
analysis." _BMC Medicine_. doi:10.1186/s12916-020-01674-y
<https://doi.org/10.1186/s12916-020-01674-y>.
Distribution: gamma (days)
Parameters:
  shape: 8.633
  scale: 1.447

# ℹ Use `parameter_tbl()` to see a summary table of the parameters.
# ℹ Explore database online at: https://epiverse-trace.github.io/epiparameter/articles/database.html

Dans la bibliothèque des paramètres épidémiologiques, on peut ne pas disposer d’un "generation" pour la maladie qui nous intéresse. À la place, nous pouvons consulter le serial intervalles pour COVID-19. Voyons ce qu’il faut prendre en compte pour cela !

Analyse systématique des données relatives aux agents pathogènes prioritaires

Les données de l’examen systématique des pathogènes prioritaires {epireview} paquet R contient des paramètres sur Ebola, Marburg et Lassa issus de revues systématiques récentes. D’autres agents pathogènes prioritaires sont prévus pour les prochaines versions. Jetez un coup d’œil à cette vignette pour plus d’informations sur l’utilisation de ces paramètres avec epiparameter.

Temps de génération vs intervalle série

Le temps de génération, conjointement avec le nombre de reproduction (\(R\)), peut fournir des indications précieuses sur le taux de croissance probable de l’épidémie et, partant, sur la mise en œuvre de mesuresde lutte. Plus la valeur de \(R\) est grande et/ou plus le temps de génération est court, plus le nombre de nouvelles infections attendues par jour est élevé, et donc plus l’incidence des cas de maladie augmentera rapidement.

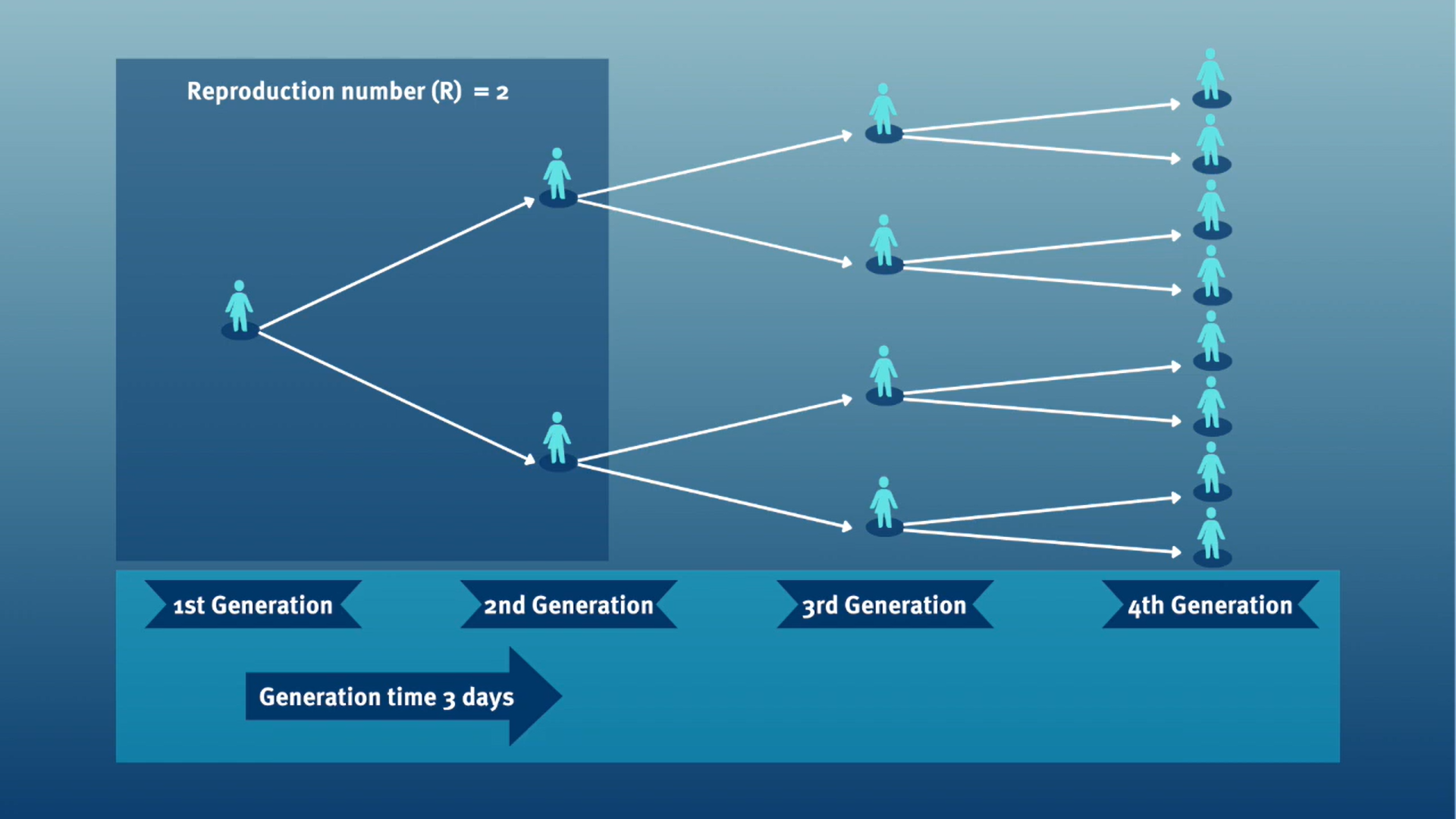
Vidéo du MRC Centre for Global Infectious Disease Analysis, Ep 76. Science In Context - Epi Parameter Review Group avec le Dr Anne Cori (27-07-2023) at https://youtu.be/VvpYHhFDIjI?si=XiUyjmSV1gKNdrrL
Vidéo du MRC Centre for Global Infectious Disease Analysis, Ep 76. Science In Context - Epi Parameter Review Group avec le Dr Anne Cori (27-07-2023) at https://youtu.be/VvpYHhFDIjI?si=XiUyjmSV1gKNdrrL

Pour calculer le nombre effectif de reproduction (\(R_{t}\)), le temps de génération (c’est-à-dire le délai entre une infection et la suivante) est souvent approximée par la distribution des temps de génération. intervalle sériel (c’est-à-dire le délai entre l’apparition des symptômes chez l’infecteur et l’apparition des symptômes chez l’infecté). Cette approximation est fréquemment utilisée car il est plus facile d’observer et d’enregistrer l’apparition des symptômes que le moment exact de l’infection.

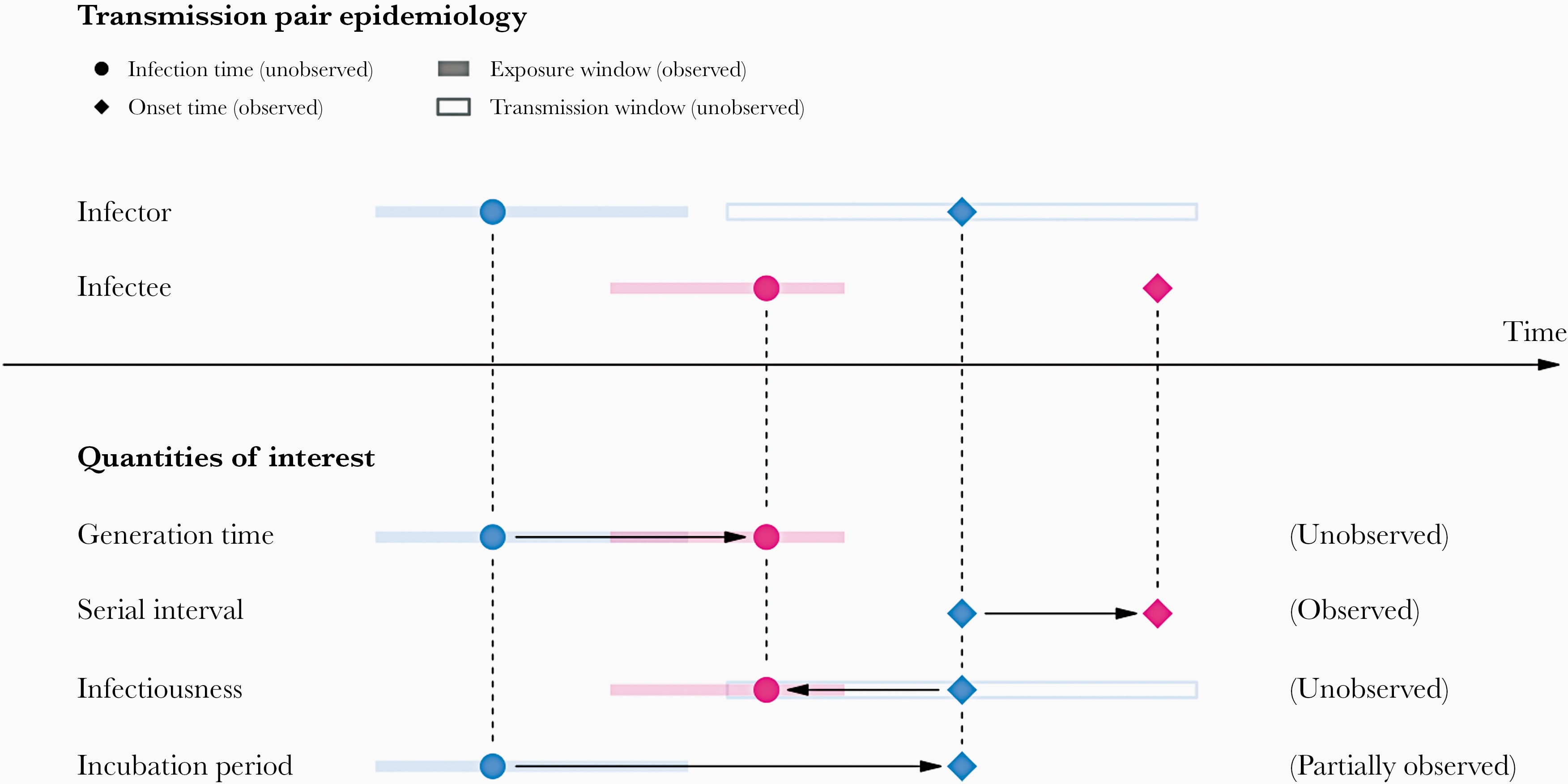
Schéma de la relation entre les différentes périodes de transmission entre un infecteur et un infecté dans une paire de transmission. La fenêtre d’exposition est définie comme l’intervalle de temps entre l’exposition au virus et la fenêtre de transmission est définie comme l’intervalle de temps pour la transmission ultérieure par rapport à la durée de l’infection (Chung Lau et al., 2021).
Schéma de la relation entre les différentes périodes de transmission entre un infecteur et un infecté dans une paire de transmission. La fenêtre d’exposition est définie comme l’intervalle de temps entre l’exposition au virus et la fenêtre de transmission est définie comme l’intervalle de temps pour la transmission ultérieure par rapport à la durée de l’infection (Chung Lau et al., 2021).

Cependant, l’utilisation de la intervalle sériel comme approximation de l’intervalle temps de génération est plus appropriée pour les maladies dans lesquelles l’infectiosité commence après l’apparition des symptômes (Chung Lau et al., 2021). Dans les cas où l’infectiosité commence avant l’apparition des symptômes, les intervalles sériels peuvent avoir des valeurs négatives, ce qui se produit lorsque l’infecté développe des symptômes avant l’infecteur dans une paire de transmission (Nishiura et al., 2020).

Des délais moyens aux distributions de probabilité

Si nous mesurons les intervalle sériel dans des données réelles, nous constatons généralement que toutes les paires de cas n’ont pas le même délai d’apparition. Nous pouvons également observer cette variabilité pour d’autres délais épidémiologiques clés, notamment le délai d’apparition de la maladie. la période d’incubation et période infectieuse.

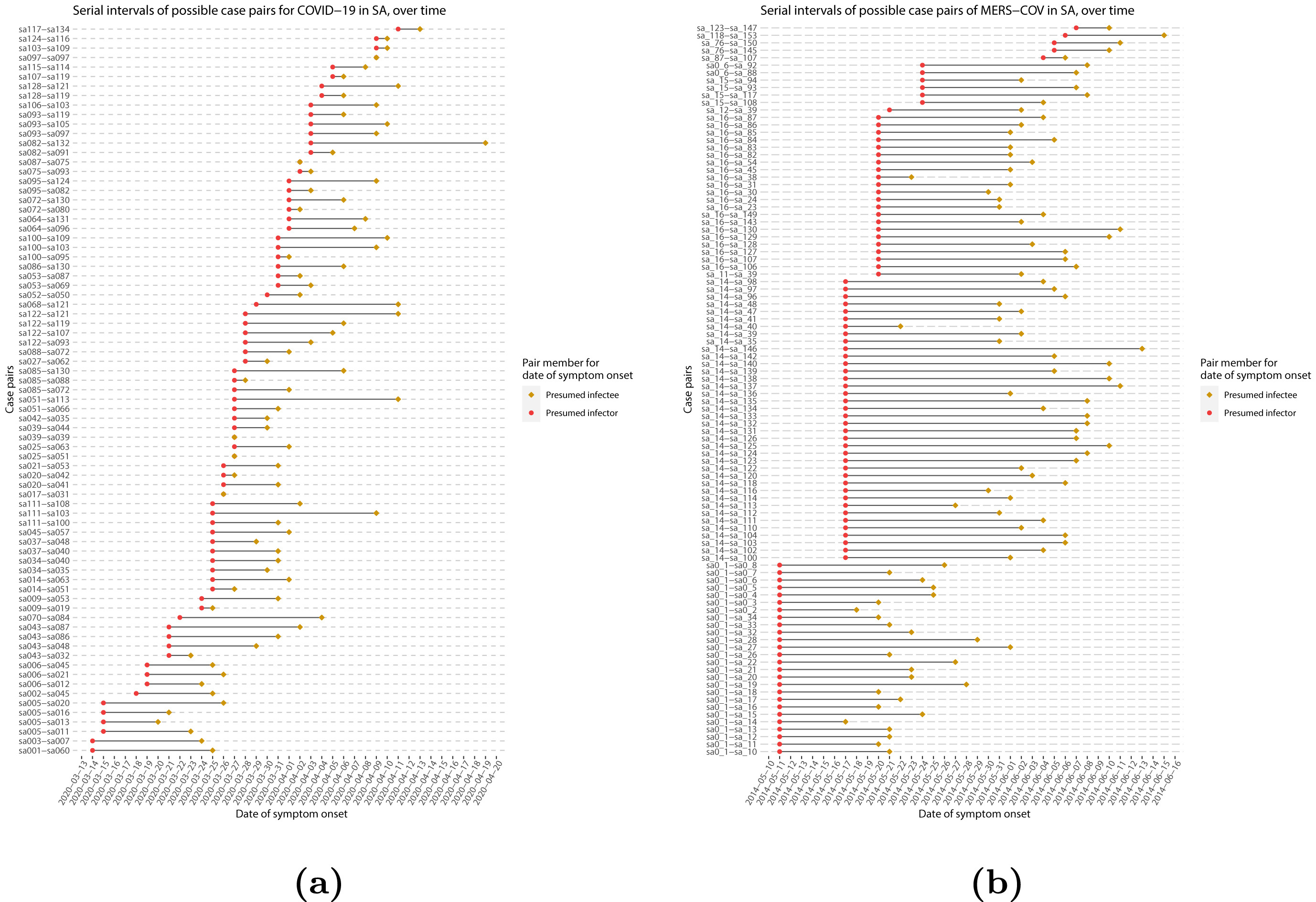
Intervalles sériels des paires de cas possibles dans (a) COVID-19 et (b) MERS-CoV. Les paires représentent un infecteur présumé et son contaminé présumé en fonction de la date d’apparition des symptômes (Althobaity et al., 2022).
Intervalles sériels des paires de cas possibles dans (a) COVID-19 et (b) MERS-CoV. Les paires représentent un infecteur présumé et son contaminé présumé en fonction de la date d’apparition des symptômes (Althobaity et al., 2022).

Pour résumer ces données relatives aux périodes individuelles et aux paires, il est donc utile de quantifier les distribution statistique des délais qui correspondent le mieux aux données, plutôt que de se concentrer sur la moyenne (McFarland et al., 2023).

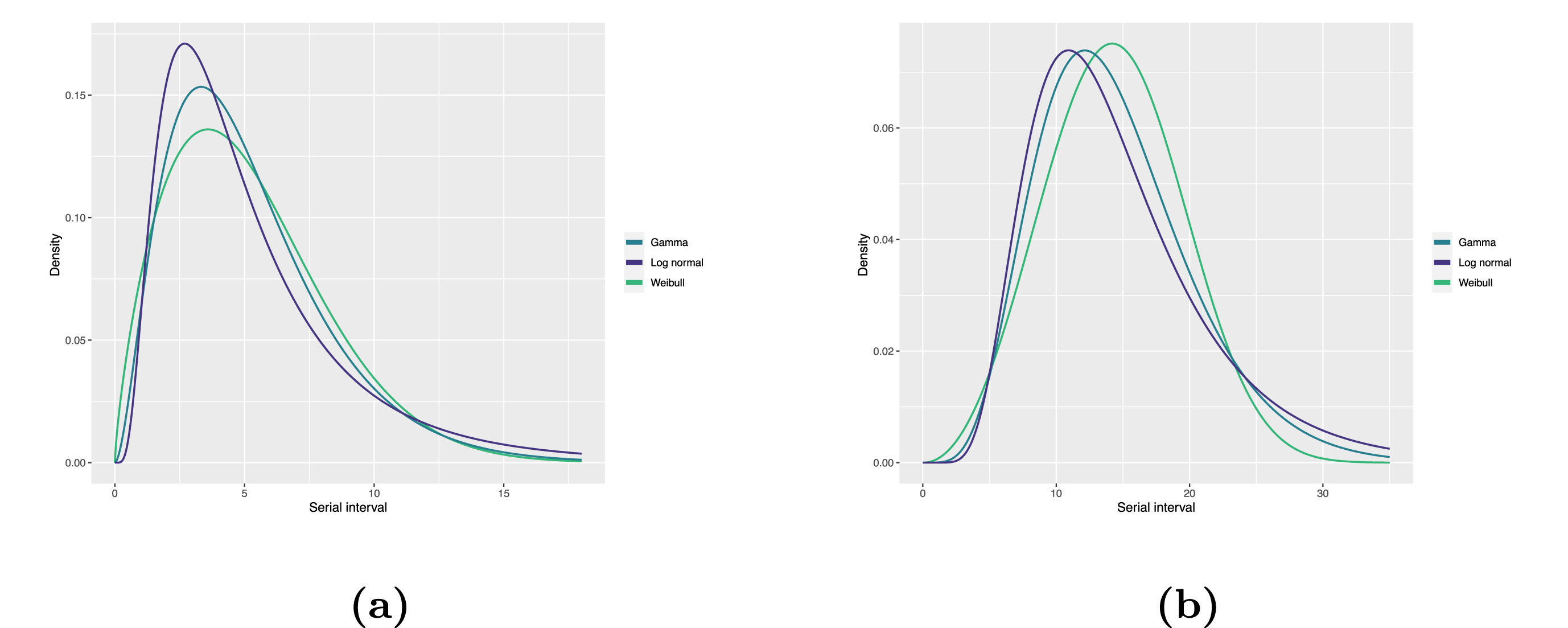
Distribution d’intervalles sériels ajustée pour (a) COVID-19 et (b) MERS-CoV sur la base des paires de transmission signalées en Arabie saoudite. Nous avons ajusté trois distributions couramment utilisées, les distributions Log normal, Gamma et Weibull, respectivement (Althobaity et al., 2022).
Distribution d’intervalles sériels ajustée pour (a) COVID-19 et (b) MERS-CoV sur la base des paires de transmission signalées en Arabie saoudite. Nous avons ajusté trois distributions couramment utilisées, les distributions Log normal, Gamma et Weibull, respectivement (Althobaity et al., 2022).

Les distributions statistiques sont résumées en fonction de leur statistiques sommaires comme l’emplacement (moyenne et percentiles) et l’étendue (variance ou écart-type) de la distribution, ou avec leur paramètres de distribution qui renseignent sur la forme (forme et taux/échelle) de la distribution. Ces valeurs estimées peuvent être rapportées avec leur incertitude (intervalles de confiance à 95 %).

Gamma moyenne forme taux/échelle
MERS-CoV 14.13(13.9-14.7) 6.31(4.88-8.52) 0.43(0.33-0.60)
COVID-19 5.1(5.0-5.5) 2.77(2.09-3.88) 0.53(0.38-0.76)
Weibull moyenne forme taux/échelle
MERS-CoV 14.2(13.3-15.2) 3.07(2.64-3.63) 16.1(15.0-17.1)
COVID-19 5.2(4.6-5.9) 1.74(1.46-2.11) 5.83(5.08-6.67)
Log normal moyenne moyenne-log sd-log
MERS-CoV 14.08(13.1-15.2) 2.58(2.50-2.68) 0.44(0.39-0.5)
COVID-19 5.2(4.2-6.5) 1.45(1.31-1.61) 0.63(0.54-0.74)

Tableau : Estimations des intervalles de série à l’aide des distributions Gamma, Weibull et Log Normal. Les intervalles de confiance à 95 % pour les paramètres de forme et d’échelle (logmoy et sd pour Log Normal) sont indiqués entre parenthèses (Althobaity et al, 2022).

Intervalle de série

Supposons que COVID-19 et le SRAS aient des valeurs de nombre de reproduction similaires et que l’intervalle de série soit proche du temps de génération.

Étant donné l’intervalle sériel des deux infections dans la figure ci-dessous :

  • Laquelle serait la plus difficile à contrôler ?
  • Pourquoi en concluez-vous ainsi ?
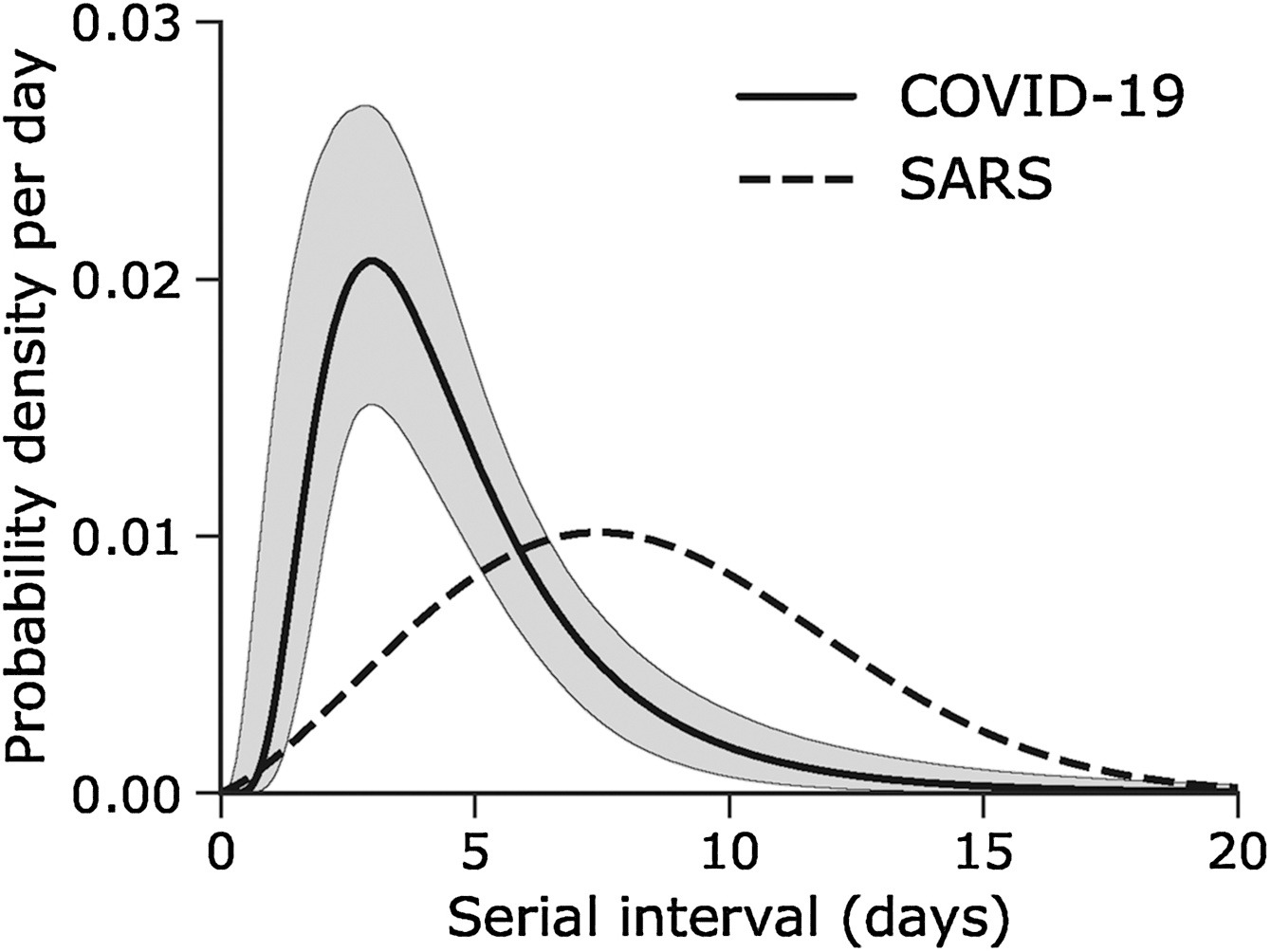
Intervalle en série des infections par le nouveau coronavirus (COVID-19) superposé à une distribution publiée du SRAS. (Nishiura et al., 2020)
Intervalle en série des infections par le nouveau coronavirus (COVID-19) superposé à une distribution publiée du SRAS. (Nishiura et al., 2020)

Le sommet de chaque courbe peut vous renseigner sur l’emplacement de la moyenne de chaque distribution. Une moyenne plus élevée indique un délai plus long entre l’apparition des symptômes chez l’infecteur et l’infecté.

Laquelle serait la plus difficile à contrôler ?

COVID-19

Pourquoi concluez-vous cela ?

L’intervalle sériel moyen de COVID-19 est plus faible. La valeur moyenne approximative de l’intervalle sériel de COVID-19 est d’environ quatre jours, alors que celle du SRAS est d’environ sept jours. Par conséquent, s’il y a beaucoup d’infections dans la population, COVID-19 produira en moyenne plus de nouvelles générations d’infections en moins de temps que le SRAS, en supposant des nombres de reproduction similaires. Cela signifie qu’il faudrait beaucoup plus de ressources pour lutter contre l’épidémie.

Choix des paramètres épidémiologiques

Dans cette section, nous utiliserons epiparameter pour obtenir l’intervalle sériel de COVID-19, comme alternative au temps de génération.

Tout d’abord, voyons combien de paramètres nous avons dans la base de données des distributions épidémiologiques (epiparameter_db()) avec l’option disease nommé covid-19. Exécutez ce code :

R 

epiparameter::epiparameter_db(
  disease = "covid"
)

A partir du epiparameter nous pouvons utiliser le paquet epiparameter_db() pour demander n’importe quel disease ainsi qu’une distribution épidémiologique spécifique (epi_name). Exécutez cette fonction dans votre console :

R 

epiparameter::epiparameter_db(
  disease = "COVID",
  epi_name = "serial"
)

Avec cette combinaison de requêtes, nous obtenons plus d’une distribution des délais (parce que la base de données a plusieurs entrées). Cette sortie est un <epiparameter> objet de classe.

INSENSIBLE À LA CASSE

epiparameter_db est insensible à la casse. Cela signifie que vous pouvez utiliser des chaînes avec des lettres en majuscules ou en minuscules indistinctement. Des chaînes comme "serial", "serial interval" ou "serial_interval" sont également valables.

Comme le suggèrent les résultats, pour résumer une <epiparameter> et obtenir les noms des colonnes de la base de données de paramètres sous-jacente, nous pouvons ajouter l’élément epiparameter::parameter_tbl() au code précédent à l’aide du tuyau %>%:

R 

epiparameter::epiparameter_db(
  disease = "covid",
  epi_name = "serial"
) %>%
  epiparameter::parameter_tbl()

SORTIE 

Returning 4 results that match the criteria (3 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SORTIE 

# Parameter table:
# A data frame:    4 × 7
  disease  pathogen   epi_name        prob_distribution author  year sample_size
  <chr>    <chr>      <chr>           <chr>             <chr>  <dbl>       <dbl>
1 COVID-19 SARS-CoV-2 serial interval <NA>              Alene…  2021        3924
2 COVID-19 SARS-CoV-2 serial interval lnorm             Nishi…  2020          28
3 COVID-19 SARS-CoV-2 serial interval weibull           Nishi…  2020          18
4 COVID-19 SARS-CoV-2 serial interval norm              Yang …  2020         131

Dans le epiparameter::parameter_tbl() nous pouvons également trouver différents types de distributions de probabilité (par exemple, Log-normal, Weibull, Normal).

epiparameter utilise la fonction base R pour les distributions. C’est pourquoi Log normal s’appelle lnorm.

Les entrées avec une valeur manquante (<NA>) dans le prob_distribution sont non paramétrés non paramétrées. Elles présentent des statistiques sommaires (par exemple, une moyenne et un écart type), mais aucune distribution de probabilité n’est spécifiée. Comparez ces deux résultats :

R 

# get an <epiparameter> object
distribution <-
  epiparameter::epiparameter_db(
    disease = "covid",
    epi_name = "serial"
  )

distribution %>%
  # pluck the first entry in the object class <list>
  pluck(1) %>%
  # check if <epiparameter> object have distribution parameters
  is_parameterised()

# check if the second <epiparameter> object
# have distribution parameters
distribution %>%
  pluck(2) %>%
  is_parameterised()

Les entrées paramétrées ont une méthode d’inférence

Comme indiqué dans ?is_parameterised une distribution paramétrée est l’entrée à laquelle est associée une distribution de probabilité fournie par une méthode d’inférence. inference_method comme indiqué dans metadata:

R 

distribution[[1]]$metadata$inference_method
distribution[[2]]$metadata$inference_method
distribution[[4]]$metadata$inference_method

Trouvez vos distributions de délais !

Prenez 2 minutes pour explorer les epiparameter bibliothèque.

Choisissez une maladie d’intérêt (par exemple, la grippe, la rougeole, etc.) et une distribution des délais (par exemple, la période d’incubation, le début de la maladie jusqu’au décès, etc.)

Trouvez :

  • Combien y a-t-il de distributions de délais pour cette maladie ?

  • Combien de types de distribution de probabilité (par exemple, gamma, log normale) y a-t-il pour un délai donné dans cette maladie ?

Posez la question :

  • Reconnaissez-vous les journaux ?

  • La revue de littérature d’{epiparameter} devrait- elle prendre en compte un autre article?

L’analyse epiparameter_db() fonction avec disease compte à elle seule le nombre d’entrées comme :

  • études, et
  • les répartitions des délais.

Les epiparameter_db() avec disease et epi_name obtient une liste de toutes les entrées avec :

  • la citation complète,
  • le type d’une distribution de probabilité, et
  • les valeurs des paramètres de la distribution.

La combinaison de epiparameter_db() plus parameter_tbl() permet d’obtenir un cadre de données de toutes les entrées avec des colonnes comme :

  • les type de la distribution de probabilité par délai, et
  • l’auteur et l’année de l’étude.

Nous avons choisi d’explorer les distributions des délais d’Ebola :

R 

# we expect 16 delay distributions for Ebola
epiparameter::epiparameter_db(
  disease = "ebola"
)

SORTIE 

Returning 17 results that match the criteria (17 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SORTIE 

# List of 17 <epiparameter> objects
Number of diseases: 1
❯ Ebola Virus Disease
Number of epi parameters: 9
❯ hospitalisation to death ❯ hospitalisation to discharge ❯ incubation period ❯ notification to death ❯ notification to discharge ❯ offspring distribution ❯ onset to death ❯ onset to discharge ❯ serial interval
[[1]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Parameter: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom (No units)
Parameters:
  mean: 1.500
  dispersion: 5.100

[[2]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Parameter: incubation period
Study: Eichner M, Dowell S, Firese N (2011). "Incubation period of ebola
hemorrhagic virus subtype zaire." _Osong Public Health and Research
Perspectives_. doi:10.1016/j.phrp.2011.04.001
<https://doi.org/10.1016/j.phrp.2011.04.001>.
Distribution: lnorm (days)
Parameters:
  meanlog: 2.487
  sdlog: 0.330

[[3]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Parameter: onset to death
Study: The Ebola Outbreak Epidemiology Team, Barry A, Ahuka-Mundeke S, Ali
Ahmed Y, Allarangar Y, Anoko J, Archer B, Abedi A, Bagaria J, Belizaire
M, Bhatia S, Bokenge T, Bruni E, Cori A, Dabire E, Diallo A, Diallo B,
Donnelly C, Dorigatti I, Dorji T, Waeber A, Fall I, Ferguson N,
FitzJohn R, Tengomo G, Formenty P, Forna A, Fortin A, Garske T,
Gaythorpe K, Gurry C, Hamblion E, Djingarey M, Haskew C, Hugonnet S,
Imai N, Impouma B, Kabongo G, Kalenga O, Kibangou E, Lee T, Lukoya C,
Ly O, Makiala-Mandanda S, Mamba A, Mbala-Kingebeni P, Mboussou F,
Mlanda T, Makuma V, Morgan O, Mulumba A, Kakoni P, Mukadi-Bamuleka D,
Muyembe J, Bathé N, Ndumbi Ngamala P, Ngom R, Ngoy G, Nouvellet P, Nsio
J, Ousman K, Peron E, Polonsky J, Ryan M, Touré A, Towner R, Tshapenda
G, Van De Weerdt R, Van Kerkhove M, Wendland A, Yao N, Yoti Z, Yuma E,
Kalambayi Kabamba G, Mwati J, Mbuy G, Lubula L, Mutombo A, Mavila O,
Lay Y, Kitenge E (2018). "Outbreak of Ebola virus disease in the
Democratic Republic of the Congo, April–May, 2018: an epidemiological
study." _The Lancet_. doi:10.1016/S0140-6736(18)31387-4
<https://doi.org/10.1016/S0140-6736%2818%2931387-4>.
Distribution: gamma (days)
Parameters:
  shape: 2.400
  scale: 3.333

# ℹ 14 more elements
# ℹ Use `print(n = ...)` to see more elements.
# ℹ Use `parameter_tbl()` to see a summary table of the parameters.
# ℹ Explore database online at: https://epiverse-trace.github.io/epiparameter/articles/database.html

Maintenant, à partir de la sortie de epiparameter::epiparameter_db() Quelle est la distribution de la descendance?

Nous choisissons de trouver les périodes d’incubation d’Ebola. Cette sortie liste tous les articles et paramètres trouvés. Exécutez-la localement si nécessaire :

R 

epiparameter::epiparameter_db(
  disease = "ebola",
  epi_name = "incubation"
)

Nous utilisons parameter_tbl() pour obtenir un récapitulatif de toutes les données :

R 

# we expect 2 different types of delay distributions
# for ebola incubation period
epiparameter::epiparameter_db(
  disease = "ebola",
  epi_name = "incubation"
) %>%
  parameter_tbl()

SORTIE 

Returning 5 results that match the criteria (5 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SORTIE 

# Parameter table:
# A data frame:    5 × 7
  disease           pathogen epi_name prob_distribution author  year sample_size
  <chr>             <chr>    <chr>    <chr>             <chr>  <dbl>       <dbl>
1 Ebola Virus Dise… Ebola V… incubat… lnorm             Eichn…  2011         196
2 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015        1798
3 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015          49
4 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015         957
5 Ebola Virus Dise… Ebola V… incubat… gamma             WHO E…  2015         792

Nous trouvons deux types de distributions de probabilités pour cette requête : log normale et gamma.

Comment le epiparameter collecte-t-elle et examine-t-elle la littérature évaluée par les pairs ? Nous vous invitons à lire la vignette sur “Protocole de collecte et de synthèse des données!

Sélectionnez une distribution unique

Les epiparameter::epiparameter_db() fonctionne comme une fonction de filtrage ou de sous-ensemble. Nous pouvons utiliser la fonction author pour conserver Hiroshi Nishiura ou l’argument subset pour conserver les paramètres des études dont la taille de l’échantillon est supérieure à 10 :

R 

epiparameter::epiparameter_db(
  disease = "covid",
  epi_name = "serial",
  author = "Nishiura",
  subset = sample_size > 10
) %>%
  epiparameter::parameter_tbl()

Nous obtenons toujours plus d’un paramètre épidémiologique. Au lieu de cela, nous pouvons définir l’argument single_epiparameter à TRUE pour n’en obtenir qu’un seul :

R 

epiparameter::epiparameter_db(
  disease = "covid",
  epi_name = "serial",
  single_epiparameter = TRUE
)

SORTIE 

Using Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>..
To retrieve the citation use the 'get_citation' function

SORTIE 

Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Parameter: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: lnorm (days)
Parameters:
  meanlog: 1.386
  sdlog: 0.568

Comment fonctionne “single_epiparameter” ?

En regardant la documentation d’aide pour ?epiparameter::epiparameter_db():

  • Si plusieurs entrées correspondent aux arguments fournis et que single_epiparameter = TRUE alors l’entrée paramétrée <epiparameter> avec l’entrée la plus grande taille d’échantillon sera renvoyée.
  • Si plusieurs entrées sont égales après ce tri, l’option première entrée de la liste sera retournée.

Qu’est-ce qu’un paramétré <epiparameter>? Regardez ?is_parameterised.

Attribuons cette <epiparameter> à l’objet de classe covid_serialint objet.

R 

covid_serialint <-
  epiparameter::epiparameter_db(
    disease = "covid",
    epi_name = "serial",
    single_epiparameter = TRUE
  )

Vous pouvez utiliser plot() pour <epiparameter> pour visualiser les objets :

  • le Fonction de densité de probabilité (PDF) et
  • la Fonction de distribution cumulative (FDC).

R 

# plot <epiparameter> object
plot(covid_serialint)

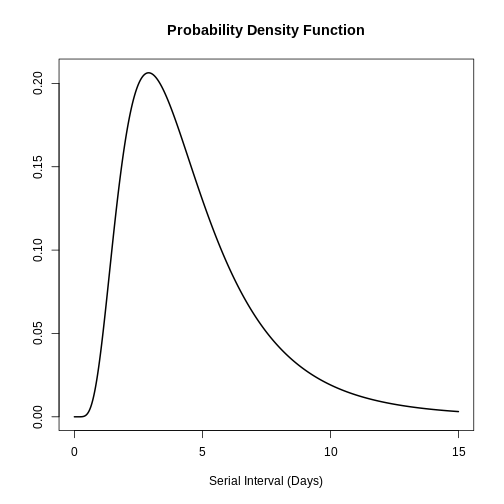
Avec la xlim vous pouvez modifier la durée ou le nombre de jours de la période d’essai. x de l’axe. Découvrez à quoi cela ressemble :

R 

# plot <epiparameter> object
plot(covid_serialint, xlim = c(1, 60))

Extrayez les statistiques récapitulatives

Nous pouvons obtenir les mean et l’écart-type (sd) à partir de ce <epiparameter> plonger dans le summary_stats l’objet :

R 

# get the mean
covid_serialint$summary_stats$mean

SORTIE 

[1] 4.7

Nous avons maintenant un paramètre épidémiologique que nous pouvons réutiliser ! Étant donné que l’objet covid_serialint est un lnorm ou une distribution log-normale, nous pouvons remplacer le statistiques sommaires que nous introduisons dans la base de données EpiNow2::LogNormal() dans la fonction

R 

generation_time <- 
  EpiNow2::LogNormal(
    mean = covid_serialint$summary_stats$mean, # replaced!
    sd = covid_serialint$summary_stats$sd, # replaced!
    max = 20
  )

Dans le prochain épisode, nous apprendrons à utiliser la fonction EpiNow2 pour spécifier correctement les distributions et estimer la transmissibilité. Ensuite, comment utiliser fonctions de distribution pour obtenir une valeur maximale (max) pour EpiNow2::LogNormal() et utiliser epiparameter dans votre analyse.

Distributions logarithmiques normales

Si vous avez besoin de la distribution log-normale de la distribution logarithmique au lieu des statistiques sommaires, vous pouvez utiliser epiparameter::get_parameters():

R 

covid_serialint_parameters <-
  epiparameter::get_parameters(covid_serialint)

covid_serialint_parameters

SORTIE 

  meanlog     sdlog
1.3862617 0.5679803

Cela permet d’obtenir un vecteur de classe <numeric> prêt à être utilisé comme entrée pour n’importe quel autre paquet !

Considérez que {EpiNow2} acceptent également les paramètres de distribution comme données d’entrée. Exécutez ?EpiNow2::LogNormal pour lire les Distributions de probabilités de référence.

Défis

L’intervalle sériel d’Ebola

Prenez 1 minute pour :

Accédez à l’intervalle de série Ebola avec la taille d’échantillon la plus élevée.

Réponse :

  • Qu’est-ce que le sd de la distribution épidémiologique ?

  • Quelle est la sample_size utilisée dans cette étude ?

Utilisez le $ et l’opérateur tabulation ou ↹ pour les explorer sous la forme d’une liste extensible :

R 

covid_serialint$

Utilisez la touche str() pour afficher la structure du <epiparameter> R.

Le paramètre de gravité d’Ebola

Un paramètre de gravité tel que la durée de l’hospitalisation pourrait compléter les informations nécessaires sur la capacité d’accueil en cas d’épidémie (Cori et al.).

Pour Ebola :

  • Qu’est-ce qui est rapporté ? estimation ponctuelle de la durée moyenne des soins de santé et de l’isolement des cas ?

Un délai informatif devrait mesurer le temps écoulé entre l’apparition des symptômes et la guérison ou le décès.

Trouver un moyen d’accéder à l’ensemble epiparameter base de données et de trouver comment ce délai peut être stocké. Les parameter_tbl() est un tableau de données.

R 

# one way to get the list of all the available parameters
epiparameter_db(disease = "all") %>%
  parameter_tbl() %>%
  as_tibble() %>%
  distinct(epi_name)

SORTIE 

Returning 125 results that match the criteria (100 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' function

SORTIE 

# A tibble: 13 × 1
   epi_name
   <chr>
 1 incubation period
 2 serial interval
 3 generation time
 4 onset to death
 5 offspring distribution
 6 hospitalisation to death
 7 hospitalisation to discharge
 8 notification to death
 9 notification to discharge
10 onset to discharge
11 onset to hospitalisation
12 onset to ventilation
13 case fatality risk

R 

ebola_severity <- epiparameter_db(
  disease = "ebola",
  epi_name = "onset to discharge"
)

SORTIE 

Returning 1 results that match the criteria (1 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' function

R 

# point estimate
ebola_severity$summary_stats$mean

SORTIE 

[1] 15.1

Vérifiez que pour certains epiparameter vous disposerez également de l’élément incertitude autour de la estimation ponctuelle de chaque statistique sommaire :

R 

# 95% confidence intervals
ebola_severity$summary_stats$mean_ci

SORTIE 

[1] 95

R 

# limits of the confidence intervals
ebola_severity$summary_stats$mean_ci_limits

SORTIE 

[1] 14.6 15.6

La distribution zoo

Explorez cette shinyapp appelée Le zoo de la distribution!

Suivez les étapes suivantes pour reproduire la forme de la distribution d’intervalles sériels COVID à partir de epiparameter (covid_serialint objet) :

  1. Accédez au https://ben18785.shinyapps.io/distribution-zoo/ site web de l’application shiny,
  2. Allez dans le panneau de gauche,
  3. Gardez l’option Catégorie de distribution: Continuous Univariate,
  4. Sélectionnez un nouveau Type de distribution: Log-Normal,
  5. Déplacez le curseurs c’est-à-dire l’élément de contrôle graphique qui vous permet d’ajuster une valeur en déplaçant une poignée le long d’une piste ou d’une barre horizontale jusqu’à l’emplacement du curseur. covid_serialint paramètres.

Reproduisez ces éléments à l’aide de l’outil distribution et tous ses éléments de liste : [[2]], [[3]] et [[4]]. Explorez comment la forme d’une distribution change lorsque ses paramètres changent.

Partagez à propos de :

  • Quelles sont les autres fonctionnalités du site web que vous trouvez utiles ?

Points clés

  • Utilisez epiparameter pour accéder au catalogue des distributions de délais épidémiologiques.
  • Utilisez cette fonction pour accéder au catalogue de la littérature sur les distributions de délais épidémiologiques. epiparameter_db() pour sélectionner une seule distribution de délais.
  • Utilisez cette option pour sélectionner les distributions à délais unique. parameter_tbl() pour obtenir une vue d’ensemble des distributions de délais multiples.
  • Réutiliser les estimations connues pour une maladie inconnue au début d’une épidémie lorsqu’il n’y a pas de données sur la recherche des contacts.