Estima la fuerza de infección a partir de encuestas serológicas usando serofoi
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo estimar retrospectivamente la Fuerza de Infección de un patógeno a partir de encuestas serológicas poblacionales de prevalencia desagregadas por edad mediante la implementación de modelos Bayesianos usando serofoi?
Objetivos
Al final de este taller usted podrá:
Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.
1. Introducción
serofoi es un paquete de R para estimar retrospectivamente la Fuerza de Infección de un patógeno a partir de encuestas serológicas poblacionales de prevalencia desagregadas por edad mediante la implementación de modelos Bayesianos. Para ello, serofoi utiliza el paquete Rstan, que proporciona una interfaz para el lenguaje de programación estadística Stan, mediante el cual se implementan métodos de Monte-Carlo basados en cadenas de Markov.
Como un caso particular, estudiaremos un brote de Chikungunya, una enfermedad viral descubierta en Tanzania en el año 1952 que se caracteriza por causar fuertes fiebres, dolor articular, jaqueca, sarpullidos, entre otros síntomas. Desde el año 2013, casos de esta enfermedad comenzaron a ser reportados en América y desde entonces la enfermedad ha sido endémica en varios países latinoamericanos. Durante este tutorial, vamos a analizar una encuesta serológica realizada entre octubre y diciembre de 2015 en Bahía, Brasil, la cual fue realizada poco tiempo después de una epidemia de esta enfermedad, con el fin de caracterizar los patrones endémicos o epidémicos en la zona.
2. Objetivos
Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.
3. Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Encuestas serologícas (sero)
Fuerza de infección (foi)
Modelos serocatalíticos
Estadística Bayesiana
Visualización e interpretación de resultados de modelos FoI
La Fuerza de Infección (FoI, por sus siglas en inglés), también conocida cómo la tasa de riesgo o la presión de infección, representa la tasa a la que los individuos susceptibles se infectan dado que estuvieron expuestos a un patógeno. En otras palabras, la FoI cuantifica el riesgo de que un individuo susceptible se infecte en un periodo de tiempo.
Como veremos a continuación, este concepto es clave en el modelamiento de enfermedades infecciosas. Para ilustrar el concepto, consideremos una población expuesta a un patógeno y llamemos \(P(t)\) a la proporción de individuos que han sido infectados al tiempo \(t\). Suponiendo que no hay sero-reversión, la cantidad \(1 - P(t)\) representa la cantidad de individuos susceptibles a la enfermedad, de tal forma que la velocidad de infección está dada por:
\[ \tag{1} \frac{dP(t)}{d t} = \lambda(t) (1- P(t)), \]
en donde \(\lambda(t)\) representa la tasa a la que los individuos susceptibles se infectan por unidad de tiempo (días, meses, años, …), es decir la FoI. La ecuación diferencial (1) se asemeja a la de una reacción química en donde \(P(t)\) representa la proporción de sustrato que no ha entrado en contacto con un reactivo catalítico, por lo que este tipo de modelos se conocen como modelos serocatalíticos (Muench, 1959).
A pesar de la simpleza del modelo representado por la ecuación (1), en comparación con modelos compartimentales (por ejemplo), la dificultad para conocer una condición inicial para la seropositividad en algún punto del pasado imposibilita su uso práctico. Para sortear esta limitación, es común aplicar el modelo para cohortes de edad en lugar de para el total de la población. Para ello, etiquetemos cada cohorte de edad de acuerdo con su año de nacimiento \(\tau\), y supongamos que los individuos son seronegativos al nacer:
\[ \frac{dP^\tau (t)}{dt} = \lambda(t) (1 - P^\tau(t)). \]
Con condiciones iniciales dadas por \(P^\tau(\tau) = 0\). Esta ecuación se puede resolver analíticamente, dando como resultado (Hens et al, 2010):
\[ P^{\tau} (t) = 1 - \exp\left(-\int_{\tau}^{t} \lambda (t') dt' \right). \]
Suponiendo que la FoI se mantiene constante a lo largo de cada año, la versión discreta de esta ecuación es:
\[ \tag{2} P^\tau(t) = 1 - \exp\left(-\sum_{i = \tau}^{t} \lambda_i \right), \]
Como un ejemplo, consideremos la FoI representada en la siguiente figura:
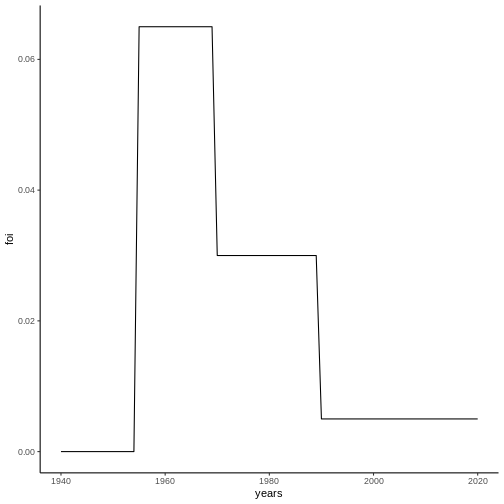
A partir de esta FoI, es posible calcular la seroprevalencia para distintas cohortes por medio de la ecuación (2):
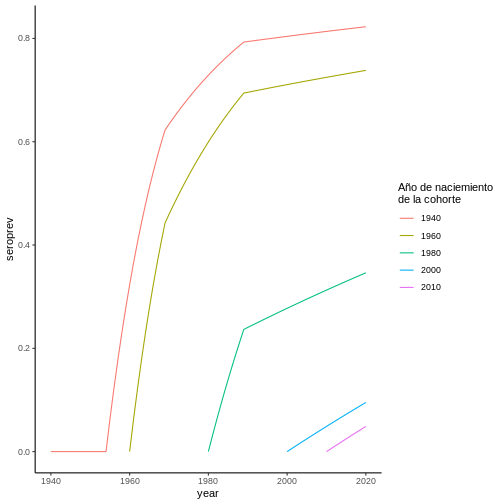
Cuando conocemos los datos de una encuesta serológica, la información a la que tenemos acceso es a una fotografía de la seroprevalencia en el momento su realización \(t_{sur}\) como función de la edad de los individuos en ese momento, la cual coincide con la ecuación (2) ya que los individuos envejecen al mismo ritmo al que pasa el tiempo; es decir:
\[ \tag{3} P^{t_{sur}}(a^\tau) = 1 - \exp\left(-\sum_{i = \tau}^{t_{sur}} \lambda_i \right). \]
En el caso del ejemplo, esto nos da la siguiente gráfica:
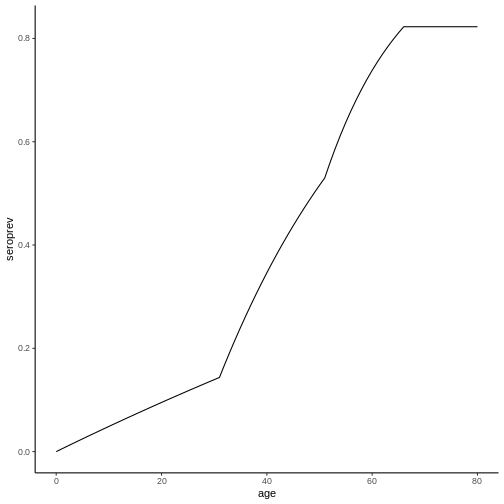
Note que los valores de seroprevalencia de cada edad en esta gráfica corresponden a los valores de seroprevalencia al momento de la encuesta (2020) en la gráfica anterior.
La misión que cumple serofoi es estimar la fuerza de infección histórica \(\lambda(t)\) a partir de esta fotografía del perfil serológico de la población al momento de la encuesta. para lo cual se requieren encuestas serológicas que cumplan con los siguientes criterios de inclusión:
- Basadas en poblacionales (no hospitalaria).
- Estudio de tipo transversal (un solo tiempo) .
- Que indique la prueba diagnóstica utilizada.
- Que identifique la edad del paciente en el momento de la encuesta.
En casos donde la FoI pueda considerarse constante, la ecuación (3) da como resultado:
\[ \tag{4} P_{sur}(a^\tau(t_{sur})) = 1 - \exp (-\lambda a^\tau), \]
en donde se tuvo en cuenta qué, al momento de la introducción del patógeno (\(t = 0\)), la proporción de individuos infectados fue \(P(0) = 0\) (condición inicial). Note que el término de la suma en la ecuación (3) da como resultado la edad de cada cohorte al considerar la fuerza de infección constante.
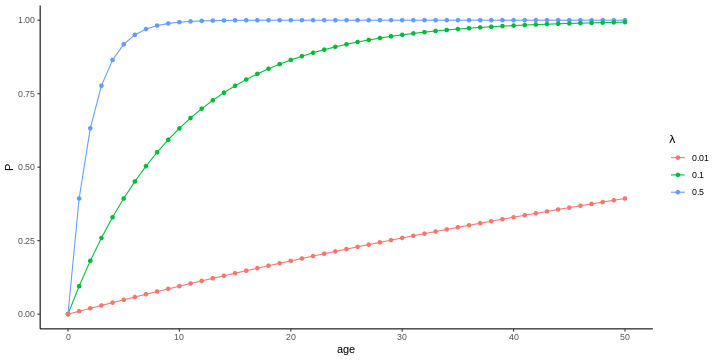
Figura 1. Curvas de prevalencia en función de la edad para distintos valores de FoI constante.
En este ejemplo hemos escogido, por simplicidad, que la FoI fuese constante; sin embargo, este no es necesariamente el caso. Identificar si la FoI sigue una tendencia constante o variante en el tiempo puede ser de vital importancia para la identificación y caracterización de la propagación de una enfermedad. Es acá donde el paquete de Rserofoi juega un papel importante, ya que este permite estimar retrospectivamente la FoI de un patógeno, recuperando así su evolución temporal, por medio de modelos Bayesianos pre-establecidos.
Los modelos actuales del paquete serofoi asumen los siguientes supuestos biológicos:
- No hay sero-reversión (sin pérdida de inmunidad).
- La FoI no depende de la edad.
- Bajos o nulos niveles de migración en las poblaciones.
- Diferencias pequeñas entre las tasas de mortalidad de susceptibles e infectados.
3.2. Modelos Bayesianos
A diferencia del enfoque frecuentista, donde la probabilidad se asocia con la frecuencia relativa de la ocurrencia de los eventos, la estadística Bayesiana se basa en el uso de la probabilidad condicional de los eventos respecto al conocimiento (o estado de información) que podamos tener sobre los datos o sobre los parámetros que queramos estimar.
Por lo general, cuando proponemos un modelo lo que buscamos es disminuir la incertidumbre sobre algún parámetro, de tal forma que nos aproximemos a su valor tan óptimamente como nos lo permita nuestro conocimiento previo del fenómeno y de las mediciones realizadas (datos).
La inferencia Bayesiana se sustenta en el teorema de Bayes, el cual establece que: dado un conjunto de datos \(\vec{y} = (y_1, …, y_N)\), el cual representa un único evento, y la variable aleatoria \(\theta\), que representa un parámetro de interés para nosotros (en nuestro caso, la FoI \(\lambda\)), la distribución de probabilidad conjunta de las variables aleatorias asociadas está dada por:
\[ \tag{4} p(\vec{y}, \theta) = p(\vec{y} | \theta) p(\theta) = p(\theta | \vec{y}) p(\vec{y}), \]
de donde se desprende la distribución aposteriori de \(\theta\), es decir una versión actualizada de la distribución de probabilidad de la FoI condicionada a nuestros datos:
\[\tag{5} p(\theta, \vec{y}) = \frac{p(\vec{y} | \theta) p(\theta)}{p(\vec{y})}, \]
La distribución \(p(\vec{y} | \theta)\), que corresponde a la información interna a los datos condicionada al valor del parámetro \(\theta\), suele estar determinada por la naturaleza del experimento: no es lo mismo escoger pelotas dentro de una caja reemplazándolas que dejándolas por fuera de la caja (e.g.). En el caso particular de la FoI, contamos con datos como el número total de encuestas por edad y el número de casos positivos, por lo que es razonable asignar una distribución binomial a la probabilidad, como veremos a continuación.
3.3.1. Modelo FoI constante
En nuestro caso particular, el parámetro que queremos estimar es la FoI (\(\lambda\)). La distribución de probabilidad apriori de \(\lambda\) representa nuestras suposiciones informadas o el conocimiento previo que tengamos sobre el comportamiento de la FoI. En este contexto, el estado de mínima información sobre \(\lambda\) está representado por una distribución uniforme:
\[\tag{6} \lambda \sim U(0, 2), \]
lo que significa que partimos de la premisa de que todos los valores de la fuerza de infección entre \(0\) y \(2\) son igualmente probables. Por otro lado, de la teoría de modelos sero-catalíticos sabemos que la seroprevalencia en un año dado está descrita por un proceso cumulativo con la edad (Hens et al, 2010):
\[\tag{7} P(a, t) = 1 - \exp\left( -\sum_{i=t-a+1}^{t} \lambda_i \right), \]
en donde \(\lambda_i\) corresponde a la FoI al tiempo \(t\). Como en este caso la FoI es constante, la ec. (7) se reduce a:
\[\tag{8} P(a, t) = 1 - \exp\left( -\lambda a \right), \]
Si \(n(a, t_{sur})\) es el número de muestras positivas por edad obtenidas en un estudio serológico desarrollado en el año \(t_{sur}\), entonces podemos estimar la distribución de los casos seropositivos por edad condicionada al valor de \(\lambda\) como una distribución binomial:
\[\tag{9} p(a, t) \sim Binom(n(a, t), P(a, t)) \\ \lambda \sim U(0, 2) \]
3.3.2. Modelo FOI dependientes del tiempo
Actualmente, serofoi permite la implementación de dos modelos dependientes del tiempo: uno de variación lenta de la FoI (time) y otro de variación rápida (time-log) de la FoI.
Cada uno de ellos se basa en distintas distribuciones previas para \(\lambda\), las cuales se muestran en la tabla 1.
| Model Type | Logarithmic Scale | Probability of positive case at age \(a\) | Prior distribution |
|---|---|---|---|
"constant" |
FALSE |
\(\sim binom(n(a,t), P(a,t))\) | \(\lambda\sim uniform(0,2)\) |
"time" |
FALSE |
\(\sim binom(n(a,t), P(a,t))\) | \(\lambda\sim normal(\lambda(t-1),\sigma)\ \lambda(t=1)\sim normal(0,1)\) |
"time" |
TRUE |
\(\sim binom(n(a,t), P(a,t))\) | \(\lambda\sim normal(log(\lambda(t-1)),\sigma)\ \lambda(t=1)\sim normal(-6,4)\) |
Tabla 1. Distribuciones a priori de los distintos modelos soportados por serofoi. \(\sigma\) representa la desviación estándar.
Como se puede observar, las distribuciones previas de \(\lambda\) en ambos casos están dadas por
distribuciones Gaussianas con desviación estándar \(\sigma\) y centradas en \(\lambda\) (modelo de variación lenta -
"time") y \(\log(\lambda)\) (modelo de variación rápida
- "time" con is_log_foi = TRUE). De esta
manera, la FoI en un tiempo \(t\) está
distribuida de acuerdo a una distribución normal alrededor del valor que
esta tenía en el tiempo inmediatamente anterior. El logaritmo en el
modelo \(\log(\lambda)\) permite
identificar cambios drásticos en la tendencia temporal de la FoI.
4. Contenido del taller
4.1 Instalación de serofoi
Previo a la instalación de serofoi, cree un proyecto en R en la carpeta de su escogencia en su máquina local; esto con el fin de organizar el espacio de trabajo en donde se guardarán los códigos que desarrolle durante la sesión.
Antes de realizar la instalación de serofoi, es necesario instalar y configurar C++ Toolchain (instrucciones para windows/ mac/ linux). Después de haber configurado C++ Toolchain, ejecute las siguientes líneas de código para instalar el paquete:
R
if(!require("pak")) install.packages("pak")
pak::pak("epiverse-trace/serofoi")
Opcionalmente, es posible modificar la configuración de R para que los modelos a implementar corran en paralelo, aprovechando los núcleos del procesador de su computador. Esto tiene el efecto de disminuir los tiempos de cómputo de las implementaciones en Stan. Para activar esta opción ejecute:
R
options(mc.cores=parallel::detectCores())
Finalmente, cargue el paquete ejecutando:
R
library(serofoi)
4.2 Caso de uso: Chikungunya
En esta sección vamos a analizar una encuesta serológica realizada
entre octubre y diciembre de 2015 en Bahía, Brasil, la cual fue
realizada poco tiempo después de una epidemia de esta enfermedad en la
zona. Nuestro objetivo es caracterizar la propagación de la enfermedad
por medio de la implementación de los distintos modelos y determinar
cuál de estos describe mejor la situación. Primero, carguemos y
preparemos los datos que utilizaremos en este análisis. La
basechik2015 contiene los datos correspondientes a esta
encuesta serológica:
R
data(chik2015)
chik2015
SALIDA
survey_year n_sample n_seropositive age_min age_max
1 2015 144 63 40 59
2 2015 148 69 60 79
3 2015 45 17 1 19
4 2015 109 55 20 39Para correr el modelo de FoI constante y visualizar los resultados del mismo, corra las siguientes líneas de código:
R
chik_constant <- fit_seromodel(serosurvey = chik2015,
model_type = "constant",
iter = 1000)
chik_constant_plot <- plot_seromodel(seromodel = chik_constant,
serosurvey = chik2015,
size_text = 12)
Ahora, corra los modelos dependientes del tiempo con
iter =1500. Luego visualice conjuntamente las tres gráficas
por medio de la función plot_grid() del paquete
cowplot:
R
install.packages("cowplot")
cowplot::plot_grid(chik_constant_plot,
chik_normal_plot,
chik_normal_log_plot,
ncol = 3)
NOTA: Debido a que el número de trayectorias es relativamente alto, con el fin de asegurar la convergencia de los modelos, el tiempo de cómputo de los modelos dependientes del tiempo puede tardar varios minutos.
Pista: Debería obtener la siguiente gráfica:
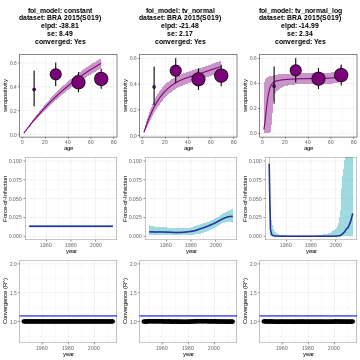
El poder predictivo de un modelo Bayesiano se puede caracterizar por medio del elpd(Expected Log Predictive Density). El modelo que mejor ajusta la encuesta epidemiológica es aquel que tiene valores más altos deelpd y valores más bajos de error estándar (se).
5. Reflexión
Discusión
Según los criterios explicados anteriormente, responda:
¿Cuál de los tres modelos se ajusta mejor a esta encuesta serológica?
¿Cómo interpreta estos resultados?
Desafío
Desafío: caso simulado
En los pasados 3 años, en zonas rurales fronterizas de dos países contíguos de América Latina se han identificado casos de encefalitis de origen desconocido en humanos. Algunos de estos casos de encefalitis han requerido hospitalización e incluso se han reportado fallecimientos. Los habitantes de la zona también señalan que una epidemia similar de casos en que las personas“perdían la conciencia después de una fuerte fiebre” habían ocurrido en la misma zona algunas décadas atrás.
En 2023 se realizó una encuesta de seroprevalencia para los 4 virus con mayor sospecha de estar circulando en la zona fronteriza donde se presentan los casos de encefalitis. Estos 4 virus son biológicamente distintivos entre ellos, es decir no tienen reacción cruzada en las pruebas serológicas. Para cada uno de estos virus, la encuesta de seroprevalencia recoge una muestra probabilística y representativa de la población de residentes de la zona con un total de 1306 individuos muestreados entre 1 y 60 años de edad. Los resultados de las pruebas serológicas para cada virus se presentan como número total de personas muestreadas por cada grupo de edad y número de personas positivas para anticuerpos IgG contra uno de los 4 virus en ese grupo de edad.
El desafío consiste en que usted y su grupo deben identificar cuál o cuáles de los 4 virus es el más probablemente implicado en esta emergencia de encefalitis viral haciendo uso de la librería serofoi.
Exploración de los datos y visualización de la seroprevalencia (30 min)
Los datos de las 4 encuestas vienen en archivos . RDS independientes que podrá encontrar en estos enlaces:
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_01.RDS
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_02.RDS
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_03.RDS
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_04.RDS
Lea los datos haciendo uso de la función readRDS(). En
esta etapa del desafío se espera que:
Exploren la estructura de los datos y analicen las características generales de una encuesta serológica transversal desagregada por edad.
Preparen los datos para el proceso de visualización por medio de funciones del paquete dplyr.
Visualicen la seroprevalencia de cada encuesta por medio de la función
plot_seroprev()y analicen cualitativamente su tendencia en cada caso.
Estimación de la fuerza de infección histórica (30 min)
Implemente los modelos que considere pertinentes a cada encuesta serológica y compare los resultados obtenidos usando métricas de comparación Bayesianas. En esta etapa se espera que:
Implementen los modelos Bayesianos disponibles en serofoi por medio de la función
fit_seromodel(). ¿Cómo afecta a sus resultados usar más o menos iteraciones?Comparación de los ajustes obtenidos por medio de la función
plot_seromodel(). ¿Cuál modelo se ajusta mejor en cada caso?
Análisis de resultados (30 min)
Con base en los resultados obtenidos anteriormente, ¿Cuál virus cree que estuvo involucrado en la epidemia reciente de encefalitis?
Para adaptar una de las cuatro bases de datos al formato necesario para {serofoi}, puede usar el siguiente código:
R
library(tidyverse)
virus_serosurvey <- readr::read_rds(
"https://epiverse-trace.github.io/epimodelac/data/serosurvey_01.RDS"
) %>%
dplyr::mutate(
age_group = vaccineff::get_age_group(
data_set = .,
col_age = "age_max",
max_val = 60,
step = 5
)
) %>%
dplyr::group_by(age_group, survey_year = tsur) %>%
dplyr::summarise(
n_sample = sum(total),
n_seropositive = sum(counts),
age_min = min(age_min),
age_max = max(age_max)
) %>%
dplyr::ungroup() %>%
dplyr::select(-age_group)
Ahora, ¿Cómo implementaría los modelos Bayesianos disponibles en
serofoi por medio de la función fit_seromodel()?
Puntos Clave
Revise si al final de esta lección adquirió estas competencias:
Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.
Sobre este documento
Este documento ha sido diseñado para el Curso Internacional: Análisis de Brotes y Modelamiento en Salud Pública, Bogotá 2023. TRACE-LAC/Javeriana.
Contribuciones
- Nicolás Torres Domínguez
- Zulma M. Cucunuba
Contribuciones son bienvenidas vía pull requests.
Referencias
Muench, H. (1959). Catalytic models in epidemiology. Harvard University Press.
Hens, N., Aerts, M., Faes, C., Shkedy, Z., Lejeune, O., Van Damme, P., & Beutels, P. (2010). Seventy-five years of estimating the force of infection from current status data. Epidemiology & Infection, 138(6), 802–812.
Cucunubá, Z. M., Nouvellet, P., Conteh, L., Vera, M. J., Angulo, V. M., Dib, J. C., … Basáñez, M. G. (2017). Modelling historical changes in the force-of-infection of Chagas disease to inform control and elimination programmes: application in Colombia. BMJ Global Health, 2(3). doi:10.1136/bmjgh-2017-000345
