Introducción al cálculo de efectividad vacunal con cohortes usando vaccineff
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo realizar el cálculo de efectividad vacunal con cohortes usando vaccineff?
Objetivos
Al final de este taller usted podrá:
Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes
1. Introducción
En esta sesión se espera que los participantes se familiaricen con
uso del paquete de Rvaccineff. Utilizaremos el diseño de
cohortes para estimar la efectividad vacunal de un conjunto de datos de
prueba y analizaremos los resultados obtenidos.
2. Objetivos
Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes
3. Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Eficacia y Efectividad vacunal
Tiempo de inducción o “delays” en el análisis de efectividad de vacunas
Diseños observacionales para el estudio de la efectividad vacunal
Diseño de cohortes para estimación de la efectividad vacunal
Estimador no paramétrico Kaplan-Meier
Modelo semi-paramétrico de Cox
Riesgos proporcionales
3.1. Eficacia vs Efectividad vacunal
Eficacia:
Se refiere a la capacidad de lograr un efecto deseado o esperado bajo condiciones ideales o controladas.
Es una medida teórica. En experimentos clínicos, por ejemplo, la eficacia de un medicamento se evalúa en condiciones controladas, donde todos los factores externos están cuidadosamente regulados para determinar el rendimiento puro del medicamento.
Puede considerarse como “lo que puede hacer” una intervención en las mejores circunstancias posibles.
Efectividad:
Se refiere a qué tan bien funciona una intervención en condiciones “reales” o prácticas, fuera de un entorno controlado.
Es una medida práctica. En el contexto de los medicamentos, la efectividad se refiere a qué tan bien funciona un medicamento en el “mundo real”, donde las condiciones no están tan controladas y hay muchos factores variables.
Puede considerarse como “lo que realmente hace” una intervención en circunstancias típicas o cotidianas.
| Un ejemplo podría ser un medicamento que en experimentos clínicos (en condiciones ideales) mostró una eficacia del 95% en prevenir el desenlace. Sin embargo, cuando se usó en el contexto general, considerando factores como la adherencia al tratamiento, interacciones con otros medicamentos y variabilidad en la población, su efectividad fue del 85%. Aquí, la eficacia muestra el potencial del medicamento bajo condiciones ideales, mientras que la efectividad muestra cómo funciona en situaciones cotidianas. |
En el caso de las vacunas la efectividad hace referencia a la disminución proporcional de casos de una enfermedad o evento en una población vacunada comparada con una población no vacunada, en condiciones del mundo real.
3.2. Tiempo de inducción
El tiempo de inducción o “delay” se refiere al periodo necesario para que la vacuna administrada induzca una respuesta inmune protectora frente a la infección o la enfermedad provocada por un patógeno. Si ocurre una infección entre el momento de la vacunación y el momento donde se prevé exista una respuesta inmune protectora, ocurrirá la infección de manera natural y no se considera un fallo de la vacuna en cuestión, puesto que la persona inmunizada aún no contaba con la protección conferida por la vacuna.
3.3. Diseños observacionales para el estudio de la efectividad vacunal
Por múltiples razones, los estudios observacionales son los más utilizados en la estimación de la efectividad vacunal. Existen múltiples diseños, entre ellos: diseño de cohortes, diseño de casos y controles, diseño de test-negativo, diseño “screening-method”. La elección del diseño, dependerá de la disponibilidad de información y los recursos disponibles para llevar a cabo el estudio.
3.4. Diseño de cohorte para el estudio de la efectividad vacunal
El término cohorte se refiere a un grupo de personas que comparten una característica común. En los estudios con diseño de cohorte, existen dos o más poblaciones que difieren en una característica o exposición y se realiza un seguimiento a ambos grupos para evaluar la aparición de uno o más desenlaces de interés y comparar la incidencia de los eventos entre ambos grupos. Para el caso de los estudios de la efectividad de vacunas, la exposición de interés corresponde a la aplicación de la vacuna y los desenlaces pueden incluir:
Infección: contagio con el patógeno de interés tras una exposición a alguien infeccioso
Enfermedad: desarrollo de signos y síntomas relacionados con la infección con un patógeno. Puede tener diferentes grados de severidad, requerir ingreso a hospitalización, UCI o incluso conducir a la muerte.
A la hora de llevar a cabo estos estudios se debe garantizar que las personas incluidas en cada población no tengan el desenlace de interés que será evaluado durante el seguimiento. Así mismo, es importante que el seguimiento se lleve a cabo de manera igual de rigurosa y por el mismo tiempo en ambos grupos.
La efectividad vacunal corresponde a la reducción relativa del riesgo de desarrollar la infección y/o enfermedad. En los estudios de cohorte se puede estimar el riesgo relativo, los odds ratio o los hazard ratio que expresa el riesgo que tiene la cohorte no expuesta comparado con la cohorte de los expuestos. La efectividad vacunal será, por lo tanto, el complemento del riesgo proporcional en la cohorte de expuestos.
Veamos esto con un ejemplo: para evaluar la efectividad de una vacuna para prevenir el desarrollo de enfermedad en una población, al cabo del seguimiento la incidencia en la cohorte vacunada fue de 1 por 1000 habitantes y en la cohorte no vacunada fue de 5 por 1000 habitantes. En este caso, tenemos que el riesgo relativo en la población vacunada fue 0.001/0.005 = 0,2. Es decir, la población vacunada tuvo una incidencia correspondiente al 20% de la incidencia de la población no vacunada. Esta reducción se puede atribuir a la vacuna y para estimarla usaríamos el complemento, que corresponde a 1 - 0,2= 0,8. Es decir que la reducción que se observó corresponde a un 80% y se puede atribuir a la vacuna, por lo tanto, la efectividad de la vacunación fue del 80% para evitar la enfermedad.
3.5. Métodos estadísticos para análisis de efectividad vacunal
En el diseño de cohortes se utilizan principalmente dos métodos: Estimación no paramétrica de Kapplan-Meier y Modelo semi-paramétrico de Cox
Estimador Kaplan-Meier
El estimador Kaplan-Meier utiliza las tasas de incidencia de un evento para cuantificar la probabilidad de supervivencia \(S(t)\) de forma no paramétrica, es decir, sin una representación matemática funcional. En general, la incidencia acumulada de cada grupo permite cuantificar el riesgo de presentar el evento como \(1 - S(t)\). Asimismo, la comparación entre el riesgo de ambos grupos en un punto del tiempo determina el riesgo relativo entre grupos (\(RR\)). A partir de esta se estima la efectividad vacunal como: \[V_{EFF} = 1 - RR\]
Modelo de Regresión de Cox
El modelo Cox, permite estimar de forma semi-paramétrica la función de riesgo instantáneo \(\lambda(t|x_i)\) de un individuo \(i\) en terminos de sus características, las cuales se asocian a un conjunto de covariables \(x_1, x_2, ..., x_n\), con lo cual se tiene:
\[\lambda(t|x_i) = \lambda_0(t) \exp(\beta_1 x_{i1} + \beta_2 x_{i2} + ....+\beta_n x_{in})\] donde \(\beta_1, \beta_2, ..., \beta_n\) son los coeficientes de la regresión y \(\lambda_0\) es una función basal no especificada, por lo que el modelo se asume como semi-paramétrico. En el caso en el que la función de riesgo instantáneo es completamente especificada, es decir, se conoce la forma funcional de \(\lambda_0(t)\), es posible calcular matemáticamente la probabilidad de supervivencia. Sin embargo, ninguna de estas funciones puede ser estimada directamente del modelo de Cox. Por el contrario, con este se busca estimar el hazard ratio, una medida de riesgos comparativa entre dos individuos \(i\) y \(j\) con características \(x_{i1}, x_{i2}, ..., x_{in}\) y \(x_{j1}, x_{j2}, ..., x_{jn}\), respectivamente. En este orden, al evaluar el riesgo de un individuo con respecto al otro se tiene:
\[HR = \frac{\lambda(t|x_i)}{\lambda(t|x_j)} = \frac{\lambda_0(t)\exp(\beta x_{i})}{\lambda_0(t)\exp(\beta x_{j})} = \exp(\beta(x_i-x_j))\] Riesgos proporcionales: Nótese que la dependencia temporal de las funciones de riesgo instantáneo individuales se canceló dentro de la expresion anterior para el Hazard ratio, por tanto se dice que los individuos \(i\) y \(j\) exhiben riesgos proporcionales en el tiempo. Esta hipótesis constituye un pilar importante de los estudios de efectividad bajo diseño de cohorte.
En el contexto de los estudios de cohorte, el modelo de Cox puede utilizarse para estimar el riesgo comparativo entre ambos grupos de presentar un desenlace de interés. En este sentido la pertenecia a un grupo se utiliza como covariable dentro de la regresión. Particularmente, para el cálculo de la efectividad vacunal se puede utilizar el \(HR\) de forma análoga al caso discutido para el estimador Kaplan-Meier, con lo que se define:
\[V_{EFF} = 1 - HR\]
4. Caso de uso del paquete
Para esta sesión se trabajará con el conjunto de datos de ejemplo
incluido en el paquete vaccineff. Adicionalmente, se
utilizarán algunas funciones de los paquetes ggplot2 y
cowplot para vizualizar algunos resultados.
Para installar vaccineff ejecute las siguientes líneas
en R:
R
# if(!require("pak")) install.packages("pak")
# pak::pak("epiverse-trace/vaccineff@dev")
Posteriormente, para cargar los paquetes en el espacio de trabajo y
el set de datos de ejemplo del vaccineff ejecute:
R
library("vaccineff")
library("ggplot2")
library("cowplot")
data(cohortdata)
head(cohortdata)
SALIDA
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2
1 <NA> <NA>
2 <NA> <NA>
3 <NA> <NA>
4 BRAND2 BRAND2
5 BRAND1 BRAND1
6 BRAND2 BRAND2Este tabla contiene información de una epidemia simulada ocurrida en 2044 sobre una población hipotética, compuesta por 100.000 habitantes, que recibió dos dosis de una vacuna para disminuir el riesgo de muerte por una enfermedad respiratoria viral. Sobre esta población se realizó seguimiento por 1 año, entre el 1 de enero y 31 de diciembre de 2044. En el conjunto de datos se presenta la información desagregada para cada uno de los participantes.
4.1 Funciones básicas de exploración de datos
4.1.1 Grupo etario
Para agrupar la población por grupo etario y graficar la distribución por edad utilizaremos la función “get_age_group”. Para esto, ejectute el siguiente comando en R:
R
cohortdata$age_group <- get_age_group(
data = cohortdata,
col_age = "age",
max_val = 80,
min_val = 0,
step = 9)
Esta función permite agrupar la población en intervalos etarios a partir de la variable “age” del conjunto de datos. En particular, para construir la agrupación por decenios se asigna el ancho del intervalo con step = 9, el mínimo valor de edad en 0 con “min_val” y el máximo valor en 80 con “max_val”. Esto significa que cualquier registro con edad mayor o igual a 80 años se agrupará en “>80”
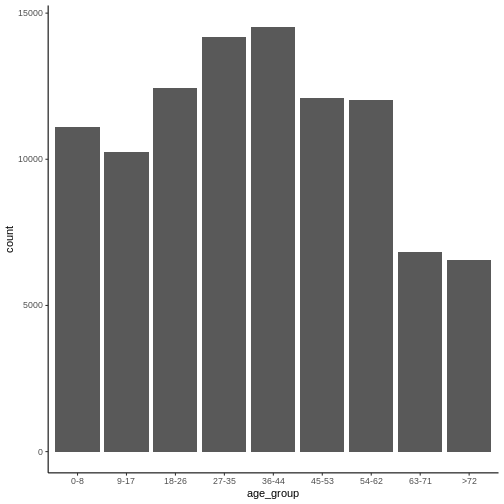
Puede graficar de forma rápida la distribución etaria asociada a la variable “age_group” utilizando la función “geom_bar” de la librería ggplot2. Para esto, ejecute el siguiente comando en R:
R
ggplot(data = cohortdata,
aes(x = age_group)) +
geom_bar() +
theme_classic()
4.1.2. Cobertura vacunal en las cohortes
En un conjunto de datos típico de un estudio de cohorte se tiene
información desagregada por persona de la(s) dosis aplicada(s) durante
el seguimiento. En este sentido, es importante dimensionar el nivel de
cobertura en la vacunación alcanzado durante el seguimiento. vaccineff
ofrece la función make_vaccineff_data y plot
que permiten llevar a cabo esta tarea con facilidad. Para esto, ejecute
el siguiente comando en R:
R
# Create `vaccineff_data`
vaccineff_data <- make_vaccineff_data(
data_set = cohortdata,
outcome_date_col = "death_date",
censoring_date_col = "death_other_causes",
vacc_date_col = "vaccine_date_2", # date of last dose
end_cohort = as.Date("2021-12-31")
)
# Plot the vaccine coverage of the total population
plot(vaccineff_data)
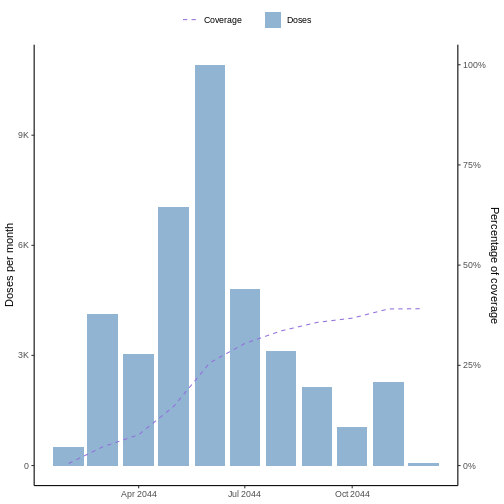
Esta función calcula la cobertura con base a la última dosis, la cual se especifica en el parámetro “vacc_date_col”. En particular, en el ejemplo anterior se utiliza la segunda dosis del conjunto de datos de ejemplo (“vaccine_date_2”).
La función make_vaccineff_data() genera nuevas columnas
en la base de datos de cohorte. La columna
immunization_date describe la fecha de inmunización según
la úlima dosis. La columna t0_follow_up describe la fecha
del inicio del periodo de seguimiento que, por defecto, es la fecha de
inicio del estudio o última dosis de vacunación. La fecha de inicio del
estudio está definida por la mínima fecha de inmunización.
R
# New columns: immunization_date, vaccine_status, t0_follow_up
head(vaccineff_data$cohort_data)
SALIDA
// linelist object
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2 age_group immunization_date vaccine_status t0_follow_up
1 <NA> <NA> 45-53 <NA> u 2021-03-11
2 <NA> <NA> 63-71 <NA> u 2021-03-11
3 <NA> <NA> >72 <NA> u 2021-03-11
4 BRAND2 BRAND2 >72 2021-05-16 v 2021-05-16
5 BRAND1 BRAND1 54-62 2021-06-22 v 2021-06-22
6 BRAND2 BRAND2 >72 2021-05-02 v 2021-05-02
// tags: outcome_date_col:death_date, censoring_date_col:death_other_causes, vacc_date_col:vaccine_date_2, immunization_date_col:immunization_date, vacc_status_col:vaccine_status, t0_follow_up_col:t0_follow_up 4.1.3. Definir la exposición: cohorte vacunada y cohorte no vacunada
La columna vaccine_status categoriza cada uno de los
sujetos según su estado vacunal, vacunados como “v” y no vacunados como
“u” (unvaccinated, en inglés) para cada uno de los registros de acuerdo
con su estado de vacunación, el cual se determina a partir de la
variable "immunization_date".
4.2 Seguimiento de la cohorte y tiempos al evento
Para llevar a cabo la estimación de la efectividad vacunal primero
debe definir la fecha de inicio y fin del seguimiento de cohortes, esto
con base en su exploración de las bases de datos. Para el caso
particular del conjunto de datos ejemplo contenidos es
vaccineff se utiliza en la funcion
make_vaccineff_data() el argumento
end_cohort.
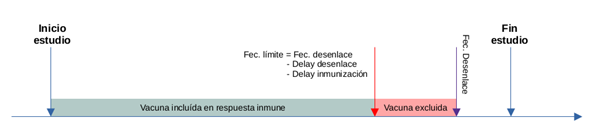
Para determinar la fecha de immunización, de un individuo
vaccineff::make_vaccineff_data() calcula la fecha de
inmunización seleccionando la vacuna que cumpla con el criterio de
fecha límite presentado en la siguiente figura.
4.2.2 Tiempo de inducción del efecto (delay)
En la figura anterior se introdujo el concepto de delay. El
delay de la immunización se refiere al tiempo que se espera que
transcurra antes de considerar que existe inmunidad protectora. Esta
variable puede controlarse en la función mediante el parámetro
immunization_delay. El valor que se asigne a esta depende
de la naturaleza del estudio. En particular, para nuestra epidemia
ejemplo utilizaremos immunization_delay = 14.
Para actualizar el objeto vaccineff_data agregue el
argumento immunization_delay = 14 en la anterior función y
ejecútela:
R
# Create `vaccineff_data`
vaccineff_data <- make_vaccineff_data(
data_set = cohortdata,
outcome_date_col = "death_date",
censoring_date_col = "death_other_causes",
vacc_date_col = "vaccine_date_2",
end_cohort = as.Date("2021-12-31"),
# Time in days before the patient is considered immune. Default is 0.
immunization_delay = 14
)
Al ejecutar este comando, se le sumará el delay a las fechas
de las columnas immunization_date y
t0_follow_up que corresponde la fecha 14 días posteriores a
la última dosis de cualquiera de las dos vacunas utilizadas en el caso
de estudio, que cumpla con el criterio de fecha límite. Puede
evidenciar la nueva columna en el conjunto de datos.
R
# Updated columns: immunization_date, t0_follow_up
head(vaccineff_data$cohort_data)
SALIDA
// linelist object
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2 age_group immunization_date vaccine_status t0_follow_up
1 <NA> <NA> 45-53 <NA> u 2021-03-25
2 <NA> <NA> 63-71 <NA> u 2021-03-25
3 <NA> <NA> >72 <NA> u 2021-03-25
4 BRAND2 BRAND2 >72 2021-05-30 v 2021-05-30
5 BRAND1 BRAND1 54-62 2021-07-06 v 2021-07-06
6 BRAND2 BRAND2 >72 2021-05-16 v 2021-05-16
// tags: outcome_date_col:death_date, censoring_date_col:death_other_causes, vacc_date_col:vaccine_date_2, immunization_date_col:immunization_date, vacc_status_col:vaccine_status, t0_follow_up_col:t0_follow_up 4.2.3 Definir el desenlace: estado vivo vs estado fallecido
El desenlace para este ejercicio va a ser la condición vital al final del estudio. En otros ejercicios el desenlace de interés podría ser la hospitalización o la infección, dependiendo del conjunto de datos utilizado.
Tenga en cuenta que en conjunto de datos del caso de estudio todas
las defunciones son debidas a la infección por el virus de interés. Para
definir el desenlace de interés de acuerdo a la condición vital de los
participantes en la cohorte, en la funcion
make_vaccineff_data() el argumento
outcome_date_col.
4.2.4. Calcular el tiempo al evento (desde exposición hasta desenlace)
Ahora, calcule para cada una de las personas el tiempo que fue seguido en el estudio. Recuerde que el seguimiento se hace igual para ambas cohortes (vacunada y no vacunada) y finaliza cuando termina el estudio o cuando se presenta el desenlace de interés. Para obtener este dato ejecute el siguiente comando en R:
R
# Estimate the Vaccine Effectiveness (VE)
ve <- estimate_vaccineff(vaccineff_data = vaccineff_data, at = 350)
Al ejecutar este comando se calcula la efectividad vacunal. Este
cálculo se basa en el estimador de Kaplan-Meier y en el modelo de Cox
para riesgos proporcionales del paquete survival. El
argumento at define el el número de días en los que se
estima la efectividad vacunal desde el inicio del periodo de
seguimiento.
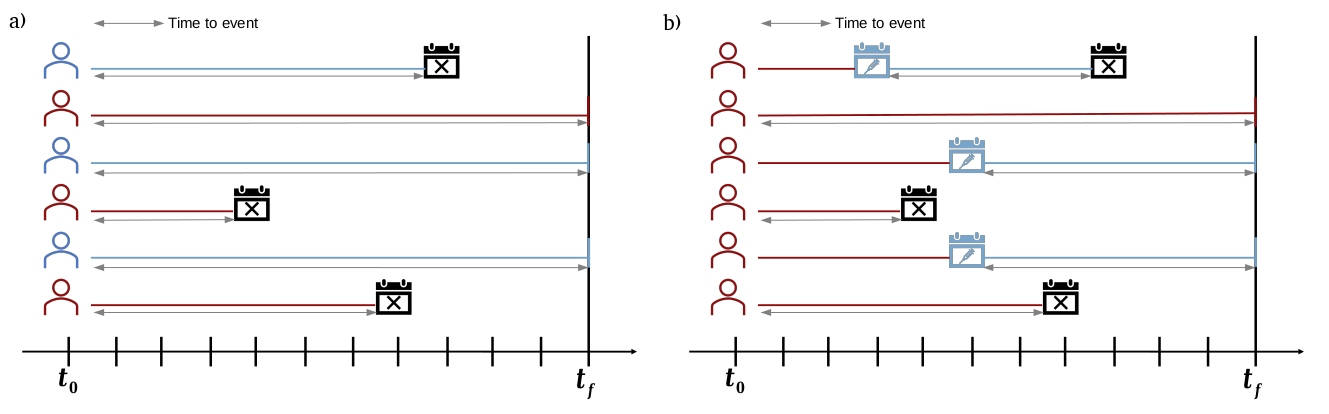
En la figura a continuación se presenta un esquema de los dos métodos de cálculo del tiempo al evento.
4.3. Curvas de riesgo acumulado y supervivencia al desenlace en cada cohorte
Como primera aproximación a la efectividad vacunal, graficaremos la curva de riesgos acumulados (1 menos la supervivencia de las poblaciones). Esta nos permite entender de forma cualitativa cuál de las poblaciones acumula mayor riesgo durante el estudio de cohorte. Y por tanto, evaluar hipótesis sobre el potencial efecto de la vacunación sobre la cohorte. Para graficar el riesgo acumulado ejecute el siguiente comando en R:
R
# Cumulative incidence
plot(ve, type = "surv", cumulative = TRUE)
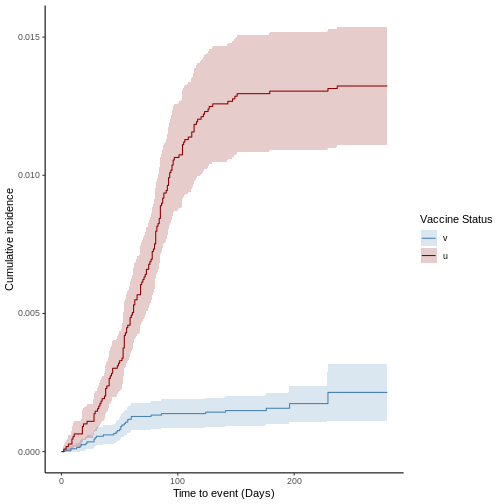
A partir de la función anterior también es posible realizar la gráfica de supervivencia de las cohortes o gráfica de Kaplan-Meier en la cual se parte del 100% de ambas cohortes en el eje de las ordenadas y en el eje de las abscisas se representa el tiempo y se observa la disminución que hay debido a las defunciones en cada cohorte. Tenga en cuenta que este no es el estimador de Kaplan-Meier, es sólo la gráfica sobre las curvas de supervivencia y de riesgo acumulado. Para obtener este gráfico, se ejecuta la misma función y se cambia el argumento “percentage” por FALSE:
R
# Generate Survival plot
plot(ve, type = "surv", cumulative = FALSE)
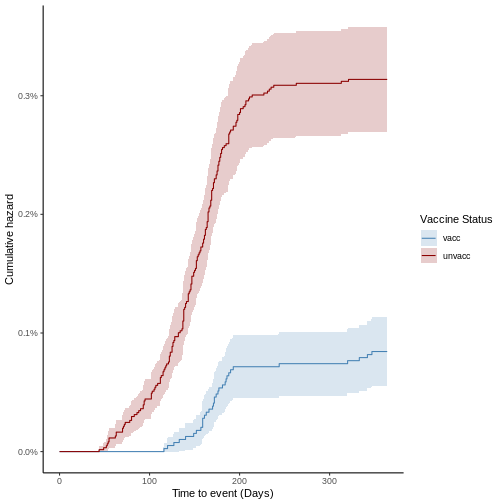
La función estimate_vaccineff() crea internamente una
tabla Kaplan-Meier.
R
head(ve$kaplan_meier)
4.4. Evaluación de la hipótesis riesgos proporcionales
Previo a la estimación de la efectividad vacunal es importante testear la hipótesis de riesgos proporcionales entre las cohortes de vacunados y no vacunados, con el fin de identificar posibles sesgos muestrales que afecten la validez de los resultados y definir estrategias de cálculo de cohortes dinámicas, emparejamiento o estratificación, entre otras, que permitar contrarestar este efecto. Un método cualitativo utilizado ampliamente en la literatura es la transformación de la probabilidad de supervivencia mediante la función logaritmo natural como \(\log[-\log[S(t)]]\). Al graficar esta función contra el logaritmo del tiempo al evento, es posible identificar si los grupos representan riesgos proporcionales cuando sus curvas se comportan de forma aproximadamente paralela.
4.5. Estimación de la efectividad vacunal
Modelo de Cox
En todos los estudios observacionales de efectividad vacunal de cohorte se compara el riesgo (o tasa de incidencia) entre los vacunados y no vacunados de desarrollar el desenlace de interés (infección, enfermedad, muerte, etc). La medida de riesgo a utilizar dependerá de las características de la cohorte y puede expresarse en términos de relative risk (RR) o hazard ratio (HR).
En este ejercicio utilizaremos el modelo de regresión de riesgos proporcionales de Cox para estimar el hazar ratio y con esta medida estimar la efectividad mediante
VE= 1-HR
Para estimar la efectividad vacunal en términos de HR, ejecute el siguiente comando en R:
R
# Print summary of VE
summary(ve)
SALIDA
Vaccine Effectiveness at 350 days computed as VE = 1 - HR:
VE lower.95 upper.95
0.872 0.8122 0.9128
Schoenfeld test for Proportional Hazards assumption:
p-value = 0.0078Podemos usar la función plot() para evaluar la hipótesis
de riesgos proporcionales:
R
# Generate loglog plot to check proportional hazards
plot(ve, type = "loglog")
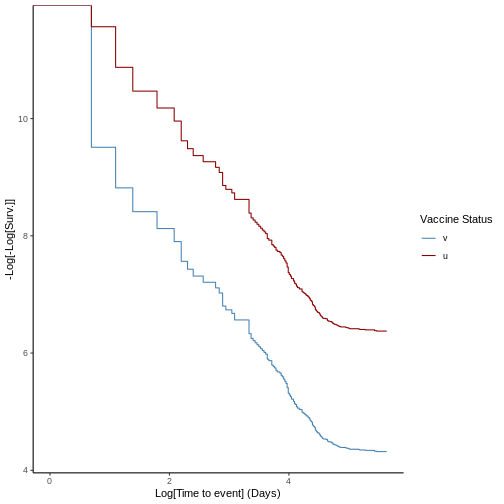
4.6 Cohorte dinámica - Emparejamiento poblacional
El comando anterior arrojó la efectividad vacunal obtenida mediante el model de Cox. Sin embargo, en la columna PH aparece la palabra rejected. Esto significa que pese a que las curvas de ambos grupos son paralelas la evaluación de la hipótesis de riesgos proporcionales haciendo uso del test de Schoenfeld no es satisfactoria. Esto debido a los potenciales sesgos muestrales inducidos por la estrategia de vacunación desplegada sobre la población. Una estrategia para contrarestas dichos sesgos es el emparejamiento dinámico de la población. En la siguiente figura se presenta un esquema de emparejamiento orientado a disminuir los sesgos muestrales.
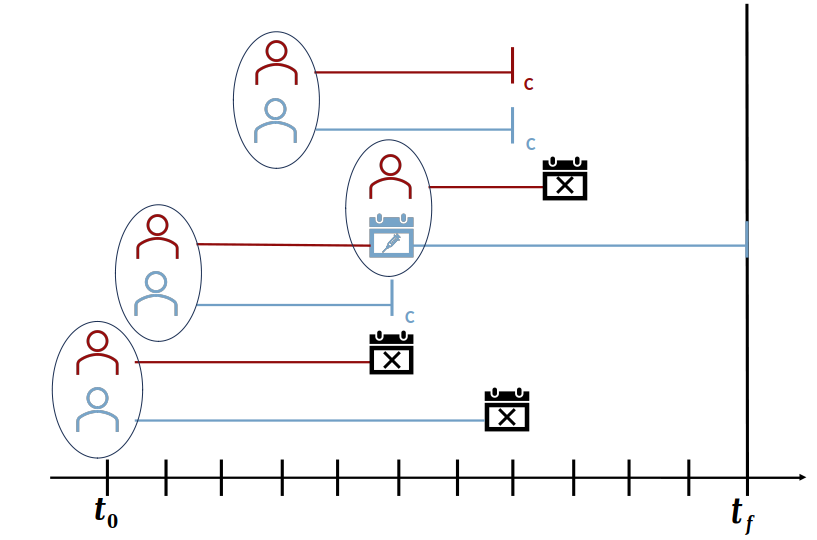
Para realizar el emparejamiento poblacional use los argumentos
match = TRUE y exact = c("age", "sex") para
emparejar por edad y sexo exactos:
R
# Create `vaccineff_data_matched`
vaccineff_data_matched <- make_vaccineff_data(
data_set = cohortdata,
outcome_date_col = "death_date",
censoring_date_col = "death_other_causes",
vacc_date_col = "vaccine_date_2",
end_cohort = as.Date("2021-12-31"),
immunization_delay = 14,
# Performe cohort matching
match = TRUE,
exact = c("age", "sex")
)
Por ejemplo, si usamos el argumento
nearest = c("age" = 2) podemos calibrar el emparejamiento
por una distancia de 2 unidades de edad.
En la base de datos emparejada identificamos nuevas columnas como
subclass, que agrupa con un código a los
emparejamientos.
R
head(vaccineff_data_matched$matching$match)
SALIDA
// linelist object
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2 age_group immunization_date vaccine_status subclass
1 <NA> <NA> 45-53 <NA> u 6226
2 <NA> <NA> 63-71 <NA> u 5023
3 <NA> <NA> >72 <NA> u 7170
4 BRAND2 BRAND2 >72 2021-05-30 v 1
5 BRAND1 BRAND1 54-62 2021-07-06 v 2
6 BRAND2 BRAND2 >72 2021-05-16 v 3
t0_follow_up censoring_after_match
1 2021-07-16 <NA>
2 2021-05-24 <NA>
3 2021-05-18 <NA>
4 2021-05-30 <NA>
5 2021-07-06 <NA>
6 2021-05-16 <NA>
// tags: outcome_date_col:death_date, censoring_date_col:censoring_after_match, vacc_date_col:vaccine_date_2, immunization_date_col:immunization_date, vacc_status_col:vaccine_status, t0_follow_up_col:t0_follow_up Las salidas de las funciones de summary() y
plot() cambiarán luego de configurado el emparejamiento.
Corre nuevamente todo el flujo de trabajo escrito en este episodio con
el objeto vaccineff_data_matched, incluyendo el gráfico de
cobertura y la estimación de la .
R
# Print summary of vaccineff data object
summary(vaccineff_data_matched)
# Plot the vaccine coverage of the total population
plot(vaccineff_data_matched)
# Estimate the Vaccine Effectiveness (VE)
ve_matched <- estimate_vaccineff(vaccineff_data = vaccineff_data_matched, at = 350)
# Generate Survival plot
plot(ve_matched, type = "surv", cumulative = FALSE)
# plot(ve, type = "surv", percentage = TRUE, cumulative = FALSE)
# Cumulative incidence
plot(ve_matched, type = "surv", cumulative = TRUE)
# Print summary of VE
summary(ve_matched)
# Generate loglog plot to check proportional hazards
plot(ve_matched, type = "loglog")
5. Reflexión
En esta sesión se llevó a cabo una estimación básica de la efectividad vacunal mediante un estudio de cohorte, haciendo uso de los estimador Kaplan-Meier y del modelo de Cox. Adicionalmente, se estudió la hipótesis de riesgos proporcionales para los grupos vacunado y no vacunado comparando la construcción de tiempos al evento de forma dinámica y fija. Se observó que pese a que la hipótesis de riesgos proporcionales se corrobora gráficamente en la consrucción de los tiempos al evento con fecha de inicio fija, al evaluar el modelo de riesgos proporcionales de Cox el test de Schoenfeld rechaza esta hipótesis. En general la decisión sobre aceptar o no los resultados es altamente dependiente del acceso a información adicional relevante que permita realizar ajustes a la estimación y capturar dinámicas relevantes.
Reto
Puntos Clave
Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes
