Content from Introducción a la analítica de brotes
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo modelar y analizar un brote?
Objetivos
Al final de este taller usted podrá:
Identificar los parámetros necesarios en casos de transmisión de enfermedades infecciosas de persona a persona.
Estimar la probabilidad de muerte (CFR).
Calcular y graficar la incidencia.
Estimar e interpretar la tasa de crecimiento y el tiempo en que se duplica la epidemia.
Estimar e interpretar el número de reproducción instantáneo de la epidemia.
Tiempos de ejecución
Explicación del taller (10 minutos)
Realización del taller (100 minutos taller)
Parte 1: Estructura de datos y CFR (15 min)
Parte 2: Incidencia y tasa de crecimiento (45 min)
Parte 3: Rt (40 min)
Discusión 30 minutos
Introducción
Un nuevo brote de virus del Ébola (EVE) en un país ficticio de África occidental
Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Transmisión de enfermedades infecciosas de persona a persona
Número de reproducción básico
Número de reproducción instantáneo
Probabilidad de muerte (IFR, CFR)
Intervalo serial
Tasa de crecimiento
Incidencia
Preparación previa
Antes de comenzar,
descargue la carpeta con los datos y el proyecto desde Carpetas de datos .
Ahí mismo encontrará un archivo
.Rpara instalar las dependencias necesarias para este taller.Recuerde abrir el archivo
RProjectdenominadoTaller-Brotes-Ebola.Rprojantes de empezar a trabajar.
Este paso no solo le ayudará a cumplir con las buenas prácticas de programación en R, sino también a mantener un directorio organizado, permitiendo un desarrollo exitoso del taller.
1. Estructura de datos
Cargue de librerías:
Cargue las librerías necesarias para el análisis epidemiológico. Los datos serán manipulados con tidyverse que es una colección de paquetes para la ciencia de datos.
R
library(tidyverse) # contiene ggplot2, dplyr, tidyr, readr, purrr, tibble
library(readxl) # para leer archivos Excel
library(binom) # para intervalos de confianza binomiales
library(knitr) # para crear tablas bonitas con kable()
library(incidence) # para calcular incidencia y ajustar modelos
library(EpiEstim) # para estimar R(t)
Cargue de bases de datos
Se le ha proporcionado la siguiente base de datos:
-
casos: una base de datos de casos que contiene información de casos hasta el 1 de julio de 2014.
Para leer en R este archivo, utilice la función read_rds
de tidyverse. Se creará una tabla de datos almacenada como
objeto de clase tibble.
R
casos <- read_rds("data/casos.rds")
Estructura de los datos
Explore la estructura de los datos. Para esto puede utilizar la
función glimpse de tidyverse, la cual nos
proporciona una visión rápida y legible de la estructura interna de
nuestro conjunto de datos.
R
glimpse(casos)
SALIDA
Rows: 166
Columns: 11
$ id_caso <chr> "d1fafd", "53371b", "f5c3d8", "6c286a", "0f58…
$ generacion <dbl> 0, 1, 1, 2, 2, 0, 3, 3, 2, 3, 4, 3, 4, 2, 4, …
$ fecha_de_infeccion <date> NA, 2014-04-09, 2014-04-18, NA, 2014-04-22, …
$ fecha_inicio_sintomas <date> 2014-04-07, 2014-04-15, 2014-04-21, 2014-04-…
$ fecha_de_hospitalizacion <date> 2014-04-17, 2014-04-20, 2014-04-25, 2014-04-…
$ fecha_desenlace <date> 2014-04-19, NA, 2014-04-30, 2014-05-07, 2014…
$ desenlace <chr> NA, NA, "Recuperacion", "Muerte", "Recuperaci…
$ genero <fct> f, m, f, f, f, f, f, f, m, m, f, f, f, f, f, …
$ hospital <fct> Military Hospital, Connaught Hospital, other,…
$ longitud <dbl> -13.21799, -13.21491, -13.22804, -13.23112, -…
$ latitud <dbl> 8.473514, 8.464927, 8.483356, 8.464776, 8.452…Como puede observar contactos tiene 11 columnas (variables) y 166
filas de datos. En un rápido vistazo puede observar el tipo de las
variables por ejemplo, la columna desenlace tiene formato
carácter (chr) y contiene entre sus valores
"Recuperación" o "Muerte".
Además, puede encontrar estas variables:
El identificador
id_casoLa generación de infectados (cuantas infecciones secundarias desde la fuente hasta el sujeto han ocurrido)
La fecha de infección
La fecha de inicio de síntomas
La fecha de hospitalización
La fecha del desenlace que, como se puede observar, en la siguiente variable puede tener entre sus opciones
NA(no hay información hasta ese momento o no hay registro), recuperación y muerteLa variable género que puede ser
fde femenino omde masculinoEl lugar de hospitalización, en la variable hospital
Y las variables longitud y latitud
Note que las fechas ya están en formato fecha
(date).
2. CFR
Probabilidad de muerte en los casos reportados (CFR,
por Case Fatality Risk)
R
table(casos$desenlace, useNA = "ifany")
SALIDA
Muerte Recuperacion <NA>
60 43 63 Desafío 1
Calcule la probabilidad de muerte en los casos reportados
(CFR) tomando el número de muertes y el número de casos con
desenlace final conocido del objeto casos. Esta vez se
calculará el CFR con el método Naive. Los cálculos
Naive (inocentes) tienen el problema de que pueden
presentar sesgos, por lo que no deberían ser utilizados para informar
decisiones de salud pública. Hablaremos de estos sesgos en profundidad
en el día 4.
Durante este taller se le presentarán algunos retos, para los cuales
obtendrá algunas pistas, por ejemplo en el presente reto se le presenta
una pista, la cual es un fragmento del código que usted debe completar
para alcanzar la solución. En los espacios donde dice
COMPLETE por favor diligencie el código faltante.
R
muertes <- COMPLETE
casos_desenlace_final_conocido <- sum(casos$desenlace %in% c("Muerte", "Recuperacion"))
CFR <- COMPLETE / COMPLETE
Ejemplo,
R
# Reto
muertes <- COMPLETE
#Solución
muertes <- sum(casos$desenlace %in% "Muerte")
SALIDA
[1] 0.5825243Para complementar el calculo del CFR se pueden calcular sus
intervalos de confianza por medio de la función
binom.confint. La función binom.confint se
utiliza para calcular intervalos de confianza para una proporción en una
distribución binomial, que corresponde, por ejemplo, a cuando tenemos el
total de infecciones con desenlace final conocido (recuperado o muerte).
Esta función pide tres argumentos: 1) el número de muertes y 2) el
número total de casos con desenlace final conocido, es decir sin
importar que hayan muerto o se hayan recuperado, pero sin cuenta los
datos con NA; 3) el método que se utilizará para calcular
los intervalos de confianza, en este caso “exact” (método
Clopper-Pearson).
Desafío 2
Determine el CFR con sus intervalos de confianza utilizando la
función binom.confint. Y obtenga este resultado:
| method | x | n | mean | lower | upper |
|---|---|---|---|---|---|
| exact | 60 | 103 | 0.5825243 | 0.4812264 | 0.6789504 |
Recuerde diligenciar los espacios donde dice COMPLETE. Y
obtenga este resultado
R
CFR_con_CI <- binom.confint(COMPLETE, COMPLETE, method = "COMPLETE") %>%
kable(caption = "**COMPLETE ¿QUE TITULO LE PONDRÍA?**")
CFR_con_CI
3. Incidencia
3.1. Curva de incidencia diaria
El paquete incidence es de gran utilidad para el
análisis epidemiológico de datos de incidencia de enfermedades
infecciosas, dado que permite calcular la incidencia a partir del
intervalo temporal suministrado (e.g. diario o semanal). Dentro de este
paquete esta la función incidence la cual cuenta con los
siguientes argumentos:
datescontiene una variable con fechas que representan cuándo ocurrieron eventos individuales, como por ejemplo la fecha de inicio de los síntomas de una enfermedad en un conjunto de pacientes.intervales un intervalo de tiempo fijo por el que se quiere calcular la incidencia. Por ejemplo,interval = 365para un año. Si no se especifica, el valor por defecto es diario.last_datefecha donde se establecerá un limite temporal para los datos. Por ejemplo, la última fecha de hospitalización. Para este tercer argumento, podemos incluir la opciónmaxy la opciónna.rm. La primera para obtener la última fecha de una variable y la segunda para ignorar losNAen caso de que existan.
Por ejemplo, se podría escribir
last_date = max(base_de_datos$vector_ultima_fecha, na.rm = TRUE)
Con esta información la función agrupa los casos según el intervalo de tiempo especificado y cuenta el número de eventos (como casos de enfermedad) que ocurrieron dentro de cada intervalo.
Desafío 3
Calcule la incidencia diaria usando únicamente el primer argumento de
la función incidence ¿Qué fecha sería la más adecuada?
Tenga en cuenta que se espera que esta sea la que pueda dar mejor
información, es decir la menor cantidad de NAs.
R
incidencia_diaria <- incidence(COMPLETE)
incidencia_diaria
El resultado es un objeto de clase incidencia
(incidence) que contiene el recuento de casos para cada
intervalo de tiempo, lo que facilita su visualización y análisis
posterior. Como puede observar la función produjo los siguientes
datos:
SALIDA
<incidence object>
[166 cases from days 2014-04-07 to 2014-06-29]
$counts: matrix with 84 rows and 1 columns
$n: 166 cases in total
$dates: 84 dates marking the left-side of bins
$interval: 1 day
$timespan: 84 days
$cumulative: FALSEComo resultado de la función se produjo un objeto tipo lista. Este
objeto arroja estos datos: 166 casos contemplados entre los
días 2014-04-07 al 2014-06-29 para un total de
84 días; se menciona que el intervalo es de
1 día, dado que no se utilizo específico explicitamente el
parámetro por lo cual quedó su valor por defecto. Finalmente se menciona
“cumulative : FALSE” lo que quiere decir que no se esta
haciendo el acumulado de la incidencia, es decir que los casos
corresponden a los del intervalo interval: 1 day, es decir
a los casos nuevos cada día en específico.
Ahora haga una gráfica de la incidencia diaria.
R
plot(incidencia_diaria, border = "black")
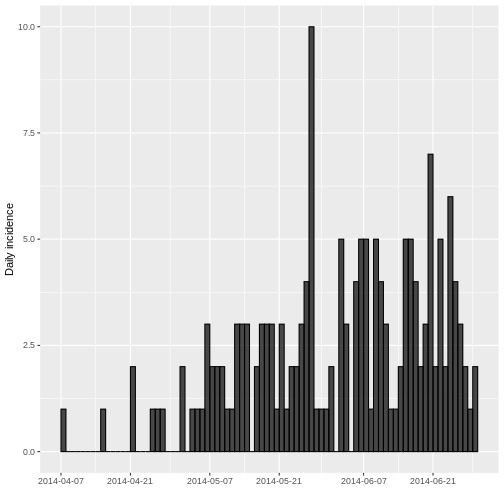
En el Eje X (Fechas): Se puede observar fechas van desde
el 7 de abril de 2014 hasta una fecha posterior al
21 de junio de 2014. Estas fechas representan el período de
observación del brote.
En el Eje Y (Incidencia Diaria): La altura de las barras
indica el número de nuevos casos reportados cada fecha según el tipo de
fecha escogido.
Dado que no se agregó el parámetro interval la
incidencia quedó por defecto diaria, produciéndose un histograma en el
que cada barra representa la incidencia de un día, es decir, los casos
nuevos. Los días sin barras sugieren que no hubo casos nuevos para esa
fecha o que los datos podrían no estar disponibles para esos días.
A pesar de que hay una curva creciente, hay periodos con pocos o ningún caso. ¿Porque cree que podrían darse estos periodos de pocos a pesar de la curva creciente?
3.2. Cálculo de la incidencia semanal
Teniendo en cuenta lo aprendido con respecto a la incidencia diaria,
cree una variable para incidencia semanal. Luego, interprete el
resultado y haga una gráfica. Para escoger la fecha que utilizará como
última fecha debe asignarle un valor al argumento last_date
de la función incidence ¿Qué fecha sería la más adecuada?
Tenga en cuenta que la fecha debe ser posterior a la fecha que se haya
escogido como el primer argumento.
Desafío 4
R
incidencia_semanal <- incidence(PRIMER ARGUMENTO, #COMPLETE
SEGUNDO ARGUMENTO, #COMPLETE
TERCER ARGUMENTO) #COMPLETESALIDA
<incidence object>
[166 cases from days 2014-04-07 to 2014-06-30]
[166 cases from ISO weeks 2014-W15 to 2014-W27]
$counts: matrix with 13 rows and 1 columns
$n: 166 cases in total
$dates: 13 dates marking the left-side of bins
$interval: 7 days
$timespan: 85 days
$cumulative: FALSE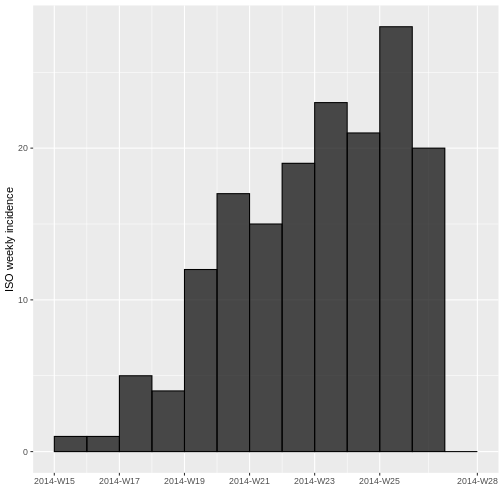
Compare la gráfica de incidencia diaria con la de incidencia semanal. ¿Qué observa? ¿Los datos se comportan diferente? ¿Es lo que esperaba? ¿Logra observar alguna tendencia?
4. Tasa de crecimiento
4.1. Modelo log-lineal
Estimación de la tasa de crecimiento mediante un modelo log-lineal
Para observar mejor las tendencias de crecimiento en el número de casos se puede visualizar la incidencia semanal en una escala logarítmica. Esto es particularmente útil para identificar patrones exponenciales en los datos.
Grafique la incidencia transformada logarítmicamente:
R
ggplot(as.data.frame(incidencia_semanal)) +
geom_point(aes(x = dates, y = log(counts))) +
scale_x_incidence(incidencia_semanal) +
xlab("Semana") +
ylab("Incidencia semanal logarítmica") +
theme_minimal()
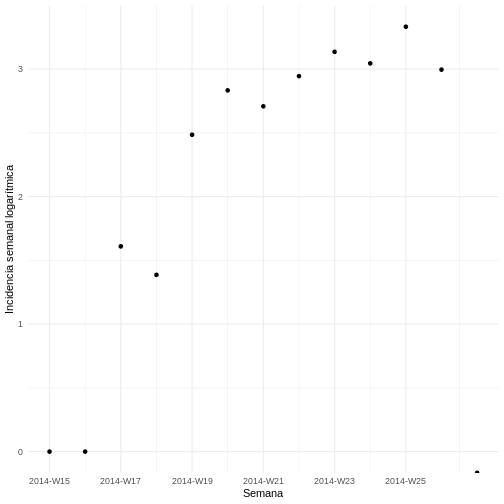
Ajuste un modelo log-lineal a los datos de incidencia semanal
R
ajuste_modelo <- incidence::fit(incidencia_semanal)
ajuste_modelo
SALIDA
<incidence_fit object>
$model: regression of log-incidence over time
$info: list containing the following items:
$r (daily growth rate):
[1] 0.04145251
$r.conf (confidence interval):
2.5 % 97.5 %
[1,] 0.02582225 0.05708276
$doubling (doubling time in days):
[1] 16.72148
$doubling.conf (confidence interval):
2.5 % 97.5 %
[1,] 12.14285 26.84302
$pred: data.frame of incidence predictions (12 rows, 5 columns)Desafío 5
¿Qué observa en este resultado?
$model: Indica que se ha realizado una regresión
logarítmica de la incidencia en función del tiempo. Esto implica que la
relación entre el tiempo y la incidencia de la enfermedad ha sido
modelada como una función lineal en escala logarítmica en la incidencia
con el fin de entender mejor las tendencias de crecimiento.
$info: Contiene varios componentes importantes del
análisis:
-
$r (daily growth rate)Tasa de crecimiento diaria:0.04145251
La tasa de crecimiento diaria estimada del brote es de
0.0415. Esto significa que cada día la cantidad de casos
está creciendo en un 4.15% con respecto al día anterior,
bajo la suposición de un crecimiento exponencial constante durante el
periodo modelado.
Si quisiera acceder a esta información sin ingresar al modelo podría hacerlo con el siguiente código:
R
tasa_crecimiento_diaria <- ajuste_modelo$info$r
cat("La tasa de crecimiento diaria es:", tasa_crecimiento_diaria, "\n")
SALIDA
La tasa de crecimiento diaria es: 0.04145251 -
$r.conf(confidence interval): 2.5 % 0.02582225 97.5 % 0.05708276
El intervalo de confianza del 95% para la tasa de
crecimiento diaria está entre 0.0258 (2.58%) y
0.0571 (5.71%).
$doubling (doubling time in days): 16.72148
- El tiempo de duplicación estimado del número de casos nuevos es de
aproximadamente
16.72 días. Esto significa que, bajo el modelo actual y con la tasa de crecimiento estimada, se espera que el número de casos de la curva epidémica actual se duplique cada16.72 días.
$doubling.conf (confidence interval): 2.5 % 12.14285
97.5 % 26.84302
- El intervalo de confianza del
95%para el tiempo de duplicación está entre aproximadamente12.14y26.84 días. Este amplio rango refleja la incertidumbre en la estimación y puede ser consecuencia de la variabilidad en los datos o de un tamaño de muestra pequeño.
$pred: Contiene las predicciones de incidencia
observada. Incluye las fechas, la escala de tiempo en días desde el
inicio del brote, los valores ajustados (predicciones) y los límites
inferior y superior del intervalo de confianza para las
predicciones.
Si quiere conocer un poco más de este componente puede explorarlo con
la función glimpse.
R
glimpse(ajuste_modelo$info$pred)
¿El modelo se ajusta bien a los datos? Verifique el \(R^2\)
R
AjusteR2modelo <- summary(ajuste_modelo$model)$adj.r.squared
cat("El R cuadrado ajustado es:", AjusteR2modelo, "\n")
SALIDA
El R cuadrado ajustado es: 0.7551113 Antes de continuar ¿Considera más adecuado usar una gráfica semanal para buscar un ajuste de los datos? ¿Por qué?
¿Es preferible calcular la tasa de crecimiento diaria con el ajuste semanal y no con el ajuste diario?
Grafique la incidencia incluyendo una línea que represente el modelo.
Con plot
R
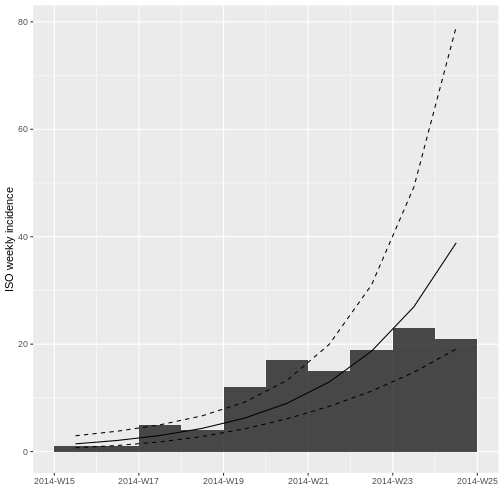
plot(incidencia_semanal, fit = ajuste_modelo)
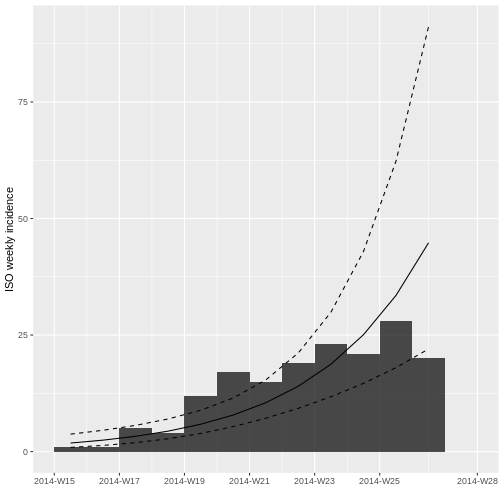
Tras ajustar el modelo log-lineal a la incidencia semanal para estimar la tasa de crecimiento de la epidemia, el gráfico muestra la curva de ajuste superpuesta a la incidencia semanal observada.
Al final del gráfico se puede observar que la incidencia semanal disminuye.
¿Porqué cree que podría estar pasando esto? ¿Cómo lo solucionaría?
4.2. Modelo log-lineal con datos truncados
Encuentre una fecha límite adecuada para el modelo log-lineal, en función de los rezagos (biológicos y administrativos).
Dado que esta epidemia es de Ébola y la mayoría de los casos van a ser hospitalizados, es muy probable que la mayoría de las notificaciones ocurran en el momento de la hospitalización. De tal manera que podríamos examinar cuánto tiempo transcurre entre la fecha de inicio de síntomas y la fecha de hospitalización para hacernos una idea del rezago para esta epidemia.
R
summary(as.numeric(casos$fecha_de_hospitalizacion - casos$fecha_inicio_sintomas))
SALIDA
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 1.00 2.00 3.53 5.00 22.00 Al restar la fecha de hospitalización a la fecha de inicio de síntomas podría haber valores negativos. ¿Cuál cree que sea su significado? ¿Ocurre en este caso?
Para evitar el sesgo debido a rezagos en la notificación, se pueden truncar los datos de incidencia. Pruebe descartar las últimas dos semanas. Este procedimiento permite concentrarse en el periodo en que los datos son más completos para un análisis más fiable.
Semanas a descartar al final de la epicurva
R
semanas_a_descartar <- 2
fecha_minima <- min(incidencia_diaria$dates)
fecha_maxima <- max(incidencia_diaria$dates) - semanas_a_descartar * 7
# Para truncar la incidencia semanal
incidencia_semanal_truncada <- subset(incidencia_semanal,
from = fecha_minima,
to = fecha_maxima) # descarte las últimas semanas de datos
# Incidencia diaria truncada. No la usamos para la regresión lineal pero se puede usar más adelante
incidencia_diaria_truncada <- subset(incidencia_diaria,
from = fecha_minima,
to = fecha_maxima) # eliminamos las últimas dos semanas de datos
Desafío 6
Ahora utilizando los datos truncados
incidencia_semanal_truncada vuelva a ajustar el modelo
logarítmico lineal.
SALIDA
<incidence_fit object>
$model: regression of log-incidence over time
$info: list containing the following items:
$r (daily growth rate):
[1] 0.05224047
$r.conf (confidence interval):
2.5 % 97.5 %
[1,] 0.03323024 0.0712507
$doubling (doubling time in days):
[1] 13.2684
$doubling.conf (confidence interval):
2.5 % 97.5 %
[1,] 9.728286 20.85893
$pred: data.frame of incidence predictions (10 rows, 5 columns)¿Cámo interpreta estos resultados? ¿Compare los \(R^2\)?
Desafío 7
Ahora utilizando los datos truncados
incidencia_semanal_truncada vuelva a graficar el modelo
logarítmico lineal.
¿Qué cambios observa?
Observe las estadísticas resumidas del ajuste:
R
summary(ajuste_modelo_truncado$model)
SALIDA
Call:
stats::lm(formula = log(counts) ~ dates.x, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.73474 -0.31655 -0.03211 0.41798 0.65311
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.186219 0.332752 0.560 0.591049
dates.x 0.052240 0.008244 6.337 0.000224 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5241 on 8 degrees of freedom
Multiple R-squared: 0.8339, Adjusted R-squared: 0.8131
F-statistic: 40.16 on 1 and 8 DF, p-value: 0.0002237El modelo muestra que hay una relación significativa
(R-squared: 0.8131) entre el tiempo (dates.x)
y la incidencia de la enfermedad, por lo que concluimos que la
enfermedad muestra un crecimiento exponencial a lo largo del tiempo.
4.3. Tasa de crecimiento y tasa de duplicación: extracción de datos
Estimacion de la tasa de crecimiento
Para estimar la tasa de crecimiento de una epidemia utilizando un modelo log-lineal es necesario realizar un ajuste de regresión a los datos de incidencia. Dado que ya tiene un objeto de incidencia truncado y un modelo log-lineal ajustado, puede proceder a calcular la tasa de crecimiento diaria y el tiempo de duplicación de la epidemia.
El modelo log-lineal proporcionará los coeficientes necesarios para estos cálculos. Note que el coeficiente asociado con el tiempo (la pendiente de la regresión) se puede interpretar como la tasa de crecimiento diaria cuando el tiempo se expresa en días.
Con el modelo ajustado truncado, es hora de realizar la estimación de
la tasa de crecimiento. Estos datos los puede encontrar en el objeto
ajuste modelo semana, que tiene los datos ajustados de
incidencia semanal truncada.
Desafío 8
Por favor escriba el código para obtener los siguientes valores:
SALIDA
La tasa de crecimiento diaria es: 0.05224047 SALIDA
Intervalo de confianza de la tasa de crecimiento diaria (95%): 0.03323024 0.0712507 Si no lo recuerda, vuelva por pistas a la sección Ajuste un modelo log-lineal a los datos de incidencia semanal
Ahora que ya ha obtenido la tasa de crecimiento diaria y sus intervalos de confianza, puede pasar a estimar el tiempo de duplicación.
Estimación del tiempo de duplicación
Esta información también la encontrará calculada y lista para
utilizar en el objeto ajuste_modelo_truncado, que tiene los
datos ajustados de incidencia semanal truncada.
Desafío 9
Por favor escriba el código para obtener los siguientes valores:
SALIDA
El tiempo de duplicación de la epidemia es 13.2684 díasSALIDA
Intervalo de confianza del tiempo de duplicación (95%): 9.728286 20.85893 Si no lo recuerda vuelva por pistas a la sección Ajuste un modelo log-lineal a los datos de incidencia semanal
5. Estimación de número de reproducción
Evaluar la velocidad a la que se propaga una infección en una población es una tarea importante a la hora de informar la respuesta de salud pública a una epidemia.
Los números de reproducción son métricas típicas para monitorear el desarrollo de epidemias y son informativos sobre su velocidad de propagación. El Número de reproducción básico \(R_0\), por ejemplo, mide el número promedio de casos secundarios producidos por un individuo infeccioso dada una población completamente susceptible. Esta hipótesis suele ser válida solo al inicio de una epidemia.
Para caracterizar el la propagación en tiempo real es más común utilizar el Número de reproducción instantáneo \(R_t\), el cual describe el número promedio de casos secundarios generados por un individuo infeccioso en el tiempo \(t\) dado que no han habido cambios en las condiciones actuales.
En esta sección exploraremos los conceptos necesarios para calcular el Número de reproducción instantáneo, así como los pasos a seguir para estimarlo por medio del paquete de R EpiEstim.
5.1. Intervalo serial (SI)
¿Qué es el intervalo serial?
El intervalo serial en epidemiología se refiere al tiempo que transcurre entre el momento en que una persona infectada (el caso primario) comienza a mostrar síntomas y el momento en que la persona que fue infectada por ella (el caso secundario) comienza a mostrar síntomas.
Este intervalo es importante porque ayuda a entender qué tan rápido se está propagando una enfermedad y a diseñar estrategias de control como el rastreo de contactos y la cuarentena. Si el intervalo serial es corto, puede significar que la enfermedad se propaga rápidamente y que es necesario actuar con urgencia para contenerla. Si es largo, puede haber más tiempo para intervenir antes de que la enfermedad se disemine ampliamente.
Para este brote de Ébola asumiremos que el intervalo serial está
descrito por una distribución Gamma de media (mean_si) de
8.7 días y con una desviación estándar
(std_si) de 6.1 días. En la práctica del día 4
estudiaremos cómo estimar el intervalo serial.
R
# Parametros de la distribución gamma para el invertavlo serial
mean_si <- 8.7
std_si <- 6.1
config <- make_config(list(mean_si = mean_si, std_si = std_si))
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.
5.2. Estimación de la transmisibilidad variable en el tiempo, R(t)
Cuando la suposición de que (\(R\))
es constante en el tiempo se vuelve insostenible, una alternativa es
estimar la transmisibilidad variable en el tiempo utilizando el Número
de reproducción instantáneo (\(R_t\)).
Este enfoque, introducido por Cori et al. (2013), se implementa en el
paquete EpiEstim, el cual estima el \(R_t\) para ventanas de tiempo
personalizadas, utilizando una distribución de Poisson. A continuación,
estimamos la transmisibilidad para ventanas de tiempo deslizantes de 1
semana (el valor predeterminado de estimate_R):
R
config <- make_config(list(mean_si = mean_si, std_si = std_si))
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.
R
# use estimate_R using method = "parametric_si"
estimacion_rt <- estimate_R(incidencia_diaria_truncada, method = "parametric_si",
si_data = si_data,
config = config)
# Observamos las primeras estimaciones de R(t)
head(estimacion_rt$R[, c("t_start", "t_end", "Median(R)",
"Quantile.0.025(R)", "Quantile.0.975(R)")])
SALIDA
t_start t_end Median(R) Quantile.0.025(R) Quantile.0.975(R)
1 2 8 NA NA NA
2 3 9 2.173592 0.3136801 7.215718
3 4 10 2.148673 0.3100840 7.132996
4 5 11 2.060726 0.2973920 6.841036
5 6 12 1.960940 0.2829915 6.509775
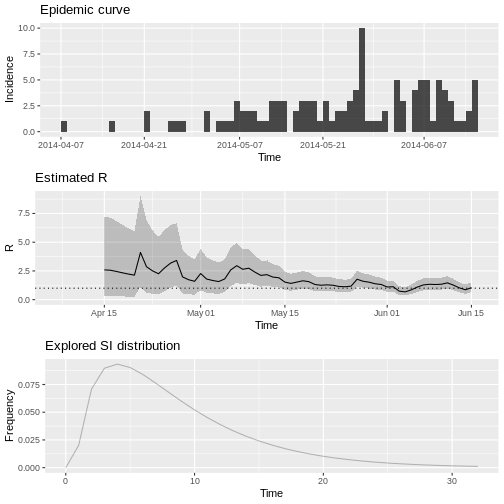
6 7 13 1.869417 0.2697834 6.205943Grafique la estimación de \(R\) como función del tiempo:
R
plot(estimacion_rt, legend = FALSE)
Sobre este documento
Este documento ha sido una adaptación de los materiales originales disponibles en RECON Learn
Contribuciones
Autores originales:
Anne Cori
Natsuko Imai
Finlay Campbell
Zhian N. Kamvar
Thibaut Jombart
Cambios menores y adaptación a español:
José M. Velasco-España
Cándida Díaz-Brochero
Nicolas Torres
Zulma M. Cucunubá
Puntos clave
Revise si al final de esta lección adquirió estas competencias:
Identificar los parámetros necesarios en casos de transmisión de enfermedades infecciosas de persona a persona.
Estimar la probabilidad de muerte (CFR).
Calcular y graficar la incidencia.
Estimar e interpretar la tasa de crecimiento y el tiempo en el que se duplica la epidemia.
Estimar e interpretar el número de reproducción instantáneo de la epidemia.
Content from Construyendo un modelo matemático simple para Zika
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo construir un modelo simplificado de zika?
Objetivos
Al final de este taller usted podrá:
- Aplicar conceptos como parámetros, \(R_0\) e inmunidad de rebaño, aprendidos en la sesión A del taller
- Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
- Realizar un modelo simple en R para una enfermedad transmitida por vector
- Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección
1. Introducción
En este taller usted aplicará los conceptos básicos del modelamiento de Enfermedades Transmitidas por Vectores (ETV) mediante el uso del lenguaje R con énfasis en el funcionamiento de los métodos, utilizando como ejemplo un modelo básico de infección por un arbovirus: el virus del Zika.
2. Agenda
- Instrucciones (5 mins)
- Desarrollo taller Zika Parte B (45 mins con acompañamiento de monitores)
- Revisión grupal del código (10 mins)
- Revisión de resultados (20 mins)
- Descanso (25 mins)
- Discusión final (60 mins)
3. Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
- Modelo SIR para ETV Zika
- Parametrización de un modelo dinámico
- Evaluación de un modelo dinámico
- Parametrización de intervenciones de control (fumigación, mosquiteros y vacunación) para una ETV
4. Paquetes requeridos
Cargue los paquetes necesarios ingresando en R los siguientes comandos:
R
library(deSolve) # Paquete deSolve para resolver las ecuaciones diferenciales
library(tidyverse) # Paquetes ggplot2 y dplyr de tidyverse
library(cowplot) # Paquete gridExtra para unir gráficos.
- Si desea puede tomar notas en el script de R, para esto se recomienda usar el símbolo de comentario # después de cada línea de código (ver ejemplo arriba). O podría utilizar un archivo Rmd para tener un aspecto similar al del taller.
5. Compartimentos del modelo básico de Zika
- \(S_h\) : Humanos susceptibles
- \(I_h\) : Humanos infecciosos
- \(R_h\) : Humanos recuperados de la infección (inmunizados frente a nueva infección)
- \(S_v\) : Vectores susceptibles
- \(E_v\) : Vectores expuestos
- \(I_v\) : Vectores infecciosos
6. Parámetros del modelo
Ahora se usarán los parámetros que discutimos en la parte A del taller. Si aún no los tiene, estos se pueden encontrar en la guía de aprendizaje de la parte A del taller.
Desafío 1
Busque los valores de los parámetros del modelo y diligéncielos en el recuadro de abajo. Tenga en cuenta que todos los parámetros usados tienen la misma unidad de tiempo (días).
R
Lv <- # Esperanza de vida de los mosquitos (en días)
Lh <- # Esperanza de vida de los humanos (en días)
PIh <- # Periodo infeccioso en humanos (en días)
PIv <- # Periodo infeccioso en vectores (en días)
PEI <- # Período extrínseco de incubación en mosquitos adultos (en días)
muv <- # Tasa per capita de mortalidad del vector (1/Lv)
muh <- # Tasa per capita de mortalidad del hospedador (1/Lh)
alphav <- # Tasa per capita de natalidad del vector
alphah <- # Tasa per capita de natalidad del hospedador
gamma <- # Tasa de recuperación en humanos (1/PIh)
delta <- # Tasa extrínseca de incubación (1/PEI)
ph <- # Probabilidad de transmisión del vector al hospedador dada una picadura por un mosquito infeccioso a un humano susceptible
pv <- # Probabilidad de transmisión del hospedador al vector dada una picadura por un mosquito susceptible a un humano infeccioso
Nh <- # Número de humanos
m <- # Densidad de mosquitos hembra por humano
Nv <- # Número de vectores (m * Nh)
R0 <- # Número reproductivo básico
b <- sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
(m * ph * pv * delta)) # Tasa de picadura
betah <- # Coeficiente de transmisión del mosquito al humano
betav <- # Coeficiente de transmisión del humano al mosquito
TIME <- # Número de años que se va a simular 7. Ecuaciones del modelo
Para este modelo emplearemos las siguientes ecuaciones diferenciales:
8. Fórmula para calcular \(R_0\) (Número reproductivo básico)
Fórmula necesaria para estimar \(R_0\):
\[ R_0 = \frac{mb^2 p_h p_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma)} \]
9. Modelo en R
Es hora de implementar el modelo en R. Para lograrlo, usaremos la
función ode del paquete desolve. Para el ejercicio
se emplearán 4 argumentos de la función esta función: el primero son las
condiciones iniciales del modelo (argumento y); el segundo
es la secuencia temporal donde se ejecutará el modelo (argumento
times); el tercero es una función que contiene las
ecuaciones diferenciales que entrarán al sistema (argumento
fun); por último un vector que contiene los parámetros con
los que se calculará el sistema (argumento parms).
R
# NO la copie a R sólo tiene fines ilustrativos.
ode(y = # Condiciones iniciales,
times = # Tiempo,
fun = # Modelo o función que lo contenga,
parms = # Parámetros
)Desafío 2
En esta sección se empezará por crear la función (argumento
fun), para ello es necesario traducir las ecuaciones del
modelo a R. Abajo encontrará la función ya construida, por favor
reemplace los parámetros faltantes (Cambie PAR por los
parámetro correspondientes) en las ecuaciones:
R
arbovmodel <- function(t, x, params) {
Sh <- x[1] # Humanos susceptibles
Ih <- x[2] # Humanos infecciosos
Rh <- x[3] # Humanos recuperados
Sv <- x[4] # Vectores susceptibles
Ev <- x[5] # Vectores expuestos
Iv <- x[6] # Vectores infecciosos
with(as.list(params), # entorno local para evaluar derivados
{
# Humanos
dSh <- PAR * Nh - PAR * (Iv/Nh) * Sh - PAR * Sh
dIh <- PAR * (Iv/Nh) * Sh - (PAR + PAR) * Ih
dRh <- PAR * Ih - PAR * Rh
# Vectores
dSv <- alphav * Nv - PAR * (Ih/Nh) * Sv - PAR * Sv
dEv <- PAR * (Ih/Nh) * Sv - (PAR + PAR)* Ev
dIv <- PAR * Ev - PAR * Iv
dx <- c(dSh, dIh, dRh, dSv, dEv, dIv)
list(dx)
}
)
}
10. Resuelva el Sistema
En esta sección se crearán los tres argumentos faltantes para usar la
función ode y se creará un objeto de clase
data.frame con los resultados de la función
ode. Por favor complete y comente el código para:
Los VALORES de las condiciones iniciales del sistema.
Los ARGUMENTOS de la función
odeen el paquete deSolve.
Desafío 3
R
# Secuencia temporal (times)
times <- seq(1, 365 * TIME , by = 1)
# Los parámetros (parms)
params <- c(
muv = muv,
muh = muh,
alphav = alphav,
alphah = alphah,
gamma = gamma,
delta = delta,
betav = betav,
betah = betah,
Nh = Nh,
Nv = Nv
)
# Condiciones iniciales del sistema (y)
xstart <- c(Sh = VALOR?, # COMPLETE Y COMENTE
Ih = VALOR?, # COMPLETE Y COMENTE
Rh = VALOR?, # COMPLETE Y COMENTE
Sv = VALOR?, # COMPLETE Y COMENTE
Ev = VALOR?, # COMPLETE Y COMENTE
Iv = VALOR?) # COMPLETE Y COMENTE
# Resuelva las ecuaciones
out <- as.data.frame(ode(y = ARGUMENTO?, # COMPLETE Y COMENTE
times = ARGUMENTO?, # COMPLETE Y COMENTE
fun = ARGUMENTO?, # COMPLETE Y COMENTE
parms = ARGUMENTO?)) # COMPLETE Y COMENTE11. Resultados
Observe el comportamiento del modelo en distintas escalas de tiempo (semanas y años):
11.1 Comportamiento General (Población humana)
R
# Revise el comportamiento general del modelo para 100 años
p1h <- ggplot(data = out, aes(y = (Rh + Ih + Sh), x = years)) +
geom_line(color = 'grey68', size = 1) +
ggtitle('Población humana total') +
theme_bw() + ylab('Número') + xlab('Años')
p2h <- ggplot(data = out, aes(y = Sh, x = years)) +
geom_line(color = 'royalblue', size = 1) +
ggtitle('Población humana susceptible') +
theme_bw() + ylab('Número') + xlab('Años')
p3h <- ggplot(data = out, aes(y = Ih, x = years)) +
geom_line(color = 'firebrick', size = 1) +
ggtitle('Población humana infecciosa') +
theme_bw() + ylab('Número') + xlab('Años')
p4h <- ggplot(data = out, aes(y = Rh, x = years)) +
geom_line(color = 'olivedrab', size = 1) +
ggtitle('Población humana recuperada') +
theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1h, p2h, p3h, p4h, ncol = 2)
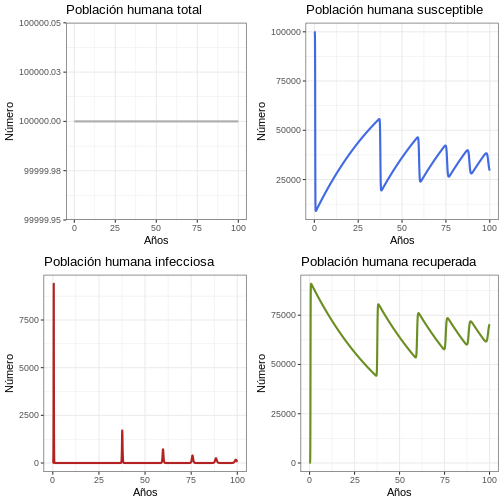
11.2 Comportamiento General (Población de vectores)
R
# Revise el comportamiento general del modelo
p1v <- ggplot(data = out, aes(y = (Sv + Ev + Iv), x = years)) +
geom_line(color = 'grey68', size = 1) +
ggtitle('Población total de mosquitos') +
theme_bw() + ylab('Número') + xlab('Años')
p2v <- ggplot(data = out, aes(y = Sv, x = years)) +
geom_line(color = 'royalblue', size = 1) +
ggtitle('Población susceptible de mosquitos') +
theme_bw() + ylab('Número') + xlab('Años')
p3v <- ggplot(data = out, aes(y = Ev, x = years)) +
geom_line(color = 'orchid', size = 1) +
ggtitle('Población expuesta de mosquitos') +
theme_bw() + ylab('Número') + xlab('Años')
p4v <- ggplot(data = out, aes(y = Iv, x = years)) +
geom_line(color = 'firebrick', size = 1) +
ggtitle('Población infecciosa de mosquitos') +
theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1v, p2v, p3v, p4v, ncol = 2)
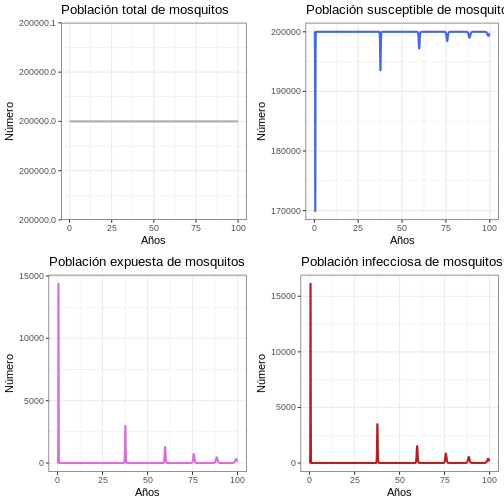
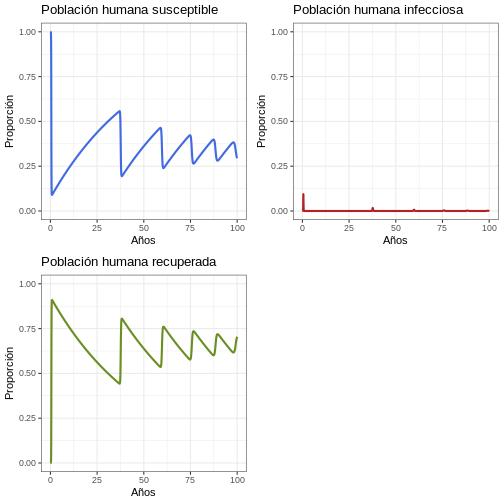
11.3 Proporción
Por favor dé una mirada más cuidadosa a las proporciones y discútalas
R
p1 <- ggplot(data = out, aes(y = Sh/(Sh+Ih+Rh), x = years)) +
geom_line(color = 'royalblue', size = 1) +
ggtitle('Población humana susceptible') +
theme_bw() + ylab('Proporción') + xlab('Años') +
coord_cartesian(ylim = c(0,1))
p2 <- ggplot(data = out, aes(y = Ih/(Sh+Ih+Rh), x = years)) +
geom_line(color = 'firebrick', size = 1) +
ggtitle('Población humana infecciosa') +
theme_bw() + ylab('Proporción') + xlab('Años') +
coord_cartesian(ylim = c(0,1))
p3 <- ggplot(data = out, aes(y = Rh/(Sh+Ih+Rh), x = years)) +
geom_line(color = 'olivedrab', size = 1) +
ggtitle('Población humana recuperada') +
theme_bw() + ylab('Proporción') + xlab('Años') +
coord_cartesian(ylim = c(0,1))
plot_grid(p1, p2, p3, ncol = 2)
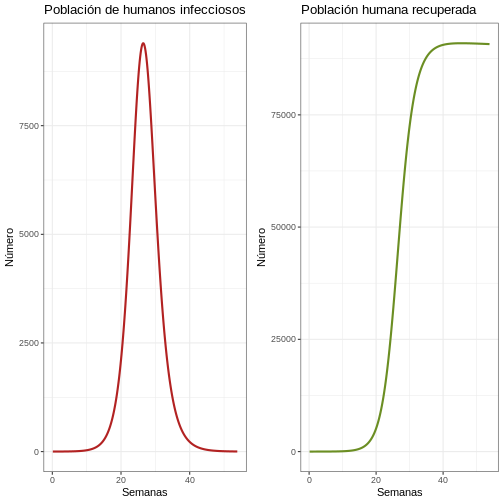
11.4 La primera epidemia
R
# Revise la primera epidemia
dat <- out %>% filter(weeks < 54)
p1e <- ggplot(dat, aes(y = Ih, x = weeks)) +
geom_line(color = 'firebrick', size = 1) +
ggtitle('Población de humanos infecciosos') +
theme_bw() + ylab('Número') + xlab('Semanas')
p2e <- ggplot(dat, aes(y = Rh, x = weeks)) +
geom_line(color = 'olivedrab', size = 1) +
ggtitle('Población humana recuperada') +
theme_bw() + ylab('Número') + xlab('Semanas')
plot_grid(p1e, p2e)
11.5 Algunos aspectos por discutir
- ¿Qué tan sensible es el modelo a cambios en el \(R_0\)?
- ¿Qué razones hay (según el modelo) para el intervalo de tiempo entre estas epidemias simuladas?
- ¿Cómo se puede calcular la tasa de ataque?
11.6 Modele una o más intervenciones de control
Ahora, utilizando este modelo básico, modelar por grupos el impacto de las siguientes intervenciones:
- Grupo 1. Fumigación contra mosquitos
- Grupo 2. Mosquiteros/angeos
- Grupo 3. Vacunación que previene frente a infecciones
Para cada intervención:
Indique en qué parte del modelo haría los cambios.
De acuerdo a la literatura que explique estas intervenciones y describa cómo parametrizará el modelo. ¿Todas estas intervenciones son viables en la actualidad?
Sobre este documento
Contribuciones
- Zulma Cucunuba & Pierre Nouvellet: Versión inicial
- Kelly Charinga & Zhian N. Kamvar: Edición
- José M. Velasco-España: Traducción de Inglés a Español y Edición
- Andree Valle-Campos: Ediciones menores
Contribuciones son bienvenidas vía pull requests. El archivo fuente del documento original puede ser encontrado aquí.
Asuntos legales
Licencia: CC-BY Copyright: Zulma Cucunuba & Pierre Nouvellet, 2017
Puntos clave
Revise si al final de esta lección adquirió estas competencias:
- Aplicar conceptos como parámetros, \(R_0\) e inmunidad de rebaño, aprendidos en la sesión A del taller
- Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
- Realizar un modelo simple en R para una enfermedad transmitida por vector
- Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección
Content from Estimación de las distribuciones de rezagos epidemiológicos: Enfermedad X
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo responder ante un brote de una enfermedad desconocida?
Objetivos
Al final de este taller usted podrá:
Comprender los conceptos clave de las distribuciones de rezagos epidemiológicos para la Enfermedad X.
Comprender las estructuras de datos y las herramientas para el análisis de datos de rastreo de contactos.
Aprender a ajustar las estimaciones del intervalo serial y el período de incubación de la Enfermedad X teniendo en cuenta la censura por intervalo utilizando un marco de trabajo Bayesiano.
Aprender a utilizar estos parámetros para informar estrategias de control en un brote de un patógeno desconocido.
1. Introducción
La Enfermedad X representa un hipotético, pero plausible, brote de una enfermedad infecciosa en el futuro. Este término fue acuñado por la Organización Mundial de la Salud (OMS) y sirve como un término general para un patógeno desconocido que podría causar una epidemia grave a nivel internacional. Este concepto representa la naturaleza impredecible de la aparición de enfermedades infecciosas y resalta la necesidad de una preparación global y mecanismos de respuesta rápida. La Enfermedad X simboliza el potencial de una enfermedad inesperada y de rápida propagación, y resalta la necesidad de sistemas de salud flexibles y adaptables, así como capacidades de investigación para identificar, comprender y combatir patógenos desconocidos.
En esta práctica, va a aprender a estimar los rezagos epidemiológicos, el tiempo entre dos eventos epidemiológicos, utilizando un conjunto de datos simulado de la Enfermedad X.
La Enfermedad X es causada por un patógeno desconocido y se transmite directamente de persona a persona. Específicamente, la practica se centrará en estimar el período de incubación y el intervalo serial.
2. Agenda
Parte 1. Individual o en grupo.
Parte 2. En grupos de 6 personas. Construir estrategia de rastreo de contactos y aislamiento y preparar presentación de máximo 10 mins.
3. Conceptos claves
3.1. Rezagos epidemiológicos: Período de incubación e intervalo serial
En epidemiología, las distribuciones de rezagos se refieren a los retrasos temporales entre dos eventos clave durante un brote. Por ejemplo: el tiempo entre el inicio de los síntomas y el diagnóstico, el tiempo entre la aparición de síntomas y la muerte, entre muchos otros.
Este taller se enfocará en dos rezagos clave conocidos como el período de incubación y el intervalo serial. Ambos son cruciales para informar la respuesta de salud pública.
El período de incubación es el tiempo entre la infección y la aparición de síntomas.
El intervalo serial es el tiempo entre la aparición de síntomas entre el caso primario y secundario.
La relación entre estos parámetros tiene un impacto en si la enfermedad se transmite antes (transmisión pre-sintomática) o después de que los síntomas (transmisión sintomática) se hayan desarrollado en el caso primario (Figura 1).
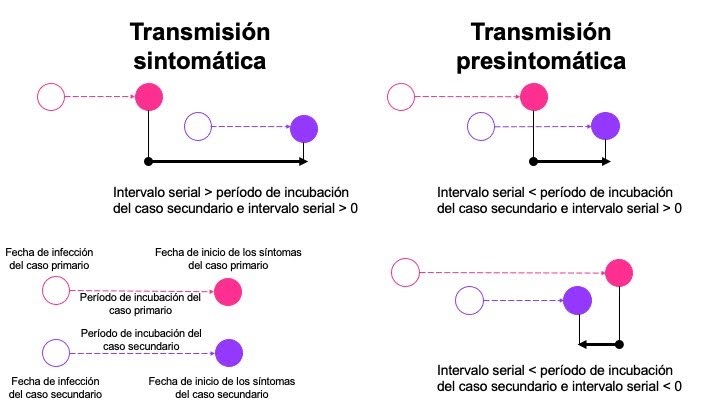
Figura 1. Relación entre el período de incubación y el intervalo serial en el momento de la transmisión (Adaptado de Nishiura et al. 2020)
3.2. Distribuciones comunes de rezagos y posibles sesgos
3.2.1 Sesgos potenciales
Cuando se estiman rezagos epidemiológicos, es importante considerar posibles sesgos:
Censura significa que sabemos que un evento ocurrió, pero no sabemos exactamente cuándo sucedió. La mayoría de los datos epidemiológicos están “doblemente censurados” debido a la incertidumbre que rodea tanto los tiempos de eventos primarios como secundarios. No tener en cuenta la censura puede llevar a estimaciones sesgadas de la desviación estándar del resago (Park et al. en progreso).
Truncamiento a la derecha es un tipo de sesgo de muestreo relacionado con el proceso de recolección de datos. Surge porque solo se pueden observar los casos que han sido reportados. No tener en cuenta el truncamiento a la derecha durante la fase de crecimiento de una epidemia puede llevar a una subestimación del rezago medio (Park et al. en progreso).
El sesgo dinámico (o de fase epidémica) es otro tipo de sesgo de muestreo. Afecta a los datos retrospectivos y está relacionado con la fase de la epidemia: durante la fase de crecimiento exponencial, los casos que desarrollaron síntomas recientemente están sobrerrepresentados en los datos observados, mientras que durante la fase de declive, estos casos están subrepresentados, lo que lleva a la estimación de intervalos de retraso más cortos y más largos, respectivamente (Park et al. en progreso).
3.2.2 Distribuciones de rezagos
Tres distribuciones de probabilidad comunes utilizadas para caracterizar rezagos en epidemiología de enfermedades infecciosas (Tabla 1):
| Distribución | Parámetros |
|---|---|
| Weibull |
shape y scale (forma y
escala) |
| gamma |
shape y scale (forma y
escala) |
| log normal |
log mean y
log standard deviation (media y desviación estándar
logarítmica) |
4. Paquetes de R para la practica
En esta practica se usarán los siguientes paquetes de
R:
dplyrpara manejo de datosepicontactspara visualizar los datos de rastreo de contactosggplot2ypatchworkpara gráficarincidencepara visualizar curvas epidemicasrstanpara estimar el período de incubacióncoarseDataToolsviaEpiEstimpara estimar el intervalo serial
Instrucciones de instalación para los paquetes:
Para cargar los paquetes, escriba:
R
library(dplyr)
library(epicontacts)
library(incidence)
library(coarseDataTools)
library(EpiEstim)
library(ggplot2)
library(loo)
library(patchwork)
library(rstan)
Para este taller, las autoras han creado algunas funciones que serán necesarias para el buen funcionamiento del mismo. Por favor, copie el siguiente texto, selecciónelo y ejecútelo para tener estas funciones en su ambiente global y poderlas utilizar.
R
## Calcule la verosimilitud DIC mediante integración
diclik <- function(par1, par2, EL, ER, SL, SR, dist){
## Si la ventana de síntomas es mayor que la ventana de exposición
if(SR-SL>ER-EL){
dic1 <- integrate(fw1, lower=SL-ER, upper=SL-EL,
subdivisions=10,
par1=par1, par2=par2,
EL=EL, ER=ER, SL=SL, SR=SR,
dist=dist)$value
if (dist == "W"){
dic2 <- (ER-EL)*
(pweibull(SR-ER, shape=par1, scale=par2) - pweibull(SL-EL, shape=par1, scale=par2))
} else if (dist == "off1W"){
dic2 <- (ER-EL)*
(pweibullOff1(SR-ER, shape=par1, scale=par2) - pweibullOff1(SL-EL, shape=par1, scale=par2))
} else if (dist == "G"){
dic2 <- (ER-EL)*
(pgamma(SR-ER, shape=par1, scale=par2) - pgamma(SL-EL, shape=par1, scale=par2))
} else if (dist == "off1G"){
dic2 <- (ER-EL)*
(pgammaOff1(SR-ER, shape=par1, scale=par2) - pgammaOff1(SL-EL, shape=par1, scale=par2))
} else if (dist == "L") {
dic2 <- (ER-EL)*
(plnorm(SR-ER, par1, par2) - plnorm(SL-EL, par1, par2))
} else if (dist == "off1L") {
dic2 <- (ER-EL)*
(plnormOff1(SR-ER, par1, par2) - plnormOff1(SL-EL, par1, par2))
} else {
stop("distribution not supported")
}
dic3 <- integrate(fw3, lower=SR-ER, upper=SR-EL,
subdivisions=10,
par1=par1, par2=par2,
EL=EL, ER=ER, SL=SL, SR=SR,
dist=dist)$value
return(dic1 + dic2 + dic3)
}
## Si la ventana de exposición es mayor que la ventana de síntomas
else{
dic1 <- integrate(fw1, lower=SL-ER, upper=SR-ER, subdivisions=10,
par1=par1, par2=par2,
EL=EL, ER=ER, SL=SL, SR=SR,
dist=dist)$value
if (dist == "W"){
dic2 <- (SR-SL)*
(pweibull(SL-EL, shape=par1, scale=par2) - pweibull(SR-ER, shape=par1, scale=par2))
} else if (dist == "off1W"){
dic2 <- (SR-SL)*
(pweibullOff1(SL-EL, shape=par1, scale=par2) - pweibullOff1(SR-ER, shape=par1, scale=par2))
} else if (dist == "G"){
dic2 <- (SR-SL)*
(pgamma(SL-EL, shape=par1, scale=par2) - pgamma(SR-ER, shape=par1, scale=par2))
} else if (dist == "off1G"){
dic2 <- (SR-SL)*
(pgammaOff1(SL-EL, shape=par1, scale=par2) - pgammaOff1(SR-ER, shape=par1, scale=par2))
} else if (dist == "L"){
dic2 <- (SR-SL)*
(plnorm(SL-EL, par1, par2) - plnorm(SR-ER, par1, par2))
} else if (dist == "off1L"){
dic2 <- (SR-SL)*
(plnormOff1(SL-EL, par1, par2) - plnormOff1(SR-ER, par1, par2))
} else {
stop("distribution not supported")
}
dic3 <- integrate(fw3, lower=SL-EL, upper=SR-EL,
subdivisions=10,
par1=par1, par2=par2,
EL=EL, ER=ER, SL=SL, SR=SR,
dist=dist)$value
return(dic1 + dic2 + dic3)
}
}
## Esta verosimilitud DIC está diseñada para datos que tienen intervalos superpuestos
diclik2 <- function(par1, par2, EL, ER, SL, SR, dist){
if(SL>ER) {
return(diclik(par1, par2, EL, ER, SL, SR, dist))
} else {
lik1 <- integrate(diclik2.helper1, lower=EL, upper=SL,
SL=SL, SR=SR, par1=par1, par2=par2, dist=dist)$value
lik2 <- integrate(diclik2.helper2, lower=SL, upper=ER,
SR=SR, par1=par1, par2=par2, dist=dist)$value
return(lik1+lik2)
}
}
## Funciones de verosimilitud para diclik2
diclik2.helper1 <- function(x, SL, SR, par1, par2, dist){
if (dist =="W"){
pweibull(SR-x, shape=par1, scale=par2) - pweibull(SL-x, shape=par1, scale=par2)
} else if (dist =="off1W") {
pweibullOff1(SR-x, shape=par1, scale=par2) - pweibullOff1(SL-x, shape=par1, scale=par2)
} else if (dist =="G") {
pgamma(SR-x, shape=par1, scale=par2) - pgamma(SL-x, shape=par1, scale=par2)
} else if (dist=="off1G"){
pgammaOff1(SR-x, shape=par1, scale=par2) - pgammaOff1(SL-x, shape=par1, scale=par2)
} else if (dist == "L"){
plnorm(SR-x, par1, par2) - plnorm(SL-x, par1, par2)
} else if (dist == "off1L"){
plnormOff1(SR-x, par1, par2) - plnormOff1(SL-x, par1, par2)
} else {
stop("distribution not supported")
}
}
diclik2.helper2 <- function(x, SR, par1, par2, dist){
if (dist =="W"){
pweibull(SR-x, shape=par1, scale=par2)
} else if (dist =="off1W") {
pweibullOff1(SR-x, shape=par1, scale=par2)
} else if (dist =="G") {
pgamma(SR-x, shape=par1, scale=par2)
} else if (dist =="off1G") {
pgammaOff1(SR-x, shape=par1, scale=par2)
} else if (dist=="L"){
plnorm(SR-x, par1, par2)
} else if (dist=="off1L"){
plnormOff1(SR-x, par1, par2)
} else {
stop("distribution not supported")
}
}
## Funciones que manipulan/calculan la verosimilitud para los datos censurados
## Las funciones codificadas aquí se toman directamente de las
## notas de verosimilitud censurada por intervalos dobles.
fw1 <- function(t, EL, ER, SL, SR, par1, par2, dist){
## Función que calcula la primera función para la integral DIC
if (dist=="W"){
(ER-SL+t) * dweibull(x=t,shape=par1,scale=par2)
} else if (dist=="off1W") {
(ER-SL+t) * dweibullOff1(x=t,shape=par1,scale=par2)
} else if (dist=="G") {
(ER-SL+t) * dgamma(x=t, shape=par1, scale=par2)
} else if (dist=="off1G") {
(ER-SL+t) * dgammaOff1(x=t, shape=par1, scale=par2)
} else if (dist =="L"){
(ER-SL+t) * dlnorm(x=t, meanlog=par1, sdlog=par2)
} else if (dist =="off1L"){
(ER-SL+t) * dlnormOff1(x=t, meanlog=par1, sdlog=par2)
} else {
stop("distribution not supported")
}
}
fw3 <- function(t, EL, ER, SL, SR, par1, par2, dist){
## Función que calcula la tercera función para la integral DIC
if (dist == "W"){
(SR-EL-t) * dweibull(x=t, shape=par1, scale=par2)
} else if (dist == "off1W"){
(SR-EL-t) * dweibullOff1(x=t, shape=par1, scale=par2)
} else if (dist == "G"){
(SR-EL-t) * dgamma(x=t, shape=par1, scale=par2)
} else if (dist == "off1G"){
(SR-EL-t) * dgammaOff1(x=t, shape=par1, scale=par2)
} else if (dist == "L") {
(SR-EL-t) * dlnorm(x=t, meanlog=par1, sdlog=par2)
} else if (dist == "off1L"){
(SR-EL-t) * dlnormOff1(x=t, meanlog=par1, sdlog=par2)
} else {
stop("distribution not supported")
}
}
5. Datos
Esta práctica está partida en dos grupos para abordar dos enfermedades desconocidas con diferentes modos de transmisión.
Cargue los datos simulados que están guardados como un archivo .RDS, de acuerdo a su grupo asignado. Puede encontrar esta información en la carpeta Enfermedad X. Descargue la carpeta, extráigala en el computador y abra el proyecto de R.
Hay dos elementos de interés:
linelist, un archivo que contiene una lista de casos de la Enfermedad X, un caso por fila.contacts, un archivo con datos de rastreo de contactos que contiene información sobre pares de casos primarios y secundarios.
R
# Grupo 1
dat <- readRDS("data/practical_data_group1.RDS")
linelist <- dat$linelist
contacts <- dat$contacts
6. Exploración de los datos
6.1. Exploración de los datos en
linelist
Empiece con linelist. Estos datos fueron recolectados
como parte de la vigilancia epidemiológica rutinaria. Cada fila
representa un caso de la Enfermedad X, y hay 7 variables:
id: número único de identificación del casodate_onset: fecha de inicio de los síntomas del pacientesex: : M = masculino; F = femeninoage: edad del paciente en añosexposure: información sobre cómo el paciente podría haber estado expuestoexposure_start: primera fecha en que el paciente estuvo expuestoexposure_end: última fecha en que el paciente estuvo expuesto
💡 Preguntas (1)
¿Cuántos casos hay en los datos de
linelist?¿Qué proporción de los casos son femeninos?
¿Cuál es la distribución de edades de los casos?
¿Qué tipo de información sobre la exposición está disponible?
R
# Inspecionar los datos
head(linelist)
SALIDA
id date_onset sex age exposure exposure_start exposure_end
1 1 2023-10-01 M 34 Close, skin-to-skin contact <NA> <NA>
2 2 2023-10-03 F 38 Close, skin-to-skin contact 2023-09-29 2023-09-29
3 3 2023-10-06 F 38 Close, skin-to-skin contact 2023-09-28 2023-09-28
4 4 2023-10-10 F 37 <NA> 2023-09-25 2023-09-27
5 5 2023-10-11 F 33 <NA> 2023-10-05 2023-10-05
6 6 2023-10-12 F 34 Close, skin-to-skin contact 2023-10-10 2023-10-10R
# P1
nrow(linelist)
SALIDA
[1] 166R
# P2
table(linelist$sex)[2]/nrow(linelist)
SALIDA
M
0.6144578 R
# P3
summary(linelist$age)
SALIDA
Min. 1st Qu. Median Mean 3rd Qu. Max.
22.00 33.00 36.00 35.51 38.00 47.00 R
# P4
table(linelist$exposure, exclude = F)[1]/nrow(linelist)
SALIDA
Close, skin-to-skin contact
0.6626506 💡 Discusión
¿Por qué cree que falta la información de exposición en algunos casos?
Ahora, grafique la curva epidémica. ¿En qué parte del brote cree que está (principio, medio, final)?
R
i <- incidence(linelist$date_onset)
plot(i) +
theme_classic() +
scale_fill_manual(values = "purple") +
theme(legend.position = "none")
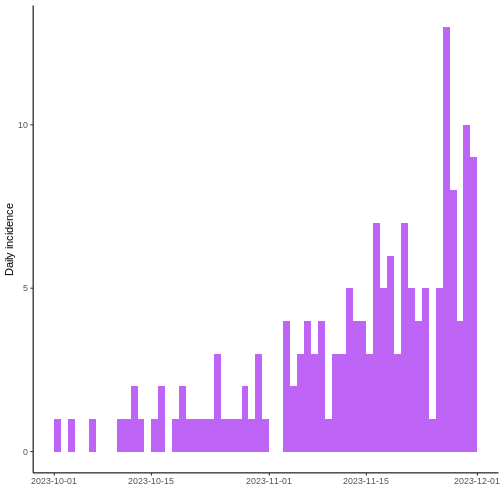
Parece que la epidemia todavía podría esta creciendo.
6.2. Exploración de los datos de
rastreo de contactos
Ahora vea los datos de rastreo de contactos, que se obtuvieron a través de entrevistas a los pacientes. A los pacientes se les preguntó sobre actividades e interacciones recientes para identificar posibles fuentes de infección. Se emparejaron pares de casos primarios y secundarios si el caso secundario nombraba al caso primario como un contacto. Solo hay información de un subconjunto de los casos porque no todos los pacientes pudieron ser contactados para una entrevista.
Note que para este ejercicio, se asumirá que los casos secundarios solo tenían un posible infectante. En realidad, la posibilidad de que un caso tenga múltiples posibles infectantes necesita ser evaluada.
Los datos de rastreo de contactos tienen 4 variables:
primary_case_id: número de identificación único para el caso primario (infectante)secondary_case_id: número de identificación único para el caso secundario (infectado)primary_onset_date: fecha de inicio de síntomas del caso primariosecondary_onset_date: fecha de inicio de síntomas del caso secundario
R
x <- make_epicontacts(linelist = linelist,
contacts = contacts,
from = "primary_case_id",
to = "secondary_case_id",
directed = TRUE) # Esto indica que los contactos son directos (i.e., este gráfico traza una flecha desde los casos primarios a los secundarios)
plot(x)
💡 Preguntas (2)
- Describa los grupos (clusters).
- ¿Ve algún evento potencial de superpropagación (donde un caso propaga el patógeno a muchos otros casos)?
_______Pausa 1 _________
7. Estimación del período de incubación
Ahora, enfoquese en el período de incubación. Se utilizará los datos
del linelist para esta parte. Se necesitan ambos el tiempo
de inicio de sintomas y el timpo de la posible exposición. Note que en
los datos hay dos fechas de exposición, una de inicio y una de final.
Algunas veces la fecha exacta de exposición es desconocida y en su lugar
se obtiene la ventana de exposición durante la entrevista.
💡 Preguntas (3)
¿Para cuántos casos tiene datos tanto de la fecha de inicio de síntomas como de exposición?
Calcule las ventanas de exposición. ¿Cuántos casos tienen una única fecha de exposición?
R
ip <- filter(linelist, !is.na(exposure_start) &
!is.na(exposure_end))
nrow(ip)
SALIDA
[1] 50R
ip$exposure_window <- as.numeric(ip$exposure_end - ip$exposure_start)
table(ip$exposure_window)
SALIDA
0 1 2
34 11 5 7.1. Estimación naive del período de incubación
Empiece calculando una estimación naive del período de incubación.
R
# Máximo tiempo de período de incubación
ip$max_ip <- ip$date_onset - ip$exposure_start
summary(as.numeric(ip$max_ip))
SALIDA
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 3.00 4.50 6.38 7.75 20.00 R
# Mínimo tiempo de período de incubación
ip$min_ip <- ip$date_onset - ip$exposure_end
summary(as.numeric(ip$min_ip))
SALIDA
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.00 4.00 5.96 7.75 19.00 7.2. Censura estimada ajustada del período de incubación
Ahora, ajuste tres distribuciones de probabilidad a los datos del
período de incubación teniendo en cuenta la censura doble. Adapte un
código de stan que fue publicado por Miura et al. durante
el brote global de mpox de 2022. Este método no tiene en cuenta el
truncamiento a la derecha ni el sesgo dinámico.
Recuerde que el interés principal es considerar tres distribuciones de probabilidad: Weibull, gamma y log normal (Ver Tabla 1).
Stan es un programa de software que implementa el
algoritmo Monte Carlo Hamiltoniano (HMC por su siglas en inglés de
Hamiltonian Monte Carlo). HMC es un método de Monte Carlo de cadena de
Markov (MCMC) para ajustar modelos complejos a datos utilizando
estadísticas bayesianas.
7.1.1. Corra el modelo en Stan
Ajuste las tres distribuciones en este bloque de código.
R
# Prepare los datos
earliest_exposure <- as.Date(min(ip$exposure_start))
ip <- ip |>
mutate(date_onset = as.numeric(date_onset - earliest_exposure),
exposure_start = as.numeric(exposure_start - earliest_exposure),
exposure_end = as.numeric(exposure_end - earliest_exposure)) |>
select(id, date_onset, exposure_start, exposure_end)
# Configure algunas opciones para ejecutar las cadenas MCMC en paralelo
# Ejecución de las cadenas MCMC en paralelo significa que se ejecutaran varias cadenas al mismo tiempo usando varios núcleos de su computador
options(mc.cores=parallel::detectCores())
input_data <- list(N = length(ip$exposure_start), # NNúmero de observaciones
tStartExposure = ip$exposure_start,
tEndExposure = ip$exposure_end,
tSymptomOnset = ip$date_onset)
# tres distribuciones de probabilidad
distributions <- c("weibull", "gamma", "lognormal")
# Código de Stan
code <- sprintf("
data{
int<lower=1> N;
vector[N] tStartExposure;
vector[N] tEndExposure;
vector[N] tSymptomOnset;
}
parameters{
real<lower=0> par[2];
vector<lower=0, upper=1>[N] uE; // Uniform value for sampling between start and end exposure
}
transformed parameters{
vector[N] tE; // infection moment
tE = tStartExposure + uE .* (tEndExposure - tStartExposure);
}
model{
// Contribution to likelihood of incubation period
target += %s_lpdf(tSymptomOnset - tE | par[1], par[2]);
}
generated quantities {
// likelihood for calculation of looIC
vector[N] log_lik;
for (i in 1:N) {
log_lik[i] = %s_lpdf(tSymptomOnset[i] - tE[i] | par[1], par[2]);
}
}
", distributions, distributions)
names(code) <- distributions
# La siguiente línea puede tomar ~1.5 min
models <- mapply(stan_model, model_code = code)
# Toma ~40 sec.
fit <- mapply(sampling, models, list(input_data),
iter=3000, # Número de iteraciones (largo de la cadena MCMC)
warmup=1000, # Número de muestras a descartar al inicio de MCMC
chain=4) # Número de cadenas MCMC a ejecutar
R
pos <- mapply(function(z) rstan::extract(z)$par, fit, SIMPLIFY=FALSE) # muestreo posterior
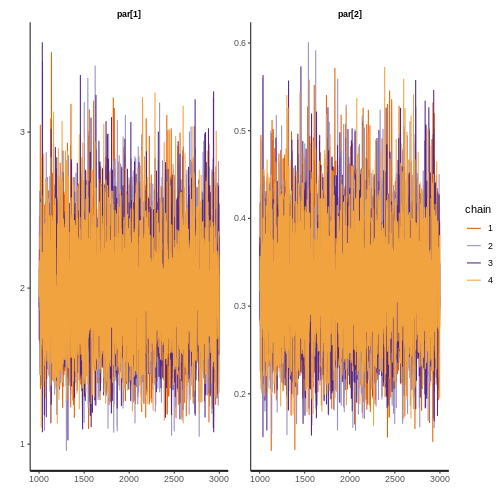
7.1.2. Revisar si hay convergencia
Ahora verifique la convergencia del modelo. Observe los valores de r-hat, los tamaños de muestra efectivos y las trazas MCMC. R-hat compara las estimaciones entre y dentro de cadenas para los parámetros del modelo; valores cercanos a 1 indican que las cadenas se han mezclado bien (Vehtari et al. 2021). El tamaño de muestra efectivo estima el número de muestras independientes después de tener en cuenta la dependencia en las cadenas MCMC (Lambert 2018). Para un modelo con 4 cadenas MCMC, se recomienda un tamaño total de muestra efectiva de al menos 400 (Vehtari et al. 2021).
Para cada modelo con distribución ajustada:
💡 Preguntas (4)
¿Los valores de r-hat son cercanos a 1?
¿Las 4 cadenas MCMC generalmente se superponen y permanecen alrededor de los mismos valores (se ven como orugas peludas)?
7.1.2.1. Convergencia para Gamma
R
print(fit$gamma, digits = 3, pars = c("par[1]","par[2]"))
SALIDA
Inference for Stan model: anon_model.
4 chains, each with iter=3000; warmup=1000; thin=1;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
par[1] 1.976 0.003 0.352 1.345 1.726 1.958 2.205 2.722 11841 1
par[2] 0.324 0.001 0.065 0.210 0.278 0.319 0.364 0.466 10930 1
Samples were drawn using NUTS(diag_e) at Mon Feb 9 10:50:08 2026.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).R
rstan::traceplot(fit$gamma, pars = c("par[1]","par[2]"))
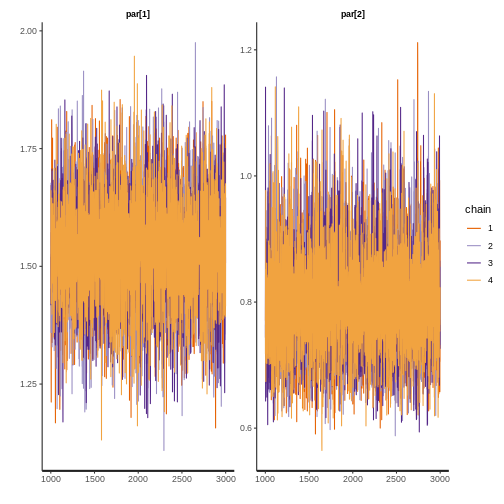
7.1.2.2. Convergencia para log normal
R
print(fit$lognormal, digits = 3, pars = c("par[1]","par[2]"))
SALIDA
Inference for Stan model: anon_model.
4 chains, each with iter=3000; warmup=1000; thin=1;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
par[1] 1.529 0.001 0.115 1.302 1.455 1.529 1.604 1.755 10940 1
par[2] 0.800 0.001 0.082 0.660 0.743 0.793 0.850 0.984 10310 1
Samples were drawn using NUTS(diag_e) at Mon Feb 9 10:50:15 2026.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).R
rstan::traceplot(fit$lognormal, pars = c("par[1]","par[2]"))
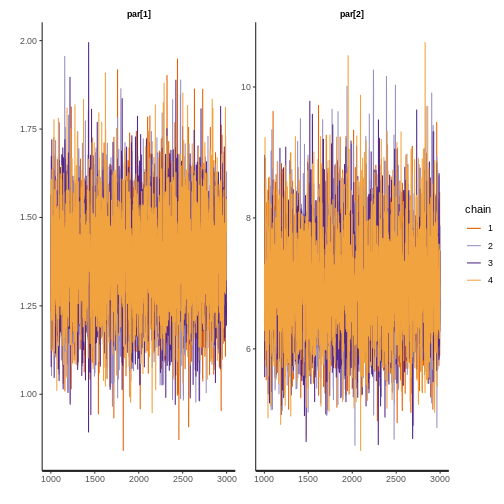
7.1.2.3. Convergencia para Weibull
R
print(fit$weibull, digits = 3, pars = c("par[1]","par[2]"))
SALIDA
Inference for Stan model: anon_model.
4 chains, each with iter=3000; warmup=1000; thin=1;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
par[1] 1.373 0.001 0.145 1.099 1.274 1.368 1.470 1.668 10607 1
par[2] 6.952 0.008 0.768 5.551 6.419 6.921 7.442 8.545 10094 1
Samples were drawn using NUTS(diag_e) at Mon Feb 9 10:50:00 2026.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).R
rstan::traceplot(fit$weibull, pars = c("par[1]","par[2]"))
7.1.3. Calcule los criterios de comparación de los modelos
Calcule el criterio de información ampliamente aplicable (WAIC) y el criterio de información de dejar-uno-fuera (LOOIC) para comparar los ajustes de los modelos. El modelo con mejor ajuste es aquel con el WAIC o LOOIC más bajo. En esta sección también se resumirá las distribuciones y se hará algunos gráficos.
💡 Preguntas (5)
- ¿Qué modelo tiene mejor ajuste?
R
# Calcule WAIC para los tres modelos
waic <- mapply(function(z) waic(extract_log_lik(z))$estimates[3,], fit)
waic
SALIDA
weibull gamma lognormal
Estimate 278.05599 275.87614 272.79644
SE 11.96422 13.38055 13.85682R
# Para looic, se necesita proveer los tamaños de muestra relativos
# al llamar a loo. Este paso lleva a mejores estimados de los tamaños de
# muestra PSIS efectivos y del error de Monte Carlo
# Extraer la verosimilitud puntual logarítmica para la distribución Weibull
loglik <- extract_log_lik(fit$weibull, merge_chains = FALSE)
# Obtener los tamaños de muestra relativos efectivos
r_eff <- relative_eff(exp(loglik), cores = 2)
# Calcula LOOIC
loo_w <- loo(loglik, r_eff = r_eff, cores = 2)$estimates[3,]
# Imprimir los resultados
loo_w[1]
SALIDA
Estimate
278.0684 R
# Extraer la verosimilitud puntual logarítmica para la distribución gamma
loglik <- extract_log_lik(fit$gamma, merge_chains = FALSE)
r_eff <- relative_eff(exp(loglik), cores = 2)
loo_g <- loo(loglik, r_eff = r_eff, cores = 2)$estimates[3,]
loo_g[1]
SALIDA
Estimate
275.8943 R
# Extraer la verosimilitud puntual logarítmica para la distribución log normal
loglik <- extract_log_lik(fit$lognormal, merge_chains = FALSE)
r_eff <- relative_eff(exp(loglik), cores = 2)
loo_l <- loo(loglik, r_eff = r_eff, cores = 2)$estimates[3,]
loo_l[1]
SALIDA
Estimate
272.8118 7.1.4. Reporte los resultados
La cola derecha de la distribución del período de incubación es importante para diseñar estrategias de control (por ejemplo, cuarentena), los percentiles del 25 al 75 informan sobre el momento más probable en que podría ocurrir la aparición de síntomas, y la distribución completa puede usarse como una entrada en modelos matemáticos o estadísticos, como para pronósticos (Lessler et al. 2009).
Obtenga las estadísticas resumidas.
R
# Necesitamos convertir los parámetros de las distribuciones a la media y desviación estándar del rezago
# En Stan, los parámetros de las distribuciones son:
# Weibull: forma y escala
# Gamma: forma e inversa de la escala (aka rate)
# Log Normal: mu y sigma
# Referencia: https://mc-stan.org/docs/2_21/functions-reference/positive-continuous-distributions.html
# Calcule las medias
means <- cbind(
pos$weibull[, 2] * gamma(1 + 1 / pos$weibull[, 1]), # media de Weibull
pos$gamma[, 1] / pos$gamma[, 2], # media de gamma
exp(pos$lognormal[, 1] + pos$lognormal[, 2]^2 / 2) # media de log normal
)
# Calcule las desviaciones estándar
standard_deviations <- cbind(
sqrt(pos$weibull[, 2]^2 * (gamma(1 + 2 / pos$weibull[, 1]) - (gamma(1 + 1 / pos$weibull[, 1]))^2)),
sqrt(pos$gamma[, 1] / (pos$gamma[, 2]^2)),
sqrt((exp(pos$lognormal[, 2]^2) - 1) * (exp(2 * pos$lognormal[, 1] + pos$lognormal[, 2]^2)))
)
# Imprimir los rezagos medios e intervalos creíbles del 95%
probs <- c(0.025, 0.5, 0.975)
res_means <- apply(means, 2, quantile, probs)
colnames(res_means) <- colnames(waic)
res_means
SALIDA
weibull gamma lognormal
2.5% 5.164347 5.078392 5.007976
50% 6.337619 6.112832 6.334840
97.5% 7.850407 7.496816 8.444604R
res_sds <- apply(standard_deviations, 2, quantile, probs)
colnames(res_sds) <- colnames(waic)
res_sds
SALIDA
weibull gamma lognormal
2.5% 3.691537 3.457163 4.008989
50% 4.653073 4.369482 5.907518
97.5% 6.321367 5.781967 10.047042R
# Informe la mediana e intervalos creíbles del 95% para los cuantiles de cada distribución
quantiles_to_report <- c(0.025, 0.05, 0.5, 0.95, 0.975, 0.99)
# Weibull
cens_w_percentiles <- sapply(quantiles_to_report, function(p) quantile(qweibull(p = p, shape = pos$weibull[,1], scale = pos$weibull[,2]), probs = probs))
colnames(cens_w_percentiles) <- quantiles_to_report
print(cens_w_percentiles)
SALIDA
0.025 0.05 0.5 0.95 0.975 0.99
2.5% 0.2185794 0.4150134 4.099327 12.55829 14.42785 16.72733
50% 0.4706396 0.7889995 5.294549 15.36799 17.88761 21.02426
97.5% 0.8397393 1.2861955 6.608721 20.01634 23.85980 28.77434R
# Gamma
cens_g_percentiles <- sapply(quantiles_to_report, function(p) quantile(qgamma(p = p, shape = pos$gamma[,1], rate = pos$gamma[,2]), probs = probs))
colnames(cens_g_percentiles) <- quantiles_to_report
print(cens_g_percentiles)
SALIDA
0.025 0.05 0.5 0.95 0.975 0.99
2.5% 0.3348797 0.5685104 4.112440 11.95506 13.93216 16.44182
50% 0.7211879 1.0629929 5.109289 14.60152 17.17792 20.50946
97.5% 1.1692585 1.5868347 6.245905 18.63239 22.23866 26.83433R
# Log normal
cens_ln_percentiles <- sapply(quantiles_to_report, function(p) quantile(qlnorm(p = p, meanlog = pos$lognormal[,1], sdlog= pos$lognormal[,2]), probs = probs))
colnames(cens_ln_percentiles) <- quantiles_to_report
print(cens_ln_percentiles)
SALIDA
0.025 0.05 0.5 0.95 0.975 0.99
2.5% 0.6267077 0.8429198 3.676783 12.61397 15.69763 20.19985
50% 0.9764945 1.2533841 4.614666 16.99725 21.81898 29.15079
97.5% 1.3681210 1.7016561 5.780718 25.05917 33.67253 47.96688Para cada modelo, encuentre estos elementos para el período de incubación estimado en la salida de arriba y escribalos abajo.
Media e intervalo de credibilidad del 95%
Desviación estándar e intervalo de credibilidad del 95%
Percentiles (e.g., 2.5, 5, 25, 50, 75, 95, 97.5, 99)
Los parámetros de las distribuciones ajustadas (e.g., shape y scale para distribución gamma)
7.1.5. Grafique los resultados
R
# Prepare los resultados para graficarlos
df <- data.frame(
#Tome los valores de las medias para trazar la función de densidad acumulatica empirica
inc_day = ((input_data$tSymptomOnset-input_data$tEndExposure)+(input_data$tSymptomOnset-input_data$tStartExposure))/2
)
x_plot <- seq(0, 30, by=0.1) # Esto configura el rango del eje x (número de días)
Gam_plot <- as.data.frame(list(dose= x_plot,
pred= sapply(x_plot, function(q) quantile(pgamma(q = q, shape = pos$gamma[,1], rate = pos$gamma[,2]), probs = c(0.5))),
low = sapply(x_plot, function(q) quantile(pgamma(q = q, shape = pos$gamma[,1], rate = pos$gamma[,2]), probs = c(0.025))),
upp = sapply(x_plot, function(q) quantile(pgamma(q = q, shape = pos$gamma[,1], rate = pos$gamma[,2]), probs = c(0.975)))
))
Wei_plot <- as.data.frame(list(dose= x_plot,
pred= sapply(x_plot, function(q) quantile(pweibull(q = q, shape = pos$weibull[,1], scale = pos$weibull[,2]), probs = c(0.5))),
low = sapply(x_plot, function(q) quantile(pweibull(q = q, shape = pos$weibull[,1], scale = pos$weibull[,2]), probs = c(0.025))),
upp = sapply(x_plot, function(q) quantile(pweibull(q = q, shape = pos$weibull[,1], scale = pos$weibull[,2]), probs = c(0.975)))
))
ln_plot <- as.data.frame(list(dose= x_plot,
pred= sapply(x_plot, function(q) quantile(plnorm(q = q, meanlog = pos$lognormal[,1], sdlog= pos$lognormal[,2]), probs = c(0.5))),
low = sapply(x_plot, function(q) quantile(plnorm(q = q, meanlog = pos$lognormal[,1], sdlog= pos$lognormal[,2]), probs = c(0.025))),
upp = sapply(x_plot, function(q) quantile(plnorm(q = q, meanlog = pos$lognormal[,1], sdlog= pos$lognormal[,2]), probs = c(0.975)))
))
# Grafique las curvas de la distribución acumulada
gamma_ggplot <- ggplot(df, aes(x=inc_day)) +
stat_ecdf(geom = "step")+
xlim(c(0, 30))+
geom_line(data=Gam_plot, aes(x=x_plot, y=pred), color=RColorBrewer::brewer.pal(11, "RdBu")[11], linewidth=1) +
geom_ribbon(data=Gam_plot, aes(x=x_plot,ymin=low,ymax=upp), fill = RColorBrewer::brewer.pal(11, "RdBu")[11], alpha=0.1) +
theme_bw(base_size = 11)+
labs(x="Incubation period (days)", y = "Proportion")+
ggtitle("Gamma")
weibul_ggplot <- ggplot(df, aes(x=inc_day)) +
stat_ecdf(geom = "step")+
xlim(c(0, 30))+
geom_line(data=Wei_plot, aes(x=x_plot, y=pred), color=RColorBrewer::brewer.pal(11, "RdBu")[11], linewidth=1) +
geom_ribbon(data=Wei_plot, aes(x=x_plot,ymin=low,ymax=upp), fill = RColorBrewer::brewer.pal(11, "RdBu")[11], alpha=0.1) +
theme_bw(base_size = 11)+
labs(x="Incubation period (days)", y = "Proportion")+
ggtitle("Weibull")
lognorm_ggplot <- ggplot(df, aes(x=inc_day)) +
stat_ecdf(geom = "step")+
xlim(c(0, 30))+
geom_line(data=ln_plot, aes(x=x_plot, y=pred), color=RColorBrewer::brewer.pal(11, "RdBu")[11], linewidth=1) +
geom_ribbon(data=ln_plot, aes(x=x_plot,ymin=low,ymax=upp), fill = RColorBrewer::brewer.pal(11, "RdBu")[11], alpha=0.1) +
theme_bw(base_size = 11)+
labs(x="Incubation period (days)", y = "Proportion")+
ggtitle("Log normal")
(lognorm_ggplot|gamma_ggplot|weibul_ggplot) + plot_annotation(tag_levels = 'A')
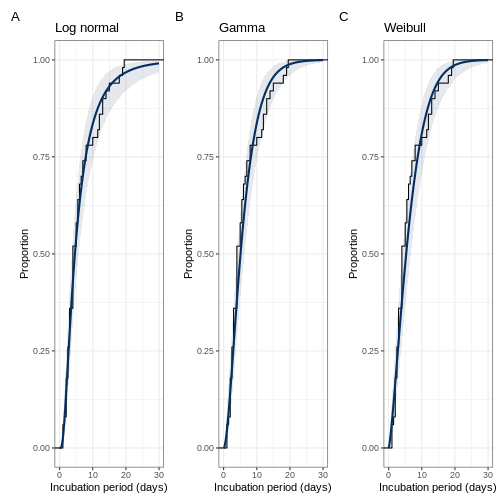
En los gráficos anteriores, la línea negra es la distribución acumulativa empírica (los datos), mientras que la curva azul es la distribución de probabilidad ajustada con los intervalos de credibilidad del 95%. Asegúrese de que la curva azul esté sobre la línea negra.
💡 Preguntas (6)
- ¿Son los ajustes de las distribuciones lo que espera?
_______Pausa 2 _________
8. Estimación del intervalo serial
Ahora, estime el intervalo serial. Nuevamente, se realizará primero una estimación navie calculando la diferencia entre la fecha de inicio de síntomas entre el par de casos primario y secundario.
¿Existen casos con intervalos seriales negativos en los datos (por ejemplo, el inicio de los síntomas en el caso secundario ocurrió antes del inicio de los síntomas en el caso primario)?
Informe la mediana del intervalo serial, así como el mínimo y el máximo.
Grafique la distribución del intervalo serial.
8.1. Estimación naive
R
contacts$diff <- as.numeric(contacts$secondary_onset_date - contacts$primary_onset_date)
summary(contacts$diff)
SALIDA
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 4.000 6.000 7.625 10.000 23.000 R
hist(contacts$diff, xlab = "Serial interval (days)", breaks = 25, main = "", col = "pink")
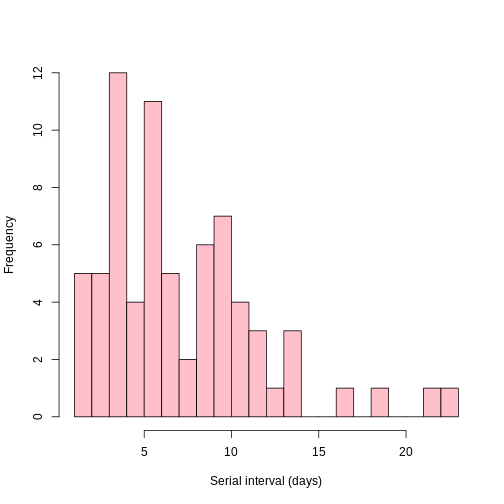
8.2. Estimación ajustada por censura
Ahora se estimará el intervalo serial utilizando una implementación
del paquete courseDataTools dentro del paquete R
EpiEstim. Este método tiene en cuenta la censura doble y
permite comparar diferentes distribuciones de probabilidad, pero no se
ajusta por truncamiento a la derecha o sesgo dinámico.
Se considerará tres distribuciones de probabilidad y deberá seleccionar la que mejor se ajuste a los datos utilizando WAIC o LOOIC. Recuerde que la distribución con mejor ajuste tendrá el WAIC o LOOIC más bajo.
Ten en cuenta que en coarseDataTools, los parámetros
para las distribuciones son ligeramente diferentes que en rstan. Aquí,
los parámetros para la distribución gamma son shape y scale (forma y
escala) (https://cran.r-project.org/web/packages/coarseDataTools/coarseDataTools.pdf).
Solo se ejecutará una cadena MCMC para cada distribución en interés del tiempo, pero en la práctica debería ejecutar más de una cadena para asegurarse de que el MCMC converge en la distribución objetivo. Usará las distribuciones a priori predeterminadas, que se pueden encontrar en la documentación del paquete (ver ‘detalles’ para la función dic.fit.mcmc aquí: (https://cran.r-project.org/web/packages/coarseDataTools/coarseDataTools.pdf).
8.2.1. Preparación de los datos
R
# Formatee los datos de intervalos censurados del intervalo serial
# Cada línea representa un evento de transmisión
# EL/ER muestran el límite inferior/superior de la fecha de inicio de los síntomas en el caso primario (infector)
# SL/SR muestran lo mismo para el caso secundario (infectado)
# type tiene entradas 0 que corresponden a datos censurados doblemente por intervalo
# (ver Reich et al. Statist. Med. 2009)
si_data <- contacts |>
select(-primary_case_id, -secondary_case_id, -primary_onset_date, -secondary_onset_date,) |>
rename(SL = diff) |>
mutate(type = 0, EL = 0, ER = 1, SR = SL + 1) |>
select(EL, ER, SL, SR, type)
8.2.2. Ajuste una distribución gamma para el SI
Primero, ajuste una distribución gamma al intervalo serial.
R
overall_seed <- 3 # semilla para el generador de números aleatorios para MCMC
MCMC_seed <- 007
# Ejecutaremos el modelo durante 4000 iteraciones con las primeras 1000 muestras descartadas como burning
n_mcmc_samples <- 3000 # número de muestras a extraer de la posterior (después del burning)
params = list(
dist = "G", # Ajuste de una distribución Gamma para el Intervalo Serial (SI)
method = "MCMC", # MCMC usando coarsedatatools
burnin = 1000, # número de muestras de burning (muestras descartadas al comienzo de MCMC)
n1 = 50, # n1 es el número de pares de media y desviación estándar del SI que se extraen
n2 = 50) # n2 es el tamaño de la muestra posterior extraída para cada par de media y desviación estándar del SI
mcmc_control <- make_mcmc_control(
seed = MCMC_seed,
burnin = params$burnin)
dist <- params$dist
config <- make_config(
list(
si_parametric_distr = dist,
mcmc_control = mcmc_control,
seed = overall_seed,
n1 = params$n1,
n2 = params$n2))
# Ajuste el SI
si_fit_gamma <- coarseDataTools::dic.fit.mcmc(
dat = si_data,
dist = dist,
init.pars = init_mcmc_params(si_data, dist),
burnin = mcmc_control$burnin,
n.samples = n_mcmc_samples,
seed = mcmc_control$seed)
SALIDA
Running 4000 MCMC iterations
MCMCmetrop1R iteration 1 of 4000
function value = -201.95281
theta =
1.04012
0.99131
Metropolis acceptance rate = 0.00000
MCMCmetrop1R iteration 1001 of 4000
function value = -202.42902
theta =
0.95294
1.05017
Metropolis acceptance rate = 0.55445
MCMCmetrop1R iteration 2001 of 4000
function value = -201.88547
theta =
1.18355
0.82124
Metropolis acceptance rate = 0.56522
MCMCmetrop1R iteration 3001 of 4000
function value = -202.11109
theta =
1.26323
0.77290
Metropolis acceptance rate = 0.55148
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
The Metropolis acceptance rate was 0.55500
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@Ahora observe los resultados.
R
# Verificar convergencia de las cadenas MCMC
converg_diag_gamma <- check_cdt_samples_convergence(si_fit_gamma@samples)
SALIDA
Gelman-Rubin MCMC convergence diagnostic was successful.R
converg_diag_gamma
SALIDA
[1] TRUER
# Guardar las muestras MCMC en un dataframe
si_samples_gamma <- data.frame(
type = 'Symptom onset',
shape = si_fit_gamma@samples$var1,
scale = si_fit_gamma@samples$var2,
p50 = qgamma(
p = 0.5,
shape = si_fit_gamma@samples$var1,
scale = si_fit_gamma@samples$var2)) |>
mutate( # La ecuación de conversión se encuentra aquí: https://en.wikipedia.org/wiki/Gamma_distribution
mean = shape*scale,
sd = sqrt(shape*scale^2)
)
# Obtener la media, desviación estándar y 95% CrI
si_summary_gamma <-
si_samples_gamma %>%
summarise(
mean_mean = quantile(mean,probs=.5),
mean_l_ci = quantile(mean,probs=.025),
mean_u_ci = quantile(mean,probs=.975),
sd_mean = quantile(sd, probs=.5),
sd_l_ci = quantile(sd,probs=.025),
sd_u_ci = quantile(sd,probs=.975)
)
si_summary_gamma
SALIDA
mean_mean mean_l_ci mean_u_ci sd_mean sd_l_ci sd_u_ci
1 7.659641 6.65395 8.707372 4.342087 3.602425 5.481316R
# Obtenga las mismas estadísticas de resumen para los parámetros de la distribución
si_samples_gamma |>
summarise(
shape_mean = quantile(shape, probs=.5),
shape_l_ci = quantile(shape, probs=.025),
shape_u_ci = quantile(shape, probs=.975),
scale_mean = quantile(scale, probs=.5),
scale_l_ci = quantile(scale, probs=.025),
scale_u_ci = quantile(scale, probs=.975)
)
R
# Necesita esto para hacer gráficos más tarde
gamma_shape <- si_fit_gamma@ests['shape',][1]
gamma_rate <- 1 / si_fit_gamma@ests['scale',][1]
8.2.3. Ajuste de una distribución log normal para el intervalo serial
Ahora, ajuste una distribución log normal a los datos del intervalo serial.
R
# Ejecute el modelo durante 4000 iteraciones, descartando las primeras 1000 muestras como burning
n_mcmc_samples <- 3000 # número de muestras a extraer de la posterior (después del burning)
params = list(
dist = "L", # Ajustando una distribución log-normal para el Intervalo Serial (SI)
method = "MCMC", # MCMC usando coarsedatatools
burnin = 1000, # número de muestras de burning (muestras descartadas al comienzo de MCMC)
n1 = 50, # n1 es el número de pares de media y desviación estándar de SI que se extraen
n2 = 50) # n2 es el tamaño de la muestra posterior extraída para cada par de media y desviación estándar de SI
mcmc_control <- make_mcmc_control(
seed = MCMC_seed,
burnin = params$burnin)
dist <- params$dist
config <- make_config(
list(
si_parametric_distr = dist,
mcmc_control = mcmc_control,
seed = overall_seed,
n1 = params$n1,
n2 = params$n2))
# Ajuste del intervalo serial
si_fit_lnorm <- coarseDataTools::dic.fit.mcmc(
dat = si_data,
dist = dist,
init.pars = init_mcmc_params(si_data, dist),
burnin = mcmc_control$burnin,
n.samples = n_mcmc_samples,
seed = mcmc_control$seed)
SALIDA
Running 4000 MCMC iterations
MCMCmetrop1R iteration 1 of 4000
function value = -216.54581
theta =
1.94255
-0.47988
Metropolis acceptance rate = 1.00000
MCMCmetrop1R iteration 1001 of 4000
function value = -216.21549
theta =
1.81272
-0.47418
Metropolis acceptance rate = 0.56643
MCMCmetrop1R iteration 2001 of 4000
function value = -215.86791
theta =
1.85433
-0.52118
Metropolis acceptance rate = 0.57221
MCMCmetrop1R iteration 3001 of 4000
function value = -216.32347
theta =
1.93196
-0.52205
Metropolis acceptance rate = 0.55948
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
The Metropolis acceptance rate was 0.56875
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@Revise los resultados.
R
# Revise la convergencia de las cadenas MCMC
converg_diag_lnorm <- check_cdt_samples_convergence(si_fit_lnorm@samples)
SALIDA
Gelman-Rubin MCMC convergence diagnostic was successful.R
converg_diag_lnorm
SALIDA
[1] TRUER
# Guarde las muestras de MCMC en un dataframe
si_samples_lnorm <- data.frame(
type = 'Symptom onset',
meanlog = si_fit_lnorm@samples$var1,
sdlog = si_fit_lnorm@samples$var2,
p50 = qlnorm(
p = 0.5,
meanlog = si_fit_lnorm@samples$var1,
sdlog = si_fit_lnorm@samples$var2)) |>
mutate( # La ecuación para la conversión está aquí https://en.wikipedia.org/wiki/Log-normal_distribution
mean = exp(meanlog + (sdlog^2/2)),
sd = sqrt((exp(sdlog^2)-1) * (exp(2*meanlog + sdlog^2)))
)
R
# Obtenga la media, desviación estándar e intervalo de credibilidad del 95%
si_summary_lnorm <-
si_samples_lnorm %>%
summarise(
mean_mean = quantile(mean,probs=.5),
mean_l_ci = quantile(mean,probs=.025),
mean_u_ci = quantile(mean,probs=.975),
sd_mean = quantile(sd, probs=.5),
sd_l_ci = quantile(sd,probs=.025),
sd_u_ci = quantile(sd,probs=.975)
)
si_summary_lnorm
SALIDA
mean_mean mean_l_ci mean_u_ci sd_mean sd_l_ci sd_u_ci
1 7.780719 6.692829 9.300588 5.189349 3.936678 7.289224R
# Obtenga las estadísticas resumen para los parámetros de la distribución
si_samples_lnorm |>
summarise(
meanlog_mean = quantile(meanlog, probs=.5),
meanlog_l_ci = quantile(meanlog, probs=.025),
meanlog_u_ci = quantile(meanlog, probs=.975),
sdlog_mean = quantile(sdlog, probs=.5),
sdlog_l_ci = quantile(sdlog, probs=.025),
sdlog_u_ci = quantile(sdlog, probs=.975)
)
SALIDA
meanlog_mean meanlog_l_ci meanlog_u_ci sdlog_mean sdlog_l_ci sdlog_u_ci
1 1.866779 1.724069 2.015255 0.6086726 0.5107204 0.725803R
lognorm_meanlog <- si_fit_lnorm@ests['meanlog',][1]
lognorm_sdlog <- si_fit_lnorm@ests['sdlog',][1]
8.2.4. Ajuste de una distribución Weibull para el intervalo serial
Finalmente, ajuste de una distribución Weibull para los datos del intervalo serial.
R
# Ejecutaremos el modelo durante 4000 iteraciones, descartando las primeras 1000 muestras como burning
n_mcmc_samples <- 3000 # número de muestras a extraer de la posterior (después del burning)
params = list(
dist = "W", # Ajustando una distribución Weibull para el Intervalo Serial (SI)
method = "MCMC", # MCMC usando coarsedatatools
burnin = 1000, # número de muestras de burning (muestras descartadas al comienzo de MCMC)
n1 = 50, # n1 es el número de pares de media y desviación estándar de SI que se extraen
n2 = 50) # n2 es el tamaño de la muestra posterior extraída para cada par de media y desviación estándar de SI
mcmc_control <- make_mcmc_control(
seed = MCMC_seed,
burnin = params$burnin)
dist <- params$dist
config <- make_config(
list(
si_parametric_distr = dist,
mcmc_control = mcmc_control,
seed = overall_seed,
n1 = params$n1,
n2 = params$n2))
# Ajuste el intervalo serial
si_fit_weibull <- coarseDataTools::dic.fit.mcmc(
dat = si_data,
dist = dist,
init.pars = init_mcmc_params(si_data, dist),
burnin = mcmc_control$burnin,
n.samples = n_mcmc_samples,
seed = mcmc_control$seed)
Revise los resultados.
R
# Revise covengencia
converg_diag_weibull <- check_cdt_samples_convergence(si_fit_weibull@samples)
SALIDA
Gelman-Rubin MCMC convergence diagnostic was successful.R
converg_diag_weibull
SALIDA
[1] TRUER
# Guarde las muestra MCMC en un dataframe
si_samples_weibull <- data.frame(
type = 'Symptom onset',
shape = si_fit_weibull@samples$var1,
scale = si_fit_weibull@samples$var2,
p50 = qweibull(
p = 0.5,
shape = si_fit_weibull@samples$var1,
scale = si_fit_weibull@samples$var2)) |>
mutate( # La ecuación para conversión está aquí https://en.wikipedia.org/wiki/Weibull_distribution
mean = scale*gamma(1+1/shape),
sd = sqrt(scale^2*(gamma(1+2/shape)-(gamma(1+1/shape))^2))
)
R
# Obtenga las estadísticas resumen
si_summary_weibull <-
si_samples_weibull %>%
summarise(
mean_mean = quantile(mean,probs=.5),
mean_l_ci = quantile(mean,probs=.025),
mean_u_ci = quantile(mean,probs=.975),
sd_mean = quantile(sd, probs=.5),
sd_l_ci = quantile(sd,probs=.025),
sd_u_ci = quantile(sd,probs=.975)
)
si_summary_weibull
SALIDA
mean_mean mean_l_ci mean_u_ci sd_mean sd_l_ci sd_u_ci
1 7.692701 6.677548 8.809715 4.418743 3.797158 5.456492R
# Obtenga las estadísticas resumen para los parámetros de la distribución.
si_samples_weibull |>
summarise(
shape_mean = quantile(shape, probs=.5),
shape_l_ci = quantile(shape, probs=.025),
shape_u_ci = quantile(shape, probs=.975),
scale_mean = quantile(scale, probs=.5),
scale_l_ci = quantile(scale, probs=.025),
scale_u_ci = quantile(scale, probs=.975)
)
SALIDA
shape_mean shape_l_ci shape_u_ci scale_mean scale_l_ci scale_u_ci
1 1.791214 1.50812 2.090071 8.631295 7.481234 9.943215R
weibull_shape <- si_fit_weibull@ests['shape',][1]
weibull_scale <- si_fit_weibull@ests['scale',][1]
8.2.5. Grafique los resultados para el intervalo serial
Ahora, grafique el ajuste de las tres distribuciones. Asegúrese que la distribución ajuste bien los datos del intervalo serial.
R
ggplot()+
theme_classic()+
geom_bar(data = contacts, aes(x=diff), fill = "#FFAD05") +
scale_y_continuous(limits = c(0,14), breaks = c(0,2,4,6,8,10,12,14), expand = c(0,0)) +
stat_function(
linewidth=.8,
fun = function(z, shape, rate)(dgamma(z, shape, rate) * length(contacts$diff)),
args = list(shape = gamma_shape, rate = gamma_rate),
aes(linetype = 'Gamma')
) +
stat_function(
linewidth=.8,
fun = function(z, meanlog, sdlog)(dlnorm(z, meanlog, sdlog) * length(contacts$diff)),
args = list(meanlog = lognorm_meanlog, sdlog = lognorm_sdlog),
aes(linetype ='Log normal')
) +
stat_function(
linewidth=.8,
fun = function(z, shape, scale)(dweibull(z, shape, scale) * length(contacts$diff)),
args = list(shape = weibull_shape, scale = weibull_scale),
aes(linetype ='Weibull')
) +
scale_linetype_manual(values = c('solid','twodash','dotted')) +
labs(x = "Days", y = "Number of case pairs") +
theme(
legend.position = c(0.75, 0.75),
plot.margin = margin(.2,5.2,.2,.2, "cm"),
legend.title = element_blank(),
)
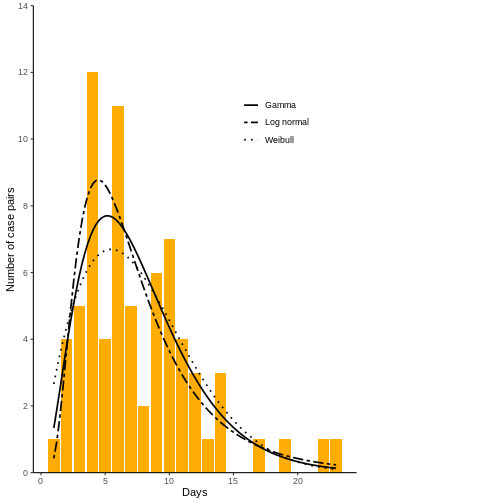
Ahora calcule el WAIC y LOOIC. coarseDataTools no tiene
una forma integrada de hacer esto, por lo que se necesita calcular la
verosimilitud a partir de las cadenas MCMC y utilizar el paquete
loo en R.
R
# Cargue las funciones de verosimilitud de coarseDataTools
calc_looic_waic <- function(symp, symp_si, dist){
# Prepare los datos y parámetros para el paquete loo
# Se necesita: una matriz de tamaño S por N, donde S es el tamaño de la muestra posterior (con todas las cadenas fusionadas)
# y N es el número de puntos de datos
mat <- matrix(NA, nrow = length(symp_si@samples$var1), ncol = nrow(si_data))
for (i in 1:nrow(symp)) {
for (j in 1:length(symp_si@samples$var1)){
L <- diclik2(par1 = symp_si@samples$var1[j],
par2 = symp_si@samples$var2[j],
EL = symp$EL[i], ER = symp$ER[i], SL = symp$SL[i], SR = symp$SR[i],
dist = dist)
mat[j,i] <- L
}
}
return(list(waic = waic(log(mat)),
looic = loo(log(mat)))) # now we have to take the log to get log likelihood
}
compare_gamma <- calc_looic_waic(symp = si_data, symp_si = si_fit_gamma, dist = "G")
compare_lnorm <- calc_looic_waic(symp = si_data, symp_si = si_fit_lnorm, dist = "L")
compare_weibull <- calc_looic_waic(symp = si_data, symp_si = si_fit_weibull, dist = "W")
# Imprima resultados
compare_gamma[["waic"]]$estimates
SALIDA
Estimate SE
elpd_waic -202.009546 7.0118463
p_waic 1.936991 0.4409454
waic 404.019093 14.0236925R
compare_lnorm[["waic"]]$estimates
SALIDA
Estimate SE
elpd_waic -202.215546 7.0178113
p_waic 1.874728 0.4106866
waic 404.431092 14.0356226R
compare_weibull[["waic"]]$estimates
SALIDA
Estimate SE
elpd_waic -203.941362 6.9020056
p_waic 2.083623 0.6633186
waic 407.882723 13.8040112R
compare_gamma[["looic"]]$estimates
SALIDA
Estimate SE
elpd_loo -202.015856 7.0144149
p_loo 1.943301 0.4437589
looic 404.031713 14.0288297R
compare_lnorm[["looic"]]$estimates
SALIDA
Estimate SE
elpd_loo -202.218954 7.0182826
p_loo 1.878136 0.4114664
looic 404.437909 14.0365651R
compare_weibull[["looic"]]$estimates
SALIDA
Estimate SE
elpd_loo -203.956018 6.9097884
p_loo 2.098279 0.6725387
looic 407.912036 13.8195768Incluya lo siguiente cuando reporte el intervalo serial:
Media e intervalo de credibilidad del 95%
Desviación estándar y e intervalo de credibilidad del 95%
Los parámetros de la distribución ajustada (e.g., shape y scale para distribución gamma)
💡 Preguntas (7)
- ¿Qué distribución tiene el menor WAIC y LOOIC??
R
si_summary_gamma
SALIDA
mean_mean mean_l_ci mean_u_ci sd_mean sd_l_ci sd_u_ci
1 7.659641 6.65395 8.707372 4.342087 3.602425 5.481316R
si_summary_lnorm
SALIDA
mean_mean mean_l_ci mean_u_ci sd_mean sd_l_ci sd_u_ci
1 7.780719 6.692829 9.300588 5.189349 3.936678 7.289224R
si_summary_weibull
SALIDA
mean_mean mean_l_ci mean_u_ci sd_mean sd_l_ci sd_u_ci
1 7.692701 6.677548 8.809715 4.418743 3.797158 5.456492
_______Pausa 3 _________
9. Medidas de control
9.1 Analicemos el resultado juntos
Ahora ha finalizado el análisis estadístico 🥳
Compare el período de incubación y el intervalo serial.
¿Cuál es más largo?
¿Ocurre la transmisión pre-sintomática con la Enfermedad X?
¿Serán medidas efectivas aislar a los individuos sintomáticos y rastrear y poner en cuarentena a sus contactos?
Si no lo son, ¿qué otras medidas se pueden implementar para frenar el brote?
10. Valores verdaderos
Los valores verdaderos usados para simular las epidemías fueron:
| Distribución | Media (días) | Desviación estándar (días) | |||
| Grupo 1 | Log normal | 5.7 | 4.6 | |
| Grupo 2 | Weibull | 7.1 | 3.7 | |
| Distribución | Media (días) | Desviación estándar (días) | |||
| Group 1 | Gamma | 8.4 | 4.9 | |
| Group 2 | Gamma | 4.8 | 3.3 | |
¿Cómo se comparan sus estimaciones con los valores verdaderos? Discuta las posibles razones para las diferencias.
Puntos Clave
Revise si al final de esta lección adquirió estas competencias:
Comprender los conceptos clave de las distribuciones de retrasos epidemiológicos para la Enfermedad X.
Entender las estructuras de datos y las herramientas para el análisis de datos de rastreo de contactos.
Aprender cómo ajustar las estimaciones del intervalo serial y del período de incubación de la Enfermedad X teniendo en cuenta la censura por intervalo usando un marco de trabajo Bayesiano.
Aprender a utilizar estos parámetros para informar estrategias de control en un brote de un patógeno desconocido.
11. Recursos adicionales
En este práctica, en gran medida se ignoraron los sesgos de
truncamiento a la derecha y sesgo dinámico, en parte debido a la falta
de herramientas fácilmente disponibles que implementen las mejores
prácticas. Para aprender más sobre cómo estos sesgos podrían afectar la
estimación de las distribuciones de retraso epidemiológico en tiempo
real, recomendamos un tutorial sobre el paquete
dynamicaltruncation en R de Sam Abbott y Sang Woo Park (https://github.com/parksw3/epidist-paper).
13. Referencias
- Reich NG et al. Estimating incubation period distributions with coarse data. Stat Med. 2009;28:2769–84. PubMed https://doi.org/10.1002/sim.3659
- Miura F et al. Estimated incubation period for monkeypox cases confirmed in the Netherlands, May 2022. Euro Surveill. 2022;27(24):pii=2200448. https://doi.org/10.2807/1560-7917.ES.2022.27.24.2200448
- Abbott S, Park Sang W. Adjusting for common biases in infectious disease data when estimating distributions. 2022 [cited 7 November 2023]. https://github.com/parksw3/dynamicaltruncation
- Lessler J et al. Incubation periods of acute respiratory viral infections: a systematic review, The Lancet Infectious Diseases. 2009;9(5):291-300. https://doi.org/10.1016/S1473-3099(09)70069-6.
- Cori A et al. Estimate Time Varying Reproduction Numbers from Epidemic Curves. 2022 [cited 7 November 2023]. https://github.com/mrc-ide/EpiEstim
- Lambert B. A Student’s Guide to Bayesian Statistics. Los Angeles, London, New Delhi, Singapore, Washington DC, Melbourne: SAGE, 2018.
- Vehtari A et al. Rank-normalization, folding, and localization: An improved R-hat for assessing convergence of MCMC. Bayesian Analysis 2021: Advance publication 1-28. https://doi.org/10.1214/20-BA1221
- Nishiura H et al. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. 2020;93:284-286. https://doi.org/10.1016/j.ijid.2020.02.060
Content from Generar reportes a partir de bases de datos de vigilancia epidemiológica usando sivirep
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo obtener un informe automatico de datos de SIVIGILA usando
sivirep?
Objetivos
Al final de este taller usted podrá:
Conocer el paquete
sivirepIdentificar las funcionalidades principales de
sivireppara generar un reporte básico.Hacer uso de
sivireppara el análisis de una de las enfermedades con mayor impacto en la región, como herramienta para la toma de decisiones y análisis.
Introducción
Colombia ha mejorado a lo largo de los años la calidad, la accesibilidad y la transparencia de su sistema oficial de vigilancia epidemiológica, SIVIGILA. Este sistema está regulado por el Instituto Nacional de Salud de Colombia y es operado por miles de trabajadores de la salud en las secretarías de salud locales, hospitales y unidades primarias generadoras de datos.
Sin embargo, todavía existen desafíos, especialmente a nivel local, en cuanto a la oportunidad y la calidad del análisis epidemiológico y de los informes epidemiológicos. Estas tareas pueden requerir una gran cantidad de trabajo manual debido a limitaciones en el entrenamiento para el análisis de datos, el tiempo que se requiere invertir, la tecnología y la calidad del acceso a internet en algunas regiones de Colombia.
Objetivos
- Conocer el paquete
sivirep - Identificar las funcionalidades principales de
sivireppara generar un reporte básico. - Hacer uso de
sivireppara el análisis de una de las enfermedades con mayor impacto en la región, como herramienta para la toma de decisiones y análisis.
Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Función: conjunto de instrucciones que se encargan de transformar las entradas en los resultados deseados.
Modulo: cojunto de funciones que son agrupadas debido a su relación conceptual, resultados proporcionados y definición de responsabilidades.
R Markdown: es una extensión del formato Markdown que permite combinar texto con código R incrustado en el documento. Es una herramienta para generar informes automatizados y documentos técnicos interactivos.
SIVIGILA: Sistema de Notificación y Vigilancia en Salud Pública de Colombia.
Microdatos: Son los datos sobre las características de las unidades de estudio de una población (individuos, hogares, establecimientos, entre otras) que se encuentran consolidados en una base de datos.
Evento: Conjunto de sucesos o circunstancias que pueden modificar o incidir en la situación de salud de una comunidad.
Incidencia: Es la cantidad de casos nuevos de un evento o una enfermedad que se presenta durante un período de tiempo específico. Usualmente, se presentá como el número de casos por población a riesgo, y por ello el denominador podría variar dependiendo del evento o enfermedad.
Departamento: En Colombia, existen 32 unidades geográficas administrativas (adm1) llamadas departamentos.
Municipio: Corresponden al segundo nivel de división administrativa en Colombia, que mediante agrupación conforman los departamentos. Colombia posee 1104 municipios registrados.
Reporte: análisis descriptivo de una enfermedad o evento del SIVIGILA.
Contenido del taller
Ha llegado el momento de explorar sivirep, de conocer
cómo generar reportes automatizados con el paquete y sus funcionalidades
principales.
El evento que analizaremos es Dengue en el departamento del Cauca para el año 2022, ya que ha sido una de las regiones más afectadas en Colombia a lo largo del tiempo por esta enfermedad.
Iniciaremos instalando e importando el paquete a través de los siguientes comandos:
R
remove.packages("sivirep")
if (!require("pak")) install.packages("pak")
pak::pak("epiverse-trace/sivirep") # Comando para instalar sivirep
rm(list = ls()) # Comando para limpiar el ambiente de R
library(sivirep) # Comando para importar sivirep
Verificar que el evento o enfermedad se encuentren disponibles para
su descarga en la lista que provee sivirep, la cual se
puede obtener ejecutando el siguiente comando:
Reporte automatizado
Ahora generaremos un reporte automatizado a partir de la plantilla
que provee el paquete llamada Reporte Básico {sivirep}, la
cual contiene seis secciones y recibe los siguientes parámetros de
entrada: el nombre del evento o enfermedad, el año, el nombre de
departamento (opcional) y nombre del municipio (opcional) para descargar
los datos de la fuente de SIVIGILA.
Para hacer uso de la plantilla se deben seguir los siguientes pasos:
- En RStudio hacer click ‘File/New File/R’ Markdown:

- Selecciona la opción del panel izquierdo: ‘From
Template’, después haz clic en el template llamado
Reporte Básico {sivirep}, indica el nombre que deseas para el reporte (i.e. Reporte_Laura), la ubicación donde deseas guardarlo y presiona ‘Ok’.

- En la parte superior de **‘RStudio’*, presiona el botón ‘Knit’, despliega las opciones y selecciona ‘Knit with parameters’.

- A continuación, aparecerá una pantalla donde podrás indicar el nombre de la enfermedad o evento, el año y el departamento del reporte. Esta acción descargará los datos deseados y también proporcionará la plantilla en un archivo R Markdown (.Rmd), al hacer clic en el botón ‘Knit’.

- Espera unos segundos mientras el informe se genera en un archivo HTML.
!Felicitaciones has generado tu primer reporte automatizado con sivirep!
Actividad exploratoria
Para conocer las funciones principales del paquete realizaremos una
actividad exploratoria siguiendo el flujo de datos de
sivirep.
Construiremos un informe en R Markdown para Dengue, departamento del Cauca, año 2022 (no se debe utilizar la plantilla de reporte vista en la sección anterior) que de respuesta a las siguientes preguntas:
- ¿Cómo es la distribución por sexo y semana epidemiológica de la enfermedad?
- ¿Esta distribución sugiere que la enfermedad afecta más a un sexo o a otro? ¿sí, no y por qué?
- ¿Cómo afecta la enfermedad los distintos grupos etarios?
- ¿Cuál es el municipio que más se ve afectado por la enfermedad en la región?
1. Preparación y configuración del documento R Markdown
Realizaremos la configuración y preparación del documento en R Markdown a través de los siguientes pasos:
- Crear un documento en R Mardown vacio:
- Insertar un chunk en el documento con las siguientes opciones de configuración:
R
knitr::opts_chunk$set(
collapse = TRUE,
comment = "#>",
fig.path = "figures/",
include = TRUE,
error = FALSE,
warning = FALSE,
message = FALSE
)
2. Importación de datos de SIVIGILA
Iniciaremos con la importación de los datos del evento o enfermedad
utilizando la función import_data_event la cual permite
descargar los datos desde la fuente de SIVIGILA utilizando un formato
parametrizado basado en el nombre del evento y el año.
R
data_dengue <- import_data_event(nombre_event = "dengue",
year = 2022)
3. Exploración de la base de datos
Recomendamos explorar la base de datos, sus variables, tipos de datos, registros y otras caracteristicas que pueden ser relavantes para su análisis y permitan responder correctamente a las preguntas planteadas en la actividad.
Si tiene alguna duda respecto a las variables o desconoce su significado puede dirigirse al diccionario de datos del SIVIGILA.
4. Limpieza de datos de SIVIGILA
Para limpiar los datos utilizaremos una función genérica que
proporciona sivirep llamada
limpiar_data_sivigila, la cual envuelve diversas tareas
para identificar y corregir errores, inconsistencias y discrepancias en
los conjuntos de datos con el fin de mejorar su calidad y precisión.
Este proceso puede incluir la corrección de errores tipográficos, el
reemplazo de valores faltantes y la validación de datos, entre otras
tareas, como eliminar fechas improbables, limpiar códigos de
geolocalización y estandarizar los nombres de las columnas y las
categorías de edad.
R
data_limpia <- limpiar_data_sivigila(data_event = data_dengue)
data_limpia
5. Filtrar casos
Ahora debemos filtrar los datos del evento o enfermedad por el
departamento de Cauca, utilizando la función de
sivirep llamada geo_filtro. Esta función
permite al usuario crear informes a nivel subnacional, seleccionando
casos específicos basados en la ubicación geográfica.
R
data_filtrada <- geo_filtro(data_event = data_limpia, dpto = "Cauca")
data_filtrada
6. Variable de sexo
Agruparemos los datos de la enfermedad por la variable sexo para
poder visualizar su distribución y obtener los porcentajes a través de
la función que proporciona sivirep:
R
casos_sex <- agrupar_sex(data_event = data_filtrada,
porcentaje = TRUE)
casos_sex
Además, sivirep cuenta con una función para generar el
gráfico por esta variable llamada plot_sex:
R
plot_sex(data_agrupada = casos_sex)
La distribución de casos por sexo y semana epidemiológica se puede
generar utilizando la función agrupar_sex_semanaepi
proporcionada por sivirep.
R
casos_sex_semanaepi <- agrupar_sex_semanaepi(data_event = data_filtrada)
casos_sex_semanaepi
La función de visualización correspondiente es
plot_sex_semanaepi, que sivirep proporciona
para mostrar la distribución de casos por sexo y semana
epidemiológica.
R
plot_sex_semanaepi(data_agrupada = casos_sex_semanaepi)
7. Variable de edad
sivirep proporciona una función llamada
agrupar_edad, que puede agrupar los datos de enfermedades
por grupos de edad. De forma predeterminada, esta función produce rangos
de edad con intervalos de 10 años.
R
casos_edad <- agrupar_edad(data_event = data_limpia, interval_edad = 10)
casos_edad
La función de visualización correspondiente es
plot_edad.
R
plot_edad(data_agrupada = casos_edad)
8. Distribución espacial de casos
Obtener la distribución espacial de los casos es útil para identificar áreas con una alta concentración de casos, agrupaciones de enfermedades y factores de riesgo ambientales o sociales.
En Colombia, existen 32 unidades geográficas administrativas (adm1)
llamadas departamentos. sivirep proporciona una función
llamada agrupar_mpio que permite obtener un data.frame de
casos agrupados por departamento o municipio.
R
dist_esp_dept <- agrupar_mpio(data_event = data_filtrada)
dist_esp_dept
Con la función llamada plot_map, podremos generar un
mapa estático que muestra la distribución de casos por municipios.
R
mapa <- plot_map(data_agrupada = dist_esp_dept)
mapa
9. Análisis de resultados
Analiza los resultados obtenidos en la ejecución de las funciones y responde las preguntas planteadas en el enunciado de la actividad exploratoria.
Dentro del R Markdown desarrolla dos (2) conclusiones pertinentes a la enfermedad teniendo en cuenta el contexto de la región y las estrategias que podrían contribuir a su mitigación.
Reflexión
Conformaremos grupos de 4-5 personas y discutiremos sobre la disponibilidad de los datos y el impacto que esto tiene en la construcción de análisis y en las acciones que se pueden emprender para mitigar el efecto de esta enfermedad sobre la población.
Desafio
En el siguiente enlace podrán encontrar el desafío que debérán
desarrollar con sivirep: - https://docs.google.com/document/d/1_79eyXHTaQSPSvUzlikx9DKpBvICaiqy/edit?usp=sharing&ouid=113064166206309718856&rtpof=true&sd=true
Content from Estima la fuerza de infección a partir de encuestas serológicas usando serofoi
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo estimar retrospectivamente la Fuerza de Infección de un patógeno a partir de encuestas serológicas poblacionales de prevalencia desagregadas por edad mediante la implementación de modelos Bayesianos usando serofoi?
Objetivos
Al final de este taller usted podrá:
Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.
1. Introducción
serofoi es un paquete de R para estimar retrospectivamente la Fuerza de Infección de un patógeno a partir de encuestas serológicas poblacionales de prevalencia desagregadas por edad mediante la implementación de modelos Bayesianos. Para ello, serofoi utiliza el paquete Rstan, que proporciona una interfaz para el lenguaje de programación estadística Stan, mediante el cual se implementan métodos de Monte-Carlo basados en cadenas de Markov.
Como un caso particular, estudiaremos un brote de Chikungunya, una enfermedad viral descubierta en Tanzania en el año 1952 que se caracteriza por causar fuertes fiebres, dolor articular, jaqueca, sarpullidos, entre otros síntomas. Desde el año 2013, casos de esta enfermedad comenzaron a ser reportados en América y desde entonces la enfermedad ha sido endémica en varios países latinoamericanos. Durante este tutorial, vamos a analizar una encuesta serológica realizada entre octubre y diciembre de 2015 en Bahía, Brasil, la cual fue realizada poco tiempo después de una epidemia de esta enfermedad, con el fin de caracterizar los patrones endémicos o epidémicos en la zona.
2. Objetivos
Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.
3. Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Encuestas serologícas (sero)
Fuerza de infección (foi)
Modelos serocatalíticos
Estadística Bayesiana
Visualización e interpretación de resultados de modelos FoI
La Fuerza de Infección (FoI, por sus siglas en inglés), también conocida cómo la tasa de riesgo o la presión de infección, representa la tasa a la que los individuos susceptibles se infectan dado que estuvieron expuestos a un patógeno. En otras palabras, la FoI cuantifica el riesgo de que un individuo susceptible se infecte en un periodo de tiempo.
Como veremos a continuación, este concepto es clave en el modelamiento de enfermedades infecciosas. Para ilustrar el concepto, consideremos una población expuesta a un patógeno y llamemos \(P(t)\) a la proporción de individuos que han sido infectados al tiempo \(t\). Suponiendo que no hay sero-reversión, la cantidad \(1 - P(t)\) representa la cantidad de individuos susceptibles a la enfermedad, de tal forma que la velocidad de infección está dada por:
\[ \tag{1} \frac{dP(t)}{d t} = \lambda(t) (1- P(t)), \]
en donde \(\lambda(t)\) representa la tasa a la que los individuos susceptibles se infectan por unidad de tiempo (días, meses, años, …), es decir la FoI. La ecuación diferencial (1) se asemeja a la de una reacción química en donde \(P(t)\) representa la proporción de sustrato que no ha entrado en contacto con un reactivo catalítico, por lo que este tipo de modelos se conocen como modelos serocatalíticos (Muench, 1959).
A pesar de la simpleza del modelo representado por la ecuación (1), en comparación con modelos compartimentales (por ejemplo), la dificultad para conocer una condición inicial para la seropositividad en algún punto del pasado imposibilita su uso práctico. Para sortear esta limitación, es común aplicar el modelo para cohortes de edad en lugar de para el total de la población. Para ello, etiquetemos cada cohorte de edad de acuerdo con su año de nacimiento \(\tau\), y supongamos que los individuos son seronegativos al nacer:
\[ \frac{dP^\tau (t)}{dt} = \lambda(t) (1 - P^\tau(t)). \]
Con condiciones iniciales dadas por \(P^\tau(\tau) = 0\). Esta ecuación se puede resolver analíticamente, dando como resultado (Hens et al, 2010):
\[ P^{\tau} (t) = 1 - \exp\left(-\int_{\tau}^{t} \lambda (t') dt' \right). \]
Suponiendo que la FoI se mantiene constante a lo largo de cada año, la versión discreta de esta ecuación es:
\[ \tag{2} P^\tau(t) = 1 - \exp\left(-\sum_{i = \tau}^{t} \lambda_i \right), \]
Como un ejemplo, consideremos la FoI representada en la siguiente figura:
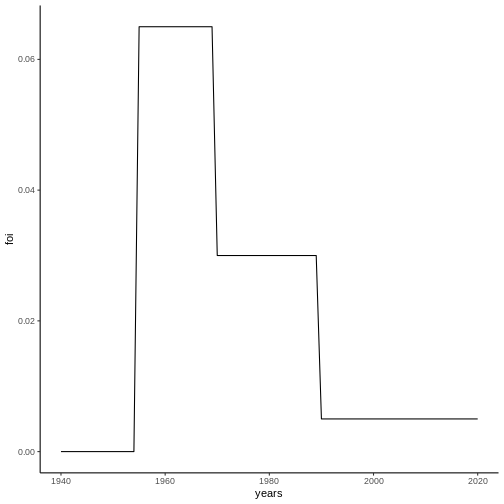
A partir de esta FoI, es posible calcular la seroprevalencia para distintas cohortes por medio de la ecuación (2):
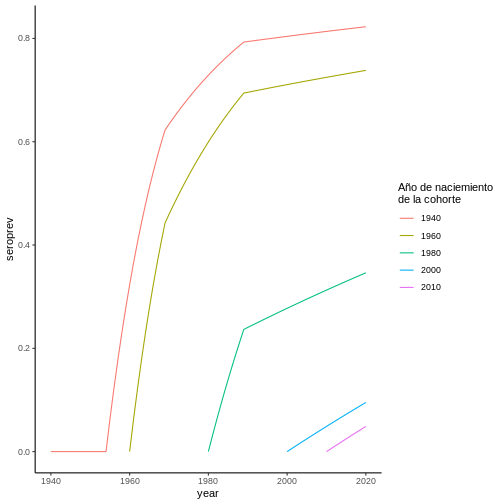
Cuando conocemos los datos de una encuesta serológica, la información a la que tenemos acceso es a una fotografía de la seroprevalencia en el momento su realización \(t_{sur}\) como función de la edad de los individuos en ese momento, la cual coincide con la ecuación (2) ya que los individuos envejecen al mismo ritmo al que pasa el tiempo; es decir:
\[ \tag{3} P^{t_{sur}}(a^\tau) = 1 - \exp\left(-\sum_{i = \tau}^{t_{sur}} \lambda_i \right). \]
En el caso del ejemplo, esto nos da la siguiente gráfica:
Note que los valores de seroprevalencia de cada edad en esta gráfica corresponden a los valores de seroprevalencia al momento de la encuesta (2020) en la gráfica anterior.
La misión que cumple serofoi es estimar la fuerza de infección histórica \(\lambda(t)\) a partir de esta fotografía del perfil serológico de la población al momento de la encuesta. para lo cual se requieren encuestas serológicas que cumplan con los siguientes criterios de inclusión:
- Basadas en poblacionales (no hospitalaria).
- Estudio de tipo transversal (un solo tiempo) .
- Que indique la prueba diagnóstica utilizada.
- Que identifique la edad del paciente en el momento de la encuesta.
En casos donde la FoI pueda considerarse constante, la ecuación (3) da como resultado:
\[ \tag{4} P_{sur}(a^\tau(t_{sur})) = 1 - \exp (-\lambda a^\tau), \]
en donde se tuvo en cuenta qué, al momento de la introducción del patógeno (\(t = 0\)), la proporción de individuos infectados fue \(P(0) = 0\) (condición inicial). Note que el término de la suma en la ecuación (3) da como resultado la edad de cada cohorte al considerar la fuerza de infección constante.
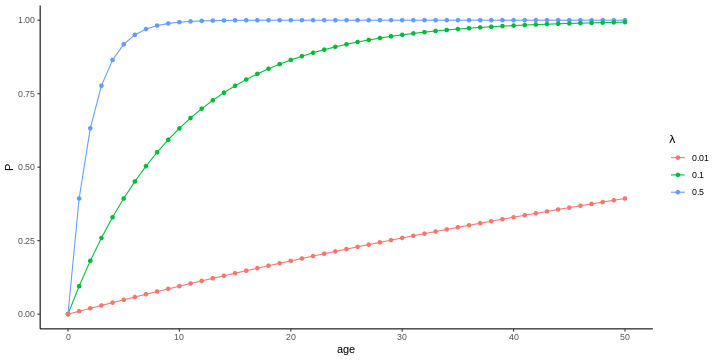
Figura 1. Curvas de prevalencia en función de la edad para distintos valores de FoI constante.
En este ejemplo hemos escogido, por simplicidad, que la FoI fuese constante; sin embargo, este no es necesariamente el caso. Identificar si la FoI sigue una tendencia constante o variante en el tiempo puede ser de vital importancia para la identificación y caracterización de la propagación de una enfermedad. Es acá donde el paquete de Rserofoi juega un papel importante, ya que este permite estimar retrospectivamente la FoI de un patógeno, recuperando así su evolución temporal, por medio de modelos Bayesianos pre-establecidos.
Los modelos actuales del paquete serofoi asumen los siguientes supuestos biológicos:
- No hay sero-reversión (sin pérdida de inmunidad).
- La FoI no depende de la edad.
- Bajos o nulos niveles de migración en las poblaciones.
- Diferencias pequeñas entre las tasas de mortalidad de susceptibles e infectados.
3.2. Modelos Bayesianos
A diferencia del enfoque frecuentista, donde la probabilidad se asocia con la frecuencia relativa de la ocurrencia de los eventos, la estadística Bayesiana se basa en el uso de la probabilidad condicional de los eventos respecto al conocimiento (o estado de información) que podamos tener sobre los datos o sobre los parámetros que queramos estimar.
Por lo general, cuando proponemos un modelo lo que buscamos es disminuir la incertidumbre sobre algún parámetro, de tal forma que nos aproximemos a su valor tan óptimamente como nos lo permita nuestro conocimiento previo del fenómeno y de las mediciones realizadas (datos).
La inferencia Bayesiana se sustenta en el teorema de Bayes, el cual establece que: dado un conjunto de datos \(\vec{y} = (y_1, …, y_N)\), el cual representa un único evento, y la variable aleatoria \(\theta\), que representa un parámetro de interés para nosotros (en nuestro caso, la FoI \(\lambda\)), la distribución de probabilidad conjunta de las variables aleatorias asociadas está dada por:
\[ \tag{4} p(\vec{y}, \theta) = p(\vec{y} | \theta) p(\theta) = p(\theta | \vec{y}) p(\vec{y}), \]
de donde se desprende la distribución aposteriori de \(\theta\), es decir una versión actualizada de la distribución de probabilidad de la FoI condicionada a nuestros datos:
\[\tag{5} p(\theta, \vec{y}) = \frac{p(\vec{y} | \theta) p(\theta)}{p(\vec{y})}, \]
La distribución \(p(\vec{y} | \theta)\), que corresponde a la información interna a los datos condicionada al valor del parámetro \(\theta\), suele estar determinada por la naturaleza del experimento: no es lo mismo escoger pelotas dentro de una caja reemplazándolas que dejándolas por fuera de la caja (e.g.). En el caso particular de la FoI, contamos con datos como el número total de encuestas por edad y el número de casos positivos, por lo que es razonable asignar una distribución binomial a la probabilidad, como veremos a continuación.
3.3.1. Modelo FoI constante
En nuestro caso particular, el parámetro que queremos estimar es la FoI (\(\lambda\)). La distribución de probabilidad apriori de \(\lambda\) representa nuestras suposiciones informadas o el conocimiento previo que tengamos sobre el comportamiento de la FoI. En este contexto, el estado de mínima información sobre \(\lambda\) está representado por una distribución uniforme:
\[\tag{6} \lambda \sim U(0, 2), \]
lo que significa que partimos de la premisa de que todos los valores de la fuerza de infección entre \(0\) y \(2\) son igualmente probables. Por otro lado, de la teoría de modelos sero-catalíticos sabemos que la seroprevalencia en un año dado está descrita por un proceso cumulativo con la edad (Hens et al, 2010):
\[\tag{7} P(a, t) = 1 - \exp\left( -\sum_{i=t-a+1}^{t} \lambda_i \right), \]
en donde \(\lambda_i\) corresponde a la FoI al tiempo \(t\). Como en este caso la FoI es constante, la ec. (7) se reduce a:
\[\tag{8} P(a, t) = 1 - \exp\left( -\lambda a \right), \]
Si \(n(a, t_{sur})\) es el número de muestras positivas por edad obtenidas en un estudio serológico desarrollado en el año \(t_{sur}\), entonces podemos estimar la distribución de los casos seropositivos por edad condicionada al valor de \(\lambda\) como una distribución binomial:
\[\tag{9} p(a, t) \sim Binom(n(a, t), P(a, t)) \\ \lambda \sim U(0, 2) \]
3.3.2. Modelo FOI dependientes del tiempo
Actualmente, serofoi permite la implementación de dos modelos dependientes del tiempo: uno de variación lenta de la FoI (time) y otro de variación rápida (time-log) de la FoI.
Cada uno de ellos se basa en distintas distribuciones previas para \(\lambda\), las cuales se muestran en la tabla 1.
| Model Type | Logarithmic Scale | Probability of positive case at age \(a\) | Prior distribution |
|---|---|---|---|
"constant" |
FALSE |
\(\sim binom(n(a,t), P(a,t))\) | \(\lambda\sim uniform(0,2)\) |
"time" |
FALSE |
\(\sim binom(n(a,t), P(a,t))\) | \(\lambda\sim normal(\lambda(t-1),\sigma)\ \lambda(t=1)\sim normal(0,1)\) |
"time" |
TRUE |
\(\sim binom(n(a,t), P(a,t))\) | \(\lambda\sim normal(log(\lambda(t-1)),\sigma)\ \lambda(t=1)\sim normal(-6,4)\) |
Tabla 1. Distribuciones a priori de los distintos modelos soportados por serofoi. \(\sigma\) representa la desviación estándar.
Como se puede observar, las distribuciones previas de \(\lambda\) en ambos casos están dadas por
distribuciones Gaussianas con desviación estándar \(\sigma\) y centradas en \(\lambda\) (modelo de variación lenta -
"time") y \(\log(\lambda)\) (modelo de variación rápida
- "time" con is_log_foi = TRUE). De esta
manera, la FoI en un tiempo \(t\) está
distribuida de acuerdo a una distribución normal alrededor del valor que
esta tenía en el tiempo inmediatamente anterior. El logaritmo en el
modelo \(\log(\lambda)\) permite
identificar cambios drásticos en la tendencia temporal de la FoI.
4. Contenido del taller
4.1 Instalación de serofoi
Previo a la instalación de serofoi, cree un proyecto en R en la carpeta de su escogencia en su máquina local; esto con el fin de organizar el espacio de trabajo en donde se guardarán los códigos que desarrolle durante la sesión.
Antes de realizar la instalación de serofoi, es necesario instalar y configurar C++ Toolchain (instrucciones para windows/ mac/ linux). Después de haber configurado C++ Toolchain, ejecute las siguientes líneas de código para instalar el paquete:
R
if(!require("pak")) install.packages("pak")
pak::pak("epiverse-trace/serofoi")
Opcionalmente, es posible modificar la configuración de R para que los modelos a implementar corran en paralelo, aprovechando los núcleos del procesador de su computador. Esto tiene el efecto de disminuir los tiempos de cómputo de las implementaciones en Stan. Para activar esta opción ejecute:
R
options(mc.cores=parallel::detectCores())
Finalmente, cargue el paquete ejecutando:
R
library(serofoi)
4.2 Caso de uso: Chikungunya
En esta sección vamos a analizar una encuesta serológica realizada
entre octubre y diciembre de 2015 en Bahía, Brasil, la cual fue
realizada poco tiempo después de una epidemia de esta enfermedad en la
zona. Nuestro objetivo es caracterizar la propagación de la enfermedad
por medio de la implementación de los distintos modelos y determinar
cuál de estos describe mejor la situación. Primero, carguemos y
preparemos los datos que utilizaremos en este análisis. La
basechik2015 contiene los datos correspondientes a esta
encuesta serológica:
R
data(chik2015)
chik2015
SALIDA
survey_year n_sample n_seropositive age_min age_max
1 2015 144 63 40 59
2 2015 148 69 60 79
3 2015 45 17 1 19
4 2015 109 55 20 39Para correr el modelo de FoI constante y visualizar los resultados del mismo, corra las siguientes líneas de código:
R
chik_constant <- fit_seromodel(serosurvey = chik2015,
model_type = "constant",
iter = 1000)
chik_constant_plot <- plot_seromodel(seromodel = chik_constant,
serosurvey = chik2015,
size_text = 12)
Ahora, corra los modelos dependientes del tiempo con
iter =1500. Luego visualice conjuntamente las tres gráficas
por medio de la función plot_grid() del paquete
cowplot:
R
install.packages("cowplot")
cowplot::plot_grid(chik_constant_plot,
chik_normal_plot,
chik_normal_log_plot,
ncol = 3)
NOTA: Debido a que el número de trayectorias es relativamente alto, con el fin de asegurar la convergencia de los modelos, el tiempo de cómputo de los modelos dependientes del tiempo puede tardar varios minutos.
Pista: Debería obtener la siguiente gráfica:
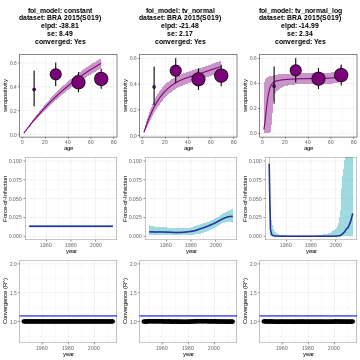
El poder predictivo de un modelo Bayesiano se puede caracterizar por medio del elpd(Expected Log Predictive Density). El modelo que mejor ajusta la encuesta epidemiológica es aquel que tiene valores más altos deelpd y valores más bajos de error estándar (se).
5. Reflexión
Discusión
Según los criterios explicados anteriormente, responda:
¿Cuál de los tres modelos se ajusta mejor a esta encuesta serológica?
¿Cómo interpreta estos resultados?
Desafío
Desafío: caso simulado
En los pasados 3 años, en zonas rurales fronterizas de dos países contíguos de América Latina se han identificado casos de encefalitis de origen desconocido en humanos. Algunos de estos casos de encefalitis han requerido hospitalización e incluso se han reportado fallecimientos. Los habitantes de la zona también señalan que una epidemia similar de casos en que las personas“perdían la conciencia después de una fuerte fiebre” habían ocurrido en la misma zona algunas décadas atrás.
En 2023 se realizó una encuesta de seroprevalencia para los 4 virus con mayor sospecha de estar circulando en la zona fronteriza donde se presentan los casos de encefalitis. Estos 4 virus son biológicamente distintivos entre ellos, es decir no tienen reacción cruzada en las pruebas serológicas. Para cada uno de estos virus, la encuesta de seroprevalencia recoge una muestra probabilística y representativa de la población de residentes de la zona con un total de 1306 individuos muestreados entre 1 y 60 años de edad. Los resultados de las pruebas serológicas para cada virus se presentan como número total de personas muestreadas por cada grupo de edad y número de personas positivas para anticuerpos IgG contra uno de los 4 virus en ese grupo de edad.
El desafío consiste en que usted y su grupo deben identificar cuál o cuáles de los 4 virus es el más probablemente implicado en esta emergencia de encefalitis viral haciendo uso de la librería serofoi.
Exploración de los datos y visualización de la seroprevalencia (30 min)
Los datos de las 4 encuestas vienen en archivos . RDS independientes que podrá encontrar en estos enlaces:
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_01.RDS
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_02.RDS
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_03.RDS
- https://epiverse-trace.github.io/epimodelac/data/serosurvey_04.RDS
Lea los datos haciendo uso de la función readRDS(). En
esta etapa del desafío se espera que:
Exploren la estructura de los datos y analicen las características generales de una encuesta serológica transversal desagregada por edad.
Preparen los datos para el proceso de visualización por medio de funciones del paquete dplyr.
Visualicen la seroprevalencia de cada encuesta por medio de la función
plot_seroprev()y analicen cualitativamente su tendencia en cada caso.
Estimación de la fuerza de infección histórica (30 min)
Implemente los modelos que considere pertinentes a cada encuesta serológica y compare los resultados obtenidos usando métricas de comparación Bayesianas. En esta etapa se espera que:
Implementen los modelos Bayesianos disponibles en serofoi por medio de la función
fit_seromodel(). ¿Cómo afecta a sus resultados usar más o menos iteraciones?Comparación de los ajustes obtenidos por medio de la función
plot_seromodel(). ¿Cuál modelo se ajusta mejor en cada caso?
Análisis de resultados (30 min)
Con base en los resultados obtenidos anteriormente, ¿Cuál virus cree que estuvo involucrado en la epidemia reciente de encefalitis?
Para adaptar una de las cuatro bases de datos al formato necesario para {serofoi}, puede usar el siguiente código:
R
library(tidyverse)
virus_serosurvey <- readr::read_rds(
"https://epiverse-trace.github.io/epimodelac/data/serosurvey_01.RDS"
) %>%
dplyr::mutate(
age_group = vaccineff::get_age_group(
data_set = .,
col_age = "age_max",
max_val = 60,
step = 5
)
) %>%
dplyr::group_by(age_group, survey_year = tsur) %>%
dplyr::summarise(
n_sample = sum(total),
n_seropositive = sum(counts),
age_min = min(age_min),
age_max = max(age_max)
) %>%
dplyr::ungroup() %>%
dplyr::select(-age_group)
Ahora, ¿Cómo implementaría los modelos Bayesianos disponibles en
serofoi por medio de la función fit_seromodel()?
Puntos Clave
Revise si al final de esta lección adquirió estas competencias:
Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.
Sobre este documento
Este documento ha sido diseñado para el Curso Internacional: Análisis de Brotes y Modelamiento en Salud Pública, Bogotá 2023. TRACE-LAC/Javeriana.
Contribuciones
- Nicolás Torres Domínguez
- Zulma M. Cucunuba
Contribuciones son bienvenidas vía pull requests.
Referencias
Muench, H. (1959). Catalytic models in epidemiology. Harvard University Press.
Hens, N., Aerts, M., Faes, C., Shkedy, Z., Lejeune, O., Van Damme, P., & Beutels, P. (2010). Seventy-five years of estimating the force of infection from current status data. Epidemiology & Infection, 138(6), 802–812.
Cucunubá, Z. M., Nouvellet, P., Conteh, L., Vera, M. J., Angulo, V. M., Dib, J. C., … Basáñez, M. G. (2017). Modelling historical changes in the force-of-infection of Chagas disease to inform control and elimination programmes: application in Colombia. BMJ Global Health, 2(3). doi:10.1136/bmjgh-2017-000345
Content from Introducción al cálculo de efectividad vacunal con cohortes usando vaccineff
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo realizar el cálculo de efectividad vacunal con cohortes usando vaccineff?
Objetivos
Al final de este taller usted podrá:
Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes
1. Introducción
En esta sesión se espera que los participantes se familiaricen con
uso del paquete de Rvaccineff. Utilizaremos el diseño de
cohortes para estimar la efectividad vacunal de un conjunto de datos de
prueba y analizaremos los resultados obtenidos.
2. Objetivos
Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes
3. Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Eficacia y Efectividad vacunal
Tiempo de inducción o “delays” en el análisis de efectividad de vacunas
Diseños observacionales para el estudio de la efectividad vacunal
Diseño de cohortes para estimación de la efectividad vacunal
Estimador no paramétrico Kaplan-Meier
Modelo semi-paramétrico de Cox
Riesgos proporcionales
3.1. Eficacia vs Efectividad vacunal
Eficacia:
Se refiere a la capacidad de lograr un efecto deseado o esperado bajo condiciones ideales o controladas.
Es una medida teórica. En experimentos clínicos, por ejemplo, la eficacia de un medicamento se evalúa en condiciones controladas, donde todos los factores externos están cuidadosamente regulados para determinar el rendimiento puro del medicamento.
Puede considerarse como “lo que puede hacer” una intervención en las mejores circunstancias posibles.
Efectividad:
Se refiere a qué tan bien funciona una intervención en condiciones “reales” o prácticas, fuera de un entorno controlado.
Es una medida práctica. En el contexto de los medicamentos, la efectividad se refiere a qué tan bien funciona un medicamento en el “mundo real”, donde las condiciones no están tan controladas y hay muchos factores variables.
Puede considerarse como “lo que realmente hace” una intervención en circunstancias típicas o cotidianas.
| Un ejemplo podría ser un medicamento que en experimentos clínicos (en condiciones ideales) mostró una eficacia del 95% en prevenir el desenlace. Sin embargo, cuando se usó en el contexto general, considerando factores como la adherencia al tratamiento, interacciones con otros medicamentos y variabilidad en la población, su efectividad fue del 85%. Aquí, la eficacia muestra el potencial del medicamento bajo condiciones ideales, mientras que la efectividad muestra cómo funciona en situaciones cotidianas. |
En el caso de las vacunas la efectividad hace referencia a la disminución proporcional de casos de una enfermedad o evento en una población vacunada comparada con una población no vacunada, en condiciones del mundo real.
3.2. Tiempo de inducción
El tiempo de inducción o “delay” se refiere al periodo necesario para que la vacuna administrada induzca una respuesta inmune protectora frente a la infección o la enfermedad provocada por un patógeno. Si ocurre una infección entre el momento de la vacunación y el momento donde se prevé exista una respuesta inmune protectora, ocurrirá la infección de manera natural y no se considera un fallo de la vacuna en cuestión, puesto que la persona inmunizada aún no contaba con la protección conferida por la vacuna.
3.3. Diseños observacionales para el estudio de la efectividad vacunal
Por múltiples razones, los estudios observacionales son los más utilizados en la estimación de la efectividad vacunal. Existen múltiples diseños, entre ellos: diseño de cohortes, diseño de casos y controles, diseño de test-negativo, diseño “screening-method”. La elección del diseño, dependerá de la disponibilidad de información y los recursos disponibles para llevar a cabo el estudio.
3.4. Diseño de cohorte para el estudio de la efectividad vacunal
El término cohorte se refiere a un grupo de personas que comparten una característica común. En los estudios con diseño de cohorte, existen dos o más poblaciones que difieren en una característica o exposición y se realiza un seguimiento a ambos grupos para evaluar la aparición de uno o más desenlaces de interés y comparar la incidencia de los eventos entre ambos grupos. Para el caso de los estudios de la efectividad de vacunas, la exposición de interés corresponde a la aplicación de la vacuna y los desenlaces pueden incluir:
Infección: contagio con el patógeno de interés tras una exposición a alguien infeccioso
Enfermedad: desarrollo de signos y síntomas relacionados con la infección con un patógeno. Puede tener diferentes grados de severidad, requerir ingreso a hospitalización, UCI o incluso conducir a la muerte.
A la hora de llevar a cabo estos estudios se debe garantizar que las personas incluidas en cada población no tengan el desenlace de interés que será evaluado durante el seguimiento. Así mismo, es importante que el seguimiento se lleve a cabo de manera igual de rigurosa y por el mismo tiempo en ambos grupos.
La efectividad vacunal corresponde a la reducción relativa del riesgo de desarrollar la infección y/o enfermedad. En los estudios de cohorte se puede estimar el riesgo relativo, los odds ratio o los hazard ratio que expresa el riesgo que tiene la cohorte no expuesta comparado con la cohorte de los expuestos. La efectividad vacunal será, por lo tanto, el complemento del riesgo proporcional en la cohorte de expuestos.
Veamos esto con un ejemplo: para evaluar la efectividad de una vacuna para prevenir el desarrollo de enfermedad en una población, al cabo del seguimiento la incidencia en la cohorte vacunada fue de 1 por 1000 habitantes y en la cohorte no vacunada fue de 5 por 1000 habitantes. En este caso, tenemos que el riesgo relativo en la población vacunada fue 0.001/0.005 = 0,2. Es decir, la población vacunada tuvo una incidencia correspondiente al 20% de la incidencia de la población no vacunada. Esta reducción se puede atribuir a la vacuna y para estimarla usaríamos el complemento, que corresponde a 1 - 0,2= 0,8. Es decir que la reducción que se observó corresponde a un 80% y se puede atribuir a la vacuna, por lo tanto, la efectividad de la vacunación fue del 80% para evitar la enfermedad.
3.5. Métodos estadísticos para análisis de efectividad vacunal
En el diseño de cohortes se utilizan principalmente dos métodos: Estimación no paramétrica de Kapplan-Meier y Modelo semi-paramétrico de Cox
Estimador Kaplan-Meier
El estimador Kaplan-Meier utiliza las tasas de incidencia de un evento para cuantificar la probabilidad de supervivencia \(S(t)\) de forma no paramétrica, es decir, sin una representación matemática funcional. En general, la incidencia acumulada de cada grupo permite cuantificar el riesgo de presentar el evento como \(1 - S(t)\). Asimismo, la comparación entre el riesgo de ambos grupos en un punto del tiempo determina el riesgo relativo entre grupos (\(RR\)). A partir de esta se estima la efectividad vacunal como: \[V_{EFF} = 1 - RR\]
Modelo de Regresión de Cox
El modelo Cox, permite estimar de forma semi-paramétrica la función de riesgo instantáneo \(\lambda(t|x_i)\) de un individuo \(i\) en terminos de sus características, las cuales se asocian a un conjunto de covariables \(x_1, x_2, ..., x_n\), con lo cual se tiene:
\[\lambda(t|x_i) = \lambda_0(t) \exp(\beta_1 x_{i1} + \beta_2 x_{i2} + ....+\beta_n x_{in})\] donde \(\beta_1, \beta_2, ..., \beta_n\) son los coeficientes de la regresión y \(\lambda_0\) es una función basal no especificada, por lo que el modelo se asume como semi-paramétrico. En el caso en el que la función de riesgo instantáneo es completamente especificada, es decir, se conoce la forma funcional de \(\lambda_0(t)\), es posible calcular matemáticamente la probabilidad de supervivencia. Sin embargo, ninguna de estas funciones puede ser estimada directamente del modelo de Cox. Por el contrario, con este se busca estimar el hazard ratio, una medida de riesgos comparativa entre dos individuos \(i\) y \(j\) con características \(x_{i1}, x_{i2}, ..., x_{in}\) y \(x_{j1}, x_{j2}, ..., x_{jn}\), respectivamente. En este orden, al evaluar el riesgo de un individuo con respecto al otro se tiene:
\[HR = \frac{\lambda(t|x_i)}{\lambda(t|x_j)} = \frac{\lambda_0(t)\exp(\beta x_{i})}{\lambda_0(t)\exp(\beta x_{j})} = \exp(\beta(x_i-x_j))\] Riesgos proporcionales: Nótese que la dependencia temporal de las funciones de riesgo instantáneo individuales se canceló dentro de la expresion anterior para el Hazard ratio, por tanto se dice que los individuos \(i\) y \(j\) exhiben riesgos proporcionales en el tiempo. Esta hipótesis constituye un pilar importante de los estudios de efectividad bajo diseño de cohorte.
En el contexto de los estudios de cohorte, el modelo de Cox puede utilizarse para estimar el riesgo comparativo entre ambos grupos de presentar un desenlace de interés. En este sentido la pertenecia a un grupo se utiliza como covariable dentro de la regresión. Particularmente, para el cálculo de la efectividad vacunal se puede utilizar el \(HR\) de forma análoga al caso discutido para el estimador Kaplan-Meier, con lo que se define:
\[V_{EFF} = 1 - HR\]
4. Caso de uso del paquete
Para esta sesión se trabajará con el conjunto de datos de ejemplo
incluido en el paquete vaccineff. Adicionalmente, se
utilizarán algunas funciones de los paquetes ggplot2 y
cowplot para vizualizar algunos resultados.
Para installar vaccineff ejecute las siguientes líneas
en R:
R
# if(!require("pak")) install.packages("pak")
# pak::pak("epiverse-trace/vaccineff@dev")
Posteriormente, para cargar los paquetes en el espacio de trabajo y
el set de datos de ejemplo del vaccineff ejecute:
R
library("vaccineff")
library("ggplot2")
library("cowplot")
data(cohortdata)
head(cohortdata)
SALIDA
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2
1 <NA> <NA>
2 <NA> <NA>
3 <NA> <NA>
4 BRAND2 BRAND2
5 BRAND1 BRAND1
6 BRAND2 BRAND2Este tabla contiene información de una epidemia simulada ocurrida en 2044 sobre una población hipotética, compuesta por 100.000 habitantes, que recibió dos dosis de una vacuna para disminuir el riesgo de muerte por una enfermedad respiratoria viral. Sobre esta población se realizó seguimiento por 1 año, entre el 1 de enero y 31 de diciembre de 2044. En el conjunto de datos se presenta la información desagregada para cada uno de los participantes.
4.1 Funciones básicas de exploración de datos
4.1.1 Grupo etario
Para agrupar la población por grupo etario y graficar la distribución por edad utilizaremos la función “get_age_group”. Para esto, ejectute el siguiente comando en R:
R
cohortdata$age_group <- get_age_group(
data = cohortdata,
col_age = "age",
max_val = 80,
min_val = 0,
step = 9)
Esta función permite agrupar la población en intervalos etarios a partir de la variable “age” del conjunto de datos. En particular, para construir la agrupación por decenios se asigna el ancho del intervalo con step = 9, el mínimo valor de edad en 0 con “min_val” y el máximo valor en 80 con “max_val”. Esto significa que cualquier registro con edad mayor o igual a 80 años se agrupará en “>80”
Puede graficar de forma rápida la distribución etaria asociada a la variable “age_group” utilizando la función “geom_bar” de la librería ggplot2. Para esto, ejecute el siguiente comando en R:
R
ggplot(data = cohortdata,
aes(x = age_group)) +
geom_bar() +
theme_classic()
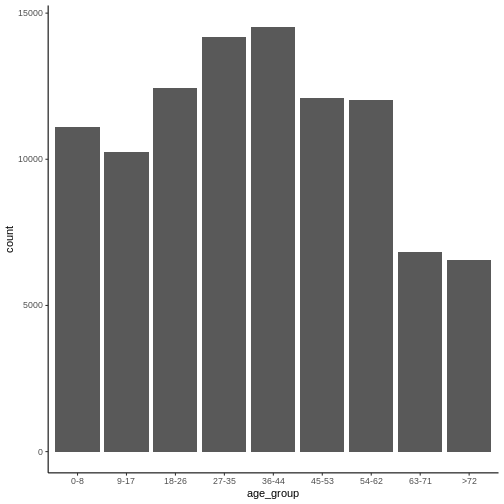
4.1.2. Cobertura vacunal en las cohortes
En un conjunto de datos típico de un estudio de cohorte se tiene
información desagregada por persona de la(s) dosis aplicada(s) durante
el seguimiento. En este sentido, es importante dimensionar el nivel de
cobertura en la vacunación alcanzado durante el seguimiento. vaccineff
ofrece la función make_vaccineff_data y plot
que permiten llevar a cabo esta tarea con facilidad. Para esto, ejecute
el siguiente comando en R:
R
# Create `vaccineff_data`
vaccineff_data <- make_vaccineff_data(
data_set = cohortdata,
outcome_date_col = "death_date",
censoring_date_col = "death_other_causes",
vacc_date_col = "vaccine_date_2", # date of last dose
end_cohort = as.Date("2021-12-31")
)
# Plot the vaccine coverage of the total population
plot(vaccineff_data)
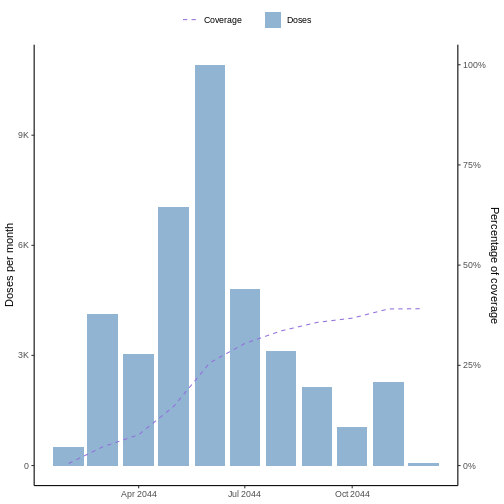
Esta función calcula la cobertura con base a la última dosis, la cual se especifica en el parámetro “vacc_date_col”. En particular, en el ejemplo anterior se utiliza la segunda dosis del conjunto de datos de ejemplo (“vaccine_date_2”).
La función make_vaccineff_data() genera nuevas columnas
en la base de datos de cohorte. La columna
immunization_date describe la fecha de inmunización según
la úlima dosis. La columna t0_follow_up describe la fecha
del inicio del periodo de seguimiento que, por defecto, es la fecha de
inicio del estudio o última dosis de vacunación. La fecha de inicio del
estudio está definida por la mínima fecha de inmunización.
R
# New columns: immunization_date, vaccine_status, t0_follow_up
head(vaccineff_data$cohort_data)
SALIDA
// linelist object
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2 age_group immunization_date vaccine_status t0_follow_up
1 <NA> <NA> 45-53 <NA> u 2021-03-11
2 <NA> <NA> 63-71 <NA> u 2021-03-11
3 <NA> <NA> >72 <NA> u 2021-03-11
4 BRAND2 BRAND2 >72 2021-05-16 v 2021-05-16
5 BRAND1 BRAND1 54-62 2021-06-22 v 2021-06-22
6 BRAND2 BRAND2 >72 2021-05-02 v 2021-05-02
// tags: outcome_date_col:death_date, censoring_date_col:death_other_causes, vacc_date_col:vaccine_date_2, immunization_date_col:immunization_date, vacc_status_col:vaccine_status, t0_follow_up_col:t0_follow_up 4.1.3. Definir la exposición: cohorte vacunada y cohorte no vacunada
La columna vaccine_status categoriza cada uno de los
sujetos según su estado vacunal, vacunados como “v” y no vacunados como
“u” (unvaccinated, en inglés) para cada uno de los registros de acuerdo
con su estado de vacunación, el cual se determina a partir de la
variable "immunization_date".
4.2 Seguimiento de la cohorte y tiempos al evento
Para llevar a cabo la estimación de la efectividad vacunal primero
debe definir la fecha de inicio y fin del seguimiento de cohortes, esto
con base en su exploración de las bases de datos. Para el caso
particular del conjunto de datos ejemplo contenidos es
vaccineff se utiliza en la funcion
make_vaccineff_data() el argumento
end_cohort.
Para determinar la fecha de immunización, de un individuo
vaccineff::make_vaccineff_data() calcula la fecha de
inmunización seleccionando la vacuna que cumpla con el criterio de
fecha límite presentado en la siguiente figura.
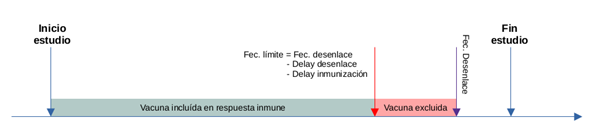
4.2.2 Tiempo de inducción del efecto (delay)
En la figura anterior se introdujo el concepto de delay. El
delay de la immunización se refiere al tiempo que se espera que
transcurra antes de considerar que existe inmunidad protectora. Esta
variable puede controlarse en la función mediante el parámetro
immunization_delay. El valor que se asigne a esta depende
de la naturaleza del estudio. En particular, para nuestra epidemia
ejemplo utilizaremos immunization_delay = 14.
Para actualizar el objeto vaccineff_data agregue el
argumento immunization_delay = 14 en la anterior función y
ejecútela:
R
# Create `vaccineff_data`
vaccineff_data <- make_vaccineff_data(
data_set = cohortdata,
outcome_date_col = "death_date",
censoring_date_col = "death_other_causes",
vacc_date_col = "vaccine_date_2",
end_cohort = as.Date("2021-12-31"),
# Time in days before the patient is considered immune. Default is 0.
immunization_delay = 14
)
Al ejecutar este comando, se le sumará el delay a las fechas
de las columnas immunization_date y
t0_follow_up que corresponde la fecha 14 días posteriores a
la última dosis de cualquiera de las dos vacunas utilizadas en el caso
de estudio, que cumpla con el criterio de fecha límite. Puede
evidenciar la nueva columna en el conjunto de datos.
R
# Updated columns: immunization_date, t0_follow_up
head(vaccineff_data$cohort_data)
SALIDA
// linelist object
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2 age_group immunization_date vaccine_status t0_follow_up
1 <NA> <NA> 45-53 <NA> u 2021-03-25
2 <NA> <NA> 63-71 <NA> u 2021-03-25
3 <NA> <NA> >72 <NA> u 2021-03-25
4 BRAND2 BRAND2 >72 2021-05-30 v 2021-05-30
5 BRAND1 BRAND1 54-62 2021-07-06 v 2021-07-06
6 BRAND2 BRAND2 >72 2021-05-16 v 2021-05-16
// tags: outcome_date_col:death_date, censoring_date_col:death_other_causes, vacc_date_col:vaccine_date_2, immunization_date_col:immunization_date, vacc_status_col:vaccine_status, t0_follow_up_col:t0_follow_up 4.2.3 Definir el desenlace: estado vivo vs estado fallecido
El desenlace para este ejercicio va a ser la condición vital al final del estudio. En otros ejercicios el desenlace de interés podría ser la hospitalización o la infección, dependiendo del conjunto de datos utilizado.
Tenga en cuenta que en conjunto de datos del caso de estudio todas
las defunciones son debidas a la infección por el virus de interés. Para
definir el desenlace de interés de acuerdo a la condición vital de los
participantes en la cohorte, en la funcion
make_vaccineff_data() el argumento
outcome_date_col.
4.2.4. Calcular el tiempo al evento (desde exposición hasta desenlace)
Ahora, calcule para cada una de las personas el tiempo que fue seguido en el estudio. Recuerde que el seguimiento se hace igual para ambas cohortes (vacunada y no vacunada) y finaliza cuando termina el estudio o cuando se presenta el desenlace de interés. Para obtener este dato ejecute el siguiente comando en R:
R
# Estimate the Vaccine Effectiveness (VE)
ve <- estimate_vaccineff(vaccineff_data = vaccineff_data, at = 350)
Al ejecutar este comando se calcula la efectividad vacunal. Este
cálculo se basa en el estimador de Kaplan-Meier y en el modelo de Cox
para riesgos proporcionales del paquete survival. El
argumento at define el el número de días en los que se
estima la efectividad vacunal desde el inicio del periodo de
seguimiento.
En la figura a continuación se presenta un esquema de los dos métodos de cálculo del tiempo al evento.
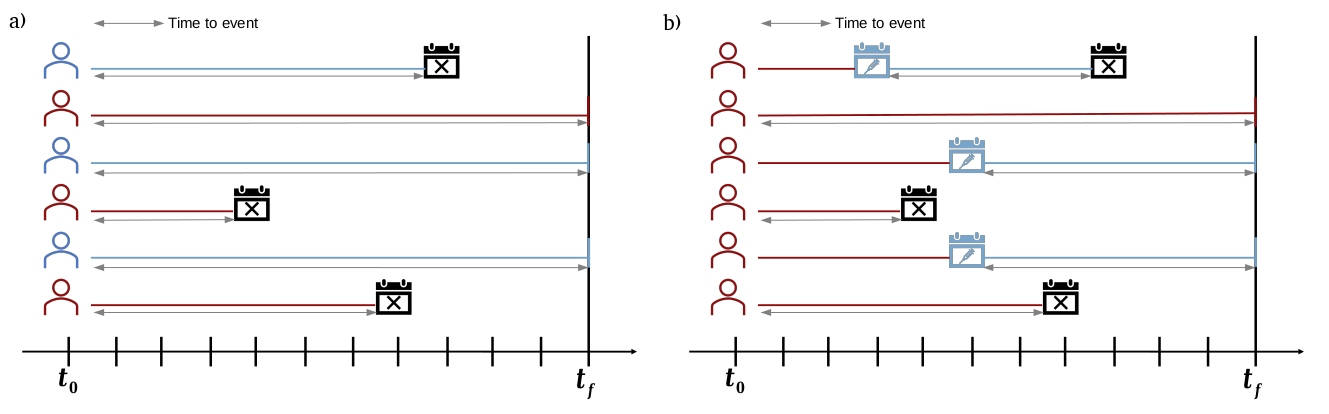
4.3. Curvas de riesgo acumulado y supervivencia al desenlace en cada cohorte
Como primera aproximación a la efectividad vacunal, graficaremos la curva de riesgos acumulados (1 menos la supervivencia de las poblaciones). Esta nos permite entender de forma cualitativa cuál de las poblaciones acumula mayor riesgo durante el estudio de cohorte. Y por tanto, evaluar hipótesis sobre el potencial efecto de la vacunación sobre la cohorte. Para graficar el riesgo acumulado ejecute el siguiente comando en R:
R
# Cumulative incidence
plot(ve, type = "surv", cumulative = TRUE)
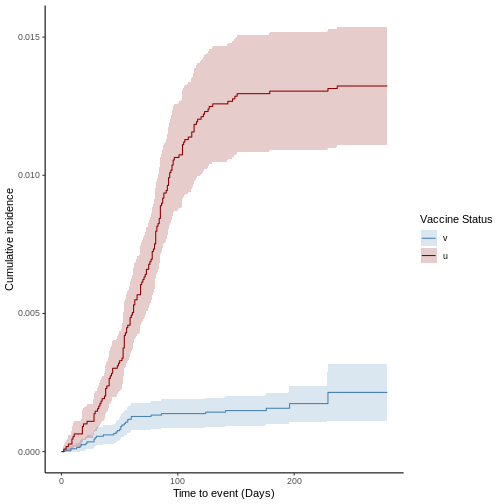
A partir de la función anterior también es posible realizar la gráfica de supervivencia de las cohortes o gráfica de Kaplan-Meier en la cual se parte del 100% de ambas cohortes en el eje de las ordenadas y en el eje de las abscisas se representa el tiempo y se observa la disminución que hay debido a las defunciones en cada cohorte. Tenga en cuenta que este no es el estimador de Kaplan-Meier, es sólo la gráfica sobre las curvas de supervivencia y de riesgo acumulado. Para obtener este gráfico, se ejecuta la misma función y se cambia el argumento “percentage” por FALSE:
R
# Generate Survival plot
plot(ve, type = "surv", cumulative = FALSE)
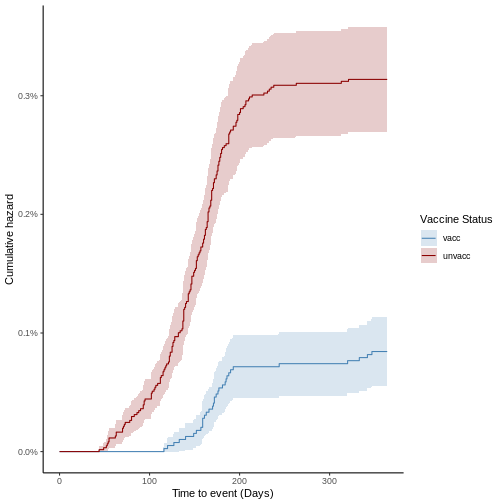
La función estimate_vaccineff() crea internamente una
tabla Kaplan-Meier.
R
head(ve$kaplan_meier)
4.4. Evaluación de la hipótesis riesgos proporcionales
Previo a la estimación de la efectividad vacunal es importante testear la hipótesis de riesgos proporcionales entre las cohortes de vacunados y no vacunados, con el fin de identificar posibles sesgos muestrales que afecten la validez de los resultados y definir estrategias de cálculo de cohortes dinámicas, emparejamiento o estratificación, entre otras, que permitar contrarestar este efecto. Un método cualitativo utilizado ampliamente en la literatura es la transformación de la probabilidad de supervivencia mediante la función logaritmo natural como \(\log[-\log[S(t)]]\). Al graficar esta función contra el logaritmo del tiempo al evento, es posible identificar si los grupos representan riesgos proporcionales cuando sus curvas se comportan de forma aproximadamente paralela.
4.5. Estimación de la efectividad vacunal
Modelo de Cox
En todos los estudios observacionales de efectividad vacunal de cohorte se compara el riesgo (o tasa de incidencia) entre los vacunados y no vacunados de desarrollar el desenlace de interés (infección, enfermedad, muerte, etc). La medida de riesgo a utilizar dependerá de las características de la cohorte y puede expresarse en términos de relative risk (RR) o hazard ratio (HR).
En este ejercicio utilizaremos el modelo de regresión de riesgos proporcionales de Cox para estimar el hazar ratio y con esta medida estimar la efectividad mediante
VE= 1-HR
Para estimar la efectividad vacunal en términos de HR, ejecute el siguiente comando en R:
R
# Print summary of VE
summary(ve)
SALIDA
Vaccine Effectiveness at 350 days computed as VE = 1 - HR:
VE lower.95 upper.95
0.872 0.8122 0.9128
Schoenfeld test for Proportional Hazards assumption:
p-value = 0.0078Podemos usar la función plot() para evaluar la hipótesis
de riesgos proporcionales:
R
# Generate loglog plot to check proportional hazards
plot(ve, type = "loglog")
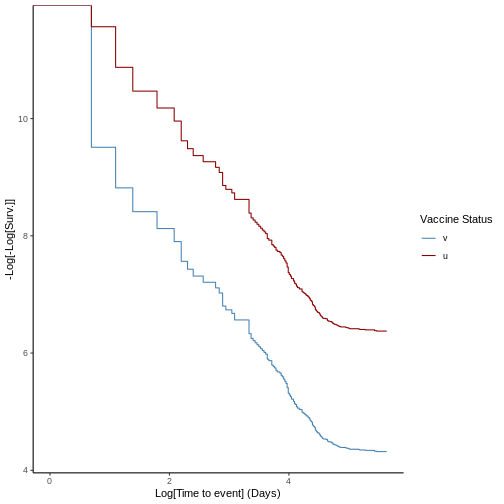
4.6 Cohorte dinámica - Emparejamiento poblacional
El comando anterior arrojó la efectividad vacunal obtenida mediante el model de Cox. Sin embargo, en la columna PH aparece la palabra rejected. Esto significa que pese a que las curvas de ambos grupos son paralelas la evaluación de la hipótesis de riesgos proporcionales haciendo uso del test de Schoenfeld no es satisfactoria. Esto debido a los potenciales sesgos muestrales inducidos por la estrategia de vacunación desplegada sobre la población. Una estrategia para contrarestas dichos sesgos es el emparejamiento dinámico de la población. En la siguiente figura se presenta un esquema de emparejamiento orientado a disminuir los sesgos muestrales.
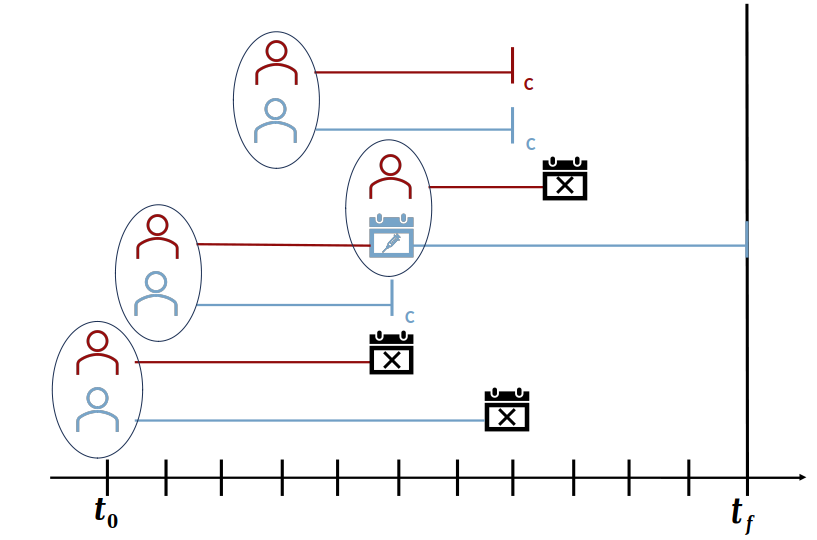
Para realizar el emparejamiento poblacional use los argumentos
match = TRUE y exact = c("age", "sex") para
emparejar por edad y sexo exactos:
R
# Create `vaccineff_data_matched`
vaccineff_data_matched <- make_vaccineff_data(
data_set = cohortdata,
outcome_date_col = "death_date",
censoring_date_col = "death_other_causes",
vacc_date_col = "vaccine_date_2",
end_cohort = as.Date("2021-12-31"),
immunization_delay = 14,
# Performe cohort matching
match = TRUE,
exact = c("age", "sex")
)
Por ejemplo, si usamos el argumento
nearest = c("age" = 2) podemos calibrar el emparejamiento
por una distancia de 2 unidades de edad.
En la base de datos emparejada identificamos nuevas columnas como
subclass, que agrupa con un código a los
emparejamientos.
R
head(vaccineff_data_matched$matching$match)
SALIDA
// linelist object
id sex age death_date death_other_causes vaccine_date_1 vaccine_date_2
1 04edf85a M 50 <NA> <NA> <NA> <NA>
2 c5a83f56 M 66 <NA> <NA> <NA> <NA>
3 82991731 M 81 <NA> <NA> <NA> <NA>
4 afbab268 M 74 <NA> <NA> 2021-03-30 2021-05-16
5 3faf2474 M 54 <NA> <NA> 2021-06-01 2021-06-22
6 97df7bdc M 79 <NA> <NA> 2021-03-21 2021-05-02
vaccine_1 vaccine_2 age_group immunization_date vaccine_status subclass
1 <NA> <NA> 45-53 <NA> u 6226
2 <NA> <NA> 63-71 <NA> u 5023
3 <NA> <NA> >72 <NA> u 7170
4 BRAND2 BRAND2 >72 2021-05-30 v 1
5 BRAND1 BRAND1 54-62 2021-07-06 v 2
6 BRAND2 BRAND2 >72 2021-05-16 v 3
t0_follow_up censoring_after_match
1 2021-07-16 <NA>
2 2021-05-24 <NA>
3 2021-05-18 <NA>
4 2021-05-30 <NA>
5 2021-07-06 <NA>
6 2021-05-16 <NA>
// tags: outcome_date_col:death_date, censoring_date_col:censoring_after_match, vacc_date_col:vaccine_date_2, immunization_date_col:immunization_date, vacc_status_col:vaccine_status, t0_follow_up_col:t0_follow_up Las salidas de las funciones de summary() y
plot() cambiarán luego de configurado el emparejamiento.
Corre nuevamente todo el flujo de trabajo escrito en este episodio con
el objeto vaccineff_data_matched, incluyendo el gráfico de
cobertura y la estimación de la .
R
# Print summary of vaccineff data object
summary(vaccineff_data_matched)
# Plot the vaccine coverage of the total population
plot(vaccineff_data_matched)
# Estimate the Vaccine Effectiveness (VE)
ve_matched <- estimate_vaccineff(vaccineff_data = vaccineff_data_matched, at = 350)
# Generate Survival plot
plot(ve_matched, type = "surv", cumulative = FALSE)
# plot(ve, type = "surv", percentage = TRUE, cumulative = FALSE)
# Cumulative incidence
plot(ve_matched, type = "surv", cumulative = TRUE)
# Print summary of VE
summary(ve_matched)
# Generate loglog plot to check proportional hazards
plot(ve_matched, type = "loglog")
5. Reflexión
En esta sesión se llevó a cabo una estimación básica de la efectividad vacunal mediante un estudio de cohorte, haciendo uso de los estimador Kaplan-Meier y del modelo de Cox. Adicionalmente, se estudió la hipótesis de riesgos proporcionales para los grupos vacunado y no vacunado comparando la construcción de tiempos al evento de forma dinámica y fija. Se observó que pese a que la hipótesis de riesgos proporcionales se corrobora gráficamente en la consrucción de los tiempos al evento con fecha de inicio fija, al evaluar el modelo de riesgos proporcionales de Cox el test de Schoenfeld rechaza esta hipótesis. En general la decisión sobre aceptar o no los resultados es altamente dependiente del acceso a información adicional relevante que permita realizar ajustes a la estimación y capturar dinámicas relevantes.
Reto
Puntos Clave
Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes
Content from Indicadores demográficos, canales endémicos y clusters de incidencia usando epiCo
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo simular una sala de análisis de riesgo?
Objetivos
Al final de este taller usted podrá:
- Navegar por la codificación de la División Política Administrativa de Colombia (DIVIPOLA).
- Consultar, visualizar e interpretar pirámides poblacionales a distintas escalas administrativas.
- Familiarizarse con la información epidemiológica proporcionada por el SIVIGILA.
- Describir las características demográficas de la información epidemiológica.
- Estimar tasas de incidencia acumulada a distintas escalas espaciales y temporales.
- Realizar una evaluación del riesgo etario integrando información epidemiológica con información sobre la estructura poblacional de una región.
epiCo
epiCo ofrece herramientas estadísticas y de visualización para el análisis de indicadores demográficos, comportamiento espaciotemporal como mapas de riesgo, y caracterización de los brotes a través de canales endémicos de las ETVs en Colombia.
Instalación
Puede descargar la última versión estable de epiCo a través del repositorio en GitHub con los siguientes comandos:
R
# if(!require("remotes")) install.packages("remotes")
# if(!require("epico")) remotes::install_github("epiverse-trace/epiCo")
Motivación
- Incluir evaluaciones de riesgos espaciales y demográficos en informes epidemiológicos rutinarios para mejorar la identificación de grupos vulnerables.
- Facilitar la comprensión de los diferentes perfiles epidemiológicos dentro de una región de Colombia en cuanto al inicio, duración, magnitud y frecuencia de los brotes.
- Reforzar la transparencia de los métodos utilizados para el análisis de brotes.
Indicadores demográficos en epiCo
El módulo demográfico de epiCo es una herramienta de análisis descriptivo y evaluación del riesgo basado en las variables reportadas por el Sistema de Vigilancia en Salud Pública en Colombia (SIVIGILA) y en datos del Departamento Administrativo Nacional de Estadística (DANE).
1. Navegando por la codificación de la División Política Administrativa de Colombia (DIVIPOLA)
El sistema DIVIPOLA es una nomenclatura estándar diseñada por el DANE para la identificación de entidades territoriales (departamentos, distritos y municipios), áreas no municipalizadas, y centros poblados a través de un código numérico único.
Colombia posee:
- 32 departamentos (División administrativa nivel 1)
- 1102 municipios (División administrativa nivel 2)
- 1 isla
- 18 áreas no municipalizadas
- 6678 centros poblados
Dos dígitos son usados para codificar los departamentos, y tres
dígitos adicionales son usados para codificar los municipios.
epiCo proporciona la lista completa de códigos a través
de un dataset interno llamado divipola_table.
R
# Se cargan las librerías necesarias.
library(epiCo)
library(incidence)
# Listado de códigos para cada uno de los municipios.
data("divipola_table")
head(divipola_table)
SALIDA
COD_DPTO NOM_DPTO COD_REG NOM_REG COD_MPIO NOM_MPIO LATITUD
1 05 ANTIOQUIA 03 CENTRO_OCCIDENTE 05001 MEDELLIN 6.257590
2 05 ANTIOQUIA 03 CENTRO_OCCIDENTE 05002 ABEJORRAL 5.803728
3 05 ANTIOQUIA 03 CENTRO_OCCIDENTE 05004 ABRIAQUI 6.627569
4 05 ANTIOQUIA 03 CENTRO_OCCIDENTE 05021 ALEJANDRIA 6.365534
5 05 ANTIOQUIA 03 CENTRO_OCCIDENTE 05030 AMAGA 6.032922
6 05 ANTIOQUIA 03 CENTRO_OCCIDENTE 05031 AMALFI 6.977789
LONGITUD
1 -75.61103
2 -75.43847
3 -76.08598
4 -75.09060
5 -75.70800
6 -74.981242. Pirámides poblacionales
epiCo cuenta con datos internos sobre las proyecciones poblaciones de Colombia a nivel nacional, departamental y municipal (información proveniente del DANE).
Los usuarios pueden realizar consultas a epiCo
utilizando la función population_pyramid, la cual requiere
el codigo DIVIPOLA de la entidad de interés y el año que se desea
consultar.
R
tolima_codigo <- "73" # Código DIVIPOLA para el departamento del Tolima.
año <- 2021 # Año a consultar.
tolima_piramide_2021 <- population_pyramid(tolima_codigo, año) # Pirámide
# poblacional del departamento del tolima para el año 2021.
head(tolima_piramide_2021)
SALIDA
age population sex
1 0 42889 F
2 5 47378 F
3 10 51141 F
4 15 54694 F
5 20 53866 F
6 25 50014 FepiCo presenta los datos agrupados en intervalos de 5 años de forma predeterminada; sin embargo, puede modificar parámetros para tener rangos distintos, separar la pirámide por género binario, obtener los datos como conteos totales o proporciones y/o desplegar una gráfica de la pirámide.
R
tolima_codigo <- "73" # Código DIVIPOLA para el departamento del Tolima.
año <- 2021 # Año a consultar.
rango_edad <- 10 #Rango de edades o ventana.
# Pirámide poblacional del departamento del tolima para el año 2021.
tolima_piramide_2021 <- population_pyramid(divipola_code = tolima_codigo,
year = año,
range = rango_edad,
sex = TRUE, total = TRUE,
plot = TRUE)
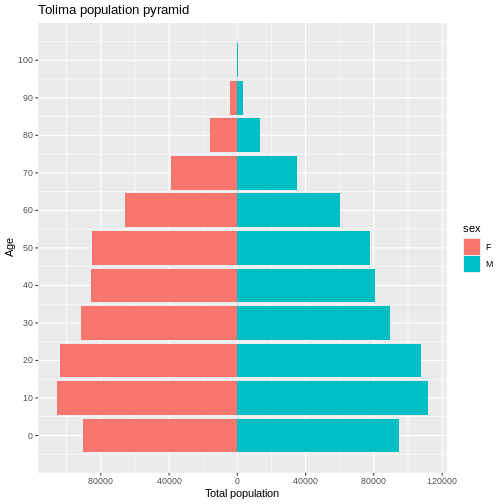
3. Datos epidemiológicos
epiCo es una herramienta que produce análisis basados en datos epidemiológicos como los que provee el SIVIGILA. El paquete cuenta con un data set llamado epi_data, que cuenta con la información y estructura que requiere la librería para sus funciones y que utiliza los casos de dengue reportados en el departamento del Tolima del 2012 al 2021 a manera de ejemplo.
R
# Datos epimdeiológicos.
data("epi_data")
head(epi_data)
SALIDA
# A tibble: 6 × 16
fec_not cod_pais_o cod_dpto_o cod_mun_o cod_pais_r cod_dpto_r cod_mun_r
<chr> <chr> <chr> <chr> <chr> <chr> <chr>
1 2012-02-04 170 73 73671 170 73 73671
2 2012-11-18 170 73 73268 170 73 73268
3 2012-07-12 170 73 73001 170 11 11001
4 2012-11-24 170 73 73275 170 73 73275
5 2012-03-29 170 73 73268 170 73 73268
6 2012-02-19 170 73 73001 170 73 73001
# ℹ 9 more variables: cod_dpto_n <chr>, cod_mun_n <chr>, edad <dbl>,
# sexo <chr>, per_etn <dbl>, ocupacion <chr>, estrato <chr>, ini_sin <chr>,
# cod_eve <dbl>4. Variables demográficas
epiCo proporciona un diccionario para consultar las
categorías étnicas usadas por el sistema SIVIGILA a través de la función
describe_ethnicity.
R
# Descripción de las etnicidades reportadas en la base de datos.
describe_ethnicity(unique(epi_data$per_etn))
SALIDA
code
1 1
2 2
3 3
4 4
5 5
6 6
description
1 A person of Amerindian descent who shares feelings of identification with their aboriginal past, maintaining traits and values of their traditional culture, as well as their own forms of organization and social control
2 They are communities that have their own ethnic and cultural identity; They are characterized by a nomadic tradition, and have their own language, which is Romanesque
3 Population located in the Archipelago of San Andres, Providencia and Santa Catalina, with Afro-Anglo-Antillean cultural roots, whose members have clearly differentiated sociocultural and linguistic traits from the rest of the Afro-Colombian population
4 Population located in the municipality of San Basilio de Palenque, department of Bolivar, where palenquero is spoken, a Creole language
5 Person of Afro-Colombian descent who have their own culture, and have their own traditions and customs within the rural-populated relationship
6 <NA>Para calcular la distribución de las ocupaciones en estos años,
epiCo usa la columna que nos indica la ocupación de
cada uno de los casos presentados en estos años. Esta ocupación está
codificada por el sistema ISCO-88 como se puede observar en la tabla
isco88_table, y epiCo cuenta con la función
occupation_plot para visualizar de forma proporcional el
número de casos pertenecientes a una labor.
R
# Tabla de ocupaciones del sistema ISCO-88.
data("isco88_table")
head(isco88_table)
SALIDA
major major_label sub_major
1 1 Legislators, Senior Officials and Managers 11
2 1 Legislators, Senior Officials and Managers 11
3 1 Legislators, Senior Officials and Managers 11
4 1 Legislators, Senior Officials and Managers 11
5 1 Legislators, Senior Officials and Managers 11
6 1 Legislators, Senior Officials and Managers 11
sub_major_label minor
1 Legislators and Senior Officials 111
2 Legislators and Senior Officials 112
3 Legislators and Senior Officials 113
4 Legislators and Senior Officials 114
5 Legislators and Senior Officials 114
6 Legislators and Senior Officials 114
minor_label unit
1 Legislators 1110
2 Senior Government Officials 1120
3 Traditional Chiefs and Heads of Villages 1130
4 Senior Officials of Special-Interest Organisations 1141
5 Senior Officials of Special-Interest Organisations 1142
6 Senior Officials of Special-Interest Organisations 1143
unit_label
1 Legislators
2 Senior government officials
3 Traditional chiefs and heads of villages
4 Senior officials of political-party organisations
5 Senior officials of employers', workers' and other economic-interest organisations
6 Senior officials of humanitarian and other special-interest organisations R
# Se calcula la distribución de ocupaciones.
occupation <- describe_occupation(isco_codes = as.integer(epi_data$ocupacion), sex = epi_data$sexo, plot = "treemap")
ADVERTENCIA
Warning in describe_occupation(isco_codes = as.integer(epi_data$ocupacion), :
NAs introduced by coercionSALIDA
59870 codes are invalid.
5. Estimación de las tasas de incidencia
La función incidence_rate de epiCo
requiere del paquete incidence para producir un objeto
incidence modificado. En lugar de un vector (o matriz) de conteos,
transforma el objeto para proporcionar un elemento de tasa que
representa el número de casos en el periodo dividido por el número total
de habitantes en la región en las fechas específicas.
epiCo usa como denominadores las proyecciones poblacionales del DANE; por lo que es necesario proporcionar el nivel de administración en el que se calculan las incidencias.
R
# Se crea el objeto incidence a partir de las fechas y municiíos presentadas en
# epi_data.
incidence_objecto <- incidence(
dates = epi_data$fec_not,
groups = epi_data$cod_mun_o,
interval = "1 epiweek"
)
# Calcular la tasa de incidencia para cada uno de los municipios del Tolima.
incidence_tasa_objecto <- incidence_rate(incidence_objecto, level = 2)
head(incidence_tasa_objecto$counts)
SALIDA
73001 73024 73026 73030 73043 73055 73067 73124 73148 73152 73168 73200
[1,] 7 0 0 0 0 0 0 0 0 0 2 0
[2,] 20 0 0 0 0 0 0 1 2 0 2 3
[3,] 17 0 1 1 0 0 0 0 2 0 3 0
[4,] 15 0 0 0 0 0 1 0 2 0 3 0
[5,] 18 0 0 0 0 0 0 0 4 0 8 0
[6,] 25 0 0 0 0 1 1 0 2 0 5 0
73217 73226 73236 73268 73270 73275 73283 73319 73347 73349 73352 73408
[1,] 0 0 0 5 0 0 0 5 0 0 0 0
[2,] 1 0 0 10 0 2 2 6 0 1 0 1
[3,] 1 1 0 20 0 3 0 3 0 5 0 5
[4,] 0 0 0 16 0 4 0 2 0 1 0 3
[5,] 0 1 0 18 0 4 0 3 0 0 0 2
[6,] 0 0 0 12 0 1 0 4 0 2 0 5
73411 73443 73449 73461 73483 73504 73520 73547 73555 73563 73585 73616
[1,] 0 1 1 0 0 1 0 0 0 0 0 0
[2,] 0 1 2 0 0 0 0 1 0 0 0 0
[3,] 0 1 1 0 1 0 0 0 0 0 0 0
[4,] 1 1 3 0 0 0 0 9 0 2 0 0
[5,] 0 1 2 0 2 2 0 0 0 0 0 0
[6,] 1 1 1 0 0 0 0 0 0 0 0 1
73622 73624 73671 73675 73678 73686 73770 73854 73861 73870 73873
[1,] 0 0 0 0 0 0 0 0 0 0 0
[2,] 0 2 0 0 0 0 1 1 0 0 0
[3,] 0 1 0 1 0 0 0 0 4 0 0
[4,] 0 0 0 1 0 0 0 0 6 0 0
[5,] 0 0 2 0 0 0 0 0 1 0 0
[6,] 0 0 1 0 0 0 0 0 1 0 06. Estimación del riesgo etario
La normalización de los datos es un aspecto clave de la
epidemiología. epiCo utiliza la distribución por edades
de los casos y normaliza los datos epidemiológicos con la estructura de
edades de una población a tarvés de la función age_risk.
Esta normalización nos permite estimar el riesgo por edad de sufrir una
enfermedad según la estructura de edad de la población general de un
municipio, departamento o país en un año determinado.
R
# Se filtran los datos del SIVIGILA para el año 2021.
data_tolima_2021 <- epi_data[lubridate::year(epi_data$fec_not) == 2021, ]
# Se calcula las tasas por edades para el año 2021.
incidence_rate_2019 <- age_risk(age = data_tolima_2021$edad,
population_pyramid = tolima_piramide_2021,
sex = data_tolima_2021$sexo,
plot = TRUE)
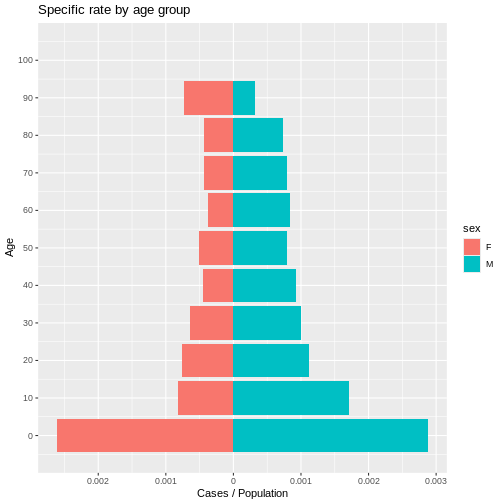
Construir un canal endémico con epiCo
El módulo de canal endémico de epiCo es una herramienta que permite estimar una línea de tendencia central y los límites superior e inferior del número esperado de casos de una enfermedad a partir de los datos históricos proporcionados por el usuario y un conjunto de parámetros personalizados.
En el siguiente tutorial, los usuarios aprenderán:
- Qué es un canal endémico y cuáles son sus ventajas, inconvenientes y precauciones.
- Un ejemplo de los datos históricos necesarios para construir un canal endémico.
- Cómo utilizar la función
endemic_channel.
1. ¿Qué es un canal endémico?
El uso de un canal endémico es una estrategia visual para representar el comportamiento histórico de una enfermedad en una región específica en una curva epidémica que define la tendencia central de los casos durante un año y los límites superior e inferior donde se espera que varíen los casos. Este gráfico proporciona tres zonas denominadas “\(\color{green}{\text{Safety - Seguridad}}\)”, “\(\color{yellow}{\text{Warning - Alerta}}\)” y “\(\color{red}{\text{Epidemic - Epidemia}}\)”, que posteriormente se utilizan para definir la situación epidemiológica de la región en función de los casos actuales.
La definición más amplia y la metodología para el canal endémico fueron proporcionadas por Bormant (1999).
Los datos necesarios para construir un canal endémico son la
incidencia semanal o mensual de la enfermedad durante los años
anteriores en la región de interés. epiCo pide al menos
un año de datos, pero los canales endémicos suelen tener entre 5 y 7
años de información. Es natural suponer que más años proporcionan
mejores estimaciones ya que los análisis estadísticos serán más
robustos, pero es importante disponer de información contextual para
asegurar que las condiciones de transmisión, vigilancia o demográficas
(entre otros factores) no han cambiado durante este periodo de tiempo.
En cuanto a la frecuencia de los datos, la incidencia semanal puede
proporcionar información más útil sobre el comportamiento de la
enfermedad y el momento en que se debe plantear una alerta
epidemiológica; sin embargo, depende de la experiencia de los usuarios y
de su contexto que se pueda lograr esta resolución de los datos. Otra
decisión común mientras se construye un canal endémico es ignorar los
años epidémicos anteriores para evitar tergiversar la dinámica de
transmisión tradicional. epiCo no sugiere años
epidémicos automáticamente, pero su función endemic_channel
ofrece la opción de anotar los años atípicos y decidir si incluirlos,
ignorarlos o ajustarlos. Más adelante en esta viñeta se ofrecen más
consejos y fuentes para la recopilación de datos.
2. Datos históricos necesarios para construir un canal endémico
En esta sección se presentan algunas estrategias para obtener, manejar y recopilar los datos históricos necesarios para construir un canal endémico. Se asume que el usuario cuenta con los datos de incidencia de la enfermedad de interés o tiene la posibilidad de consultar datos históricos del SIVIGILA.
Independientemente del caso del usuario, el objetivo de esta sección
es crear un objeto incidence con datos históricos de la
enfermedad. Este objeto debe dar cuenta de la incidencia de una sola
región (no se permiten grupos en la función
endemic_channel), debe tener un intervalo semanal o mensual
(también se permiten semanas epidemiológicas) y debe representar al
menos un año de información.
Para comprender mejor el paquete de incidence, consulte
sus viñetas.
Incidencia histórica a partir de los datos propios o de los datos SIVIGILA
El canal endémico es más útil cuando se dispone de datos hasta el año inmediatamente anterior; sin embargo, esto no siempre es posible para los usuarios ajenos a las instituciones de vigilancia. Como opción, los usuarios pueden acceder a los datos del SIVIGILA que normalmente se hacen públicos hasta el segundo semestre del año (es decir, los datos de 2022 se publicaron en el segundo semestre de 2023). Para este ejemplo se utilizarán los datos suministrados en la carpeta de datos del paquete. Estos datos presentan los casos de dengue para todos los municipios del Tolima para los años 2012 a 2021. En este caso, utilizaremos los casos del municipio de Espinal para calcular el respectivo canal endémico.
R
# Se cargan las librerías necesarias.
library(epiCo)
library(incidence)
#Se cargan los datos epidemiológicos del paquete.
data("epi_data")
data_espinal <- epi_data[epi_data$cod_mun_o == 73268, ]
# Se construyen el objeto incidence para el municipio del Espinal.
incidencia_espinal <- incidence(data_espinal$fec_not,
interval = "1 epiweek"
)
# Se filtra el objeto incidence para obtener el historico de los 7 años
# anteriores al año de interes. En este caso el 2021.
incidencia_historica <- incidencia_espinal[
incidencia_espinal$date <= as.Date("2020-12-31") &
incidencia_espinal$date >= as.Date("2014-01-01"), ]
print(incidencia_historica)
SALIDA
<incidence object>
[4808 cases from days 2014-01-05 to 2020-12-27]
[4808 cases from MMWR weeks 2014-W02 to 2020-W53]
$counts: matrix with 365 rows and 1 columns
$n: 4808 cases in total
$dates: 365 dates marking the left-side of bins
$interval: 1 week
$timespan: 2549 days
$cumulative: FALSECuando los usuarios tienen sus propios datos, el objetivo es el
mismo: limpiar y manejar los datos para construir el objeto
incidence (llamado incidencia_histórica en el
ejemplo anterior). El mensaje clave es que se necesita una lista de
fechas que den cuenta del evento de interés para luego utilizarla en el
paquete incidence.
3. Uso de la función canal_endémico de epico
Tras recopilar los datos de incidencia, los usuarios están listos para pedir a epiCo que construya un canal endémico.
La función endemic_channel tiene los siguientes
parámetros:
incidence_historic: Un objeto de incidencia con los recuentos de casos de los años anteriores.observations: Un vector numérico con las observaciones actuales (por defecto = NULL).method: Una cadena con el método de cálculo de la media de preferencia (“median”, “mean” o “geometric”) o método “unusual_behavior” (Prueba de distribución de Poisson) (por defecto = “geométrica”).geom_method: Una cadena con el método seleccionado para el cálculo de la media geométrica (véase la funcióngeom_meande epiCo) (por defecto = “shifted”).outlier_years: Un vector numérico con los años atípicos (epidémicos) (por defecto = NULL).-
outliers_handling: Una cadena con la decisión de tratamiento de los años atípicos:- ignored = los datos de los años atípicos no se tendrán en cuenta (por defecto).
- included = se tendrán en cuenta los datos de los años atípicos.
- replaced_by_median = los datos de los años atípicos se sustituirán por la mediana y se tendrán en cuenta.
- replaced_by_mean = los datos de los años atípicos se sustituirán por la media y se tendrán en cuenta.
- replaced_by_geom_mean = los datos de los años atípicos se sustituirán por la media geométrica y se tendrán en cuenta.
ci: Un valor numérico para especificar el intervalo de confianza a utilizar con el método geométrico (por defecto = 0.95).plot: Un booleano para mostrar un gráfico (por defecto = FALSE).
La salida de la función endemic_channel de
epiCo es una tabla de datos con las observaciones, la
media histórica y los intervalos de confianza, y un gráfico que muestra
las tres bandas epidemiológicas, las observaciones actuales (si se
proporcionan) y los métodos y el manejo de valores atípicos establecidos
por el usuario.
Ejemplo
El siguiente ejemplo utiliza la incidencia histórica a la que se ha accedido previamente desde la fuente de datos SIVIGILA para construir el canal endémico 2021 para el municipio del Espinal.
R
# Se toman el conteo de casos del 2020 como las observaciones.
observaciones <- incidencia_espinal[
incidencia_espinal$date >= as.Date("2021-01-01") &
incidencia_espinal$date <= as.Date("2021-12-31"), ]$counts
# Se especifican los años hiper endemicos que deben ser ignorados en la
# constucción del canal endémico.
años_atipicos <- c(2016, 2019)
# Se construye el canal endémico y se plotea el resultado.
espinal_endemic_chanel <- endemic_channel(
incidence_historic = incidencia_historica,
observations = observaciones,
outlier_years = años_atipicos,
plot = TRUE
)
SALIDA
Data prior to 2015-01-04 were not used for the endemic channel calculation.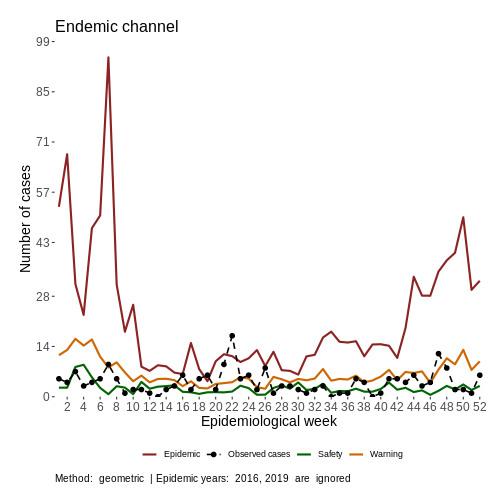
Análisis espaciotemporales con epico
El módulo espaciotemporal de epico es una herramienta que permite analizar la correlación espacial de los casos a partir de sus coordenadas de notificación y los tiempos reales de desplazamiento dentro del territorio colombiano.
En el siguiente tutorial aprenderás:
- A utilizar la función
morans_indexde epico. - Cómo interpretar y comunicar los resultados.
1. La función morans_index de
epico
epiCo proporciona una función para realizar un
análisis del índice
de Moran Local a partir de un objeto incidence con
observaciones únicas para un conjunto de municipios colombianos.
Internamente, la función lee los grupos del objeto
incidence como los códigos DIVIPOLA para:
- Estimar las tasas de incidencia utilizando la función
incidence_ratede epico. - Evaluarlas en la función
neighborhoodsde epico.
Es necesario que el usuario proporcione el nivel administrativo al que corresponden los grupos (0: nivel nacional, 1: nivel departamental, 2: nivel municipal), la escala a la que se deben estimar las tasas de incidencia (casos por número de habitantes) y el umbral de tiempo de viaje para la definición del barrio. En el siguiente ejemplo se utilizan los casos de los municipios del Tolima para el año 2021.
R
# Se cargan las librerías necesarias.
library(epiCo)
library(incidence)
data("epi_data")
# Se filtran los datos epidemiológicos para el año de interés.
data_tolima <- epi_data[lubridate::year(epi_data$fec_not) == 2021, ]
# Se crea el objeto incidence para los datos del tolima en el 2021.
incidence_object <- incidence(
dates = data_tolima$fec_not,
groups = data_tolima$cod_mun_o,
interval = "12 months"
)
# Se realiza el analisis espaciotemporal, especificando la escala de nivel
# municipal
monrans_tolima <- morans_index(incidence_object = incidence_object, threshold = 2)
SALIDA
Significant municipalities are:SALIDA
73043 with Low-High (incidence - spatial correlation)
73168 with Low-High (incidence - spatial correlation)
73483 with High-Low (incidence - spatial correlation)
73504 with Low-Low (incidence - spatial correlation)ADVERTENCIA
Warning: sf layer has inconsistent datum (+proj=longlat +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +no_defs).
Need '+proj=longlat +datum=WGS84'R
monrans_tolima$plot
2. Interpretación de los resultados del mapa
El metodo del indice de moran local divide los datos espaciales en 4 cuadrantes:
- High-High: donde se ubican los municipios cuya incidencia está sobre la media de la región, y se encuentran rodeados de municipios que también se encuentran sobre la media de la región.
- Low-High: municipios cuya incidencia está debajo de la media de la región, y se encuentran rodeados de municipios que se encuentran sobre la media de la región. Este cuadrante marca municipios candidatos a ser casos atípicos espaciales.
- Low-Low: municipios cuya incidencia está debajo de la media de la región, y se encuentran rodeados de municipios que se encuentran debajo de la media media de la región.
- High-Low, municipios cuya incidencia está sobre la media de la región, y se encuentran rodeados de municipios que se encuentran debajo de la media de la región. Este cuadrante marca municipios candidatos a ser casos atípicos espaciales.
Reto
Reto ***
Puntos Clave
Revise si al final de esta lección adquirió estas competencias:
- Navegar por la codificación de la División Política Administrativa de Colombia (DIVIPOLA).
- Consultar, visualizar e interpretar pirámides poblacionales a distintas escalas administrativas.
- Familiarizarse con la información epidemiológica proporcionada por el SIVIGILA.
- Describir las características demográficas de la información epidemiológica.
- Estimar tasas de incidencia acumulada a distintas escalas espaciales y temporales.
- Realizar una evaluación del riesgo etario integrando información epidemiológica con información sobre la estructura poblacional de una región.
Sobre este documento
Este documento ha sido diseñado por Juan Daniel Umaña Caro y Juan Montenegro-Torres para el Curso Internacional: Análisis de Brotes y Modelamiento en Salud Pública, Bogotá 2023. TRACE-LAC/Javeriana.
Contribuciones
- Juan D. Umaña (author)
- Juan Montenegro-Torres (author)
- Julian Otero (author)
- Mauricio Santos-Vega (contributor)
- Catalina Gonzalez Uribe (contributor)
- Juan Manuel Cordovez (contributor)
