Introducción a la analítica de brotes
Última actualización: 2026-02-09 | Mejora esta página
Hoja de ruta
Preguntas
- ¿Cómo modelar y analizar un brote?
Objetivos
Al final de este taller usted podrá:
Identificar los parámetros necesarios en casos de transmisión de enfermedades infecciosas de persona a persona.
Estimar la probabilidad de muerte (CFR).
Calcular y graficar la incidencia.
Estimar e interpretar la tasa de crecimiento y el tiempo en que se duplica la epidemia.
Estimar e interpretar el número de reproducción instantáneo de la epidemia.
Tiempos de ejecución
Explicación del taller (10 minutos)
Realización del taller (100 minutos taller)
Parte 1: Estructura de datos y CFR (15 min)
Parte 2: Incidencia y tasa de crecimiento (45 min)
Parte 3: Rt (40 min)
Discusión 30 minutos
Introducción
Un nuevo brote de virus del Ébola (EVE) en un país ficticio de África occidental
Conceptos básicos a desarrollar
En esta práctica se desarrollarán los siguientes conceptos:
Transmisión de enfermedades infecciosas de persona a persona
Número de reproducción básico
Número de reproducción instantáneo
Probabilidad de muerte (IFR, CFR)
Intervalo serial
Tasa de crecimiento
Incidencia
Preparación previa
Antes de comenzar,
descargue la carpeta con los datos y el proyecto desde Carpetas de datos .
Ahí mismo encontrará un archivo
.Rpara instalar las dependencias necesarias para este taller.Recuerde abrir el archivo
RProjectdenominadoTaller-Brotes-Ebola.Rprojantes de empezar a trabajar.
Este paso no solo le ayudará a cumplir con las buenas prácticas de programación en R, sino también a mantener un directorio organizado, permitiendo un desarrollo exitoso del taller.
1. Estructura de datos
Cargue de librerías:
Cargue las librerías necesarias para el análisis epidemiológico. Los datos serán manipulados con tidyverse que es una colección de paquetes para la ciencia de datos.
R
library(tidyverse) # contiene ggplot2, dplyr, tidyr, readr, purrr, tibble
library(readxl) # para leer archivos Excel
library(binom) # para intervalos de confianza binomiales
library(knitr) # para crear tablas bonitas con kable()
library(incidence) # para calcular incidencia y ajustar modelos
library(EpiEstim) # para estimar R(t)
Cargue de bases de datos
Se le ha proporcionado la siguiente base de datos:
-
casos: una base de datos de casos que contiene información de casos hasta el 1 de julio de 2014.
Para leer en R este archivo, utilice la función read_rds
de tidyverse. Se creará una tabla de datos almacenada como
objeto de clase tibble.
R
casos <- read_rds("data/casos.rds")
Estructura de los datos
Explore la estructura de los datos. Para esto puede utilizar la
función glimpse de tidyverse, la cual nos
proporciona una visión rápida y legible de la estructura interna de
nuestro conjunto de datos.
R
glimpse(casos)
SALIDA
Rows: 166
Columns: 11
$ id_caso <chr> "d1fafd", "53371b", "f5c3d8", "6c286a", "0f58…
$ generacion <dbl> 0, 1, 1, 2, 2, 0, 3, 3, 2, 3, 4, 3, 4, 2, 4, …
$ fecha_de_infeccion <date> NA, 2014-04-09, 2014-04-18, NA, 2014-04-22, …
$ fecha_inicio_sintomas <date> 2014-04-07, 2014-04-15, 2014-04-21, 2014-04-…
$ fecha_de_hospitalizacion <date> 2014-04-17, 2014-04-20, 2014-04-25, 2014-04-…
$ fecha_desenlace <date> 2014-04-19, NA, 2014-04-30, 2014-05-07, 2014…
$ desenlace <chr> NA, NA, "Recuperacion", "Muerte", "Recuperaci…
$ genero <fct> f, m, f, f, f, f, f, f, m, m, f, f, f, f, f, …
$ hospital <fct> Military Hospital, Connaught Hospital, other,…
$ longitud <dbl> -13.21799, -13.21491, -13.22804, -13.23112, -…
$ latitud <dbl> 8.473514, 8.464927, 8.483356, 8.464776, 8.452…Como puede observar contactos tiene 11 columnas (variables) y 166
filas de datos. En un rápido vistazo puede observar el tipo de las
variables por ejemplo, la columna desenlace tiene formato
carácter (chr) y contiene entre sus valores
"Recuperación" o "Muerte".
Además, puede encontrar estas variables:
El identificador
id_casoLa generación de infectados (cuantas infecciones secundarias desde la fuente hasta el sujeto han ocurrido)
La fecha de infección
La fecha de inicio de síntomas
La fecha de hospitalización
La fecha del desenlace que, como se puede observar, en la siguiente variable puede tener entre sus opciones
NA(no hay información hasta ese momento o no hay registro), recuperación y muerteLa variable género que puede ser
fde femenino omde masculinoEl lugar de hospitalización, en la variable hospital
Y las variables longitud y latitud
Note que las fechas ya están en formato fecha
(date).
2. CFR
Probabilidad de muerte en los casos reportados (CFR,
por Case Fatality Risk)
R
table(casos$desenlace, useNA = "ifany")
SALIDA
Muerte Recuperacion <NA>
60 43 63 Desafío 1
Calcule la probabilidad de muerte en los casos reportados
(CFR) tomando el número de muertes y el número de casos con
desenlace final conocido del objeto casos. Esta vez se
calculará el CFR con el método Naive. Los cálculos
Naive (inocentes) tienen el problema de que pueden
presentar sesgos, por lo que no deberían ser utilizados para informar
decisiones de salud pública. Hablaremos de estos sesgos en profundidad
en el día 4.
Durante este taller se le presentarán algunos retos, para los cuales
obtendrá algunas pistas, por ejemplo en el presente reto se le presenta
una pista, la cual es un fragmento del código que usted debe completar
para alcanzar la solución. En los espacios donde dice
COMPLETE por favor diligencie el código faltante.
R
muertes <- COMPLETE
casos_desenlace_final_conocido <- sum(casos$desenlace %in% c("Muerte", "Recuperacion"))
CFR <- COMPLETE / COMPLETE
Ejemplo,
R
# Reto
muertes <- COMPLETE
#Solución
muertes <- sum(casos$desenlace %in% "Muerte")
SALIDA
[1] 0.5825243Para complementar el calculo del CFR se pueden calcular sus
intervalos de confianza por medio de la función
binom.confint. La función binom.confint se
utiliza para calcular intervalos de confianza para una proporción en una
distribución binomial, que corresponde, por ejemplo, a cuando tenemos el
total de infecciones con desenlace final conocido (recuperado o muerte).
Esta función pide tres argumentos: 1) el número de muertes y 2) el
número total de casos con desenlace final conocido, es decir sin
importar que hayan muerto o se hayan recuperado, pero sin cuenta los
datos con NA; 3) el método que se utilizará para calcular
los intervalos de confianza, en este caso “exact” (método
Clopper-Pearson).
Desafío 2
Determine el CFR con sus intervalos de confianza utilizando la
función binom.confint. Y obtenga este resultado:
| method | x | n | mean | lower | upper |
|---|---|---|---|---|---|
| exact | 60 | 103 | 0.5825243 | 0.4812264 | 0.6789504 |
Recuerde diligenciar los espacios donde dice COMPLETE. Y
obtenga este resultado
R
CFR_con_CI <- binom.confint(COMPLETE, COMPLETE, method = "COMPLETE") %>%
kable(caption = "**COMPLETE ¿QUE TITULO LE PONDRÍA?**")
CFR_con_CI
3. Incidencia
3.1. Curva de incidencia diaria
El paquete incidence es de gran utilidad para el
análisis epidemiológico de datos de incidencia de enfermedades
infecciosas, dado que permite calcular la incidencia a partir del
intervalo temporal suministrado (e.g. diario o semanal). Dentro de este
paquete esta la función incidence la cual cuenta con los
siguientes argumentos:
datescontiene una variable con fechas que representan cuándo ocurrieron eventos individuales, como por ejemplo la fecha de inicio de los síntomas de una enfermedad en un conjunto de pacientes.intervales un intervalo de tiempo fijo por el que se quiere calcular la incidencia. Por ejemplo,interval = 365para un año. Si no se especifica, el valor por defecto es diario.last_datefecha donde se establecerá un limite temporal para los datos. Por ejemplo, la última fecha de hospitalización. Para este tercer argumento, podemos incluir la opciónmaxy la opciónna.rm. La primera para obtener la última fecha de una variable y la segunda para ignorar losNAen caso de que existan.
Por ejemplo, se podría escribir
last_date = max(base_de_datos$vector_ultima_fecha, na.rm = TRUE)
Con esta información la función agrupa los casos según el intervalo de tiempo especificado y cuenta el número de eventos (como casos de enfermedad) que ocurrieron dentro de cada intervalo.
Desafío 3
Calcule la incidencia diaria usando únicamente el primer argumento de
la función incidence ¿Qué fecha sería la más adecuada?
Tenga en cuenta que se espera que esta sea la que pueda dar mejor
información, es decir la menor cantidad de NAs.
R
incidencia_diaria <- incidence(COMPLETE)
incidencia_diaria
El resultado es un objeto de clase incidencia
(incidence) que contiene el recuento de casos para cada
intervalo de tiempo, lo que facilita su visualización y análisis
posterior. Como puede observar la función produjo los siguientes
datos:
SALIDA
<incidence object>
[166 cases from days 2014-04-07 to 2014-06-29]
$counts: matrix with 84 rows and 1 columns
$n: 166 cases in total
$dates: 84 dates marking the left-side of bins
$interval: 1 day
$timespan: 84 days
$cumulative: FALSEComo resultado de la función se produjo un objeto tipo lista. Este
objeto arroja estos datos: 166 casos contemplados entre los
días 2014-04-07 al 2014-06-29 para un total de
84 días; se menciona que el intervalo es de
1 día, dado que no se utilizo específico explicitamente el
parámetro por lo cual quedó su valor por defecto. Finalmente se menciona
“cumulative : FALSE” lo que quiere decir que no se esta
haciendo el acumulado de la incidencia, es decir que los casos
corresponden a los del intervalo interval: 1 day, es decir
a los casos nuevos cada día en específico.
Ahora haga una gráfica de la incidencia diaria.
R
plot(incidencia_diaria, border = "black")
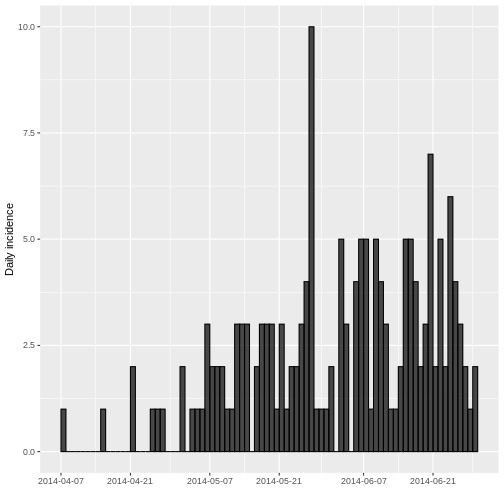
En el Eje X (Fechas): Se puede observar fechas van desde
el 7 de abril de 2014 hasta una fecha posterior al
21 de junio de 2014. Estas fechas representan el período de
observación del brote.
En el Eje Y (Incidencia Diaria): La altura de las barras
indica el número de nuevos casos reportados cada fecha según el tipo de
fecha escogido.
Dado que no se agregó el parámetro interval la
incidencia quedó por defecto diaria, produciéndose un histograma en el
que cada barra representa la incidencia de un día, es decir, los casos
nuevos. Los días sin barras sugieren que no hubo casos nuevos para esa
fecha o que los datos podrían no estar disponibles para esos días.
A pesar de que hay una curva creciente, hay periodos con pocos o ningún caso. ¿Porque cree que podrían darse estos periodos de pocos a pesar de la curva creciente?
3.2. Cálculo de la incidencia semanal
Teniendo en cuenta lo aprendido con respecto a la incidencia diaria,
cree una variable para incidencia semanal. Luego, interprete el
resultado y haga una gráfica. Para escoger la fecha que utilizará como
última fecha debe asignarle un valor al argumento last_date
de la función incidence ¿Qué fecha sería la más adecuada?
Tenga en cuenta que la fecha debe ser posterior a la fecha que se haya
escogido como el primer argumento.
Desafío 4
R
incidencia_semanal <- incidence(PRIMER ARGUMENTO, #COMPLETE
SEGUNDO ARGUMENTO, #COMPLETE
TERCER ARGUMENTO) #COMPLETESALIDA
<incidence object>
[166 cases from days 2014-04-07 to 2014-06-30]
[166 cases from ISO weeks 2014-W15 to 2014-W27]
$counts: matrix with 13 rows and 1 columns
$n: 166 cases in total
$dates: 13 dates marking the left-side of bins
$interval: 7 days
$timespan: 85 days
$cumulative: FALSE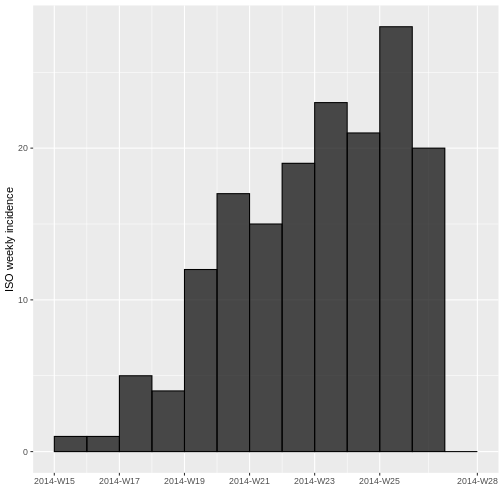
Compare la gráfica de incidencia diaria con la de incidencia semanal. ¿Qué observa? ¿Los datos se comportan diferente? ¿Es lo que esperaba? ¿Logra observar alguna tendencia?
4. Tasa de crecimiento
4.1. Modelo log-lineal
Estimación de la tasa de crecimiento mediante un modelo log-lineal
Para observar mejor las tendencias de crecimiento en el número de casos se puede visualizar la incidencia semanal en una escala logarítmica. Esto es particularmente útil para identificar patrones exponenciales en los datos.
Grafique la incidencia transformada logarítmicamente:
R
ggplot(as.data.frame(incidencia_semanal)) +
geom_point(aes(x = dates, y = log(counts))) +
scale_x_incidence(incidencia_semanal) +
xlab("Semana") +
ylab("Incidencia semanal logarítmica") +
theme_minimal()
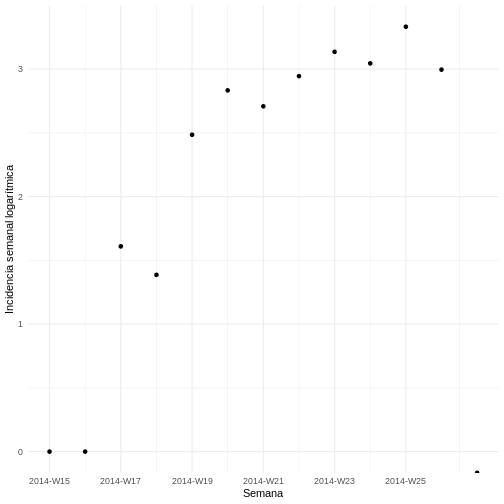
Ajuste un modelo log-lineal a los datos de incidencia semanal
R
ajuste_modelo <- incidence::fit(incidencia_semanal)
ajuste_modelo
SALIDA
<incidence_fit object>
$model: regression of log-incidence over time
$info: list containing the following items:
$r (daily growth rate):
[1] 0.04145251
$r.conf (confidence interval):
2.5 % 97.5 %
[1,] 0.02582225 0.05708276
$doubling (doubling time in days):
[1] 16.72148
$doubling.conf (confidence interval):
2.5 % 97.5 %
[1,] 12.14285 26.84302
$pred: data.frame of incidence predictions (12 rows, 5 columns)Desafío 5
¿Qué observa en este resultado?
$model: Indica que se ha realizado una regresión
logarítmica de la incidencia en función del tiempo. Esto implica que la
relación entre el tiempo y la incidencia de la enfermedad ha sido
modelada como una función lineal en escala logarítmica en la incidencia
con el fin de entender mejor las tendencias de crecimiento.
$info: Contiene varios componentes importantes del
análisis:
-
$r (daily growth rate)Tasa de crecimiento diaria:0.04145251
La tasa de crecimiento diaria estimada del brote es de
0.0415. Esto significa que cada día la cantidad de casos
está creciendo en un 4.15% con respecto al día anterior,
bajo la suposición de un crecimiento exponencial constante durante el
periodo modelado.
Si quisiera acceder a esta información sin ingresar al modelo podría hacerlo con el siguiente código:
R
tasa_crecimiento_diaria <- ajuste_modelo$info$r
cat("La tasa de crecimiento diaria es:", tasa_crecimiento_diaria, "\n")
SALIDA
La tasa de crecimiento diaria es: 0.04145251 -
$r.conf(confidence interval): 2.5 % 0.02582225 97.5 % 0.05708276
El intervalo de confianza del 95% para la tasa de
crecimiento diaria está entre 0.0258 (2.58%) y
0.0571 (5.71%).
$doubling (doubling time in days): 16.72148
- El tiempo de duplicación estimado del número de casos nuevos es de
aproximadamente
16.72 días. Esto significa que, bajo el modelo actual y con la tasa de crecimiento estimada, se espera que el número de casos de la curva epidémica actual se duplique cada16.72 días.
$doubling.conf (confidence interval): 2.5 % 12.14285
97.5 % 26.84302
- El intervalo de confianza del
95%para el tiempo de duplicación está entre aproximadamente12.14y26.84 días. Este amplio rango refleja la incertidumbre en la estimación y puede ser consecuencia de la variabilidad en los datos o de un tamaño de muestra pequeño.
$pred: Contiene las predicciones de incidencia
observada. Incluye las fechas, la escala de tiempo en días desde el
inicio del brote, los valores ajustados (predicciones) y los límites
inferior y superior del intervalo de confianza para las
predicciones.
Si quiere conocer un poco más de este componente puede explorarlo con
la función glimpse.
R
glimpse(ajuste_modelo$info$pred)
¿El modelo se ajusta bien a los datos? Verifique el \(R^2\)
R
AjusteR2modelo <- summary(ajuste_modelo$model)$adj.r.squared
cat("El R cuadrado ajustado es:", AjusteR2modelo, "\n")
SALIDA
El R cuadrado ajustado es: 0.7551113 Antes de continuar ¿Considera más adecuado usar una gráfica semanal para buscar un ajuste de los datos? ¿Por qué?
¿Es preferible calcular la tasa de crecimiento diaria con el ajuste semanal y no con el ajuste diario?
Grafique la incidencia incluyendo una línea que represente el modelo.
Con plot
R
plot(incidencia_semanal, fit = ajuste_modelo)
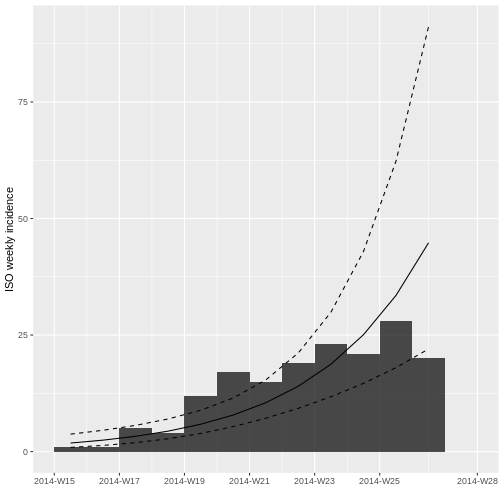
Tras ajustar el modelo log-lineal a la incidencia semanal para estimar la tasa de crecimiento de la epidemia, el gráfico muestra la curva de ajuste superpuesta a la incidencia semanal observada.
Al final del gráfico se puede observar que la incidencia semanal disminuye.
¿Porqué cree que podría estar pasando esto? ¿Cómo lo solucionaría?
4.2. Modelo log-lineal con datos truncados
Encuentre una fecha límite adecuada para el modelo log-lineal, en función de los rezagos (biológicos y administrativos).
Dado que esta epidemia es de Ébola y la mayoría de los casos van a ser hospitalizados, es muy probable que la mayoría de las notificaciones ocurran en el momento de la hospitalización. De tal manera que podríamos examinar cuánto tiempo transcurre entre la fecha de inicio de síntomas y la fecha de hospitalización para hacernos una idea del rezago para esta epidemia.
R
summary(as.numeric(casos$fecha_de_hospitalizacion - casos$fecha_inicio_sintomas))
SALIDA
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 1.00 2.00 3.53 5.00 22.00 Al restar la fecha de hospitalización a la fecha de inicio de síntomas podría haber valores negativos. ¿Cuál cree que sea su significado? ¿Ocurre en este caso?
Para evitar el sesgo debido a rezagos en la notificación, se pueden truncar los datos de incidencia. Pruebe descartar las últimas dos semanas. Este procedimiento permite concentrarse en el periodo en que los datos son más completos para un análisis más fiable.
Semanas a descartar al final de la epicurva
R
semanas_a_descartar <- 2
fecha_minima <- min(incidencia_diaria$dates)
fecha_maxima <- max(incidencia_diaria$dates) - semanas_a_descartar * 7
# Para truncar la incidencia semanal
incidencia_semanal_truncada <- subset(incidencia_semanal,
from = fecha_minima,
to = fecha_maxima) # descarte las últimas semanas de datos
# Incidencia diaria truncada. No la usamos para la regresión lineal pero se puede usar más adelante
incidencia_diaria_truncada <- subset(incidencia_diaria,
from = fecha_minima,
to = fecha_maxima) # eliminamos las últimas dos semanas de datos
Desafío 6
Ahora utilizando los datos truncados
incidencia_semanal_truncada vuelva a ajustar el modelo
logarítmico lineal.
SALIDA
<incidence_fit object>
$model: regression of log-incidence over time
$info: list containing the following items:
$r (daily growth rate):
[1] 0.05224047
$r.conf (confidence interval):
2.5 % 97.5 %
[1,] 0.03323024 0.0712507
$doubling (doubling time in days):
[1] 13.2684
$doubling.conf (confidence interval):
2.5 % 97.5 %
[1,] 9.728286 20.85893
$pred: data.frame of incidence predictions (10 rows, 5 columns)¿Cámo interpreta estos resultados? ¿Compare los \(R^2\)?
Desafío 7
Ahora utilizando los datos truncados
incidencia_semanal_truncada vuelva a graficar el modelo
logarítmico lineal.
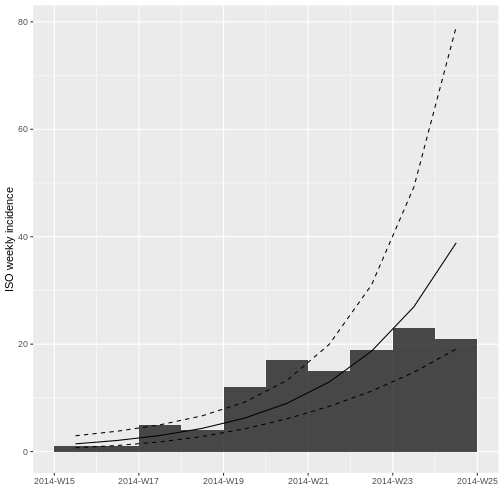
¿Qué cambios observa?
Observe las estadísticas resumidas del ajuste:
R
summary(ajuste_modelo_truncado$model)
SALIDA
Call:
stats::lm(formula = log(counts) ~ dates.x, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.73474 -0.31655 -0.03211 0.41798 0.65311
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.186219 0.332752 0.560 0.591049
dates.x 0.052240 0.008244 6.337 0.000224 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5241 on 8 degrees of freedom
Multiple R-squared: 0.8339, Adjusted R-squared: 0.8131
F-statistic: 40.16 on 1 and 8 DF, p-value: 0.0002237El modelo muestra que hay una relación significativa
(R-squared: 0.8131) entre el tiempo (dates.x)
y la incidencia de la enfermedad, por lo que concluimos que la
enfermedad muestra un crecimiento exponencial a lo largo del tiempo.
4.3. Tasa de crecimiento y tasa de duplicación: extracción de datos
Estimacion de la tasa de crecimiento
Para estimar la tasa de crecimiento de una epidemia utilizando un modelo log-lineal es necesario realizar un ajuste de regresión a los datos de incidencia. Dado que ya tiene un objeto de incidencia truncado y un modelo log-lineal ajustado, puede proceder a calcular la tasa de crecimiento diaria y el tiempo de duplicación de la epidemia.
El modelo log-lineal proporcionará los coeficientes necesarios para estos cálculos. Note que el coeficiente asociado con el tiempo (la pendiente de la regresión) se puede interpretar como la tasa de crecimiento diaria cuando el tiempo se expresa en días.
Con el modelo ajustado truncado, es hora de realizar la estimación de
la tasa de crecimiento. Estos datos los puede encontrar en el objeto
ajuste modelo semana, que tiene los datos ajustados de
incidencia semanal truncada.
Desafío 8
Por favor escriba el código para obtener los siguientes valores:
SALIDA
La tasa de crecimiento diaria es: 0.05224047 SALIDA
Intervalo de confianza de la tasa de crecimiento diaria (95%): 0.03323024 0.0712507 Si no lo recuerda, vuelva por pistas a la sección Ajuste un modelo log-lineal a los datos de incidencia semanal
Ahora que ya ha obtenido la tasa de crecimiento diaria y sus intervalos de confianza, puede pasar a estimar el tiempo de duplicación.
Estimación del tiempo de duplicación
Esta información también la encontrará calculada y lista para
utilizar en el objeto ajuste_modelo_truncado, que tiene los
datos ajustados de incidencia semanal truncada.
Desafío 9
Por favor escriba el código para obtener los siguientes valores:
SALIDA
El tiempo de duplicación de la epidemia es 13.2684 díasSALIDA
Intervalo de confianza del tiempo de duplicación (95%): 9.728286 20.85893 Si no lo recuerda vuelva por pistas a la sección Ajuste un modelo log-lineal a los datos de incidencia semanal
5. Estimación de número de reproducción
Evaluar la velocidad a la que se propaga una infección en una población es una tarea importante a la hora de informar la respuesta de salud pública a una epidemia.
Los números de reproducción son métricas típicas para monitorear el desarrollo de epidemias y son informativos sobre su velocidad de propagación. El Número de reproducción básico \(R_0\), por ejemplo, mide el número promedio de casos secundarios producidos por un individuo infeccioso dada una población completamente susceptible. Esta hipótesis suele ser válida solo al inicio de una epidemia.
Para caracterizar el la propagación en tiempo real es más común utilizar el Número de reproducción instantáneo \(R_t\), el cual describe el número promedio de casos secundarios generados por un individuo infeccioso en el tiempo \(t\) dado que no han habido cambios en las condiciones actuales.
En esta sección exploraremos los conceptos necesarios para calcular el Número de reproducción instantáneo, así como los pasos a seguir para estimarlo por medio del paquete de R EpiEstim.
5.1. Intervalo serial (SI)
¿Qué es el intervalo serial?
El intervalo serial en epidemiología se refiere al tiempo que transcurre entre el momento en que una persona infectada (el caso primario) comienza a mostrar síntomas y el momento en que la persona que fue infectada por ella (el caso secundario) comienza a mostrar síntomas.
Este intervalo es importante porque ayuda a entender qué tan rápido se está propagando una enfermedad y a diseñar estrategias de control como el rastreo de contactos y la cuarentena. Si el intervalo serial es corto, puede significar que la enfermedad se propaga rápidamente y que es necesario actuar con urgencia para contenerla. Si es largo, puede haber más tiempo para intervenir antes de que la enfermedad se disemine ampliamente.
Para este brote de Ébola asumiremos que el intervalo serial está
descrito por una distribución Gamma de media (mean_si) de
8.7 días y con una desviación estándar
(std_si) de 6.1 días. En la práctica del día 4
estudiaremos cómo estimar el intervalo serial.
R
# Parametros de la distribución gamma para el invertavlo serial
mean_si <- 8.7
std_si <- 6.1
config <- make_config(list(mean_si = mean_si, std_si = std_si))
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.
5.2. Estimación de la transmisibilidad variable en el tiempo, R(t)
Cuando la suposición de que (\(R\))
es constante en el tiempo se vuelve insostenible, una alternativa es
estimar la transmisibilidad variable en el tiempo utilizando el Número
de reproducción instantáneo (\(R_t\)).
Este enfoque, introducido por Cori et al. (2013), se implementa en el
paquete EpiEstim, el cual estima el \(R_t\) para ventanas de tiempo
personalizadas, utilizando una distribución de Poisson. A continuación,
estimamos la transmisibilidad para ventanas de tiempo deslizantes de 1
semana (el valor predeterminado de estimate_R):
R
config <- make_config(list(mean_si = mean_si, std_si = std_si))
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.
R
# use estimate_R using method = "parametric_si"
estimacion_rt <- estimate_R(incidencia_diaria_truncada, method = "parametric_si",
si_data = si_data,
config = config)
# Observamos las primeras estimaciones de R(t)
head(estimacion_rt$R[, c("t_start", "t_end", "Median(R)",
"Quantile.0.025(R)", "Quantile.0.975(R)")])
SALIDA
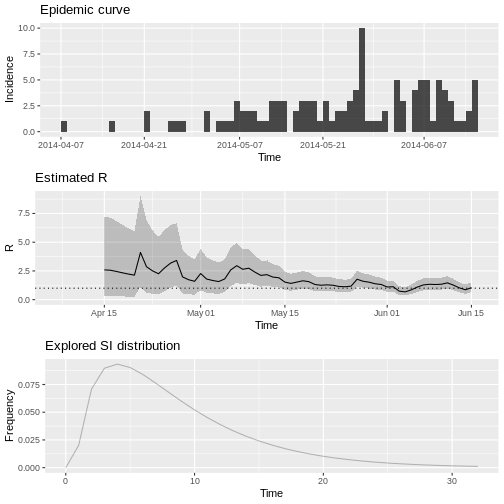
t_start t_end Median(R) Quantile.0.025(R) Quantile.0.975(R)
1 2 8 NA NA NA
2 3 9 2.173592 0.3136801 7.215718
3 4 10 2.148673 0.3100840 7.132996
4 5 11 2.060726 0.2973920 6.841036
5 6 12 1.960940 0.2829915 6.509775
6 7 13 1.869417 0.2697834 6.205943Grafique la estimación de \(R\) como función del tiempo:
R
plot(estimacion_rt, legend = FALSE)
Sobre este documento
Este documento ha sido una adaptación de los materiales originales disponibles en RECON Learn
Contribuciones
Autores originales:
Anne Cori
Natsuko Imai
Finlay Campbell
Zhian N. Kamvar
Thibaut Jombart
Cambios menores y adaptación a español:
José M. Velasco-España
Cándida Díaz-Brochero
Nicolas Torres
Zulma M. Cucunubá
Puntos clave
Revise si al final de esta lección adquirió estas competencias:
Identificar los parámetros necesarios en casos de transmisión de enfermedades infecciosas de persona a persona.
Estimar la probabilidad de muerte (CFR).
Calcular y graficar la incidencia.
Estimar e interpretar la tasa de crecimiento y el tiempo en el que se duplica la epidemia.
Estimar e interpretar el número de reproducción instantáneo de la epidemia.
