Construyendo un modelo matemático simple para Zika

Última actualización: 2024-11-19 | Mejora esta página

Hoja de ruta

Preguntas

  • ¿Cómo construir un modelo simplificado de zika?

Objetivos

Al final de este taller usted podrá:

  • Aplicar conceptos como parámetros, \(R_0\) e inmunidad de rebaño, aprendidos en la sesión A del taller
  • Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
  • Realizar un modelo simple en R para una enfermedad transmitida por vector
  • Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección

1. Introducción

En este taller usted aplicará los conceptos básicos del modelamiento de Enfermedades Transmitidas por Vectores (ETV) mediante el uso del lenguaje R con énfasis en el funcionamiento de los métodos, utilizando como ejemplo un modelo básico de infección por un arbovirus: el virus del Zika.

2. Agenda

  • Instrucciones (5 mins)
  • Desarrollo taller Zika Parte B (45 mins con acompañamiento de monitores)
  • Revisión grupal del código (10 mins)
  • Revisión de resultados (20 mins)
  • Descanso (25 mins)
  • Discusión final (60 mins)

3. Conceptos básicos a desarrollar

En esta práctica se desarrollarán los siguientes conceptos:

  • Modelo SIR para ETV Zika
  • Parametrización de un modelo dinámico
  • Evaluación de un modelo dinámico
  • Parametrización de intervenciones de control (fumigación, mosquiteros y vacunación) para una ETV

4. Paquetes requeridos

Cargue los paquetes necesarios ingresando en R los siguientes comandos:

R 

library(deSolve)   # Paquete deSolve para resolver las ecuaciones diferenciales
library(tidyverse) # Paquetes ggplot2 y dplyr de tidyverse
library(cowplot) # Paquete gridExtra para unir gráficos.
  • Si desea puede tomar notas en el script de R, para esto se recomienda usar el símbolo de comentario # después de cada línea de código (ver ejemplo arriba). O podría utilizar un archivo Rmd para tener un aspecto similar al del taller.

5. Compartimentos del modelo básico de Zika

  • \(S_h\) : Humanos susceptibles
  • \(I_h\) : Humanos infecciosos
  • \(R_h\) : Humanos recuperados de la infección (inmunizados frente a nueva infección)
  • \(S_v\) : Vectores susceptibles
  • \(E_v\) : Vectores expuestos
  • \(I_v\) : Vectores infecciosos

6. Parámetros del modelo

Ahora se usarán los parámetros que discutimos en la parte A del taller. Si aún no los tiene, estos se pueden encontrar en la guía de aprendizaje de la parte A del taller.

Desafío 1

Busque los valores de los parámetros del modelo y diligéncielos en el recuadro de abajo. Tenga en cuenta que todos los parámetros usados tienen la misma unidad de tiempo (días).

R 

Lv       <-        # Esperanza de vida de los mosquitos (en días)
Lh       <-        # Esperanza de vida de los humanos (en días)
PIh      <-        # Periodo infeccioso en humanos (en días)
PIv      <-        # Periodo infeccioso en vectores (en días)
PEI      <-        # Período extrínseco de incubación en mosquitos adultos (en días)
muv      <-        # Tasa per capita de mortalidad del vector (1/Lv)
muh      <-        # Tasa per capita de mortalidad del hospedador (1/Lh)
alphav   <-        # Tasa per capita de natalidad del vector
alphah   <-        # Tasa per capita de natalidad del hospedador
gamma    <-        # Tasa de recuperación en humanos (1/PIh)
delta    <-        # Tasa extrínseca de incubación (1/PEI)
ph       <-        # Probabilidad de transmisión del vector al hospedador dada una picadura por un mosquito infeccioso a un humano susceptible
pv       <-        # Probabilidad de transmisión del hospedador al vector dada una picadura por un mosquito susceptible a un humano infeccioso
Nh       <-        # Número de humanos
m        <-        # Densidad de mosquitos hembra por humano
Nv       <-        # Número de vectores (m * Nh)
R0       <-        # Número reproductivo básico
b        <-        sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
                   (m * ph * pv * delta)) # Tasa de picadura
betah    <-        # Coeficiente de transmisión del mosquito al humano
betav    <-        # Coeficiente de transmisión del humano al mosquito
TIME     <-        # Número de años que se va a simular

7. Ecuaciones del modelo

Para este modelo emplearemos las siguientes ecuaciones diferenciales:

7.1 Humanos

\[\ \frac{dSh}{dt} = \alpha_h N_h - \beta_h \frac {I_v}{N_h}S_h - \mu_h S_h \]

\[\ \frac{dIh}{dt} = \beta_h \frac {I_v}{N_h}S_h - (\gamma + \mu_h) I_h \]

\[\ \frac{dRh}{dt} = \gamma I_h - \mu_h R_h\]

7.2 Vectores

\[\ \frac{dSv}{dt} = \alpha_v N_v - \beta_v \frac{ I_h} {N_h}S_v - \mu_v Sv\]

\[\ \frac{dE_v}{dt} = \beta_v \frac{I_h} {N_h}S_v- (\delta + \mu_v) Ev\]

\[\ \frac{dI_v}{dt} = \delta Ev - \mu_v I_v\]

8. Fórmula para calcular \(R_0\) (Número reproductivo básico)

Fórmula necesaria para estimar \(R_0\):

\[ R_0 = \frac{mb^2 p_h p_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma)} \]

9. Modelo en R

Es hora de implementar el modelo en R. Para lograrlo, usaremos la función ode del paquete desolve. Para el ejercicio se emplearán 4 argumentos de la función esta función: el primero son las condiciones iniciales del modelo (argumento y); el segundo es la secuencia temporal donde se ejecutará el modelo (argumento times); el tercero es una función que contiene las ecuaciones diferenciales que entrarán al sistema (argumento fun); por último un vector que contiene los parámetros con los que se calculará el sistema (argumento parms).

R 

# NO la copie a R sólo tiene fines ilustrativos.
ode(y      = # Condiciones iniciales,
    times  = # Tiempo,
    fun    = # Modelo o función que lo contenga,
    parms  = # Parámetros
)

Desafío 2

En esta sección se empezará por crear la función (argumento fun), para ello es necesario traducir las ecuaciones del modelo a R. Abajo encontrará la función ya construida, por favor reemplace los parámetros faltantes (Cambie PAR por los parámetro correspondientes) en las ecuaciones:

R 

arbovmodel <- function(t, x, params) {
  
  Sh <- x[1]    # Humanos susceptibles
  Ih <- x[2]    # Humanos infecciosos 
  Rh <- x[3]    # Humanos recuperados
  Sv <- x[4]    # Vectores susceptibles
  Ev <- x[5]    # Vectores expuestos
  Iv <- x[6]    # Vectores infecciosos
  
  with(as.list(params), # entorno local para evaluar derivados
       {
         # Humanos
         dSh   <-  PAR * Nh - PAR * (Iv/Nh) * Sh - PAR * Sh   
         dIh   <-  PAR * (Iv/Nh) * Sh - (PAR + PAR) * Ih
         dRh   <-  PAR * Ih  - PAR * Rh
         
         # Vectores
         dSv  <-  alphav * Nv - PAR * (Ih/Nh) * Sv - PAR * Sv 
         dEv  <-  PAR * (Ih/Nh) * Sv - (PAR + PAR)* Ev
         dIv  <-  PAR * Ev - PAR * Iv
         
         dx   <- c(dSh, dIh, dRh, dSv, dEv, dIv)
         list(dx)
       }
  )
}

10. Resuelva el Sistema

En esta sección se crearán los tres argumentos faltantes para usar la función ode y se creará un objeto de clase data.frame con los resultados de la función ode. Por favor complete y comente el código para:

  • Los VALORES de las condiciones iniciales del sistema.

  • Los ARGUMENTOS de la función ode en el paquete deSolve.

Desafío 3

R 

# Secuencia temporal (times)
times  <- seq(1, 365 * TIME , by = 1)
# Los parámetros (parms)
params <- c(
  muv      = muv,     
  muh      = muh, 
  alphav   = alphav,
  alphah   = alphah,
  gamma    = gamma,   
  delta    = delta,   
  betav    = betav,       
  betah    = betah,   
  Nh       = Nh,      
  Nv       = Nv
)
# Condiciones iniciales del sistema (y)
xstart <- c(Sh = VALOR?,        # COMPLETE Y COMENTE
            Ih = VALOR?,        # COMPLETE Y COMENTE
            Rh = VALOR?,        # COMPLETE Y COMENTE
            Sv = VALOR?,        # COMPLETE Y COMENTE
            Ev = VALOR?,        # COMPLETE Y COMENTE
            Iv = VALOR?)        # COMPLETE Y COMENTE
# Resuelva las ecuaciones
out <- as.data.frame(ode(y      = ARGUMENTO?,   # COMPLETE Y COMENTE
                         times  = ARGUMENTO?,   # COMPLETE Y COMENTE
                         fun    = ARGUMENTO?,   # COMPLETE Y COMENTE
                         parms  = ARGUMENTO?))  # COMPLETE Y COMENTE

11. Resultados

Desafío 4

Para tener una visualización más significativa de los resultados, convierta las unidades de tiempo de días a años y a semanas.

R 

# Cree las opciones de tiempo para años y semanas 
out$years <- 
out$weeks <-

Observe el comportamiento del modelo en distintas escalas de tiempo (semanas y años):

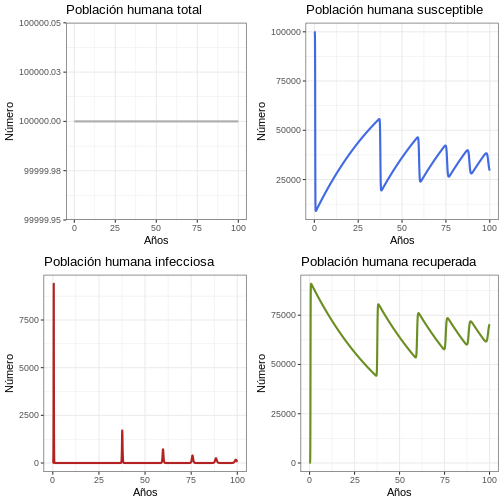
11.1 Comportamiento General (Población humana)

R 

# Revise el comportamiento general del modelo para 100 años
p1h <- ggplot(data = out, aes(y = (Rh + Ih + Sh), x = years)) +
  geom_line(color = 'grey68', size = 1) +
  ggtitle('Población humana total') +
  theme_bw() + ylab('Número') + xlab('Años')
p2h <- ggplot(data = out, aes(y = Sh, x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('Número') + xlab('Años')
p3h <- ggplot(data = out, aes(y = Ih, x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población humana infecciosa') +
  theme_bw() + ylab('Número') + xlab('Años')
p4h <- ggplot(data = out, aes(y = Rh, x = years)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1h, p2h, p3h, p4h, ncol = 2)

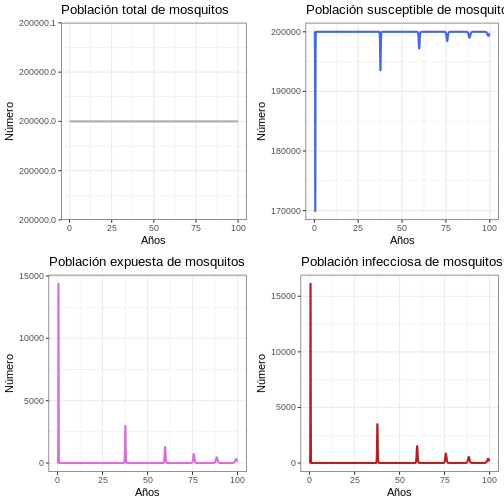
11.2 Comportamiento General (Población de vectores)

R 

# Revise el comportamiento general del modelo
p1v <- ggplot(data = out, aes(y = (Sv + Ev + Iv), x = years)) +
  geom_line(color = 'grey68', size = 1) +
  ggtitle('Población total de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p2v <- ggplot(data = out, aes(y = Sv, x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población susceptible de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p3v <- ggplot(data = out, aes(y = Ev, x = years)) +
  geom_line(color = 'orchid', size = 1) +
  ggtitle('Población expuesta de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p4v <- ggplot(data = out, aes(y = Iv, x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población infecciosa de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1v, p2v, p3v, p4v, ncol = 2)

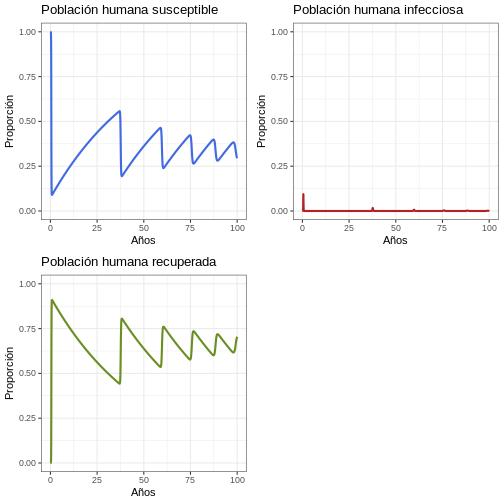
11.3 Proporción

Por favor dé una mirada más cuidadosa a las proporciones y discútalas

R 

p1 <- ggplot(data = out, aes(y = Sh/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
p2 <- ggplot(data = out, aes(y = Ih/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población humana infecciosa') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
p3 <- ggplot(data = out, aes(y = Rh/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
plot_grid(p1, p2, p3, ncol = 2)

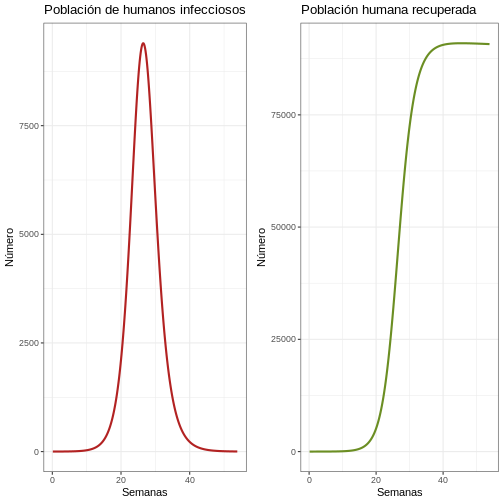
11.4 La primera epidemia

R 

# Revise la primera epidemia
dat <- out %>% filter(weeks < 54)
p1e <- ggplot(dat, aes(y = Ih, x = weeks)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población de humanos infecciosos') +
  theme_bw() + ylab('Número') + xlab('Semanas')
p2e <- ggplot(dat, aes(y = Rh, x = weeks)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Número') + xlab('Semanas')
plot_grid(p1e, p2e)

11.5 Algunos aspectos por discutir

  • ¿Qué tan sensible es el modelo a cambios en el \(R_0\)?
  • ¿Qué razones hay (según el modelo) para el intervalo de tiempo entre estas epidemias simuladas?
  • ¿Cómo se puede calcular la tasa de ataque?

11.6 Modele una o más intervenciones de control

Ahora, utilizando este modelo básico, modelar por grupos el impacto de las siguientes intervenciones:

  1. Grupo 1. Fumigación contra mosquitos
  2. Grupo 2. Mosquiteros/angeos
  3. Grupo 3. Vacunación que previene frente a infecciones

Para cada intervención:

  1. Indique en qué parte del modelo haría los cambios.

  2. De acuerdo a la literatura que explique estas intervenciones y describa cómo parametrizará el modelo. ¿Todas estas intervenciones son viables en la actualidad?

Sobre este documento

Contribuciones

  • Zulma Cucunuba & Pierre Nouvellet: Versión inicial
  • Kelly Charinga & Zhian N. Kamvar: Edición
  • José M. Velasco-España: Traducción de Inglés a Español y Edición
  • Andree Valle-Campos: Ediciones menores

Contribuciones son bienvenidas vía pull requests. El archivo fuente del documento original puede ser encontrado aquí.

Asuntos legales

Licencia: CC-BY Copyright: Zulma Cucunuba & Pierre Nouvellet, 2017

Puntos clave

Revise si al final de esta lección adquirió estas competencias:

  • Aplicar conceptos como parámetros, \(R_0\) e inmunidad de rebaño, aprendidos en la sesión A del taller
  • Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
  • Realizar un modelo simple en R para una enfermedad transmitida por vector
  • Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección