Acceder a las distribuciones de retrasos epidemiológicos
Figura 1
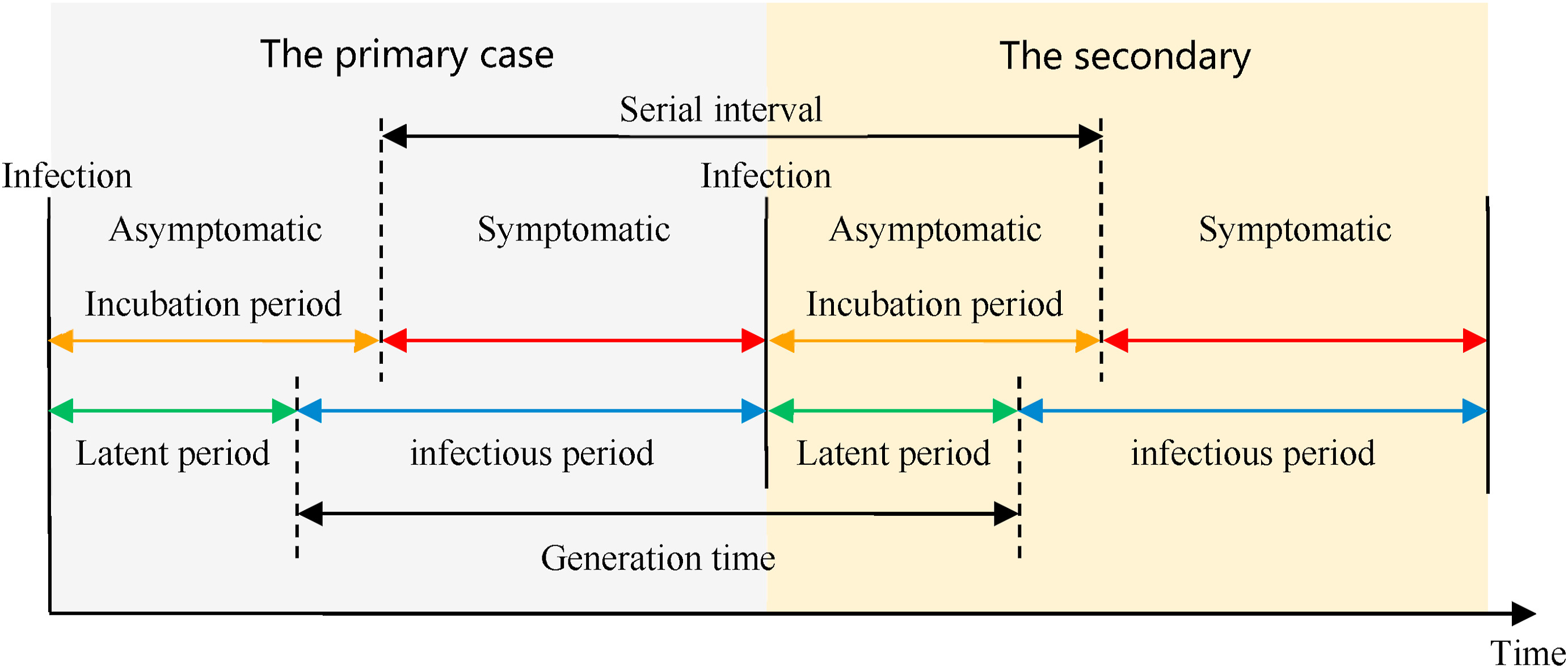
Definición de los periodos de tiempo clave. En
Xiang
et al, 2021
Figura 2
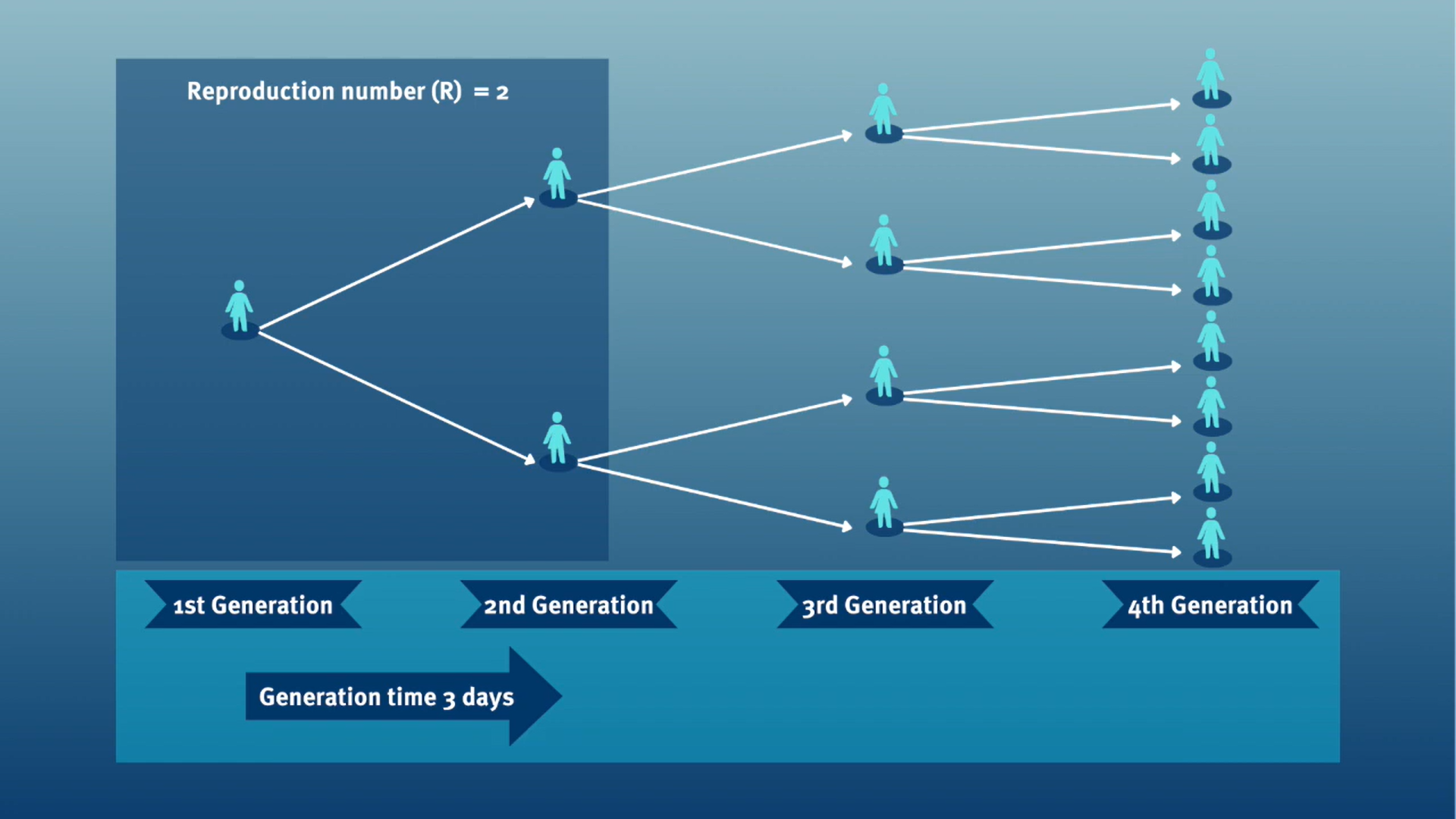
Vídeo del Centro MRC para el Análisis Global de
las Enfermedades Infecciosas, Ep 76. Ciencia en Contexto - Grupo de
Revisión de Parámetros Epi con la Dra. Anne Cori (27-07-2023) en https://youtu.be/VvpYHhFDIjI?si=XiUyjmSV1gKNdrrL
Figura 3
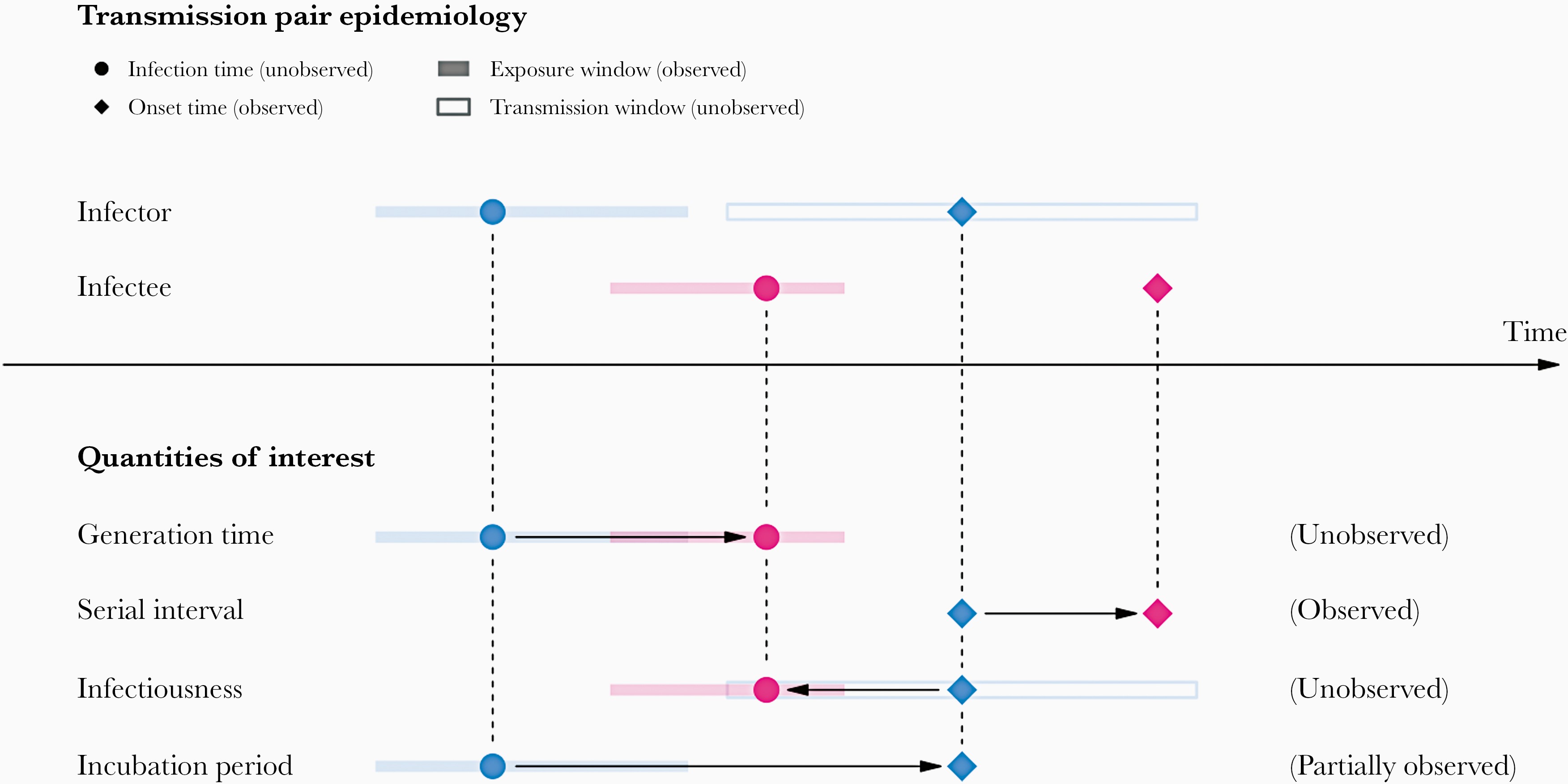
Un Esquema de la relación de los distintos
periodos de tiempo de transmisión entre un infector y un infectado en un
par de transmisión. La ventana de exposición se define como el intervalo
de tiempo que tiene la exposición viral, y la ventana de transmisión se
define como el intervalo de tiempo para la transmisión posterior con
respecto al tiempo de infección (Chung
Lau et al., 2021).
Figura 4
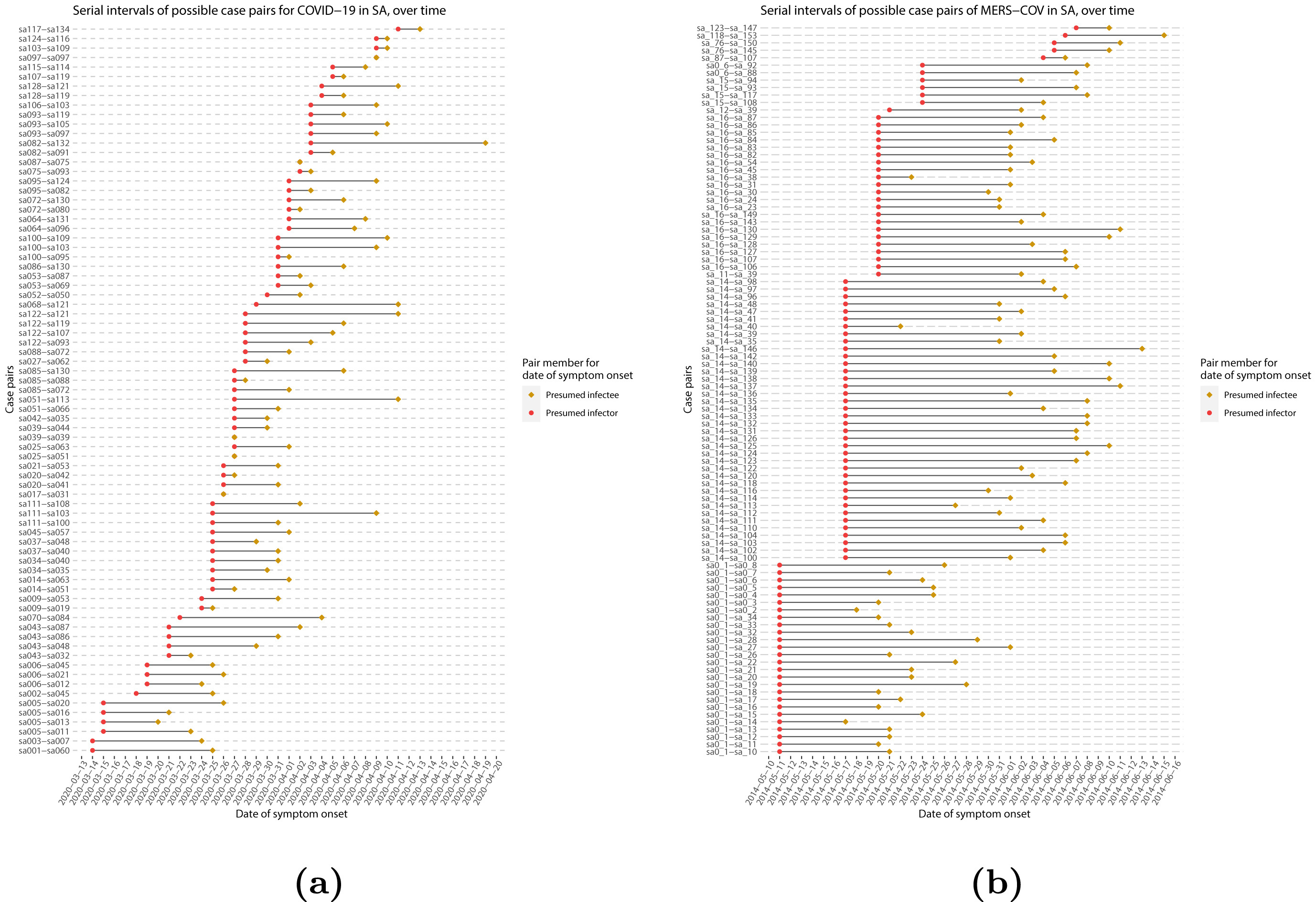
Intervalos seriales de posibles parejas de casos
en (a) COVID-19 y (b) MERS-CoV. Los pares representan un supuesto
infector y su presunto infectado trazados por fecha de inicio de los
síntomas (Althobaity
et al., 2022).
Figura 5
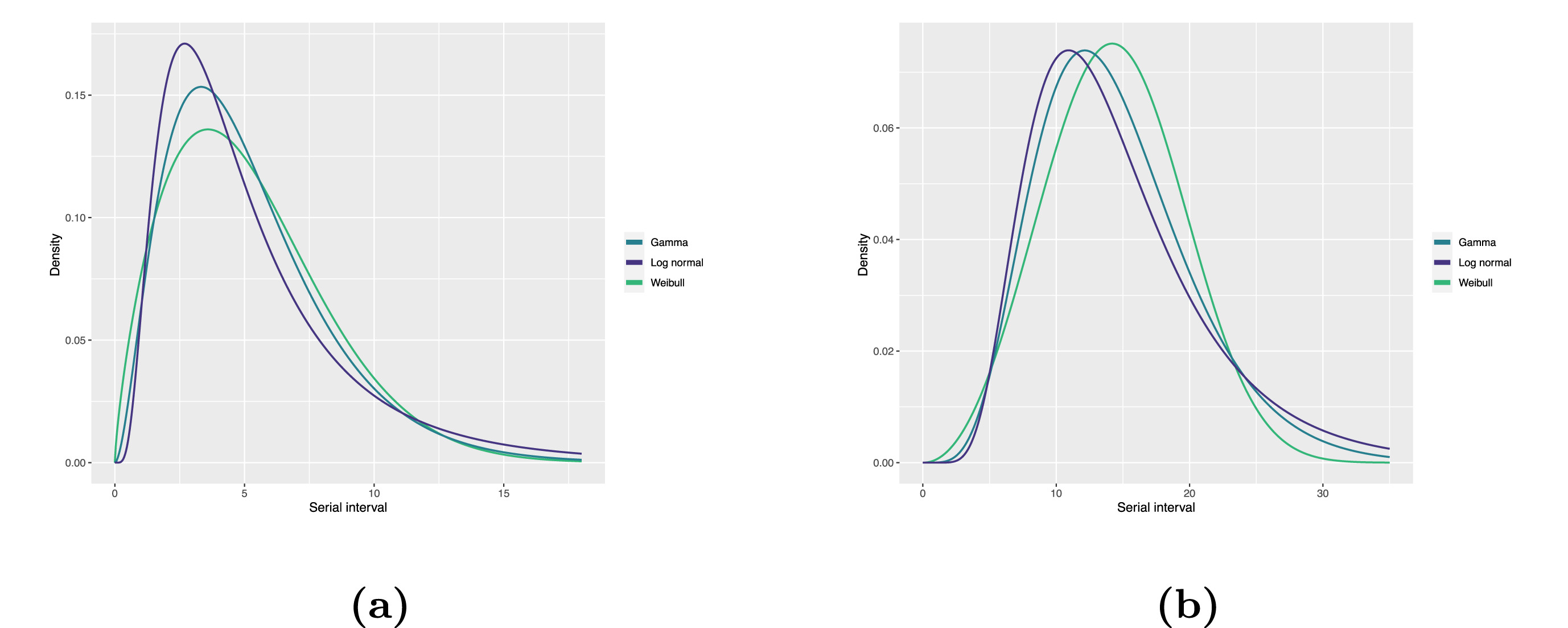
Distribución ajustada del intervalo serial para
(a) COVID-19 y (b) MERS-CoV basada en pares de transmisión notificados
en Arabia Saudí. Ajustamos tres distribuciones comunmente usadas, Log
normal, Gamma y Weibull, respectivamente (Althobaity
et al., 2022).
Figura 6
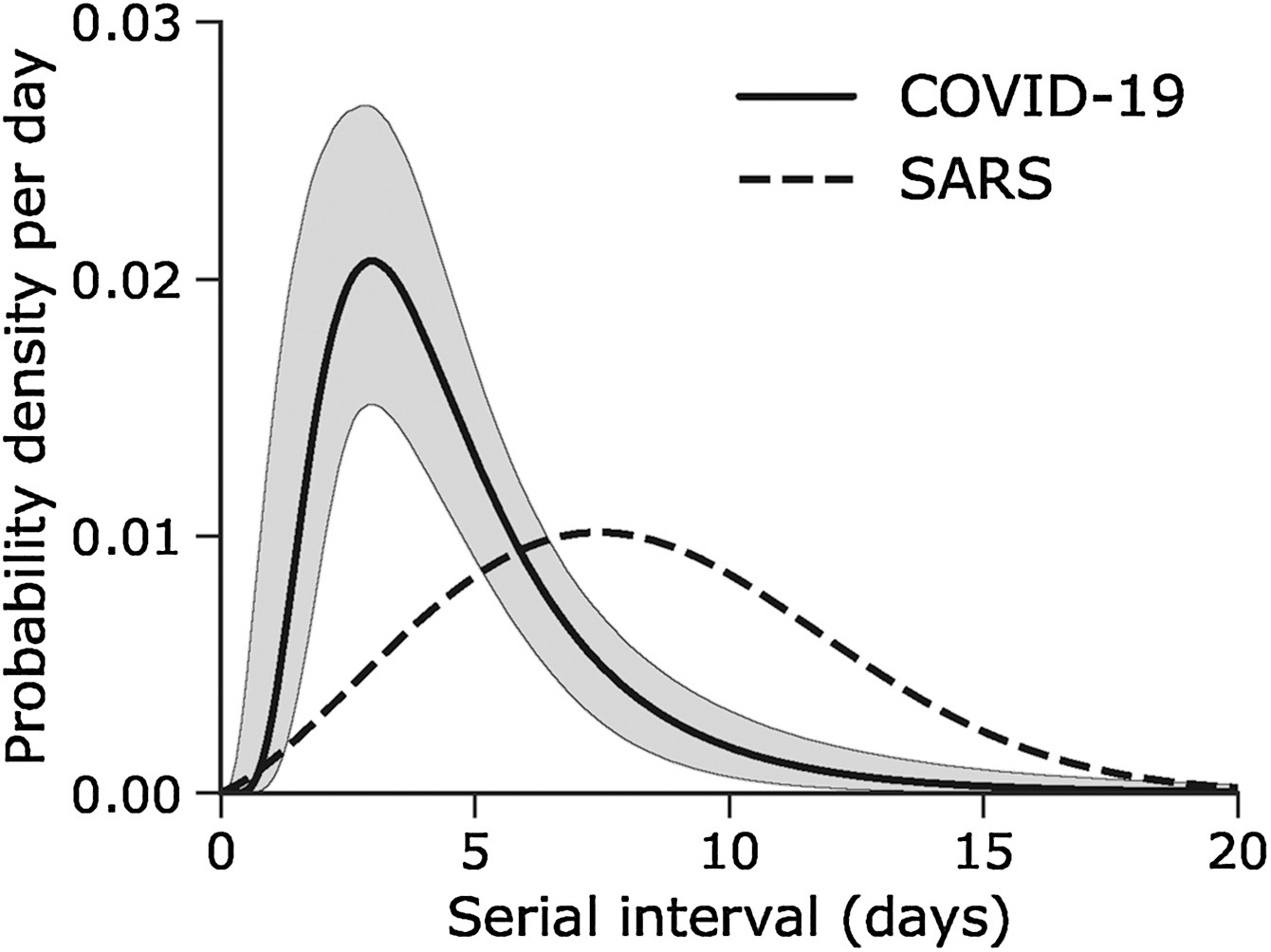
El Intervalo serial de nuevas infecciones por
coronavirus (COVID-19) superpuesto a una distribución publicada del
SRAS. (Nishiura
et al., 2020)
Figura 7
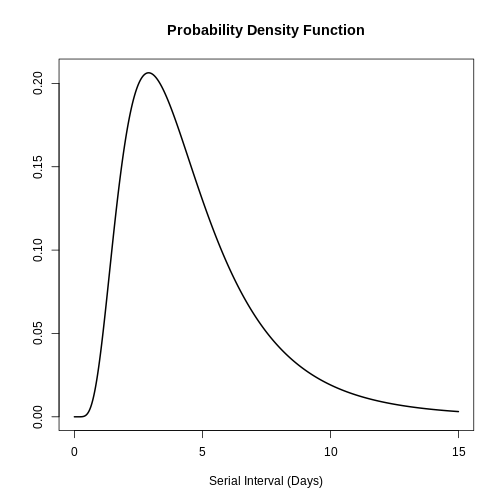
Cuantificar la transmisión
Figura 1
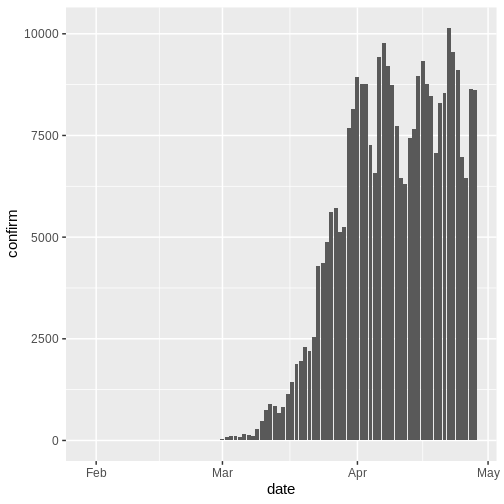
Figura 2
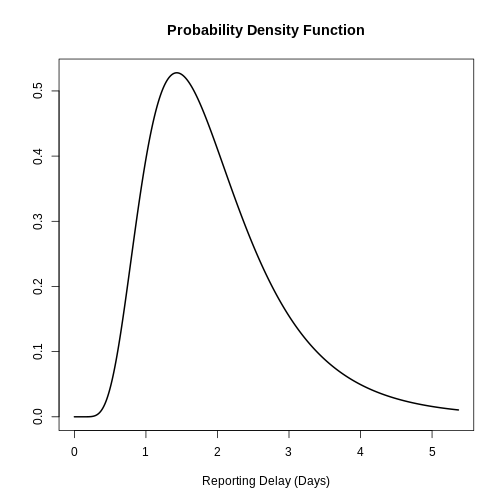
Figura 3
Figura 4
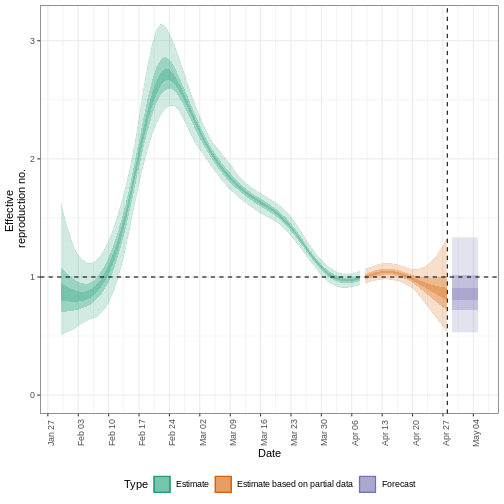
Figura 5
Figura 6
Utilizar distribuciones de retraso en el análisis
Figura 1
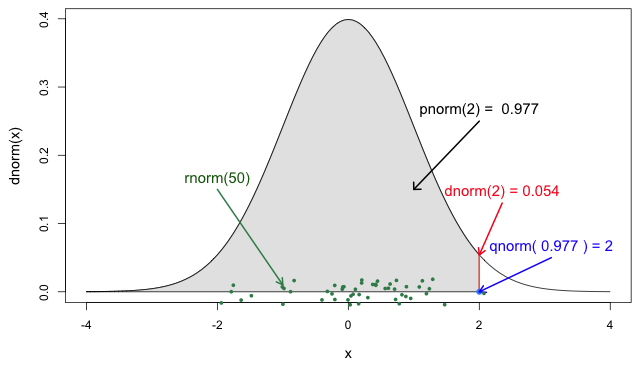
Las cuatro funciones de probabilidad de la
distribución normal (Jack
Weiss, 2012)
Figura 2
Figura 3
Figura 4
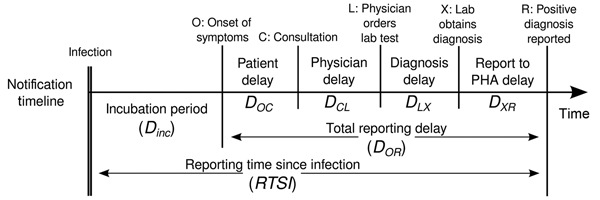
Calendario de notificación de la cadena
de enfermedades, Países Bajos. Lab, laboratorio; PHA, autoridad
sanitaria pública. En Marinović
y otros, 2015
Figura 5
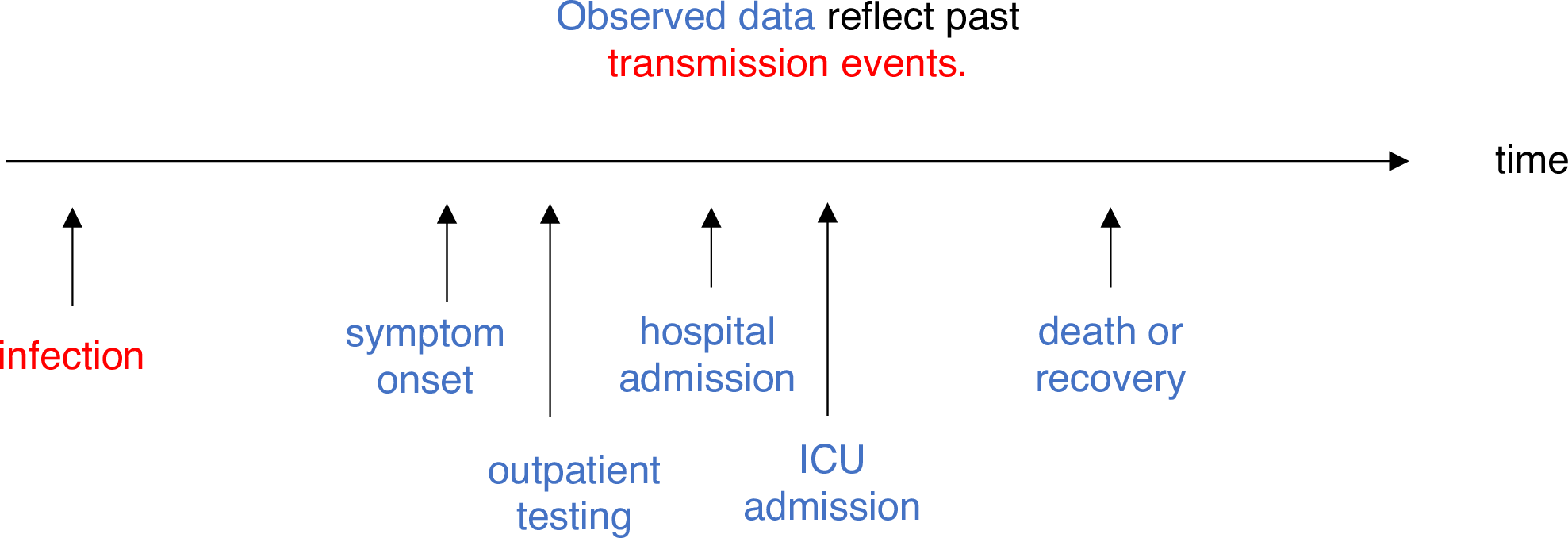
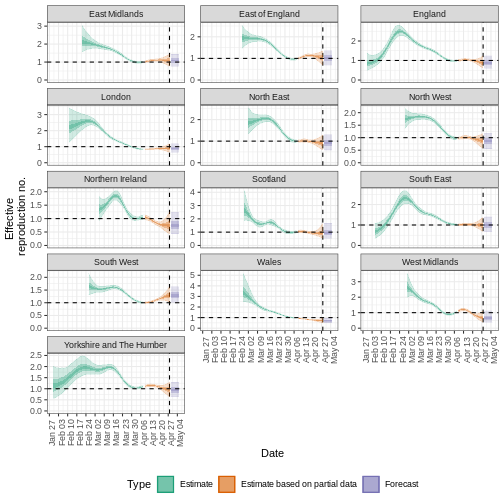
\(R_{t}\) es una medida de la transmisión en
el momento \(t\).
Observaciones después del tiempo \(t\)
deben ajustarse. UCI, unidad de cuidados intensivos. En Gostic
et al., 2020
Figura 6
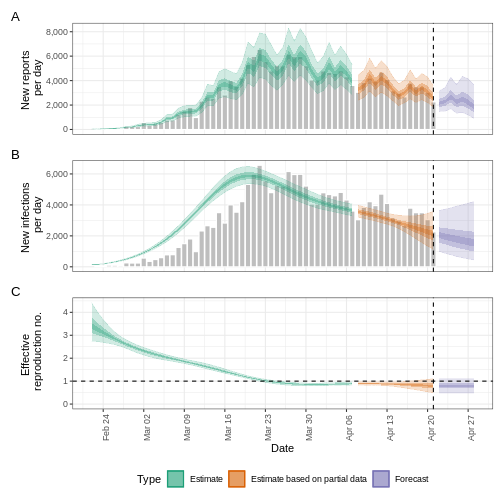
Figura 7
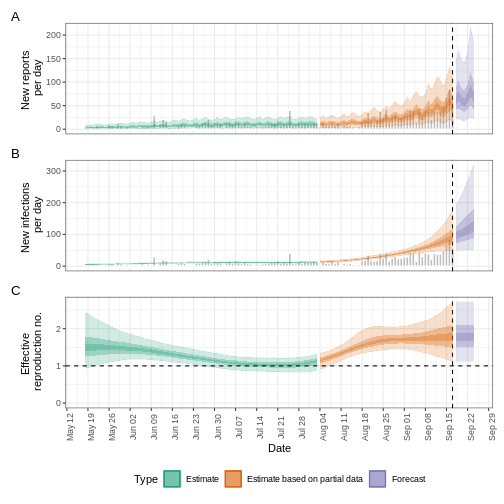
Figura 8
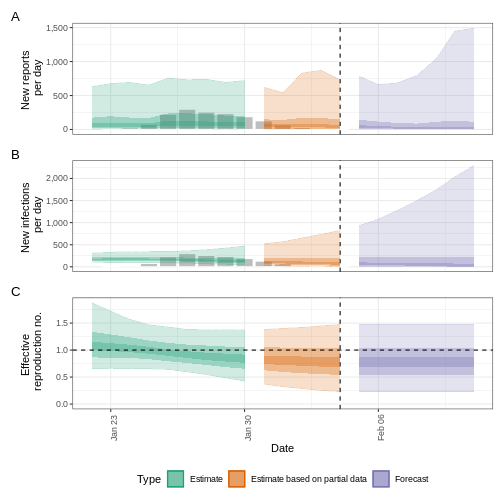
Crear una previsión a corto plazo
Figura 1

Figura 2

Figura 3

Figura 4

Figura 5

Estimación de la severidad del brote
Figura 1
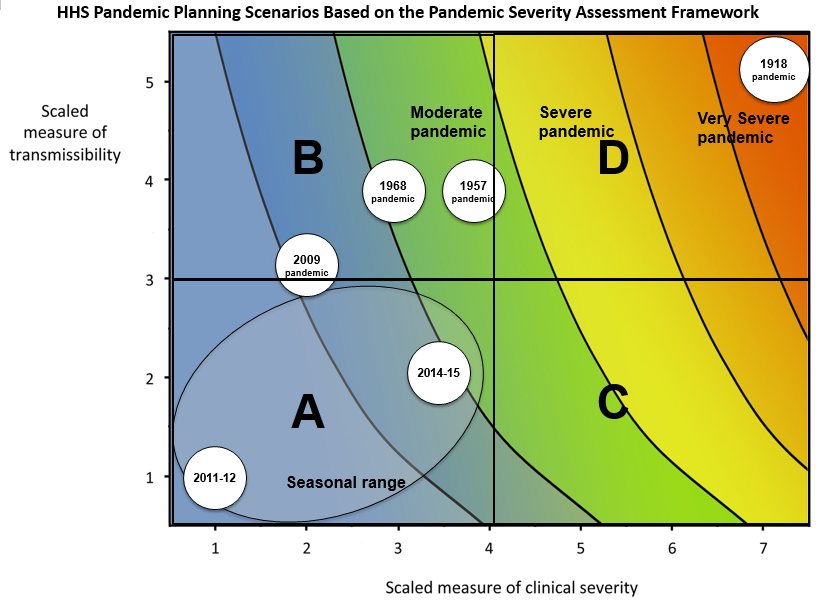
Escenarios de Planificación de Pandemias del HHS
basados en el Marco de Evaluación de la Gravedad de la Pandemia. Éste
utiliza una medida combinada de gravedad clínica y transmisibilidad para
caracterizar los escenarios de pandemia de gripe. HHS:
Departamento de Salud y Servicios Humanos de los Estados Unidos (CDC,
2016).
Figura 2
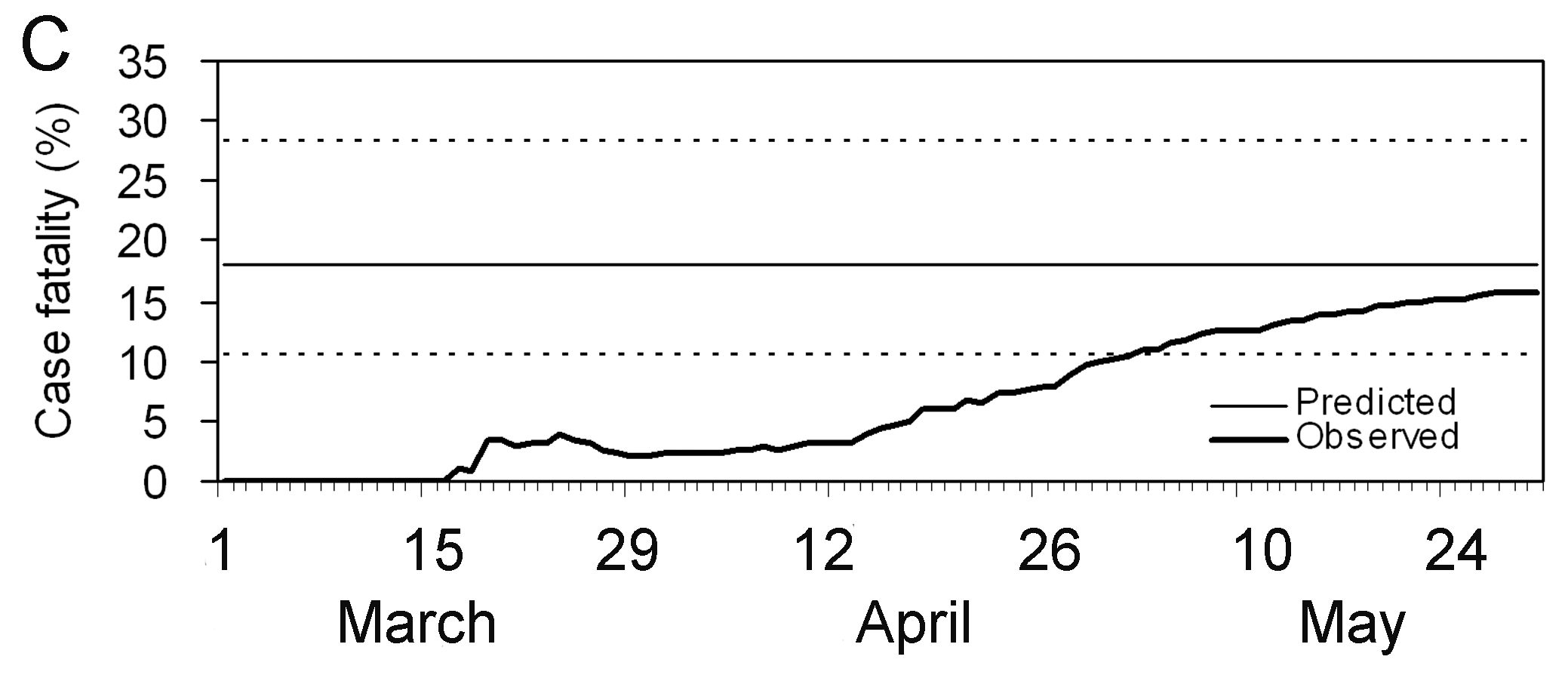
Estimaciones sesgadas de la probabilidad de
muerte como función del tiempo (línea gruesa), calculado como el número
acumulado de muertes dividido por el número de casos confirmados en el
tiempo \(t\). La estimación de la
probabilidad de muerte al final de un brote (~30 de mayo) corresponde
con la probabilidad de muerte verdadera. La línea continua horizontal y
las líneas de puntos muestran el valor esperado y los intervalos de
confianza del 95% (\(95%\) IC) de la
predicción de la probabilidad de muerte ajustada al retraso temporal
entre el periodo inicial de síntomas y muerte , utilizando los datos
observados hasta el 27 de Marzo de 2003 (Nishiura
et al., 2009)
Figura 3
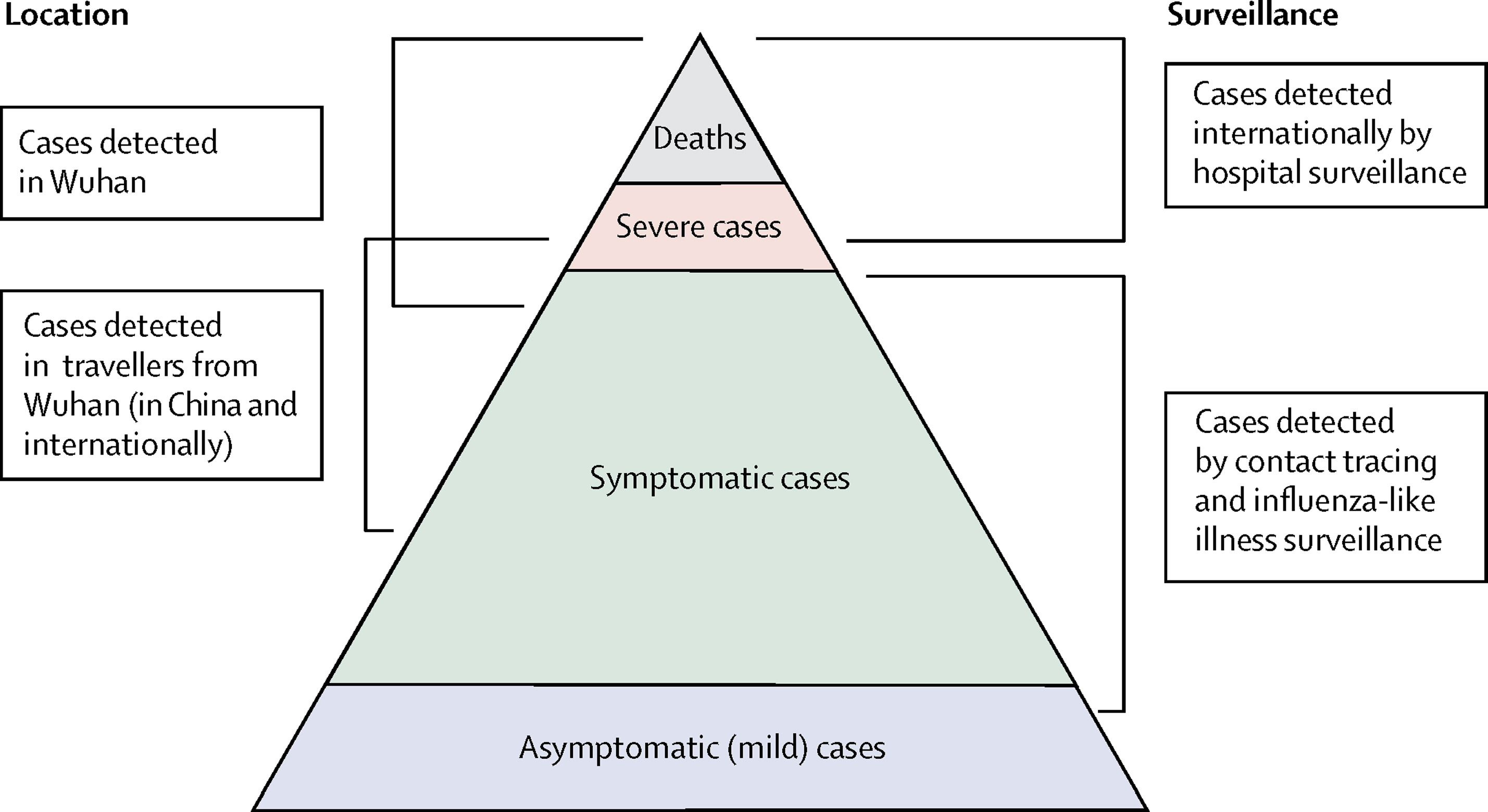
Espectro de casos de COVID-19. La probabilidad
de muerte pretende estimar la proporción de muertes entre los casos
confirmados en una epidemia. (Verity
et al., 2020)
Figura 4
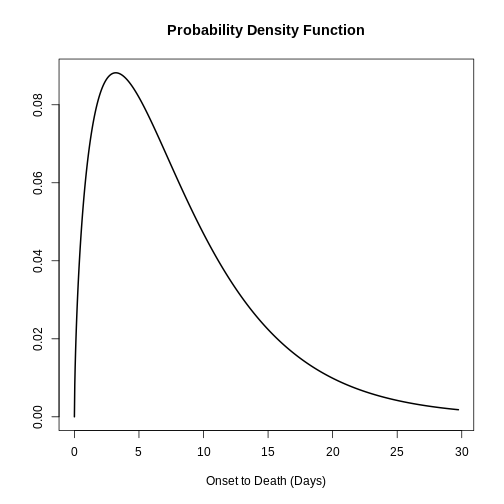
Figura 5
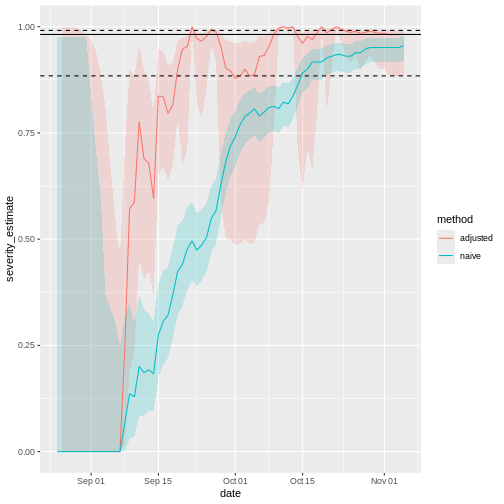
Figura 6
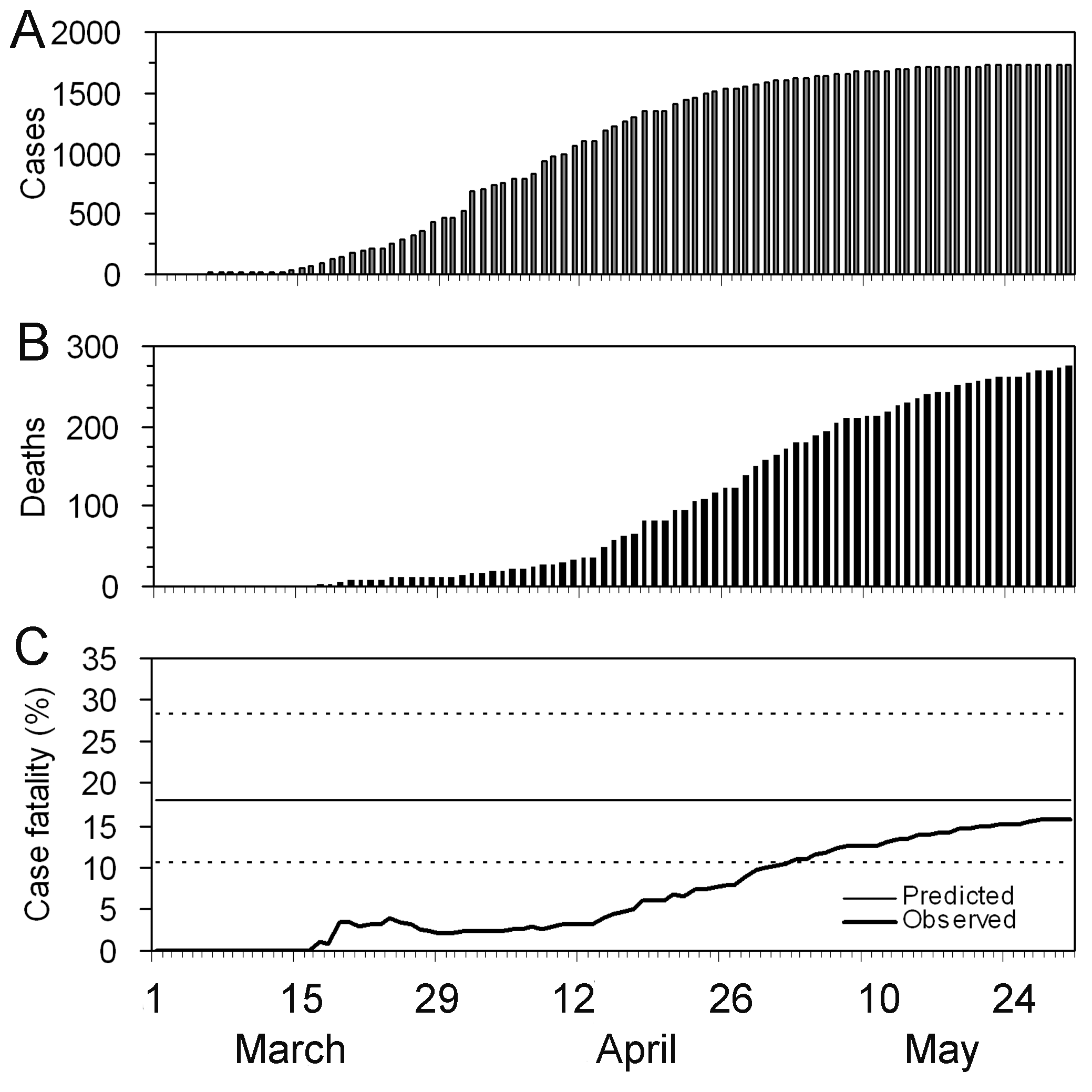
Riesgo observado (sesgado) de muerte confirmada
del síndrome respiratorio agudo grave (SRAS) en Hong Kong, 2003. (Nishiura
et al., 2009)
Figura 7
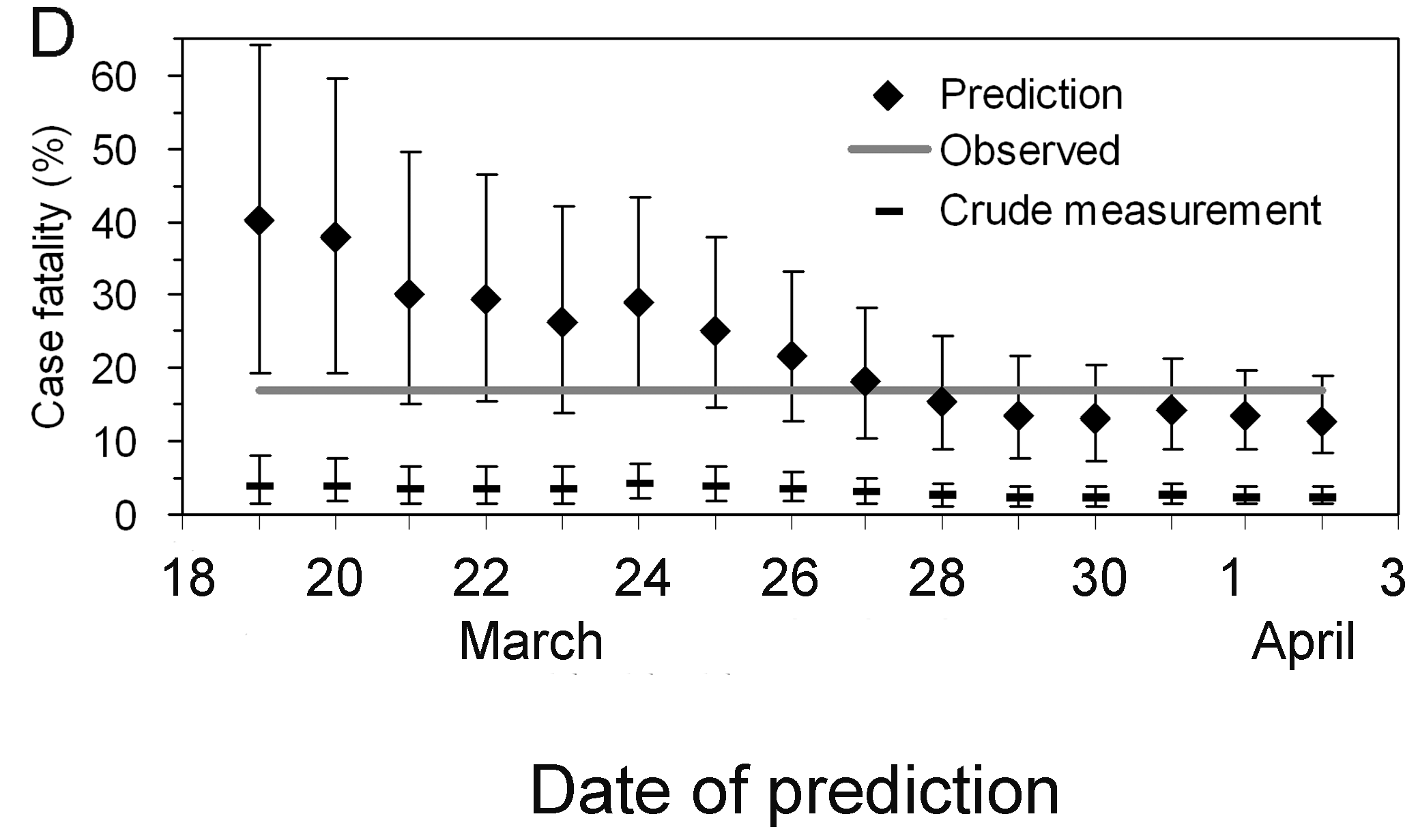
Determinación temprana del riesgo de muerte
confirmada ajustado al retraso del síndrome respiratorio agudo grave
(SRAS) en Hong Kong, 2003. (Nishiura
et al., 2009)
Figura 8

La población de casos confirmados y el proceso
de muestreo para estimar el CFR sin sesgo durante el transcurso de un
brote. (Nishiura et
al., 2009)
Figura 9
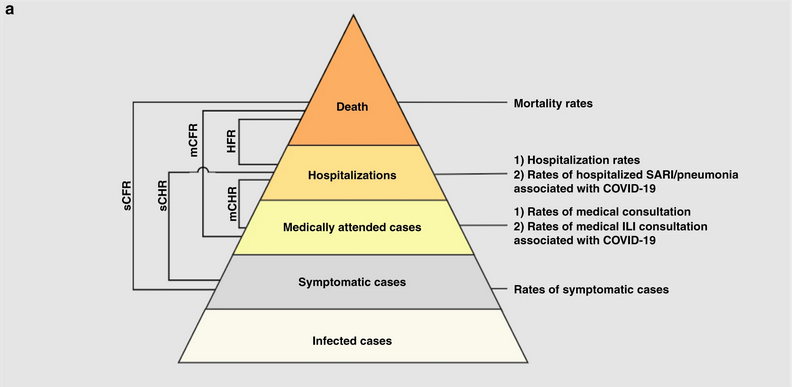
Niveles de gravedad de las infecciones por
SRAS-CoV-2 y parámetros de interés. Se supone que cada nivel es un
subconjunto del nivel inferior.
Figura 10
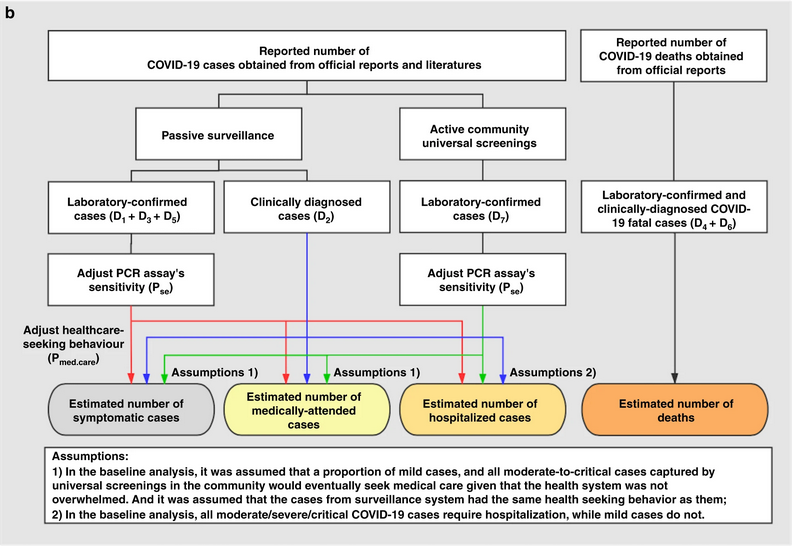
Diagrama esquemático de los análisis de
referencia. Las flechas rojas, azules y verdes indican el flujo de datos
desde los casos confirmados por laboratorio de la vigilancia pasiva, los
casos diagnosticados clínicamente y los casos confirmados por
laboratorio de los cribados activos.
Account for superspreading
Figura 1

Chains of SARS-CoV-2 transmission in
Hong Kong initiated by local or imported cases.
(a), Transmission network of a cluster of cases traced
back to a collection of four bars across Hong Kong (n = 106).
(b), Transmission network associated with a wedding
without clear infector–infectee pairs but linked back to a preceding
social gathering and local source (n = 22). (c),
Transmission network associated with a temple cluster of undetermined
source (n = 19). (d), All other clusters of SARS-CoV-2
infections where the source and transmission chain could be determined
(Adam et
al., 2020).
Figura 2

Observed offspring distribution of
SARS-CoV-2 transmission in Hong Kong. N = 91 SARS-CoV-2
infectors, N = 153 terminal infectees and N = 46 sporadic local cases.
Histogram bars indicate the proportion of onward transmission per amount
of secondary cases. Line corresponds to a fitted negative binomial
distribution (Adam et al.,
2020).
Figura 3

Figura 4

Figura 5

Figura 6

Figura 7

Figura 8

Evidence for variation in individual
reproductive number. (Left, c) Proportion of transmission
expected from the most infectious 20% of cases, for 10 outbreak or
surveillance data sets (triangles). Dashed lines show proportions
expected under the 20/80 rule (top) and homogeneity (bottom). (Right,
d), Reported superspreading events (SSEs; diamonds) relative to
estimated reproductive number R (squares) for twelve directly
transmitted infections. Crosses show the 99th-percentile proposed as
threshold for SSEs. (More figure details in Lloyd-Smith et al.,
2005)
Figura 9

Schematic representation of contact tracing
strategies. Black arrows indicate the directions of transmission, blue
and Orange arrows, a successful or failed contact tracing,
respectivelly. When there is evidence of individual-level variation in
transmission, often resulting in superspreading, backward contact
tracing from the index case (blue circle) increase the probability to
find the primary case (green circle) or clusters with a larger fraction
of cases, potentially increasing the number of quarentined cases (yellow
circles). Claire
Blackmore, 2021
Figura 10

Reported superspreading events (SSEs; diamonds)
relative to estimated reproduction number R (squares) for twelve
directly transmitted infections. Lines show 5–95 percentile range of the
number of secondary cases following a Poisson distribution with lambda
equal to the reproduction number (\(Z∼Poisson(R)\)), and crosses show the
99th-percentile proposed as threshold for SSEs. Stars represent SSEs
caused by more than one source case. ‘Other’ diseases are: 1,
Streptococcus group A; 2, Lassa fever; 3, Mycoplasma pneumonia; 4,
pneumonic plague; 5, tuberculosis. R is not shown for ‘other’ diseases,
and is off-scale for monkeypox.
Simulate transmission chains
Figura 1

Figura 2
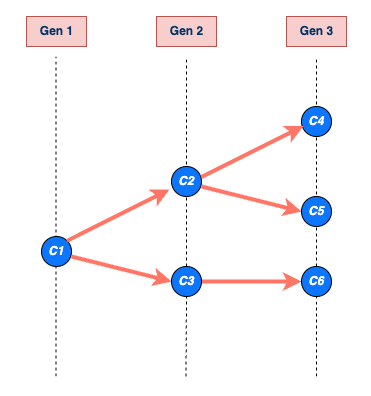
An example of a transmission chain
starting with a single case C1. Cases are represented by blue
circles and arrows indicating who infected whom. The chain grows through
generations Gen 1, Gen 2, and Gen 3, producing cases C2, C3, C4, C5, and
C6. The chain ends at generation Gen 3 with cases C4, C5, and C6. The
size of C1’s chain is 6, including C1 (that is, the sum of all blue
circles), and the length is 3, which includes Gen 1 (maximum number of
generations reached by C1’s chain) (Azam
& Funk, 2024).
Figura 3

A schematic of the relationship of different
time periods of transmission between an infector and an infectee in a
transmission pair. Exposure window is defined as the time interval
having viral exposure, and transmission window is defined as the time
interval for onward transmission with respect to the infection time (Chung
Lau et al., 2021).
Figura 4

Figura 5

Figura 6

Figura 7

Figura 8

Growth of simulated outbreaks with R =
1.5 and one initial case, conditional on non-extinction. Boxes
show the median and interquartile range (IQR) of the first disease
generation with 100 cases; whiskers show the most extreme values within
1.5 × IQR of the boxes, and crosses show outliers. Percentages show the
proportion of 10,000 simulated outbreaks that reached the 100-case
threshold (Lloyd-Smith et al.,
2005).
Figura 9

Figura 10

Figura 11

