Utilizar distribuciones de retraso en el análisis

Última actualización: 2024-11-19 | Mejora esta página

Tiempo estimado: 30 minutos

Hoja de ruta

Preguntas

¿Cómo reutilizar los retrasos almacenados en el paquete {epiparameter} con mi flujo de análisis existente?

Objetivos

Utilizar funciones de distribución para distribuciones continuas y discretas almacenadas como objetos <epidist>.
Convertir una distribución continua en discreta con {epiparameter}.
Conectar las salidas de {epiparameter} con entradas de EpiNow2.

Requisitos previos

Completar el tutorial Cuantificar la transmisión

Este episodio requiere que estés familiarizado con:

Ciencia de datos : Programación básica con R.

Estadística : Distribuciones de probabilidad.

Teoría epidémica Parámetros epidemiológicos, periodos de tiempo, número reproductivo efectivo.

Introducción

{epiparameter} nos ayuda a elegir un conjunto específico de parámetros epidemiológicos de la bibliografía, en lugar de copiarlos/pegarlos a mano:

R

covid_serialint <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "serial",
    author = "Nishiura",
    single_epidist = TRUE
  )

¡Ahora tenemos un parámetro epidemiológico que podemos utilizar en nuestro análisis! En el bloque de abajo hemos sustituido uno de los parámetros de estadísticas de resumen por EpiNow2::LogNormal()

R

generation_time <- 
  EpiNow2::LogNormal(
    mean = covid_serialint$summary_stats$mean, # replaced!
    sd = covid_serialint$summary_stats$sd, # replaced!
    max = 20
  )

En este episodio, utilizaremos las funciones de distribución que {epiparameter} proporciona para obtener un valor máximo (max) para este y cualquier otro paquete aguas abajo en tu flujo de análisis.

Carguemos los paquetes {epiparameter} y EpiNow2. En EpiNow2 estableceremos 4 núcleos para utilizarlos en cálculos paralelos. Utilizaremos el operador pipe %>%, algunos verbos de dplyr y ggplot2, así que llamemos también al paquete tidyverse:

R

library(epiparameter)
library(EpiNow2)
library(tidyverse)

withr::local_options(list(mc.cores = 4))

El doble punto

El doble punto :: en R te permite llamar a una función específica de un paquete sin cargar todo el paquete en el entorno actual.

Por ejemplo dplyr::filter(data, condition) utiliza filter() del paquete dplyr.

Esto nos ayuda a recordar las funciones del paquete y a evitar conflictos con los nombres de las funciones.

Funciones de distribución

En R, todas las distribuciones estadísticas tienen funciones para acceder a lo siguiente:

density(): Función de densidad de probabilidad (PDF, por sus siglas en inglés),
cdf(): Función de distribución acumulada (CDF, por sus siglas en inglés),
quantile(): Cuantil y
generate(): Generar valores aleatorios de la distribución dada.

Funciones para la distribución Normal

Si lo necesitas, ¡lee en detalle acerca de las funciones de probabilidad de R para la distribución normal, cada una de sus definiciones e identifica en qué parte de una distribución se encuentran!

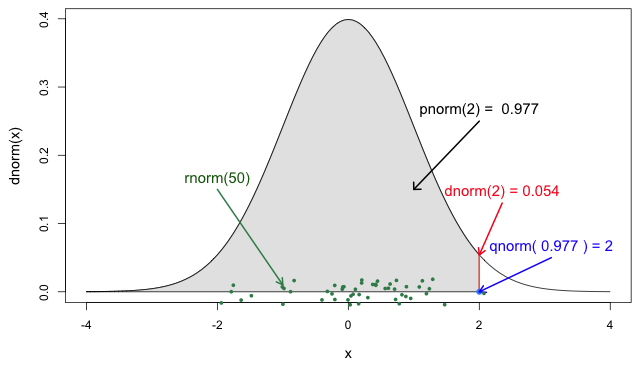
Las cuatro funciones de probabilidad de la distribución normal (Jack Weiss, 2012)

Si consultas ?stats::Distributions, cada tipo de distribución tiene un conjunto único de funciones. Sin embargo, ¡{epiparameter} te ofrece las mismas cuatro funciones para acceder a cada uno de los valores anteriores para cualquier objeto <epidist> que quieras!

R

# Grafica esto para tener una imagen de referencia
plot(covid_serialint, day_range = 0:20)

R

# El valor de densidad cuando el cuantil tiene un valor de 10 (días)
density(covid_serialint, at = 10)

SALIDA

[1] 0.01911607

R

# La probabilidad acumulada cuando el cuantil tiene un valor de 10 (días)
cdf(covid_serialint, q = 10)

SALIDA

[1] 0.9466605

R

# El valor del cuantil (día) cuando la probabilidad acumulada es 60%
quantile(covid_serialint, p = 0.6)

SALIDA

[1] 4.618906

R

# Generar 10 valores aleatorios (días) dada una familia de distribuciones y
# sus parámetros
generate(covid_serialint, times = 10)

SALIDA

 [1]  5.702350  8.846805  4.247009 10.232628  7.698895  4.088730 12.172251
 [8]  4.556690  5.119388  2.796879

Notas de la instructora

El acceso a la documentación de referencia (archivos de ayuda) de estas funciones es accesible con la notación de tres dobles puntos: epiparameter:::

?epiparameter:::density.epidist()
?epiparameter:::cdf.epidist()
?epiparameter:::quantile.epidist()
?epiparameter:::generate.epidist()

Ventana para el rastreo de contactos y el intervalo en serie

El intervalo serial es importante en la optimización del rastreo de contactos, ya que proporciona una ventana temporal para la contención de la propagación de una enfermedad (Fine, 2003). A partir del intervalo serial, podemos evaluar la necesidad de ampliar el número de días previos a tener en cuenta para iniciar el rastreo de contactos e incluir más contactos retrospectivos (Davis et al., 2020).

Con el intervalo de serie COVID-19 (covid_serialint) calcula:

¿Cuántos más casos atrasados se podrían captar si el método de rastreo de contactos considerara los contactos de hasta 6 días antes del inicio en comparación con los de 2 días antes del inicio?

Dar una pista

En la Figura 5 de las funciones de probabilidad de R para la distribución normal, la sección sombreada representa una probabilidad acumulada de 0.997 para el valor del cuantil en x = 2.

Mostrar la solución

R

plot(covid_serialint)

R

cdf(covid_serialint, q = 2)

SALIDA

[1] 0.1111729

R

cdf(covid_serialint, q = 6)

SALIDA

[1] 0.7623645

Dado el intervalo de serie COVID-19:

Un método de rastreo de contactos que considere los contactos hasta 2 días antes del inicio captará alrededor del 11,1% de los casos retrospectivos.
Si este periodo se amplía a 6 días antes del inicio, se podría incluir el 76,2% de los contactos retrospectivos.

¿Y si

intercambiamos la pregunta entre días y probabilidad acumulada a:

Al considerar los casos secundarios, ¿cuántos días después del inicio de los síntomas de los casos primarios podemos esperar que se produzca un 55% de inicio de los síntomas?

R

quantile(covid_serialint, p = 0.55)

Una interpretación podría ser

El 55% del inicio de los síntomas de los casos secundarios ocurrirá después de 4,2 días del inicio de los síntomas de los casos primarios.

Discretizar una distribución continua

¡Nos acercamos al final! EpiNow2::LogNormal() todavía necesita un valor máximo (max).

Una forma de hacerlo es obtener el valor del cuantil del percentil 99 de la distribución o la probabilidad acumulada de 0.99 . Para ello, necesitamos acceder al conjunto de funciones de distribución de nuestro objeto <epidist>.

Podemos utilizar el conjunto de funciones de distribución de una distribución continua (como arriba). Sin embargo, estos valores serán continuos. Podemos discretizar la distribución continua almacenada en nuestro objeto <epidist> para obtener valores discretos a partir de una distribución continua.

Cuando usamos epiparameter::discretise() sobre la distribución continua, obtenemos una distribución discreta (o discretizada):

R

covid_serialint_discrete <-
  epiparameter::discretise(covid_serialint)

covid_serialint_discrete

SALIDA

Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Distribution: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: discrete lnorm
Parameters:
  meanlog: 1.386
  sdlog: 0.568

Identificamos este cambio en la línea de salida Distribution: del objeto <epidist>. Comprueba de nuevo esta línea:

Distribution: discrete lnorm

Mientras que para una distribución continua trazamos la Función de densidad de probabilidad (PDF) para una distribución discreta, trazamos la función de masa de probabilidad (PMF):

R

# continua
plot(covid_serialint)

# discreta
plot(covid_serialint_discrete)

Para obtener finalmente un valor máximo (max), accedamos al valor del cuantil del percentil 99 o cuando la probabilidad acumulada es 0.99 usando prob_dist$q de forma similar a como accedemos a los valores de estadísticas de resumen (summary_stats).

R

covid_serialint_discrete_max <-
  quantile(covid_serialint_discrete, p = 0.99)

Duración del periodo de cuarentena e incubación

El periodo de incubación es un retraso útil para evaluar la duración de la vigilancia activa o la cuarentena (Lauer et al., 2020). Del mismo modo, los retrasos desde la aparición de los síntomas hasta la recuperación (o la muerte) determinarán la duración necesaria de la asistencia sanitaria y el aislamiento del caso (Cori et al., 2017).

Calcula:

¿En qué plazo exacto de tiempo el 99% de las personas que presentan síntomas de COVID-19 después de la infección los presentan?

Dar una pista

¿Qué distribución del retraso mide el tiempo entre la infección y la aparición de los síntomas?

¡Las funciones de probabilidad discretas para <epidist> son las mismas que utilizamos para las continuas!

R

# Grafica esto para tener una imagen de referencia
plot(covid_serialint_discrete, day_range = 0:20)

# El valor de la densidad cuando el cuantil tiene un valor de 10 (días)
density(covid_serialint_discrete, at = 10)

# La probabilidad acumulada cuando el cuantil tiene un valor de 10 (días)
cdf(covid_serialint_discrete, q = 10)

# El valor del cuantil (días) cuando la probabilidad acumulada es 60%
quantile(covid_serialint_discrete, p = 0.6)

# Generar valores aleatorios
generate(covid_serialint_discrete, times = 10)

Mostrar la solución

R

covid_incubation <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "incubation",
    single_epidist = TRUE
  )

SALIDA

Using Linton N, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov A, Jung S, Yuan
B, Kinoshita R, Nishiura H (2020). "Incubation Period and Other
Epidemiological Characteristics of 2019 Novel Coronavirus Infections
with Right Truncation: A Statistical Analysis of Publicly Available
Case Data." _Journal of Clinical Medicine_. doi:10.3390/jcm9020538
<https://doi.org/10.3390/jcm9020538>..
To retrieve the citation use the 'get_citation' function

R

covid_incubation_discrete <- epiparameter::discretise(covid_incubation)

quantile(covid_incubation_discrete, p = 0.99)

SALIDA

[1] 19

El 99% de los que desarrollan síntomas de COVID-19 lo harán en los 16 días posteriores a la infección.

Ahora, ¿es esperable este resultado en términos epidemiológicos?

¿Cómo crear un gráfico de distribución?

A partir de un valor máximo con quantile() podemos crear una secuencia de valores de cuantiles como un vector numérico y calcular density() para cada uno:

R

# Crear la visualización para una distribución discreta
# a partir de un valor máximo de la distribución
quantile(covid_serialint_discrete, p = 0.99) %>%
  # Generar un vector de cuantiles
  # como una secuencia para cada número natural
  seq(1L, to = ., by = 1L) %>%
  # Convertir el vector numérico en un data.frame (tibble)
  as_tibble_col(column_name = "quantile_values") %>%
  mutate(
    # Calcular los valores de densidad
    # para cada cuantul en la función de densidad
    density_values =
      density(
        x = covid_serialint_discrete,
        at = quantile_values
      )
  ) %>%
  # Graficar
  ggplot(
    aes(
      x = quantile_values,
      y = density_values
    )
  ) +
  geom_col()

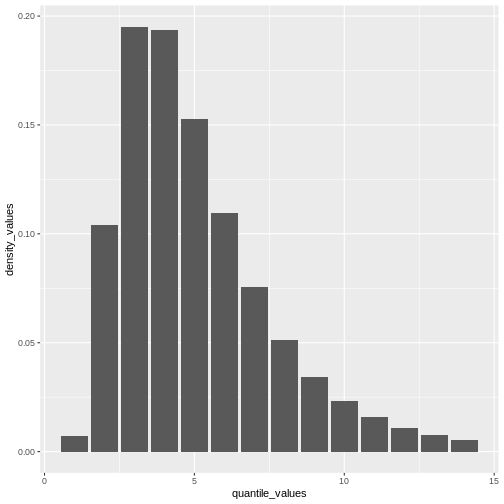
Recuerda: En las infecciones con transmisión presintomática, los intervalos seriales pueden tener valores negativos (Nishiura et al., 2020). ¡Cuando utilizamos el intervalo serial para aproximar el tiempo de generación necesitamos hacer esta distribución sólo con valores positivos!

Plug-in `{epiparameter}` a `{EpiNow2}`

¡Ahora podemos introducirlo todo en la función EpiNow2::LogNormal()!

Las estadísticas de resumen: media (mean) y desviación estándar (sd) de la distribución,
un valor máximo (max),
el nombre de la distribución (distribution).

Cuando utilices EpiNow2::LogNormal() para definir una distribución log normal como la del intervalo serial del COVID-19 (covid_serialint) podemos especificar la media (mean) y la desviación estándar (sd) como parámetros. Alternativamente, para obtener los parámetros “naturales” de una distribución log normal podemos convertir sus estadísticos de resumen en parámetros de distribución denominados meanlog y sdlog. Con {epiparameter} podemos obtener directamente los parámetros de la distribución utilizando epiparameter::get_parameters():

R

covid_serialint_parameters <-
  epiparameter::get_parameters(covid_serialint)

Entonces, tenemos:

R

serial_interval_covid <-
  EpiNow2::LogNormal(
    meanlog = covid_serialint_parameters["meanlog"],
    sdlog = covid_serialint_parameters["sdlog"],
    max = covid_serialint_discrete_max
  )

serial_interval_covid

SALIDA

- lognormal distribution (max: 14):
  meanlog:
    1.4
  sdlog:
    0.57

Suponiendo un escenario con COVID-19, utilicemos los primeros 60 días del conjunto de datos example_confirmed del paquete EpiNow2 como casos reportados(reported_cases) y el recientemente creado intervalo serial COVID (serial_interval_covid) como entradas para estimar el número reproductivo variable en el tiempo utilizando EpiNow2::epinow().

R

epinow_estimates_cg <- epinow(
  # casos
  data = example_confirmed[1:60],
  # retrasos
  generation_time = generation_time_opts(serial_interval_covid)
)

SALIDA

WARN [2024-11-19 02:33:14] epinow: There were 2 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:33:14] epinow: Examine the pairs() plot to diagnose sampling problems
 -

R

base::plot(epinow_estimates_cg)

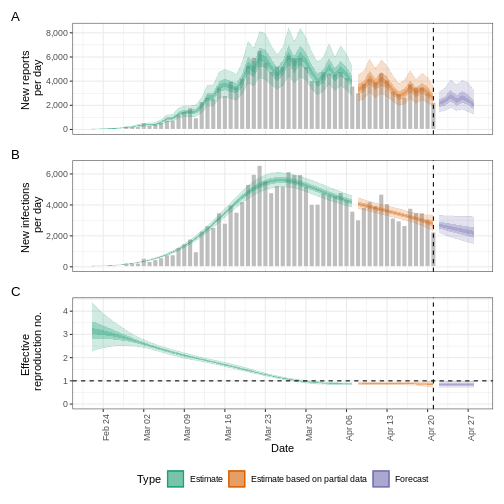
plot() incluye los casos estimados por fecha de infección, que se reconstruyen a partir de los casos notificados y los retrasos.

Advertencia

Utilizar el intervalo serial en lugar del tiempo de generación es una alternativa que puede propagar sesgos en tus estimaciones, más aún en enfermedades con transmisión presintomática reportada. (Chung Lau et al., 2021)

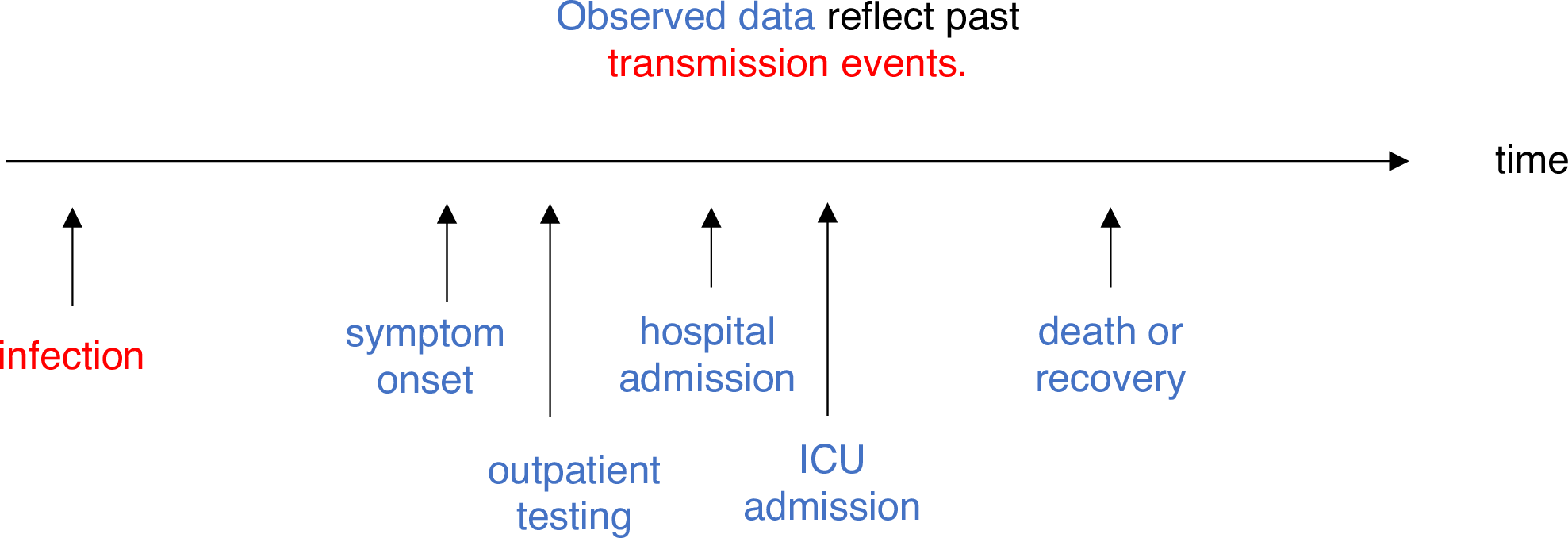
Ajuste por retrasos en la notificación

Estimar $R_t$ requiere datos sobre el número diario de nuevas infecciones. Debido a los retrasos en el desarrollo de cargas víricas detectables, la aparición de síntomas, la búsqueda de atención sanitaria y la notificación, estas cifras no están fácilmente disponibles. Todas las observaciones reflejan eventos de transmisión de algún momento del pasado. En otras palabras, si $d$ es el tiempo transcurrido desde la infección hasta la observación, las observaciones en el momento $t$ informan a $R_{t−d}$ no $R_t$. (Gostic et al., 2020)

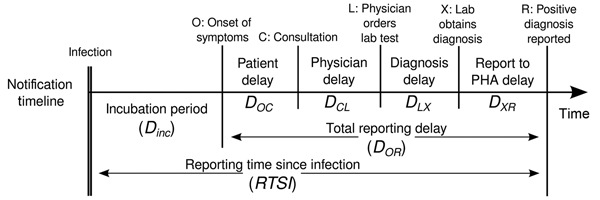
Calendario de notificación de la cadena de enfermedades, Países Bajos. Lab, laboratorio; PHA, autoridad sanitaria pública. En Marinović y otros, 2015

La distribución del retraso podría inferirse conjuntamente con los tiempos de infección subyacentes o estimarse como la suma del periodo de incubación y la distribución de los retrasos desde el inicio de los síntomas hasta la observación a partir de los datos (retraso en la notificación). En EpiNow2 podemos especificar estas dos distribuciones de retraso complementarias con el argumento delays.

R_{t} es una medida de la transmisión en el momento t. Observaciones después del tiempo t deben ajustarse. UCI, unidad de cuidados intensivos. En Gostic et al., 2020

Utiliza un periodo de incubación de COVID-19 para estimar Rt

Estima el número reproductivo variable en el tiempo para los primeros 60 días del conjunto de datos example_confirmed de EpiNow2. Accede a un periodo de incubación para COVID-19 a partir de {epiparameter} para utilizarlo como retraso de notificación.

Utiliza el último cálculo de epinow() usando el argumento delays y la función auxiliar delay_opts().

El argumento delays y la función auxiliar delay_opts() son análogos al argumento generation_time y la función auxiliar generation_time_opts().

R

epinow_estimates <- epinow(
  # casos
  reported_cases = example_confirmed[1:60],
  # retrasos
  generation_time = generation_time_opts(covid_serial_interval),
  delays = delay_opts(covid_incubation_time)
)

Mostrar la solución

R

# Tiempo de generación ---------------------------------------------------------

# Intervalo serial covid
covid_serialint <-
  epiparameter::epidist_db(
    disease = "covid",
    epi_dist = "serial",
    author = "Nishiura",
    single_epidist = TRUE
  )

# adaptar epidist para epinow2
covid_serialint_discrete_max <- covid_serialint %>%
  epiparameter::discretise() %>%
  quantile(p = 0.99)

covid_serialint_parameters <-
  epiparameter::get_parameters(covid_serialint)

covid_serial_interval <-
  EpiNow2::LogNormal(
    meanlog = covid_serialint_parameters["meanlog"],
    sdlog = covid_serialint_parameters["sdlog"],
    max = covid_serialint_discrete_max
  )

# Periodo de incubación -------------------------------------------------------

# Periodo de incubación
covid_incubation <- epiparameter::epidist_db(
  disease = "covid",
  epi_dist = "incubation",
  author = "Natalie",
  single_epidist = TRUE
)

# Adaptar epiparameter para epinow2
covid_incubation_discrete_max <- covid_incubation %>%
  epiparameter::discretise() %>%
  quantile(p = 0.99)

covid_incubation_parameters <-
  epiparameter::get_parameters(covid_incubation)

covid_incubation_time <-
  EpiNow2::LogNormal(
    meanlog = covid_incubation_parameters["meanlog"],
    sdlog = covid_incubation_parameters["sdlog"],
    max = covid_incubation_discrete_max
  )

# epinow ------------------------------------------------------------------

# usar epinow
epinow_estimates_cgi <- epinow(
  # casos
  data = example_confirmed[1:60],
  # retrasos
  generation_time = generation_time_opts(covid_serial_interval),
  delays = delay_opts(covid_incubation_time)
)

SALIDA

WARN [2024-11-19 02:34:51] epinow: There were 11 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:34:51] epinow: Examine the pairs() plot to diagnose sampling problems
 -

R

base::plot(epinow_estimates_cgi)

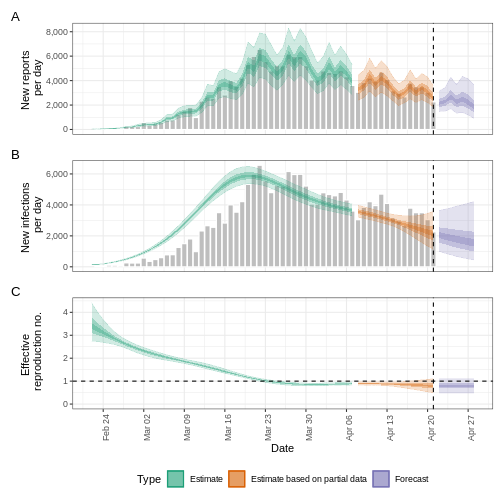
Intenta complementar el argumento delays con un retraso de notificación como el objeto reporting_delay_fixed del episodio anterior.

¿Cuánto ha cambiado?

Tras añadir el periodo de incubación, debata acerca de:

¿Cambia la tendencia del ajuste del modelo en la sección estimación (“Estimate”)?
¿Ha cambiado la incertidumbre?
¿Cómo explicaría o interpretaría estos cambios?

Compara todas las figuras generadas con EpiNow2 anteriormente.

Desafíos

Un consejo para completar código

Si escribimos el [ ] luego del objeto covid_serialint_parameters[ ], dentro de [ ] podemos utilizar el la tecla Tab en el teclado ↹ para usar la función de completado de código

Usar esto permite acceder rápidamente a covid_serialint_parameters["meanlog"] y covid_serialint_parameters["sdlog"].

¡Te invitamos a probarlo en otros bloques de código y en la consola de R!

Número de reproducción efectiva del ébola ajustado por retrasos en la notificación

Descarga y lee el conjunto de datos de ébola:

Estime el número reproductivo efectivo utilizando EpiNow2
Ajuste la estimación según los retrasos de notificación disponibles en {epiparameter}
¿Por qué eligió ese parámetro?

Para calcular el $R_t$ utilizando EpiNow2 necesitamos

Los datos de incidencia agregada con los casos confirmados por día, y
La distribución del tiempo de generación.
Opcionalmente, informar las distribuciones de retrasos cuando estén disponibles (por ejemplo, el periodo de incubación).

Para obtener las distribuciones de retrasos utilizando {epiparameter} podemos utilizar funciones como:

epiparameter::epidist_db()
epiparameter::parameter_tbl()
discretise()
quantile()

Mostrar la solución

R

# Leer datos
# e.j.: Si la ruta al archivo es data/raw-data/ebola_cases.csv entonces:
ebola_confirmed <-
  read_csv(here::here("data", "raw-data", "ebola_cases.csv"))

# Listar las distribuciones
epiparameter::epidist_db(disease = "ebola") %>%
  epiparameter::parameter_tbl()

R

# Tiempo de generación ---------------------------------------------------------

# Filtrar una distribución para el tiempo de generación
ebola_serial <- epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "serial",
  single_epidist = TRUE
)

# adaptar epiparameter para epinow2
ebola_serial_discrete <- epiparameter::discretise(ebola_serial)

serial_interval_ebola <-
  EpiNow2::Gamma(
    mean = ebola_serial$summary_stats$mean,
    sd = ebola_serial$summary_stats$sd,
    max = quantile(ebola_serial_discrete, p = 0.99)
  )

# Tiempo de incubación  -------------------------------------------------------

# Filtrar una distribución para el retraso del periodo de incubación
ebola_incubation <- epiparameter::epidist_db(
  disease = "ebola",
  epi_dist = "incubation",
  single_epidist = TRUE
)

# adaptar epiparameter para epinow2
ebola_incubation_discrete <- epiparameter::discretise(ebola_incubation)

incubation_period_ebola <-
  EpiNow2::Gamma(
    mean = ebola_incubation$summary_stats$mean,
    sd = ebola_incubation$summary_stats$sd,
    max = quantile(ebola_serial_discrete, p = 0.99)
  )

# epinow ------------------------------------------------------------------

# Usar epinow
epinow_estimates_egi <- epinow(
  # casos
  data = ebola_confirmed,
  # retrasos
  generation_time = generation_time_opts(serial_interval_ebola),
  delays = delay_opts(incubation_period_ebola)
)

SALIDA

WARN [2024-11-19 02:37:24] epinow: There were 181 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2024-11-19 02:37:24] epinow: Examine the pairs() plot to diagnose sampling problems
 -
WARN [2024-11-19 02:37:26] epinow: The largest R-hat is NA, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2024-11-19 02:37:27] epinow: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2024-11-19 02:37:28] epinow: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -

R

plot(epinow_estimates_egi)

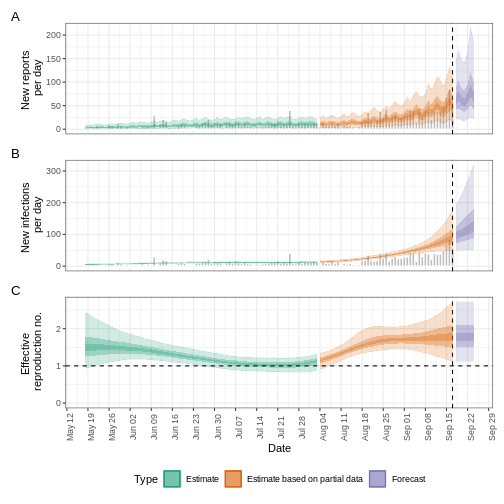
¿Qué hacer con las distribuciones de Weibull?

Utiliza el conjunto de datos influenza_england_1978_school del paquete outbreaks para calcular el número reproductivo efectivo mediante EpiNow2, ajustando por los retrasos de notificación disponibles en {epiparameter}.

EpiNow2::NonParametric() acepta Funciones de Masa de Probabilidad (PMF) de cualquier familia de distribuciones. Lee la guía de referencia sobre Distribuciones de probabilidad.

Mostrar la solución

R

# ¿Qué parámetros hay disponibles para Influenza?
epiparameter::epidist_db(disease = "influenza") %>%
  epiparameter::parameter_tbl() %>%
  count(epi_distribution)

SALIDA

# Parameter table:
# A data frame:    3 × 2
  epi_distribution      n
  <chr>             <int>
1 generation time       1
2 incubation period    15
3 serial interval       1

R

# Tiempo de generación  -------------------------------------------------------

# Leer tiempo de generación
influenza_generation <-
  epiparameter::epidist_db(
    disease = "influenza",
    epi_dist = "generation"
  )

influenza_generation

SALIDA

Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Distribution: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull
Parameters:
  shape: 2.360
  scale: 3.180

R

# EpiNow2 permite usar distribuciones Gamma o LogNormal
# Se puede introducir una PMF

influenza_generation_discrete <-
  epiparameter::discretise(influenza_generation)

influenza_generation_max <-
  quantile(influenza_generation_discrete, p = 0.99)

influenza_generation_pmf <-
  density(
    influenza_generation_discrete,
    at = 1:influenza_generation_max
  )

influenza_generation_pmf

SALIDA

[1] 0.06312336 0.22134988 0.29721220 0.23896828 0.12485164 0.04309454

R

# EpiNow2::NonParametric() también puede recibir valores de PMF
generation_time_influenza <-
  EpiNow2::NonParametric(
    pmf = influenza_generation_pmf
  )

# Periodo de incubación  -------------------------------------------------------

# Leer el periodo de incubación
influenza_incubation <-
  epiparameter::epidist_db(
    disease = "influenza",
    epi_dist = "incubation",
    single_epidist = TRUE
  )

# Discretizar el periodo de incubación
influenza_incubation_discrete <-
  epiparameter::discretise(influenza_incubation)

influenza_incubation_max <-
  quantile(influenza_incubation_discrete, p = 0.99)

influenza_incubation_pmf <-
  density(
    influenza_incubation_discrete,
    at = 1:influenza_incubation_max
  )

influenza_incubation_pmf

SALIDA

[1] 0.05749151 0.16687705 0.22443092 0.21507632 0.16104546 0.09746609 0.04841928

R

# EpiNow2::NonParametric() también puede recibit valores de PMF
incubation_time_influenza <-
  EpiNow2::NonParametric(
    pmf = influenza_incubation_pmf
  )

# epinow ------------------------------------------------------------------

# Leer datos
influenza_cleaned <-
  outbreaks::influenza_england_1978_school %>%
  select(date, confirm = in_bed)

# Usar epinow
epinow_estimates_igi <- epinow(
  # casos
  data = influenza_cleaned,
  # retrasos
  generation_time = generation_time_opts(generation_time_influenza),
  delays = delay_opts(incubation_time_influenza)
)

plot(epinow_estimates_igi)

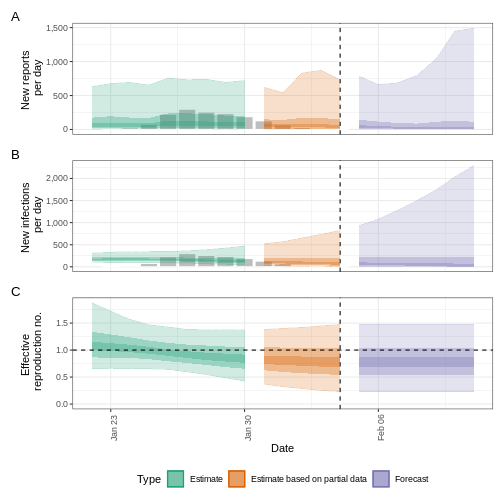
Próximos pasos

¿Cómo obtener parámetros de distribución a partir de distribuciones estadísticas?

¿Cómo obtener la media y la desviación típica de un tiempo de generación con sólo parámetros de distribución pero sin estadísticas de resumen como mean o sd para EpiNow2::Gamma() o EpiNow2::LogNormal()?

¡Mira en {epiparameter} la viñeta extracción y conversión de parámetros y sus casos de uso !

¿Cómo estimar las distribuciones de retraso de la Enfermedad X?

Consulta este excelente tutorial sobre la estimación del intervalo serial y el período de incubación de la Enfermedad X, teniendo en cuenta la censura por medio de inferencia bayesiana con paquetes como rstan y coarseDataTools.

Tutorial en Inglés: https://rpubs.com/tracelac/diseaseX
Tutorial en Español: https://epiverse-trace.github.io/epimodelac/EnfermedadX.html

Luego, después de obtener tus valores estimados, ¡puedes crear manualmente tus propios objetos con clase <epidist> por medio de epiparameter::epidist()! Echa un vistazo a su guía de referencia sobre “Crear un objeto <epidist>” ¡!

Por último, echa un vistazo al último paquete de R {epidist} que proporciona métodos para abordar los principales retos de la estimación de distribuciones, como el truncamiento, la censura por intervalos y los sesgos dinámicos.

Puntos Clave

Utilizar funciones de distribución con <epidist> para obtener estadísticas de resumen y parámetros informativos de las intervenciones de salud pública, como la Ventana de rastreo de contactos y la Duración de la cuarentena.
Utilizar discretise() para convertir distribuciones de retraso continuas en discretas.
Utilizar {epiparameter} para obtener los retrasos de información necesarios en las estimaciones de transmisibilidad.

Utilizar distribuciones de retraso en el análisis

Hoja de ruta

Preguntas

Objetivos

Requisitos previos

Introducción

R

R

R

El doble punto

Funciones de distribución

Funciones para la distribución Normal

R

R

SALIDA

R

SALIDA

R

SALIDA

R

SALIDA

Notas de la instructora

Ventana para el rastreo de contactos y el intervalo en serie

Dar una pista

Mostrar la solución

R

R

SALIDA

R

SALIDA

¿Y si

R

Discretizar una distribución continua

R

SALIDA

R

R

Duración del periodo de cuarentena e incubación

Dar una pista

R

Mostrar la solución

R

SALIDA

R

SALIDA

¿Cómo crear un gráfico de distribución?

R

Plug-in {epiparameter} a {EpiNow2}

R

R

SALIDA

R

SALIDA

R

Advertencia

Ajuste por retrasos en la notificación

Utiliza un periodo de incubación de COVID-19 para estimar Rt

R

Mostrar la solución

R

SALIDA

R

¿Cuánto ha cambiado?

Desafíos

Un consejo para completar código

Número de reproducción efectiva del ébola ajustado por retrasos en la notificación

Mostrar la solución

R

R

SALIDA

R

¿Qué hacer con las distribuciones de Weibull?

Mostrar la solución

R

SALIDA

R

SALIDA

R

SALIDA

R

Plug-in `{epiparameter}` a `{EpiNow2}`