Cuantificar la transmisión
Última actualización: 2024-11-19 | Mejora esta página
Tiempo estimado: 30 minutos
Hoja de ruta
Preguntas
- ¿Cómo puedo estimar el número de reproducción variable en el tiempo (\(Rt\)) y la tasa de crecimiento a partir de una serie temporal de datos de casos?
- ¿Cómo puedo cuantificar la heterogeneidad geográfica a partir de estas métricas de transmisión?
Objetivos
- Aprender a estimar las métricas de transmisión a partir de una serie
temporal de datos de casos utilizando el paquete R
EpiNow2
Requisitos previos
Los alumnos deben familiarizarse con los siguientes conceptos antes de trabajar con este tutorial:
Estadística Distribuciones de probabilidad y principio del análisis bayesiano.
Teoría epidémica Número de reproducción efectiva.
Ciencia de los datos Transformación y visualización de datos. Puedes revisar el episodio en Agregar y visualizar datos de incidencia.
Recordatorio: el Número de Reproducción Efectiva, \(R_t\)
El número básico de reproducción, \(R_0\) es el número medio de casos causados por un individuo infeccioso en una población totalmente susceptible.
Pero en un brote en curso, la población no permanece totalmente susceptible, ya que los que se recuperan de la infección suelen ser inmunes. Además, puede haber cambios de comportamiento u otros factores que afecten la transmisión. Por lo tanto, cuando nos interesa controlar los cambios en la transmisión, es más importante tener en cuenta el valor del número de reproducción efectiva, \(R_t\) y el número medio de casos causados por un individuo infeccioso en la población en el momento \(t\).
Introducción
La intensidad de la transmisión de un brote se cuantifica mediante dos métricas clave: el número de reproducción, que informa sobre la fuerza de la transmisión indicando cuántos casos nuevos se esperan de cada caso existente; y la tasa de crecimiento que informa sobre la velocidad de la transmisión, indicando la rapidez con que el brote se propaga o disminuye (tiempo de duplicación/desaparición) dentro de una población. Para más detalles sobre la distinción entre velocidad y fuerza de transmisión y las implicaciones para el control, revisa Dushoff y Park, 2021.
Para estimar estas métricas clave utilizando datos de casos, debemos tener en cuenta los retrasos entre la fecha de las infecciones y la fecha de los casos notificados. En una situación de brote, normalmente sólo se dispone de datos sobre las fechas notificadas, por lo que debemos utilizar métodos de estimación para tener en cuenta estos retrasos cuando intentemos comprender los cambios en la transmisión a lo largo del tiempo.
En los próximos tutoriales nos centraremos en cómo utilizar las funciones de EpiNow2 para estimar las métricas de transmisión de los datos de casos. No cubriremos el trasfondo teórico de los modelos ni el marco de inferencia; para más detalles sobre estos conceptos, consulta la viñeta.
En este tutorial vamos a aprender a utilizar el paquete
EpiNow2 para estimar el número de reproducción variable
en el tiempo. Obtendremos los datos de entrada de
incidence2. Utilizaremos el paquete tidyr
y dplyr para ordenar algunas de sus salidas,
ggplot2 para visualizar la distribución de casos, y el
operador tubería %>% para conectar algunas de sus
funciones, así que también llamaremos al paquete
tidyverse:
R
library(EpiNow2)
library(incidence2)
library(tidyverse)
El doble punto
El doble punto :: en R te permite llamar a una función
específica de un paquete sin cargar todo el paquete en el entorno
actual.
Por ejemplo dplyr::filter(data, condition) utiliza la
función filter() del paquete dplyr.
Esto nos ayuda a recordar las funciones del paquete y a evitar conflictos de espacio de nombres.
Este tutorial muestra el uso de la función epinow() para
estimar el número de reproducción variable en el tiempo y los tiempos de
infección, las entradas necesarias para el modelo y las limitaciones de
su resultado.
Inferencia bayesiana
El paquete R EpiNow2 utiliza inferencia bayesiana para estimar las
cifras de reproducción y los tiempos de infección basándose en las
fechas de notificación.
En la inferencia bayesiana, utilizamos el conocimiento previo (distribuciones previas) con los datos (en una función de verosimilitud) para hallar la probabilidad posterior.
Probabilidad posterior \(\propto\) verosimilitud \(\times\) probabilidad previa
Consulta la distribución de probabilidad a priori y la probabilidad posterior.
En la “Expected change in daily cases”
por “la probabilidad posterior de que \(R_t
< 1\)”, nos referimos específicamente a la área bajo la
curva de distribución de probabilidad po.
Distribuciones de retrasos y datos de casos
Datos de casos
Para explorar las funciones de EpiNow2 utilizaremos los
datos del brote del inicio de la pandemia COVID-19 del Reino Unido. Los
datos están disponibles en el paquete R incidence2.
R
dplyr::as_tibble(incidence2::covidregionaldataUK)
SALIDA
# A tibble: 6,370 × 13
date region region_code cases_new cases_total deaths_new deaths_total
<date> <chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 2020-01-30 East Mi… E12000004 NA NA NA NA
2 2020-01-30 East of… E12000006 NA NA NA NA
3 2020-01-30 England E92000001 2 2 NA NA
4 2020-01-30 London E12000007 NA NA NA NA
5 2020-01-30 North E… E12000001 NA NA NA NA
6 2020-01-30 North W… E12000002 NA NA NA NA
7 2020-01-30 Norther… N92000002 NA NA NA NA
8 2020-01-30 Scotland S92000003 NA NA NA NA
9 2020-01-30 South E… E12000008 NA NA NA NA
10 2020-01-30 South W… E12000009 NA NA NA NA
# ℹ 6,360 more rows
# ℹ 6 more variables: recovered_new <dbl>, recovered_total <dbl>,
# hosp_new <dbl>, hosp_total <dbl>, tested_new <dbl>, tested_total <dbl>Para utilizar los datos, debemos darles formato para que tengan dos columnas:
-
date: la fecha (para validar si un objeto es de tipo fecha ver?is.Date()), -
confirmnúmero de casos confirmados en esa fecha.
Utilicemos tidyr y incidence2 para ello:
R
cases <- incidence2::covidregionaldataUK %>%
# use {tidyr} to preprocess missing values
tidyr::replace_na(base::list(cases_new = 0)) %>%
# use {incidence2} to compute the daily incidence
incidence2::incidence(
date_index = "date",
counts = "cases_new",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable)
Con incidence2::incidence() agregamos casos en distintos
tiempos intervalos (es decir, días, semanas o meses) o por
grupo categorías. También podemos tener fechas completas para
todo el rango de fechas por categoría de grupo utilizando
complete_dates = TRUE Explora más adelante la incidence2::incidence()
manual de referencia
Podemos obtener un objeto similar a cases de la tabla de
datos (data.frame)
incidence2::covidregionaldataUK utilizando las siguientes
funciones del paquete dplyr:
R
incidence2::covidregionaldataUK %>%
dplyr::select(date, cases_new) %>%
dplyr::group_by(date) %>%
dplyr::summarise(confirm = sum(cases_new, na.rm = TRUE)) %>%
dplyr::ungroup()
Sin embargo, la función incidence2::incidence() contiene
argumentos prácticos como complete_dates que facilitan la
obtención de un objeto de incidencia con el mismo rango de fechas para
cada agrupación sin necesidad de líneas de código adicionales ni de un
paquete de series temporales.
Hay datos de casos disponibles para 490 días, pero en una situación de brote es probable que sólo tuviéramos acceso al principio de este conjunto de datos. Por lo tanto, suponemos que sólo disponemos de los primeros 90 días de estos datos.
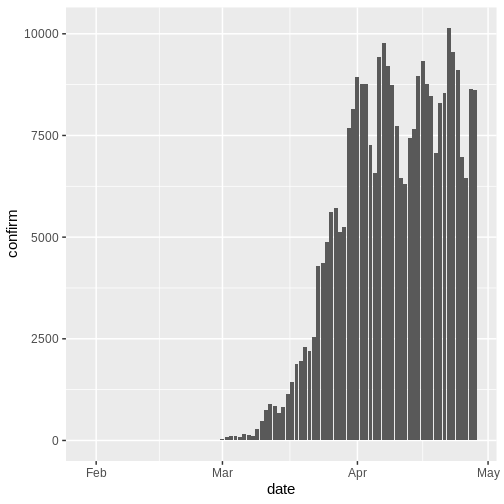
Distribuciones de retraso
Suponemos que hay retrasos desde el momento de la infección hasta el momento en que se notifica un caso. Especificamos estos retrasos como distribuciones para tener en cuenta la incertidumbre en las diferencias a nivel individual. El retraso puede consistir en múltiples tipos de retrasos/procesos. Un retraso típico desde el momento de la infección hasta la notificación del caso puede consistir en:
tiempo desde la infección hasta la aparición de los síntomas (el período de incubación) + tiempo desde el inicio de los síntomas hasta la notificación del caso (el tiempo de notificación).
La distribución del retraso para cada uno de estos procesos puede
estimarse a partir de los datos u obtenerse de la bibliografía. Podemos
expresar la incertidumbre sobre cuáles son los parámetros correctos de
las distribuciones, suponiendo que las distribuciones tienen parámetros
fijos (_fixed) o si tienen parámetros
variables (_variable). Para entender la
diferencia entre distribuciones fijas y
variables, consideremos el periodo de incubación.
Retrasos y datos
El número de retrasos y su tipo son una entrada flexible que depende de los datos. Los siguientes ejemplos muestran cómo se pueden especificar los retrasos para distintas fuentes de datos:
| Fuente de datos | Retraso(s) |
|---|---|
| Hora de inicio de los síntomas | Periodo de incubación |
| Hora del informe del caso | Periodo de incubación + tiempo desde el inicio de los síntomas hasta la notificación del caso |
| Tiempo de hospitalización | Periodo de incubación + tiempo desde el inicio de los síntomas hasta la hospitalización |
Distribución del periodo de incubación
La distribución del periodo de incubación de muchas enfermedades
suele obtenerse de la bibliografía. El paquete
{epiparameter} contiene una biblioteca de parámetros
epidemiológicos de distintas enfermedades obtenidos de la
literatura.
Especificamos una distribución gamma (fija) con media \(\mu = 4\) y desviación estándar \(\sigma= 2\) (forma = \(4\), escala = \(1\)) mediante la función
Gamma() de la siguiente manera:
R
incubation_period_fixed <- EpiNow2::Gamma(
mean = 4,
sd = 2,
max = 20
)
incubation_period_fixed
SALIDA
- gamma distribution (max: 20):
shape:
4
rate:
1El argumento max es el valor máximo que puede tomar la
distribución, en este ejemplo 20 días.
¿Por qué una distribución gamma?
El periodo de incubación debe tener un valor positivo. Por lo tanto, tenemos que especificar una distribución en EpiNow2 que sea sólo para valores positivos.
Gamma() admite distribuciones Gamma y
LogNormal() Distribuciones logarítmicas normales, que son
distribuciones sólo para valores positivos.
Para todos los tipos de retraso, tendremos que utilizar distribuciones sólo para valores positivos: ¡no queremos incluir retrasos de días negativos en nuestro análisis!
Incluyendo la incertidumbre de distribución
Para especificar una distribución variable, incluimos la incertidumbre en torno a la media \(\mu\) y la desviación estándar \(\sigma\) de nuestra distribución gamma. Si nuestra distribución del periodo de incubación tiene una media \(\mu\) y una desviación estándar \(\sigma\) entonces suponemos que la media (\(\mu\)) sigue una distribución Normal con desviación estándar \(\sigma_{\mu}\):
\[\mbox{Normal}(\mu,\sigma_{\mu}^2)\]
y una desviación estándar (\(\sigma\)) sigue una distribución Normal con desviación estándar \(\sigma_{\sigma}\):
\[\mbox{Normal}(\sigma,\sigma_{\sigma}^2).\]
Lo especificamos utilizando Normal() para cada
argumento: la media (\(\mu=4\) con
\(\sigma_{\mu}=0.5\)) y la desviación
estándar (\(\sigma=2\) con \(\sigma_{\sigma}=0.5\)).
R
incubation_period_variable <- EpiNow2::Gamma(
mean = EpiNow2::Normal(mean = 4, sd = 0.5),
sd = EpiNow2::Normal(mean = 2, sd = 0.5),
max = 20
)
incubation_period_variable
SALIDA
- gamma distribution (max: 20):
shape:
- normal distribution:
mean:
4
sd:
0.61
rate:
- normal distribution:
mean:
1
sd:
0.31Retrasos en los informes
Tras el periodo de incubación, habrá un retraso adicional desde el inicio de los síntomas hasta la notificación del caso: el retraso de notificación. Podemos especificarlo como una distribución fija o variable, o estimar una distribución a partir de los datos.
Al especificar una distribución, es útil visualizar la densidad de probabilidad para ver el pico y la dispersión de la distribución, en este caso utilizaremos una log normal logarítmica normal.
Si queremos suponer que la media del retraso en la notificación es de 2 días (con una desviación estándar de 1 día), escribimos:
Utilizando la media y la desviación estándar de la distribución log
normal, podemos especificar una distribución fija o variable utilizando
LogNormal() como antes:
R
reporting_delay_variable <- EpiNow2::LogNormal(
mean = EpiNow2::Normal(mean = 2, sd = 0.5),
sd = EpiNow2::Normal(mean = 1, sd = 0.5),
max = 10
)
Utilizando epiparameter::epidist() podemos crear una
distribución personalizada. La distribución log normal tendrá el
siguiente aspecto:
R
library(epiparameter)
R
epiparameter::epidist(
disease = "covid",
epi_dist = "reporting delay", # retraso del reporte
prob_distribution = "lnorm",
summary_stats = epiparameter::create_epidist_summary_stats(
mean = 2,
sd = 1
)
) %>%
plot()
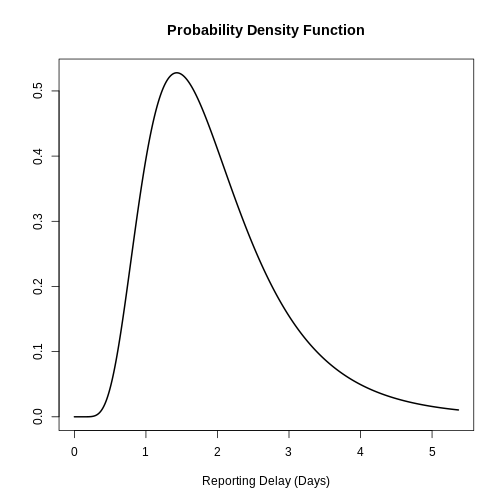
Podemos trazar distribuciones simples y combinadas generadas por
EpiNow2 utilizando plot(). Combinemos en un
gráfico el retraso desde la infección hasta la notificación, que incluye
el periodo de incubación y el retraso en la notificación:
R
plot(incubation_period_variable + reporting_delay_variable)
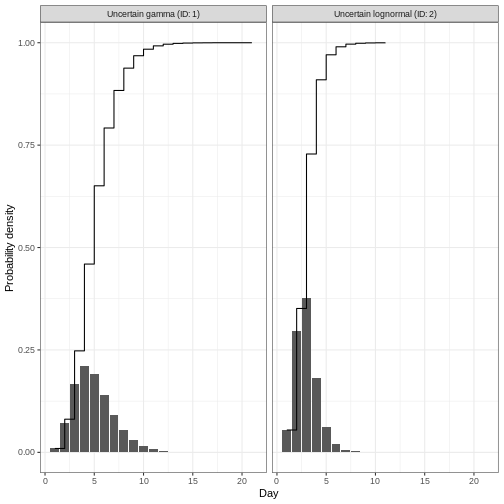
Aviso
Si disponemos de datos sobre el tiempo transcurrido entre el inicio
de los síntomas y la notificación, podemos utilizar la función
estimate_delay() para estimar una distribución log normal a
partir de un vector de retrasos. El siguiente código muestra cómo
utilizar estimate_delay() con datos sintéticos de
retrasos.
R
delay_data <- rlnorm(500, log(5), 1) # datos de retraso sintéticos
reporting_delay <- EpiNow2::estimate_delay(
delay_data,
samples = 1000,
bootstraps = 10
)
Tiempo de generación
También debemos especificar una distribución para el tiempo de generación. Aquí utilizaremos una distribución log normal con media 3.6 y desviación estándar 3.1 (Ganyani et al. 2020).
R
generation_time_variable <- EpiNow2::LogNormal(
mean = EpiNow2::Normal(mean = 3.6, sd = 0.5),
sd = EpiNow2::Normal(mean = 3.1, sd = 0.5),
max = 20
)
Estimaciones de hallazgos
La función epinow() es una envoltura de la función
estimate_infections() utilizada para estimar los casos por
fecha de infección. La distribución del tiempo de generación y las
distribuciones del retraso deben pasarse utilizando las funciones
generation_time_opts() y delay_opts()
respectivamente.
Hay muchas otras entradas que se pueden pasar a epinow()
ver ?EpiNow2::epinow() para más detalles. Una entrada
opcional es especificar una log normal para el número de
reproducción efectivo \(R_t\) al inicio
del brote. Especificamos una media de 2 días y una desviación estándar
de 2 días como argumentos de prior dentro de
rt_opts():
R
# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = base::list(mean = 2, sd = 2))
Inferencia bayesiana con Stan
La inferencia bayesiana se realiza utilizando métodos MCMC con el
programa Stan. Hay una serie de
entradas por defecto para las funciones Stan, incluido el número de
cadenas y el número de muestras por cadena (ver
?EpiNow2::stan_opts()).
Para reducir el tiempo de cálculo, podemos ejecutar las cadenas en
paralelo. Para ello, debemos establecer el número de núcleos que se van
a utilizar. Por defecto, se ejecutan 4 cadenas MCMC (ver
stan_opts()$chains), por lo que podemos establecer un
número igual de núcleos para que se utilicen en paralelo de la siguiente
manera:
R
withr::local_options(base::list(mc.cores = 4))
Para averiguar el número máximo de núcleos disponibles en tu máquina,
utiliza parallel::detectCores().
Lista de verificación
Nota: En el siguiente código _fixed se
utilizan distribuciones en lugar de _variable
(distribuciones de retraso con incertidumbre). Esto se hace para
acelerar el tiempo de cálculo. En general, se recomienda utilizar
distribuciones variables que tengan en cuenta la incertidumbre
adicional.
R
# alternativas: distribuciones con parámetros fijos
generation_time_fixed <- EpiNow2::LogNormal(
mean = 3.6,
sd = 3.1,
max = 20
)
reporting_delay_fixed <- EpiNow2::LogNormal(
mean = 2,
sd = 1,
max = 10
)
Ahora estás listo para ejecutar EpiNow2::epinow() para
estimar el número de reproducción variable en el tiempo durante los
primeros 90 días:
R
reported_cases <- cases %>%
dplyr::slice_head(n = 90)
R
estimates <- EpiNow2::epinow(
# casos
data = reported_cases,
# retrasos
generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
# prior
rt = rt_prior
)
No esperes a que esto continúe
Para efectos de este tutorial, podemos utilizar opcionalmente
EpiNow2::stan_opts() para reducir el tiempo de cálculo.
Podemos especificar un número fijo de samples = 1000 y
chains = 3 al argumento stan de la función
EpiNow2::epinow(). Esperamos que esto lleve aproximadamente
3 minutos.
R
# puedes adicionar el argumento `stan`
EpiNow2::epinow(
...,
stan = EpiNow2::stan_opts(samples = 1000, chains = 3)
)
Recuerda: Utilizar un número adecuado de muestras y cadenas es crucial para garantizar la convergencia y obtener estimaciones fiables en los cálculos bayesianos con Stan. Los resultados más precisos se obtienen a costa de la velocidad.
Resultados
Podemos extraer y visualizar estimaciones del número de reproducción efectivo a lo largo del tiempo:
R
estimates$plots$R
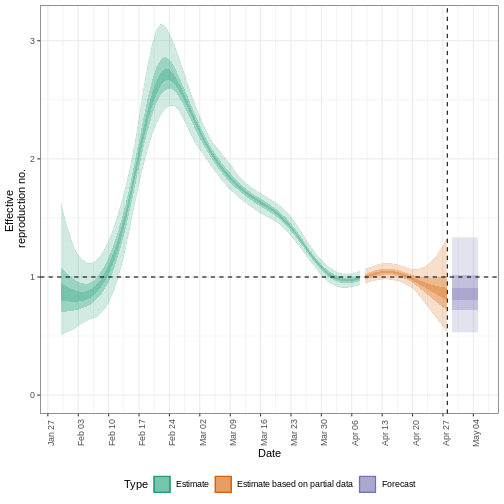
La incertidumbre de las estimaciones aumenta con el tiempo. Esto se debe a que las estimaciones se basan en datos del pasado, dentro de los periodos de retraso. Esta diferencia de incertidumbre se clasifica en Estimación (verde) utiliza todos los datos y Estimación basada en datos parciales (naranja) estimaciones que se basan en menos datos (porque es más probable que las infecciones que se produjeron en su momento no se hayan observado todavía), por este motivo, tienen intervalos cada vez más amplios hacia la fecha del último punto de datos. Por último, el Pronóstico (morado) es una proyección a futuro.
También podemos visualizar la estimación de la tasa de crecimiento a lo largo del tiempo:
R
estimates$plots$growth_rate
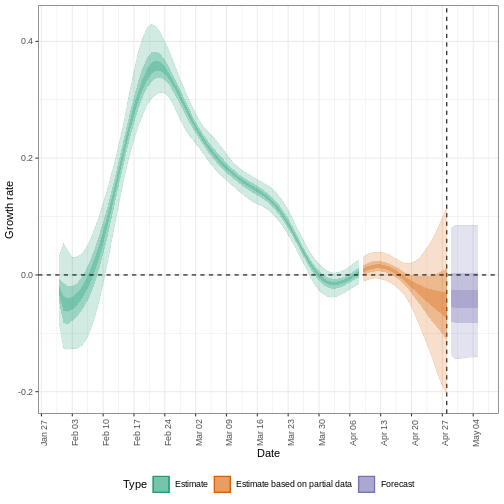
Para extraer un resumen de las métricas clave de transmisión en la última fecha de los datos:
R
summary(estimates)
SALIDA
measure estimate
<char> <char>
1: New infections per day 6476 (2738 -- 13517)
2: Expected change in daily reports Likely decreasing
3: Effective reproduction no. 0.87 (0.51 -- 1.3)
4: Rate of growth -0.046 (-0.22 -- 0.11)
5: Doubling/halving time (days) -15 (6.4 -- -3.2)Como estas estimaciones se basan en datos parciales, tienen un amplio intervalo de incertidumbre.
Del resumen de nuestro análisis se desprende que el cambio esperado en los casos diarios es de con la estimación de nuevos casos confirmados .
El número de reproducción efectivo \(R_t\) estimado (en la última fecha de los datos) es 0.87 (0.51 – 1.3).
La tasa de crecimiento exponencial del número de casos es -0.046 (-0.22 – 0.11).
El tiempo de duplicación (el tiempo que tarda en duplicarse el número de casos) es -15 (6.4 – -3.2).
Expected change in daily cases
Un factor que describe el cambio esperado en los casos diarios, basado en la probabilidad posterior de que \(R_t < 1\).
| Probabilidad (\(p\)) | Cambio esperado |
|---|---|
| \(p < 0,05\) | Aumentando |
| \(0,05 \leq p< 0,4\) | Probable aumento |
| \(0,4 \leq p< 0,6\) | Estable |
| \(0,6 \leq p < 0,95\) | Probable disminución |
| \(0,95 \leq p \leq 1\) | En disminución |
Cuantificar la heterogeneidad geográfica
Los datos del brote del inicio de la pandemia COVID-19 del Reino Unido del paquete R incidence2 incluyen la región en la que se registraron los casos. Para encontrar estimaciones regionales del número de reproducción efectiva y de casos, debemos dar formato a los datos para que tengan tres columnas:
-
date: la fecha. -
region: la región. -
confirm: número de casos confirmados para una región en una fecha determinada.
R
regional_cases <- incidence2::covidregionaldataUK %>%
# usar {tidyr} para pre-procesar los valores faltantes
tidyr::replace_na(base::list(cases_new = 0)) %>%
# usar {incidence2} para convertir datos agregados en datos de incidencia
incidence2::incidence(
date_index = "date",
groups = "region",
counts = "cases_new",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable)
# mantener las primeras 90 fechas para todas las regiones
# obtener el vector de las primeras 90 fechas
date_range <- regional_cases %>%
dplyr::distinct(date) %>%
# desde {incidence2}, las fechas ya están ordenadas en orden ascendente
dplyr::slice_head(n = 90) %>%
dplyr::pull(date)
# filtrar las fechas en la variable date_range
regional_cases <- regional_cases %>%
dplyr::filter(magrittr::is_in(x = date, table = date_range))
dplyr::as_tibble(regional_cases)
SALIDA
# A tibble: 1,170 × 3
date region confirm
<date> <chr> <dbl>
1 2020-01-30 East Midlands 0
2 2020-01-30 East of England 0
3 2020-01-30 England 2
4 2020-01-30 London 0
5 2020-01-30 North East 0
6 2020-01-30 North West 0
7 2020-01-30 Northern Ireland 0
8 2020-01-30 Scotland 0
9 2020-01-30 South East 0
10 2020-01-30 South West 0
# ℹ 1,160 more rowsPara hallar las estimaciones regionales, utilizamos los mismos datos
que epinow() para la función
regional_epinow():
R
estimates_regional <- EpiNow2::regional_epinow(
# casos
data = regional_cases,
# retrasos
generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
# prior
rt = rt_prior
)
SALIDA
INFO [2024-11-19 01:34:09] Producing following optional outputs: regions, summary, samples, plots, latest
INFO [2024-11-19 01:34:09] Reporting estimates using data up to: 2020-04-28
INFO [2024-11-19 01:34:09] No target directory specified so returning output
INFO [2024-11-19 01:34:09] Producing estimates for: East Midlands, East of England, England, London, North East, North West, Northern Ireland, Scotland, South East, South West, Wales, West Midlands, Yorkshire and The Humber
INFO [2024-11-19 01:34:09] Regions excluded: none
INFO [2024-11-19 02:31:34] Completed regional estimates
INFO [2024-11-19 02:31:34] Regions with estimates: 13
INFO [2024-11-19 02:31:34] Regions with runtime errors: 0
INFO [2024-11-19 02:31:34] Producing summary
INFO [2024-11-19 02:31:34] No summary directory specified so returning summary output
INFO [2024-11-19 02:31:34] No target directory specified so returning timingsR
estimates_regional$summary$summarised_results$table
SALIDA
Region New infections per day
<char> <char>
1: East Midlands 346 (185 -- 618)
2: East of England 483 (258 -- 857)
3: England 3163 (1598 -- 5887)
4: London 291 (167 -- 486)
5: North East 239 (108 -- 493)
6: North West 515 (256 -- 938)
7: Northern Ireland 37 (15 -- 101)
8: Scotland 272 (108 -- 769)
9: South East 588 (300 -- 1099)
10: South West 469 (304 -- 726)
11: Wales 81 (46 -- 133)
12: West Midlands 202 (83 -- 451)
13: Yorkshire and The Humber 444 (224 -- 816)
Expected change in daily reports Effective reproduction no.
<fctr> <char>
1: Likely increasing 1.1 (0.77 -- 1.4)
2: Stable 1 (0.69 -- 1.3)
3: Likely decreasing 0.87 (0.58 -- 1.2)
4: Likely decreasing 0.89 (0.66 -- 1.2)
5: Likely decreasing 0.91 (0.59 -- 1.3)
6: Likely decreasing 0.87 (0.58 -- 1.2)
7: Likely decreasing 0.75 (0.43 -- 1.3)
8: Stable 0.95 (0.55 -- 1.7)
9: Stable 0.98 (0.65 -- 1.4)
10: Increasing 1.3 (1 -- 1.6)
11: Decreasing 0.7 (0.49 -- 0.94)
12: Likely decreasing 0.68 (0.38 -- 1.1)
13: Likely decreasing 0.93 (0.63 -- 1.3)
Rate of growth Doubling/halving time (days)
<char> <char>
1: 0.022 (-0.099 -- 0.12) 31 (5.6 -- -7)
2: -0.0081 (-0.14 -- 0.1) -86 (6.9 -- -5.1)
3: -0.046 (-0.18 -- 0.084) -15 (8.3 -- -3.8)
4: -0.029 (-0.13 -- 0.069) -24 (10 -- -5.2)
5: -0.027 (-0.17 -- 0.11) -26 (6.5 -- -4)
6: -0.043 (-0.17 -- 0.064) -16 (11 -- -4.1)
7: -0.071 (-0.24 -- 0.13) -9.7 (5.5 -- -2.9)
8: -0.0099 (-0.18 -- 0.21) -70 (3.2 -- -3.9)
9: -0.0096 (-0.15 -- 0.12) -73 (5.8 -- -4.6)
10: 0.079 (-0.0084 -- 0.17) 8.8 (4 -- -82)
11: -0.093 (-0.2 -- 0.0083) -7.5 (83 -- -3.5)
12: -0.11 (-0.28 -- 0.074) -6.1 (9.3 -- -2.5)
13: -0.028 (-0.17 -- 0.092) -24 (7.5 -- -4.2)R
estimates_regional$summary$plots$R
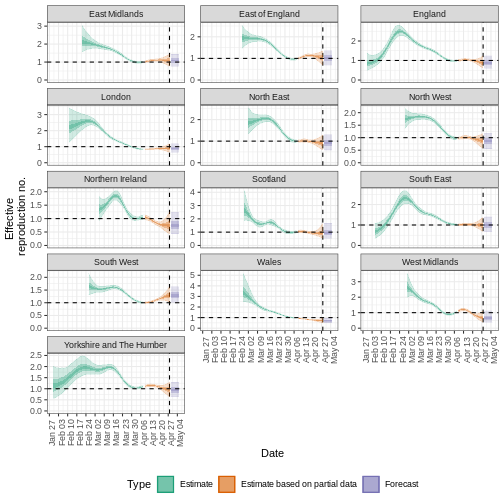
Resumen
EpiNow2 puede utilizarse para estimar las métricas de
transmisión a partir de los datos de casos en cualquier momento del
curso de un brote. La fiabilidad de estas estimaciones depende de la
calidad de los datos y de la elección adecuada de las distribuciones de
retraso. En el siguiente tutorial aprenderemos a hacer previsiones e
investigaremos algunas de las opciones adicionales de inferencia
disponibles en EpiNow2.
Puntos Clave
- Las métricas de transmisión pueden estimarse a partir de los datos del caso tras tener en cuenta los retrasos
- La incertidumbre puede tenerse en cuenta en las distribuciones de retrasos
