Access epidemiological delay distributions
Last updated on 2024-06-18 | Edit this page
Estimated time: 30 minutes
Overview
Questions
- How to get access to disease delay distributions from a pre-established database for use in analysis?
Objectives
- Get delays from a literature search database with
{epiparameter}. - Get distribution parameters and summary statistics of delay distributions.
Introduction
Infectious diseases follow an infection cycle, which usually includes the following phases: presymptomatic period, symptomatic period and recovery period, as described by their natural history. These time periods can be used to understand transmission dynamics and inform disease prevention and control interventions.
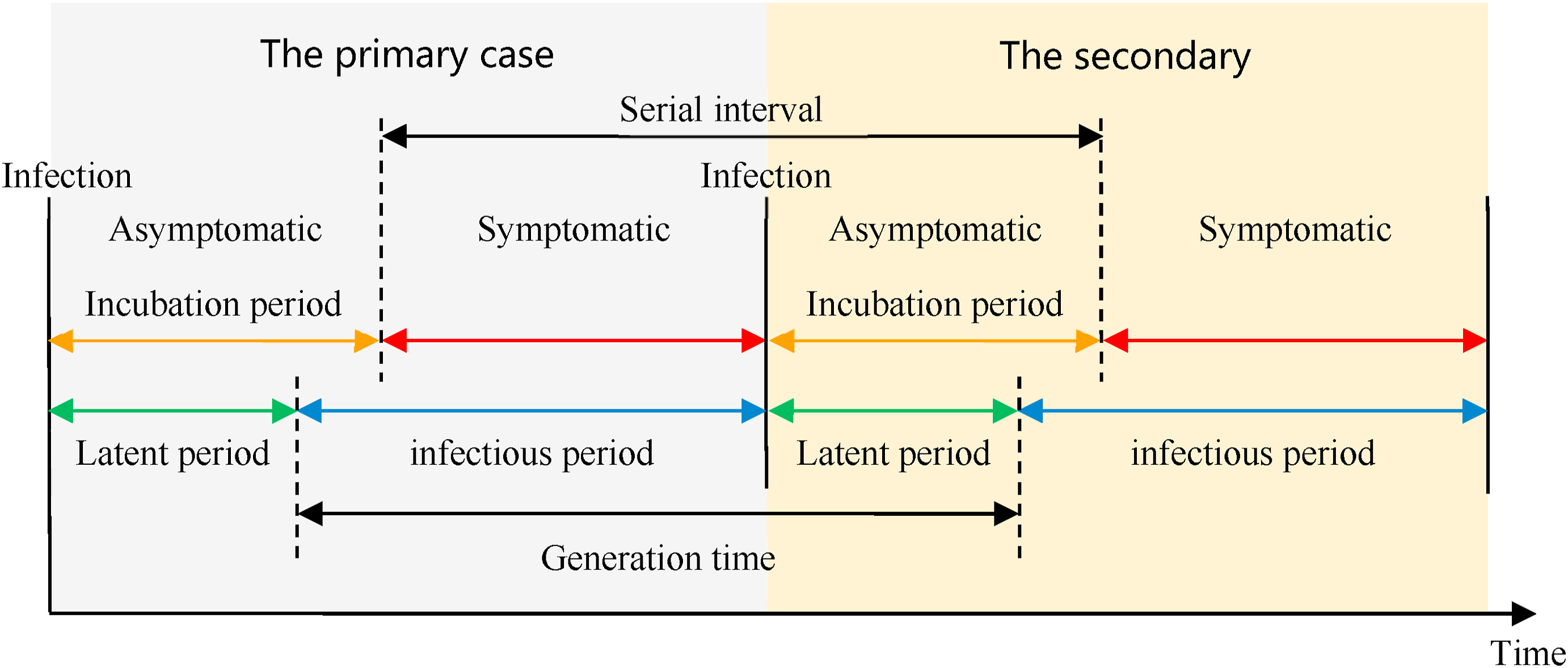
Definitions
Look at the glossary for the definitions of all the time periods of the figure above!
However, early in an epidemic, modelling efforts can be delayed by
the lack of a centralised resource that summarises input parameters for
the disease of interest (Nash et al., 2023).
Projects like {epiparameter} and {epireview}
are building online catalogues following literature synthesis protocols
that can help parametrise models by easily accessing a comprenhensive
library of previously estimated epidemiological parameters from past
outbreaks.
To exemplify how to use the {epiparameter} R package in
your analysis pipeline, our goal in this episode will be to access one
specific set of epidemiological parameters from the literature, instead
of copying-and-pasting them by hand, to plug them into an
EpiNow2 analysis workflow.
Let’s start loading the {epiparameter} package. We’ll
use the pipe %>% to connect some of their functions,
some tibble and dplyr functions, so let’s
also call to the tidyverse package:
R
library(epiparameter)
library(tidyverse)
The double-colon
The double-colon :: in R let you call a specific
function from a package without loading the entire package into the
current environment.
For example, dplyr::filter(data, condition) uses
filter() from the dplyr package.
This help us remember package functions and avoid namespace conflicts.
The problem
If we want to estimate the transmissibility of an infection, it’s
common to use a package such as EpiEstim or
EpiNow2. However, both require some epidemiological
information as an input. For example, in EpiNow2 we use
EpiNow2::Gamma() to specify a generation time as a
probability distribution adding its mean, standard
deviation (sd), and maximum value (max).
To specify a generation_time that follows a
Gamma distribution with mean \(\mu =
4\), standard deviation \(\sigma =
2\), and a maximum value of 20, we write:
R
generation_time <-
EpiNow2::Gamma(
mean = 4,
sd = 2,
max = 20
)
It is a common practice for analysts to manually search the available
literature and copy and paste the summary statistics or
the distribution parameters from scientific
publications. A challenge that is often faced is that the reporting of
different statistical distributions is not consistent across the
literature. {epiparameter}’s objective is to facilitate the
access to reliable estimates of distribution parameters for a range of
infectious diseases, so that they can easily be implemented in outbreak
analytic pipelines.
In this episode, we will access the summary statistics of
generation time for COVID-19 from the library of epidemiological
parameters provided by {epiparameter}. These metrics can be
used to estimate the transmissibility of this disease using
EpiNow2 in subsequent episodes.
Let’s start by looking at how many entries are available in the
epidemiological distributions database in
{epiparameter} using epidist_db() for the
epidemiological distribution epi_dist called generation
time with the string "generation":
R
epiparameter::epidist_db(
epi_dist = "generation"
)
OUTPUT
Returning 1 results that match the criteria (1 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionOUTPUT
Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Distribution: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull
Parameters:
shape: 2.360
scale: 3.180Currently, in the library of epidemiological parameters, we have one
"generation" time entry for Influenza. Instead, we can look
at the serial intervals for COVID-19. Let find
what we need to consider for this!
Generation time vs serial interval
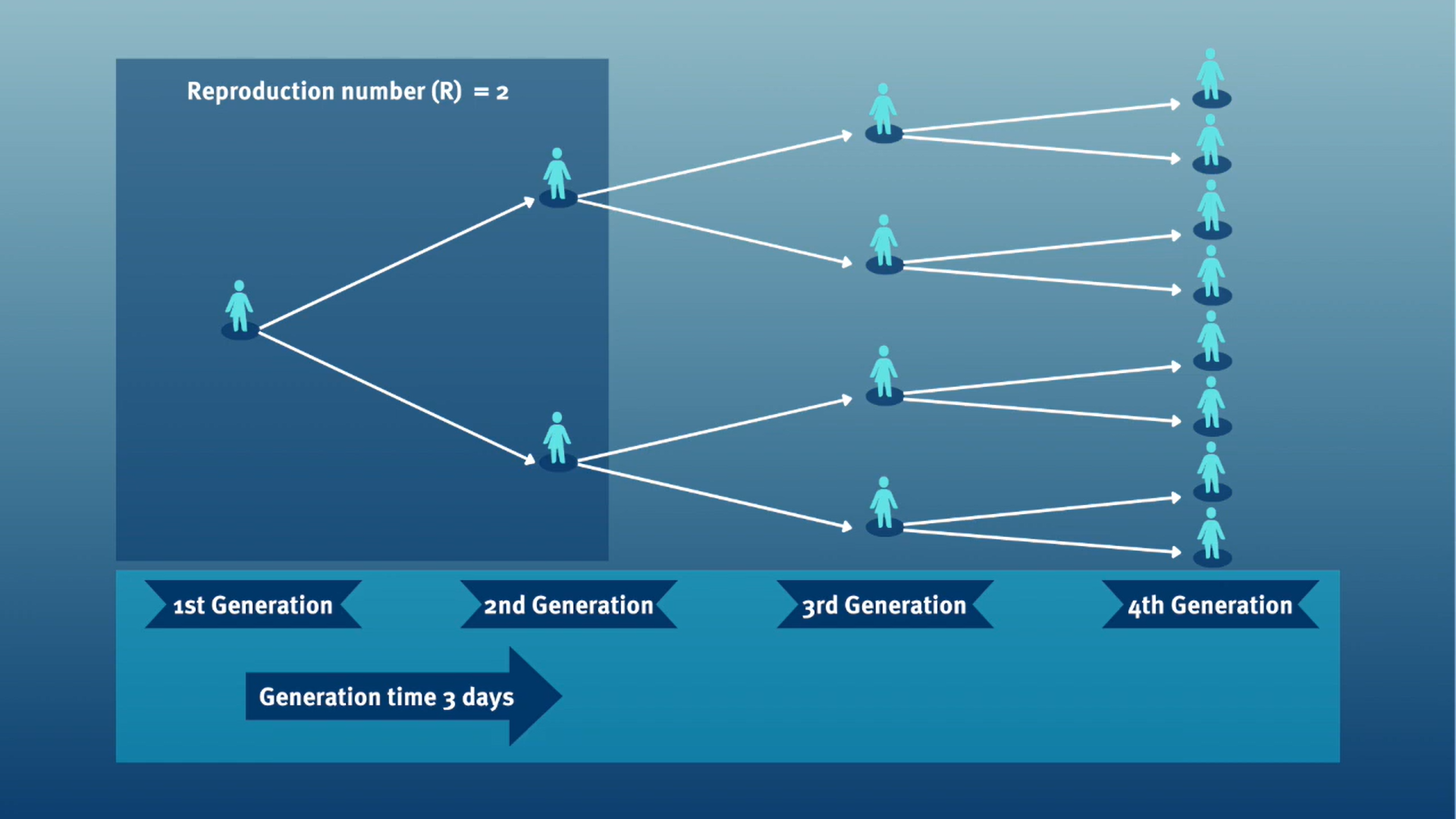
The generation time, jointly with the reproduction number (\(R\)), provide valuable insights on the strength of transmission and inform the implementation of control measures. Given a \(R>1\), the shorter the generation time, the earlier the incidence of disease cases will grow.
In calculating the effective reproduction number (\(R_{t}\)), the generation time distribution is often approximated by the serial interval distribution. This frequent approximation is because it is easier to observe and measure the onset of symptoms than the onset of infectiousness.
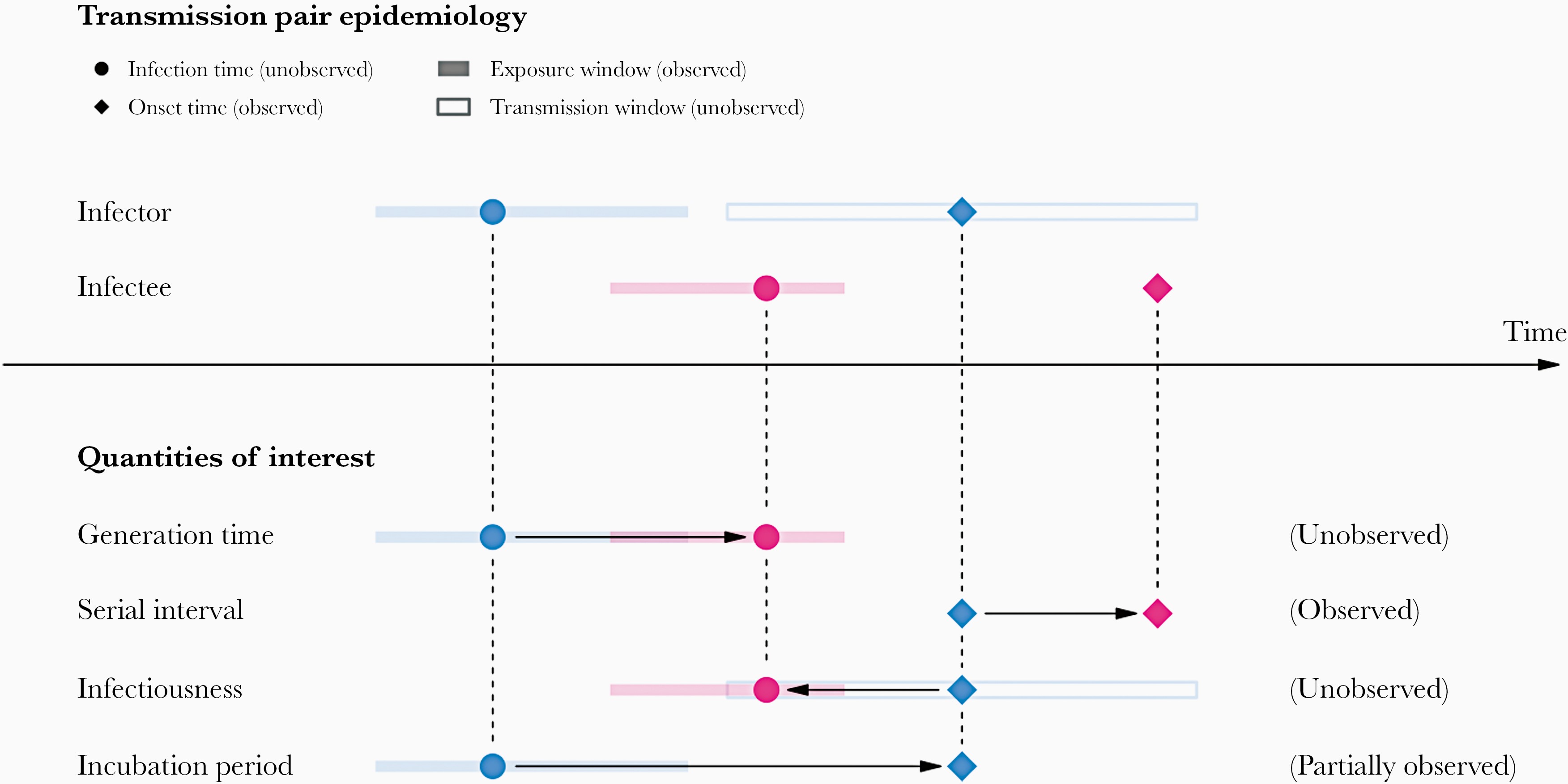
However, using the serial interval as an approximation of the generation time is primarily valid for diseases in which infectiousness starts after symptom onset (Chung Lau et al., 2021). In cases where infectiousness starts before symptom onset, the serial intervals can have negative values, which is the case for diseases with pre-symptomatic transmission (Nishiura et al., 2020).
From time periods to probability distributions.
When we calculate the serial interval, we see that not all case pairs have the same time length. We will observe this variability for any case pair and individual time period, including the incubation period and infectious period.
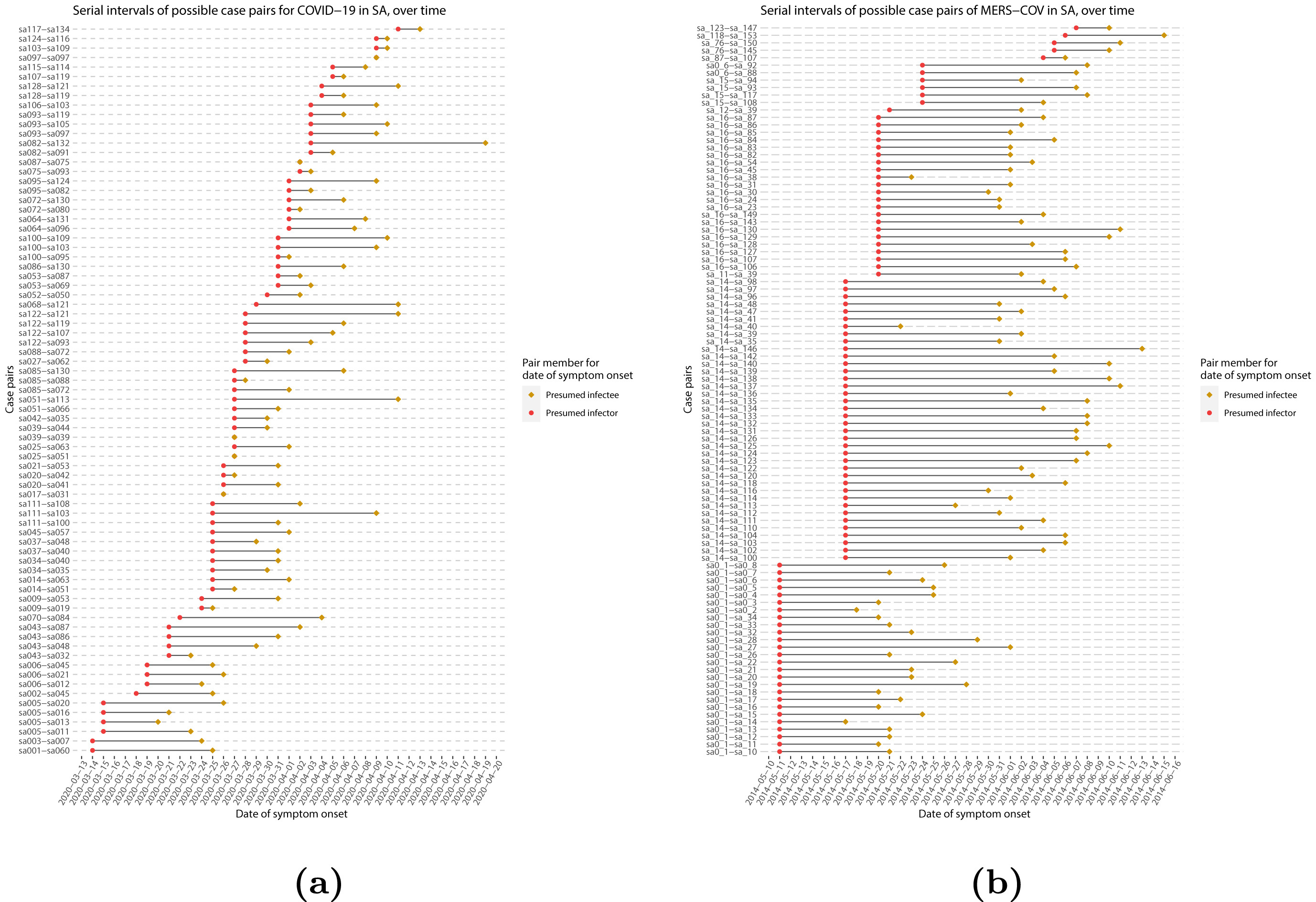
To summarise these data from individual and pair time periods, we can find the statistical distributions that best fit the data (McFarland et al., 2023).
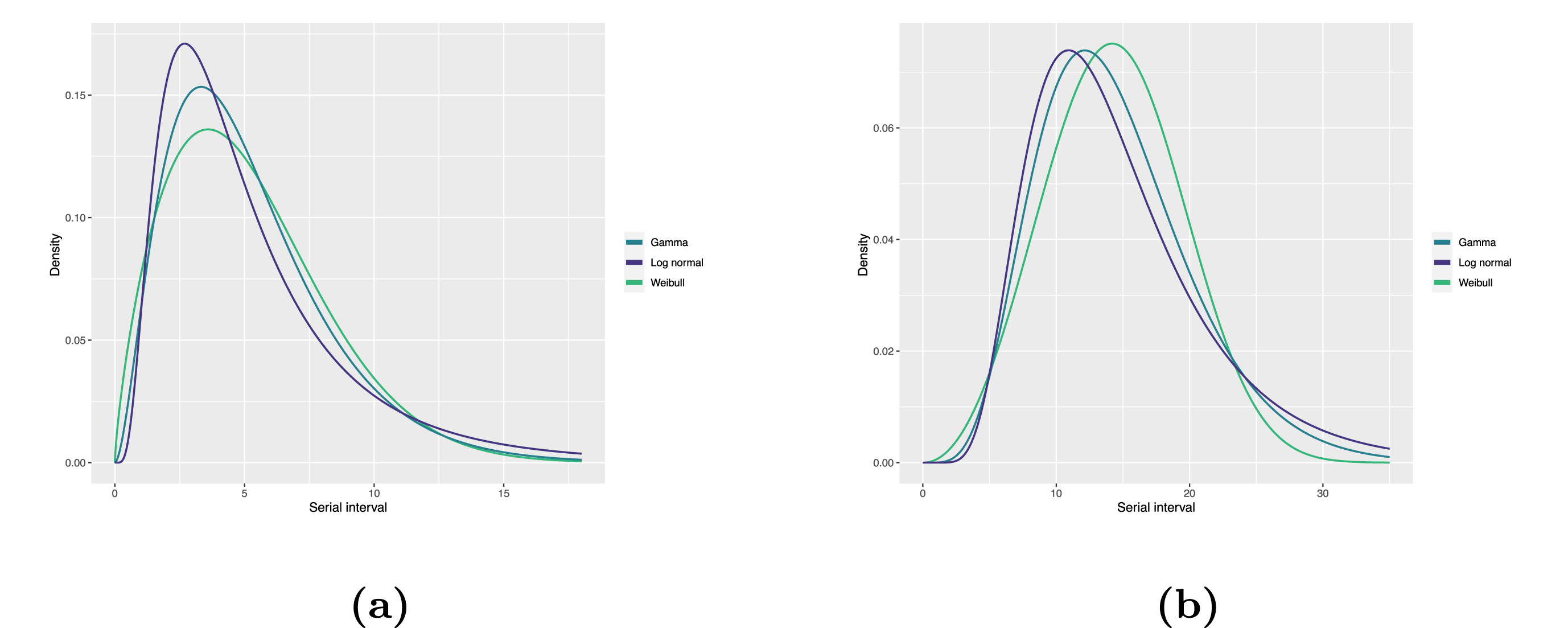
Statistical distributions are summarised in terms of their summary statistics like the location (mean and percentiles) and spread (variance or standard deviation) of the distribution, or with their distribution parameters that inform about the form (shape and rate/scale) of the distribution. These estimated values can be reported with their uncertainty (95% confidence intervals).
| Gamma | mean | shape | rate/scale |
|---|---|---|---|
| MERS-CoV | 14.13(13.9–14.7) | 6.31(4.88–8.52) | 0.43(0.33–0.60) |
| COVID-19 | 5.1(5.0–5.5) | 2.77(2.09–3.88) | 0.53(0.38–0.76) |
| Weibull | mean | shape | rate/scale |
|---|---|---|---|
| MERS-CoV | 14.2(13.3–15.2) | 3.07(2.64–3.63) | 16.1(15.0–17.1) |
| COVID-19 | 5.2(4.6–5.9) | 1.74(1.46–2.11) | 5.83(5.08–6.67) |
| Log normal | mean | mean-log | sd-log |
|---|---|---|---|
| MERS-CoV | 14.08(13.1–15.2) | 2.58(2.50–2.68) | 0.44(0.39–0.5) |
| COVID-19 | 5.2(4.2–6.5) | 1.45(1.31–1.61) | 0.63(0.54–0.74) |
Serial interval
Assume that COVID-19 and SARS have similar reproduction number values and that the serial interval approximates the generation time.
Given the serial interval of both infections in the figure below:
- Which one would be harder to control?
- Why do you conclude that?
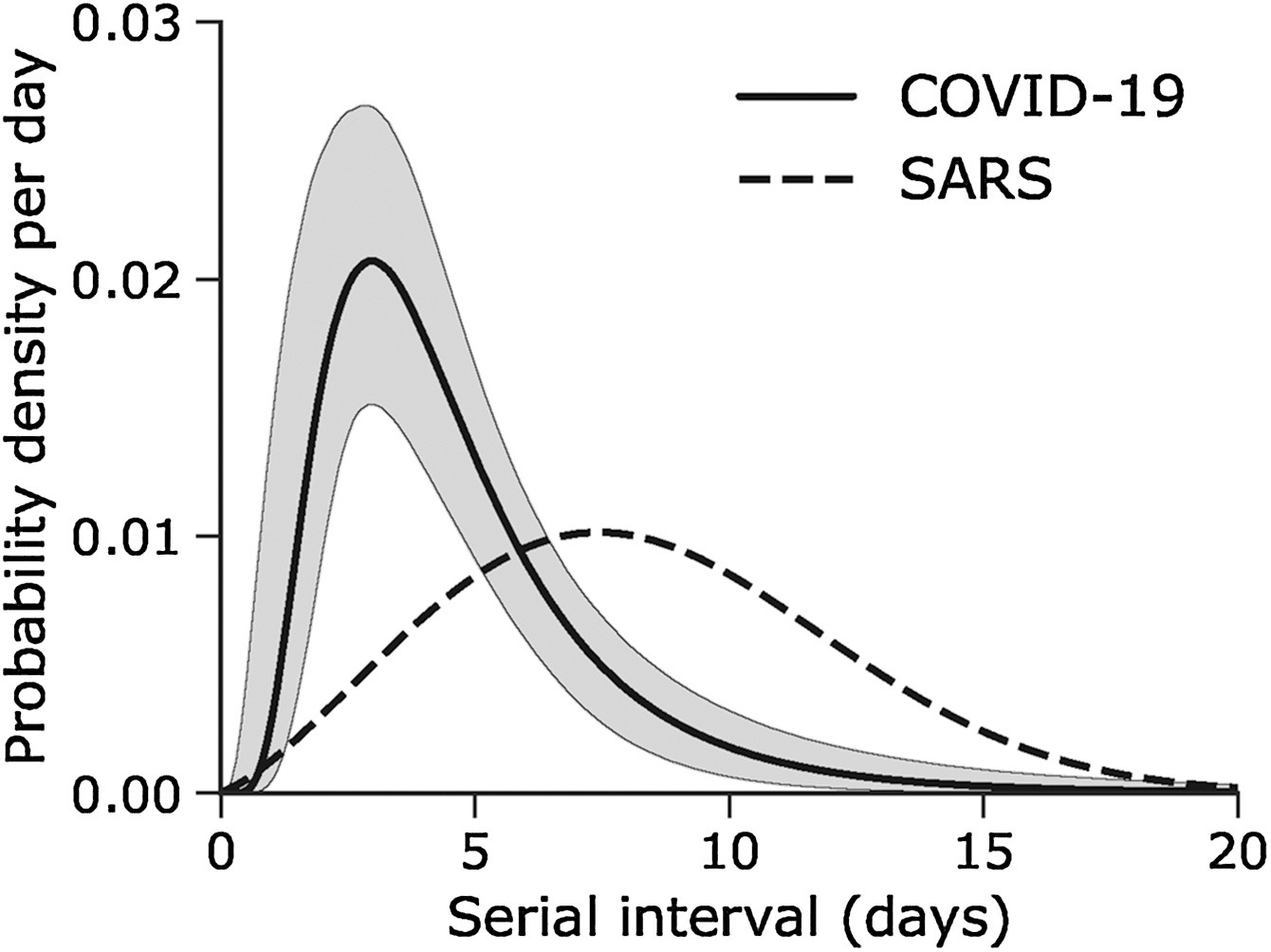
The peak of each curve can inform you about the location of the mean of each distribution. The larger the mean, the larger the serial interval.
Which one would be harder to control?
COVID-19
Why do you conclude that?
COVID-19 has the lowest mean serial interval. The approximate mean value for the serial interval of COVID-19 is around four days, and SARS is about seven days. Thus, COVID-19 will likely have newer generations in less time than SARS, assuming similar reproduction numbers.
The objective of the assessment above is to assess the interpretation of a larger or shorter generation time.
Choosing epidemiological parameters
In this section, we will use {epiparameter} to obtain
the serial interval for COVID-19, as an alternative to the generation
time.
Let’s ask now how many parameters we have in the epidemiological
distributions database (epidist_db()) with the
disease named covid-19. Run this locally!
R
epiparameter::epidist_db(
disease = "covid"
)
From the {epiparameter} package, we can use the
epidist_db() function to ask for any disease
and also for a specific epidemiological distribution
(epi_dist). Run this in your console:
R
epiparameter::epidist_db(
disease = "COVID",
epi_dist = "serial"
)
With this query combination, we get more than one delay distribution.
This output is an <epidist> class object.
CASE-INSENSITIVE
epidist_db is case-insensitive.
This means that you can use strings with letters in upper or lower case
indistinctly. Strings like "serial",
"serial interval" or "serial_interval" are
also valid.
As suggested in the outputs, to summarise an
<epidist> object and get the column names from the
underlying parameter database, we can add the
epiparameter::parameter_tbl() function to the previous code
using the pipe %>%:
R
epiparameter::epidist_db(
disease = "covid",
epi_dist = "serial"
) %>%
epiparameter::parameter_tbl()
OUTPUT
Returning 4 results that match the criteria (3 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionOUTPUT
# Parameter table:
# A data frame: 4 × 7
disease pathogen epi_distribution prob_distribution author year sample_size
<chr> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 COVID-19 SARS-CoV… serial interval <NA> Alene… 2021 3924
2 COVID-19 SARS-CoV… serial interval lnorm Nishi… 2020 28
3 COVID-19 SARS-CoV… serial interval weibull Nishi… 2020 18
4 COVID-19 SARS-CoV… serial interval norm Yang … 2020 131In the epiparameter::parameter_tbl() output, we can also
find different types of probability distributions (e.g., Log-normal,
Weibull, Normal).
{epiparameter} uses the base R naming
convention for distributions. This is why Log normal is
called lnorm.
Entries with a missing value (<NA>) in the
prob_distribution column are non-parameterised
entries. They have summary statistics but no probability distribution.
Compare these two outputs:
R
# get an <epidist> object
distribution <-
epiparameter::epidist_db(
disease = "covid",
epi_dist = "serial"
)
distribution %>%
# pluck the first entry in the object class <list>
pluck(1) %>%
# check if <epidist> object have distribution parameters
is_parameterised()
# check if the second <epidist> object
# have distribution parameters
distribution %>%
pluck(2) %>%
is_parameterised()
Parameterised entries have an Inference method
As detailed in ?is_parameterised, a parameterised
distribution is the entry that has a probability distribution associated
with it provided by an inference_method as shown in
metadata:
R
distribution[[1]]$metadata$inference_method
distribution[[2]]$metadata$inference_method
distribution[[4]]$metadata$inference_method
Find your delay distributions!
Take 2 minutes to explore the {epiparameter}
library.
Choose a disease of interest (e.g., Influenza, Measles, etc.) and a delay distribution (e.g., the incubation period, onset to death, etc.).
Find:
How many delay distributions are for that disease?
How many types of probability distribution (e.g., gamma, log normal) are for a given delay in that disease?
Ask:
Do you recognise the papers?
Should
{epiparameter}literature review consider any other paper?
The epidist_db() function with disease
alone counts the number of entries like:
- studies, and
- delay distributions.
The epidist_db() function with disease and
epi_dist gets a list of all entries with:
- the complete citation,
- the type of a probability distribution, and
- distribution parameter values.
The combo of epidist_db() plus
parameter_tbl() gets a data frame of all entries with
columns like:
- the type of the probability distribution per delay, and
- author and year of the study.
We choose to explore Ebola’s delay distributions:
R
# we expect 16 delays distributions for ebola
epiparameter::epidist_db(
disease = "ebola"
)
OUTPUT
Returning 17 results that match the criteria (17 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionOUTPUT
# List of 17 <epidist> objects
Number of diseases: 1
❯ Ebola Virus Disease
Number of epi distributions: 9
❯ hospitalisation to death ❯ hospitalisation to discharge ❯ incubation period ❯ notification to death ❯ notification to discharge ❯ offspring distribution ❯ onset to death ❯ onset to discharge ❯ serial interval
[[1]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Distribution: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom
Parameters:
mean: 1.500
dispersion: 5.100
[[2]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Distribution: incubation period
Study: Eichner M, Dowell S, Firese N (2011). "Incubation period of ebola
hemorrhagic virus subtype zaire." _Osong Public Health and Research
Perspectives_. doi:10.1016/j.phrp.2011.04.001
<https://doi.org/10.1016/j.phrp.2011.04.001>.
Distribution: lnorm
Parameters:
meanlog: 2.487
sdlog: 0.330
[[3]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Distribution: onset to death
Study: The Ebola Outbreak Epidemiology Team, Barry A, Ahuka-Mundeke S, Ali
Ahmed Y, Allarangar Y, Anoko J, Archer B, Abedi A, Bagaria J, Belizaire
M, Bhatia S, Bokenge T, Bruni E, Cori A, Dabire E, Diallo A, Diallo B,
Donnelly C, Dorigatti I, Dorji T, Waeber A, Fall I, Ferguson N,
FitzJohn R, Tengomo G, Formenty P, Forna A, Fortin A, Garske T,
Gaythorpe K, Gurry C, Hamblion E, Djingarey M, Haskew C, Hugonnet S,
Imai N, Impouma B, Kabongo G, Kalenga O, Kibangou E, Lee T, Lukoya C,
Ly O, Makiala-Mandanda S, Mamba A, Mbala-Kingebeni P, Mboussou F,
Mlanda T, Makuma V, Morgan O, Mulumba A, Kakoni P, Mukadi-Bamuleka D,
Muyembe J, Bathé N, Ndumbi Ngamala P, Ngom R, Ngoy G, Nouvellet P, Nsio
J, Ousman K, Peron E, Polonsky J, Ryan M, Touré A, Towner R, Tshapenda
G, Van De Weerdt R, Van Kerkhove M, Wendland A, Yao N, Yoti Z, Yuma E,
Kalambayi Kabamba G, Mwati J, Mbuy G, Lubula L, Mutombo A, Mavila O,
Lay Y, Kitenge E (2018). "Outbreak of Ebola virus disease in the
Democratic Republic of the Congo, April–May, 2018: an epidemiological
study." _The Lancet_. doi:10.1016/S0140-6736(18)31387-4
<https://doi.org/10.1016/S0140-6736%2818%2931387-4>.
Distribution: gamma
Parameters:
shape: 2.400
scale: 3.333
# ℹ 14 more elements
# ℹ Use `print(n = ...)` to see more elements.
# ℹ Use `parameter_tbl()` to see a summary table of the parameters.
# ℹ Explore database online at: https://epiverse-trace.github.io/epiparameter/dev/articles/database.htmlNow, from the output of epiparameter::epidist_db(), What
is an offspring
distribution?
We choose to find Ebola’s incubation periods. This output list all the papers and parameters found. Run this locally if needed:
R
epiparameter::epidist_db(
disease = "ebola",
epi_dist = "incubation"
)
We use parameter_tbl() to get a summary display of
all:
R
# we expect 2 different types of delay distributions
# for ebola incubation period
epiparameter::epidist_db(
disease = "ebola",
epi_dist = "incubation"
) %>%
parameter_tbl()
OUTPUT
Returning 5 results that match the criteria (5 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionOUTPUT
# Parameter table:
# A data frame: 5 × 7
disease pathogen epi_distribution prob_distribution author year sample_size
<chr> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 Ebola Vi… Ebola V… incubation peri… lnorm Eichn… 2011 196
2 Ebola Vi… Ebola V… incubation peri… gamma WHO E… 2015 1798
3 Ebola Vi… Ebola V… incubation peri… gamma WHO E… 2015 49
4 Ebola Vi… Ebola V… incubation peri… gamma WHO E… 2015 957
5 Ebola Vi… Ebola V… incubation peri… gamma WHO E… 2015 792We find two types of probability distributions for this query: log normal and gamma.
How does {epiparameter} do the collection and review of
peer-reviewed literature? We invite you to read the vignette on “Data
Collation and Synthesis Protocol”!
Select a single distribution
The epiparameter::epidist_db() function works as a
filtering or subset function. Let’s use the author argument
to filter Hiroshi Nishiura parameters:
R
epiparameter::epidist_db(
disease = "covid",
epi_dist = "serial",
author = "Hiroshi"
) %>%
epiparameter::parameter_tbl()
OUTPUT
Returning 2 results that match the criteria (2 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionOUTPUT
# Parameter table:
# A data frame: 2 × 7
disease pathogen epi_distribution prob_distribution author year sample_size
<chr> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 COVID-19 SARS-CoV… serial interval lnorm Nishi… 2020 28
2 COVID-19 SARS-CoV… serial interval weibull Nishi… 2020 18We still get more than one epidemiological parameter. We can set the
single_epidist argument to TRUE to only
one:
R
epiparameter::epidist_db(
disease = "covid",
epi_dist = "serial",
author = "Hiroshi",
single_epidist = TRUE
)
OUTPUT
Using Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>..
To retrieve the citation use the 'get_citation' functionOUTPUT
Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Distribution: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: lnorm
Parameters:
meanlog: 1.386
sdlog: 0.568How does ‘single_epidist’ works?
Looking at the help documentation for
?epiparameter::epidist_db():
- If multiple entries match the arguments supplied and
single_epidist = TRUE, then the parameterised<epidist>with the largest sample size will be returned. - If multiple entries are equal after this sorting, the first entry will be returned.
What is a parametrised <epidist>? Look at
?is_parameterised.
Let’s assign this <epidist> class object to the
covid_serialint object.
R
covid_serialint <-
epiparameter::epidist_db(
disease = "covid",
epi_dist = "serial",
author = "Nishiura",
single_epidist = TRUE
)
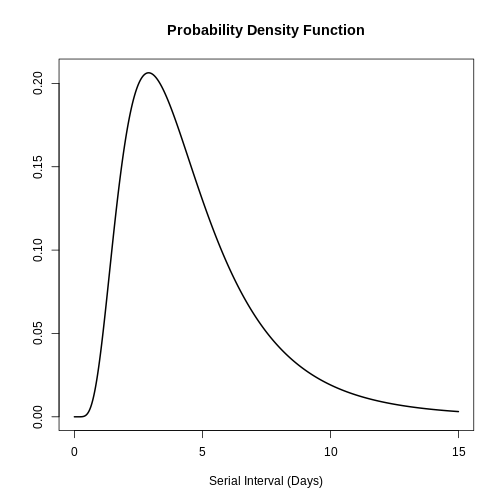
You can use plot() to <epidist>
objects to visualise:
- the Probability Density Function (PDF) and
- the Cumulative Distribution Function (CDF).
R
# plot <epidist> object
plot(covid_serialint)
With the day_range argument, you can change the length
or number of days in the x axis. Explore what this looks
like:
R
# plot <epidist> object
plot(covid_serialint, day_range = 0:20)
Extract the summary statistics
We can get the mean and standard deviation
(sd) from this <epidist> diving into the
summary_stats object:
R
# get the mean
covid_serialint$summary_stats$mean
OUTPUT
[1] 4.7Now, we have an epidemiological parameter we can reuse! Given that
the covid_serialint is a lnorm or log normal
distribution, we can replace the summary statistics
numbers we plug into the EpiNow2::LogNormal() function:
R
generation_time <-
EpiNow2::LogNormal(
mean = covid_serialint$summary_stats$mean, # replaced!
sd = covid_serialint$summary_stats$sd, # replaced!
max = 20
)
In the next episode we’ll learn how to use EpiNow2 to
correctly specify distributions, estimate transmissibility. Then, how to
use distribution functions to get a maximum value
(max) for EpiNow2::LogNormal() and use
{epiparameter} in your analysis.
Log normal distributions
If you need the log normal distribution parameters
instead of the summary statistics, we can use
epiparameter::get_parameters():
R
covid_serialint_parameters <-
epiparameter::get_parameters(covid_serialint)
covid_serialint_parameters
OUTPUT
meanlog sdlog
1.3862617 0.5679803 This gets a vector of class <numeric> ready to use
as input for any other package!
Challenges
R
# ebola serial interval
ebola_serial <-
epiparameter::epidist_db(
disease = "ebola",
epi_dist = "serial",
single_epidist = TRUE
)
OUTPUT
Using WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>..
To retrieve the citation use the 'get_citation' functionR
ebola_serial
OUTPUT
Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Distribution: serial interval
Study: WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>.
Distribution: gamma
Parameters:
shape: 2.188
scale: 6.490R
# get the sd
ebola_serial$summary_stats$sd
OUTPUT
[1] 9.6R
# get the sample_size
ebola_serial$metadata$sample_size
OUTPUT
[1] 305Try to visualise this distribution using plot().
Also, explore all the other nested elements within the
<epidist> object.
Share about:
- What elements do you find useful for your analysis?
- What other elements would you like to see in this object? How?
An interesting element is the method_assess nested
entry, which refers to the methods used by the study authors to assess
for bias while estimating the serial interval distribution.
R
covid_serialint$method_assess
OUTPUT
$censored
[1] TRUE
$right_truncated
[1] TRUE
$phase_bias_adjusted
[1] FALSEWe will explore these concepts following episodes!
Ebola’s severity parameter
A severity parameter like the duration of hospitalisation could add to the information needed about the bed capacity in response to an outbreak (Cori et al., 2017).
For Ebola:
- What is the reported point estimate of the mean duration of health care and case isolation?
An informative delay should measure the time from symptom onset to recovery or death.
Find a way to access the whole {epiparameter} database
and find how that delay may be stored. The parameter_tbl()
output is a dataframe.
R
# one way to get the list of all the available parameters
epidist_db(disease = "all") %>%
parameter_tbl() %>%
as_tibble() %>%
distinct(epi_distribution)
OUTPUT
Returning 122 results that match the criteria (99 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionOUTPUT
# A tibble: 12 × 1
epi_distribution
<chr>
1 incubation period
2 serial interval
3 generation time
4 onset to death
5 offspring distribution
6 hospitalisation to death
7 hospitalisation to discharge
8 notification to death
9 notification to discharge
10 onset to discharge
11 onset to hospitalisation
12 onset to ventilation R
ebola_severity <- epidist_db(
disease = "ebola",
epi_dist = "onset to discharge"
)
OUTPUT
Returning 1 results that match the criteria (1 are parameterised).
Use subset to filter by entry variables or single_epidist to return a single entry.
To retrieve the citation for each use the 'get_citation' functionR
# point estimate
ebola_severity$summary_stats$mean
OUTPUT
[1] 15.1Check that for some {epiparameter} entries you will also
have the uncertainty around the point estimate of each
summary statistic:
R
# 95% confidence intervals
ebola_severity$summary_stats$mean_ci
OUTPUT
[1] 95R
# limits of the confidence intervals
ebola_severity$summary_stats$mean_ci_limits
OUTPUT
[1] 14.6 15.6The distribution zoo
Explore this shinyapp called The Distribution Zoo!
Follow these steps to reproduce the form of the COVID serial interval
distribution from {epiparameter}
(covid_serialint object):
- Access the https://ben18785.shinyapps.io/distribution-zoo/ shiny app website,
- Go to the left panel,
- Keep the Category of distribution:
Continuous Univariate, - Select a new Type of distribution:
Log-Normal, - Move the sliders, i.e. the graphical control
element that allows you to adjust a value by moving a handle along a
horizontal track or bar to the
covid_serialintparameters.
Replicate these with the distribution object and all its
list elements: [[2]], [[3]], and
[[4]]. Explore how the shape of a distribution changes when
its parameters change.
Share about:
- What other features of the website do you find helpful?
In the context of user interfaces and graphical user interfaces (GUIs), like the Distribution Zoo shiny app, a slider is a graphical control element that allows users to adjust a value by moving a handle along a track or bar. Conceptually, it provides a way to select a numeric value within a specified range by visually sliding or dragging a pointer (the handle) along a continuous axis.
Key Points
- Use
{epiparameter}to access the literature catalogue of epidemiological delay distributions. - Use
epidist_db()to select single delay distributions. - Use
parameter_tbl()for an overview of multiple delay distributions. - Reuse known estimates for unknown disease in the early stage of an outbreak when no contact tracing data is available.
