Notes de l'instructeur

Instructor notes

Accéder aux distribution des délais épidémiologiques

Remarque de l'instructeur

Les premiers modèles pour COVID-19 utilisaient des paramètres d’autres coronavirus. https://www.thelancet.com/article/S1473-3099(20)30144-4/fulltext

Remarque de l'instructeur

L’objectif de l’évaluation ci-dessus est d’évaluer l’interprétation d’un temps de génération plus long ou plus court.

R

# ebola serial interval
ebola_serial <-
  epiparameter::epiparameter_db(
    disease = "ebola",
    epi_name = "serial",
    single_epiparameter = TRUE
  )

SORTIE

Using WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>..
To retrieve the citation use the 'get_citation' function

R

ebola_serial

SORTIE

Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Parameter: serial interval
Study: WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>.
Distribution: gamma (days)
Parameters:
  shape: 2.188
  scale: 6.490

R

# get the sd
ebola_serial$summary_stats$sd

SORTIE

[1] 9.6

R

# get the sample_size
ebola_serial$metadata$sample_size

SORTIE

[1] 305

Essayez de visualiser cette distribution en utilisant plot().

Explorez également tous les autres éléments imbriqués dans l’élément <epiparameter> à l’intérieur de l’objet.

Partagez sur :

Quels sont les éléments que vous trouvez utiles pour votre analyse ?
Quels autres éléments souhaiteriez-vous voir figurer dans cet objet ? Comment ?

Un élément intéressant est le method_assess qui fait référence aux méthodes utilisées par les auteurs de l’étude pour évaluer les biais lors de l’estimation de la distribution des intervalles sériels.

R

covid_serialint$method_assess

SORTIE

$censored
[1] TRUE

$right_truncated
[1] TRUE

$phase_bias_adjusted
[1] FALSE

Nous explorerons ces concepts au fil des épisodes !

Remarque de l'instructeur

Dans le contexte des interfaces utilisateurs et des interfaces graphiques (GUI), comme le Zoo de la distribution une application glissière est un élément de contrôle graphique qui permet aux utilisateurs d’ajuster une valeur en déplaçant une poignée le long d’une piste ou d’une barre. Conceptuellement, il permet de sélectionner une valeur numérique dans une plage spécifiée en faisant glisser visuellement un pointeur (la poignée) le long d’un axe continu.

Quantifier la transmission

Remarque de l'instructeur

Ce tutoriel illustre l’utilisation de epinow() pour estimer le nombre de reproduction et les durées d’infection variables dans le temps. Les étudiants doivent comprendre les données d’entrée nécessaires au modèle et les limites des résultats du modèle.

Remarque de l'instructeur

Faites référence à la distribution de probabilité a priori et à la probabilité a posteriori a posteriori.

Dans la “Expected change in reports”, l’appel par “la probabilité a posteriori que \(R_t < 1\)”nous nous référons spécifiquement à la aire sous la courbe de distribution de la probabilité a posteriori.

Utiliser les distributions de délais dans l'analyse

Remarque de l'instructeur

L’accès à la documentation de référence (fichiers d’aide) de ces fonctions est accessible avec la notation à trois doubles points : epiparameter:::

?epiparameter:::density.epiparameter()
?epiparameter:::cdf.epiparameter()
?epiparameter:::quantile.epiparameter()
?epiparameter:::generate.epiparameter()

Remarque de l'instructeur

We can stop the livecoding at this stage and move on with the practical.

Établir des prévisions à court terme

Estimation de la gravité d'une épidémie

Remarque de l'instructeur

Les périodes sont pertinentes : Période 1 – 15 jours où le RL est nul, ce qui indique qu’aucun décès n’a été signalé ; Période du 15 mars au 26 avril où le RL semble augmenter ; Période du 30 avril au 30 mai où l’estimation du RL se stabilise.

Remarque de l'instructeur

Vous trouverez plus d’informations concernant l’effet des délais dans l’estimation du RL dans cette section de la vignette de la librairie {cfr}.

Remarque de l'instructeur

Il y a presque un mois de différence.

Notez que l’estimation présente une incertitude considérable au début de la série chronologique. Après deux semaines, le RL corrigé au délai se rapproche de l’estimation globale du RL à la fin de l’épidémie.

Ce schéma est-il similaire à celui d’autres épidémies ? Nous vous invitons à utiliser les ensembles de données dans les défis de cet épisode pour le découvrir.

Tenir compte du phénomène hypercontagieux

Remarque de l'instructeur

R

# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
  R = ebola_offspring$estimate["mu"],
  k = ebola_offspring$estimate["size"],
  cluster_size = c(5, 10, 25)
)

SORTIE

          R         k prop_5 prop_10 prop_25
1 0.3675993 0.8539443  2.64%      0%      0%

La probabilité d’avoir des grappes de cinq personnes est de 1,8 %. À ce stade, compte tenu des paramètres de distribution de la descendance, une stratégie rétrospective n’augmentera peut-être pas la probabilité de contenir et de mettre en quarantaine davantage de cas en amont.

Simuler des chaînes de transmission

Remarque de l'instructeur

La fonction permettant de générer un nombre aléatoire à partir d’un objet de classe <epiparameter> peut également accepter cette notation :

R

as.function(x = serial_interval, func_type = "generate")

Remarque de l'instructeur

R

# load packages -----------------------------------------------------------

library(epiparameter)
library(tidyverse)

# delays ------------------------------------------------------------------

mpox_offspring_epiparam <- epiparameter::epiparameter_db(
  disease = "mpox",
  epi_name = "offspring",
  single_epiparameter = TRUE
)

mpox_offspring <- epiparameter::get_parameters(mpox_offspring_epiparam)

mpox_serialint <- epiparameter::epiparameter_db(
  disease = "mpox",
  epi_name = "serial interval",
  single_epiparameter = TRUE
)

# iterate -----------------------------------------------------------------

# Set seed for random number generator
set.seed(33)

simulated_chains_mpox <- epichains::simulate_chains(
  n_chains = 1000,
  statistic = "size",
  offspring_dist = rnbinom,
  mu = mpox_offspring["mean"],
  size = mpox_offspring["dispersion"],
  generation_time = function(x) generate(x = mpox_serialint, times = x)
)

# visualize ---------------------------------------------------------------

# daily aggregate of cases
simulated_chains_mpox_day <- simulated_chains_mpox %>%
  # use data.frame output from <epichains> object
  as_tibble() %>%
  # Count the daily number of cases in each chain
  mutate(day = ceiling(time)) %>%
  count(chain, day, name = "cases") %>%
  # Calculate the cumulative number of cases for each chain
  group_by(chain) %>%
  mutate(cumulative_cases = cumsum(cases)) %>%
  ungroup()

# Visualize transmission chains by cumulative cases
simulated_chains_mpox_day %>%
  # Create grouped chain trajectories
  ggplot(aes(x = day, y = cumulative_cases, group = chain)) +
  geom_line(color = "black", alpha = 0.25, show.legend = FALSE) +
  # Define a 100-case threshold
  geom_hline(aes(yintercept = 100), lty = 2) +
  labs(x = "Day", y = "Cumulative cases")

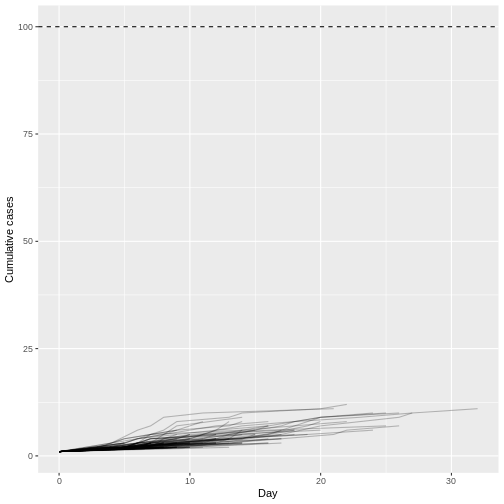
Dans l’hypothèse d’une épidémie de variole du singe avec \(R\) = 0.32 et \(k\) = 0.58, il n’y a pas de trajectoire parmi 1000 simulations qui atteignent plus de 100 cas infectés. Par rapport au MERS (\(R\) = 0.6 et \(k\) = 0.02).

Remarque de l'instructeur

R

# load packages ---------------------------
library(epichains)
library(epiparameter)
library(fitdistrplus)
library(tidyverse)

R

# fit a negative binomial distribution ------------------------------------

# Fitting a negative binomial distribution to the number of secondary cases
fit.cases <- fitdistrplus::fitdist(c0, "nbinom")
fit.cases

SORTIE

Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
      estimate Std. Error
size 0.1814260 0.03990278
mu   0.9537995 0.19812301

R

# serial interval parameters ----------------------------------------------

ebola_serialinter <- epiparameter::epiparameter_db(
  disease = "ebola",
  epi_name = "serial interval",
  single_epiparameter = TRUE
)

# simulate outbreak trajectories ------------------------------------------

# Set seed for random number generator
set.seed(645)
sim_multiple_chains <- epichains::simulate_chains(
  n_chains = 100,
  statistic = "size",
  offspring_dist = rnbinom,
  mu = fit.cases$estimate["mu"],
  size = fit.cases$estimate["size"],
  generation_time = function(x) generate(x = ebola_serialinter, times = x)
)

# summarise ----------------------------------------

summary(sim_multiple_chains)

SORTIE

`epichains_summary` object

  [1]    9    1    2    1    1    4    1   20   14    1    1  131    1    2    1
 [16]    1    7    1    2 2889    1    1    1   13    3    1    1    1    1    1
 [31]    5    6    1    1    1    1    1    1    1    1    2    1    1    2    1
 [46]    1    1    1    1    1    1    1    1    1  335    1   11    3   24    6
 [61]    1    1    1    1    1    1    1    1    1    1    1    1    1    1  111
 [76]    1    1    1    1    1    1    2    1  544    1    1    1    3    1    2
 [91]    6    1    1    1    1    1    1    1 2091    1

 Simulated sizes:

Max: 2889
Min: 1

R

# visualize ----------------------------------------

sim_chains_aggregate <-
  sim_multiple_chains %>%
  # use data.frame output from <epichains> object
  as_tibble() %>%
  # Count the daily number of cases in each chain
  mutate(day = ceiling(time)) %>%
  count(chain, day, name = "cases") %>%
  # Calculate the cumulative number of cases for each chain
  group_by(chain) %>%
  mutate(cumulative_cases = cumsum(cases)) %>%
  ungroup()

sim_chains_aggregate %>%
  # Create grouped chain trajectories
  ggplot(aes(x = day, y = cumulative_cases, group = chain)) +
  geom_line() +
  # Define a 100-case threshold
  geom_hline(aes(yintercept = 100), lty = 2) +
  ylim(0, 100) +
  xlim(0, 100) +
  labs(x = "Day", y = "Cumulative cases")

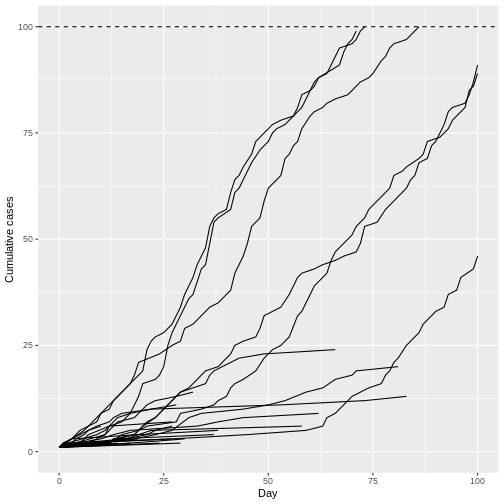
Fait remarquable, même avec R0 inférieur à 1 (R = 0.95), nous pouvons avoir des épidémies potentiellement explosives. La variation observée de la contagiosité individuelle dans le cas d’Ebola signifie que, bien que la probabilité d’extinction soit élevée, les nouveaux cas index ont également le potentiel d’une repousse explosive de l’épidémie.