Content from Accéder aux distribution des délais épidémiologiques
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 30 minutes
Vue d'ensemble
Questions
- Comment accéder aux distributions des délais des maladies à partir d’une base de données préétablie pour les utiliser dans l’analyse ?
Objectifs
- Obtenez les délais à partir d’une base de données de recherche documentaire avec epiparameter.
- Obtenez les paramètres de distribution et les statistiques sommaires des distributions de délais.
Conditions préalables
Cet épisode nécessite que vous soyez familier avec :
la science des données Programmation de base avec R.
Théorie des épidémies La théorie des épidémies est basée sur les paramètres épidémiologiques, les périodes de la maladie, telles que la période d’incubation, le temps de génération et l’intervalle sériel.
Introduction
Les maladies infectieuses suivent un cycle infectieux qui comprend généralement les phases suivantes : période présymptomatique, période symptomatique et période de guérison, comme le décrivent leurs histoire naturelle. Ces périodes peuvent être utilisées pour comprendre la dynamique de la transmission et informer les interventions de prévention et de contrôle des maladies.
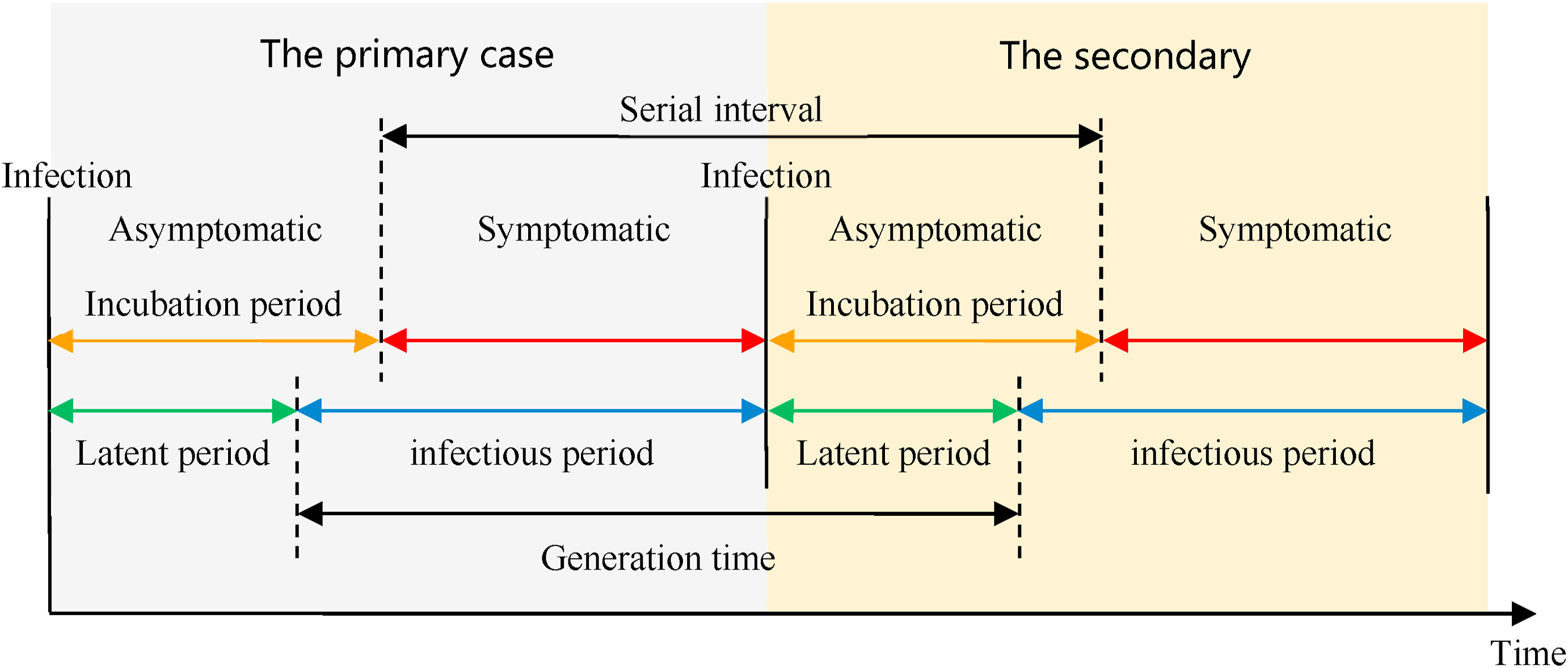
Définitions
Regardez le glossaire pour connaître les définitions de toutes les périodes de la figure ci-dessus !
Toutefois, au début d’une épidémie, les efforts visant à comprendre
l’épidémie et les implications pour la lutte peuvent être retardés par
l’absence d’un moyen facile d’accéder aux paramètres clés de la maladie
en question (Nash et al.,
2023). Des projets tels que epiparameter et
{epireview} construisent des catalogues en ligne en suivant
des protocoles de synthèse de la littérature qui peuvent aider à
informer l’analyse et à paramétrer les modèles en fournissant une
bibliothèque de paramètres épidémiologiques précédemment estimés à
partir d’épidémies passées.
Les premiers modèles pour COVID-19 utilisaient des paramètres d’autres coronavirus. https://www.thelancet.com/article/S1473-3099(20)30144-4/fulltext
Pour illustrer l’utilisation de l’outil epiparameter R dans votre pipeline d’analyse, notre objectif dans cet épisode sera d’accéder à un ensemble spécifique de paramètres épidémiologiques de la littérature, au lieu d’extraire des articles et de les copier-coller à la main. Nous les insérerons ensuite dans un EpiNow2 flux de travail d’analyse.
Commençons par charger le fichier epiparameter
paquetage. Nous utiliserons le tube %>% pour connecter
certaines de ses fonctions, certaines tibble et
dplyr donc appelons aussi à la fonction
tidyverse paquetage :
R
library(epiparameter)
library(tidyverse)
Le double point-virgule
Le double point-virgule :: dans R vous permet d’appeler
une fonction spécifique d’un paquetage sans charger l’ensemble du
paquetage dans l’environnement actuel.
Par exemple, vous pouvez appeler une fonction spécifique d’un package
sans charger le package entier dans l’environnement actuel,
dplyr::filter(data, condition) utilise
filter() à partir de l’outil dplyr
paquet.
Cela nous permet de nous souvenir des fonctions du paquet et d’éviter les conflits d’espace de noms.
Le problème
Si nous voulons estimer la transmissibilité d’une infection, il est
courant d’utiliser un package tel que EpiEstim ou
EpiNow2. Le paquet EpiEstim permet
d’estimer en temps réel le nombre de reproductions à l’aide des données
relatives aux cas dans le temps, reflétant ainsi l’évolution de la
transmission en fonction de la date d’apparition des symptômes. Pour
estimer la transmission en fonction du moment où les personnes ont été
effectivement infectées (plutôt que de l’apparition des symptômes), le
logiciel EpiNow2 étend cette idée en la combinant avec un
modèle qui tient compte des délais dans les données observées. Les deux
logiciels requièrent certaines informations épidémiologiques en entrée.
Par exemple, dans EpiNow2 nous utilisons
EpiNow2::Gamma() pour spécifier un temps de génération sous la
forme d’une distribution de probabilité ajoutant son mean
l’écart-type (sd) et sa valeur maximale
(max).
Pour spécifier une valeur generation_time qui suit un
Gamma avec une moyenne \(\mu =
4\) écart-type \(\sigma = 2\) et
une valeur maximale de 20, nous écrivons :
R
generation_time <-
EpiNow2::Gamma(
mean = 4,
sd = 2,
max = 20
)
Il est courant que les analystes recherchent manuellement la littérature disponible et copient et collent les résultats de la recherche. statistiques sommaires ou les paramètres de distribution des publications scientifiques. Une difficulté à laquelle on est souvent confronté est que la présentation des différentes distributions statistiques n’est pas cohérente dans la littérature (par exemple, un article peut ne présenter que la moyenne, plutôt que la distribution sous-jacente complète). epiparameter L’objectif du projet est de faciliter l’accès à des estimations fiables des paramètres de distribution pour une série de maladies infectieuses, afin qu’elles puissent être facilement mises en œuvre dans les pipelines d’analyse des épidémies.
Dans cet épisode, nous allons accéder les statistiques sommaires du temps de génération pour COVID-19 à partir de la bibliothèque de paramètres épidémiologiques fournie par l’Agence européenne pour la sécurité et la santé au travail (ESA). epiparameter. Ces paramètres peuvent être utilisés pour estimer la transmissibilité de cette maladie à l’aide de l’outil EpiNow2 dans les épisodes suivants.
Commençons par examiner le nombre d’entrées actuellement disponibles
dans la base de données des base de données des distributions
épidémiologiques en epiparameter en utilisant
epiparameter_db() pour la distribution épidémiologique
epi_name appelé temps de génération avec la chaîne
"generation":
R
epiparameter::epiparameter_db(
epi_name = "generation"
)
SORTIE
Returning 3 results that match the criteria (2 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' functionSORTIE
# List of 3 <epiparameter> objects
Number of diseases: 2
❯ Chikungunya ❯ Influenza
Number of epi parameters: 1
❯ generation time
[[1]]
Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Parameter: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull (days)
Parameters:
shape: 2.360
scale: 3.180
[[2]]
Disease: Chikungunya
Pathogen: Chikungunya Virus
Epi Parameter: generation time
Study: Salje H, Cauchemez S, Alera M, Rodriguez-Barraquer I, Thaisomboonsuk B,
Srikiatkhachorn A, Lago C, Villa D, Klungthong C, Tac-An I, Fernandez
S, Velasco J, Roque Jr V, Nisalak A, Macareo L, Levy J, Cummings D,
Yoon I (2015). "Reconstruction of 60 Years of Chikungunya Epidemiology
in the Philippines Demonstrates Episodic and Focal Transmission." _The
Journal of Infectious Diseases_. doi:10.1093/infdis/jiv470
<https://doi.org/10.1093/infdis/jiv470>.
Parameters: <no parameters>
Mean: 14 (days)
[[3]]
Disease: Chikungunya
Pathogen: Chikungunya Virus
Epi Parameter: generation time
Study: Guzzetta G, Vairo F, Mammone A, Lanini S, Poletti P, Manica M, Rosa R,
Caputo B, Solimini A, della Torre A, Scognamiglio P, Zumla A, Ippolito
G, Merler S (2020). "Spatial modes for transmission of chikungunya
virus during a large chikungunya outbreak in Italy: a modeling
analysis." _BMC Medicine_. doi:10.1186/s12916-020-01674-y
<https://doi.org/10.1186/s12916-020-01674-y>.
Distribution: gamma (days)
Parameters:
shape: 8.633
scale: 1.447
# ℹ Use `parameter_tbl()` to see a summary table of the parameters.
# ℹ Explore database online at: https://epiverse-trace.github.io/epiparameter/articles/database.htmlDans la bibliothèque des paramètres épidémiologiques, on peut ne pas
disposer d’un "generation" pour la maladie qui nous
intéresse. À la place, nous pouvons consulter le serial
intervalles pour COVID-19. Voyons ce qu’il faut prendre en compte pour
cela !
Analyse systématique des données relatives aux agents pathogènes prioritaires
Les données de l’examen systématique des pathogènes prioritaires {epireview}
paquet R contient des paramètres sur Ebola, Marburg et Lassa issus
de revues systématiques récentes. D’autres agents pathogènes
prioritaires sont prévus pour les prochaines versions. Jetez un coup
d’œil à cette
vignette pour plus d’informations sur l’utilisation de ces
paramètres avec epiparameter.
Temps de génération vs intervalle série
Le temps de génération, conjointement avec le nombre de reproduction (\(R\)), peut fournir des indications précieuses sur le taux de croissance probable de l’épidémie et, partant, sur la mise en œuvre de mesuresde lutte. Plus la valeur de \(R\) est grande et/ou plus le temps de génération est court, plus le nombre de nouvelles infections attendues par jour est élevé, et donc plus l’incidence des cas de maladie augmentera rapidement.
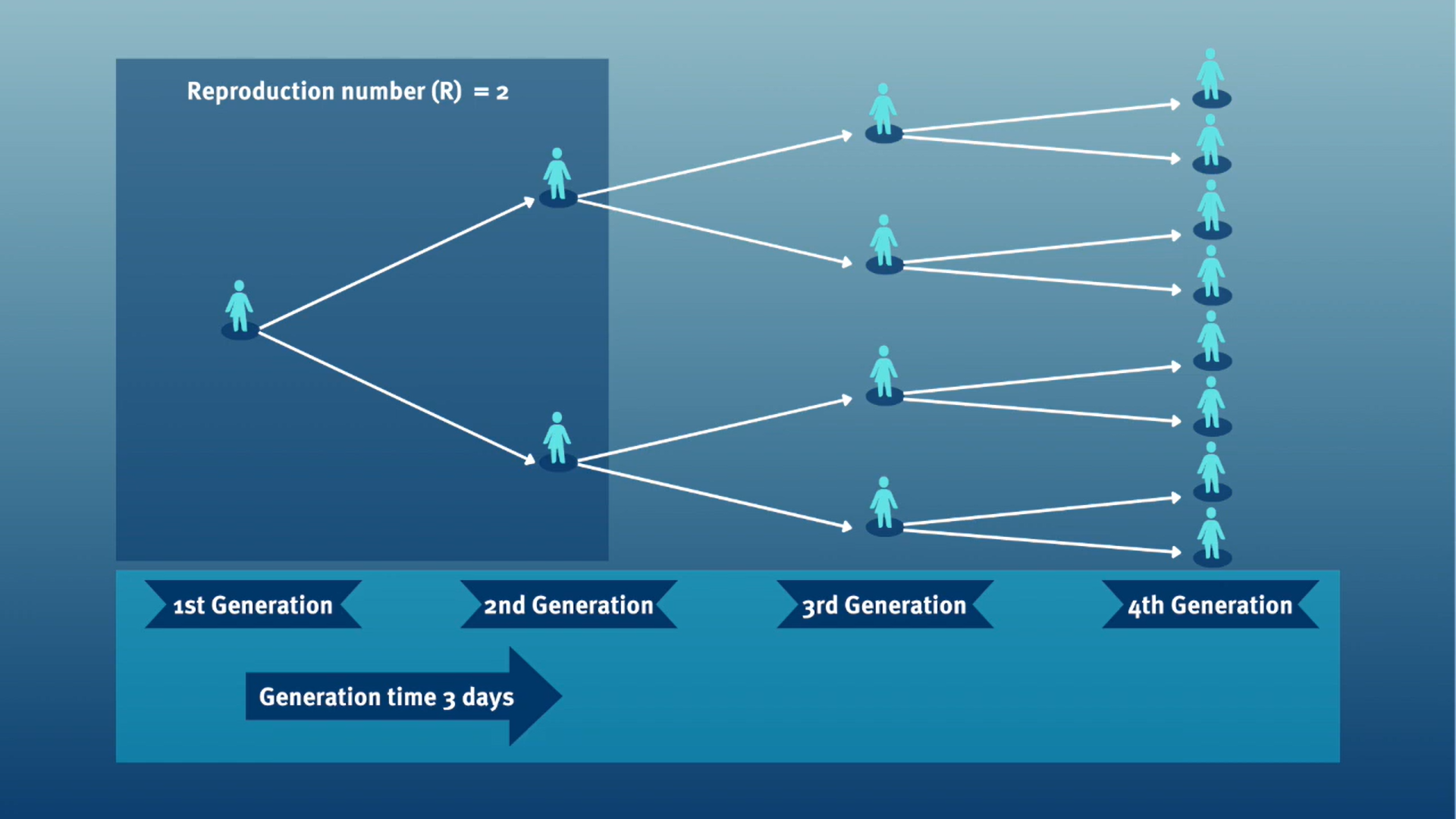
Pour calculer le nombre effectif de reproduction (\(R_{t}\)), le temps de génération (c’est-à-dire le délai entre une infection et la suivante) est souvent approximée par la distribution des temps de génération. intervalle sériel (c’est-à-dire le délai entre l’apparition des symptômes chez l’infecteur et l’apparition des symptômes chez l’infecté). Cette approximation est fréquemment utilisée car il est plus facile d’observer et d’enregistrer l’apparition des symptômes que le moment exact de l’infection.
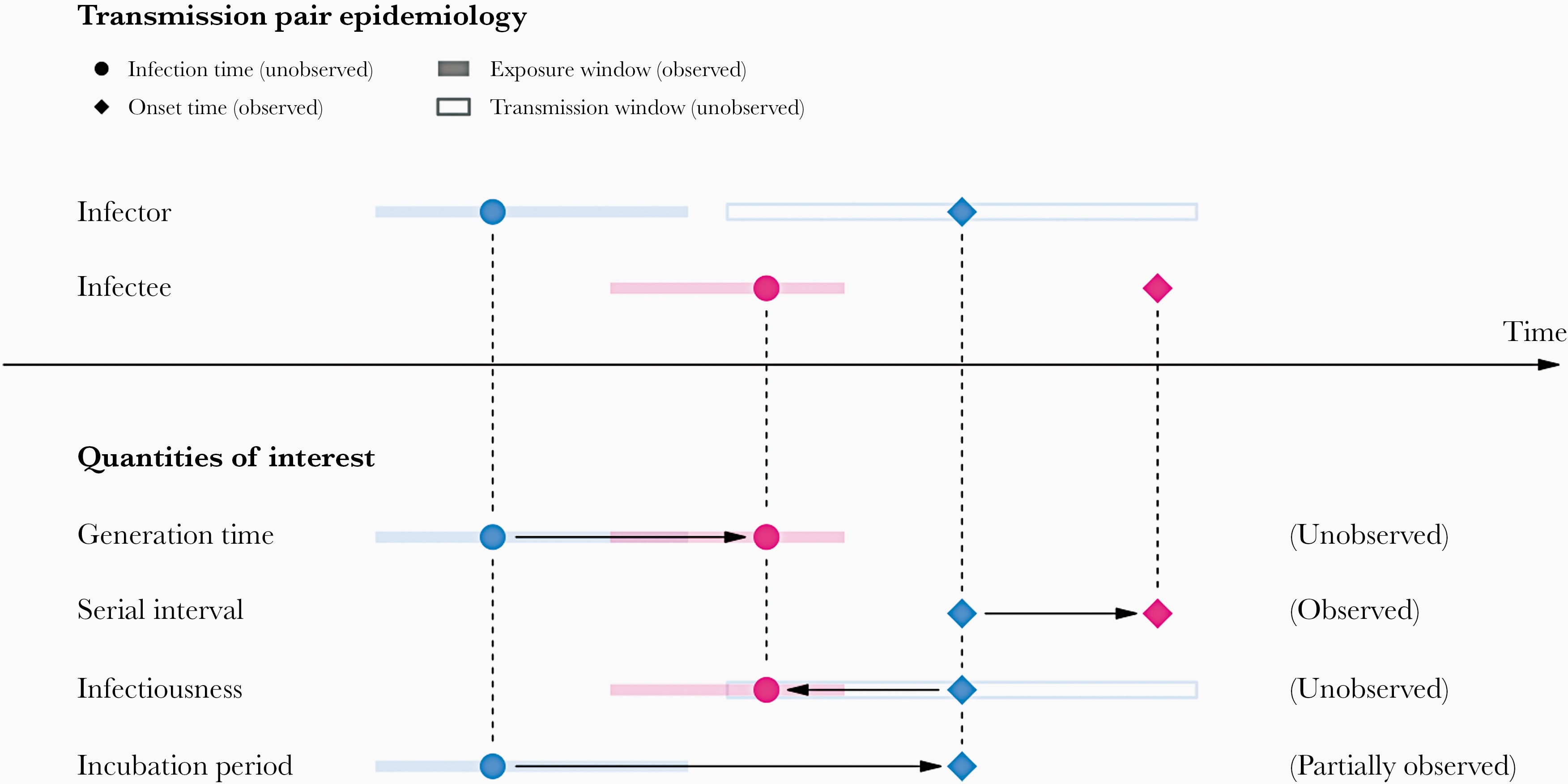
Cependant, l’utilisation de la intervalle sériel comme approximation de l’intervalle temps de génération est plus appropriée pour les maladies dans lesquelles l’infectiosité commence après l’apparition des symptômes (Chung Lau et al., 2021). Dans les cas où l’infectiosité commence avant l’apparition des symptômes, les intervalles sériels peuvent avoir des valeurs négatives, ce qui se produit lorsque l’infecté développe des symptômes avant l’infecteur dans une paire de transmission (Nishiura et al., 2020).
Des délais moyens aux distributions de probabilité
Si nous mesurons les intervalle sériel dans des données réelles, nous constatons généralement que toutes les paires de cas n’ont pas le même délai d’apparition. Nous pouvons également observer cette variabilité pour d’autres délais épidémiologiques clés, notamment le délai d’apparition de la maladie. la période d’incubation et période infectieuse.
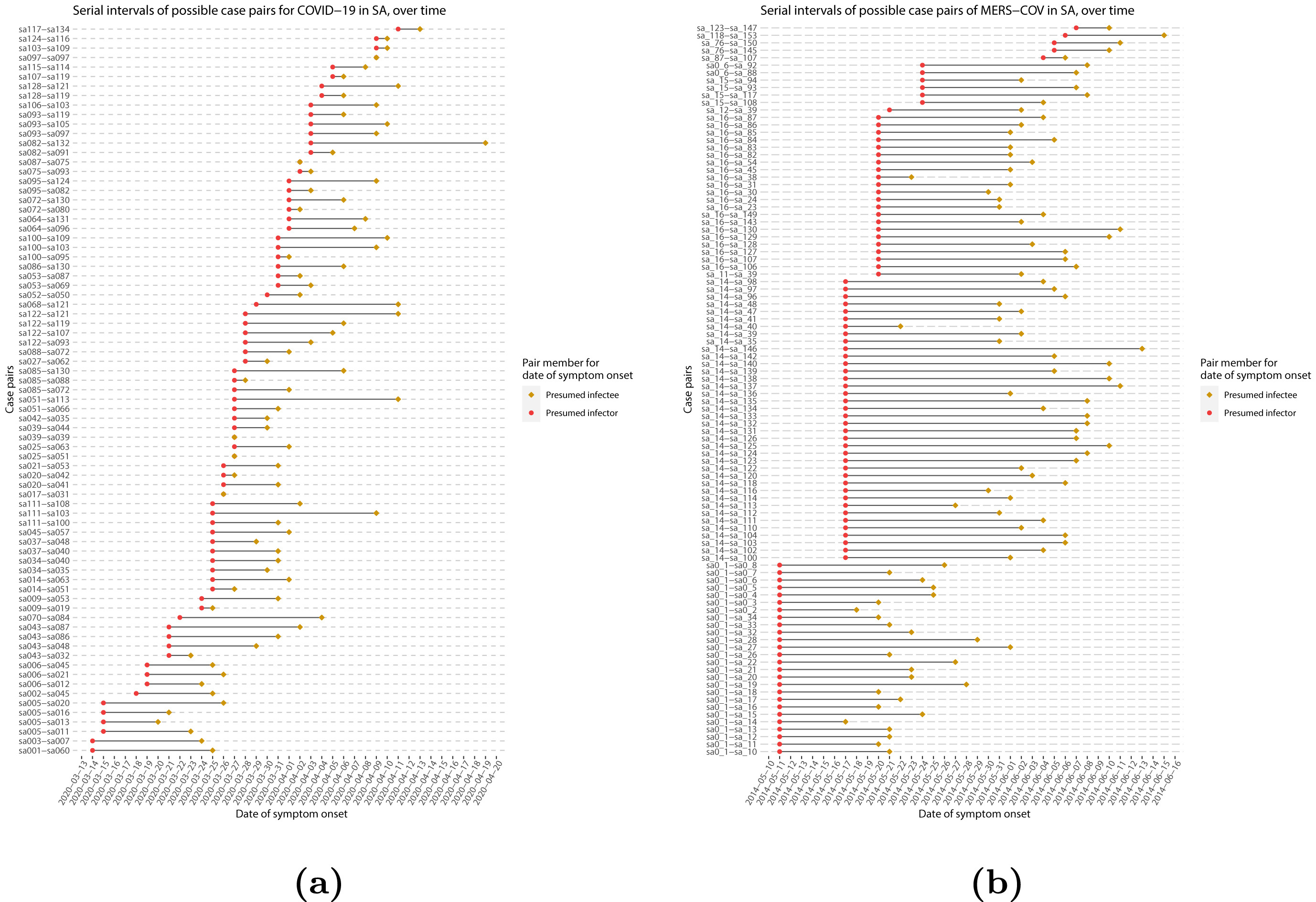
Pour résumer ces données relatives aux périodes individuelles et aux paires, il est donc utile de quantifier les distribution statistique des délais qui correspondent le mieux aux données, plutôt que de se concentrer sur la moyenne (McFarland et al., 2023).
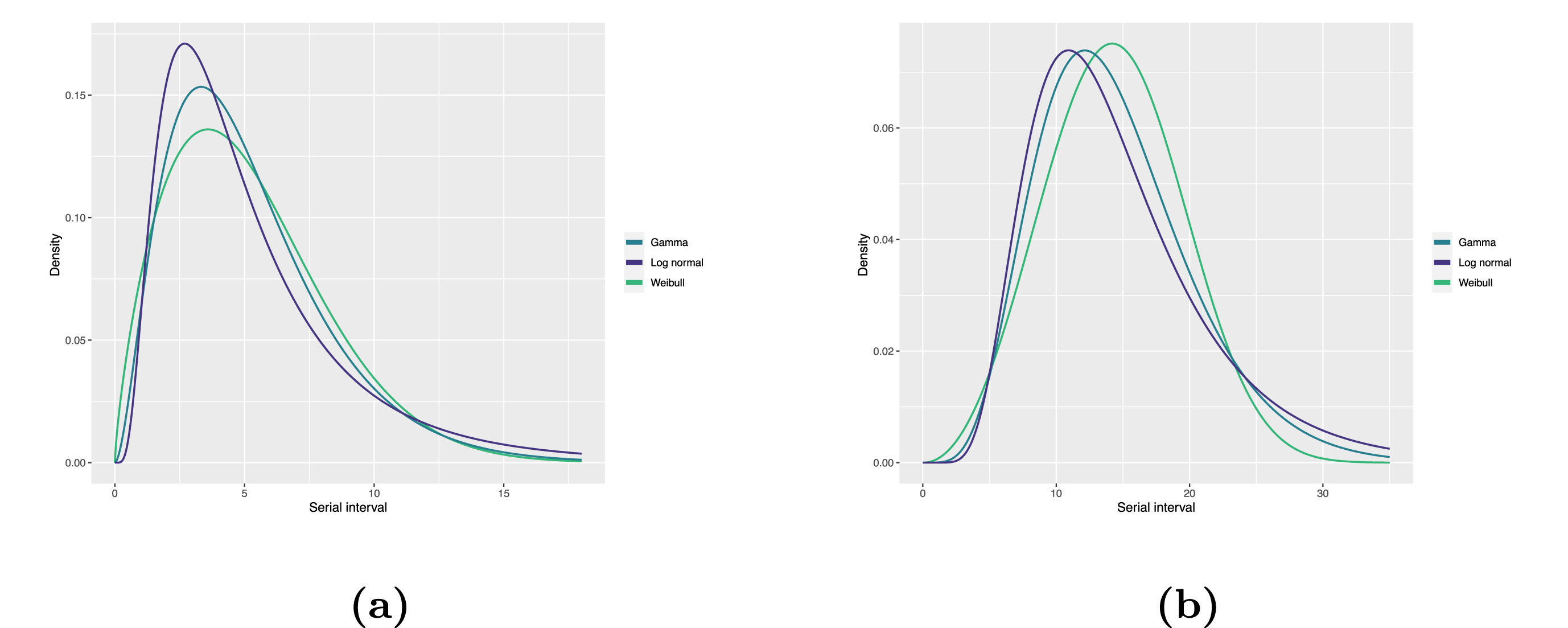
Les distributions statistiques sont résumées en fonction de leur statistiques sommaires comme l’emplacement (moyenne et percentiles) et l’étendue (variance ou écart-type) de la distribution, ou avec leur paramètres de distribution qui renseignent sur la forme (forme et taux/échelle) de la distribution. Ces valeurs estimées peuvent être rapportées avec leur incertitude (intervalles de confiance à 95 %).
| Gamma | moyenne | forme | taux/échelle |
|---|---|---|---|
| MERS-CoV | 14.13(13.9-14.7) | 6.31(4.88-8.52) | 0.43(0.33-0.60) |
| COVID-19 | 5.1(5.0-5.5) | 2.77(2.09-3.88) | 0.53(0.38-0.76) |
| Weibull | moyenne | forme | taux/échelle |
|---|---|---|---|
| MERS-CoV | 14.2(13.3-15.2) | 3.07(2.64-3.63) | 16.1(15.0-17.1) |
| COVID-19 | 5.2(4.6-5.9) | 1.74(1.46-2.11) | 5.83(5.08-6.67) |
| Log normal | moyenne | moyenne-log | sd-log |
|---|---|---|---|
| MERS-CoV | 14.08(13.1-15.2) | 2.58(2.50-2.68) | 0.44(0.39-0.5) |
| COVID-19 | 5.2(4.2-6.5) | 1.45(1.31-1.61) | 0.63(0.54-0.74) |
Tableau : Estimations des intervalles de série à l’aide des distributions Gamma, Weibull et Log Normal. Les intervalles de confiance à 95 % pour les paramètres de forme et d’échelle (logmoy et sd pour Log Normal) sont indiqués entre parenthèses (Althobaity et al, 2022).
Intervalle de série
Supposons que COVID-19 et le SRAS aient des valeurs de nombre de reproduction similaires et que l’intervalle de série soit proche du temps de génération.
Étant donné l’intervalle sériel des deux infections dans la figure ci-dessous :
- Laquelle serait la plus difficile à contrôler ?
- Pourquoi en concluez-vous ainsi ?
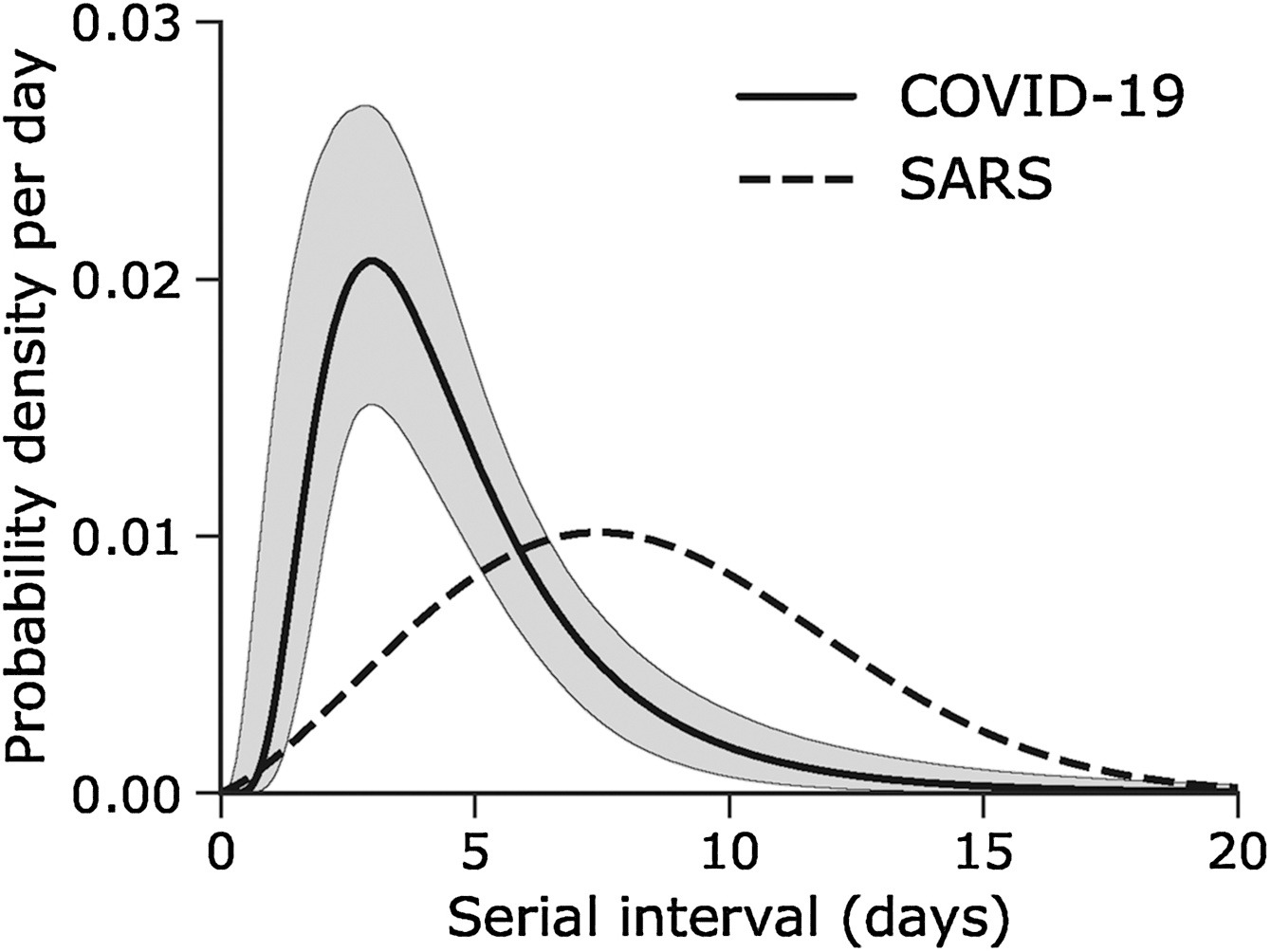
Le sommet de chaque courbe peut vous renseigner sur l’emplacement de la moyenne de chaque distribution. Une moyenne plus élevée indique un délai plus long entre l’apparition des symptômes chez l’infecteur et l’infecté.
Laquelle serait la plus difficile à contrôler ?
COVID-19
Pourquoi concluez-vous cela ?
L’intervalle sériel moyen de COVID-19 est plus faible. La valeur moyenne approximative de l’intervalle sériel de COVID-19 est d’environ quatre jours, alors que celle du SRAS est d’environ sept jours. Par conséquent, s’il y a beaucoup d’infections dans la population, COVID-19 produira en moyenne plus de nouvelles générations d’infections en moins de temps que le SRAS, en supposant des nombres de reproduction similaires. Cela signifie qu’il faudrait beaucoup plus de ressources pour lutter contre l’épidémie.
L’objectif de l’évaluation ci-dessus est d’évaluer l’interprétation d’un temps de génération plus long ou plus court.
Choix des paramètres épidémiologiques
Dans cette section, nous utiliserons epiparameter pour obtenir l’intervalle sériel de COVID-19, comme alternative au temps de génération.
Tout d’abord, voyons combien de paramètres nous avons dans la base de
données des distributions épidémiologiques
(epiparameter_db()) avec l’option disease
nommé covid-19. Exécutez ce code :
R
epiparameter::epiparameter_db(
disease = "covid"
)
A partir du epiparameter nous pouvons utiliser le
paquet epiparameter_db() pour demander n’importe quel
disease ainsi qu’une distribution épidémiologique
spécifique (epi_name). Exécutez cette fonction dans votre
console :
R
epiparameter::epiparameter_db(
disease = "COVID",
epi_name = "serial"
)
Avec cette combinaison de requêtes, nous obtenons plus d’une
distribution des délais (parce que la base de données a plusieurs
entrées). Cette sortie est un <epiparameter> objet de
classe.
INSENSIBLE À LA CASSE
epiparameter_db est insensible
à la casse. Cela signifie que vous pouvez utiliser des chaînes avec
des lettres en majuscules ou en minuscules indistinctement. Des chaînes
comme "serial", "serial interval" ou
"serial_interval" sont également valables.
Comme le suggèrent les résultats, pour résumer une
<epiparameter> et obtenir les noms des colonnes de la
base de données de paramètres sous-jacente, nous pouvons ajouter
l’élément epiparameter::parameter_tbl() au code précédent à
l’aide du tuyau %>%:
R
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial"
) %>%
epiparameter::parameter_tbl()
SORTIE
Returning 4 results that match the criteria (3 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' functionSORTIE
# Parameter table:
# A data frame: 4 × 7
disease pathogen epi_name prob_distribution author year sample_size
<chr> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 COVID-19 SARS-CoV-2 serial interval <NA> Alene… 2021 3924
2 COVID-19 SARS-CoV-2 serial interval lnorm Nishi… 2020 28
3 COVID-19 SARS-CoV-2 serial interval weibull Nishi… 2020 18
4 COVID-19 SARS-CoV-2 serial interval norm Yang … 2020 131Dans le epiparameter::parameter_tbl() nous pouvons
également trouver différents types de distributions de probabilité (par
exemple, Log-normal, Weibull, Normal).
epiparameter utilise la fonction base R
pour les distributions. C’est pourquoi Log normal
s’appelle lnorm.
Les entrées avec une valeur manquante (<NA>) dans
le prob_distribution sont non paramétrés non
paramétrées. Elles présentent des statistiques sommaires (par exemple,
une moyenne et un écart type), mais aucune distribution de probabilité
n’est spécifiée. Comparez ces deux résultats :
R
# get an <epiparameter> object
distribution <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial"
)
distribution %>%
# pluck the first entry in the object class <list>
pluck(1) %>%
# check if <epiparameter> object have distribution parameters
is_parameterised()
# check if the second <epiparameter> object
# have distribution parameters
distribution %>%
pluck(2) %>%
is_parameterised()
Les entrées paramétrées ont une méthode d’inférence
Comme indiqué dans ?is_parameterised une distribution
paramétrée est l’entrée à laquelle est associée une distribution de
probabilité fournie par une méthode d’inférence.
inference_method comme indiqué dans
metadata:
R
distribution[[1]]$metadata$inference_method
distribution[[2]]$metadata$inference_method
distribution[[4]]$metadata$inference_method
Trouvez vos distributions de délais !
Prenez 2 minutes pour explorer les epiparameter bibliothèque.
Choisissez une maladie d’intérêt (par exemple, la grippe, la rougeole, etc.) et une distribution des délais (par exemple, la période d’incubation, le début de la maladie jusqu’au décès, etc.)
Trouvez :
Combien y a-t-il de distributions de délais pour cette maladie ?
Combien de types de distribution de probabilité (par exemple, gamma, log normale) y a-t-il pour un délai donné dans cette maladie ?
Posez la question :
Reconnaissez-vous les journaux ?
La revue de littérature d’{epiparameter} devrait- elle prendre en compte un autre article?
L’analyse epiparameter_db() fonction avec
disease compte à elle seule le nombre d’entrées comme :
- études, et
- les répartitions des délais.
Les epiparameter_db() avec disease et
epi_name obtient une liste de toutes les entrées avec :
- la citation complète,
- le type d’une distribution de probabilité, et
- les valeurs des paramètres de la distribution.
La combinaison de epiparameter_db() plus
parameter_tbl() permet d’obtenir un cadre de données de
toutes les entrées avec des colonnes comme :
- les type de la distribution de probabilité par délai, et
- l’auteur et l’année de l’étude.
Nous avons choisi d’explorer les distributions des délais d’Ebola :
R
# we expect 16 delay distributions for Ebola
epiparameter::epiparameter_db(
disease = "ebola"
)
SORTIE
Returning 17 results that match the criteria (17 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' functionSORTIE
# List of 17 <epiparameter> objects
Number of diseases: 1
❯ Ebola Virus Disease
Number of epi parameters: 9
❯ hospitalisation to death ❯ hospitalisation to discharge ❯ incubation period ❯ notification to death ❯ notification to discharge ❯ offspring distribution ❯ onset to death ❯ onset to discharge ❯ serial interval
[[1]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Parameter: offspring distribution
Study: Lloyd-Smith J, Schreiber S, Kopp P, Getz W (2005). "Superspreading and
the effect of individual variation on disease emergence." _Nature_.
doi:10.1038/nature04153 <https://doi.org/10.1038/nature04153>.
Distribution: nbinom (No units)
Parameters:
mean: 1.500
dispersion: 5.100
[[2]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Parameter: incubation period
Study: Eichner M, Dowell S, Firese N (2011). "Incubation period of ebola
hemorrhagic virus subtype zaire." _Osong Public Health and Research
Perspectives_. doi:10.1016/j.phrp.2011.04.001
<https://doi.org/10.1016/j.phrp.2011.04.001>.
Distribution: lnorm (days)
Parameters:
meanlog: 2.487
sdlog: 0.330
[[3]]
Disease: Ebola Virus Disease
Pathogen: Ebola Virus-Zaire Subtype
Epi Parameter: onset to death
Study: The Ebola Outbreak Epidemiology Team, Barry A, Ahuka-Mundeke S, Ali
Ahmed Y, Allarangar Y, Anoko J, Archer B, Abedi A, Bagaria J, Belizaire
M, Bhatia S, Bokenge T, Bruni E, Cori A, Dabire E, Diallo A, Diallo B,
Donnelly C, Dorigatti I, Dorji T, Waeber A, Fall I, Ferguson N,
FitzJohn R, Tengomo G, Formenty P, Forna A, Fortin A, Garske T,
Gaythorpe K, Gurry C, Hamblion E, Djingarey M, Haskew C, Hugonnet S,
Imai N, Impouma B, Kabongo G, Kalenga O, Kibangou E, Lee T, Lukoya C,
Ly O, Makiala-Mandanda S, Mamba A, Mbala-Kingebeni P, Mboussou F,
Mlanda T, Makuma V, Morgan O, Mulumba A, Kakoni P, Mukadi-Bamuleka D,
Muyembe J, Bathé N, Ndumbi Ngamala P, Ngom R, Ngoy G, Nouvellet P, Nsio
J, Ousman K, Peron E, Polonsky J, Ryan M, Touré A, Towner R, Tshapenda
G, Van De Weerdt R, Van Kerkhove M, Wendland A, Yao N, Yoti Z, Yuma E,
Kalambayi Kabamba G, Mwati J, Mbuy G, Lubula L, Mutombo A, Mavila O,
Lay Y, Kitenge E (2018). "Outbreak of Ebola virus disease in the
Democratic Republic of the Congo, April–May, 2018: an epidemiological
study." _The Lancet_. doi:10.1016/S0140-6736(18)31387-4
<https://doi.org/10.1016/S0140-6736%2818%2931387-4>.
Distribution: gamma (days)
Parameters:
shape: 2.400
scale: 3.333
# ℹ 14 more elements
# ℹ Use `print(n = ...)` to see more elements.
# ℹ Use `parameter_tbl()` to see a summary table of the parameters.
# ℹ Explore database online at: https://epiverse-trace.github.io/epiparameter/articles/database.htmlMaintenant, à partir de la sortie de
epiparameter::epiparameter_db() Quelle est la distribution de la
descendance?
Nous choisissons de trouver les périodes d’incubation d’Ebola. Cette sortie liste tous les articles et paramètres trouvés. Exécutez-la localement si nécessaire :
R
epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "incubation"
)
Nous utilisons parameter_tbl() pour obtenir un
récapitulatif de toutes les données :
R
# we expect 2 different types of delay distributions
# for ebola incubation period
epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "incubation"
) %>%
parameter_tbl()
SORTIE
Returning 5 results that match the criteria (5 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' functionSORTIE
# Parameter table:
# A data frame: 5 × 7
disease pathogen epi_name prob_distribution author year sample_size
<chr> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 Ebola Virus Dise… Ebola V… incubat… lnorm Eichn… 2011 196
2 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 1798
3 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 49
4 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 957
5 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 792Nous trouvons deux types de distributions de probabilités pour cette requête : log normale et gamma.
Comment le epiparameter collecte-t-elle et examine-t-elle la littérature évaluée par les pairs ? Nous vous invitons à lire la vignette sur “Protocole de collecte et de synthèse des données!
Sélectionnez une distribution unique
Les epiparameter::epiparameter_db() fonctionne comme une
fonction de filtrage ou de sous-ensemble. Nous pouvons utiliser la
fonction author pour conserver
Hiroshi Nishiura ou l’argument subset pour
conserver les paramètres des études dont la taille de l’échantillon est
supérieure à 10 :
R
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
author = "Nishiura",
subset = sample_size > 10
) %>%
epiparameter::parameter_tbl()
Nous obtenons toujours plus d’un paramètre épidémiologique. Au lieu
de cela, nous pouvons définir l’argument
single_epiparameter à TRUE pour n’en obtenir
qu’un seul :
R
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
single_epiparameter = TRUE
)
SORTIE
Using Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>..
To retrieve the citation use the 'get_citation' functionSORTIE
Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Parameter: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: lnorm (days)
Parameters:
meanlog: 1.386
sdlog: 0.568Attribuons cette <epiparameter> à l’objet de
classe covid_serialint objet.
R
covid_serialint <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
single_epiparameter = TRUE
)
Vous pouvez utiliser plot() pour
<epiparameter> pour visualiser les objets :
- le Fonction de densité de probabilité (PDF) et
- la Fonction de distribution cumulative (FDC).
R
# plot <epiparameter> object
plot(covid_serialint)
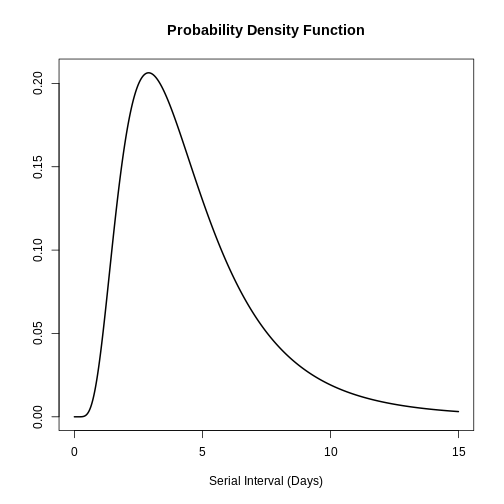
Avec la xlim vous pouvez modifier la durée ou le nombre
de jours de la période d’essai. x de l’axe. Découvrez à
quoi cela ressemble :
R
# plot <epiparameter> object
plot(covid_serialint, xlim = c(1, 60))
Extrayez les statistiques récapitulatives
Nous pouvons obtenir les mean et l’écart-type
(sd) à partir de ce <epiparameter>
plonger dans le summary_stats l’objet :
R
# get the mean
covid_serialint$summary_stats$mean
SORTIE
[1] 4.7Nous avons maintenant un paramètre épidémiologique que nous pouvons
réutiliser ! Étant donné que l’objet covid_serialint est un
lnorm ou une distribution log-normale, nous pouvons
remplacer le statistiques sommaires que nous
introduisons dans la base de données EpiNow2::LogNormal()
dans la fonction
R
generation_time <-
EpiNow2::LogNormal(
mean = covid_serialint$summary_stats$mean, # replaced!
sd = covid_serialint$summary_stats$sd, # replaced!
max = 20
)
Dans le prochain épisode, nous apprendrons à utiliser la fonction
EpiNow2 pour spécifier correctement les distributions et
estimer la transmissibilité. Ensuite, comment utiliser fonctions
de distribution pour obtenir une valeur maximale
(max) pour EpiNow2::LogNormal() et utiliser
epiparameter dans votre analyse.
Distributions logarithmiques normales
Si vous avez besoin de la distribution log-normale de la
distribution logarithmique au lieu des statistiques sommaires,
vous pouvez utiliser epiparameter::get_parameters():
R
covid_serialint_parameters <-
epiparameter::get_parameters(covid_serialint)
covid_serialint_parameters
SORTIE
meanlog sdlog
1.3862617 0.5679803 Cela permet d’obtenir un vecteur de classe
<numeric> prêt à être utilisé comme entrée pour
n’importe quel autre paquet !
Considérez que {EpiNow2} acceptent également les paramètres de
distribution comme données d’entrée. Exécutez
?EpiNow2::LogNormal pour lire les Distributions
de probabilités de référence.
Défis
L’intervalle sériel d’Ebola
Prenez 1 minute pour :
Accédez à l’intervalle de série Ebola avec la taille d’échantillon la plus élevée.
Réponse :
Qu’est-ce que le
sdde la distribution épidémiologique ?Quelle est la
sample_sizeutilisée dans cette étude ?
R
# ebola serial interval
ebola_serial <-
epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "serial",
single_epiparameter = TRUE
)
SORTIE
Using WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>..
To retrieve the citation use the 'get_citation' functionR
ebola_serial
SORTIE
Disease: Ebola Virus Disease
Pathogen: Ebola Virus
Epi Parameter: serial interval
Study: WHO Ebola Response Team, Agua-Agum J, Ariyarajah A, Aylward B, Blake I,
Brennan R, Cori A, Donnelly C, Dorigatti I, Dye C, Eckmanns T, Ferguson
N, Formenty P, Fraser C, Garcia E, Garske T, Hinsley W, Holmes D,
Hugonnet S, Iyengar S, Jombart T, Krishnan R, Meijers S, Mills H,
Mohamed Y, Nedjati-Gilani G, Newton E, Nouvellet P, Pelletier L,
Perkins D, Riley S, Sagrado M, Schnitzler J, Schumacher D, Shah A, Van
Kerkhove M, Varsaneux O, Kannangarage N (2015). "West African Ebola
Epidemic after One Year — Slowing but Not Yet under Control." _The New
England Journal of Medicine_. doi:10.1056/NEJMc1414992
<https://doi.org/10.1056/NEJMc1414992>.
Distribution: gamma (days)
Parameters:
shape: 2.188
scale: 6.490R
# get the sd
ebola_serial$summary_stats$sd
SORTIE
[1] 9.6R
# get the sample_size
ebola_serial$metadata$sample_size
SORTIE
[1] 305Essayez de visualiser cette distribution en utilisant
plot().
Explorez également tous les autres éléments imbriqués dans l’élément
<epiparameter> à l’intérieur de l’objet.
Partagez sur :
- Quels sont les éléments que vous trouvez utiles pour votre analyse ?
- Quels autres éléments souhaiteriez-vous voir figurer dans cet objet ? Comment ?
Un élément intéressant est le method_assess qui fait
référence aux méthodes utilisées par les auteurs de l’étude pour évaluer
les biais lors de l’estimation de la distribution des intervalles
sériels.
R
covid_serialint$method_assess
SORTIE
$censored
[1] TRUE
$right_truncated
[1] TRUE
$phase_bias_adjusted
[1] FALSENous explorerons ces concepts au fil des épisodes !
Le paramètre de gravité d’Ebola
Un paramètre de gravité tel que la durée de l’hospitalisation pourrait compléter les informations nécessaires sur la capacité d’accueil en cas d’épidémie (Cori et al.).
Pour Ebola :
- Qu’est-ce qui est rapporté ? estimation ponctuelle de la durée moyenne des soins de santé et de l’isolement des cas ?
Un délai informatif devrait mesurer le temps écoulé entre l’apparition des symptômes et la guérison ou le décès.
Trouver un moyen d’accéder à l’ensemble epiparameter
base de données et de trouver comment ce délai peut être stocké. Les
parameter_tbl() est un tableau de données.
R
# one way to get the list of all the available parameters
epiparameter_db(disease = "all") %>%
parameter_tbl() %>%
as_tibble() %>%
distinct(epi_name)
SORTIE
Returning 125 results that match the criteria (100 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' functionSORTIE
# A tibble: 13 × 1
epi_name
<chr>
1 incubation period
2 serial interval
3 generation time
4 onset to death
5 offspring distribution
6 hospitalisation to death
7 hospitalisation to discharge
8 notification to death
9 notification to discharge
10 onset to discharge
11 onset to hospitalisation
12 onset to ventilation
13 case fatality risk R
ebola_severity <- epiparameter_db(
disease = "ebola",
epi_name = "onset to discharge"
)
SORTIE
Returning 1 results that match the criteria (1 are parameterised).
Use subset to filter by entry variables or single_epiparameter to return a single entry.
To retrieve the citation for each use the 'get_citation' functionR
# point estimate
ebola_severity$summary_stats$mean
SORTIE
[1] 15.1Vérifiez que pour certains epiparameter vous disposerez également de l’élément incertitude autour de la estimation ponctuelle de chaque statistique sommaire :
R
# 95% confidence intervals
ebola_severity$summary_stats$mean_ci
SORTIE
[1] 95R
# limits of the confidence intervals
ebola_severity$summary_stats$mean_ci_limits
SORTIE
[1] 14.6 15.6La distribution zoo
Explorez cette shinyapp appelée Le zoo de la distribution!
Suivez les étapes suivantes pour reproduire la forme de la
distribution d’intervalles sériels COVID à partir de
epiparameter (covid_serialint objet) :
- Accédez au https://ben18785.shinyapps.io/distribution-zoo/ site web de l’application shiny,
- Allez dans le panneau de gauche,
- Gardez l’option Catégorie de distribution:
Continuous Univariate, - Sélectionnez un nouveau Type de distribution:
Log-Normal, - Déplacez le curseurs c’est-à-dire l’élément de
contrôle graphique qui vous permet d’ajuster une valeur en déplaçant une
poignée le long d’une piste ou d’une barre horizontale jusqu’à
l’emplacement du curseur.
covid_serialintparamètres.
Reproduisez ces éléments à l’aide de l’outil
distribution et tous ses éléments de liste :
[[2]], [[3]] et [[4]]. Explorez
comment la forme d’une distribution change lorsque ses paramètres
changent.
Partagez à propos de :
- Quelles sont les autres fonctionnalités du site web que vous trouvez utiles ?
Dans le contexte des interfaces utilisateurs et des interfaces graphiques (GUI), comme le Zoo de la distribution une application glissière est un élément de contrôle graphique qui permet aux utilisateurs d’ajuster une valeur en déplaçant une poignée le long d’une piste ou d’une barre. Conceptuellement, il permet de sélectionner une valeur numérique dans une plage spécifiée en faisant glisser visuellement un pointeur (la poignée) le long d’un axe continu.
Points clés
- Utilisez epiparameter pour accéder au catalogue des distributions de délais épidémiologiques.
- Utilisez cette fonction pour accéder au catalogue de la littérature
sur les distributions de délais épidémiologiques.
epiparameter_db()pour sélectionner une seule distribution de délais. - Utilisez cette option pour sélectionner les distributions à délais
unique.
parameter_tbl()pour obtenir une vue d’ensemble des distributions de délais multiples. - Réutiliser les estimations connues pour une maladie inconnue au début d’une épidémie lorsqu’il n’y a pas de données sur la recherche des contacts.
Content from Quantifier la transmission
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 30 minutes
Vue d'ensemble
Questions
- Comment puis-je estimer le nombre de reproduction variable dans le temps (\(Rt\)) et le taux de croissance à partir d’une série chronologique de données de cas ?
- Comment quantifier l’hétérogénéité géographique à partir de ces paramètres de transmission ?
Objectifs
- Apprenez à estimer les paramètres de transmission à partir d’une
série chronologique de données sur les cas à l’aide du package
EpiNow2.
Conditions préalables
Les étudiants doivent se familiariser avec les concepts suivants avant de suivre ce tutoriel :
Statistiques: distributions de probabilités, principe de l’analyse bayésienne.
Théorie des épidémies: Nombre de reproduction effectif.
Science des données: la transformation et la visualisation des données. Vous pouvez revoir l’épisode sur Agréger et visualiser les données d’incidence.
Rappel : le nombre de reproduction effectif, \(R_t\)
Le nombre de reproduction de base, \(R_0\) est le nombre moyen de cas causés par un individu infectieux dans une population entièrement susceptible.
Mais dans une épidémie en cours, la population ne reste pas entièrement susceptible, car les personnes qui se remettent de l’infection sont généralement immunisées. En outre, il peut y avoir des changements de comportement ou d’autres facteurs qui affectent la transmission. Lorsque nous voulons surveiller les changements dans la transmission, nous nous intéressons donc davantage à la valeur du nombre de reproduction effectif, \(R_t\) qui représente le nombre moyen de cas causés par un individu infectieux dans la population au temps \(t\) compte tenu de l’état actuel de la population (y compris les niveaux d’immunité et les mesures de contrôle).
Introduction
L’intensité de la transmission d’une épidémie est quantifiée à l’aide de deux paramètres clés : le nombre de reproduction, qui renseigne sur la force de la transmission en indiquant le nombre de nouveaux cas attendus pour chaque cas existant, et le nombre de décès. taux de croissance qui renseigne sur la vitesse de transmission en indiquant la rapidité avec laquelle l’épidémie se propage ou décline (temps de doublement/dédoublement) au sein d’une population. Pour plus de détails sur la distinction entre la vitesse et la force de la transmission et les implications pour la lutte, consultez le site Dushoff & Park, 2021.
Pour estimer ces paramètres clés à l’aide des données relatives aux cas, nous devons tenir compte des délais entre les dates d’infections et les dates de cas déclarés. Lors d’une épidémie, les données ne sont généralement disponibles qu’à partir des dates déclarées. Nous devons donc utiliser des méthodes d’estimation pour tenir compte de ces retards lorsque nous essayons de comprendre les changements dans la transmission au fil du temps.
Dans les prochains tutoriels, nous nous concentrerons sur la manière d’utiliser les fonctions de EpiNow2 pour estimer les paramètres de transmission des données de cas. Nous ne couvrirons pas le contexte théorique des modèles ou du cadre d’inférence, pour plus de détails sur ces concepts, consultez la vignette..
Dans ce tutoriel, nous allons apprendre à utiliser le package
EpiNow2 pour estimer le nombre de reproduction variable
dans le temps. Nous obtiendrons les données d’entrée de
incidence2. Nous utiliserons le package
tidyr et dplyr pour organiser certains de
ses résultats, ggplot2 pour visualiser la distribution
des cas, et le tuyau %>% pour relier certaines de leurs
fonctions, alors appelons aussi le package tidyverse
:
R
library(EpiNow2)
library(incidence2)
library(tidyverse)
Le double point-virgule
Le double deux-points :: dans R vous permet d’appeler
une fonction spécifique d’un package sans charger l’ensemble du package
dans l’environnement actuel.
Par exemple, vous pouvez appeler une fonction spécifique d’un package
sans charger le package entier dans l’environnement actuel,
dplyr::filter(data, condition) utilise
filter() à partir du package dplyr.
Cela nous permet de nous souvenir des fonctions du package et d’éviter les conflits d’espace de noms.
Ce tutoriel illustre l’utilisation de epinow() pour
estimer le nombre de reproduction et les durées d’infection variables
dans le temps. Les étudiants doivent comprendre les données d’entrée
nécessaires au modèle et les limites des résultats du modèle.
Inférence bayésienne
Le package R EpiNow2 utilise une méthode d’inférence
bayésienne inférence bayésienne
pour estimer les nombres de reproduction et les durées d’infection sur
la base des dates déclarées. En d’autres termes, il estime la
transmission en fonction de la date à laquelle les personnes ont été
effectivement infectées (plutôt que de l’apparition des symptômes), en
tenant compte des retards dans les données observées. En revanche,
l’approche EpiEstim permet une estimation en temps réel
plus rapide et plus simple du nombre de reproductions en utilisant
uniquement les données de cas au fil du temps, reflétant la façon dont
la transmission change en fonction du moment où les symptômes
apparaissent.
Dans l’inférence bayésienne, nous utilisons les connaissances a priori (distributions a priori) et les données (via une fonction de vraisemblance) pour obtenir la probabilité a posteriori :
\(\text{Probabilité a posteriori} \propto \text{vraisemblance} \times \text{probabilité a priori}\)
Faites référence à la distribution de probabilité a priori et à la probabilité a posteriori a posteriori.
Dans la “Expected change in reports”,
l’appel par “la probabilité a posteriori que \(R_t < 1\)”nous nous référons
spécifiquement à la aire sous la
courbe de distribution de la probabilité a posteriori.
Distributions de délais et données de cas
Données de cas
Pour illustrer les fonctions des EpiNow2 nous
utiliserons les données relatives au début de la pandémie de COVID-19 au
Royaume-Uni, mais uniquement pour les 90 premiers jours observés. Les
données sont disponibles dans le package R
incidence2.
R
dplyr::as_tibble(incidence2::covidregionaldataUK)
SORTIE
# A tibble: 6,370 × 13
date region region_code cases_new cases_total deaths_new deaths_total
<date> <chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 2020-01-30 East Mi… E12000004 NA NA NA NA
2 2020-01-30 East of… E12000006 NA NA NA NA
3 2020-01-30 England E92000001 2 2 NA NA
4 2020-01-30 London E12000007 NA NA NA NA
5 2020-01-30 North E… E12000001 NA NA NA NA
6 2020-01-30 North W… E12000002 NA NA NA NA
7 2020-01-30 Norther… N92000002 NA NA NA NA
8 2020-01-30 Scotland S92000003 NA NA NA NA
9 2020-01-30 South E… E12000008 NA NA NA NA
10 2020-01-30 South W… E12000009 NA NA NA NA
# ℹ 6,360 more rows
# ℹ 6 more variables: recovered_new <dbl>, recovered_total <dbl>,
# hosp_new <dbl>, hosp_total <dbl>, tested_new <dbl>, tested_total <dbl>Pour utiliser les données, nous devons les formater de manière à ce qu’elles comportent deux colonnes :
-
datela date (en tant qu’objet date, voir?is.Date()), -
confirm: nombre de cas déclarés (confirmés) à cette date.
Utilisons tidyr et incidence2 pour cela :
R
cases_sliced <- incidence2::covidregionaldataUK %>%
dplyr::as_tibble() %>%
# Preprocess missing values
tidyr::replace_na(base::list(cases_new = 0)) %>%
# Compute the daily incidence
incidence2::incidence(
date_index = "date",
counts = "cases_new",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
# Keep the first 90 dates
dplyr::slice_head(n = 90)
Avec incidence2::incidence() nous agrégeons des cas sur
différentes périodes de temps (intervalles, c’est-à-dire des
jours, des semaines ou des mois) ou par groupe. Nous pouvons également
obtenir les dates complètes pour tous les intervalles de dates par
catégorie de groupe à l’aide de la fonction
complete_dates = TRUE Explorez plus tard les incidence2::incidence()
manuel de référence
Pouvons-nous reproduire {incidence2} avec {dplyr}?
Nous pouvons obtenir un objet similaire à cases à partir
de l’objet incidence2::covidregionaldataUK à l’aide du
package dplyr.
R
incidence2::covidregionaldataUK %>%
dplyr::select(date, cases_new) %>%
dplyr::group_by(date) %>%
dplyr::summarise(confirm = sum(cases_new, na.rm = TRUE)) %>%
dplyr::ungroup() %>%
dplyr::slice_head(n = 90)
Cependant, incidence2::incidence() contient des
arguments pratiques comme complete_dates qui facilitent
l’obtention d’un objet d’incidence avec le même intervalle de dates pour
chaque groupe sans nécessiter de lignes de code supplémentaires ou un
package de séries temporelles.
Dans une situation d’épidémie, il est probable que nous n’ayons accès qu’au début de l’ensemble des données d’entrée. Nous supposons donc que nous ne disposons que des 90 premiers jours de ces données.
R
plot(cases_sliced)
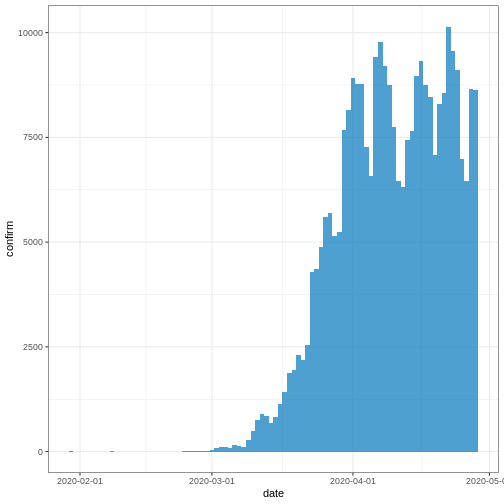
Pour transmettre les résultats de incidence2 à
EpiNow2, nous devons supprimer une colonne de l’objet
cases_filter :
R
# Drop column for {EpiNow2} input format
cases <- cases_sliced %>%
dplyr::select(-count_variable)
cases
SORTIE
# A tibble: 90 × 2
date confirm
<date> <dbl>
1 2020-01-30 3
2 2020-01-31 0
3 2020-02-01 0
4 2020-02-02 0
5 2020-02-03 0
6 2020-02-04 0
7 2020-02-05 2
8 2020-02-06 0
9 2020-02-07 0
10 2020-02-08 8
# ℹ 80 more rowsDistribution des délais
Nous supposons qu’il existe des délais entre le moment de l’infection et le moment où un cas est signalé. Nous spécifions ces délais sous forme de distributions pour tenir compte de l’incertitude des différences au niveau individuel. Le délai peut impliquer plusieurs types de processus. Un délai typique entre le moment de l’infection et la déclaration du cas peut consister en ce qui suit
le temps écoulé entre l’infection et l’apparition des symptômes (le période d’incubation) + délai entre l’apparition des symptômes et la notification du cas (délai de déclaration) .
La distribution des délais pour chacun de ces processus peut être estimée à partir de données ou obtenue à partir de la littérature. Nous pouvons exprimer l’incertitude quant aux paramètres corrects des distributions en supposant que les distributions ont fixe fixes ou qu’elles ont variables variables. Pour comprendre la différence entre fixe et variables considérons la période d’incubation.
Délais et données
Le nombre de retards et le type de retard sont des données flexibles qui dépendent des données. Les exemples ci-dessous montrent comment les délais peuvent être spécifiés pour différentes sources de données :
| Source de données | Délai (s) |
|---|---|
| Heure d’apparition des symptômes | Période d’incubation |
| Date de la déclaration du cas | Période d’incubation + délai entre l’apparition des symptômes et la notification du cas |
| Durée de l’hospitalisation | Période d’incubation + temps écoulé entre l’apparition des symptômes et l’hospitalisation |
Distribution de la période d’incubation
La distribution de la période d’incubation pour de nombreuses maladies peut généralement être obtenue à partir de la littérature. L’ensemble epiparameter contient une bibliothèque de paramètres épidémiologiques pour différentes maladies, obtenus à partir de la littérature.
Nous spécifions une distribution gamma (fixe) avec moyenne \(\mu = 4\) et un écart-type \(\sigma = 2\) (forme = \(4\), échelle = \(1\)) en utilisant la fonction
Gamma() comme suit :
R
incubation_period_fixed <- EpiNow2::Gamma(
mean = 4,
sd = 2,
max = 20
)
incubation_period_fixed
SORTIE
- gamma distribution (max: 20):
shape:
4
rate:
1L’argument max est la valeur maximale que la
distribution peut prendre ; dans cet exemple, 20 jours.
Nous pouvons tracer les distributions générées par
EpiNow2 en utilisant plot().
R
plot(incubation_period_fixed)
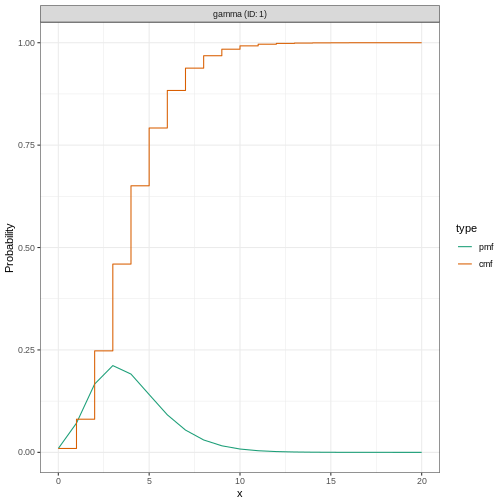
Pourquoi une distribution gamma ?
La période d’incubation doit être une valeur positive. Nous devons donc spécifier une distribution en EpiNow2 qui ne concerne que les valeurs positives.
Gamma() prend en charge les distributions Gamma et
LogNormal() les distributions log-normales, qui sont des
distributions pour les valeurs positives uniquement.
Pour tous les types de retard, nous devrons utiliser des distributions pour les valeurs positives uniquement - nous ne voulons pas inclure les retards de jours négatifs dans notre analyse !
Prise en compte de l’incertitude de la distribution
Pour spécifier une distribution variable nous incluons l’incertitude autour de la moyenne \(\mu\) et de l’écart-type \(\sigma\) de notre distribution gamma. Si notre distribution de la période d’incubation a une moyenne \(\mu\) et un écart-type \(\sigma\) nous supposons que la moyenne (\(\mu\)) suit une distribution normale avec un écart type \(\sigma_{\mu}\):
\[\mbox{Normal}(\mu,\sigma_{\mu}^2)\]
et un écart-type (\(\sigma\)) suit une distribution normale avec un écart type \(\sigma_{\sigma}\):
\[\mbox{Normal}(\sigma,\sigma_{\sigma}^2).\]
Nous spécifions ceci en utilisant Normal() pour chaque
argument : la moyenne (\(\mu = 4\) avec
\(\sigma_{\mu} = 0.5\)) et l’écart-type
(\(\sigma = 2\) avec \(\sigma_{\sigma} = 0.5\)).
R
incubation_period_variable <- EpiNow2::Gamma(
mean = EpiNow2::Normal(mean = 4, sd = 0.5),
sd = EpiNow2::Normal(mean = 2, sd = 0.5),
max = 20
)
incubation_period_variable
SORTIE
- gamma distribution (max: 20):
shape:
- normal distribution:
mean:
4
sd:
0.61
rate:
- normal distribution:
mean:
1
sd:
0.31Traçons la distribution que nous venons de configurer :
R
plot(incubation_period_variable)
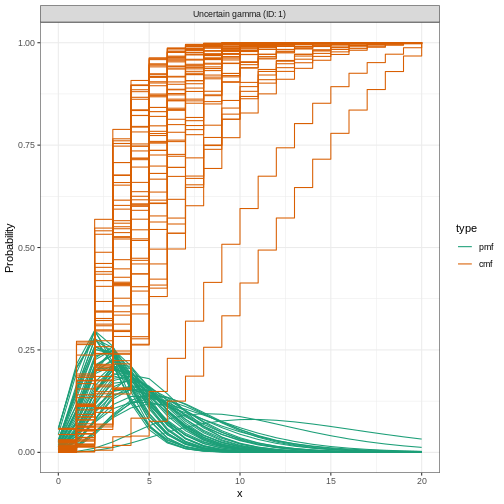
Retards dans l’établissement des rapports
Après la période d’incubation, il s’écoule un délai supplémentaire entre l’apparition des symptômes et la notification du cas : le délai de déclaration. Nous pouvons le spécifier comme une distribution fixe ou variable, ou estimer une distribution à partir de données.
Lorsque vous spécifiez une distribution, il est utile de visualiser la densité de probabilité pour voir le pic et l’étendue de la distribution. Dans cet example, nous allons utiliser une distribution log normale.
Si nous voulons supposer que le délai de déclaration moyen est de 2
jours (avec une incertitude de 0,5 jour) et que l’écart type est de 1
jour (avec une incertitude de 0,5 jour), nous pouvons spécifier une
distribution variable à l’aide de la commande LogNormal()
comme précédemment :
R
reporting_delay_variable <- EpiNow2::LogNormal(
meanlog = EpiNow2::Normal(mean = 2, sd = 0.5),
sdlog = EpiNow2::Normal(mean = 1, sd = 0.5),
max = 10
)
Visualisez une distribution log-normale en utilisant {epiparameter}
En utilisant epiparameter::epiparameter() nous pouvons
créer une distribution personnalisée. La distribution normale à
logarithme fixe aura l’aspect suivant :
R
library(epiparameter)
R
epiparameter::epiparameter(
disease = "covid",
epi_name = "reporting delay",
prob_distribution =
epiparameter::create_prob_distribution(
prob_distribution = "lnorm",
prob_distribution_params = c(
meanlog = 2,
sdlog = 1
)
)
) %>%
plot()
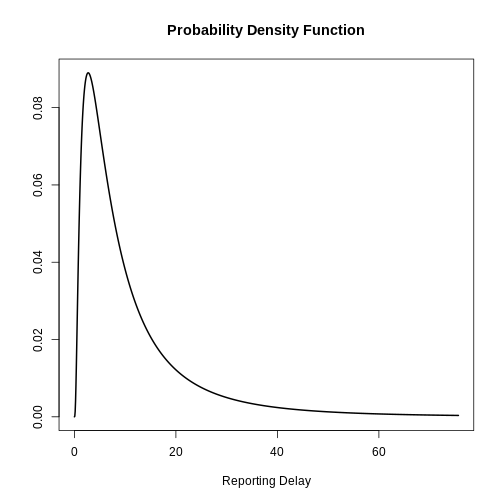
Comment obtenir le délai de reporting à partir des données ?
Si l’on dispose de données sur le délai entre l’apparition des
symptômes et la déclaration, on peut utiliser la fonction
estimate_delay() pour estimer une distribution log-normale
à partir d’un vecteur de délais. Le code ci-dessous illustre comment
utiliser la fonction estimate_delay() avec des données
synthétiques sur les délais.
R
library(tidyverse)
# Steps:
# - get Ebola data from package {outbreaks}
# - keep a subset of columns for this example only
# - calculate the time difference between two dates in linelist
# - extract the time difference as a vector class object
# - estimate the delay parameters using {EpiNow2}
outbreaks::ebola_sim_clean$linelist %>%
tibble::as_tibble() %>%
dplyr::select(case_id, date_of_onset, date_of_hospitalisation) %>%
dplyr::mutate(reporting_delay = date_of_hospitalisation - date_of_onset) %>%
dplyr::pull(reporting_delay) %>%
EpiNow2::estimate_delay(
samples = 1000,
bootstraps = 10
)
SORTIE
WARN [2025-11-11 01:32:57] dist_fit (chain: 1): The largest R-hat is 1.11, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-11-11 01:32:57] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:32:57] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:00] dist_fit (chain: 1): The largest R-hat is 1.06, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-11-11 01:33:00] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:00] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:02] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:02] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:04] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:04] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:06] dist_fit (chain: 1): The largest R-hat is 1.12, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-11-11 01:33:06] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:06] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:08] dist_fit (chain: 1): The largest R-hat is 1.15, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-11-11 01:33:08] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:08] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:11] dist_fit (chain: 1): The largest R-hat is 1.11, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-11-11 01:33:11] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:11] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:13] dist_fit (chain: 1): The largest R-hat is 1.1, indicating chains have not mixed.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#r-hat -
WARN [2025-11-11 01:33:13] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:13] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:15] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:15] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess -
WARN [2025-11-11 01:33:17] dist_fit (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess -
WARN [2025-11-11 01:33:17] dist_fit (chain: 1): Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess - SORTIE
- lognormal distribution (max: 22):
meanlog:
- normal distribution:
mean:
0.21
sd:
0.16
sdlog:
- normal distribution:
mean:
1
sd:
0.12Temps de génération
Nous devons également spécifier une distribution pour le temps de génération. Nous utiliserons ici une distribution log-normale avec une moyenne de 3,6 et un écart-type de 3,1 (Ganyani et al. 2020).
R
generation_time_variable <- EpiNow2::LogNormal(
mean = EpiNow2::Normal(mean = 3.6, sd = 0.5),
sd = EpiNow2::Normal(mean = 3.1, sd = 0.5),
max = 20
)
Trouver des estimations
La fonction epinow() est une “enveloppe” pour la
fonction estimate_infections() utilisée pour estimer les
cas par date d’infection. La distribution du temps de génération et la
distribution des délais doivent être transmises à l’aide des fonctions
generation_time_opts() et delay_opts()
respectivement.
Il existe de nombreuses autres entrées qui peuvent être transmises à
epinow() voir ?EpiNow2::epinow() pour plus de
détails. Une entrée optionnelle consiste à spécifier un a priori
log-normal pour le nombre de reproduction effectif \(R_t\) au début de l’épidémie. Nous
spécifions une moyenne de 2 jours et un écart-type de 2 jours comme
arguments de la commande prior dans
rt_opts():
R
# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = EpiNow2::LogNormal(mean = 2, sd = 2))
Inférence bayésienne à l’aide de Stan
L’inférence bayésienne est réalisée à l’aide de méthodes MCMC avec le
programme Stan. Les fonctions Stan
disposent d’un certain nombre d’entrées par défaut, notamment le nombre
de chaînes et le nombre d’échantillons par chaîne (voir
?EpiNow2::stan_opts()).
Pour réduire le temps de calcul, nous pouvons exécuter les chaînes en
parallèle. Pour ce faire, nous devons définir le nombre de cœurs à
utiliser. Par défaut, 4 chaînes MCMC sont exécutées (voir
stan_opts()$chains), nous pouvons donc définir un nombre
égal de cœurs à utiliser en parallèle comme suit :
R
withr::local_options(base::list(mc.cores = 4))
Pour connaître le nombre maximal de cœurs disponibles sur votre
machine, utilisez la commande parallel::detectCores().
Liste de vérification
Note : Dans le code ci-dessous _fixed
les distributions sont utilisées à la place de _variable
(distributions de retard avec incertitude). Cela permet d’accélérer le
temps de calcul. Il est généralement recommandé d’utiliser des
distributions variables qui tiennent compte d’une incertitude
supplémentaire.
R
# fixed alternatives
generation_time_fixed <- EpiNow2::LogNormal(
mean = 3.6,
sd = 3.1,
max = 20
)
reporting_delay_fixed <- EpiNow2::LogNormal(
mean = 2,
sd = 1,
max = 10
)
Vous êtes maintenant prêt à exécuter EpiNow2::epinow()
pour estimer le nombre de reproduction variable dans le temps pour les
90 premiers jours :
R
estimates <- EpiNow2::epinow(
# reported cases
data = cases,
# delays
generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
# prior
rt = rt_prior
)
N’attendez pas que cela se poursuive
Pour les besoins de ce tutoriel, nous pouvons optionnellement
utiliser EpiNow2::stan_opts() pour réduire le temps de
calcul. Nous pouvons spécifier un nombre fixe de
samples = 1000 et chains = 2 aux
stan l’argument de la EpiNow2::epinow() de la
fonction. Cette opération devrait prendre environ 3 minutes.
<Nous pouvons optionnellement définir
stan = stan_opts(method = "vb") pour utiliser une méthode
d’échantillonnage approximative. Cela devrait prendre moins d’une
minute. –>
R
# you can add the `stan` argument
EpiNow2::epinow(
...,
stan = EpiNow2::stan_opts(samples = 1000, chains = 3)
)
Rappelez-vous : En utilisant un nombre approprié d’ échantillons et de chaînes est cruciale pour garantir la convergence et obtenir des estimations fiables dans les calculs bayésiens utilisant Stan. L’obtention de résultats plus précis se fait au détriment de la vitesse.
Résultats
Nous pouvons extraire et visualiser des estimations du nombre de reproductions effectives au fil du temps :
R
estimates$plots$R
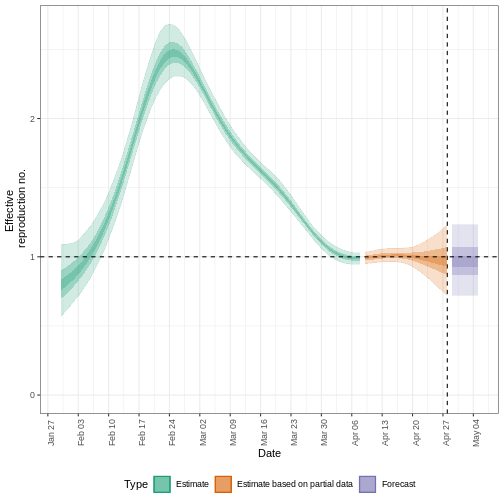
L’incertitude des estimations augmente avec le temps. Cela s’explique par le fait que les estimations sont fondées sur des données antérieures, c’est-à-dire sur les périodes de retard. Cette différence d’incertitude est classée dans les catégories suivantes Estimation (vert) utilise toutes les données et Estimation basée sur des données partielles (orange) des estimations basées sur moins de données (parce que les infections qui se sont produites à l’époque sont plus susceptibles de ne pas avoir encore été observées) et qui ont donc des intervalles de plus en plus larges vers la date du dernier point de données. Enfin, les Prévision (violet) est une projection dans le temps.
Nous pouvons également visualiser l’estimation du taux de croissance dans le temps :
R
estimates$plots$growth_rate
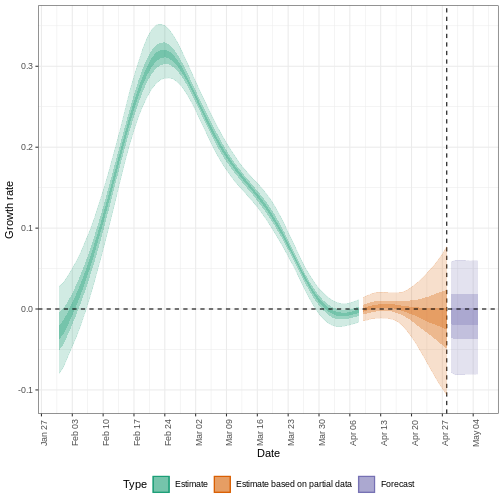
Pour extraire un résumé des principaux paramètres de transmission à dernière date* dans les données :
R
summary(estimates)
SORTIE
measure estimate
<char> <char>
1: New infections per day 7821 (4823 -- 13140)
2: Expected change in reports Likely decreasing
3: Effective reproduction no. 0.96 (0.75 -- 1.2)
4: Rate of growth -0.012 (-0.099 -- 0.079)
5: Doubling/halving time (days) -56 (8.8 -- -7)Ces estimations étant basées sur des données partielles, elles présentent un large intervalle d’incertitude.
Le résumé de notre analyse montre que le changement attendu dans les déclarations est de Likely decreasing avec l’estimation des nouvelles infections 7821 (4823 – 13140).
Le nombre effectif de reproduction \(R_t\) (à la dernière date des données) est de 0.96 (0.75 – 1.2).
Le taux de croissance exponentiel du nombre de cas est de -0.012 (-0.099 – 0.079).
Le temps de doublement (le temps nécessaire pour que le nombre de cas double) est de -56 (8.8 – -7).
Expected change in reports
Un facteur décrivant l’évolution attendue des déclarations sur la base de la probabilité a posteriori que \(R_t < 1\).
| Probabilité (\(p\)) | Changement attendu (\(p\)) |
|---|---|
| p < 0.05$ | Augmentation |
| 0,05$ p< 0,4$ | Augmentation probable |
| 0,4$ p< 0,6$ | Stable |
| 0,6$ p < 0,95$ | Vraisemblablement décroissante |
| 0,95$ p $ | Décroissante |
Intervalles crédibles
En tout EpiNow2 les régions ombrées reflètent les intervalles de crédibilité de 90 %, 50 % et 20 %, du plus clair au plus foncé.
Liste de vérification
EpiNow2 peut être utilisé pour estimer les paramètres de
transmission à partir des données relatives aux cas, à tout moment de
l’évolution d’une épidémie. La fiabilité de ces estimations dépend de la
qualité des données et du choix approprié des distributions de délais.
Dans le prochain tutoriel, nous apprendrons à faire des prévisions et
nous étudierons certaines des options d’inférence supplémentaires
disponibles dans le logiciel EpiNow2.
Défi
Défi
Quantifier l’hétérogénéité géographique
Les données relatives au début de la pandémie de COVID-19 au Royaume-Uni proviennent du package R incidence2 comprennent la région dans laquelle les cas ont été enregistrés. Pour obtenir des estimations régionales du nombre effectif de reproductions et de cas, nous devons formater les données de manière à ce qu’elles comportent trois colonnes :
-
datela date, -
region: la région, -
confirmle nombre de déclarations de maladies (confirmées) pour une région à une date donnée.
Générer des estimations régionales de Rt à partir des
incidence2::covidregionaldataUK à partir de la base de
données :
- utiliser incidence2 pour convertir les données
agrégées en données d’incidence par la variable
region, - conserver les 90 premières dates pour toutes les régions,
- estimer le Rt par région en utilisant le temps de génération défini et les retards dans cet épisode.
R
regional_cases <- incidence2::covidregionaldataUK %>%
# use {tidyr} to preprocess missing values
tidyr::replace_na(base::list(cases_new = 0))
Pour manipuler les données, vous pouvez
R
regional_cases <- incidence2::covidregionaldataUK %>%
# use {tidyr} to preprocess missing values
tidyr::replace_na(base::list(cases_new = 0)) %>%
# use {incidence2} to convert aggregated data to incidence data
incidence2::incidence(
date_index = "date",
groups = "region",
counts = "cases_new",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable) %>%
dplyr::filter(date < ymd(20200301))
Pour apprendre à faire l’estimation régionale de Rt, lisez la section
de la vignette “Get started” sur regional_epinow() à
l’adresse https://epiforecasts.io/EpiNow2/articles/EpiNow2.html#regional_epinow
Pour obtenir des estimations régionales, nous utilisons les mêmes
arguments de epinow() dans la fonction
regional_epinow():
R
estimates_regional <- EpiNow2::regional_epinow(
# cases
data = regional_cases,
# delays
generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
# prior
rt = rt_prior
)
Visualisez les résultats avec :
R
estimates_regional$summary$summarised_results$table
estimates_regional$summary$plots$R
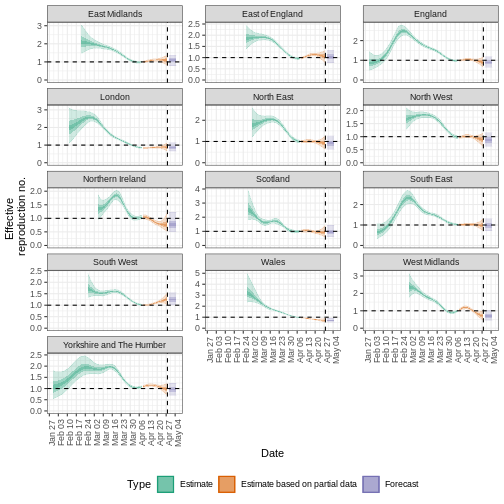
Points clés
- Les paramètres de transmission peuvent être estimés à partir des données du cas après prise en compte des retards.
- L’incertitude peut être prise en compte dans la distribution des retards.
Content from Utiliser les distributions de délais dans l'analyse
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 30 minutes
Vue d'ensemble
Questions
- Comment réutiliser les délais enregistrés dans le epiparameter avec mon pipeline d’analyse existant ?
Objectifs
- Utilisez les fonctions de distribution pour les distributions
continues et discrètes enregistrées en tant que objets
<epiparameter>. - Convertissez une distribution continue en distribution discrète à l’aide de la fonction epiparameter.
- Connecter les sorties de epiparameter avec les entrées EpiNow2.
Conditions préalables
- Compléter le tutoriel Accéder aux distribution des délais épidémiologiques
- Compléter le tutoriel Quantifier la transmission
Pour cet épisode, vous devez vous familiariser avec :
Science des données Programmation de base avec R.
Statistiques : Distributions de probabilité.
Théorie des épidémies : paramètres épidémiologiques, périodes de temps, nombre reproductif effectif.
Introduction
Cet épisode intégrera le contenu des deux épisodes précédents.
Commençons par charger le packageepiparameter et
EpiNow2 . Nous utiliserons le tube %>%,
quelques verbes de dplyr et ggplot2 et
donc appelons aussi à le package tidyverse :
R
library(epiparameter)
library(EpiNow2)
library(tidyverse)
Pour résumer, nous avons appris que epiparameter nous aide à choisir un ensemble spécifique de paramètres épidémiologiques issus de la littérature, au lieu de les copier/coller à la main:
R
covid_serialint <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
single_epiparameter = TRUE
)
Nous avons maintenant un paramètre épidémiologique que nous pouvons
utiliser dans notre analyse ! Par exemple, pour quantifier la
transmission, nous pouvons utiliser l’intervalle sériel comme
approximation du temps de génération. Dans le bloc de code ci-dessous,
nous avons remplacé un des paramètres statistiques
sommaires en EpiNow2::LogNormal()
R
generation_time <-
EpiNow2::LogNormal(
mean = covid_serialint$summary_stats$mean, # replaced!
sd = covid_serialint$summary_stats$sd, # replaced!
max = 20
)
Dans cet épisode, nous utiliserons les fonctions de
distribution qui epiparameter fournit pour
obtenir une médiane, valeur maximale (max), percentiles ou
quantiles pour tout objet de classe <epiparameter>.
Ils vous seront utiles en aval dans votre pipeline d’analyse !
Le double point-virgule
Le double point-virgule :: dans R vous permet d’appeler
une fonction spécifique d’un package sans charger l’ensemble du package
dans l’environnement actuel.
Par example, dplyr::filter(data, condition) utilise la
fonctionfilter() du paquet `{dplyr}’.
Cela nous permet de nous souvenir des fonctions du paquet et d’éviter les conflits d’espace de noms en spécifiant explicitement la fonction du paquet à utiliser lorsque plusieurs paquets ont des fonctions portant le même nom.
Fonctions de distribution
w En R, toutes les distributions statistiques disposent de fonctions qui permettant d’accéder aux éléments suivants :
-
density(): fonction de densité de probabilité (FDP), -
cdf()fonction de distribution cumulative (FDC), -
quantile(): Quantile et -
generate(): Aléatoire valeurs aléatoires de la distribution donnée.
Fonctions pour la loi normale
Si vous en avez besoin, lisez en détail la rubrique Fonctions de probabilité R pour la loinormale Pour en savoir plus sur les fonctions de probabilité de la loi normale, lisez les définitions de chacune d’entre elles et identifiez la partie de la loi dans laquelle elles se situent !
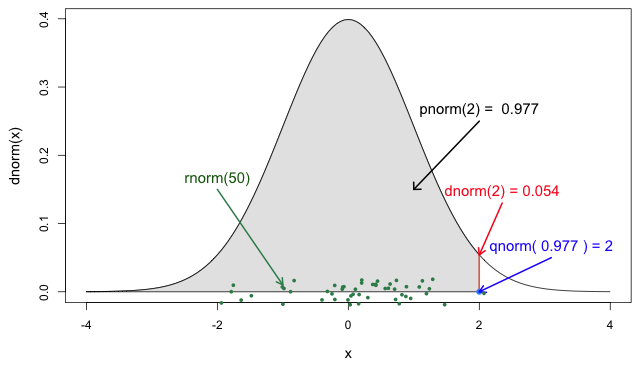
Si vous regardez ?stats::Distributions, chaque type de
distribution possède un ensemble unique de fonctions. Cependant,
epiparameter vous donne les mêmes quatre fonctions pour
accéder à chacune des valeurs ci-dessus pour n’importe quelle objet
<epiparameter> de votre choix !
R
# plot this to have a visual reference
# continuous distribution
plot(covid_serialint, xlim = c(0, 20))
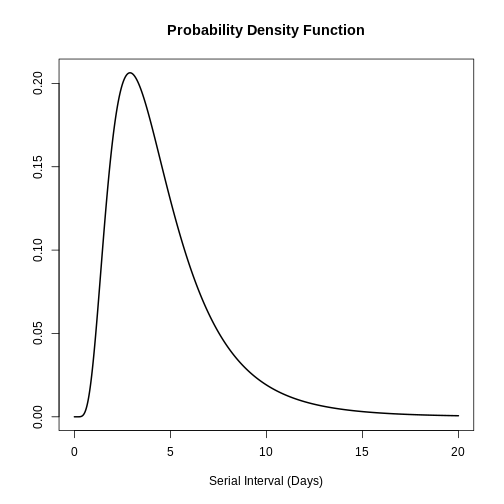
R
# the density value at quantile value of 10 (days)
density(covid_serialint, at = 10)
SORTIE
[1] 0.01911607R
# the cumulative probability at quantile value of 10 (days)
epiparameter::cdf(covid_serialint, q = 10)
SORTIE
[1] 0.9466605R
# the quantile value (day) at a cumulative probability of 60%
quantile(covid_serialint, p = 0.6)
SORTIE
[1] 4.618906R
# generate 10 random values (days) given
# the distribution family and its parameters
epiparameter::generate(covid_serialint, times = 10)
SORTIE
[1] 2.382512 7.554113 1.688063 6.682228 3.708993 3.796628 3.902427 2.665439
[9] 4.138396 3.374977L’accès à la documentation de référence (fichiers d’aide) de ces
fonctions est accessible avec la notation à trois doubles points :
epiparameter:::
?epiparameter:::density.epiparameter()?epiparameter:::cdf.epiparameter()?epiparameter:::quantile.epiparameter()?epiparameter:::generate.epiparameter()
Fenêtre pour la recherche de contact et l’intervalle sériel
L’intervalle sériel est important pour l’optimisation de la recherche des contacts, car il fournit une fenêtre temporelle pour l’endiguement de la propagation d’une maladie (Fine, 2003). En fonction de l’intervalle sériel, nous pouvons évaluer la nécessité d’augmenter le nombre de jours pris en compte pour la recherche des contacts afin d’inclure un plus grand nombre de contacts rétrospectifs (Davis et al., 2020).
Avec l’intervalle sériel COVID-19 (covid_serialint),
calculez :
- Quelle proportion supplémentaire des cas rétrospectifs pourrait être capturée si la méthode de recherche des contacts prenait en compte les contacts jusqu’à 6 jours avant l’apparition de la maladie par rapport à 2 jours avant l’apparition de la maladie ?
Dans la figure 5 du Fonctions
de probabilité R pour la loi normale la partie ombrée représente une
probabilité cumulée de 0.997 pour la valeur du quantile à
x = 2.
R
plot(covid_serialint)
R
epiparameter::cdf(covid_serialint, q = 2)
SORTIE
[1] 0.1111729R
epiparameter::cdf(covid_serialint, q = 6)
SORTIE
[1] 0.7623645Étant donné l’intervalle sériel COVID-19 :
Une méthode de recherche des contacts prenant en compte les contacts jusqu’à 2 jours avant l’apparition de la maladie permettra d’identifier environ 11,1 % des cas rétrospectifs.
Si cette période est étendue à 6 jours avant l’apparition de la maladie, 76,2 % des cas rétrospectifs pourraient être pris en compte.
Si nous échangeons la question entre les jours et la probabilité cumulée à :
- Considèrent les cas secondaires, combien de jours après l’apparition des symptômes des cas primaires peut-on s’attendre à ce que 55 % des symptômes apparaissent ?
R
quantile(covid_serialint, p = 0.55)
L’interprétation pourrait être la suivante :
- Les 55 % de cas secondaires seront devenus symptômatique 4,2 jours après l’apparition des symptômes des cas primaires.
Discrétiser une distribution continue
Nous nous rapprochons de la fin ! EpiNow2::LogNormal() a
encore besoin d’une valeur maximale (max).
Une façon d’y parvenir est d’obtenir la valeur du quantile pour le
99e percentile de la distribution ou 0.99 probabilité
cumulative de la distribution. Pour le faire, nous devons accéder à
l’ensemble des fonctions de distribution de notre objet
<epiparameter>.
Nous pouvons utiliser l’ensemble des fonctions de distribution d’un
distribution continue (comme ci-dessus). Cependant, ces valeurs seront
des nombres continus. Nous pouvons discrétiser la
distribution continue enregistréedans notre
objet<epiparameter> pour obtenir des valeurs
discrètes à partir d’une distribution continue.
Lorsque nous epiparameter::discretise() la distribution
continue, nous obtenons une distribution discrète :
R
covid_serialint_discrete <-
epiparameter::discretise(covid_serialint)
covid_serialint_discrete
SORTIE
Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Parameter: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: discrete lnorm (days)
Parameters:
meanlog: 1.386
sdlog: 0.568Nous identifions ce changement dans la Distribution:
ligne de sortie de l’objet <epiparameter>. Vérifiez à
nouveau cette ligne :
Distribution: discrete lnormAlors que pour une distribution continue nous traçons la courbe de la Fonction de densité de probabilité (FDP) pour une distribution discrète, nous traçons la Fonction de masse de probabilité (FMP):
R
# discrete distribution
plot(covid_serialint_discrete)
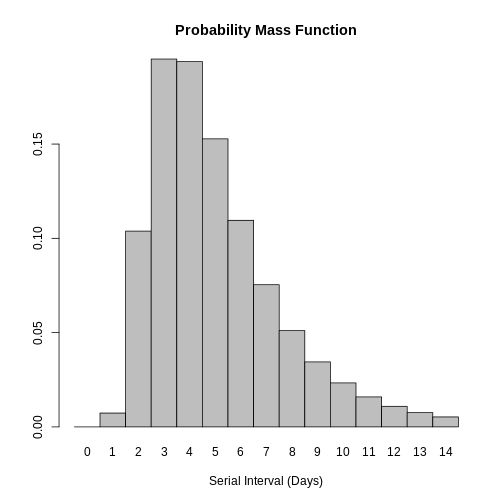
Pour obtenir enfin une max, accédons à la valeur du
quantile du 99e percentile ou 0.99 de la distribution à
l’aide de la fonction prob_dist$q de la même manière que
nous accédons à les valeurs summary_stats.
R
covid_serialint_discrete_max <-
quantile(covid_serialint_discrete, p = 0.99)
Durée de la quarantaine et de la période d’incubation
La période d’incubation est un délai utile pour évaluer la durée de la surveillance active ou de la quarantaine (Lauer et al., 2020). De même, les délais entre l’apparition des symptômes et la guérison (ou le décès) détermineront la durée nécessaire des soins de santé et de l’isolement des cas (Cori et al.).
Calculez :
- Dans quel délai précis 99 % des personnes présentant les symptômes de COVID-19 les manifestent-elles après l’infection ?
Quelle est la distribution des délais qui mesure le temps écoulé entre l’infection et l’apparition des symptômes ?
Les fonctions de probabilité pour les distributions
<epiparameter> discrètes sont les
mêmes que celles que nous avons utilisées pour les distributions
continues !
R
# plot to have a visual reference
plot(covid_serialint_discrete, xlim = c(0, 20))
# density value at quantile value 10 (day)
density(covid_serialint_discrete, at = 10)
# cumulative probability at quantile value 10 (day)
epiparameter::cdf(covid_serialint_discrete, q = 10)
# In what quantile value (days) do we have the 60% cumulative probability?
quantile(covid_serialint_discrete, p = 0.6)
# generate random values
epiparameter::generate(covid_serialint_discrete, times = 10)
R
covid_incubation <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "incubation",
single_epiparameter = TRUE
)
SORTIE
Using Linton N, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov A, Jung S, Yuan
B, Kinoshita R, Nishiura H (2020). "Incubation Period and Other
Epidemiological Characteristics of 2019 Novel Coronavirus Infections
with Right Truncation: A Statistical Analysis of Publicly Available
Case Data." _Journal of Clinical Medicine_. doi:10.3390/jcm9020538
<https://doi.org/10.3390/jcm9020538>..
To retrieve the citation use the 'get_citation' functionR
covid_incubation_discrete <- epiparameter::discretise(covid_incubation)
quantile(covid_incubation_discrete, p = 0.99)
SORTIE
[1] 1999% des personnes qui développent les symptômes du COVID-19 le feront dans les 16 jours suivant l’infection.
Réfléchissez-y, ce résultat est-il attendu en termes épidémiologiques ?
A partir d’une valeur maximale avec quantile() nous
pouvons créer une séquence de valeurs de quantiles sous la forme d’un
tableau numérique et calculer density() pour chacune
d’entre elles :
R
# create a discrete distribution visualisation
# from a maximum value from the distribution
quantile(covid_serialint_discrete, p = 0.99) %>%
# generate quantile values
# as a sequence for each natural number
seq(1L, to = ., by = 1L) %>%
# coerce numeric vector to data frame
as_tibble_col(column_name = "quantile_values") %>%
mutate(
# calculate density values
# for each quantile in the density function
density_values =
density(
x = covid_serialint_discrete,
at = quantile_values
)
) %>%
# create plot
ggplot(
aes(
x = quantile_values,
y = density_values
)
) +
geom_col()
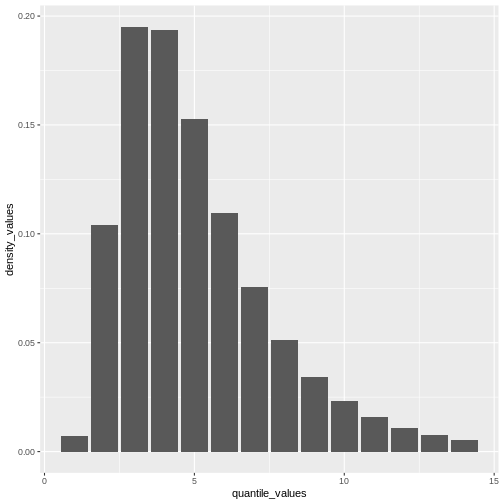
Rappelez-vous : Dans les infections à transmission pré-symptomatique, les intervalles sériels peuvent avoir des valeurs négatives (Nishiura et al., 2020). Lorsque nous utilisons la méthode intervalle sériel pour approximer le temps de génération nous devons effectuer cette distribution avec des valeurs positives uniquement !
Plug-in {epiparameter} pour {EpiNow2}
Maintenant, nous pouvons brancher le tout dans le fonction
EpiNow2::LogNormal() !
- les statistiques sommaires
meanetsdde la distribution, - une valeur maximale
max, - le nom de la
distribution.
Lors qu’on utilise EpiNow2::LogNormal() pour définir une
loi log-normale comme celle de
l’objetcovid_serialint, nous pouvons spécifier la moyenne
et l’écart-type comme paramètres. Pour obtenir les paramètres “naturels”
d’une loi log-normale, nous pouvons également convertir ces statistiques
sommaires en paramètres de distribution nommés meanlog et
sdlog. Avec epiparameter nous pouvons
obtenir directement les paramètres de distribution en utilisant
epiparameter::get_parameters():
R
covid_serialint_parameters <-
epiparameter::get_parameters(covid_serialint)
On a alors :
R
serial_interval_covid <-
EpiNow2::LogNormal(
meanlog = covid_serialint_parameters["meanlog"],
sdlog = covid_serialint_parameters["sdlog"],
max = covid_serialint_discrete_max
)
serial_interval_covid
SORTIE
- lognormal distribution (max: 14):
meanlog:
1.4
sdlog:
0.57Dans l’hypothèse d’un scénario COVID-19, utilisons les 60 premiers
jours de l’ensemble de données . example_confirmed du
package EpiNow2 comme reported_cases et
l’objet récemment créé serial_interval_covid en tant que
données d’entrée pour estimer le nombre de reproduction variable dans le
temps à l’aide du fonction EpiNow2::epinow().
R
# Set 4 cores to be used in parallel computations
withr::local_options(list(mc.cores = 4))
epinow_estimates_cg <- EpiNow2::epinow(
# cases
data = example_confirmed[1:60],
# delays
generation_time = EpiNow2::generation_time_opts(serial_interval_covid)
)
base::plot(epinow_estimates_cg)
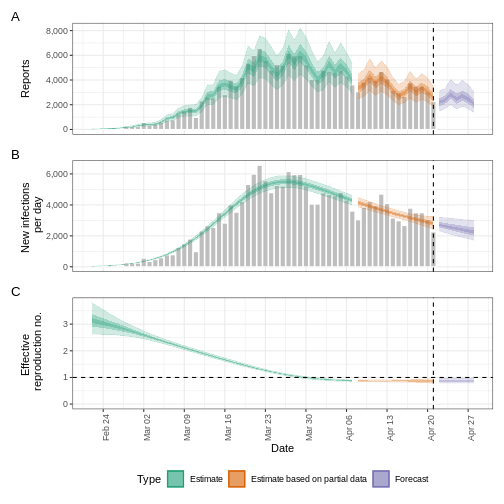
La sortie plot() comprend les cas estimés par date
d’infection, qui sont reconstitués à partir des cas déclarés et des
retards.
Avertissement
L’utilisation de l’intervalle sériel au lieu du temps de génération est une alternative qui peut propager un biais dans vos estimations, d’autant plus pour les maladies dont la transmission pré-symptomatique est signalée. (Chung Lau et al, 2021)
We can stop the livecoding at this stage and move on with the practical.
Ajustement pour tenir compte des délais de déclaration
L’estimation de \(R_t\) nécessite des données sur le nombre quotidien de nouvelles infections. En raison des délais dans le développement de charges virales détectables, l’apparition des symptômes, la recherche de soins et la déclaration, ces chiffres ne sont pas facilement disponibles. Toutes les observations reflètent des événements de transmission survenus dans le passé. En d’autres termes, si \(d\) est le délai entre l’infection et l’observation, alors les observations au temps \(t\) informent \(R_{t−d}\) et non \(R_t\). (Gostic et al., 2020)
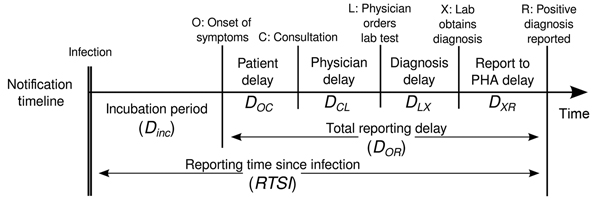
La distribution des délais pourrait être déduite
conjointement avec les temps d’infection sous-jacents, ou estimée comme
la somme des distributions de la . période d’incubation et du délais
entre l’apparition des symptômes et l’observation à partir des données
de la liste d’attente (délai de
déclaration). Pour EpiNow2, nous pouvons spécifier
ces deux distributions de délais complémentaires dans l’argument
delays.
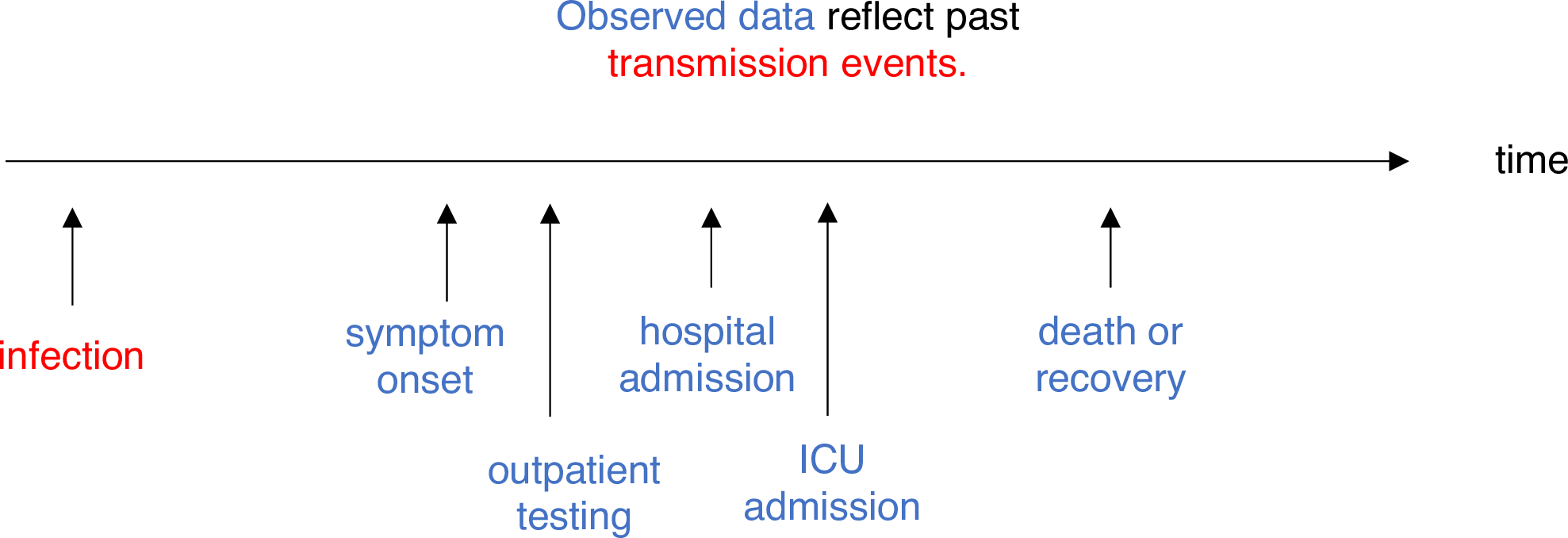
Utiliser une période d’incubation pour COVID-19 afin d’estimer Rt
Estimez le nombre de reproduction variable dans le temps pour les 60
premiers jours de l’ensemble de données example_confirmed
de EpiNow2. Accédez à une période d’incubation pour
COVID-19 à partir de epiparameter pour l’utiliser comme
délai de déclaration.
Utilisez le dernier calcul d’ epinow() à l’aide de
l’argument delays et la fonction d’aide
delay_opts() e.
L’argument delays et la fonction
d’aidedelay_opts() sont analogues à l’argument
generation_time et à la fonction d’aide
generation_time_opts().
R
epinow_estimates <- EpiNow2::epinow(
# cases
reported_cases = example_confirmed[1:60],
# delays
generation_time = EpiNow2::generation_time_opts(covid_serial_interval),
delays = EpiNow2::delay_opts(covid_incubation_time)
)
R
# generation time ---------------------------------------------------------
# get covid serial interval
covid_serialint <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
covid_serialint_discrete_max <- covid_serialint %>%
epiparameter::discretise() %>%
quantile(p = 0.99)
covid_serialint_parameters <-
epiparameter::get_parameters(covid_serialint)
covid_serial_interval <-
EpiNow2::LogNormal(
meanlog = covid_serialint_parameters["meanlog"],
sdlog = covid_serialint_parameters["sdlog"],
max = covid_serialint_discrete_max
)
# incubation time ---------------------------------------------------------
# get covid incubation period
covid_incubation <- epiparameter::epiparameter_db(
disease = "covid",
epi_name = "incubation",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
covid_incubation_discrete_max <- covid_incubation %>%
epiparameter::discretise() %>%
quantile(p = 0.99)
covid_incubation_parameters <-
epiparameter::get_parameters(covid_incubation)
covid_incubation_time <-
EpiNow2::LogNormal(
meanlog = covid_incubation_parameters["meanlog"],
sdlog = covid_incubation_parameters["sdlog"],
max = covid_incubation_discrete_max
)
# epinow ------------------------------------------------------------------
# run epinow
epinow_estimates_cgi <- EpiNow2::epinow(
# cases
data = example_confirmed[1:60],
# delays
generation_time = EpiNow2::generation_time_opts(covid_serial_interval),
delays = EpiNow2::delay_opts(covid_incubation_time)
)
base::plot(epinow_estimates_cgi)
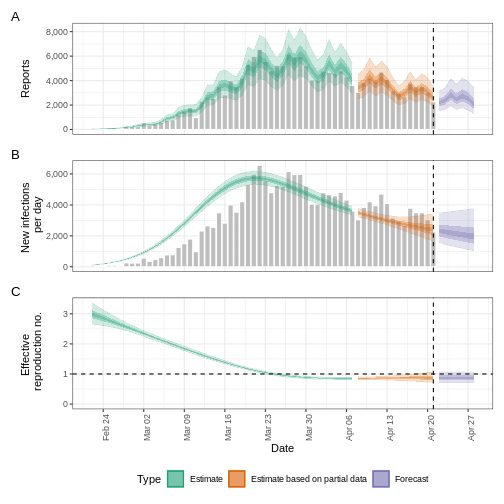
Essayez de compléter le delays avec un délai de
déclaration comme le reporting_delay_fixed de l’épisode
précédent.
Dans quelle mesure a-t-il changé ?
Après avoir ajouté la période d’incubation, discutez-en :
- La tendance de l’ajustement du modèle dans la section “Estimation” change-t-elle ?
- L’incertitude a-t-elle changé ?
- Comment expliqueriez-vous ou interpréteriez-vous ces changements ?
Comparez toutes les figures EpiNow2 générées précédemment.
Défis
Une astuce pour compléter le code
Si nous écrivons l’élément [] à côté de l’objet
covid_serialint_parameters[] à l’intérieur de
[] nous pouvons utiliser le touche de tabulation
↹ pour accéder à la fonctionnalité
de complétion de code
Elle permet d’accéder rapidement aux éléments suivants
covid_serialint_parameters["meanlog"] et
covid_serialint_parameters["sdlog"].
Nous vous invitons à tester ceci dans des blocs de code et dans la console R !
Nombre de reproduction effectif d’Ebola ajusté en fonction des délais de déclaration
Téléchargez et lisez les données Ebola:
- Estimez le nombre de reproduction effectif en utilisant EpiNow2
- Ajustez l’estimation en fonction des délais de déclaration disponibles en epiparameter
- Pourquoi avez-vous choisi ce paramètre ?
Pour calculer la \(R_t\) en utilisant EpiNow2 nous avons besoin de :
- L’incidence agrégée
dataavec les cas confirmés par jour, et - La distribution du temps
generation. - Optionnellement, les distributions des délais de déclaration lorsqu’elles sont disponibles (par exemple, la période d’incubation).
Pour obtenir la distribution des délais à l’aide de epiparameter, nous pouvons utiliser des fonctions comme :
epiparameter::epiparameter_db()epiparameter::parameter_tbl()discretise()quantile()
R
# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
ebola_confirmed <-
read_csv(here::here("data", "raw-data", "ebola_cases.csv")) %>%
incidence2::incidence(
date_index = "date",
counts = "confirm",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable)
# list distributions
epiparameter::epiparameter_db(disease = "ebola") %>%
epiparameter::parameter_tbl()
R
# generation time ---------------------------------------------------------
# subset one distribution for the generation time
ebola_serial <- epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "serial",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
ebola_serial_discrete <- epiparameter::discretise(ebola_serial)
serial_interval_ebola <-
EpiNow2::Gamma(
mean = ebola_serial$summary_stats$mean,
sd = ebola_serial$summary_stats$sd,
max = quantile(ebola_serial_discrete, p = 0.99)
)
# incubation time ---------------------------------------------------------
# subset one distribution for delay of the incubation period
ebola_incubation <- epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "incubation",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
ebola_incubation_discrete <- epiparameter::discretise(ebola_incubation)
incubation_period_ebola <-
EpiNow2::Gamma(
mean = ebola_incubation$summary_stats$mean,
sd = ebola_incubation$summary_stats$sd,
max = quantile(ebola_serial_discrete, p = 0.99)
)
# epinow ------------------------------------------------------------------
# run epinow
epinow_estimates_egi <- EpiNow2::epinow(
# cases
data = ebola_confirmed,
# delays
generation_time = EpiNow2::generation_time_opts(serial_interval_ebola),
delays = EpiNow2::delay_opts(incubation_period_ebola)
)
SORTIE
WARN [2025-11-11 01:40:14] epinow: There were 1 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2025-11-11 01:40:14] epinow: Examine the pairs() plot to diagnose sampling problems
- R
plot(epinow_estimates_egi)
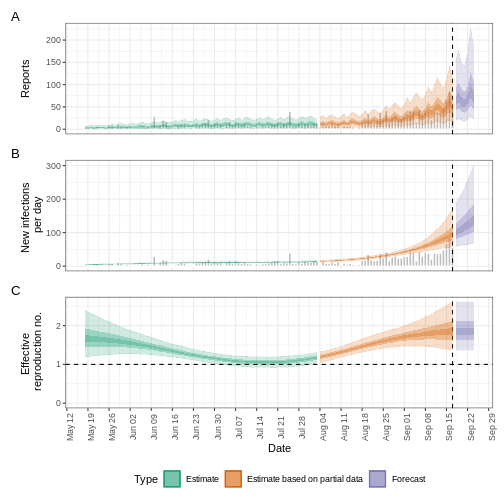
Que faire avec les distributions de Weibull ?
Utilisez les données influenza_england_1978_school du
package outbreaks pour calculer le nombre de reproduction
effectif à l’aide de EpiNow2 en ajustant en fonction des
délais de déclaration disponibles dans epiparameter.
EpiNow2::NonParametric() accepte les fonctions de masse
de probabilité (FMP) de n’importe quelle famille de distribution. Lisez
le guide de référence sur les Distributions
de probabilités.
R
# What parameters are available for Influenza?
epiparameter::epiparameter_db(disease = "influenza") %>%
epiparameter::parameter_tbl() %>%
count(epi_name)
SORTIE
# Parameter table:
# A data frame: 3 × 2
epi_name n
<chr> <int>
1 generation time 1
2 incubation period 15
3 serial interval 1R
# generation time ---------------------------------------------------------
# Read the generation time
influenza_generation <-
epiparameter::epiparameter_db(
disease = "influenza",
epi_name = "generation"
)
influenza_generation
SORTIE
Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Parameter: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull (days)
Parameters:
shape: 2.360
scale: 3.180R
# EpiNow2 currently accepts Gamma or LogNormal
# other can pass the PMF function
influenza_generation_discrete <-
epiparameter::discretise(influenza_generation)
influenza_generation_max <-
quantile(influenza_generation_discrete, p = 0.99)
influenza_generation_pmf <-
density(
influenza_generation_discrete,
at = 0:influenza_generation_max
)
influenza_generation_pmf
SORTIE
[1] 0.00000000 0.06312336 0.22134988 0.29721220 0.23896828 0.12485164 0.04309454R
# EpiNow2::NonParametric() can also accept the PMF values
generation_time_influenza <-
EpiNow2::NonParametric(
pmf = influenza_generation_pmf
)
# incubation period -------------------------------------------------------
# Read the incubation period
influenza_incubation <-
epiparameter::epiparameter_db(
disease = "influenza",
epi_name = "incubation",
single_epiparameter = TRUE
)
# Discretize incubation period
influenza_incubation_discrete <-
epiparameter::discretise(influenza_incubation)
influenza_incubation_max <-
quantile(influenza_incubation_discrete, p = 0.99)
influenza_incubation_pmf <-
density(
influenza_incubation_discrete,
at = 0:influenza_incubation_max
)
influenza_incubation_pmf
SORTIE
[1] 0.00000000 0.05749151 0.16687705 0.22443092 0.21507632 0.16104546 0.09746609
[8] 0.04841928R
# EpiNow2::NonParametric() can also accept the PMF values
incubation_time_influenza <-
EpiNow2::NonParametric(
pmf = influenza_incubation_pmf
)
# epinow ------------------------------------------------------------------
# Read data
influenza_cleaned <-
outbreaks::influenza_england_1978_school %>%
select(date, confirm = in_bed)
# Run epinow()
epinow_estimates_igi <- EpiNow2::epinow(
# cases
data = influenza_cleaned,
# delays
generation_time = EpiNow2::generation_time_opts(generation_time_influenza),
delays = EpiNow2::delay_opts(incubation_time_influenza)
)
plot(epinow_estimates_igi)
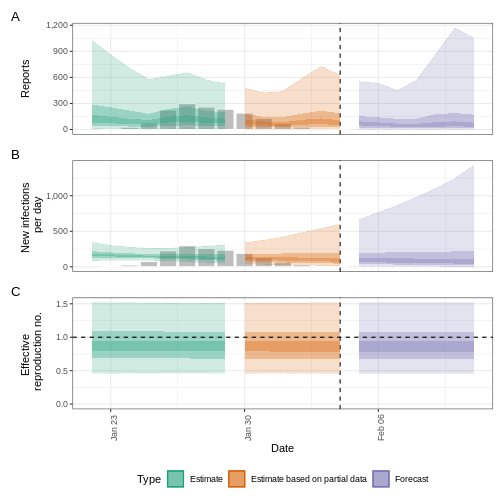
Prochaines étapes
Comment obtenir des paramètres de distribution à partir de distributions statistiques ?
Comment obtenir la moyenne et l’écart-type d’un temps de génération
avec seulement des paramètres de distribution mais aucune
statistique sommaire tel que mean ou sd pour
EpiNow2::Gamma() ou EpiNow2::LogNormal()?
Regardez la vignette epiparameter sur l’extraction et la conversion des paramètres et sescas d’utilisations!
Comment estimer la distribution des délais pour la maladie X ?
Consultez cet excellent tutoriel sur l’estimation de l’intervalle sériel et de la période d’incubation de la maladie X en tenant compte de la censure en utilisant l’inférence bayésienne avec des packages comme rstan et coarseDataTools.
- Tutoriel en anglais : https://rpubs.com/tracelac/diseaseX
- Tutoriel en Español : https://epiverse-trace.github.io/epimodelac/EnfermedadX.html
Ensuite, Après avoir obtenu vos valeurs estimées,
vous pouvez créer manuellement vos propres objets de classe
<epiparameter> à l’aide de la fonction
epiparameter::epiparameter()! Jetez un coup d’œil à songuide
de référence sur “Créer un objet
<epiparameter>”!
Enfin, jetez un coup d’œil au derniers packages R {epidist} et {primarycensored}
qui fournissent des méthodes pour relever les principaux défis de
l’estimation des distributions, y compris la troncature, la censure par
intervalle et les biais dynamiques.
Points clés
- Utilisez les fonctions de distribution avec
<epiparameter>pour obtenir des statistiques sommaires et des paramètres informatifs pour les interventions de santé publique, comme la fenêtre de recherche des contacts et la durée de la quarantaine. - Utilisez
discretise()pour convertir les distributions de délais continues en distributions discrètes. - Utilisez epiparameter pour obtenir les délais de déclaration requis dans les estimations de transmissibilité.
Content from Établir des prévisions à court terme
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 60 minutes
Vue d'ensemble
Questions
- Comment créer des prévisions à court terme à partir de données de cas ?
- Comment tenir compte des rapports incomplets dans les prévisions ?
Objectifs
- Apprendre à faire des prévisions de cas à l’aide du logiciel R
EpiNow2 - Apprendre à inclure un processus d’observation dans l’estimation
Conditions préalables
- Compléter le tutoriel Quantifier la transmission
Les apprenants doivent se familiariser avec les dépendances conceptuelles suivantes avant de suivre ce tutoriel :
Statistiques: distributions de probabilités, principe d’ Analyse bayésienne.
Théorie des épidémies: Nombre de reproduction effectif.
Introduction
À partir des données relatives aux cas d’ épidémie, il est possible d’estimer le nombre actuel et futur de cas en tenant compte à la fois des délais de la déclaration et de la sous-déclaration. Pour faire des prévisions sur l’évolution future de l’épidémie, nous devons émettre une hypothèse sur la façon dont les observations faites jusqu’à présent sont liées à ce que nous attendons à l’avenir. La façon la plus simple de procéder est de supposer qu’il n’y a pas de changement, c’est-à-dire que le nombre de reproduction restera le même à l’avenir qu’au moment de la dernière observation. Dans ce tutoriel, nous établirons des prévisions en supposant que le nombre de reproductions restera le même que son estimation à la dernière date pour laquelle des données étaient disponibles.
Dans ce tutoriel, nous allons apprendre à utiliser la fonction EpiNow2 pour prévoir les cas en tenant compte des observations incomplètes et pour prévoir les observations secondaires telles que les décès.
Nous utiliserons le tuyau %>% pour connecter des
fonctions, donc appelons aussi l’opérateur tidyverse au
paquetage :
R
library(EpiNow2)
library(tidyverse)
Le double point-virgule
Le double point-virgule :: dans R vous permet d’appeler
une fonction spécifique d’un paquet sans charger l’intégralité du paquet
dans l’environnement actuel.
Par exemple, vous pouvez appeler une fonction spécifique d’un paquet
sans charger le paquet entier dans l’environnement actuel,
dplyr::filter(data, condition) utilise
filter() à partir de l’outil dplyr
paquet.
Cela nous permet de nous souvenir des fonctions du paquet et d’éviter les conflits d’espace de noms.
Créez une prévision à court terme
La fonction epinow() décrite dans l’épisode quantifier la transmission est
une enveloppe pour les fonctions :
-
estimate_infections()utilisée pour estimer le nombre de cas par date d’infection. -
forecast_infections()utilisée pour simuler des infections à l’aide d’un ajustement existant (estimation) aux cas observés.
Utilisons le même code que celui utilisé dans l’épisode quantifier la transmission pour obtenir les données d’entrée, les délais et les priorités :
R
# Read cases dataset
cases <- incidence2::covidregionaldataUK %>%
# use {tidyr} to preprocess missing values
tidyr::replace_na(base::list(cases_new = 0)) %>%
# use {incidence2} to compute the daily incidence
incidence2::incidence(
date_index = "date",
counts = "cases_new",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable) # Drop count_variable as no longer needed
# Incubation period
incubation_period_fixed <- EpiNow2::Gamma(
mean = 4,
sd = 2,
max = 20
)
# Log-tranformed mean
log_mean <- EpiNow2::convert_to_logmean(mean = 2, sd = 1)
# Log-transformed std
log_sd <- EpiNow2::convert_to_logsd(mean = 2, sd = 1)
# Reporting delay
reporting_delay_fixed <- EpiNow2::LogNormal(
mean = log_mean,
sd = log_sd,
max = 10
)
# Generation time
generation_time_fixed <- EpiNow2::LogNormal(
mean = 3.6,
sd = 3.1,
max = 20
)
# define Rt prior distribution
rt_prior <- EpiNow2::rt_opts(prior = EpiNow2::LogNormal(mean = 2, sd = 2))
Nous pouvons maintenant extraire les prévisions à court terme à l’aide de :
R
# Assume we only have the first 90 days of this data
reported_cases <- cases %>%
dplyr::slice(1:90)
# Estimate and forecast
estimates <- EpiNow2::epinow(
data = reported_cases,
generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
rt = rt_prior
)
SORTIE
WARN [2025-11-11 01:44:47] epinow: There were 47 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth above 12. See
https://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded -
WARN [2025-11-11 01:44:47] epinow: Examine the pairs() plot to diagnose sampling problems
- N’attendez pas que cela se termine !
Ce dernier morceau peut prendre 10 minutes à s’exécuter. Continuez à lire cet épisode du tutoriel pendant qu’il s’exécute en arrière-plan. Pour plus d’informations sur le temps de calcul, lisez la section “Inférence bayésienne à l’aide de Stan” dans la section quantification de la transmission.
Nous pouvons visualiser les estimations du nombre de reproductions
effectives et du nombre estimé de cas à l’aide de plot().
Les estimations sont réparties en trois catégories :
Estimation (vert) : utilise toutes les données,
Estimation basée sur des données partielles (orange) : contient un degré d’incertitude plus élevé car ces estimations sont basées sur moins de données,
Prévision (violet) : prévisions pour l’avenir.
R
plot(estimates)
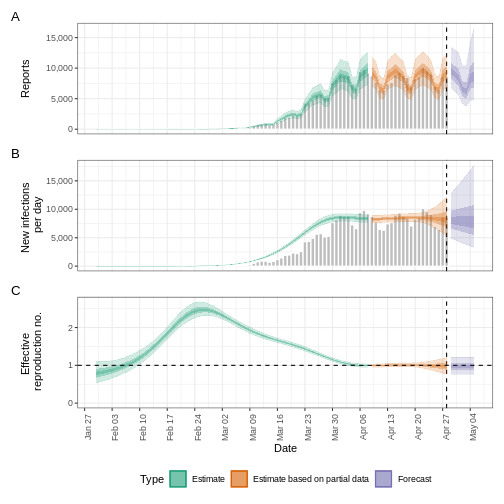
Prévision avec des observations incomplètes
Dans l’épisode de la quantification de la
transmission nous avons tenu compte des délais de déclaration. Dans
EpiNow2, nous pouvons également tenir compte des
observations incomplètes, car dans la réalité, 100 % des cas ne sont pas
déclarés. Nous passerons un argument supplémentaire appelé
obs dans le epinow() pour définir un modèle
d’observation. Le format de obs est défini par la fonction
obs_opt() (voir ?EpiNow2::obs_opts pour plus
de détails).
Supposons que nous estimions que les données de l’épidémie COVID-19
dans l’objet cases n’incluent pas tous les cas déclarés.
Nous estimons que seuls 40 % des cas réels sont déclarés. Pour spécifier
cela dans le modèle d’observation, nous devons passer un facteur
d’échelle avec une moyenne et un écart type. Si nous supposons que 40 %
des cas sont déclarés (avec un écart-type de 1 %), nous spécifions alors
le facteur d’échelle scale à obs_opts() comme
suit :
R
obs_scale <- EpiNow2::Normal(mean = 0.4, sd = 0.01)
Pour exécuter le cadre d’inférence avec ce processus d’observation,
nous ajoutons obs = obs_opts(scale = obs_scale) aux
arguments d’entrée de epinow():
R
# Define observation model
obs_scale <- EpiNow2::Normal(mean = 0.4, sd = 0.01)
# Assume we only have the first 90 days of this data
reported_cases <- cases %>%
dplyr::slice(1:90)
# Estimate and forecast
estimates <- EpiNow2::epinow(
data = reported_cases,
generation_time = EpiNow2::generation_time_opts(generation_time_fixed),
delays = EpiNow2::delay_opts(incubation_period_fixed + reporting_delay_fixed),
rt = rt_prior,
# Add observation model
obs = EpiNow2::obs_opts(scale = obs_scale)
)
base::summary(estimates)
SORTIE
measure estimate
<char> <char>
1: New infections per day 19968 (13162 -- 29794)
2: Expected change in reports Likely decreasing
3: Effective reproduction no. 0.97 (0.77 -- 1.2)
4: Rate of growth -0.012 (-0.091 -- 0.064)
5: Doubling/halving time (days) -56 (11 -- -7.6)Les estimations des mesures de transmission telles que le nombre de reproduction efficace et le taux de croissance sont similaires (ou de même valeur) par rapport à la situation où nous n’avons pas tenu compte des observations incomplètes (voir l’épisode de quantification de la transmission dans la section “Recherche d’estimations”). Cependant, le nombre de nouveaux cas confirmés par date d’infection a considérablement changé d’ampleur pour refléter l’hypothèse selon laquelle seuls 40 % des cas sont déclarés.
Nous pouvons également changer la distribution par défaut de
Binomiale négative à Poisson, supprimer l’effet de semaine par défaut
(qui tient compte des schémas hebdomadaires de déclaration) et bien
d’autres choses encore. Voir ?EpiNow2::obs_opts pour plus
de détails.
Quelles sont les implications de ce changement ?
- Comparer différents pourcentages d’observations %
- En quoi diffèrent-ils en ce qui concerne le nombre d’infections estimées ?
- Quelles sont les implications de ce changement pour la santé publique ?
Prévision des observations secondaires
L’outil EpiNow2 permet également d’estimer et de prévoir
les observations secondaires, par exemple les décès et les
hospitalisations, à partir d’une observation primaire, par exemple le
nombre de cas. Nous illustrerons ici comment prévoir le nombre de décès
découlant des cas observés de COVID-19 dans les premiers stades de
l’épidémie au Royaume-Uni.
Tout d’abord, nous devons formater nos données de manière à ce qu’elles comportent les colonnes suivantes :
-
date: la date (en tant qu’objet date, voir?is.Date()), -
primary: nombre d’observations primaires à cette date, dans cet exemple cas, -
secondary: nombre de dates d’observations secondaires, dans cet exemple décès.
R
reported_cases_deaths <- incidence2::covidregionaldataUK %>%
# use {tidyr} to preprocess missing values
tidyr::replace_na(base::list(cases_new = 0, deaths_new = 0)) %>%
# use {incidence2} to compute the daily incidence
incidence2::incidence(
date_index = "date",
counts = c(primary = "cases_new", secondary = "deaths_new"),
date_names_to = "date",
complete_dates = TRUE
) %>%
# rearrange to wide format for {EpiNow2}
pivot_wider(names_from = count_variable, values_from = count)
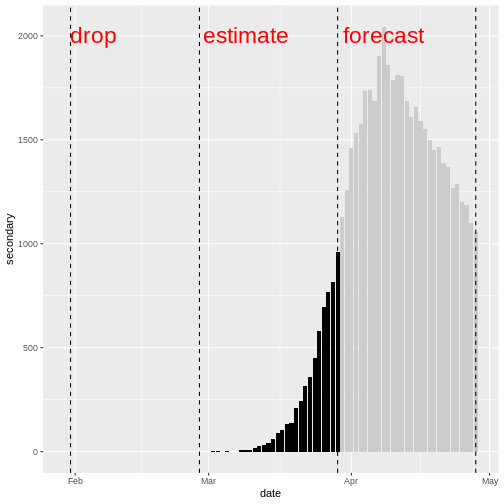
En utilisant les données sur les cas et les décès entre le 31e et le
60e jour, nous estimerons la relation entre les observations primaires
et secondaires à l’aide de la méthode suivante
estimate_secondary() puis nous prévoyons les décès futurs à
l’aide de forecast_secondary(). Pour plus de détails sur le
modèle, voir le documentation
du modèle.
Nous devons spécifier le type d’observation en utilisant
type en secondary_opts() Les options sont les
suivantes :
- “incidence” : les observations secondaires découlent d’observations primaires antérieures, c’est-à-dire de décès survenus à la suite de cas enregistrés.
- “prévalence” : les observations secondaires résultent d’une combinaison d’observations primaires actuelles et d’observations secondaires antérieures, c’est-à-dire l’utilisation des lits d’hôpitaux à partir des admissions actuelles à l’hôpital et de l’utilisation passée des lits d’hôpitaux.
Dans cet exemple, nous spécifions
secondary_opts(type = "incidence"). Voir
?EpiNow2::secondary_opts pour plus de détails.
La dernière donnée clé est la distribution des délais entre les
observations primaires et secondaires. Il s’agit ici du délai entre le
signalement du cas et le décès. Nous supposons que ce délai suit une
distribution gamma avec une moyenne de 14 jours et un écart-type de 5
jours. Nous pouvons également utiser epiparameter, comme
alternative, pour accéder
aux délais épidémiologiques). Nous utilisons Gamma()
pour spécifier une distribution gamma fixe.
Il existe d’autres fonctions d’entrée pour
estimate_secondary() qui peuvent être spécifiées, y compris
l’ajout d’un processus d’observation, voir
?EpiNow2::estimate_secondary pour plus de détails sur ces
options.
Pour trouver l’ajustement du modèle entre les cas et les décès :
R
# Estimate from day 31 to day 60 of this data
cases_to_estimate <- reported_cases_deaths %>%
slice(31:60)
# Delay distribution between case report and deaths
delay_report_to_death <- EpiNow2::Gamma(
mean = EpiNow2::Normal(mean = 14, sd = 0.5),
sd = EpiNow2::Normal(mean = 5, sd = 0.5),
max = 30
)
# Estimate secondary cases
estimate_cases_to_deaths <- EpiNow2::estimate_secondary(
data = cases_to_estimate,
secondary = EpiNow2::secondary_opts(type = "incidence"),
delays = EpiNow2::delay_opts(delay_report_to_death)
)
SORTIE
WARN [2025-11-11 01:49:02] estimate_secondary (chain: 1): Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#bulk-ess - Soyez prudent avec l’échelle de temps
Au début d’une épidémie, il peut y avoir des changements substantiels dans les tests et les rapports. Si les tests changent d’un mois à l’autre, l’ajustement du modèle sera biaisé. Vous devez donc être prudent quant à l’échelle temporelle des données utilisées dans l’ajustement du modèle et les prévisions.
Nous représentons l’ajustement du modèle (rubans ombrés) avec les observations secondaires (diagramme à barres) et les observations primaires (ligne pointillée) comme suit :
R
plot(estimate_cases_to_deaths, primary = TRUE)
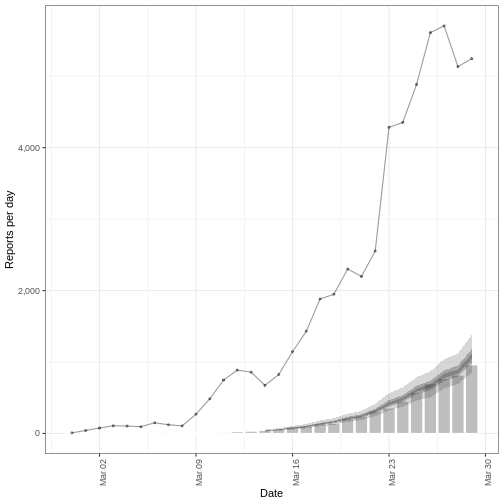
Pour utiliser cet ajustement de modèle afin de prévoir les décès, nous passons un cadre de données composé de l’observation primaire (cas) pour les dates non utilisées dans l’ajustement de modèle.
Remarque : dans cet épisode, nous utilisons des données dont nous connaissons les décès et les cas, nous créons donc une base de données en extrayant les cas. Mais dans la pratique, il s’agirait d’un ensemble de données différent composé uniquement de cas.
R
# Forecast from day 61 to day 90
cases_to_forecast <- reported_cases_deaths %>%
dplyr::slice(61:90) %>%
dplyr::mutate(value = primary)
Pour faire des prévisions, nous utilisons l’ajustement du modèle
estimate_cases_to_deaths:
R
# Forecast secondary cases
deaths_forecast <- EpiNow2::forecast_secondary(
estimate = estimate_cases_to_deaths,
primary = cases_to_forecast
)
plot(deaths_forecast)
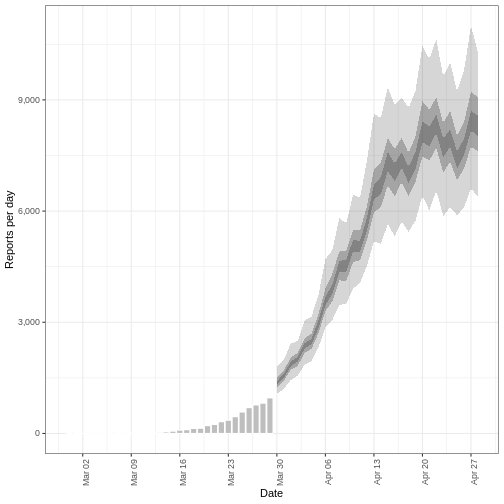
Le graphique montre les observations secondaires prévues (décès) pour
les dates pour lesquelles nous avons enregistré des cas. Il est
également possible de prévoir les décès à l’aide des cas prévus ; dans
ce cas, vous devez spécifier primary comme
estimates sortie de estimate_infections().
Intervalles crédibles
Dans tous les cas EpiNow2 les régions ombrées reflètent les intervalles de crédibilité de 90 %, 50 % et 20 %, dans l’ordre du plus clair au plus foncé.
Défi : Analyse de l’épidémie d’Ebola
Défi
Téléchargez le fichier ebola_cases.csv et lisez-le
dans R. Les données simulées sont la date d’apparition des symptômes et
le nombre de cas confirmés aux premiers stades de l’épidémie d’Ebola en
Sierra Leone en 2014.
En utilisant les 3 premiers mois (120 jours) de données :
- Estimez si les cas augmentent ou diminuent au 120e jour de l’épidémie.
- Tenir compte d’une capacité d’observation de 80 % des cas.
- Établissez une prévision à deux semaines du nombre de cas.
Vous pouvez utiliser les valeurs de paramètres suivantes pour la (les) distribution(s) des délais et la distribution du temps de génération.
- Période d’incubation : Log normal\((2.487,0.330)\) (Eichner et al. 2011 via epiparameter)
- Temps de génération : Gamma\((15.3, 10.1)\) (Équipe d’intervention de l’OMS contre Ebola 2014)
Vous pouvez inclure une certaine incertitude autour de la moyenne et de l’écart-type de ces distributions.
Nous utilisons le nombre de reproduction effectif et le taux de croissance pour estimer si les cas augmentent ou diminuent.
Nous pouvons utiliser le horizon à l’intérieur de la
forecast_opts() fourni pour forecast argument
dans epinow() pour étendre la durée de la prévision. La
valeur par défaut est de sept jours.
Assurez-vous que les données sont au bon format :
-
datela date (en tant qu’objet de date, voir?is.Date()), -
confirmnombre de cas confirmés à cette date.
Pour estimer le nombre de reproductions effectives et le taux de
croissance, nous utiliserons la fonction epinow().
Les données étant constituées de la date d’apparition des symptômes, il nous suffit de spécifier une distribution des délais pour la période d’incubation et le temps de génération.
Nous spécifions les distributions avec une certaine incertitude autour de la moyenne et de l’écart-type de la distribution log-normale pour la période d’incubation et de la distribution Gamma pour le temps de génération.
R
epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "incubation"
) %>%
epiparameter::parameter_tbl()
SORTIE
# Parameter table:
# A data frame: 5 × 7
disease pathogen epi_name prob_distribution author year sample_size
<chr> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 Ebola Virus Dise… Ebola V… incubat… lnorm Eichn… 2011 196
2 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 1798
3 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 49
4 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 957
5 Ebola Virus Dise… Ebola V… incubat… gamma WHO E… 2015 792R
ebola_eichner <- epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "incubation",
author = "Eichner"
)
ebola_eichner_parameters <- epiparameter::get_parameters(ebola_eichner)
ebola_incubation_period <- EpiNow2::LogNormal(
meanlog = EpiNow2::Normal(
mean = ebola_eichner_parameters["meanlog"],
sd = 0.5
),
sdlog = EpiNow2::Normal(
mean = ebola_eichner_parameters["sdlog"],
sd = 0.5
),
max = 20
)
ebola_generation_time <- EpiNow2::Gamma(
mean = EpiNow2::Normal(mean = 15.3, sd = 0.5),
sd = EpiNow2::Normal(mean = 10.1, sd = 0.5),
max = 30
)
Nous lisons les données en utilisant readr::read_csv().
Cette fonction reconnaît que la colonne date est une
<date> vecteur de classe.
R
# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
ebola_cases_raw <- readr::read_csv(
here::here("data", "raw-data", "ebola_cases.csv")
)
Prétraiter et adapter les données brutes pour EpiNow2:
R
ebola_cases <- ebola_cases_raw %>%
# use {tidyr} to preprocess missing values
tidyr::replace_na(base::list(confirm = 0)) %>%
# use {incidence2} to compute the daily incidence
incidence2::incidence(
date_index = "date",
counts = "confirm",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable)
dplyr::as_tibble(ebola_cases)
SORTIE
# A tibble: 123 × 2
date confirm
<date> <dbl>
1 2014-05-18 1
2 2014-05-19 0
3 2014-05-20 2
4 2014-05-21 4
5 2014-05-22 6
6 2014-05-23 1
7 2014-05-24 2
8 2014-05-25 0
9 2014-05-26 10
10 2014-05-27 8
# ℹ 113 more rowsNous définissons un modèle d’observation pour mettre à l’échelle le nombre estimé et prévu de nouvelles infections :
R
# Define observation model
# mean of 80% and standard deviation of 1%
ebola_obs_scale <- EpiNow2::Normal(mean = 0.8, sd = 0.01)
Comme nous voulons également créer une prévision sur deux semaines,
nous spécifions horizon = 14 pour prévoir 14 jours au lieu
des 7 jours par défaut.
R
ebola_estimates <- EpiNow2::epinow(
data = ebola_cases %>% dplyr::slice(1:120), # first 3 months of data only
generation_time = EpiNow2::generation_time_opts(ebola_generation_time),
delays = EpiNow2::delay_opts(ebola_incubation_period),
# Add observation model
obs = EpiNow2::obs_opts(scale = ebola_obs_scale),
# horizon needs to be 14 days to create two week forecast (default is 7 days)
forecast = EpiNow2::forecast_opts(horizon = 14)
)
SORTIE
WARN [2025-11-11 01:50:04] epinow: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess - R
summary(ebola_estimates)
SORTIE
measure estimate
<char> <char>
1: New infections per day 94 (49 -- 190)
2: Expected change in reports Increasing
3: Effective reproduction no. 1.7 (1.2 -- 2.4)
4: Rate of growth 0.042 (0.0034 -- 0.087)
5: Doubling/halving time (days) 17 (8 -- 210)Le numéro de reproduction effectif \(R_t\) (à la dernière date des données) est de 1.7 (1.2 – 2.4). Le taux de croissance exponentiel du nombre de cas est de 0.042 (0.0034 – 0.087).
Visualisez les estimations :
R
plot(ebola_estimates)
Prévision avec des estimations de \(R_t\)
Par défaut, les prévisions à court terme sont créées en utilisant la dernière estimation du nombre de reproductions \(R_t\). Cette estimation étant basée sur des données partielles, elle présente une grande incertitude.
Le nombre de reproductions projeté dans le futur peut être remplacé
par une estimation moins récente, basée sur des données plus nombreuses,
à l’aide de rt_opts():
R
EpiNow2::rt_opts(future = "estimate")
Il en résultera des prévisions moins incertaines (puisqu’elles sont basées sur les données de l \(R_t\) avec un intervalle d’incertitude plus étroit), mais les prévisions seront basées sur des estimations moins récentes de \(R_t\) et supposeront qu’il n’y a pas eu de changement depuis lors.
En outre, il est possible de projeter la valeur de \(R_t\) dans le futur à l’aide d’un modèle
générique en fixant future = "project". Comme cette option
utilise un modèle pour prévoir la valeur de \(R_t\) il en résultera des prévisions plus
incertaines que la valeur de estimate pour un exemple voir
ici.
Résumé
EpiNow2 peut être utilisé pour créer des prévisions à
court terme et pour estimer la relation entre différents résultats. Il
existe une série d’options de modèle qui peuvent être mises en œuvre
pour différentes analyses, y compris l’ajout d’un processus
d’observation pour tenir compte des déclarations incomplètes. Voir le
site web de l’Agence européenne pour la sécurité et la santé au travail.
vignette
pour plus de détails sur les différentes options de modèle dans
EpiNow2 qui ne sont pas abordées dans ces tutoriels.
Points clés
- Nous pouvons créer des prévisions à court terme en faisant des hypothèses sur le comportement futur du nombre de reproduction.
- Les estimations peuvent tenir compte des déclarations de cas incomplètes.
Content from Estimation de la gravité d'une épidémie
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 12 minutes
Vue d'ensemble
Questions
Pourquoi estime-t-on la gravité clinique d’une épidémie ?
Comment peut-on estimer le risque de létalité (RL) au début d’une épidémie en cours ?
Objectifs
Estimer le risque de létalité (RL) à partir de données épidémiologiques agrégées en utilisant la librairie cfr.
Estimer le RL ajusté au délai épidémiologique à l’aide des librairies epiparameter et cfr.
Estimer la sévérité ajustée au délai épidémiologique pour une série chronologique en expansion en utilisant le package cfr.
Pré-requis
Les concepts abordés dans cet épisode supposent que vous êtes familiers avec :
Science des données: Programmation de base avec R.
Théorie des épidémies: Distributions des délais.
R packages installés: cfr, epiparameter, outbreaks, tidyverse.
Installer les packages si elles ne le sont pas déjà:
R
# si {pak} n'est pas disponible, exécutez : install.packages("pak")
pak::pak("cfr")
pak::pak("epiparameter")
pak::pak("tidyverse")
pak::pak("outbreaks")
Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.
Introduction
Les questions les plus fréquentes au début d’une épidémie sont:
- Quel est l’impact probable de l’épidémie sur la santé publique en termes de gravité clinique ?
- Quels sont les groupes les plus gravement touchés ?
- L’épidémie risque-t-elle de provoquer une pandémie très grave ?
Nous pouvons évaluer le potentiel pandémique d’une épidémie à l’aide de deux mesures essentielles : la transmissibilité et la gravité clinique. (Fraser et al. 2009, CDC, 2016).
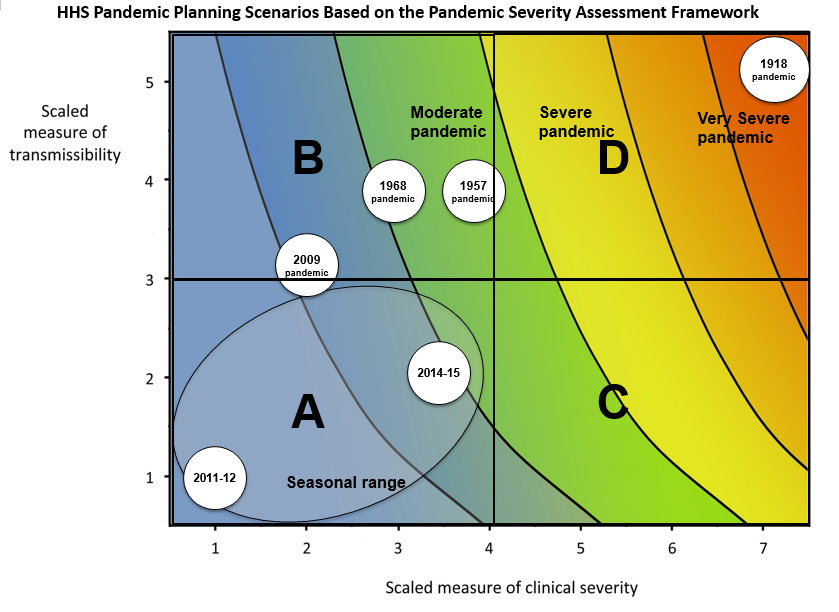
Une approche épidémiologique pour estimer la gravité clinique consiste à quantifier le risque de létalité (RL). Le risque de létalité est la probabilité conditionnelle de décès en cas de diagnostic confirmé, calculée comme le rapport entre le nombre cumulé de décès dus à une maladie infectieuse et le nombre de cas diagnostiqués confirmés. Toutefois, le calcule de ce paramètre de cette façon au cours d’une épidémie tend à aboutir à un RL naïf ou biaisé, compte tenu du délai entre l’apparition de la maladie et le décès, qui varie considérablement au fur et à mesure que l’épidémie progresse et se stabilise aux derniers stades de l’épidémie (Ghani et al. 2005).
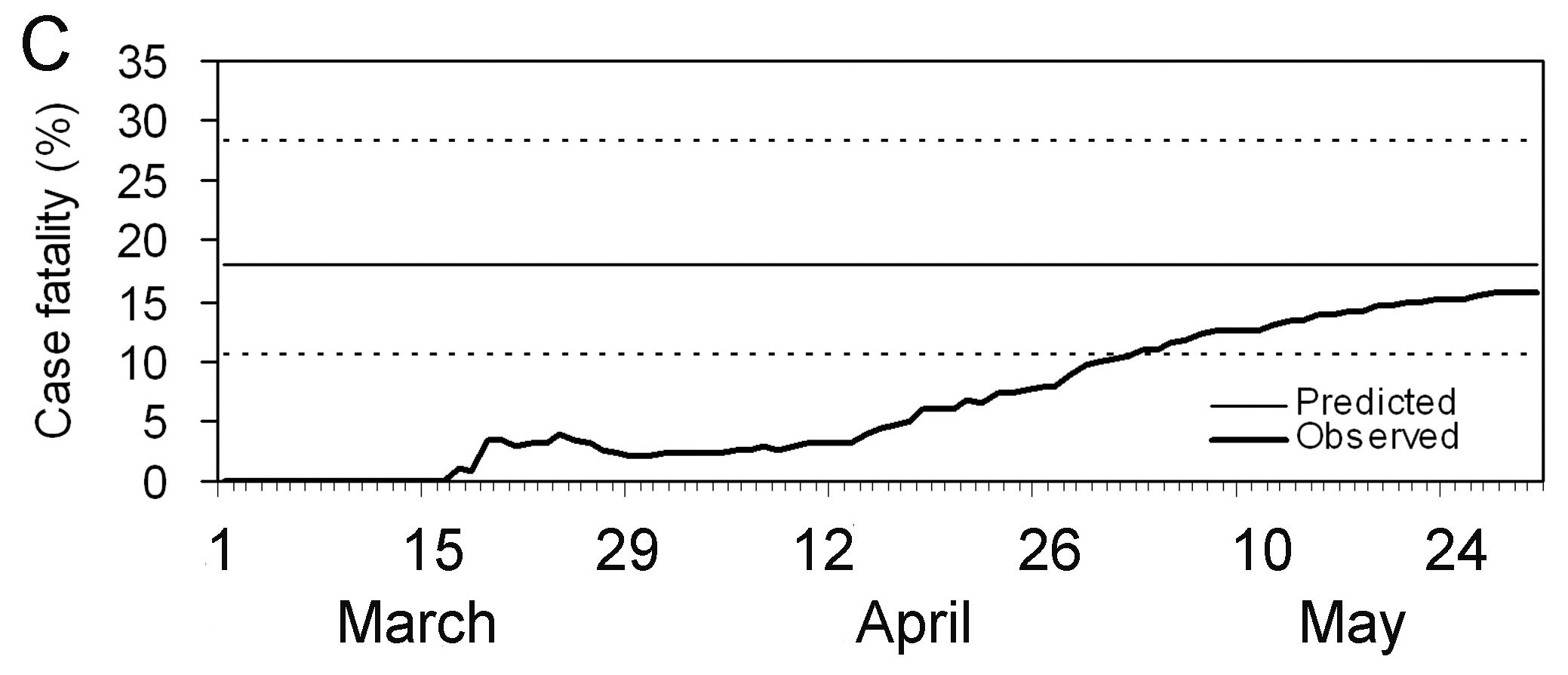
Les périodes sont pertinentes : Période 1 – 15 jours où le RL est nul, ce qui indique qu’aucun décès n’a été signalé ; Période du 15 mars au 26 avril où le RL semble augmenter ; Période du 30 avril au 30 mai où l’estimation du RL se stabilise.
Généralement, l’estimation de la gravité clinique d’une maladie peut être utile même en dehors d’un scénario de planification d’une pandémie et dans le contexte de la santé publique courante. Le fait de savoir si une épidémie a ou a eu une gravité différente de celle observée dans le passé peut motiver des recherches pour identifier les causes. Celles-ci peuvent être intrinsèques à l’agent infectieux (par exemple, une nouvelle souche plus grave) ou liées à des facteurs sous-jacents dans la population (par exemple, une immunité réduite ou des facteurs de morbidité) (Lipsitch et al., 2015).
Dans ce tutoriel, nous allons apprendre à utiliser la librairie cfr pour calculer et ajuster le risque de gravité clinique en utilisant la distribution des délais obtenue de la librairie epiparameter ou de d’autres sources, sur la base des méthodes développées par Nishiura et al. 2009. Nous allons aussi explorer la libraire cfr pour determiner comment l’utiliser pour calculer d’autres mesures de sévérité clinique.
Nous utiliserons l’opérateur pipe (%>%) de la
librairie magrittr pour relier facilement certaines
fonctions de la librairie cfr, y compris les fonctions de
la librairie de formatage de données dplyr. Nous
chargerons donc la librairie tidyverse, qui comprend à la
fois les librairies magrittr et dplyr.
R
# charger les packages
library(cfr)
library(epiparameter)
library(tidyverse)
library(outbreaks)
L’opérateur double deux-points
(::)
L’opérateur :: de R permet d’accéder aux fonctions ou
aux objets d’un package spécifique sans attacher l’intégralité du
package (sans faire appel à la function libray()). Il offre
plusieurs avantages, notamment :
- Indiquer explicitement le package d’origine d’une fonction, réduisant ainsi les ambiguïtés et les conflits potentiels lorsque plusieurs packages possèdent des fonctions portant le même nom.
- Permettre d’appeler une fonction depuis un package sans charger
l’intégralité du package avec un appel à la fonction
library().
Par exemple, la commande dplyr::filter(data, condition)
signifie que nous appelons la fonction filter() depuis la
librairie dplyr.
Discussion
Etiez-vous membre d’une équipe chargée de de concevoir des stratégies de réponse à une épidémie? Si oui:
- Comment évaluez-vous la gravité clinique de l’épidémie ?
- Quelles étaient les principales sources de biais ?
- Qu’aviez-vous fait pour prendre en compte les biais identifiés ?
- Quelle analyse complémentaire feriez-vous pour résoudre le biais ?
Sources de données pour la gravité clinique
Quelles sont les sources de données qu’on peut utiliser pour estimer la gravité clinique d’une épidémie? Verity et al, 2020 résume le spectre des cas de COVID-19 :
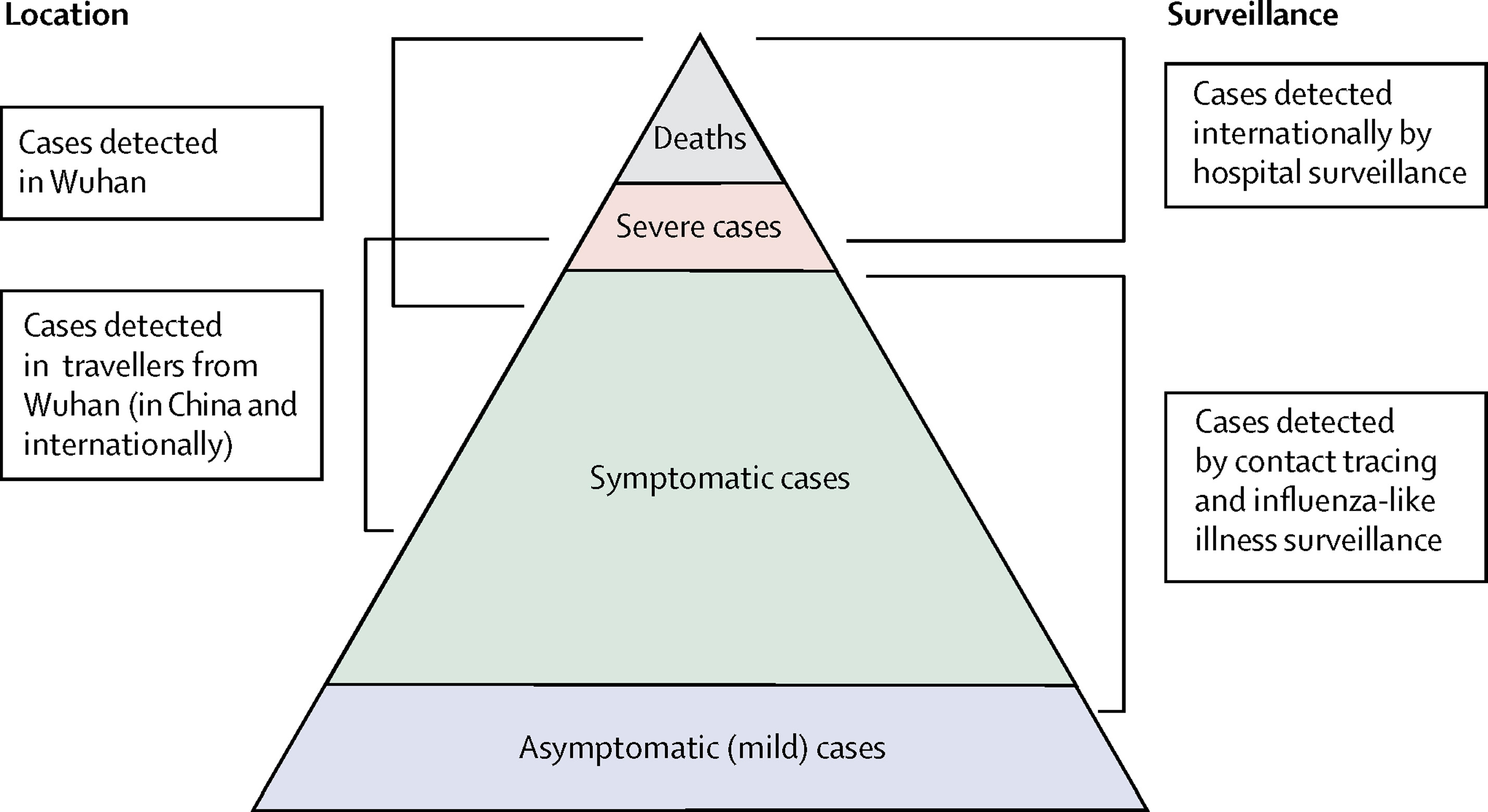
- Au sommet de la pyramide, les cas définis comme grave ou critiques selon les critères établis par l’OMS. Ces cas auraient probablement été identifiés en milieu hospitalier, présentant une pneumonie virale atypique. Ils auraient été identifiés en Chine continentale et parmi ceux classés au niveau international comme émanants d’une transmission locale.
- Beaucoup d’autres sont probablement symptomatiques (c’est-à-dire avec de la fièvre, de la toux ou des myalgies), mais ne nécessiteront peut-être pas d’hospitalisation. Ces cas auraient été identifiés grâce à leurs liens avec des voyageurs internationaux dans des zones à haut risque et grâce à la recherche des personnes en contact avec les cas confirmés. Ils pourraient être identifiés grâce à la surveillance de la population, par exemple en cas de syndrome grippal.
- La partie inférieure de la pyramide représente les cas bénins (et éventuellement asymptomatiques). Ces cas pourraient être identifiés par la recherche de cas contacts et, puis par des tests sérologiques.
Estimation du risque de létalité (RL) naïf
Nous mesurons la gravité d’une maladie en termes de risque de létalité (RL). Le RL est interprété comme la probabilité conditionnelle de décès en cas de diagnostic confirmé, calculée comme le ratio du nombre cumulé de décès \(D_{t}\) sur le nombre cumulé de cas confirmés \(C_{t}\) à un moment donné \(t\). Nous pouvons le référer au RL naïf (également RL brut ou biaisé, \(b_{t}\)) :
\[ b_{t} = \frac{D_{t}}{C_{t}} \]
Cette formule est considérée comme naïve parce qu’elle tend à produire un RL biaisé et largement sous-estimé en raison du délai entre l’apparition de la maladie et le décès, qui ne se stabilise que vers la fin de l’épidémie.
Pour calculer le RL naïf à l’aide de la librairie cfr, on a besoin d’un tableau de données comportant au minimum trois colonnes nommées :
datecasesdeaths
Explorons le tableau de données ebola1976 inclus dans le
package cfr, et qui contient les données provenant de la
première épidémie d’Ebola au Zaïre (actuelle la République Démocratique
du Congo) en 1976, comme l’ont analysé Camacho et al. (2014).
R
# charger le tableau de donnees ebola1976 du package {cfr}
data("ebola1976")
# Visualiser l'incidence du nombre de cas et de deces repertorie
ebola1976 %>%
incidence2::incidence(
date_index = "date",
counts = c("cases", "deaths")
) %>%
plot()
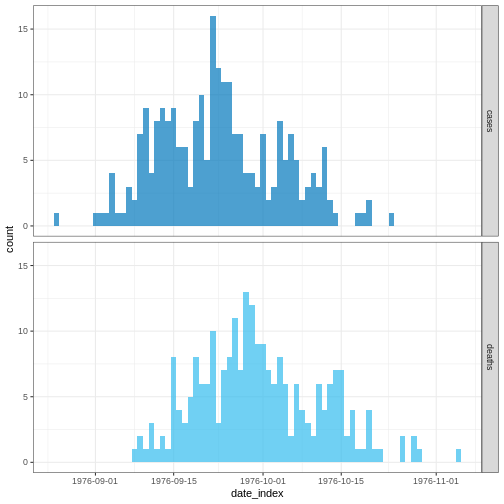
Nous supposerons que nous sommes dans le contexte d’une épidémie d’Ebola en cours où nous disposons que des données collectées durant les 30 premiers jours de l’épidémie.
R
# supposons que nous disposons des donnees des 30 premiers jours de l'epidemie
ebola_30days <- ebola1976 %>%
dplyr::slice_head(n = 30) %>%
dplyr::as_tibble()
ebola_30days
SORTIE
# A tibble: 30 × 3
date cases deaths
<date> <int> <int>
1 1976-08-25 1 0
2 1976-08-26 0 0
3 1976-08-27 0 0
4 1976-08-28 0 0
5 1976-08-29 0 0
6 1976-08-30 0 0
7 1976-08-31 0 0
8 1976-09-01 1 0
9 1976-09-02 1 0
10 1976-09-03 1 0
# ℹ 20 more rowsNous avons besoin de données d’incidence agrégées
Les données d’entrée des fonctions de la cfr sont des données d’incidence, qui sont ont été agrégées à partir des données de cas individuels.
Ces données doivent être agrégées par “unité de temps”, c’est-à-dire une observation par unité de temps, contenant le nombre de cas et de décès signalés en un temps donné. Les observations avec des valeurs nulles ou manquantes doivent également être incluses, comme pour les données de séries temporelles.
Cependant, il faut noter que la version actuelle de cfr requière des données agrégées journaliers. Les autres unités temporelles d’agrégation de données telles que les semaines, mois, etc ne sont pour le moment pas pris en charge.
Liste de vérification
Lorsque vous regroupez les cas par jour avec
incidence2, vous pouvez adapter les données pour
cfr à l’aide de cfr::prepare_data() sur les
objets <incidence2>. Pour plus de détails et un
exemple, consultez le manuel de référence cfr sur la
préparation des formats de données épidémiologiques courants pour
l’estimation du CFR (https://epiverse-trace.github.io/cfr/reference/prepare_data.html).
La fonction cfr::cfr_static() permet de calculer le RL
naïf.
R
# Calculer le RL naïf durant les 30 premiers jours
cfr::cfr_static(data = ebola_30days)
SORTIE
severity_estimate severity_low severity_high
1 0.4740741 0.3875497 0.5617606Défi
Téléchargez le fichier sarscov2_cases_deaths.csv et importez-le dans R. Puis estimez le RL naïf.
Vérifier le format des données d’entrée en répondant aux questions suivantes:
- Contient-il des données d’incidences quotidiennes ?
- Les noms des colonnes sont-ils conformes aux exigences de la
fonction
cfr_static()? - Comment renommer les noms de colonnes d’un tableau de données ?
Importez les données téléchargées à l’aide de la fonction
readr::read_csv(). Cette fonction reconnaît que la colonne
date est de type <Date>.
R
# importer les données dans R
# supposons que le chemin d'accès au fichier est data/raw-data/ebola_cases.csv
sarscov2_input <- readr::read_csv(
file = here::here("data", "raw-data", "sarscov2_cases_deaths.csv")
)
R
# voir un aperçu des données
sarscov2_input
SORTIE
# A tibble: 93 × 3
date cases_jpn deaths_jpn
<date> <dbl> <dbl>
1 2020-01-20 1 0
2 2020-01-21 1 0
3 2020-01-22 0 0
4 2020-01-23 1 0
5 2020-01-24 1 0
6 2020-01-25 3 0
7 2020-01-26 3 0
8 2020-01-27 4 0
9 2020-01-28 6 0
10 2020-01-29 7 0
# ℹ 83 more rowsNous pouvons utiliser la fonction
cleanepi::standardize_column_names() pour renommer les noms
des colonnes de sorte qu’elles soient conforment aux exigences de la
fonction cfr::cfr_static().
R
# renommer les noms des colonnes
sarscov2_input <- sarscov2_input %>%
cleanepi::standardize_column_names(
rename = c(cases = "cases_jpn", deaths = "deaths_jpn")
)
# estimer le RL naïf
cfr::cfr_static(sarscov2_input)
SORTIE
severity_estimate severity_low severity_high
1 0.01895208 0.01828832 0.01963342Biais affectant l’estimation du CFR
Deux biais qui affectent l’estimation du RL
Lipsitch et al, 2015 ont décrit deux biais potentiels qui peuvent affecter l’estimation du RL (et comment y remédier) :
Pour les maladies ayant un spectre de présentations cliniques, les cas qui sont portés à l’attention des autorités de santé publique et enregistrés dans les bases de données de surveillance sont généralement des personnes présentant les symptômes les plus graves, qui consultent un médecin, admises à l’hôpital ou décèdent.
Par conséquent, le RL sera généralement plus élevé chez les cas confirmés que dans l’ensemble de la population des cas, étant donné que cette dernière peut inclure des personnes présentant des symptômes légers, subcliniques et (selon certaines définitions de “cas”) asymptomatiques.
Lors d’une épidémie en cours, il y a un délai entre le moment où une personne décède et le moment où son décès est signalé. Par conséquent, à tout moment, la liste des cas contient des individus qui vont mourir et dont le décès n’est pas encore survenu ou qui est survenu mais n’a pas encore été signalé. Ainsi, la division du nombre cumulé de décès déclarés par le nombre cumulé de cas déclarés en un moment donné d’une épidémie sous-évaluera le véritable RL.
Les principaux facteurs déterminants de l’ampleur du biais sont, le taux de croissance de l’épidémie et la distribution des délais entre la déclaration des cas et la déclaration des décès ; plus les délais sont longs, plus le taux de croissance est rapide, et plus le biais est important.
Dans les sections suivantes de cet épisode du tutoriel, nous allons nous concentrer sur les solutions concernant spécifiquement ce biais en utilisant la librairie cfr.
Il est crucial d’améliorer l’estimation du RL ajusté au délais au début d’une épidémie pour déterminer sa virulence, mais aussi le niveau et les choix des interventions de santé publique et fournir des conseils au grand public.
En 2009, lors de l’épidémie de grippe porcine A (H1N1), le Mexique a effectué une estimation précoce biaisée du RL. Les premiers rapports du gouvernement mexicain faisaient état d’une infection virulente, alors que dans d’autres pays, le même virus était perçu comme bénin (TIME, 2009).
Aux États-Unis et au Canada, aucun décès n’a été attribué au virus durant les dix jours qui ont suivi la déclaration d’urgence de santé publique par l’OMS. Même dans des circonstances similaires, au début d’une pandémie mondiale, les responsables de la santé publique, les décideurs et le grand public veulent connaître la virulence d’un agent infectieux émergent.
Garske et al, 2009 évaluer les défis afin d’estimer la gravité de cette pandémie, en soulignant que le fait de recenser avec précision les cas pour le dénominateur peut améliorer la capacité à obtenir des estimations informatives du taux de létalité.
Vous trouverez plus d’informations concernant l’effet des délais dans
l’estimation du RL dans cette section de la vignette
de la librairie {cfr}.
RL ajusté au délai
Nishiura et al, 2009 ont développé une méthode de calcul du RL qui prend en compte les délais entre l’apparition des symptômes et le décès.
Durant certaines phases d’une épidémie en cours, il peut arriver que
le nombre de décès soit insuffisant pour déterminer la distribution du
temps entre l’apparition des symptômes et le décès. Par conséquent, nous
pouvons obtenir une estimation de la distribution de ce délai à
partir d’épidémies antérieures ou en réutilisant celles qui sont
accessibles via des librairies R tels que epiparameter ou
{epireview} qui les collectent à partir de la littérature
scientifique publiée. Lisez l’épisode accéder aux délais épidémiologiques de ce
tutoriel pour de plus amples informations.
Obtenons la distribution du délai entre la date d’apparition des symptômes et la date de décès via la librairie epiparameter.
R
# obtenir la distribution du délai
onset_to_death_ebola <- epiparameter::epiparameter_db(
disease = "Ebola",
epi_name = "onset_to_death",
single_epiparameter = TRUE
)
# visualiser la distribution du délai
plot(onset_to_death_ebola, xlim = c(0, 40))
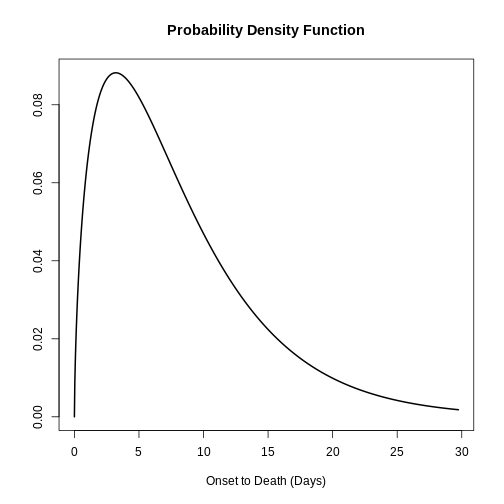
Pour prendre en compte la distribution du délai lors du calcul le RL
ajusté au délai, nous devons fournir à l’arguemt
delay_density de la fonction cfr::cfr_static()
la valeur correspondante.
R
# calculer le RL ajusté au délai pour les 30 premiers jours
cfr::cfr_static(
data = ebola_30days,
delay_density = function(x) density(onset_to_death_ebola, x)
)
SORTIE
severity_estimate severity_low severity_high
1 0.9502 0.881 0.9861Le RL ajusté au délai indique que la gravité globale de la maladie à la fin de l’épidémie ou selon les récentes données disponibles à ce moment-là est 0.9502 avec un intervalle de confiance de 95% entre 0.881 et 0.9861, légèrement supérieure à la valeur naïve.
Pour corriger le biais résultant des cas dont les résultats ne sont pas encore connus au moment de l’estimation, {cfr} tient compte de la probabilité que le résultat d’un cas soit connu après un certain délai.
Pour ce faire, il relie \(D_t\) à la fonction d’incidence \(c_t\) (c’est-à-dire le nombre de nouveaux cas confirmés au jour t) et à la fonction de densité de probabilité conditionnelle \(f_s\) du temps écoulé entre l’apparition de la maladie et le décès, étant donné le décès.
\[ D_t = p_t \times \sum_{i = 0}^t\sum_{j = 0}^\infty c_i f_{j - i} \]
Ici, \(D_t\) est le nombre cumulé de décès jusqu’au moment t, et \(p_t\) est la proportion réalisée de cas confirmés qui décèdent des suites de l’infection (c’est-à-dire le risque de létalité non biaisé, ou CFR) .
Le terme \(\sum_{i = 0}^t\sum_{j =
0}^\infty c_i f_{j - i}\) représente le nombre total
prévu de cas dont l’issue est connue au moment t.
Il additionne tous les cas incidents \(c_i\), chacun pondéré par la fonction de
densité de probabilité \(f_{j−i}\) que
leur issue soit connue après un délai de \(j−i\) jours.
Chaque jour d’analyse, cfr calcule, pour chaque cas,
le nombre attendu de résultats à l’instant
t. Lorsque vous utilisez des objets de classe
<epiparameter>, la fonction density()
peut être appliquée pour obtenir la fonction de densité de probabilité
correspondante pour chaque cas et chaque jour.
Par exemple, au jour 1, les résultats attendus sont égaux à :
- le nombre de cas observés au jour 1 multiplié par la densité au jour 0.
R
# Au jour 1, les résultats attendus sont :
ebola_30days$cases[1] *
density(onset_to_death_ebola, at = 0)
SORTIE
[1] 0Au jour 2, les résultats attendus sont égaux à :
- le nombre de cas observés au jour 1 multiplié par la densité au jour 1, plus
- le nombre de cas observés au jour 2 multiplié par la densité au jour 0
R
# Au jour 2, les résultats attendus sont les suivants :
ebola_30days$cases[1] *
density(onset_to_death_ebola, at = 1) +
ebola_30days$cases[2] *
density(onset_to_death_ebola, at = 0)
SORTIE
[1] 0.06495664Au troisième jour, les résultats attendus sont égaux à :
- le nombre de cas observés au premier jour multiplié par la densité au deuxième jour, plus
- le nombre de cas observés au deuxième jour multiplié par la densité au premier jour, plus
- le nombre de cas observés au troisième jour multiplié par la densité au jour 0.
R
# Au troisième jour, les résultats attendus sont :
ebola_30days$cases[1] *
density(onset_to_death_ebola, at = 2) +
ebola_30days$cases[2] *
density(onset_to_death_ebola, at = 1) +
ebola_30days$cases[3] *
density(onset_to_death_ebola, at = 0)
SORTIE
[1] 0.08295091Notez que les cas observés les plus récemment commencent la
distribution des délais à partir de 0, les autres
continuent avec le jour suivant.
Étant donné que la valeur d’entrée dans at varie selon
le jour pour chaque cas (at = 0, at = 1,
at = 2, …), la fonction density() doit être
exprimée en fonction de x. cfr tirera alors les valeurs
en conséquence, comme indiqué ci-dessous :
R
# {cfr} utilise la densité de la distribution à différentes valeurs de x
function(x) density(onset_to_death_ebola, at = x)
En interne, la fonction cfr::estimate_outcomes()
effectue ce calcul :
R
cfr::estimate_outcomes(
data = ebola_30days,
delay_density = function(x) density(onset_to_death_ebola, at = x)
) %>%
slice_head(n = 3) %>%
pull(estimated_outcomes)
SORTIE
[1] 0.00000000 0.06495664 0.08295091Utilisation des objets de la classe epiparameter
Lorsque vous utilisez un object de la classe
<epiparameter>, vous pouvez utiliser cette expression
comme modèle :
function(x) density(<NOM_OBJECT_EPIPARAMETER>, x)
Pour les fonctions de distribution dont les paramètres ne sont pas disponibles dans epiparameter nous vous proposons deux alternatives :
Créer un objet de la classe
<epiparameter>pour l’intégrer dans d’autres packages R d’un pipeline d’analyse épidémiologique. Lisez l’article document de référence deepiparameter::epiparameter()pour plus de clarifications.Liser la vignette de cfr portant sur l’utilisation des distributions des délais.
Pour la fonction cfr_static() et les autres de la
famille cfr_*(), les distributions les plus appropriées
sont les distributions discrets. Ceci en raison du fait
que nous travaillerons avec des données d’incidence quotidiennes sur le
nombre de cas et de décès.
Nous pouvons supposer que l’évaluation de la fonction de distribution de probabilité (FDP) d’une distribution continue est équivalente à la fonction de masse de probabilité (FMP) de la distribution discrète correspondante.
Toutefois, cette hypothèse pourrait être inappropriée en présence de
distributions présentant des pics énormes. C’est le cas, par exemple,
des maladies dont la distribution du délai entre la date d’apparition
des symptômes et la date du décès présente un pic très élevé et une
faible variance. Dans ce cas, la disparité moyenne entre la FDP et la
FMP devrait être plus prononcée que pour les distributions avec de
larges variances. Une façon d’y remédier est de discrétiser la
distribution continue en appliquant la fonction
epiparameter::discretise() à un objet de la classe
<epiparameter>.
R
onset_to_death_ebola %>%
epiparameter::discretise() %>%
plot(xlim = c(0, 40))
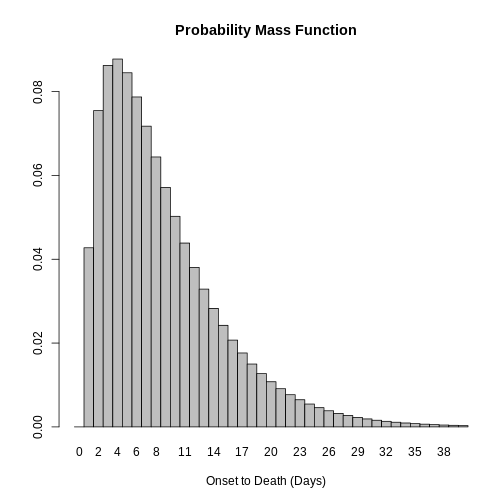
Défi
Utilisez le même fichier (sarscov2_cases_deaths.csv) que celui du défi précédent pour:
- Estimer le RL ajusté au délai en utilisant la distribution de délai adéquate.
- Comparer les résultats du RL naïf et du RL ajusté au délai.
- Trouver l’objet de la classe
<epiparameter>approprié pour ces données.
Nous utiliserons la librairie epiparameter pour accéder à une distribution des délais pour les données d’incidence du SARS-CoV-2.
R
library(epiparameter)
sarscov2_delay <- epiparameter::epiparameter_db(
disease = "covid",
epi_name = "onset to death",
single_epiparameter = TRUE
)
Les données seront importées dans R à l’aide de la fonction
readr::read_csv(). Cette fonction reconnaît que la colonne
date est de type <Date>.
R
# importer les donnees
# supposons que le chemin d'accès au fichier est: data/raw-data/ebola_cases.csv
sarscov2_input <- readr::read_csv(
file = here::here("data", "raw-data", "sarscov2_cases_deaths.csv")
)
R
# voir un apperçu des donnees
sarscov2_input
SORTIE
# A tibble: 93 × 3
date cases_jpn deaths_jpn
<date> <dbl> <dbl>
1 2020-01-20 1 0
2 2020-01-21 1 0
3 2020-01-22 0 0
4 2020-01-23 1 0
5 2020-01-24 1 0
6 2020-01-25 3 0
7 2020-01-26 3 0
8 2020-01-27 4 0
9 2020-01-28 6 0
10 2020-01-29 7 0
# ℹ 83 more rowsNous pouvons utiliser la fonction
cleanepi::standardize_column_names() pour renommer les noms
des colonnes de sorte qu’elles soient conforment à la fonction
cfr::cfr_static().
R
# renommer les noms des colonnes avant d'estimer le RL ajusté au délai
sarscov2_input %>%
cleanepi::standardize_column_names(
rename = c(cases = "cases_jpn", deaths = "deaths_jpn")
) %>%
cfr::cfr_static(
delay_density = function(x) density(sarscov2_delay, x)
)
SORTIE
severity_estimate severity_low severity_high
1 0.0734 0.071 0.0759Comparer et interpréter les estimations du RL naïfs et ajusté au délais.
Pour ajuster le RL, Nishiura et al. 2009 ont utilisé les incidences des cas et des décès pour estimer le nombre de cas dont les pronostiques vitaux sont connus :
\[ u_t = \dfrac{\sum_{i = 0}^t \sum_{j = 0}^\infty c_{i - j} f_{j}}{\sum_{i = 0} c_i}, \]
où :
- \(c_{t}\) est l’incidence quotidienne des cas à l’instant \(t\),
- \(f_{t}\) est la valeur de la fonction de masse de probabilité (FMP) de la distribution des délais entre l’apparition des symptômes et le décès, et
- \(u_{t}\) représente le facteur de sous-estimation des statuts vitals connus.
\(u_{t}\) est utilisé pour
ajuster l’échelle du nombre cumulé de cas au niveau du
dénominateur dans le calcul du RL. Ce calcul est effectué en interne à
l’aide de la fonction estimate_outcomes().
L’estimateur du RL peut être écrit comme suit :
\[p_{t} = \frac{b_{t}}{u_{t}}\]
où \(p_{t}\) est la proportion réelle de cas confirmés qui meurent de l’infection (ou le RL non biaisé), et \(b_{t}\) est l’estimation brute et biaisée du RL (ou RL naïf).
D’après cette dernière équation, nous observons que le RL non biaisé \(p_{t}\) est plus élevé que le RL biaisé \(b_{t}\), car le numérateur dans \(u_{t}\) est plus petit que le dénominateur (notez que \(f_{t}\) est la distribution de probabilité de la distribution des délais entre l’apparition des symptômes et le décès). Par conséquent, \(b_{t}\) est considérer comme l’estimateur biaisé du RL.
Lorsque nous observons toute l’évolution d’une épidémie (de \(t \rightarrow \infty\)), \(u_{t}\) tend vers 1, ce qui fait que \(b_{t}\) tend à \(p_{t}\) et devient un estimateur sans biais (Nishiura et al., 2009).
Estimation du RL au début d’une épidémie
L’estimation du RL naïf est utile pour obtenir une estimation globale de la gravité d’une épidémie (jusqu’au moment \(t\)). À la fin de l’épidémie ou lorsqu’on atteint un niveau où on a de plus en plus de décès sont signalés, le RL estimé sera alors plus proche du “véritable” RL non biaisé.
Par ailleurs, la valeur RL ajusté au délai estimée au début d’une épidémie refléte mieux la gravité d’une maladie infectieuse émergente que le RL biaisé ou naïf obtenu au cours de l’épidémie.
Nous pouvons calculer le RL ajusté au délai au début d’une
épidémie à l’aide de la fonction cfr::cfr_rolling().
À noter
cfr::cfr_rolling() est une fonction utilitaire qui
calcule automatiquement le RL à chaque jour de l’épidémie à l’aide des
données disponibles au jour de l’estimation, permettant ainsi à
l’utilisateur de gagner du temps.
cfr::cfr_rolling() montre le RL estimé à chaque jour de
l’épidémie, étant donné que les données futures sur les nombres de cas
et de décès ne sont pas disponibles à ce moment-là. Pour un même jeu de
données, la valeur finale de cfr::cfr_rolling() est
identique à celle de cfr::cfr_static().
R
# Calculer le RL naïf quotidien à chacun des 73 jours dans un jeu de donnees
# d'Ebola
rolling_cfr_naive <- cfr::cfr_rolling(data = ebola1976)
SORTIE
`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.R
# Calculer le RL quotidien ajusté au délai à chacun des 73 jours dans un jeu de
# donnees d'Ebola
rolling_cfr_adjusted <- cfr::cfr_rolling(
data = ebola1976,
delay_density = function(x) density(onset_to_death_ebola, x)
)
SORTIE
`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.SORTIE
Some daily ratios of total deaths to total cases with known outcome are below 0.01%: some CFR estimates may be unreliable.FALSEAvec la fonction utils::tail() nous pouvons monter les
dernières estimations du RL. On voit que les intervalles de confiance à
95% des valeurs naïves et corrigées se chevauchent.
R
# voir un aperçu des dernieres valeurs du RL
utils::tail(rolling_cfr_naive)
utils::tail(rolling_cfr_adjusted)
Visualisons maintenant les deux résultats dans une série chronologique. Quelle serait la performance des estimations naïves et ajustées au délai en temps réel ?
R
# concatener les deux resultats
dplyr::bind_rows(
list(
naive = rolling_cfr_naive,
adjusted = rolling_cfr_adjusted
),
.id = "method"
) %>%
# visualiser les valeurs journalieres du RL naif et corrige
ggplot() +
geom_ribbon(
aes(
date,
ymin = severity_low,
ymax = severity_high,
fill = method
),
alpha = 0.2, show.legend = FALSE
) +
geom_line(
aes(date, severity_estimate, colour = method)
)
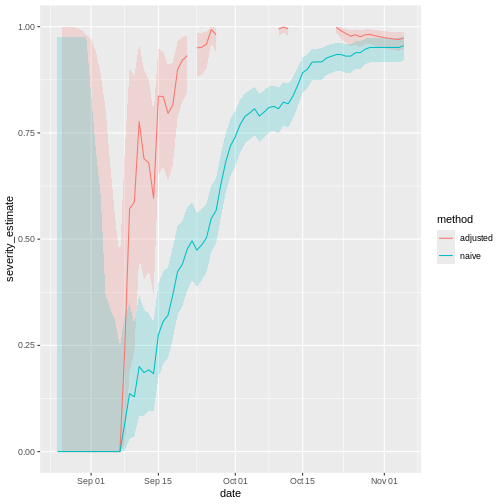
Les lignes rouges et bleues représentent respectivement le RL journalier ajusté au délai et naïf tout au long de l’épidémie. Les bandes autour d’elles représentent les intervalles de confiance à 95% (IC 95%).
Notez que le calcul du RL ajusté au délai est particulièrement utile lorsqu’une courbe épidémique de cas confirmés est la seule donnée disponible (c’est-à-dire lorsque les données concernant le temps entre l’apparition des symptômes jusqu’au décès ne sont pas disponibles, comme c’est le cas au début de l’épidémie). Lorsqu’il y a peu ou pas de décès, une hypothèse sur la distribution des délais entre l’apparition des symptômes et le décès doit être formulée, par exemple à partir de la littérature basée sur les épidémies précédentes. Nishiura et al. 2009 illustrent ce phénomène dans les figures à l’aide de données relatives à l’épidémie de SARS survenue à Hong Kong en 2003.
Les figures A et B montrent les nombres cumulés de cas et de décès dus au SARS, et la figure C montre les estimations observées (biaisées) du RL en fonction du temps, c’est-à-dire le nombre cumulé de décès par rapport au nombre de cas à l’instant \(t\). En raison du délai entre l’apparition des symptômes et le décès, l’estimation biaisée du RL au temps \(t\) est inférieure au RL obtenu à la fin de l’épidémie (302/1755 = 17,2 %).
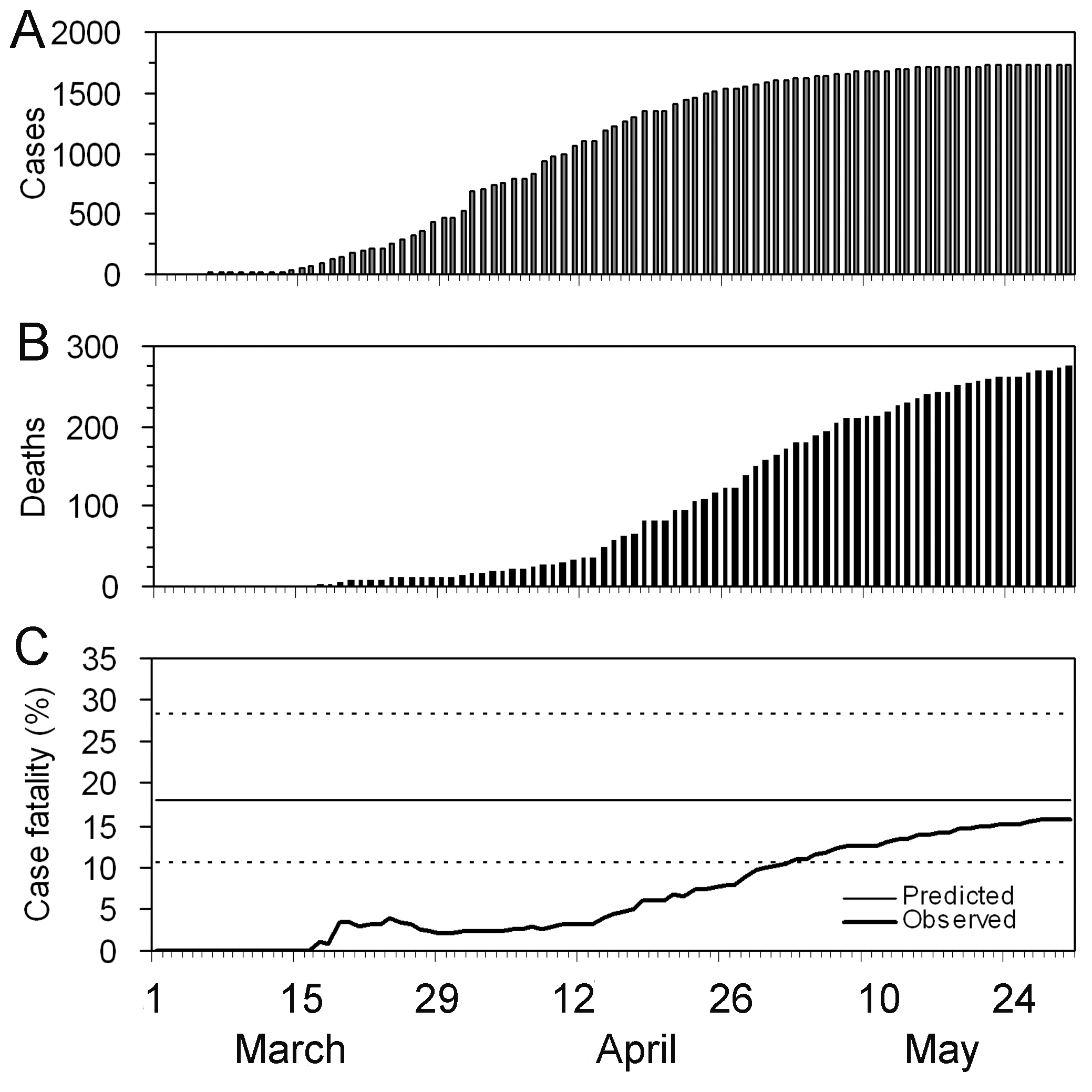
Néanmoins, même en n’utilisant que les données observées sur la
période du 19 mars au 2 avril, cfr::cfr_static() peut
produire une prédiction appropriée (figure D), par exemple le RL ajusté
au délai au 27 mars est de 18,1% (IC 95% : 10,5 - 28,1). Une
surestimation est notée au tout début de l’épidémie, mais les limites de
l’intervalle de confiance à 95% pour les phases ultérieures incluent le
RL réel (c’est-à-dire 17,2 %).
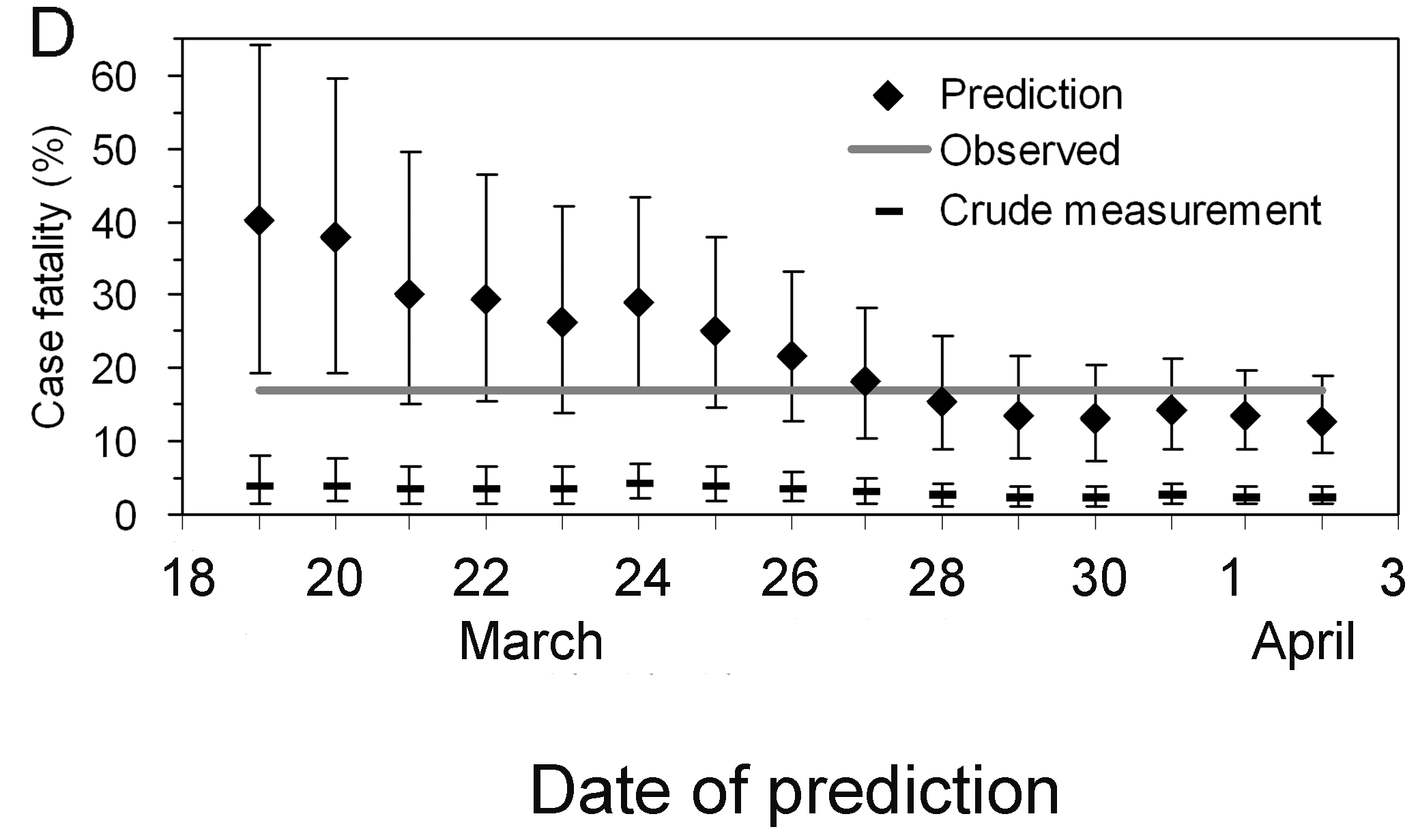
Interpréter l’estimation du RL au début de l’épidémie
Sur la base de la figure ci-dessus :
- Quelle est la différence, en jours, entre la date à laquelle l’IC à 95% du RL ajusté aux délais et du RL naïf se croisent avec le RL estimé à la fin de l’épidémie ?
Discutez-en :
- En quoi le fait de disposer d’un RL ajusté aux délai peut-il influer sur les stratégies de santé publique ?
Nous pouvons soit inspecter visuellement ou analyser les tableaux des données de sortie.
Il y a presque un mois de différence.
Notez que l’estimation présente une incertitude considérable au début de la série chronologique. Après deux semaines, le RL corrigé au délai se rapproche de l’estimation globale du RL à la fin de l’épidémie.
Ce schéma est-il similaire à celui d’autres épidémies ? Nous vous invitons à utiliser les ensembles de données dans les défis de cet épisode pour le découvrir.
Liste de vérification
Avec cfr nous estimons le RL comme la proportion de décès parmi les cas confirmés.
En n’utilisant que les cas confirmés il est clair que tous les cas qui ne cherchent pas de traitement médical ou qui ne sont pas notifiés ne sont pas pris en compte, de même que tous les cas asymptomatiques. Cela signifie que le RL estimé est plus élevé que la proportion de décès parmi l’ensemble des personnes infectées.
La méthode de la librairie cfr vise à obtenir un estimateur non biaisé “bien avant” d’observer toute l’évolution de l’épidémie. Pour ce faire, cfr utilise le facteur de sous-estimation \(u_{t}\) pour estimer le RL non biaisé \(p_{t}\) à l’aide de la méthode du maximum de vraisemblance, étant donné le processus d’échantillonnage défini par Nishiura et al, 2009.

Nous connaissons le nombre cumulé de cas confirmés et de décès \(C_{t}\) et \(D_{t}\) à l’instant \(t\) à partir des données d’incidence agrégées et souhaitons estimer le RL non biaisé \(\pi\) au moyen du facteur de sous-estimation \(u_{t}\).
Si nous connaissions le facteur de sous-estimation \(u_{t}\) nous pourrions préciser la taille de la population des cas confirmés qui ne sont plus à risque (\(u_{t}C_{t}\), ombré), bien que nous ne sachions pas quels individus survivants appartiennent à ce groupe. Une proportion \(\pi\) de ceux qui font partie du groupe de cas encore à risque (taille \((1- u_{t})C_{t}\), non ombré) devrait mourir.
Parce que chaque cas qui n’est plus à risque avait une probabilité indépendante de mourir, \(\pi\) le nombre de décès, \(D_{t}\) est un échantillon d’une distribution binomiale avec une taille d’échantillon de \(u_{t}C_{t}\) et la probabilité de décès \(p_{t}\) = \(\pi\).
Ceci est représenté par la fonction de vraisemblance suivante permettant d’obtenir l’estimation du maximum de vraisemblance du RL non biaisé \(p_{t}\) = \(\pi\):
\[ {\sf L}(\pi | C_{t},D_{t},u_{t}) = \log{\dbinom{u_{t}C_{t}}{D_{t}}} + D_{t} \log{\pi} + (u_{t}C_{t} - D_{t})\log{(1 - \pi)}, \]
Ce calcule est réalisé par la fonction interne
?cfr:::estimate_severity().
- Le RL ajusté aux délais ne prend pas en charge toutes les sources d’erreur dans les données, telle que la non-détection de toutes les personnes infectées.
Challenges
Autres mesures de sévérité
Supposons que nous ayons besoin d’évaluer la gravité clinique de l’épidémie dans un contexte autre aue la surveillance épidémiologique, comme la gravité parmi les cas qui arrivent à l’hôpital ou les cas que vous avez recueillis lors d’une enquête sérologique représentative.
En utilisant cfr nous pouvons modifier les valeurs du
numérateur (cases) et du dénominateur (deaths)
pour estimer des mesures plus sévères comme le risque d’infection
mortelle (RIM) ou le risque d’hospitalisation mortelle (RHM). Nous
pouvons suivre analogie ci-après :
Si pour le risque de décès (RL) d’un cas, nous exigeons :
- les données sur l’incidence des cas et des décès, avec une
- distribution des délais entre les cas et les décès (ou une approximation proche, comme le délai entre l’apparition des symptômes et le décès).
Dans ce cas, le risque d’infection mortelle (RIM) nécessite :
- les données sur l’incidence des infections et des décès, avec une
- distribution des délais entre l’exposition et le décès (ou une approximation proche).
De la même manière, le risque d’hospitalisation mortelle requière :
- les données d’incidence des cas d’hospitalisation et de décès, ainsi qu’une
- distribution des délais entre l’hospitalisation et le décès.
Yang et al, 2020 résume les différentes définitions et sources de données :
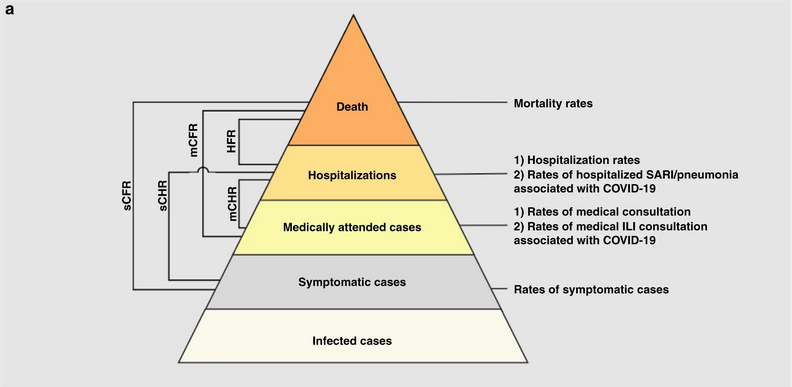
- sCFR risque de létalité des cas symptomatiques (sRL),
- sCHR risque d’hospitalisation des cas symptomatiques (sRH),
- mCFR risque de létalité des cas médicalement pris en charge (mRL),
- mCHR risque d’hospitalisation d’un cas médicalement pris en charge (mRH),
- HFR risque d’hospitalisation mortelle (RHM).
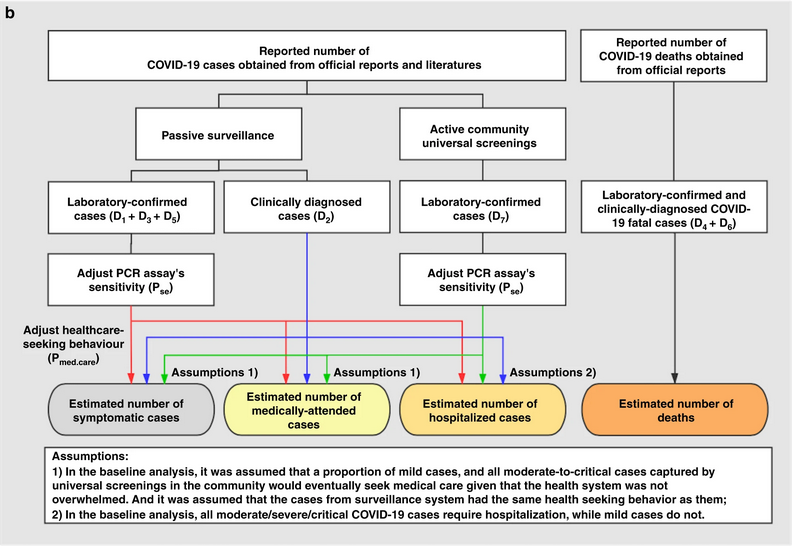
Les données agrégées diffèrent des données de cas individuels (linelist)
Les données d’incidence agrégées diffèrent des linelist où chaque observation contient des données concernant un cas individuel.
R
outbreaks::ebola_sierraleone_2014 %>% as_tibble()
SORTIE
# A tibble: 11,903 × 8
id age sex status date_of_onset date_of_sample district chiefdom
<int> <dbl> <fct> <fct> <date> <date> <fct> <fct>
1 1 20 F confirmed 2014-05-18 2014-05-23 Kailahun Kissi Teng
2 2 42 F confirmed 2014-05-20 2014-05-25 Kailahun Kissi Teng
3 3 45 F confirmed 2014-05-20 2014-05-25 Kailahun Kissi Tonge
4 4 15 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
5 5 19 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
6 6 55 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
7 7 50 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
8 8 8 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
9 9 54 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
10 10 57 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
# ℹ 11,893 more rowsUtilisez {incidence2} pour réorganiser vos données
Comment réorganiser les données d’entrée ?
Le réorganisation des données d’entrée durant le processus d’analyse des données peut prendre beaucoup de temps. Pour obtenir des données d’incidence agrégées prêtes à être analysées nous vous encourageons à utiliser le package incidence2.
Tout d’abord, consultez la vignette Get
started de la librairie incidence2 pour savoir
comment utiliser l’argument date_index lors de la lecture
d’un linelist contenant plusieurs colonnes de type
<Date>.
Ensuite, référez-vous au
manuel de référence sur la façon d’utiliser la fonction
cfr::prepare_data() sur les objets de classe
<incidence2>.
R
# charger les packages
library(cfr)
library(epiparameter)
library(incidence2)
library(outbreaks)
library(tidyverse)
# Acceder a la distribution des delais
mers_delay <- epiparameter::epiparameter_db(
disease = "mers",
epi_name = "onset to death",
single_epiparameter = TRUE
)
# lire le linelist
mers_korea_2015$linelist %>%
as_tibble() %>%
select(starts_with("dt_"))
SORTIE
# A tibble: 162 × 6
dt_onset dt_report dt_start_exp dt_end_exp dt_diag dt_death
<date> <date> <date> <date> <date> <date>
1 2015-05-11 2015-05-19 2015-04-18 2015-05-04 2015-05-20 NA
2 2015-05-18 2015-05-20 2015-05-15 2015-05-20 2015-05-20 NA
3 2015-05-20 2015-05-20 2015-05-16 2015-05-16 2015-05-21 2015-06-04
4 2015-05-25 2015-05-26 2015-05-16 2015-05-20 2015-05-26 NA
5 2015-05-25 2015-05-27 2015-05-17 2015-05-17 2015-05-26 NA
6 2015-05-24 2015-05-28 2015-05-15 2015-05-17 2015-05-28 2015-06-01
7 2015-05-21 2015-05-28 2015-05-16 2015-05-17 2015-05-28 NA
8 2015-05-26 2015-05-29 2015-05-15 2015-05-15 2015-05-29 NA
9 NA 2015-05-29 2015-05-15 2015-05-17 2015-05-29 NA
10 2015-05-21 2015-05-29 2015-05-16 2015-05-16 2015-05-29 NA
# ℹ 152 more rowsR
# utiliser {incidence2} pour determiner les incidences journalieres
mers_incidence <- mers_korea_2015$linelist %>%
# convertir en objet incidence2
incidence2::incidence(date_index = c("dt_onset", "dt_death")) %>%
# completer les dates du début a la fin
incidence2::complete_dates()
# voir un aperçu des donnees d'incidence
mers_incidence
SORTIE
# incidence: 72 x 3
# count vars: dt_death, dt_onset
date_index count_variable count
<date> <chr> <int>
1 2015-05-11 dt_death 0
2 2015-05-11 dt_onset 1
3 2015-05-12 dt_death 0
4 2015-05-12 dt_onset 0
5 2015-05-13 dt_death 0
6 2015-05-13 dt_onset 0
7 2015-05-14 dt_death 0
8 2015-05-14 dt_onset 0
9 2015-05-15 dt_death 0
10 2015-05-15 dt_onset 0
# ℹ 62 more rowsR
# Preparer les donnees d'incidence pour utilisation dans {cfr}
mers_incidence %>%
cfr::prepare_data(
cases_variable = "dt_onset",
deaths_variable = "dt_death"
)
SORTIE
date deaths cases
1 2015-05-11 0 1
2 2015-05-12 0 0
3 2015-05-13 0 0
4 2015-05-14 0 0
5 2015-05-15 0 0
6 2015-05-16 0 0
7 2015-05-17 0 1
8 2015-05-18 0 1
9 2015-05-19 0 0
10 2015-05-20 0 5
11 2015-05-21 0 6
12 2015-05-22 0 2
13 2015-05-23 0 4
14 2015-05-24 0 2
15 2015-05-25 0 3
16 2015-05-26 0 1
17 2015-05-27 0 2
18 2015-05-28 0 1
19 2015-05-29 0 3
20 2015-05-30 0 5
21 2015-05-31 0 10
22 2015-06-01 2 16
23 2015-06-02 0 11
24 2015-06-03 1 7
25 2015-06-04 1 12
26 2015-06-05 1 9
27 2015-06-06 0 7
28 2015-06-07 0 7
29 2015-06-08 2 6
30 2015-06-09 0 1
31 2015-06-10 2 6
32 2015-06-11 1 3
33 2015-06-12 0 0
34 2015-06-13 0 2
35 2015-06-14 0 0
36 2015-06-15 0 1R
# Estimer le RL ajuste au delai
mers_incidence %>%
cfr::prepare_data(
cases_variable = "dt_onset",
deaths_variable = "dt_death"
) %>%
cfr::cfr_static(delay_density = function(x) density(mers_delay, x))
SORTIE
severity_estimate severity_low severity_high
1 0.1377 0.0716 0.2288Hétérogénéité de la gravité
Le RL peut varier d’une population à l’autre (par exemple en fonction de l’âge, l’espace géographique, du traitement, etc) ; la quantification de ces hétérogénéités peut aider à mobiliser les ressources de manière appropriée et à comparer différents régimes de soins (Cori et al., 2017).
Utilisez le tableau de données cfr::covid_data pour
estimer un RL ajusté aux délais, stratifié par pays.
Une façon d’effectuer une analyse stratifiée consiste à
appliquer un modèle à des données imbriquées. Cette vignette
de la librairie {tidyr} vignette vous montre comment
appliquer la méthode dplyr::group_by() +
tidyr::nest() aux données de imbriquées, puis
dplyr::mutate() + purrr::map() pour appliquer
le modèle.
R
library(cfr)
library(epiparameter)
library(tidyverse)
covid_data %>% dplyr::glimpse()
SORTIE
Rows: 20,786
Columns: 4
$ date <date> 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2…
$ country <chr> "Argentina", "Brazil", "Colombia", "France", "Germany", "India…
$ cases <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ deaths <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…R
delay_onset_death <- epiparameter::epiparameter_db(
disease = "covid",
epi_name = "onset to death",
single_epiparameter = TRUE
)
covid_data %>%
dplyr::group_by(country) %>%
tidyr::nest() %>%
dplyr::mutate(
temp = purrr::map(
.x = data,
.f = cfr::cfr_static,
delay_density = function(x) density(delay_onset_death, x)
)
) %>%
tidyr::unnest(cols = temp)
SORTIE
# A tibble: 19 × 5
# Groups: country [19]
country data severity_estimate severity_low severity_high
<chr> <list> <dbl> <dbl> <dbl>
1 Argentina <tibble> 0.0133 0.0133 0.0133
2 Brazil <tibble> 0.0195 0.0195 0.0195
3 Colombia <tibble> 0.0225 0.0224 0.0226
4 France <tibble> 0.0044 0.0044 0.0044
5 Germany <tibble> 0.0045 0.0045 0.0045
6 India <tibble> 0.0119 0.0119 0.0119
7 Indonesia <tibble> 0.024 0.0239 0.0241
8 Iran <tibble> 0.0191 0.0191 0.0192
9 Italy <tibble> 0.0075 0.0075 0.0075
10 Mexico <tibble> 0.0461 0.046 0.0462
11 Peru <tibble> 0.0502 0.0501 0.0504
12 Poland <tibble> 0.0186 0.0186 0.0187
13 Russia <tibble> 0.0182 0.0182 0.0182
14 South Africa <tibble> 0.0254 0.0253 0.0255
15 Spain <tibble> 0.0087 0.0087 0.0087
16 Turkey <tibble> 0.006 0.006 0.006
17 Ukraine <tibble> 0.0204 0.0203 0.0205
18 United Kingdom <tibble> 0.009 0.009 0.009
19 United States <tibble> 0.0111 0.0111 0.0111C’est génial ! Vous pouvez maintenant utiliser un code similaire pour stratifier vos analyses en fonction de l’âge, des régions ou autres facteurs utiles.
Mais comment interpréter le fait qu’on ait une variabilité nationale de la gravité clinique pour un même agent pathogène diagnostiqué ?
Des facteurs locaux tels que la capacité de test, la définition de cas et le régime d’échantillonnage peuvent influer sur la déclaration des cas et des décès, et donc sur la détermination de la grvité clinique. Jetez un coup d’œil à la vignette de cfr sur Estimation de la proportion de cas confirmés au cours d’une épidémie.
Annexe
La librairie cfr possède une fonction appelée
cfr_time_varying() dont la fonctionnalité diffère de celle
de cfr_rolling().
Quand doit-on utiliser cfr_rolling() ?
cfr::cfr_rolling() calcule le RL estimé à chaque jour de
l’épidémie, vue que les données futures sur les cas et les décès ne sont
pas disponibles à ce moment-là. La valeur finale de
cfr_rolling() est identique à celle de
cfr_static() pour les mêmes données.
Rappelez-vous, comme indiqué ci-dessus, cfr_rolling()
est utile pour obtenir des estimations du RL à un stade précoce de
l’épidémie et vérifier si l’estimation du RL d’une épidémie s’est
stabilisée. C’est pourquoi, cfr_rolling() n’est pas
sensible à la durée ou à la taille de l’épidémie.
Quand doit-on utiliser
cfr_time_varying() ?
D’autre part, cfr::cfr_time_varying(), utilisée pour
calculer le RL mobile (RL par intervalle de temps régulier), aide à
comprendre les variations du RL dues à des changements durant
l’épidémie, comme par exemple en raison d’un nouveau variant du
pathogène ou d’une immunité accrue due à la vaccination.
Cependant, cfr_time_varying() est sensible à
l’incertitude de l’échantillonnage. Son résultat est donc sensible à la
taille de l’épidémie. Plus le nombre de cas dont on connaitra le
pronostique au moment de l’estimation est élevé, plus nous obtiendrons
des estimations raisonnables du RL variable par intervalle de temps
consécutif.
Par exemple, avec 100 cas, le taux de létalité estimé aura, grosso
modo, un intervalle de confiance de 95% ± 10% de la valeur moyenne (IC
binomial). Donc, si le nombre de cas dont on connaitra le pronostique à
un jour donné est supérieur 100, nous pouvons obtenir des
estimations raisonnables du RL mobile. Mais si nous disposons que de
>100 cas sur toute la durée de l’épidémie nous devrons
probablement nous appuyer sur la fonction cfr_rolling() qui
utilise les données cumulées.
Nous vous invitons à lire la vignette
sur la fonction cfr_time_varying().
Points clés
Utilisez la librairie cfr pour estimer la gravité clinique
Utilisez la fonction
cfr::cfr_static()pour estimer le RL global à l’aide des plus récentes données disponibles.Utilisez la fonction
cfr::cfr_rolling()pour obtenir les estimations du RL durant chaque jour de l’épidémie.Utiliser l’argument
delay_densitypour ajuster les valeurs du RL au délai épidémiologique en fonction de la distribution des délais correspondants.
Content from Tenir compte du phénomène hypercontagieux
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 32 minutes
Vue d'ensemble
Questions
- Comment peut-on estimer la variation de la transmission au niveau individuel (c’est-à-dire le potentiel de super propagation) à partir des données de traçage des contacts ?
- Quelles sont les implications de la variation de la transmission pour la prise de décision ?
Objectifs
- Estimez la distribution de descendance (c’est-à-dire le nombre de cas secondaires) à partir des données de l’épidémie à l’aide de epicontacts.
- Estimez l’ampleur de la variation au niveau individuel (c’est-à-dire le paramètre de dispersion) de la distribution de la descendance à l’aide de fitdistrplus.
- Estimez la proportion de la transmission liée à des “événements de super propagation” à l’aide de superspreading.
Pré-requis
Les apprenants doivent se familiariser avec les concepts suivants avant de suivre ce tutoriel :
Statistiques: distributions de probabilités courantes, en particulier Poisson et binôme négatif.
Théorie épidémique Le nombre de reproduction, R.
R packages installés: epicontacts, fitdistrplus, superspreading, outbreaks, tidyverse.
Installer les packages si elles ne le sont pas déjà:
R
# si {pak} n'est pas disponible, exécutez : install.packages("pak")
pak::pak("epicontacts")
pak::pak("fitdistrplus")
pak::pak("superspreading")
pak::pak("outbreaks")
pak::pak("tidyverse")
Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.
Introduction
De la variole au coronavirus du syndrome respiratoire aigu sévère 2 (SRAS-CoV-2), certaines personnes infectées transmettent l’infection à un plus grand nombre de personnes que d’autres. La transmission de la maladie est le résultat d’une combinaison de facteurs biologiques et sociaux, et ces facteurs s’équilibrent dans une certaine mesure au niveau de la population lors d’une grande épidémie. C’est pourquoi les chercheurs utilisent souvent les moyennes de la population pour évaluer le potentiel de propagation de la maladie. Toutefois, au début ou à la fin d’une épidémie, les différences individuelles en matière de contagiosité peuvent être plus importantes. En particulier, elles augmentent le risque d’événements de super propagation (ESS), qui peuvent déclencher des épidémies explosives et influencer les chances de contrôler la transmission (Lloyd-Smith et al., 2005).
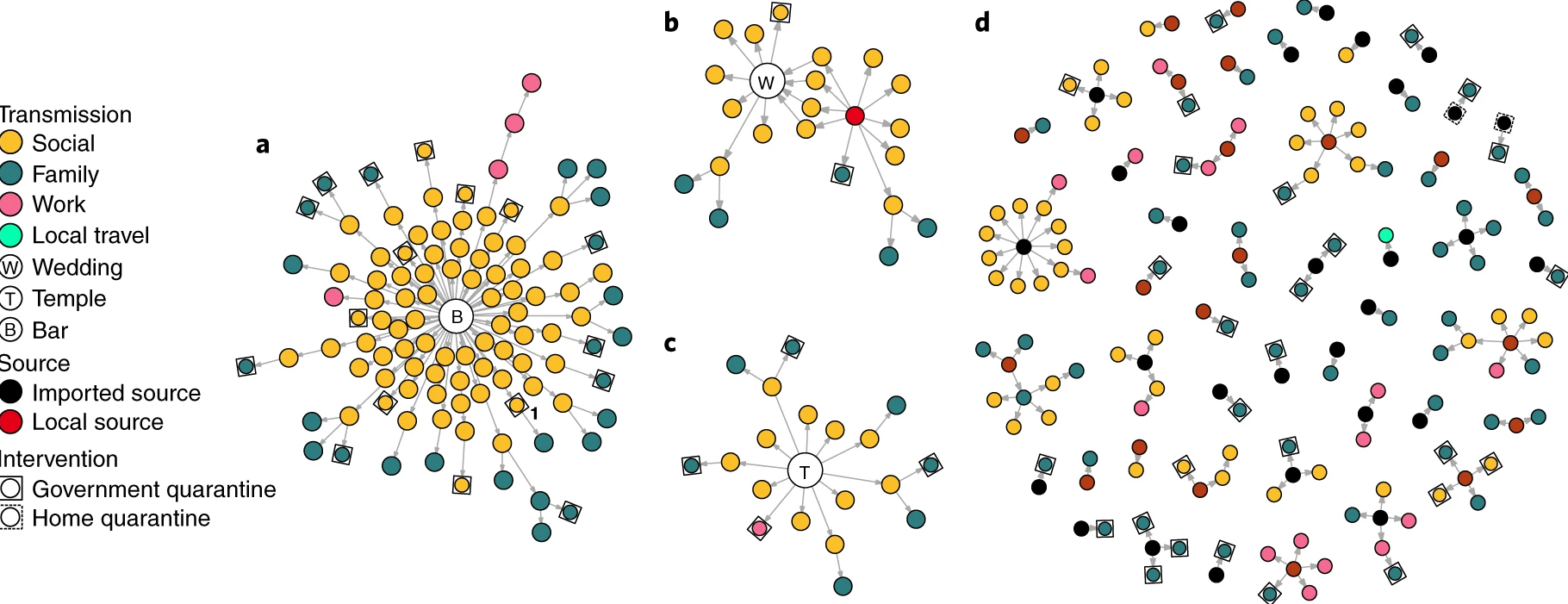
Le nombre de reproduction de base, \(R_{0}\) mesure le nombre moyen de cas causés par un individu infectieux dans une population entièrement susceptible. Les estimations de \(R_{0}\) sont utiles pour comprendre la dynamique moyenne d’une épidémie au niveau de la population, mais elles peuvent masquer des variations individuelles considérables dans la contagiosité. Cela a été mis en évidence lors de l’émergence mondiale du SRAS-CoV-2 par de nombreux “événements de super propagation” au cours desquels certains individus infectieux ont généré un nombre anormalement élevé de cas secondaires (LeClerc et al, 2020).
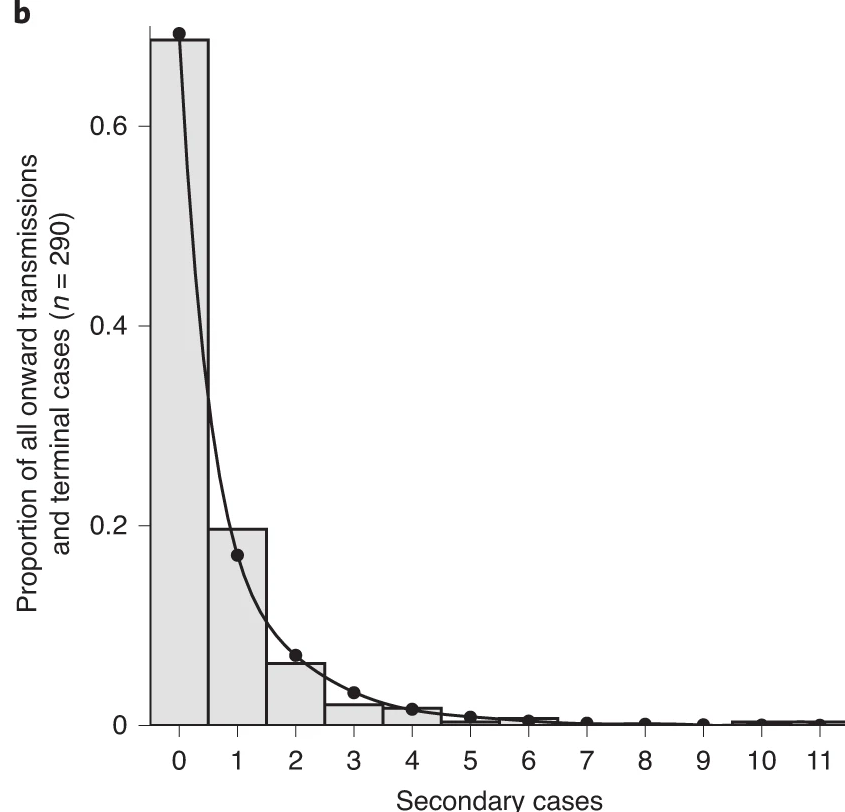
Dans ce tutoriel, nous allons quantifier la variation individuelle de la transmission, et donc estimer le potentiel d’événements d’hypercontagion. Nous utiliserons ensuite ces estimations pour explorer les implications de l’hypercontagion pour les interventions de recherche de contacts.
Nous allons utiliser les données de l’étude outbreaks et gérer la liste des lignes et les données sur les contacts à l’aide de l’outil epicontacts et estimer les paramètres de distribution avec fitdistrplus. Enfin, nous allons utiliser superspreading pour explorer les implications de la variation de la transmission sur la prise de décision.
Nous utiliserons le tuyau %>% pour relier certaines
des fonctions de ces packages, donc appelons aussi le package
tidyverse .
R
library(outbreaks)
library(epicontacts)
library(fitdistrplus)
library(superspreading)
library(tidyverse)
Le double point-virgule
Le double point-virgule :: dans R vous permettent
d’appeler une fonction spécifique d’un package sans charger le package
entier dans l’environnement actuel.
Par exemple, vous pouvez appeler une fonction spécifique d’un package
sans charger le package entier dans l’environnement actuel,
dplyr::filter(data, condition) utilise
filter() à partir de l’outil dplyr
package.
Cela nous permet de nous souvenir des fonctions du package et d’éviter les conflits d’espace de noms.
Le numéro de reproduction individuel
Le nombre de reproduction individuel est défini comme le nombre de cas secondaires causés par un individu infecté.
Au début d’une épidémie, nous pouvons utiliser les données de contact pour reconstruire les chaînes de transmission (c’est-à-dire qui a infecté qui) et calculer le nombre de cas secondaires générés par chaque individu. Cette reconstruction des événements de transmission liés à partir des données de contact peut permettre de comprendre comment différents individus ont contribué à la transmission au cours d’une épidémie (Cori et al., 2017).
Mettons cela en pratique en utilisant l’outil
mers_korea_2015 et les données de contact de la base de
données outbreaks et les intégrons à l’application
epicontacts pour calculer la distribution des cas
secondaires lors de l’épidémie de MERS-CoV de 2015 en Corée du Sud (Campbell,
2022) :
R
## first, make an epicontacts object
epi_contacts <-
epicontacts::make_epicontacts(
linelist = outbreaks::mers_korea_2015$linelist,
contacts = outbreaks::mers_korea_2015$contacts,
directed = TRUE
)
Avec l’argument directed = TRUE nous configurons un
graphe orienté. Ces directions intègrent notre hypothèse de la paire
“infecteur-infecté”.
R
# visualise contact network
plot(epi_contacts)

Les données de contact d’une chaîne de transmission peuvent fournir
des informations sur les personnes infectées qui sont entrées en contact
avec d’autres. Nous nous attendons à ce que l’infecteur
(from) et la personne infectée (to), ainsi que
des colonnes supplémentaires de variables liées à leur contact, telles
que le lieu (exposure) et la date du contact.
À la suite de mettre de l’ordre dans les données l’unité d’observation dans notre cadre de données de contact est la paire infecteur-infecté. Bien qu’un infecteur puisse infecter plusieurs personnes, les enquêtes de recherche de contacts peuvent enregistrer des contacts liés à plus d’un infecteur (par exemple, au sein d’un ménage). Mais nous devrions nous attendre à avoir des paires infecteur-infecté uniques, car chaque personne infectée a généralement contracté l’infection auprès d’une seule autre personne.
Pour garantir l’unicité de ces paires, nous pouvons vérifier les réplicats pour les personnes infectées :
R
# no infector-infectee pairs are replicated
epi_contacts %>%
purrr::pluck("contacts") %>%
dplyr::group_by(to) %>%
dplyr::filter(dplyr::n() > 1)
SORTIE
# A tibble: 5 × 4
# Groups: to [2]
from to exposure diff_dt_onset
<chr> <chr> <fct> <int>
1 SK_16 SK_107 Emergency room 17
2 SK_87 SK_107 Emergency room 2
3 SK_14 SK_39 Hospital room 16
4 SK_11 SK_39 Hospital room 13
5 SK_12 SK_39 Hospital room 12Notre objectif est d’obtenir le nombre de cas secondaires causés par les individus infectés observés. Dans la base de données des contacts, lorsque chaque paire infecteur-infecté est unique, le nombre de lignes par infecteur correspond au nombre de cas secondaires générés par cet individu.
R
# count secondary cases per infector in contacts
epi_contacts %>%
purrr::pluck("contacts") %>%
dplyr::count(from, name = "secondary_cases")
SORTIE
from secondary_cases
1 SK_1 26
2 SK_11 1
3 SK_118 1
4 SK_12 1
5 SK_123 1
6 SK_14 38
7 SK_15 4
8 SK_16 21
9 SK_6 2
10 SK_76 2
11 SK_87 1Mais cette sortie ne contient que le nombre de cas secondaires pour
les infectieux déclarés dans les données de contact, et non pour les cas
de tous les individus de l’ensemble des
<epicontacts> l’objet.
Au lieu de cela, à partir de epicontacts nous pouvons
utiliser la fonction epicontacts::get_degree(). L’argument
type = "out" permet d’obtenir la valeur de degré de
sortie de chaque nœud dans le réseau de
contact à partir du <epicontacts> objet de la classe.
Dans un réseau dirigé, le degré de sortie est le nombre d’arêtes
sortantes (infectés) émanant d’un nœud (infecteur) (Nykamp DQ,
consulté le : 2025).
De même, l’argument only_linelist = TRUE n’inclura que
les individus figurant dans le cadre de données de la liste de
référence. Lors des enquêtes sur les épidémies, nous nous attendons à ce
qu’un registre de toutes les les personnes infectées
observées dans les données de la liste de référence. Cependant, toute
personne qui n’est pas liée à un infecteur ou un infecté potentiel
n’apparaîtra pas dans les données de contact. Par conséquent, l’argument
only_linelist = TRUE nous permettra de ne pas manquer ce
dernier groupe d’individus lorsque nous compterons le nombre de cas
secondaires causés par tous les individus infectés observés. Ils
apparaîtront dans les <integer> sous la forme
0 cas secondaires.
R
# Count secondary cases per subject in contacts and linelist
all_secondary_cases <- epicontacts::get_degree(
x = epi_contacts,
type = "out",
only_linelist = TRUE
)
Caution
À epicontacts::get_degree() nous utilisons l’argument
only_linelist = TRUE. Il s’agit de compter le nombre de cas
secondaires causés par toutes les personnes infectées observées, ce qui
inclut les individus figurant dans les bases de données des contacts et
des listes de diffusion.
L’hypothèse selon laquelle “la liste de référence inclura toutes les personnes figurant dans les contacts et la liste de référence”. peut ne pas fonctionner dans toutes les situations.
Par exemple, si au cours du registre des infections observées, les
données de contact comprenaient plus de sujets que ceux disponibles dans
les données de la liste de référence, vous ne devez prendre en compte
que les individus figurant dans les données de contact. Dans ce cas,
vous devez prendre en compte uniquement les personnes figurant dans les
données de contact, à epicontacts::get_degree() nous
utilisons l’argument only_linelist = FALSE.
Vous trouverez ici une version imprimée exemple reproductible:
R
# Three subjects on linelist
sample_linelist <- tibble::tibble(
id = c("id1", "id2", "id3")
)
# Four infector-infectee pairs with Five subjects in contact data
sample_contact <- tibble::tibble(
from = c("id1","id1","id2","id4"),
to = c("id2","id3","id4","id5")
)
# make an epicontacts object
sample_net <- epicontacts::make_epicontacts(
linelist = sample_linelist,
contacts = sample_contact,
directed = TRUE
)
# count secondary cases per subject from linelist only
epicontacts::get_degree(x = sample_net, type = "out", only_linelist = TRUE)
#> id1 id2 id3
#> 2 1 0
# count secondary cases per subject from contact only
epicontacts::get_degree(x = sample_net, type = "out", only_linelist = FALSE)
#> id1 id2 id4 id3 id5
#> 2 1 1 0 0
A partir d’un histogramme des all_secondary_cases de
l’objet, nous pouvons identifier les variation au niveau
individuel dans le nombre de cas secondaires. Trois cas étaient
liés à plus de 20 cas secondaires, tandis que les cas complémentaires
comptaient moins de cinq ou aucun cas secondaire.
<La visualisation du nombre de cas secondaires sur un histogramme nous aidera à faire le lien avec la distribution statistique à ajuster : –>
R
## plot the distribution
all_secondary_cases %>%
tibble::enframe() %>%
ggplot(aes(value)) +
geom_histogram(binwidth = 1) +
labs(
x = "Number of secondary cases",
y = "Frequency"
)
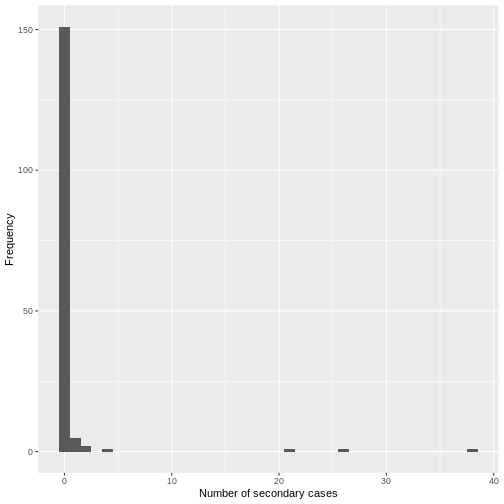
Le nombre de cas secondaires peut être utilisé pour estimer de manière empirique la distribution de la descendance qui est le nombre de cas secondaires causées par chaque cas. Une distribution statistique candidate utilisée pour modéliser la distribution de la descendance est la distribution binomiale négative avec deux paramètres :
Moyenne qui représente la \(R_{0}\) le nombre moyen de cas (secondaires) produits par un seul individu dans une population entièrement sensible, et
Dispersion exprimée par \(k\) qui représente la variation au niveau individuel de la transmission par des individus isolés.
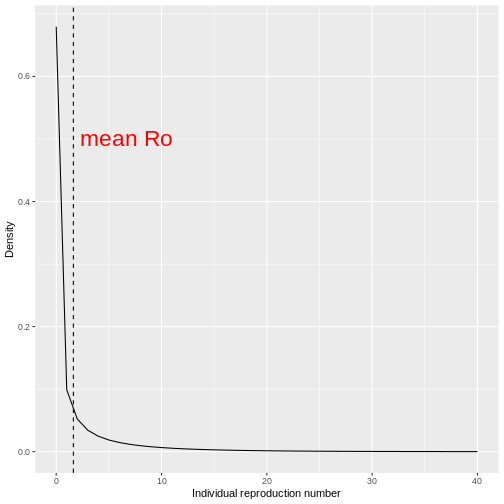
L’histogramme et le diagramme de densité montrent que la distribution de la descendance est fortement asymétrique, soit surdispersée. Dans ce cadre, les événements de surdispersion (ESS) ne sont pas arbitraires ou exceptionnels, mais simplement des réalisations de la queue droite de la distribution de la descendance, que nous pouvons quantifier et analyser (Lloyd-Smith et al., 2005).
Récapitulation terminologique
- A partir de la liste des lignes et des données de contact, nous calculons le nombre de cas secondaires causés par les personnes infectées observées.
- Alors que \(R_{0}\) représente la transmission moyenne au sein de la population, nous pouvons définir l’indicateur nombre de reproduction individuel comme le nombre d’infections secondaires causées par un individu infecté spécifique, qui varie d’un individu à l’autre.
- En raison des effets stochastiques de la transmission, le nombre d’infections secondaires causées par chaque personne infectée est décrit par la distribution de la descendance.
- La distribution des descendants peut être modélisée par l’équation suivante binomiale négative avec une moyenne \(R_{0}\) et un paramètre de dispersion \(k\), estimés à partir du nombre observé de cas secondaires.
Pour les occurrences d’événements discrets associés, nous pouvons utiliser Poisson ou des distributions binomiales négatives.
Dans une distribution de Poisson, la moyenne est égale à la variance. Mais lorsque la variance est supérieure à la moyenne, on parle de surdispersion. Dans les applications biologiques, la surdispersion se produit et une binomiale négative peut donc être considérée comme une alternative à la distribution de Poisson.
La distribution binomiale négative est particulièrement utile pour les données discrètes sur un intervalle positif non borné dont la variance de l’échantillon dépasse la moyenne de l’échantillon. En d’autres termes, les observations sont surdispersées par rapport à une distribution de Poisson, pour laquelle la moyenne est égale à la variance.
En épidémiologie, binôme négatif ont été utilisées pour modéliser la transmission de maladies infectieuses pour lesquelles le nombre probable d’infections ultérieures peut varier considérablement d’un individu à l’autre et d’un environnement à l’autre, en tenant compte de toutes les variations dans les antécédents infectieux des individus, y compris les propriétés des circonstances biologiques (c’est-à-dire le degré d’excrétion virale) et environnementales (par exemple, le type et le lieu de contact).
Défi
Calculez la distribution des cas secondaires d’Ebola à l’aide de la
méthode des ebola_sim_clean objet de
outbreaks package.
- La distribution de la descendance d’Ebola est-elle asymétrique ou surdispersée ?
⚠️ Étape facultative : Cet ensemble de données a
5829 cas. Exécution plot(<epicontacts>) peut prendre
plusieurs minutes et utiliser beaucoup de mémoire pour les grandes
épidémies telles que la liste des cas d’Ebola. Si vous utilisez un
ordinateur plus ancien ou plus lent, vous pouvez sauter cette étape.
R
## first, make an epicontacts object
ebola_contacts <-
epicontacts::make_epicontacts(
linelist = outbreaks::ebola_sim_clean$linelist,
contacts = outbreaks::ebola_sim_clean$contacts,
directed = TRUE
)
# count secondary cases per subject in contacts and linelist
ebola_secondary <- epicontacts::get_degree(
x = ebola_contacts,
type = "out",
only_linelist = TRUE
)
## plot the distribution
ebola_secondary %>%
tibble::enframe() %>%
ggplot(aes(value)) +
geom_histogram(binwidth = 1) +
labs(
x = "Number of secondary cases",
y = "Frequency"
)
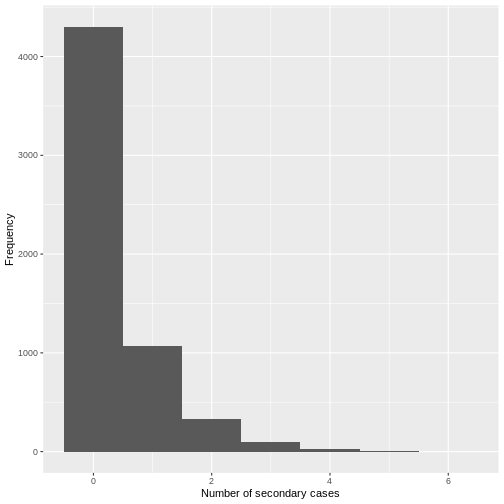
D’après une inspection visuelle, la distribution des cas secondaires
pour l’ensemble des données relatives à Ebola en
ebola_sim_clean montre une distribution asymétrique avec
des cas secondaires inférieurs ou égaux à 6. Nous devons compléter cette
observation par une analyse statistique afin d’évaluer la
surdispersion.
Estimez le paramètre de dispersion
Pour estimer empiriquement le paramètre de dispersion \(k\) nous pourrions ajuster une distribution binomiale négative au nombre de cas secondaires.
Nous pouvons ajuster des distributions aux données à l’aide de la fonction fitdistrplus qui fournit des estimations du maximum de vraisemblance.
R
library(fitdistrplus)
R
## fit distribution
offspring_fit <- all_secondary_cases %>%
fitdistrplus::fitdist(distr = "nbinom")
offspring_fit
SORTIE
Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
estimate Std. Error
size 0.02039807 0.007278299
mu 0.60452947 0.337893199Nom des paramètres
A partir de la fitdistrplus sortie :
- Le
sizefait référence au paramètre de dispersion estimé \(k\) estimé, et - L’objet
muse réfère à la moyenne estimée, qui représente l’ensemble de la population. \(R_{0}\),
À partir de la distribution du nombre de cas secondaires, nous avons estimé un paramètre de dispersion \(k\) de 0.02 avec un intervalle de confiance à 95% de 0.006 à 0.035. Comme la valeur de \(k\) est nettement inférieure à un, nous pouvons conclure qu’il existe un potentiel considérable pour les événements de superposition.
Nous pouvons superposer les valeurs de densité estimées de la distribution binomiale négative ajustée et l’histogramme du nombre de cas secondaires :
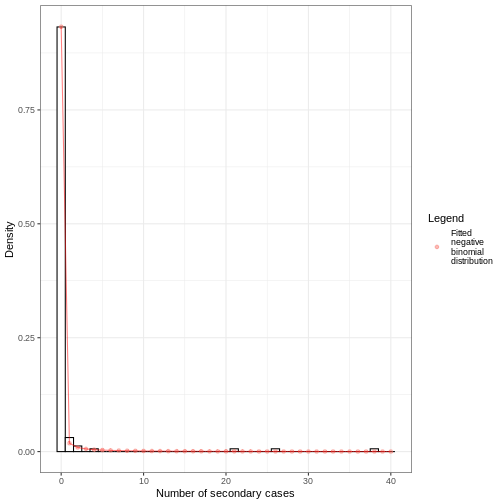
Variation de la transmission au niveau individuel
La variation de la transmission au niveau individuel est définie par la relation entre la moyenne (\(R_{0}\)), la dispersion (\(k\)) et la variance d’une distribution binomiale négative.
Le modèle binomial négatif a \(variance = R_{0}(1+\frac{R_{0}}{k})\), de sorte que les plus petites valeurs de \(k\) indiquent une plus grande variance et, par conséquent, une plus grande variation au niveau individuel de la transmission.
\[\uparrow variance = R_{0}(1+\frac{R_{0}}{\downarrow k})\]
Lorsque \(k\) s’approche de l’infini (\(k \rightarrow \infty\)), la variance est égale à la moyenne (parce que \(\frac{R_{0}}{\infty}=0\)). Cela fait du modèle de Poisson classique un cas particulier du modèle binomial négatif.
Défi
À partir de l’épreuve précédente, utilisez la distribution des cas
secondaires de l’épreuve de la ebola_sim_clean de l’objet
de outbreaks package.
Ajustez une distribution binomiale négative pour estimer la moyenne et le paramètre de dispersion de la distribution de la descendance. Essayez d’estimer l’incertitude du paramètre de dispersion à partir de l’erreur standard et des intervalles de confiance à 95 %.
- Le paramètre de dispersion estimé d’Ebola fournit-il des preuves d’une variation de la transmission au niveau individuel ?
Revoyez comment nous avons ajusté une distribution binomiale négative
à l’aide de la fonction fitdistrplus::fitdist()
fonction.
R
ebola_offspring <- ebola_secondary %>%
fitdistrplus::fitdist(distr = "nbinom")
ebola_offspring
SORTIE
Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
estimate Std. Error
size 0.8539443 0.072505326
mu 0.3675993 0.009497097R
## extract the "size" parameter
ebola_mid <- ebola_offspring$estimate[["size"]]
## calculate the 95% confidence intervals using the
## standard error estimate and
## the 0.025 and 0.975 quantiles of the normal distribution.
ebola_lower <- ebola_mid + ebola_offspring$sd[["size"]] * qnorm(0.025)
ebola_upper <- ebola_mid + ebola_offspring$sd[["size"]] * qnorm(0.975)
# ebola_mid
# ebola_lower
# ebola_upper
À partir de la distribution du nombre de cas secondaires, nous avons estimé un paramètre de dispersion \(k\) de 0.85 avec un intervalle de confiance à 95% de 0.71 à 1.
Pour les estimations du paramètre de dispersion supérieures à un, nous obtenons une faible variance de la distribution, et donc une faible variation de la transmission au niveau individuel.
Mais cela signifie-t-il que la distribution des cas secondaires ne présente pas d’événements de super propagation (ESS) ? Vous rencontrerez plus tard une difficulté supplémentaire : comment définir un seuil d’ESS pour Ebola ?
Nous pouvons utiliser les estimations du maximum de vraisemblance de
fitdistrplus pour comparer différents modèles et évaluer
la performance de l’ajustement à l’aide d’estimateurs tels que l’AIC et
le BIC. Pour en savoir plus, lisez la vignette sur Estimer
la transmission au niveau individuel et utilisez l’outil
superspreading fonction d’aide ic_tbl() pour
cela !
Le paramètre de dispersion entre les maladies
La recherche sur les maladies sexuellement transmissibles et à transmission vectorielle a précédemment suggéré une règle “20/80”, 20 % des individus contribuant à au moins 80 % du potentiel de transmission (Woolhouse et al).
En soi, le paramètre de dispersion \(k\) est difficile à interpréter intuitivement, et sa conversion en un résumé proportionnel peut faciliter la comparaison. Si l’on considère un éventail plus large d’agents pathogènes, on constate qu’il n’existe pas de règle absolue pour le pourcentage qui génère 80 % de la transmission, mais que la variation apparaît comme une caractéristique commune des maladies infectieuses.
Lorsque les 20 % de cas les plus infectieux contribuent à 80 % de la transmission (ou plus), on observe une forte variation de la transmission au niveau individuel, avec une distribution de la descendance fortement surdispersée (\(k<0.1\)), par exemple dans le cas du SRAS-1.
Lorsque les 20 % de cas les plus infectieux contribuent à environ 50 % de la transmission, la variation de la transmission au niveau individuel est faible et la distribution de la descendance est modérément dispersée (\(k > 0.1\)), par exemple la peste pulmonaire.
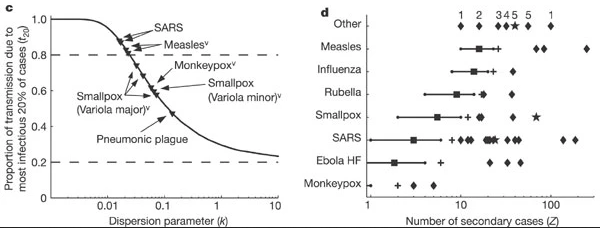
Contrôle de la superspreading avec la traçabilité des contacts
Lors d’une épidémie, il est courant d’essayer de réduire la transmission en identifiant les personnes qui ont été en contact avec une personne infectée, puis en les mettant en quarantaine au cas où elles s’avéreraient infectées par la suite. Cette recherche de contacts peut être déployée de plusieurs manières. La recherche des contacts “en amont” cible les contacts en aval susceptibles d’avoir été infectés par une infection nouvellement identifiée (c’est-à-dire le “cas index”). La recherche “en amont” vise plutôt le cas primaire en amont qui a infecté le cas index (ou un lieu ou un événement au cours duquel le cas index a été infecté), par exemple en retraçant l’historique des contacts jusqu’au point d’exposition probable. Cela permet d’identifier d’autres personnes qui ont également été potentiellement infectées par ce cas primaire antérieur.
En présence d’une variation de la transmission au niveau individuel, c’est-à-dire avec une distribution de la descendance surdispersée, si ce cas primaire est identifié, une plus grande partie de la chaîne de transmission peut être détectée en remontant l’historique de chacun des contacts de ce cas primaire (Endo et al., 2020).
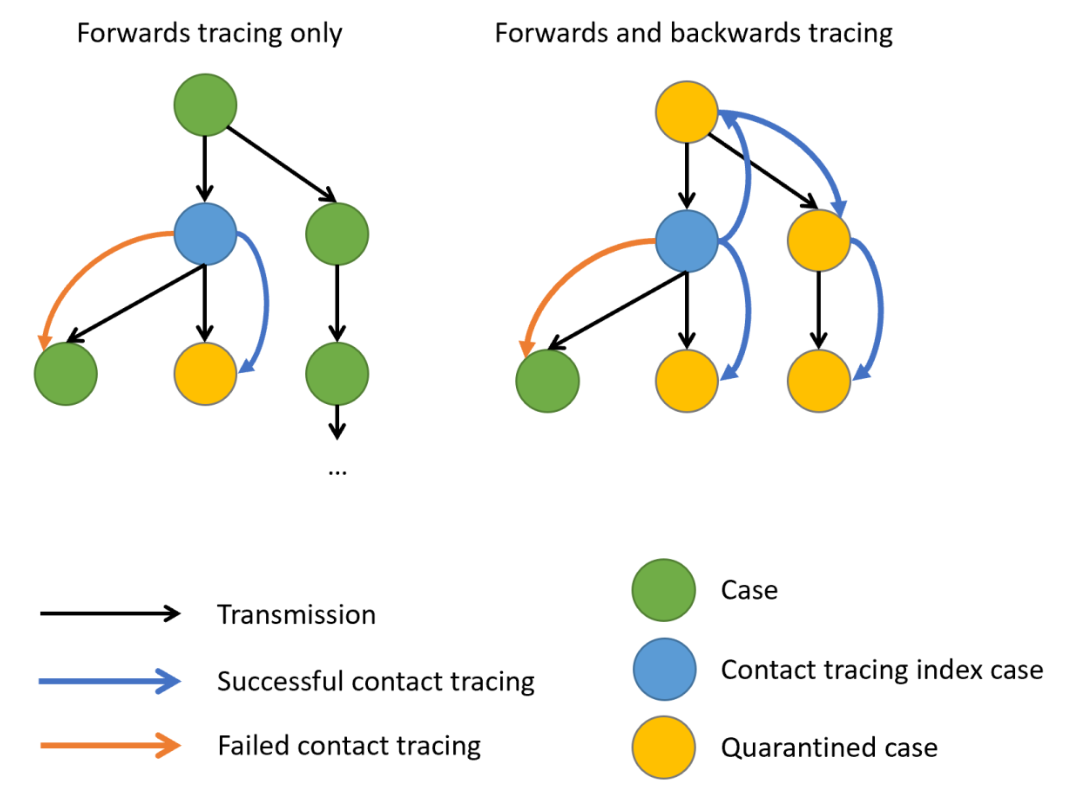
Lorsqu’il existe des preuves de variation au niveau individuel (c’est-à-dire de surdispersion), qui se traduisent souvent par ce que l’on appelle des événements de superspreading, une grande proportion d’infections peut être liée à une petite proportion de grappes d’origine. Par conséquent, la recherche et le ciblage des grappes d’origine, combinés à la réduction des infections ultérieures, peuvent considérablement améliorer l’efficacité des méthodes de dépistage (Endo et al., 2020).
Des données empiriques axées sur l’évaluation de l’efficacité de la recherche rétrospective ont permis d’identifier 42 % de cas supplémentaires par rapport à la recherche prospective, ce qui plaide en faveur de sa mise en œuvre lorsqu’une suppression rigoureuse de la transmission est justifiée (Raymenants et al, 2022)
Probabilité de cas dans un groupe donné
En utilisant superspreading nous pouvons estimer la probabilité d’avoir une grappe d’infections secondaires causées par un cas primaire identifié par traçage rétrospectif de taille \(X\) ou plus (Endo et al., 2020).
R
# Set seed for random number generator
set.seed(33)
# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
R = offspring_fit$estimate["mu"],
k = offspring_fit$estimate["size"],
cluster_size = c(5, 10, 25)
)
SORTIE
R k prop_5 prop_10 prop_25
1 0.6045295 0.02039807 87.9% 74.6% 46.1%Même si nous disposons d’un \(R<1\) une distribution de la descendance fortement surdispersée (\(k=0.02\)) signifie que si nous détectons un nouveau cas, il y a un risque d’erreur dans la distribution de la descendance. 46.1% probabilité qu’il provienne d’un groupe de 25 infections ou plus. Par conséquent, en suivant une stratégie rétrospective, les efforts de recherche des contacts augmenteront la probabilité de réussir à contenir et à mettre en quarantaine ce grand nombre de personnes précédemment infectées, plutôt que de se concentrer simplement sur le nouveau cas, qui est susceptible de n’avoir infecté personne (parce qu’il n’a pas été infecté). \(k\) est très faible).
Nous pouvons également utiliser ce nombre pour empêcher les rassemblements de certaines tailles afin de réduire l’épidémie en prévenant les événements potentiels de surpopulation. Les interventions peuvent viser à réduire le nombre de reproductions afin de réduire la probabilité d’avoir des groupes de cas secondaires.
Recherche rétrospective des contacts pour Ebola
Utilisez les paramètres estimés pour Ebola pour
ebola_sim_clean à partir de outbreaks
package.
Calculez la probabilité d’avoir un groupe d’infections secondaires causées par un cas primaire identifié par traçage rétrospectif de taille 5, 10, 15 ou plus.
La mise en œuvre d’une stratégie de traçage en amont à ce stade de l’épidémie d’Ebola augmenterait-elle la probabilité de contenir et de mettre en quarantaine un plus grand nombre de cas en aval ?
Examinez comment nous avons estimé la probabilité d’avoir des grappes
de taille fixe, compte tenu de la moyenne de la distribution de la
descendance et des paramètres de dispersion, à l’aide de la méthode des
superspreading::proportion_cluster_size() fonction.
R
# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
R = ebola_offspring$estimate["mu"],
k = ebola_offspring$estimate["size"],
cluster_size = c(5, 10, 25)
)
SORTIE
R k prop_5 prop_10 prop_25
1 0.3675993 0.8539443 2.64% 0% 0%La probabilité d’avoir des grappes de cinq personnes est de 1,8 %. À ce stade, compte tenu des paramètres de distribution de la descendance, une stratégie rétrospective n’augmentera peut-être pas la probabilité de contenir et de mettre en quarantaine davantage de cas en amont.
Défis
Le virus Ebola se propage-t-il à grande échelle ?
La notion d’“événement de surpopulation” peut revêtir des significations différentes selon les personnes. Lloyd-Smith et al, 2005 ont proposé un protocole général pour définir un événement de super propagation (ESS). Si le nombre d’infections secondaires causées par chaque cas, \(Z\) suit une distribution binomiale négative (\(R, k\)) :
- Nous définissons une ESS comme tout individu infecté qui infecte plus de \(Z(n)\) autres, où \(Z(n)\) est le nième percentile de l’échantillon de \(Poisson(R)\) distribution.
- Un SSE du 99e centile est donc tout cas causant plus d’infections qu’il n’en surviendrait dans 99 % des histoires infectieuses d’une population homogène.
À l’aide de la fonction de distribution correspondante, estimez le
seuil d’ESS pour définir un ESS pour les estimations de la distribution
de la descendance d’Ebola pour l’ensemble de la population.
ebola_sim_clean objet de outbreaks
package.
Dans une distribution de Poisson, lambda ou tau sont égaux à la valeur estimée du paramètre moyenne d’une distribution binomiale négative. Vous pouvez étudier cette question dans Le zoo de la distribution une application brillante.
Pour obtenir la valeur du quantile pour le 99ème centile, nous devons
utiliser la fonction fonction
de densité de la distribution de Poisson dpois().
R
# get mean
ebola_mu_mid <- ebola_offspring$estimate["mu"]
# get 99th-percentile from poisson distribution
# with mean equal to mu
stats::qpois(
p = 0.99,
lambda = ebola_mu_mid
)
SORTIE
[1] 2Comparez ces valeurs avec celles rapportées par Lloyd-Smith et al, 2005. Voir la figure ci-dessous :
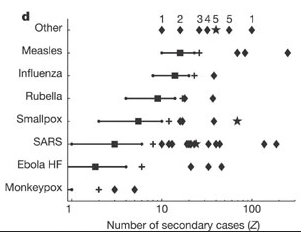
Proportion attendue de transmission
Quelle est la proportion de cas responsables de 80 % de la transmission ?
L’utilisation superspreading et comparez les estimations pour MERS en utilisant les paramètres de distribution de la descendance de cet épisode du didacticiel, avec les estimations pour le SRAS-1 et Ebola accessibles via le paramètre de distribution de la descendance epiparameter R.
Pour utiliser superspreading::proportion_transmission()
nous vous recommandons de lire le Estimer
quelle proportion de cas provoque une certaine proportion de
transmission le manuel de référence.
Actuellement, epiparameter a des distributions de
descendants pour SARS, Smallpox, Mpox, Pneumonic Plague, Hantavirus
Pulmonary Syndrome, Ebola Virus Disease. Accédons à la distribution des
descendants mean et dispersion pour SARS-1
:
R
# Load parameters
sars <- epiparameter::epiparameter_db(
disease = "SARS",
epi_name = "offspring distribution",
single_epiparameter = TRUE
)
sars_params <- epiparameter::get_parameters(sars)
sars_params
SORTIE
mean dispersion
1.63 0.16 R
#' estimate for ebola --------------
ebola_epiparameter <- epiparameter::epiparameter_db(
disease = "Ebola",
epi_name = "offspring distribution",
single_epiparameter = TRUE
)
ebola_params <- epiparameter::get_parameters(ebola_epiparameter)
ebola_params
SORTIE
mean dispersion
1.5 5.1 R
# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
R = ebola_params[["mean"]],
k = ebola_params[["dispersion"]],
prop_transmission = 0.8
)
SORTIE
R k prop_80
1 1.5 5.1 43.2%R
#' estimate for sars --------------
# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
R = sars_params[["mean"]],
k = sars_params[["dispersion"]],
prop_transmission = 0.8
)
SORTIE
R k prop_80
1 1.63 0.16 13%R
#' estimate for mers --------------
# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
R = offspring_fit$estimate["mu"],
k = offspring_fit$estimate["size"],
prop_transmission = 0.8
)
SORTIE
R k prop_80
1 0.6045295 0.02039807 2.13%Le MERS présente le pourcentage le plus faible de cas (2,1 %) responsables de 80 % de la transmission, ce qui est représentatif d’une distribution très dispersée de la descendance.
Le virus Ebola présente le pourcentage le plus élevé de cas (43 %) responsables de 80 % de la transmission. Ce pourcentage est représentatif des distributions de descendance dont les paramètres de dispersion sont élevés.
inverse-dispersion ?
Le paramètre de dispersion \(k\) peut être exprimé différemment dans la littérature.
- Dans la page Wikipédia consacrée à la binomiale négative, ce paramètre est défini sous sa forme réciproque (voir la rubrique équation de la variance).
- Dans le cas d’une le zoo de distribution shiny app, le paramètre de dispersion \(k\) est appelé “Inverse-dispersion” mais il est égal au paramètre estimé dans cet épisode. Nous vous invitons à explorer cette piste !
hétérogénéité ?
La variation de la transmission au niveau individuel est également
appelée hétérogénéité de la transmission ou degré d’hétérogénéité de la
transmission. Lloyd-Smith et al,
2005 l’infectiosité hétérogène dans les Campbell
et al, 2018 lors de l’introduction de la {outbreaker2}
package. De même, un réseau de contacts peut stocker des contacts
épidémiologiques hétérogènes, comme dans la documentation de l’étude
epicontacts package (Nagraj
et al., 2018).
Lisez ces articles de blog
Tracer la variole du singe de la JUNIPER montre l’utilité des modèles de réseau pour la recherche de contacts.
Devenir viral d’Adam Kucharski présente les conditions qui déclenchent la contagion en ligne : viralité sur YouTube, épidémies et campagnes de marketing.
Points clés
- Utiliser epicontacts pour calculer le nombre de cas secondaires causés par une personne particulière à partir de la liste de diffusion et des données de contact.
- Utiliser fitdistrplus pour estimer empiriquement la distribution de la descendance à partir de la distribution du nombre de cas secondaires.
- Utilisez superspreading pour estimer la probabilité d’avoir des grappes d’une taille donnée à partir des cas primaires et informer les efforts de recherche de contacts.
Content from Simuler des chaînes de transmission
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 32 minutes
Vue d'ensemble
Questions
- Comment simuler des chaînes de transmission basées sur les caractéristiques de l’infection ?
Objectifs
- Estimez le potentiel d’épidémies importantes suite à l’introduction d’un nouveau cas à l’aide d’un processus de ramification avec epichains.
Conditions préalables
Les apprenants devraient se familiariser avec les concepts suivants avant de suivre ce tutoriel :
Statistiques Les distributions de probabilités courantes, y compris les distributions de Poisson et binomiale négative.
Théorie des épidémies: Le nombre de reproduction, \(R\).
Introduction
La variation individuelle de la transmission peut affecter à la fois le potentiel d’établissement d’une épidémie dans une population et la facilité de sa contrôle (Cori et al., 2017).
Une plus grande variation réduit la probabilité globale qu’un nouveau cas unique soit à l’origine d’une épidémie locale de grande ampleur, car la plupart des cas infectent peu d’autres personnes et les individus qui génèrent un grand nombre de cas secondaires sont relativement rares.
Toutefois, si un “événement de super propagation” se produit et que l’épidémie s’installe, cette variation peut rendre l’épidémie plus difficile à contrôler en utilisant des interventions de masse (c’est-à-dire des interventions générales qui supposent implicitement que tout le monde contribue de manière égale à la transmission), car certains cas contribuent de manière disproportionnée : un seul cas non contrôlé peut générer un grand nombre de cas secondaires.
Inversement, la variation de la transmission peut offrir des possibilités des interventions ciblées si les individus qui contribuent le plus à la transmission (en raison de facteurs biologiques ou comportementaux), ou les environnements dans lesquels se produisent les “événements de super propagation”, partagent des caractéristiques sociodémographiques, environnementales ou géographiques qui peuvent être définies.
Comment peut-on quantifier le potentiel d’une nouvelle infection à provoquer une épidémie de grande ampleur sur la base de son nombre de reproduction \(R\) et de la dispersion \(k\) de la distribution de sa descendance ?
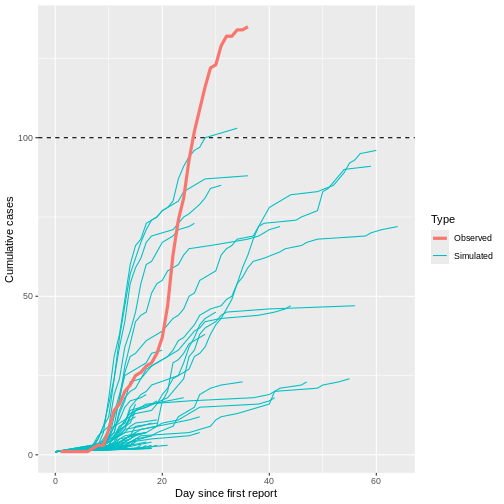
Dans cet épisode, nous utiliserons le package epichains pour simuler des chaînes de transmission et estimer le potentiel d’épidémies importantes suite à l’introduction d’un nouveau cas. Nous allons l’utiliser avec les fonctions de epiparameter, dplyr et purrrdonc il faut également charger le tidyverse package :
R
library(epichains)
library(epiparameter)
library(tidyverse)
Le double point-virgule
Le double point-virgule :: en R vous permet d’appeler
une fonction spécifique d’un package sans charger le package entier dans
l’environnement courant.
Par exemple, vous pouvez appeler une fonction spécifique d’un package
sans charger le package entier dans l’environnement actuel,
dplyr::filter(data, condition) utilise
filter() à partir de l’outil dplyr
package.
Cela nous permet de nous souvenir des fonctions du package et d’éviter les conflits d’espace de noms.
Simulation des épidémies incontrôlées
Les épidémies de maladies infectieuses se propagent dans les populations lorsqu’une chaîne d’individus infectés transmet l’infection à d’autres. Processus de ramification peuvent être utilisés pour modéliser cette transmission. Un processus de ramification est un processus stochastique (c’est-à-dire un processus aléatoire qui peut être décrit par une distribution de probabilité connue), dans lequel chaque individu infectieux donne naissance à un nombre aléatoire d’individus dans la génération suivante d’infection, en commençant par le cas index dans la génération 1. La distribution du nombre de cas secondaires générés par chaque individu est appelée distribution de la descendance (Azam & Funk, 2024).
epichains fournit des méthodes d’analyse et de simulation de la taille et longueur des processus de ramification pour une certaine distribution de la descendance. epichains met en œuvre un modèle simple et rapide pour simuler les chaînes de transmission afin d’évaluer le risque épidémique, de projeter les cas dans l’avenir et d’évaluer les interventions qui modifient \(R\).
taille et longueur de la chaîne
La taille de la chaîne de transmission est définie comme le nombre total d’individus infectés sur toutes les générations d’infection, et
la longueur de la chaîne de transmission est le nombre de générations entre le premier et le dernier cas de l’épidémie avant que la chaîne se termine.
Le calcul de la taille inclut le premier cas, et le calcul de la longueur contient la première génération lorsque le premier cas commence la chaîne (voir figure ci-dessous).
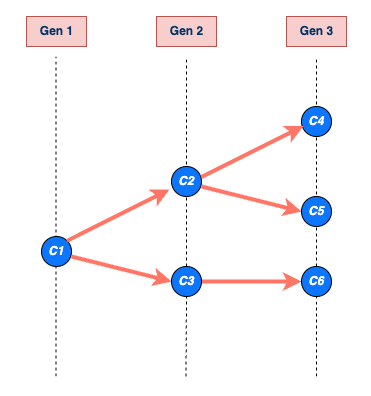
Pour utiliser epichains nous devons connaître (ou supposer) deux valeurs épidémiologiques clés : la distribution de la descendance et le temps de génération.
Obtenez la distribution de la descendance
Nous supposons ici que la distribution de la descendance du MERS suit
une distribution binomiale négative, avec une moyenne (nombre de
reproduction \(R\)) et une dispersion
\(k\) estimées à partir de la liste et
des données de contact de mers_korea_2015 dans le package
outbreaks R de l’épisode précédent.
R
mers_offspring <- c(mean = 0.60, dispersion = 0.02)
Distribution de la descendance pour épichains
Nous entrons une distribution de descendance dans
epichains en faisant référence à la fonction R qui génère
des valeurs aléatoires à partir de la distribution souhaitée. Pour une
distribution binomiale négative, nous utilisons rnbinom
avec les arguments mu et size:
En interne, epichains tire une valeur aléatoire, compte tenu des paramètres, afin de simuler le nombre de nouvelles infections à partir d’un individu infecté (transmission ultérieure).
R
# generate one random number given the distribution family and its parameters
# (run this line many times to get different values)
rnbinom(n = 1, mu = mers_offspring["mean"], size = mers_offspring["dispersion"])
Le manuel de référence en ?rnbinom nous indique les
arguments spécifiques requis.
epichains peut accepter n’importe quelle fonction R qui génère des nombres aléatoires, de sorte que les arguments spécifiés changeront en fonction de la fonction R utilisée. Pour plus de détails sur les options possibles, consultez le manuel de référence de la fonction.
Par exemple, disons que nous voulons utiliser une distribution de
Poisson pour la distribution de la descendance. Tout d’abord, lisez
l’argument requis ?rpois dans le manuel de référence.
Ensuite, spécifiez l’argument lambda également connu sous
le nom de taux ou de moyenne dans la littérature. En
epichains cela peut ressembler à ceci :
Dans cet exemple, nous pouvons spécifier
lambda = mers_offspring["mean"] car le nombre moyen de cas
secondaires générés (c’est-à-dire \(R\)) devrait être le même quelle que soit
la distribution que nous supposons. Ce qui change, c’est la variance de
la distribution, et donc le niveau de variation de la transmission au
niveau individuel. Lorsque le paramètre de dispersion \(k\) s’approche l’infini (\(k \rightarrow \infty\)) dans une
distribution binomiale négative, la variance est égale à la moyenne.
Cela fait de la distribution de Poisson classique un cas particulier de
la distribution binomiale négative.
Obtenir le temps de génération
La distribution de l’intervalle de série est souvent utilisée pour approximer la distribution du temps de génération. Cette approximation est couramment utilisée parce qu’il est plus facile d’observer et de mesurer l’apparition des symptômes dans chaque cas que le moment précis de l’infection.

Cependant, l’utilisation de l’option intervalle de série comme approximation du temps de génération est principalement valable pour les maladies dans lesquelles l’infectiosité commence après l’apparition des symptômes (Chung Lau et al., 2021). Dans les cas où l’infectiosité commence avant l’apparition des symptômes, les intervalles sériels peuvent avoir des valeurs négatives, ce qui est le cas pour les maladies à transmission pré-symptomatique (Nishiura et al., 2020).
Utilisons le package epiparameter pour accéder à l’intervalle de série disponible pour la maladie MERS :
R
serial_interval <- epiparameter::epiparameter_db(
disease = "mers",
epi_name = "serial",
single_epiparameter = TRUE
)
plot(serial_interval, day_range = 0:25)
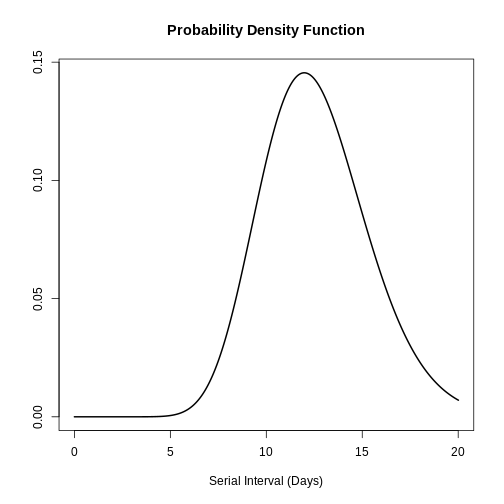
L’intervalle de série pour le MERS a une moyenne de 12.6 jours et un écart-type de 2.8 jours.
temps de génération pour epichains
Dans chaque étape de la simulation, epichains tire des
valeurs du temps de génération pour chaque nouvelle infection génèré de
la distribution de la descendance. Pour les objets de la classe
epiparameter::generate() pour cette entrée.:
R
# In step one, the number of new infections is 2, then:
# generate 2 random values given the serial interval distribution
generate(x = serial_interval, times = 2)
SORTIE
[1] 14.60507 15.06471R
# In step two, the number of new infections is 6, then:
# generate 6 random values given the serial interval distribution
generate(x = serial_interval, times = 6)
SORTIE
[1] 12.522027 16.109812 14.195049 6.875113 15.432142 12.349850Étant donné que le valeur de l’entrée pour le champ
times changera à chaque étape, nous devons intégrer
generate() dedans la fonction. epichains
tirera autant de valeurs aléatoires du temps de génération que le nombre
de nouvelles infections à cette étape. Le résultat sera le suivant :
R
function(x) generate(x = serial_interval, times = x)
Cette interface est similaire à celle que cfr utilise pour établir un lien avec epiparameter. Lisez le vignette travailler avec des distributions de retard pour plus de détails.
La fonction permettant de générer un nombre aléatoire à partir d’un
objet de classe <epiparameter> peut également
accepter cette notation :
R
as.function(x = serial_interval, func_type = "generate")
Simuler une chaîne unique
Nous sommes maintenant prêts à utiliser la fonction
simulate_chains() de epichains pour créer
un chaîne de transmission :
R
epichains::simulate_chains(
n_chains = 1,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
)
simulate_chains() nécessite au minimum trois séries
d’arguments :
-
les contrôles de simulation (
n_chainsetstatistic), -
la distribution des descendants
(
offspring_distet les paramètres de distributions requis), et - le temps de génération (
generation_time).
Dans les lignes ci-dessus, nous avons décrit comment spécifier la distribution des descendants et le temps de génération. Les contrôles la simulation comprend au moins deux arguments :
-
n_chains, qui définit le nombre de chaînes de transmission à simuler pour et -
statisticqui définit une statistique de chaîne à suivre (soit"size"ou"length") comme critère d’arrêt pour chaque chaîne simulée.
Critères d’arrêt
Il s’agit d’une fonction personnalisable de epichains.
Par défaut, les simulations de processus de ramification se terminent
lorsqu’elles se sont éteintes. Pour les chaînes de transmission de
longue durée, en simulate_chains() vous pouvez ajouter
l’argument stat_threshold
Par exemple, si on définit un critère d’arrêt pour
statistic = "size" de stat_threshold = 500 il
n’y aura plus de descendance après une chaîne de taille 500.
La sortie de simulate_chains() crée un objet de classe
<epichains> que nous pouvons ensuite analyser dans
R.
Simuler plusieurs chaînes
Nous pouvons utiliser simulate_chains() pour créer
plusieurs chaînes et augmenter la probabilité de simuler des projections
de épidémies incontrôlées en cas de distribution de la descendance trop
dispersée.
Nous devons spécifier un élément supplémentaire :
-
set.seed(<integer>), qui est une fonction de générateur de nombres aléatoires avec une valeur de semence spécifiée, le nombre<integer>afin de garantir des résultats cohérents entre les différentes exécutions de code.
Avec cette configuration, chaque chaîne représentera
un cas initial. Les cas de chaque chaîne sont
indépendants, isolés et sans interactions. Cela signifie que chaque
chaîne disposera de son propre pool de susceptibles, que tu peux
configurer à l’aide de l’option pop ou
percent_immune.
Maintenant, simulons 100 chaînes de transmission :
R
# Run all this chunk together to let set.seed() work!
# Set seed for random number generator
set.seed(33)
multiple_epichains <- epichains::simulate_chains(
n_chains = 100,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
)
Tu peux inspecter le taille total de chaque chaîne
simulée, ce qui équivaut au nombre cumulé de cas par chaîne, à l’aide de
la fonction summary() à l’objet de classe
<epichains>:
R
summary(multiple_epichains)
SORTIE
`epichains_summary` object
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[19] 7 1 1 1 1 1 1 1 1 1 1 14 1 2 1 1 2 1
[37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[55] 1 1 1 1 512 1 1 1 1 1 104 1 1 1 1 1 1 1
[73] 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1
[91] 1 1 1 1 1 1 1 1 1 1
Simulated sizes:
Max: 512
Min: 1Nous pouvons compter visuellement le nombre de chaînes qui atteignent plus de 100 cas d’infection, ainsi que les nombres maximum et minimum.
Défi
Utilise la dernière exécution de
epichains::simulate_chains() pour simuler plusieurs
chaînes. Modifie le statistic de "size" à
"length". Exécute le fonction summary().
- Pour quelle chaîne cette sortie compte-t-elle ?
Si tu as besoin d’aide, reviens à la boîte “Taille et longueur de la chaîne” depuis le début.
Lire la sortie d’épichains
Pour explorer le format de sortie de l’objet multiple_epichains du
classe <epichains>, examinons la simulation
chain nombre 30.
Utilisons dplyr::filter() pour cela :
R
chain_to_observe <- 30
R
#### get epichain summary ----------------------------------------------------
multiple_epichains %>%
dplyr::filter(chain == chain_to_observe)
SORTIE
`<epichains>` object
< epichains head (from first known infector) >
chain infector infectee generation time
2 30 1 2 2 14.100967
3 30 1 3 2 10.640301
4 30 1 4 2 15.608764
5 30 1 5 2 13.515424
6 30 1 6 2 9.967474
7 30 1 7 2 9.376222
Number of chains: 100
Number of infectors (known): 3
Number of generations: 3
Use `as.data.frame(<object_name>)` to view the full output in the console.Cette sortie contient deux parties :
- Un
head()des paires infecteur-infecté en commençant par le premier infecteur connu. - Un pied de page récapitulatif, le morceau de texte qui apparaît en bas :
SORTIE
Number of infectors (known): 3
Number of generations: 3Le chain nombre 30 simulé comporte trois infecteurs
connus et trois générations. Ces nombres sont plus visibles lorsque l’on
imprime les objets <epichains> sous la forme d’un
cadre de données (ou <tibble>).
R
#### infector-infectee data frame --------------------------------------------
multiple_epichains %>%
dplyr::filter(chain == chain_to_observe) %>%
dplyr::as_tibble()
SORTIE
# A tibble: 14 × 5
chain infector infectee generation time
<int> <dbl> <dbl> <int> <dbl>
1 30 NA 1 1 0
2 30 1 2 2 14.1
3 30 1 3 2 10.6
4 30 1 4 2 15.6
5 30 1 5 2 13.5
6 30 1 6 2 9.97
7 30 1 7 2 9.38
8 30 1 8 2 11.5
9 30 4 9 3 31.0
10 30 4 10 3 25.3
11 30 4 11 3 28.5
12 30 4 12 3 29.6
13 30 4 13 3 25.9
14 30 4 14 3 24.6 Chaîne 30 nous raconte une histoire:
“Dans la première génération de transmission à time = 0,
un sujet (ID = NA) a infecté le sujet avec
ID = 1. Sujet ID = 1 est le premier infecteur
connu.
“Ensuite, dans la deuxième génération de transmission, le sujet
ID = 1 a infecté sept sujets, de ID = 2 à
ID = 8. Ces infections se sont produites chez
time entre le 9e et le 15e jour, après la première
infection connue.
“Plus tard, lors de la troisième génération de transmission, le sujet
ID = 4 a infecté six nouveaux sujets, de
ID = 9 à ID = 14. Ces infections se sont
produites chez time entre le 24e et le 31e jour, après la
première infection connue.”
Le cadre de données de sortie recueille les infectés comme unité d’observation :
- Chaque personne infectée a un
infectee“ID”. - Chaque infecté qui se comporte comme un infecteur
est enregistré dans la base de données
infectorcolonne à l’aide deinfectee“id”. - Chaque personne infectée l’a été à un moment précis.
generationettime(continu). - Le numéro de simulation est enregistré sous le
chaincolonne.
Remarque : Le
Number of infectors (known) comprend le sujet
ID = NA sous le infector colonne. Il s’agit de
l’infecteur spécifié comme cas d’index (dans la colonne
n_chains ), qui a commencé la chaîne de transmission à
l’infecté de ID = 1 à generation = 1 et
time = 0.
Répéter les simulations
Comme précédemment, nous pouvons configurer la simulation de
plusieurs chaînes en augmentant simplement le nombre de chaînes (par ex.
n_chains = 1 à n_chains = 100). Cependant, si
nous devons supposer que chaque cas initial commence (à être infectieux)
à un moment différent, cela ne peut être configuré que dans une seule
fonction de simulation. Il faut donc itérer plusieurs
fois sur une configuration spécifique de simulation de chaîne pour
augmenter la probabilité de simuler des projections d’épidémies
incontrôlées. Le tableau suivant compare les alternatives :
| Simulations | Cas initiaux | Heure de début (t0) |
Utilise |
|---|---|---|---|
| Un | 1 | Idem |
epichains::simulate_chains() avec
n_chains = 1
|
| Multiple (100, par exemple) | 1 | Idem |
epichains::simulate_chains() avec
n_chains = 100
|
| Multiple (100, par exemple) | Plus d’un | Différents | Itère 100 fois en utilisant purrr::map() sur
epichains::simulate()
|
La différence essentielle de la troisième configuration est
l’argument t0 de epichains::simulate_chains().
L’argument t0 définit l’heure de début de chaque cas
initial par chaîne.
À noter
Un exemple d’utilisation de l’itération est disponible dans la vignette epichains sur Prévision de l’incidence des maladies infectieuses : un exemple de COVID-19. Il s’agit de simuler l’importation de 13 cas à différents moments.
R
epichains::covid19_sa[1:5, ] %>%
dplyr::mutate(start_time = date - min(date))
SORTIE
# A tibble: 5 × 3
date cases start_time
<date> <int> <drtn>
1 2020-03-05 1 0 days
2 2020-03-07 1 2 days
3 2020-03-08 1 3 days
4 2020-03-09 4 4 days
5 2020-03-11 6 6 days Au lieu d’avoir 100 chaînes commençant au même jour 0
(t0 = 0, par défaut), chaque simulation créera des chaînes
qui commenceront à un moment différent dans le temps. Elle considérera
le jour 2020-03-05 comme Jour 0. La première
chaîne commence au jour 0, une au jour 2, une au jour 3, quatre au jour
4 et six au jour 6. L’argument t0 aura cette structure
:
R
t0 <- c(0, 2, 3, rep(4, 4), rep(6, 6))
t0
SORTIE
[1] 0 2 3 4 4 4 4 6 6 6 6 6 6Pour augmenter la probabilité de simuler des projections d’épidémies incontrôlées, ce même scénario doit être itéré 100 fois. Cela nous aidera à fournir une projection avec de l’incertitude.
Dans cette section, nous allons te montrer comment construire le
itération sur epichains étape par étape.
Nous répliquerons la même simulation que précédemment : 100 chaînes de
transmission avec 1 cas initial chacune à partir du jour 0
(t0 = 0). Mais au lieu d’utiliser
n_chains = 100 nous allons itérer 100 fois sur la
simulation d’une chaîne de transmission avec un cas initial à partir du
jour 0 (n_chains = 1).
Nous devons spécifier deux éléments supplémentaires :
-
number_simulations, qui définit le nombre de simulations à effectuer. -
initial_casesdéfinit le nombre de cas initiaux à introduire dans l’argumentn_chainsexpliqué dans les lignes ci-dessus.
R
# Number of simulation runs
number_simulations <- 100
# Number of initial cases
initial_cases <- 1
number_simulations et initial_cases sont
commodément stockés dans des objets pour faciliter leur réutilisation en
aval dans le flux de travail.
Itération à l’aide de purrr
Itération vise à effectuer la même action sur différents objets de manière répétée.
Apprenez à utiliser les fonctions de base de purrr
comme map() à partir du tutoriel YouTube sur How to purrr par
Equitable Equations.
Ou, si vous avez déjà utilisé la famille de
fonctions*apply, visitez la vignette du package purrr base R
qui présente les principales différences, des traductions directes et
des exemples.
Pour obtenir plusieurs chaînes, nous devons appliquer la méthode
simulate_chains() à chaque chaîne définie par une séquence
de nombres allant de 1 à 100.
purrr et epichains
Tout d’abord, décrivons comment nous utilisons
purrr::map() avec
epichains::simulate_chains(). La fonction
map() nécessite deux arguments :
-
.x, un vecteur de nombres, et -
.fune fonction permettant d’itérer sur chaque valeur du vecteur.
R
# steps:
# - purrr::map() will run 100 times function(sim).
# - seq_len() creates a vector with sequence of numbers (simulation IDs from 1 to 100) and
# - function(sim) iterates {epichains} to each simulation ID number, then
# - dplyr::mutate() adds a column to the <epichains> output with the simulation ID number.
# - purrr::list_rbind() combines all the list class outputs (for each simulation ID) into a single data frame.
purrr::map(
.x = seq_len(number_simulations),
.f = function(sim) {
epichains::simulate_chains(...) %>% # <-- {epichains}
dplyr::mutate(simulation_id = sim)
}
) %>%
purrr::list_rbind()
# pseudo code: do not run.
L’élément sim est placé pour enregistrer le numéro
d’itération (ID de simulation) dans une nouvelle
colonne dans la sortie <epichains>. La fonction
purrr::list_rbind() a pour but de combiner toutes les
sorties de liste de map().
Pourquoi un point (.) comme préfixe ?
Dans le principes de
conception ordonnée nous avons un chapitre sur le préfixe point
!
Nous sommes maintenant prêts à utiliser purrr::map()
pour simuler de manière répétée de simulate_chains() et de
stocker dans un vecteur de 1 à 100:
R
set.seed(33)
simulated_chains_map <-
purrr::map(
.x = seq_len(number_simulations),
.f = function(sim) {
epichains::simulate_chains(
n_chains = initial_cases,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
) %>%
dplyr::mutate(simulation_id = sim)
}
) %>%
purrr::list_rbind()
Une limitation de la sortie itérative est que nous ne pouvons pas
utiliser la fonction summary(
R
simulated_chains_map %>%
dplyr::count(simulation_id) %>%
dplyr::pull(n)
SORTIE
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 9 1 1 1
[19] 1 1 1 1 113 1 1 1 1 1 1 1 1 1 19 1 1 1
[37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[55] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 22 1 1 1
[73] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[91] 1 1 1 1 1 1 1 1 1 1Visualiser plusieurs chaînes
Pour augmenter la probabilité de simuler des projections d’épidémies incontrôlées compte tenu d’une distribution surdispersée de la progéniture, simulons 1000 chaînes de transmission avec 1 cas initial pour chacune d’entre elles, à partir du jour 0.
Nous allons créer une simulation multiple sans itération pour cette section :
R
set.seed(33)
multiple_epichains <- epichains::simulate_chains(
n_chains = 1000,
statistic = "size",
offspring_dist = rnbinom,
mu = mers_offspring["mean"],
size = mers_offspring["dispersion"],
generation_time = function(x) generate(x = serial_interval, times = x)
)
Pour visualiser les chaînes simulées, nous avons besoin d’un traitement préalable :
- Utilisons dplyr pour obtenir des nombres de temps ronds qui ressemblent à des journées de surveillance.
- Compte les cas quotidiens dans chaque simulation (par
chain). - Calcule le nombre cumulé de cas dans une simulation.
R
# daily aggregate of cases
aggregate_chains <- multiple_epichains %>%
# use data.frame output from <epichains> object
dplyr::as_tibble() %>%
# get the round number (day) of infection times
dplyr::mutate(day = ceiling(time)) %>%
# count the daily number of cases in each chain
dplyr::count(chain, day, name = "cases") %>%
# calculate the cumulative number of cases for each chain
dplyr::group_by(chain) %>%
dplyr::mutate(cases_cumsum = cumsum(cases)) %>%
dplyr::ungroup()
Avant le graphique, créons un tableau de sommaire avec la durée
totale et la taille de chaque chaîne. Nous pouvons utiliser la “combo”
dplyr de group_by(),
summarise() et ungroup():
R
# Summarise the chain duration and size
summary_chains <-
aggregate_chains %>%
dplyr::group_by(chain) %>%
dplyr::summarise(
# duration
day_max = max(day),
# size
cases_total = max(cases_cumsum)
) %>%
dplyr::ungroup()
summary_chains
SORTIE
# A tibble: 1,000 × 3
chain day_max cases_total
<int> <dbl> <int>
1 1 0 1
2 2 0 1
3 3 0 1
4 4 0 1
5 5 0 1
6 6 0 1
7 7 0 1
8 8 0 1
9 9 0 1
10 10 0 1
# ℹ 990 more rowsMaintenant, nous sommes prêts à utiliser le package ggplot2 :
R
# Visualize transmission chains by cumulative cases
ggplot() +
# create grouped chain trajectories
geom_line(
data = aggregate_chains,
mapping = aes(
x = day,
y = cases_cumsum,
group = chain
),
color = "black",
alpha = 0.25,
show.legend = FALSE
) +
# define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2) +
labs(
x = "Day",
y = "Cumulative cases"
)
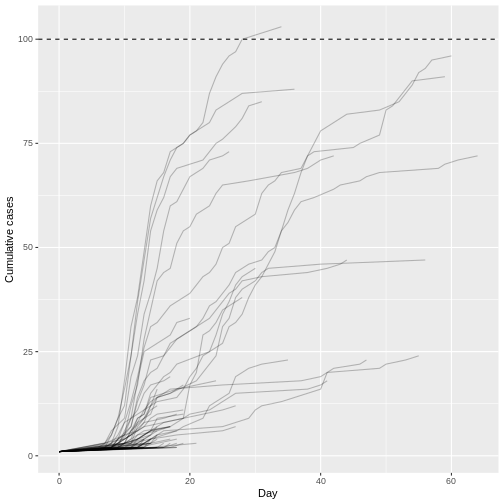
Bien que la plupart des présentations de 1 ne génèrent pas de cas secondaires (N = 934) ou que la plupart des épidémies s’éteignent rapidement (durée médiane de 17 et taille médiane de 5.5), seulement 1 trajectoires épidémiques parmi les 100 simulations (1%) peuvent atteindre plus de 100 cas infectés. Ce résultat est remarquable carle nombre de reproduction \(R\) est inférieur à 1 (moyenne de la distribution des descendants de 0.6), mais, compte tenu d’un paramètre de dispersion de la distribution de la progéniture de 0.02 il montre le potentiel de épidémies explosives de la maladie MERS.
Nous pouvons compter combien de chaînes ont atteint le seuil de 100 cas en utilisant les fonctionsdplyr. Cette sortie devrait nous donner des résultats équivalents à summary(multiple_epichains)`:
R
# number of chains that reached the 100-case threshold
summary_chains %>%
dplyr::arrange(desc(cases_total)) %>%
dplyr::filter(cases_total > 100)
SORTIE
# A tibble: 1 × 3
chain day_max cases_total
<int> <dbl> <int>
1 65 34 103Recouvrons le nombre cumulé de cas observés à l’aide de l’objet
linelist de l’ensemble de données mers_korea_2015 du
package R outbreaks. Pour préparer l’ensemble de données
afin de pouvoir tracer le nombre total de cas quotidiens au fil du
temps, nous utilisons incidence2 pour convertir la liste
de lignes en un objet <incidence2>, et compléte les
dates manquantes de la série temporelle à l’aide de
complete_dates()
R
library(outbreaks)
mers_cumcases <- mers_korea_2015$linelist %>%
# incidence2 workflow
incidence2::incidence(date_index = "dt_onset") %>%
incidence2::complete_dates() %>%
# wrangling using {dplyr}
dplyr::mutate(count_cumsum = cumsum(count)) %>%
tibble::rownames_to_column(var = "day") %>%
dplyr::mutate(day = as.numeric(day))
Utilise plot() pour faire un graphique d’incidence :
R
# plot the incidence2 object
plot(mers_cumcases)
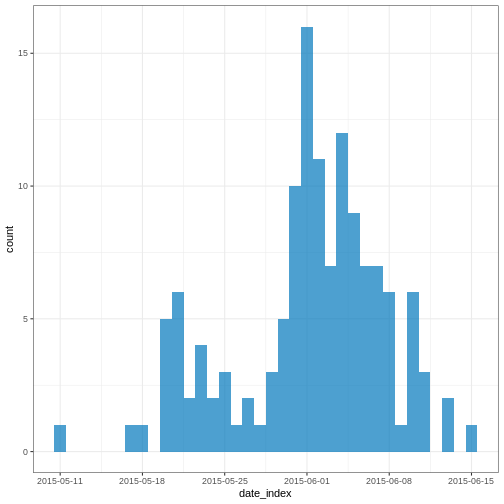
En traçant le nombre observé de cas cumulés de l’épidémie de syndrome respiratoire du Moyen-Orient (MERS) en Corée du Sud en 2015 à côté des chaînes simulées précédemment, on constate que les cas observés ont suivi une trajectoire conforme à la dynamique de l’épidémie explosive simulée (ce qui est logique, étant donné que la simulation utilise des paramètres basés sur cette épidémie spécifique).
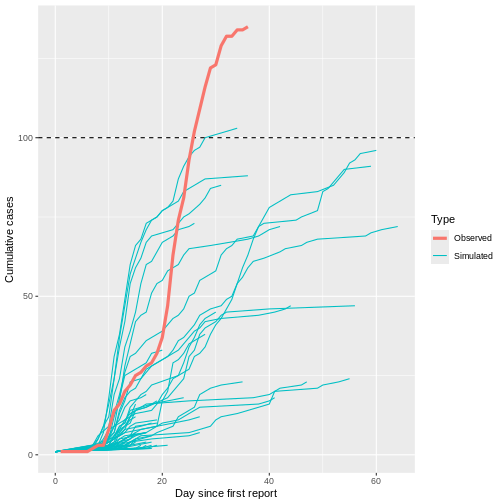
Lorsque nous augmentons le paramètre de dispersion de \(k = 0.01\) à \(k = \infty\) - et réduisons ainsi la variation de la transmission au niveau individuel - et supposons un nombre de reproduction fixe \(R = 1.5\) La proportion de épidémies simulés ayant atteint le seuil de 100 cas augmente. Cela s’explique par le fait que les épidémies simulées ont maintenant une dynamique plus cohérente, dans le sens des aiguilles d’une montre, plutôt que le niveau élevé de variabilité observé précédemment.
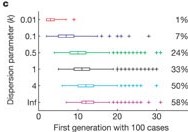
Les premières projections de propagation
Dans la phase initiale de l’épidémie, tu peux utiliser epichains pour appliquer un modèle de processus de ramification afin de prévoir le nombre de cas futurs. Même si le modèle tient compte du caractère aléatoire de la transmission et de la variation du nombre de cas secondaires, il peut y avoir des caractéristiques locales supplémentaires que nous n’avons pas prises en compte. L’analyse des premières prévisions faites pour le COVID dans différents pays à l’aide de cette structure de modèle a révélé que les prévisions étaient souvent trop confiantes (Pearson et al., 2020). Cela est probablement dû au fait que le modèle en temps réel n’incluait pas tous les changements dans la distribution de descendance qui se produisaient au niveau local à la suite des changements de comportement et des mesures de contrôle. Tu peux en savoir plus sur l’importance du contexte local dans les modèles COVID-19 dans . Eggo et al. (2020).
Nous t’invitons à lire la vignette sur Prévision de l’incidence des maladies infectieuses : un exemple de COVID-19! pour en savoir plus sur l’établissement de prévisions à l’aide de epichains.
Défis
Potentiel d’une épidémie importante de variole du singe
Évalue le potentiel d’un nouveau cas de variole du singe (Mpox) à générer une grande épidémie explosive.
- Simule 1000 chaînes de transmission avec 1 cas initial chacune à partir du jour 0.
- Utilise le paquet approprié pour accéder aux données de retard des épidémies précédentes.
- Combien de trajectoires simulées atteignent plus de 100 cas infectés ?
Avec epiparameter, tu peux accéder et utiliser les distributions des descendants et des retards des épidémies d’Ebola précédentes.
R
library(epiparameter)
library(tidyverse)
epiparameter::epiparameter_db(epi_name = "offspring") %>%
epiparameter::parameter_tbl() %>%
dplyr::count(disease, epi_name)
SORTIE
# Parameter table:
# A data frame: 6 × 3
disease epi_name n
<chr> <chr> <int>
1 Ebola Virus Disease offspring distribution 1
2 Hantavirus Pulmonary Syndrome offspring distribution 1
3 Mpox offspring distribution 1
4 Pneumonic Plague offspring distribution 1
5 SARS offspring distribution 2
6 Smallpox offspring distribution 4R
epiparameter::epiparameter_db(epi_name = "serial interval") %>%
epiparameter::parameter_tbl() %>%
dplyr::count(disease, epi_name)
SORTIE
# Parameter table:
# A data frame: 6 × 3
disease epi_name n
<chr> <chr> <int>
1 COVID-19 serial interval 4
2 Ebola Virus Disease serial interval 4
3 Influenza serial interval 1
4 MERS serial interval 2
5 Marburg Virus Disease serial interval 2
6 Mpox serial interval 5De plus, étant donné que tu n’as besoin que d’une seule chaîne par itération, commençant le même jour, il n’est peut-être pas nécessaire d’utiliser l’itération pour celle-ci.
R
# load packages -----------------------------------------------------------
library(epiparameter)
library(tidyverse)
# delays ------------------------------------------------------------------
mpox_offspring_epiparam <- epiparameter::epiparameter_db(
disease = "mpox",
epi_name = "offspring",
single_epiparameter = TRUE
)
mpox_offspring <- epiparameter::get_parameters(mpox_offspring_epiparam)
mpox_serialint <- epiparameter::epiparameter_db(
disease = "mpox",
epi_name = "serial interval",
single_epiparameter = TRUE
)
# iterate -----------------------------------------------------------------
# Set seed for random number generator
set.seed(33)
simulated_chains_mpox <- epichains::simulate_chains(
n_chains = 1000,
statistic = "size",
offspring_dist = rnbinom,
mu = mpox_offspring["mean"],
size = mpox_offspring["dispersion"],
generation_time = function(x) generate(x = mpox_serialint, times = x)
)
# visualize ---------------------------------------------------------------
# daily aggregate of cases
simulated_chains_mpox_day <- simulated_chains_mpox %>%
# use data.frame output from <epichains> object
as_tibble() %>%
# Count the daily number of cases in each chain
mutate(day = ceiling(time)) %>%
count(chain, day, name = "cases") %>%
# Calculate the cumulative number of cases for each chain
group_by(chain) %>%
mutate(cumulative_cases = cumsum(cases)) %>%
ungroup()
# Visualize transmission chains by cumulative cases
simulated_chains_mpox_day %>%
# Create grouped chain trajectories
ggplot(aes(x = day, y = cumulative_cases, group = chain)) +
geom_line(color = "black", alpha = 0.25, show.legend = FALSE) +
# Define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2) +
labs(x = "Day", y = "Cumulative cases")
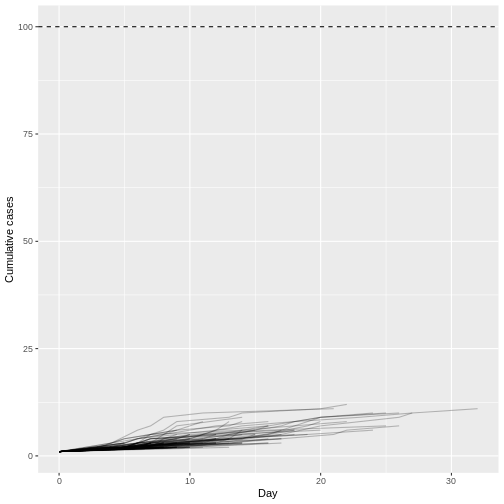
Dans l’hypothèse d’une épidémie de variole du singe avec \(R\) = 0.32 et \(k\) = 0.58, il n’y a pas de trajectoire parmi 1000 simulations qui atteignent plus de 100 cas infectés. Par rapport au MERS (\(R\) = 0.6 et \(k\) = 0.02).
Avec superspreading tu peux obtenir des solutions numériques à des processus qui epichains résoudre à l’aide de processus de branchement. Nous t’invitons à lire le vignette superspreading sur Le risque épidémique et répondre à :
- Quelle est la probabilité qu’un agent pathogène nouvellement introduit provoque une grande épidémie ?
- Quelle est la probabilité qu’une infection ne s’établisse pas, par hasard, après une ou plusieurs introductions initiales ?
- Quelle est la probabilité que l’épidémie soit contenue ?
Vérifie sices estimations varient de façon non linéaire en fonction du nombre moyen de reproduction. \(R\) et de la dispersion \(k\) d’une maladie donnée.
A partir d’une répartition des cas secondaires
Christian Althaus, 2015 a réutiliser des données publiées par Faye et al, 2015 (Figure 2) sur l’arbre de transmission de la maladie à virus Ebola à Conakry, en Guinée, en 2014.
En utilisant les données sous l’onglet “indice” :
- Estime la distribution de la descendance à partir de la distribution des cas secondaires.
- Estime ensuite le potentiel de grande épidémie à partir de ces données, en effectuant 100 simulations avec un cas initial.
- Imprime le résumé de l’objet de classe
<epichains>. Cela devrait nous aider à compter le nombre de chaînes qui atteignent unsizede plus de 100 cas infectés.
Pour des résultats reproductibles, utilise
set.seed(645).
Code avec les données de l’arbre de transmission écrites par Christian Althaus, 2015:
R
# Number of individuals in the trees
n <- 152
# Number of secondary cases for all individuals
c1 <- c(1, 2, 2, 5, 14, 1, 4, 4, 1, 3, 3, 8, 2, 1, 1,
4, 9, 9, 1, 1, 17, 2, 1, 1, 1, 4, 3, 3, 4, 2,
5, 1, 2, 2, 1, 9, 1, 3, 1, 2, 1, 1, 2)
c0 <- c(c1, rep(0, n - length(c1)))
c0 %>%
enframe() %>%
ggplot(aes(value)) +
geom_histogram(binwidth = 1)
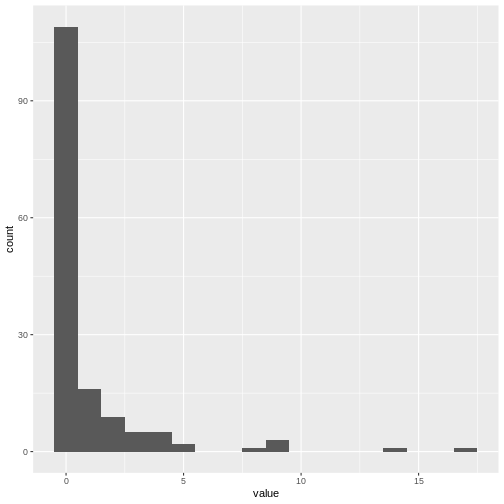
Défi facultatif :
- Reproduis la figure (B) de Christian Althaus, 2015 avec la sortie de la simulation.
R
# load packages ---------------------------
library(epichains)
library(epiparameter)
library(fitdistrplus)
library(tidyverse)
R
# fit a negative binomial distribution ------------------------------------
# Fitting a negative binomial distribution to the number of secondary cases
fit.cases <- fitdistrplus::fitdist(c0, "nbinom")
fit.cases
SORTIE
Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
estimate Std. Error
size 0.1814260 0.03990278
mu 0.9537995 0.19812301R
# serial interval parameters ----------------------------------------------
ebola_serialinter <- epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "serial interval",
single_epiparameter = TRUE
)
# simulate outbreak trajectories ------------------------------------------
# Set seed for random number generator
set.seed(645)
sim_multiple_chains <- epichains::simulate_chains(
n_chains = 100,
statistic = "size",
offspring_dist = rnbinom,
mu = fit.cases$estimate["mu"],
size = fit.cases$estimate["size"],
generation_time = function(x) generate(x = ebola_serialinter, times = x)
)
# summarise ----------------------------------------
summary(sim_multiple_chains)
SORTIE
`epichains_summary` object
[1] 9 1 2 1 1 4 1 20 14 1 1 131 1 2 1
[16] 1 7 1 2 2889 1 1 1 13 3 1 1 1 1 1
[31] 5 6 1 1 1 1 1 1 1 1 2 1 1 2 1
[46] 1 1 1 1 1 1 1 1 1 335 1 11 3 24 6
[61] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 111
[76] 1 1 1 1 1 1 2 1 544 1 1 1 3 1 2
[91] 6 1 1 1 1 1 1 1 2091 1
Simulated sizes:
Max: 2889
Min: 1R
# visualize ----------------------------------------
sim_chains_aggregate <-
sim_multiple_chains %>%
# use data.frame output from <epichains> object
as_tibble() %>%
# Count the daily number of cases in each chain
mutate(day = ceiling(time)) %>%
count(chain, day, name = "cases") %>%
# Calculate the cumulative number of cases for each chain
group_by(chain) %>%
mutate(cumulative_cases = cumsum(cases)) %>%
ungroup()
sim_chains_aggregate %>%
# Create grouped chain trajectories
ggplot(aes(x = day, y = cumulative_cases, group = chain)) +
geom_line() +
# Define a 100-case threshold
geom_hline(aes(yintercept = 100), lty = 2) +
ylim(0, 100) +
xlim(0, 100) +
labs(x = "Day", y = "Cumulative cases")
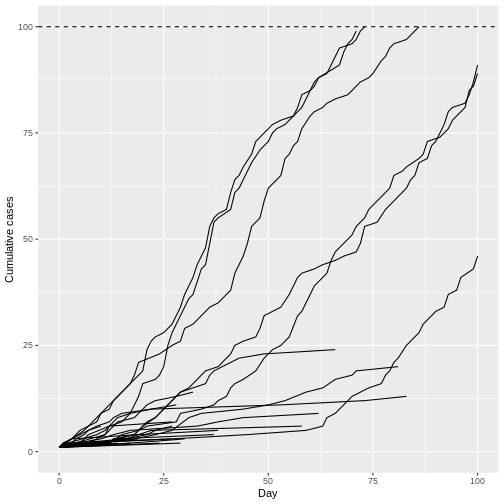
Fait remarquable, même avec R0 inférieur à 1 (R = 0.95), nous pouvons avoir des épidémies potentiellement explosives. La variation observée de la contagiosité individuelle dans le cas d’Ebola signifie que, bien que la probabilité d’extinction soit élevée, les nouveaux cas index ont également le potentiel d’une repousse explosive de l’épidémie.
Points clés
- Utilise epichains pour simuler le potentiel de grandes épidémies de maladies dont la distribution de la descendance est trop dispersée.

Comment fonctionne “single_epiparameter” ?
En regardant la documentation d’aide pour
?epiparameter::epiparameter_db():single_epiparameter = TRUEalors l’entrée paramétrée<epiparameter>avec l’entrée la plus grande taille d’échantillon sera renvoyée.Qu’est-ce qu’un paramétré
<epiparameter>? Regardez?is_parameterised.