Utiliser les distributions de délais dans l'analyse
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 30 minutes
Vue d'ensemble
Questions
- Comment réutiliser les délais enregistrés dans le epiparameter avec mon pipeline d’analyse existant ?
Objectifs
- Utilisez les fonctions de distribution pour les distributions
continues et discrètes enregistrées en tant que objets
<epiparameter>. - Convertissez une distribution continue en distribution discrète à l’aide de la fonction epiparameter.
- Connecter les sorties de epiparameter avec les entrées EpiNow2.
Conditions préalables
- Compléter le tutoriel Accéder aux distribution des délais épidémiologiques
- Compléter le tutoriel Quantifier la transmission
Pour cet épisode, vous devez vous familiariser avec :
Science des données Programmation de base avec R.
Statistiques : Distributions de probabilité.
Théorie des épidémies : paramètres épidémiologiques, périodes de temps, nombre reproductif effectif.
Introduction
Cet épisode intégrera le contenu des deux épisodes précédents.
Commençons par charger le packageepiparameter et
EpiNow2 . Nous utiliserons le tube %>%,
quelques verbes de dplyr et ggplot2 et
donc appelons aussi à le package tidyverse :
R
library(epiparameter)
library(EpiNow2)
library(tidyverse)
Pour résumer, nous avons appris que epiparameter nous aide à choisir un ensemble spécifique de paramètres épidémiologiques issus de la littérature, au lieu de les copier/coller à la main:
R
covid_serialint <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
single_epiparameter = TRUE
)
Nous avons maintenant un paramètre épidémiologique que nous pouvons
utiliser dans notre analyse ! Par exemple, pour quantifier la
transmission, nous pouvons utiliser l’intervalle sériel comme
approximation du temps de génération. Dans le bloc de code ci-dessous,
nous avons remplacé un des paramètres statistiques
sommaires en EpiNow2::LogNormal()
R
generation_time <-
EpiNow2::LogNormal(
mean = covid_serialint$summary_stats$mean, # replaced!
sd = covid_serialint$summary_stats$sd, # replaced!
max = 20
)
Dans cet épisode, nous utiliserons les fonctions de
distribution qui epiparameter fournit pour
obtenir une médiane, valeur maximale (max), percentiles ou
quantiles pour tout objet de classe <epiparameter>.
Ils vous seront utiles en aval dans votre pipeline d’analyse !
Le double point-virgule
Le double point-virgule :: dans R vous permet d’appeler
une fonction spécifique d’un package sans charger l’ensemble du package
dans l’environnement actuel.
Par example, dplyr::filter(data, condition) utilise la
fonctionfilter() du paquet `{dplyr}’.
Cela nous permet de nous souvenir des fonctions du paquet et d’éviter les conflits d’espace de noms en spécifiant explicitement la fonction du paquet à utiliser lorsque plusieurs paquets ont des fonctions portant le même nom.
Fonctions de distribution
w En R, toutes les distributions statistiques disposent de fonctions qui permettant d’accéder aux éléments suivants :
-
density(): fonction de densité de probabilité (FDP), -
cdf()fonction de distribution cumulative (FDC), -
quantile(): Quantile et -
generate(): Aléatoire valeurs aléatoires de la distribution donnée.
Fonctions pour la loi normale
Si vous en avez besoin, lisez en détail la rubrique Fonctions de probabilité R pour la loinormale Pour en savoir plus sur les fonctions de probabilité de la loi normale, lisez les définitions de chacune d’entre elles et identifiez la partie de la loi dans laquelle elles se situent !
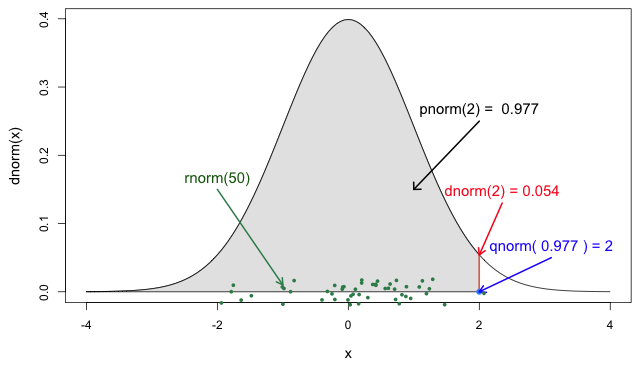
Si vous regardez ?stats::Distributions, chaque type de
distribution possède un ensemble unique de fonctions. Cependant,
epiparameter vous donne les mêmes quatre fonctions pour
accéder à chacune des valeurs ci-dessus pour n’importe quelle objet
<epiparameter> de votre choix !
R
# plot this to have a visual reference
# continuous distribution
plot(covid_serialint, xlim = c(0, 20))
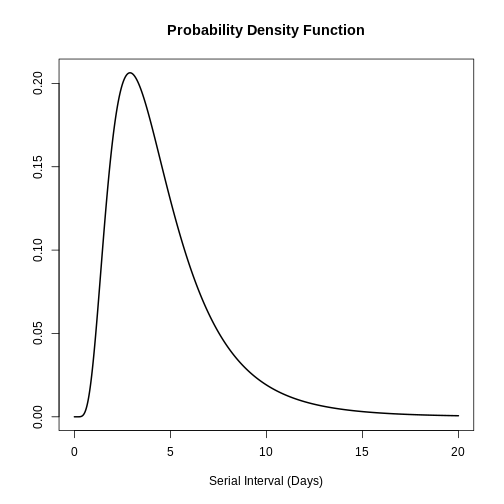
R
# the density value at quantile value of 10 (days)
density(covid_serialint, at = 10)
SORTIE
[1] 0.01911607R
# the cumulative probability at quantile value of 10 (days)
epiparameter::cdf(covid_serialint, q = 10)
SORTIE
[1] 0.9466605R
# the quantile value (day) at a cumulative probability of 60%
quantile(covid_serialint, p = 0.6)
SORTIE
[1] 4.618906R
# generate 10 random values (days) given
# the distribution family and its parameters
epiparameter::generate(covid_serialint, times = 10)
SORTIE
[1] 2.382512 7.554113 1.688063 6.682228 3.708993 3.796628 3.902427 2.665439
[9] 4.138396 3.374977L’accès à la documentation de référence (fichiers d’aide) de ces
fonctions est accessible avec la notation à trois doubles points :
epiparameter:::
?epiparameter:::density.epiparameter()?epiparameter:::cdf.epiparameter()?epiparameter:::quantile.epiparameter()?epiparameter:::generate.epiparameter()
Fenêtre pour la recherche de contact et l’intervalle sériel
L’intervalle sériel est important pour l’optimisation de la recherche des contacts, car il fournit une fenêtre temporelle pour l’endiguement de la propagation d’une maladie (Fine, 2003). En fonction de l’intervalle sériel, nous pouvons évaluer la nécessité d’augmenter le nombre de jours pris en compte pour la recherche des contacts afin d’inclure un plus grand nombre de contacts rétrospectifs (Davis et al., 2020).
Avec l’intervalle sériel COVID-19 (covid_serialint),
calculez :
- Quelle proportion supplémentaire des cas rétrospectifs pourrait être capturée si la méthode de recherche des contacts prenait en compte les contacts jusqu’à 6 jours avant l’apparition de la maladie par rapport à 2 jours avant l’apparition de la maladie ?
Dans la figure 5 du Fonctions
de probabilité R pour la loi normale la partie ombrée représente une
probabilité cumulée de 0.997 pour la valeur du quantile à
x = 2.
R
plot(covid_serialint)
R
epiparameter::cdf(covid_serialint, q = 2)
SORTIE
[1] 0.1111729R
epiparameter::cdf(covid_serialint, q = 6)
SORTIE
[1] 0.7623645Étant donné l’intervalle sériel COVID-19 :
Une méthode de recherche des contacts prenant en compte les contacts jusqu’à 2 jours avant l’apparition de la maladie permettra d’identifier environ 11,1 % des cas rétrospectifs.
Si cette période est étendue à 6 jours avant l’apparition de la maladie, 76,2 % des cas rétrospectifs pourraient être pris en compte.
Si nous échangeons la question entre les jours et la probabilité cumulée à :
- Considèrent les cas secondaires, combien de jours après l’apparition des symptômes des cas primaires peut-on s’attendre à ce que 55 % des symptômes apparaissent ?
R
quantile(covid_serialint, p = 0.55)
L’interprétation pourrait être la suivante :
- Les 55 % de cas secondaires seront devenus symptômatique 4,2 jours après l’apparition des symptômes des cas primaires.
Discrétiser une distribution continue
Nous nous rapprochons de la fin ! EpiNow2::LogNormal() a
encore besoin d’une valeur maximale (max).
Une façon d’y parvenir est d’obtenir la valeur du quantile pour le
99e percentile de la distribution ou 0.99 probabilité
cumulative de la distribution. Pour le faire, nous devons accéder à
l’ensemble des fonctions de distribution de notre objet
<epiparameter>.
Nous pouvons utiliser l’ensemble des fonctions de distribution d’un
distribution continue (comme ci-dessus). Cependant, ces valeurs seront
des nombres continus. Nous pouvons discrétiser la
distribution continue enregistréedans notre
objet<epiparameter> pour obtenir des valeurs
discrètes à partir d’une distribution continue.
Lorsque nous epiparameter::discretise() la distribution
continue, nous obtenons une distribution discrète :
R
covid_serialint_discrete <-
epiparameter::discretise(covid_serialint)
covid_serialint_discrete
SORTIE
Disease: COVID-19
Pathogen: SARS-CoV-2
Epi Parameter: serial interval
Study: Nishiura H, Linton N, Akhmetzhanov A (2020). "Serial interval of novel
coronavirus (COVID-19) infections." _International Journal of
Infectious Diseases_. doi:10.1016/j.ijid.2020.02.060
<https://doi.org/10.1016/j.ijid.2020.02.060>.
Distribution: discrete lnorm (days)
Parameters:
meanlog: 1.386
sdlog: 0.568Nous identifions ce changement dans la Distribution:
ligne de sortie de l’objet <epiparameter>. Vérifiez à
nouveau cette ligne :
Distribution: discrete lnormAlors que pour une distribution continue nous traçons la courbe de la Fonction de densité de probabilité (FDP) pour une distribution discrète, nous traçons la Fonction de masse de probabilité (FMP):
R
# discrete distribution
plot(covid_serialint_discrete)
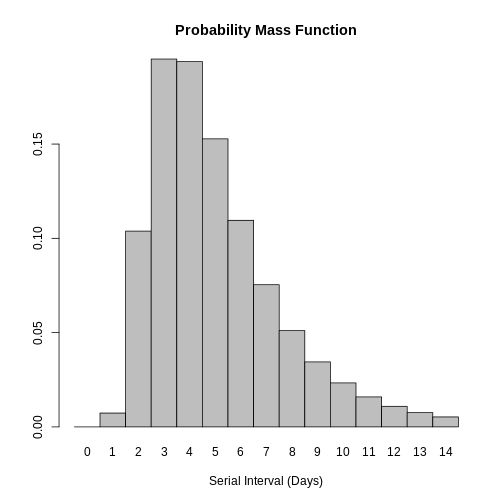
Pour obtenir enfin une max, accédons à la valeur du
quantile du 99e percentile ou 0.99 de la distribution à
l’aide de la fonction prob_dist$q de la même manière que
nous accédons à les valeurs summary_stats.
R
covid_serialint_discrete_max <-
quantile(covid_serialint_discrete, p = 0.99)
Durée de la quarantaine et de la période d’incubation
La période d’incubation est un délai utile pour évaluer la durée de la surveillance active ou de la quarantaine (Lauer et al., 2020). De même, les délais entre l’apparition des symptômes et la guérison (ou le décès) détermineront la durée nécessaire des soins de santé et de l’isolement des cas (Cori et al.).
Calculez :
- Dans quel délai précis 99 % des personnes présentant les symptômes de COVID-19 les manifestent-elles après l’infection ?
Quelle est la distribution des délais qui mesure le temps écoulé entre l’infection et l’apparition des symptômes ?
Les fonctions de probabilité pour les distributions
<epiparameter> discrètes sont les
mêmes que celles que nous avons utilisées pour les distributions
continues !
R
# plot to have a visual reference
plot(covid_serialint_discrete, xlim = c(0, 20))
# density value at quantile value 10 (day)
density(covid_serialint_discrete, at = 10)
# cumulative probability at quantile value 10 (day)
epiparameter::cdf(covid_serialint_discrete, q = 10)
# In what quantile value (days) do we have the 60% cumulative probability?
quantile(covid_serialint_discrete, p = 0.6)
# generate random values
epiparameter::generate(covid_serialint_discrete, times = 10)
R
covid_incubation <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "incubation",
single_epiparameter = TRUE
)
SORTIE
Using Linton N, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov A, Jung S, Yuan
B, Kinoshita R, Nishiura H (2020). "Incubation Period and Other
Epidemiological Characteristics of 2019 Novel Coronavirus Infections
with Right Truncation: A Statistical Analysis of Publicly Available
Case Data." _Journal of Clinical Medicine_. doi:10.3390/jcm9020538
<https://doi.org/10.3390/jcm9020538>..
To retrieve the citation use the 'get_citation' functionR
covid_incubation_discrete <- epiparameter::discretise(covid_incubation)
quantile(covid_incubation_discrete, p = 0.99)
SORTIE
[1] 1999% des personnes qui développent les symptômes du COVID-19 le feront dans les 16 jours suivant l’infection.
Réfléchissez-y, ce résultat est-il attendu en termes épidémiologiques ?
A partir d’une valeur maximale avec quantile() nous
pouvons créer une séquence de valeurs de quantiles sous la forme d’un
tableau numérique et calculer density() pour chacune
d’entre elles :
R
# create a discrete distribution visualisation
# from a maximum value from the distribution
quantile(covid_serialint_discrete, p = 0.99) %>%
# generate quantile values
# as a sequence for each natural number
seq(1L, to = ., by = 1L) %>%
# coerce numeric vector to data frame
as_tibble_col(column_name = "quantile_values") %>%
mutate(
# calculate density values
# for each quantile in the density function
density_values =
density(
x = covid_serialint_discrete,
at = quantile_values
)
) %>%
# create plot
ggplot(
aes(
x = quantile_values,
y = density_values
)
) +
geom_col()
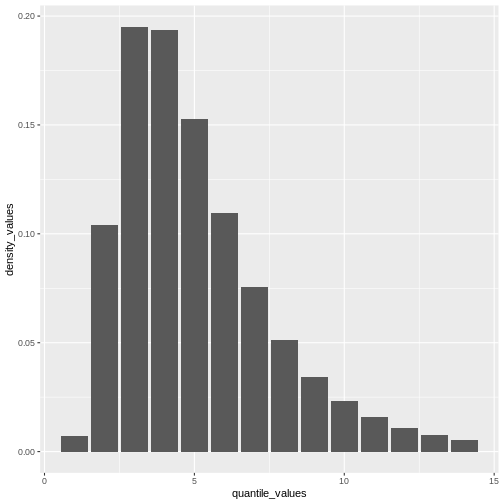
Rappelez-vous : Dans les infections à transmission pré-symptomatique, les intervalles sériels peuvent avoir des valeurs négatives (Nishiura et al., 2020). Lorsque nous utilisons la méthode intervalle sériel pour approximer le temps de génération nous devons effectuer cette distribution avec des valeurs positives uniquement !
Plug-in {epiparameter} pour {EpiNow2}
Maintenant, nous pouvons brancher le tout dans le fonction
EpiNow2::LogNormal() !
- les statistiques sommaires
meanetsdde la distribution, - une valeur maximale
max, - le nom de la
distribution.
Lors qu’on utilise EpiNow2::LogNormal() pour définir une
loi log-normale comme celle de
l’objetcovid_serialint, nous pouvons spécifier la moyenne
et l’écart-type comme paramètres. Pour obtenir les paramètres “naturels”
d’une loi log-normale, nous pouvons également convertir ces statistiques
sommaires en paramètres de distribution nommés meanlog et
sdlog. Avec epiparameter nous pouvons
obtenir directement les paramètres de distribution en utilisant
epiparameter::get_parameters():
R
covid_serialint_parameters <-
epiparameter::get_parameters(covid_serialint)
On a alors :
R
serial_interval_covid <-
EpiNow2::LogNormal(
meanlog = covid_serialint_parameters["meanlog"],
sdlog = covid_serialint_parameters["sdlog"],
max = covid_serialint_discrete_max
)
serial_interval_covid
SORTIE
- lognormal distribution (max: 14):
meanlog:
1.4
sdlog:
0.57Dans l’hypothèse d’un scénario COVID-19, utilisons les 60 premiers
jours de l’ensemble de données . example_confirmed du
package EpiNow2 comme reported_cases et
l’objet récemment créé serial_interval_covid en tant que
données d’entrée pour estimer le nombre de reproduction variable dans le
temps à l’aide du fonction EpiNow2::epinow().
R
# Set 4 cores to be used in parallel computations
withr::local_options(list(mc.cores = 4))
epinow_estimates_cg <- EpiNow2::epinow(
# cases
data = example_confirmed[1:60],
# delays
generation_time = EpiNow2::generation_time_opts(serial_interval_covid)
)
base::plot(epinow_estimates_cg)
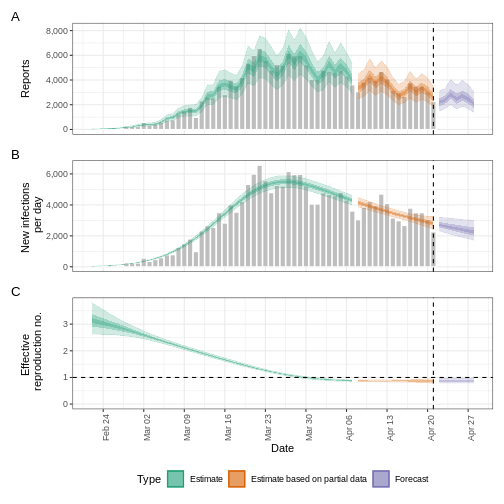
La sortie plot() comprend les cas estimés par date
d’infection, qui sont reconstitués à partir des cas déclarés et des
retards.
Avertissement
L’utilisation de l’intervalle sériel au lieu du temps de génération est une alternative qui peut propager un biais dans vos estimations, d’autant plus pour les maladies dont la transmission pré-symptomatique est signalée. (Chung Lau et al, 2021)
We can stop the livecoding at this stage and move on with the practical.
Ajustement pour tenir compte des délais de déclaration
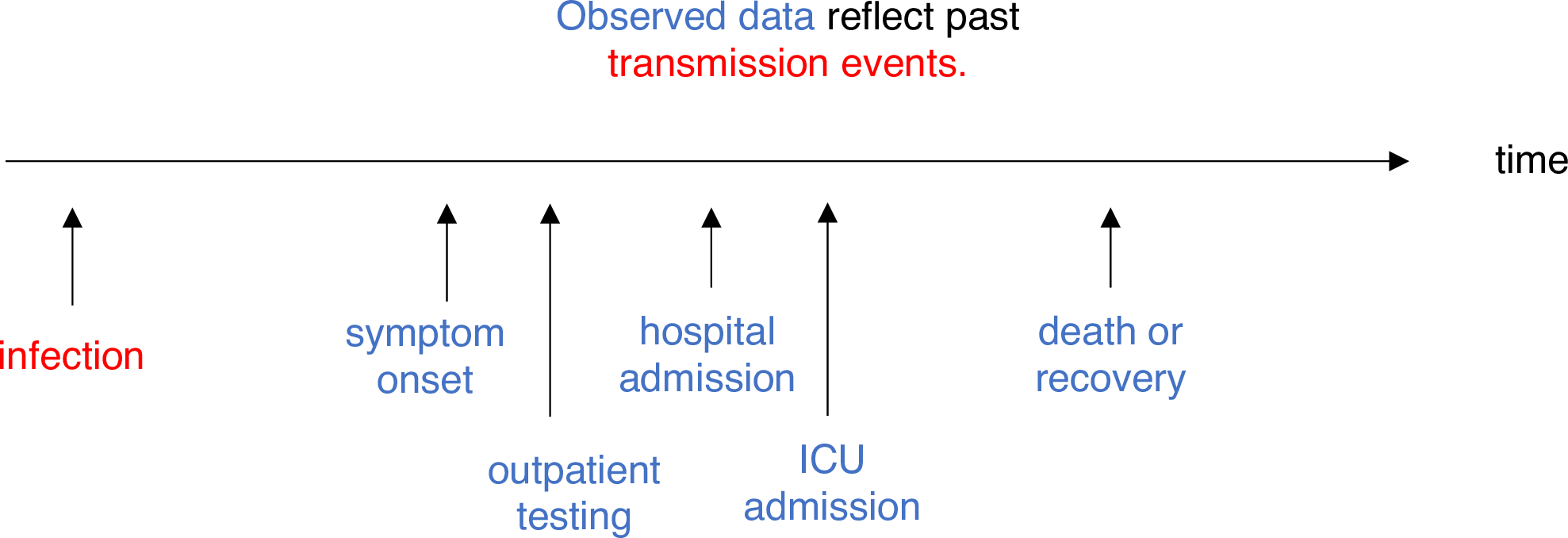
L’estimation de \(R_t\) nécessite des données sur le nombre quotidien de nouvelles infections. En raison des délais dans le développement de charges virales détectables, l’apparition des symptômes, la recherche de soins et la déclaration, ces chiffres ne sont pas facilement disponibles. Toutes les observations reflètent des événements de transmission survenus dans le passé. En d’autres termes, si \(d\) est le délai entre l’infection et l’observation, alors les observations au temps \(t\) informent \(R_{t−d}\) et non \(R_t\). (Gostic et al., 2020)
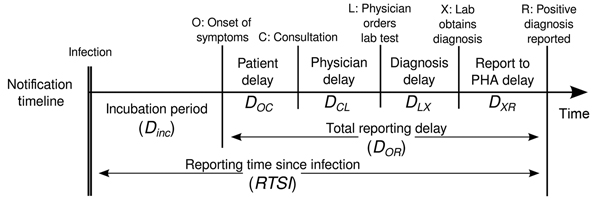
La distribution des délais pourrait être déduite
conjointement avec les temps d’infection sous-jacents, ou estimée comme
la somme des distributions de la . période d’incubation et du délais
entre l’apparition des symptômes et l’observation à partir des données
de la liste d’attente (délai de
déclaration). Pour EpiNow2, nous pouvons spécifier
ces deux distributions de délais complémentaires dans l’argument
delays.
Utiliser une période d’incubation pour COVID-19 afin d’estimer Rt
Estimez le nombre de reproduction variable dans le temps pour les 60
premiers jours de l’ensemble de données example_confirmed
de EpiNow2. Accédez à une période d’incubation pour
COVID-19 à partir de epiparameter pour l’utiliser comme
délai de déclaration.
Utilisez le dernier calcul d’ epinow() à l’aide de
l’argument delays et la fonction d’aide
delay_opts() e.
L’argument delays et la fonction
d’aidedelay_opts() sont analogues à l’argument
generation_time et à la fonction d’aide
generation_time_opts().
R
epinow_estimates <- EpiNow2::epinow(
# cases
reported_cases = example_confirmed[1:60],
# delays
generation_time = EpiNow2::generation_time_opts(covid_serial_interval),
delays = EpiNow2::delay_opts(covid_incubation_time)
)
R
# generation time ---------------------------------------------------------
# get covid serial interval
covid_serialint <-
epiparameter::epiparameter_db(
disease = "covid",
epi_name = "serial",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
covid_serialint_discrete_max <- covid_serialint %>%
epiparameter::discretise() %>%
quantile(p = 0.99)
covid_serialint_parameters <-
epiparameter::get_parameters(covid_serialint)
covid_serial_interval <-
EpiNow2::LogNormal(
meanlog = covid_serialint_parameters["meanlog"],
sdlog = covid_serialint_parameters["sdlog"],
max = covid_serialint_discrete_max
)
# incubation time ---------------------------------------------------------
# get covid incubation period
covid_incubation <- epiparameter::epiparameter_db(
disease = "covid",
epi_name = "incubation",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
covid_incubation_discrete_max <- covid_incubation %>%
epiparameter::discretise() %>%
quantile(p = 0.99)
covid_incubation_parameters <-
epiparameter::get_parameters(covid_incubation)
covid_incubation_time <-
EpiNow2::LogNormal(
meanlog = covid_incubation_parameters["meanlog"],
sdlog = covid_incubation_parameters["sdlog"],
max = covid_incubation_discrete_max
)
# epinow ------------------------------------------------------------------
# run epinow
epinow_estimates_cgi <- EpiNow2::epinow(
# cases
data = example_confirmed[1:60],
# delays
generation_time = EpiNow2::generation_time_opts(covid_serial_interval),
delays = EpiNow2::delay_opts(covid_incubation_time)
)
base::plot(epinow_estimates_cgi)
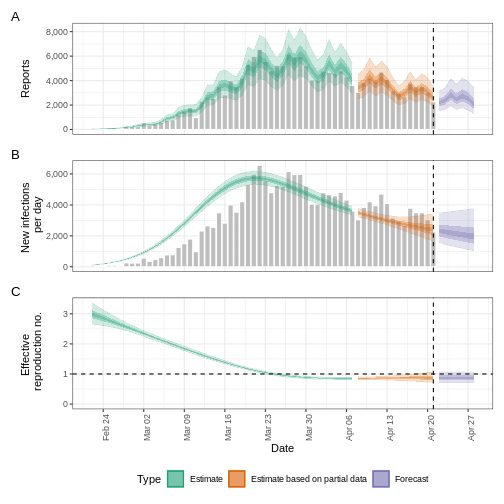
Essayez de compléter le delays avec un délai de
déclaration comme le reporting_delay_fixed de l’épisode
précédent.
Dans quelle mesure a-t-il changé ?
Après avoir ajouté la période d’incubation, discutez-en :
- La tendance de l’ajustement du modèle dans la section “Estimation” change-t-elle ?
- L’incertitude a-t-elle changé ?
- Comment expliqueriez-vous ou interpréteriez-vous ces changements ?
Comparez toutes les figures EpiNow2 générées précédemment.
Défis
Une astuce pour compléter le code
Si nous écrivons l’élément [] à côté de l’objet
covid_serialint_parameters[] à l’intérieur de
[] nous pouvons utiliser le touche de tabulation
↹ pour accéder à la fonctionnalité
de complétion de code
Elle permet d’accéder rapidement aux éléments suivants
covid_serialint_parameters["meanlog"] et
covid_serialint_parameters["sdlog"].
Nous vous invitons à tester ceci dans des blocs de code et dans la console R !
Nombre de reproduction effectif d’Ebola ajusté en fonction des délais de déclaration
Téléchargez et lisez les données Ebola:
- Estimez le nombre de reproduction effectif en utilisant EpiNow2
- Ajustez l’estimation en fonction des délais de déclaration disponibles en epiparameter
- Pourquoi avez-vous choisi ce paramètre ?
Pour calculer la \(R_t\) en utilisant EpiNow2 nous avons besoin de :
- L’incidence agrégée
dataavec les cas confirmés par jour, et - La distribution du temps
generation. - Optionnellement, les distributions des délais de déclaration lorsqu’elles sont disponibles (par exemple, la période d’incubation).
Pour obtenir la distribution des délais à l’aide de epiparameter, nous pouvons utiliser des fonctions comme :
epiparameter::epiparameter_db()epiparameter::parameter_tbl()discretise()quantile()
R
# read data
# e.g.: if path to file is data/raw-data/ebola_cases.csv then:
ebola_confirmed <-
read_csv(here::here("data", "raw-data", "ebola_cases.csv")) %>%
incidence2::incidence(
date_index = "date",
counts = "confirm",
count_values_to = "confirm",
date_names_to = "date",
complete_dates = TRUE
) %>%
dplyr::select(-count_variable)
# list distributions
epiparameter::epiparameter_db(disease = "ebola") %>%
epiparameter::parameter_tbl()
R
# generation time ---------------------------------------------------------
# subset one distribution for the generation time
ebola_serial <- epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "serial",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
ebola_serial_discrete <- epiparameter::discretise(ebola_serial)
serial_interval_ebola <-
EpiNow2::Gamma(
mean = ebola_serial$summary_stats$mean,
sd = ebola_serial$summary_stats$sd,
max = quantile(ebola_serial_discrete, p = 0.99)
)
# incubation time ---------------------------------------------------------
# subset one distribution for delay of the incubation period
ebola_incubation <- epiparameter::epiparameter_db(
disease = "ebola",
epi_name = "incubation",
single_epiparameter = TRUE
)
# adapt epiparameter to epinow2
ebola_incubation_discrete <- epiparameter::discretise(ebola_incubation)
incubation_period_ebola <-
EpiNow2::Gamma(
mean = ebola_incubation$summary_stats$mean,
sd = ebola_incubation$summary_stats$sd,
max = quantile(ebola_serial_discrete, p = 0.99)
)
# epinow ------------------------------------------------------------------
# run epinow
epinow_estimates_egi <- EpiNow2::epinow(
# cases
data = ebola_confirmed,
# delays
generation_time = EpiNow2::generation_time_opts(serial_interval_ebola),
delays = EpiNow2::delay_opts(incubation_period_ebola)
)
SORTIE
WARN [2025-11-11 01:40:14] epinow: There were 1 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them. -
WARN [2025-11-11 01:40:14] epinow: Examine the pairs() plot to diagnose sampling problems
- R
plot(epinow_estimates_egi)
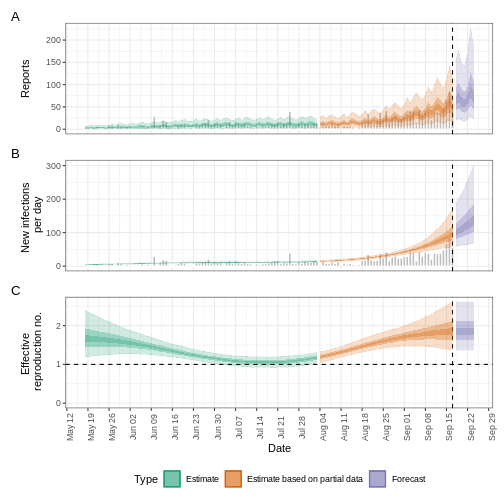
Que faire avec les distributions de Weibull ?
Utilisez les données influenza_england_1978_school du
package outbreaks pour calculer le nombre de reproduction
effectif à l’aide de EpiNow2 en ajustant en fonction des
délais de déclaration disponibles dans epiparameter.
EpiNow2::NonParametric() accepte les fonctions de masse
de probabilité (FMP) de n’importe quelle famille de distribution. Lisez
le guide de référence sur les Distributions
de probabilités.
R
# What parameters are available for Influenza?
epiparameter::epiparameter_db(disease = "influenza") %>%
epiparameter::parameter_tbl() %>%
count(epi_name)
SORTIE
# Parameter table:
# A data frame: 3 × 2
epi_name n
<chr> <int>
1 generation time 1
2 incubation period 15
3 serial interval 1R
# generation time ---------------------------------------------------------
# Read the generation time
influenza_generation <-
epiparameter::epiparameter_db(
disease = "influenza",
epi_name = "generation"
)
influenza_generation
SORTIE
Disease: Influenza
Pathogen: Influenza-A-H1N1
Epi Parameter: generation time
Study: Lessler J, Reich N, Cummings D, New York City Department of Health and
Mental Hygiene Swine Influenza Investigation Team (2009). "Outbreak of
2009 Pandemic Influenza A (H1N1) at a New York City School." _The New
England Journal of Medicine_. doi:10.1056/NEJMoa0906089
<https://doi.org/10.1056/NEJMoa0906089>.
Distribution: weibull (days)
Parameters:
shape: 2.360
scale: 3.180R
# EpiNow2 currently accepts Gamma or LogNormal
# other can pass the PMF function
influenza_generation_discrete <-
epiparameter::discretise(influenza_generation)
influenza_generation_max <-
quantile(influenza_generation_discrete, p = 0.99)
influenza_generation_pmf <-
density(
influenza_generation_discrete,
at = 0:influenza_generation_max
)
influenza_generation_pmf
SORTIE
[1] 0.00000000 0.06312336 0.22134988 0.29721220 0.23896828 0.12485164 0.04309454R
# EpiNow2::NonParametric() can also accept the PMF values
generation_time_influenza <-
EpiNow2::NonParametric(
pmf = influenza_generation_pmf
)
# incubation period -------------------------------------------------------
# Read the incubation period
influenza_incubation <-
epiparameter::epiparameter_db(
disease = "influenza",
epi_name = "incubation",
single_epiparameter = TRUE
)
# Discretize incubation period
influenza_incubation_discrete <-
epiparameter::discretise(influenza_incubation)
influenza_incubation_max <-
quantile(influenza_incubation_discrete, p = 0.99)
influenza_incubation_pmf <-
density(
influenza_incubation_discrete,
at = 0:influenza_incubation_max
)
influenza_incubation_pmf
SORTIE
[1] 0.00000000 0.05749151 0.16687705 0.22443092 0.21507632 0.16104546 0.09746609
[8] 0.04841928R
# EpiNow2::NonParametric() can also accept the PMF values
incubation_time_influenza <-
EpiNow2::NonParametric(
pmf = influenza_incubation_pmf
)
# epinow ------------------------------------------------------------------
# Read data
influenza_cleaned <-
outbreaks::influenza_england_1978_school %>%
select(date, confirm = in_bed)
# Run epinow()
epinow_estimates_igi <- EpiNow2::epinow(
# cases
data = influenza_cleaned,
# delays
generation_time = EpiNow2::generation_time_opts(generation_time_influenza),
delays = EpiNow2::delay_opts(incubation_time_influenza)
)
plot(epinow_estimates_igi)
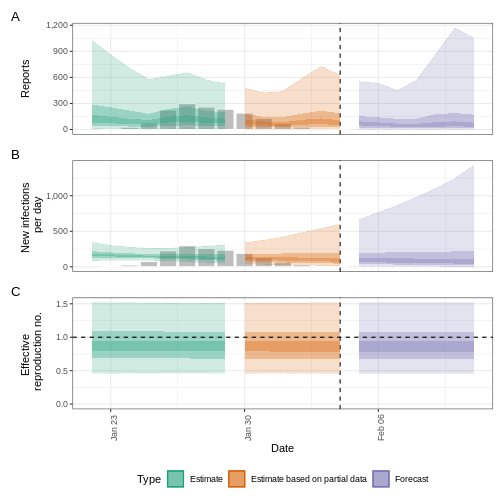
Prochaines étapes
Comment estimer la distribution des délais pour la maladie X ?
Consultez cet excellent tutoriel sur l’estimation de l’intervalle sériel et de la période d’incubation de la maladie X en tenant compte de la censure en utilisant l’inférence bayésienne avec des packages comme rstan et coarseDataTools.
- Tutoriel en anglais : https://rpubs.com/tracelac/diseaseX
- Tutoriel en Español : https://epiverse-trace.github.io/epimodelac/EnfermedadX.html
Ensuite, Après avoir obtenu vos valeurs estimées,
vous pouvez créer manuellement vos propres objets de classe
<epiparameter> à l’aide de la fonction
epiparameter::epiparameter()! Jetez un coup d’œil à songuide
de référence sur “Créer un objet
<epiparameter>”!
Enfin, jetez un coup d’œil au derniers packages R {epidist} et {primarycensored}
qui fournissent des méthodes pour relever les principaux défis de
l’estimation des distributions, y compris la troncature, la censure par
intervalle et les biais dynamiques.
Points clés
- Utilisez les fonctions de distribution avec
<epiparameter>pour obtenir des statistiques sommaires et des paramètres informatifs pour les interventions de santé publique, comme la fenêtre de recherche des contacts et la durée de la quarantaine. - Utilisez
discretise()pour convertir les distributions de délais continues en distributions discrètes. - Utilisez epiparameter pour obtenir les délais de déclaration requis dans les estimations de transmissibilité.

Comment obtenir des paramètres de distribution à partir de distributions statistiques ?
Comment obtenir la moyenne et l’écart-type d’un temps de génération avec seulement des paramètres de distribution mais aucune statistique sommaire tel que
meanousdpourEpiNow2::Gamma()ouEpiNow2::LogNormal()?Regardez la vignette epiparameter sur l’extraction et la conversion des paramètres et sescas d’utilisations!