Estimation de la gravité d'une épidémie
Dernière mise à jour le 2025-11-11 | Modifier cette page
Durée estimée : 12 minutes
Vue d'ensemble
Questions
Pourquoi estime-t-on la gravité clinique d’une épidémie ?
Comment peut-on estimer le risque de létalité (RL) au début d’une épidémie en cours ?
Objectifs
Estimer le risque de létalité (RL) à partir de données épidémiologiques agrégées en utilisant la librairie cfr.
Estimer le RL ajusté au délai épidémiologique à l’aide des librairies epiparameter et cfr.
Estimer la sévérité ajustée au délai épidémiologique pour une série chronologique en expansion en utilisant le package cfr.
Pré-requis
Les concepts abordés dans cet épisode supposent que vous êtes familiers avec :
Science des données: Programmation de base avec R.
Théorie des épidémies: Distributions des délais.
R packages installés: cfr, epiparameter, outbreaks, tidyverse.
Installer les packages si elles ne le sont pas déjà:
R
# si {pak} n'est pas disponible, exécutez : install.packages("pak")
pak::pak("cfr")
pak::pak("epiparameter")
pak::pak("tidyverse")
pak::pak("outbreaks")
Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.
Introduction
Les questions les plus fréquentes au début d’une épidémie sont:
- Quel est l’impact probable de l’épidémie sur la santé publique en termes de gravité clinique ?
- Quels sont les groupes les plus gravement touchés ?
- L’épidémie risque-t-elle de provoquer une pandémie très grave ?
Nous pouvons évaluer le potentiel pandémique d’une épidémie à l’aide de deux mesures essentielles : la transmissibilité et la gravité clinique. (Fraser et al. 2009, CDC, 2016).
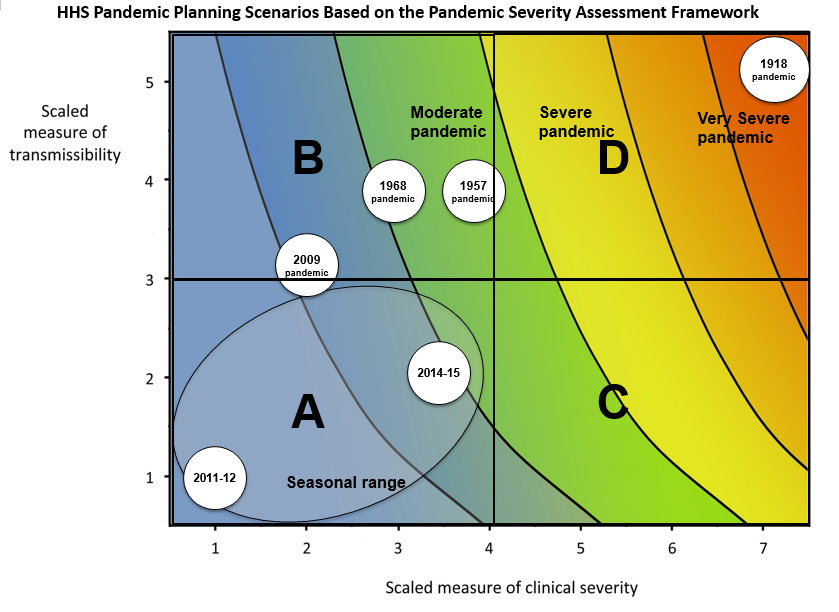
Une approche épidémiologique pour estimer la gravité clinique consiste à quantifier le risque de létalité (RL). Le risque de létalité est la probabilité conditionnelle de décès en cas de diagnostic confirmé, calculée comme le rapport entre le nombre cumulé de décès dus à une maladie infectieuse et le nombre de cas diagnostiqués confirmés. Toutefois, le calcule de ce paramètre de cette façon au cours d’une épidémie tend à aboutir à un RL naïf ou biaisé, compte tenu du délai entre l’apparition de la maladie et le décès, qui varie considérablement au fur et à mesure que l’épidémie progresse et se stabilise aux derniers stades de l’épidémie (Ghani et al. 2005).
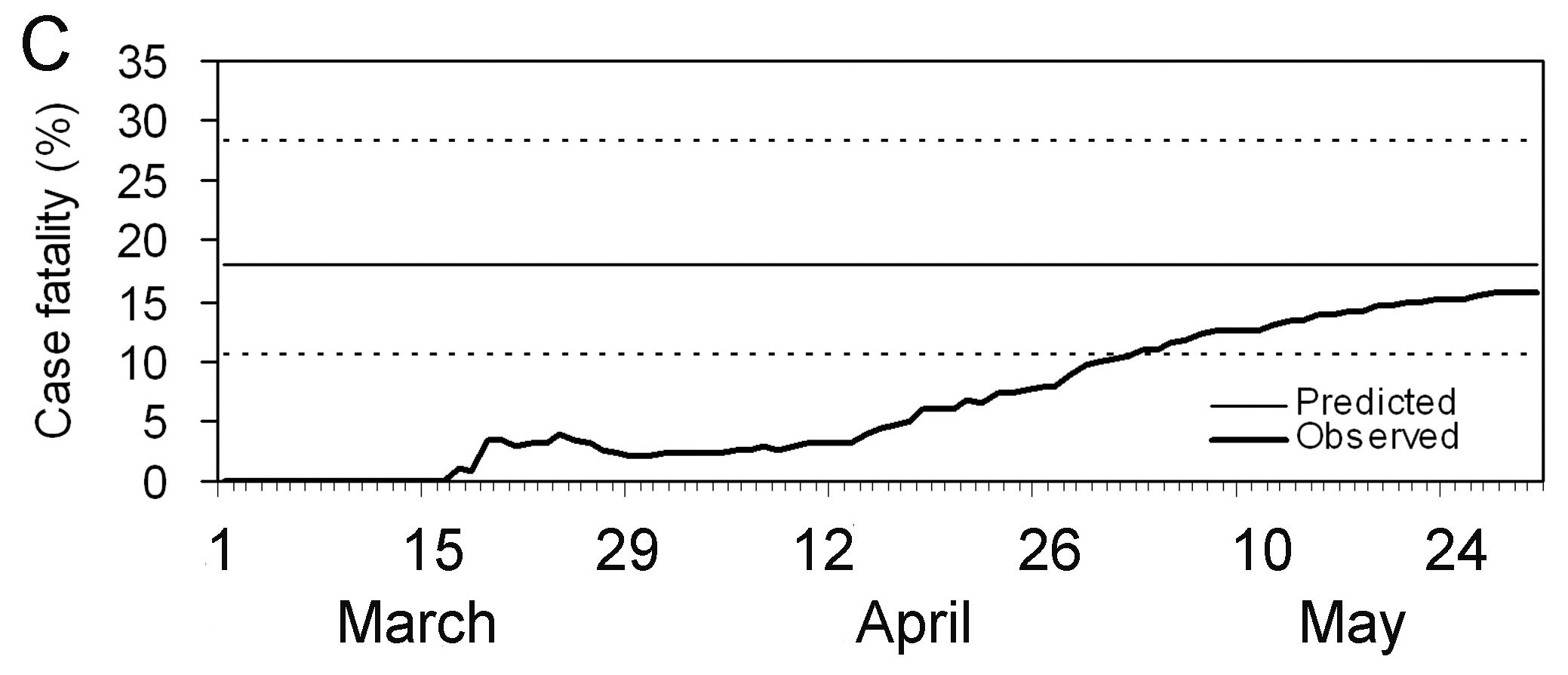
Les périodes sont pertinentes : Période 1 – 15 jours où le RL est nul, ce qui indique qu’aucun décès n’a été signalé ; Période du 15 mars au 26 avril où le RL semble augmenter ; Période du 30 avril au 30 mai où l’estimation du RL se stabilise.
Généralement, l’estimation de la gravité clinique d’une maladie peut être utile même en dehors d’un scénario de planification d’une pandémie et dans le contexte de la santé publique courante. Le fait de savoir si une épidémie a ou a eu une gravité différente de celle observée dans le passé peut motiver des recherches pour identifier les causes. Celles-ci peuvent être intrinsèques à l’agent infectieux (par exemple, une nouvelle souche plus grave) ou liées à des facteurs sous-jacents dans la population (par exemple, une immunité réduite ou des facteurs de morbidité) (Lipsitch et al., 2015).
Dans ce tutoriel, nous allons apprendre à utiliser la librairie cfr pour calculer et ajuster le risque de gravité clinique en utilisant la distribution des délais obtenue de la librairie epiparameter ou de d’autres sources, sur la base des méthodes développées par Nishiura et al. 2009. Nous allons aussi explorer la libraire cfr pour determiner comment l’utiliser pour calculer d’autres mesures de sévérité clinique.
Nous utiliserons l’opérateur pipe (%>%) de la
librairie magrittr pour relier facilement certaines
fonctions de la librairie cfr, y compris les fonctions de
la librairie de formatage de données dplyr. Nous
chargerons donc la librairie tidyverse, qui comprend à la
fois les librairies magrittr et dplyr.
R
# charger les packages
library(cfr)
library(epiparameter)
library(tidyverse)
library(outbreaks)
L’opérateur double deux-points
(::)
L’opérateur :: de R permet d’accéder aux fonctions ou
aux objets d’un package spécifique sans attacher l’intégralité du
package (sans faire appel à la function libray()). Il offre
plusieurs avantages, notamment :
- Indiquer explicitement le package d’origine d’une fonction, réduisant ainsi les ambiguïtés et les conflits potentiels lorsque plusieurs packages possèdent des fonctions portant le même nom.
- Permettre d’appeler une fonction depuis un package sans charger
l’intégralité du package avec un appel à la fonction
library().
Par exemple, la commande dplyr::filter(data, condition)
signifie que nous appelons la fonction filter() depuis la
librairie dplyr.
Discussion
Etiez-vous membre d’une équipe chargée de de concevoir des stratégies de réponse à une épidémie? Si oui:
- Comment évaluez-vous la gravité clinique de l’épidémie ?
- Quelles étaient les principales sources de biais ?
- Qu’aviez-vous fait pour prendre en compte les biais identifiés ?
- Quelle analyse complémentaire feriez-vous pour résoudre le biais ?
Sources de données pour la gravité clinique
Quelles sont les sources de données qu’on peut utiliser pour estimer la gravité clinique d’une épidémie? Verity et al, 2020 résume le spectre des cas de COVID-19 :
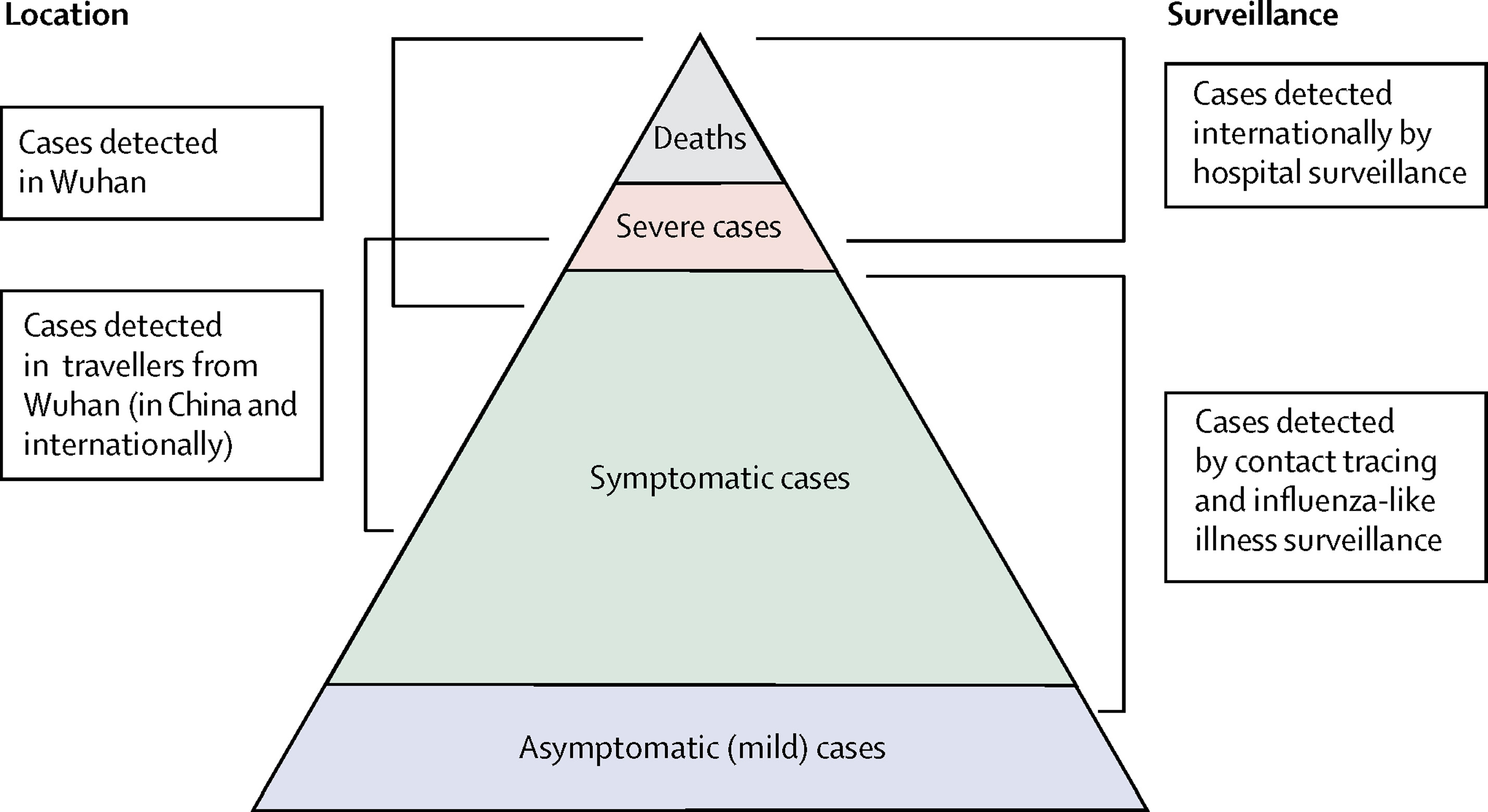
- Au sommet de la pyramide, les cas définis comme grave ou critiques selon les critères établis par l’OMS. Ces cas auraient probablement été identifiés en milieu hospitalier, présentant une pneumonie virale atypique. Ils auraient été identifiés en Chine continentale et parmi ceux classés au niveau international comme émanants d’une transmission locale.
- Beaucoup d’autres sont probablement symptomatiques (c’est-à-dire avec de la fièvre, de la toux ou des myalgies), mais ne nécessiteront peut-être pas d’hospitalisation. Ces cas auraient été identifiés grâce à leurs liens avec des voyageurs internationaux dans des zones à haut risque et grâce à la recherche des personnes en contact avec les cas confirmés. Ils pourraient être identifiés grâce à la surveillance de la population, par exemple en cas de syndrome grippal.
- La partie inférieure de la pyramide représente les cas bénins (et éventuellement asymptomatiques). Ces cas pourraient être identifiés par la recherche de cas contacts et, puis par des tests sérologiques.
Estimation du risque de létalité (RL) naïf
Nous mesurons la gravité d’une maladie en termes de risque de létalité (RL). Le RL est interprété comme la probabilité conditionnelle de décès en cas de diagnostic confirmé, calculée comme le ratio du nombre cumulé de décès \(D_{t}\) sur le nombre cumulé de cas confirmés \(C_{t}\) à un moment donné \(t\). Nous pouvons le référer au RL naïf (également RL brut ou biaisé, \(b_{t}\)) :
\[ b_{t} = \frac{D_{t}}{C_{t}} \]
Cette formule est considérée comme naïve parce qu’elle tend à produire un RL biaisé et largement sous-estimé en raison du délai entre l’apparition de la maladie et le décès, qui ne se stabilise que vers la fin de l’épidémie.
Pour calculer le RL naïf à l’aide de la librairie cfr, on a besoin d’un tableau de données comportant au minimum trois colonnes nommées :
datecasesdeaths
Explorons le tableau de données ebola1976 inclus dans le
package cfr, et qui contient les données provenant de la
première épidémie d’Ebola au Zaïre (actuelle la République Démocratique
du Congo) en 1976, comme l’ont analysé Camacho et al. (2014).
R
# charger le tableau de donnees ebola1976 du package {cfr}
data("ebola1976")
# Visualiser l'incidence du nombre de cas et de deces repertorie
ebola1976 %>%
incidence2::incidence(
date_index = "date",
counts = c("cases", "deaths")
) %>%
plot()
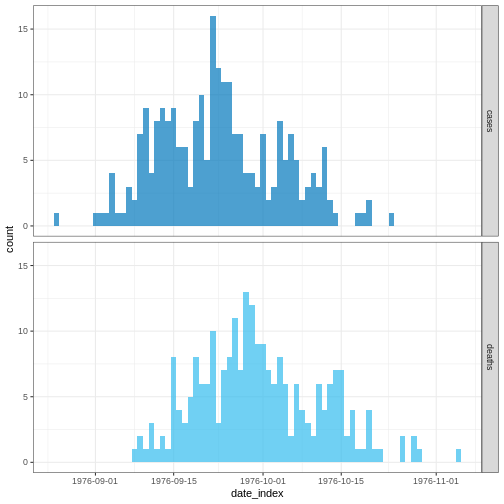
Nous supposerons que nous sommes dans le contexte d’une épidémie d’Ebola en cours où nous disposons que des données collectées durant les 30 premiers jours de l’épidémie.
R
# supposons que nous disposons des donnees des 30 premiers jours de l'epidemie
ebola_30days <- ebola1976 %>%
dplyr::slice_head(n = 30) %>%
dplyr::as_tibble()
ebola_30days
SORTIE
# A tibble: 30 × 3
date cases deaths
<date> <int> <int>
1 1976-08-25 1 0
2 1976-08-26 0 0
3 1976-08-27 0 0
4 1976-08-28 0 0
5 1976-08-29 0 0
6 1976-08-30 0 0
7 1976-08-31 0 0
8 1976-09-01 1 0
9 1976-09-02 1 0
10 1976-09-03 1 0
# ℹ 20 more rowsNous avons besoin de données d’incidence agrégées
Les données d’entrée des fonctions de la cfr sont des données d’incidence, qui sont ont été agrégées à partir des données de cas individuels.
Ces données doivent être agrégées par “unité de temps”, c’est-à-dire une observation par unité de temps, contenant le nombre de cas et de décès signalés en un temps donné. Les observations avec des valeurs nulles ou manquantes doivent également être incluses, comme pour les données de séries temporelles.
Cependant, il faut noter que la version actuelle de cfr requière des données agrégées journaliers. Les autres unités temporelles d’agrégation de données telles que les semaines, mois, etc ne sont pour le moment pas pris en charge.
Liste de vérification
Lorsque vous regroupez les cas par jour avec
incidence2, vous pouvez adapter les données pour
cfr à l’aide de cfr::prepare_data() sur les
objets <incidence2>. Pour plus de détails et un
exemple, consultez le manuel de référence cfr sur la
préparation des formats de données épidémiologiques courants pour
l’estimation du CFR (https://epiverse-trace.github.io/cfr/reference/prepare_data.html).
La fonction cfr::cfr_static() permet de calculer le RL
naïf.
R
# Calculer le RL naïf durant les 30 premiers jours
cfr::cfr_static(data = ebola_30days)
SORTIE
severity_estimate severity_low severity_high
1 0.4740741 0.3875497 0.5617606Défi
Téléchargez le fichier sarscov2_cases_deaths.csv et importez-le dans R. Puis estimez le RL naïf.
Vérifier le format des données d’entrée en répondant aux questions suivantes:
- Contient-il des données d’incidences quotidiennes ?
- Les noms des colonnes sont-ils conformes aux exigences de la
fonction
cfr_static()? - Comment renommer les noms de colonnes d’un tableau de données ?
Importez les données téléchargées à l’aide de la fonction
readr::read_csv(). Cette fonction reconnaît que la colonne
date est de type <Date>.
R
# importer les données dans R
# supposons que le chemin d'accès au fichier est data/raw-data/ebola_cases.csv
sarscov2_input <- readr::read_csv(
file = here::here("data", "raw-data", "sarscov2_cases_deaths.csv")
)
R
# voir un aperçu des données
sarscov2_input
SORTIE
# A tibble: 93 × 3
date cases_jpn deaths_jpn
<date> <dbl> <dbl>
1 2020-01-20 1 0
2 2020-01-21 1 0
3 2020-01-22 0 0
4 2020-01-23 1 0
5 2020-01-24 1 0
6 2020-01-25 3 0
7 2020-01-26 3 0
8 2020-01-27 4 0
9 2020-01-28 6 0
10 2020-01-29 7 0
# ℹ 83 more rowsNous pouvons utiliser la fonction
cleanepi::standardize_column_names() pour renommer les noms
des colonnes de sorte qu’elles soient conforment aux exigences de la
fonction cfr::cfr_static().
R
# renommer les noms des colonnes
sarscov2_input <- sarscov2_input %>%
cleanepi::standardize_column_names(
rename = c(cases = "cases_jpn", deaths = "deaths_jpn")
)
# estimer le RL naïf
cfr::cfr_static(sarscov2_input)
SORTIE
severity_estimate severity_low severity_high
1 0.01895208 0.01828832 0.01963342Biais affectant l’estimation du CFR
Deux biais qui affectent l’estimation du RL
Lipsitch et al, 2015 ont décrit deux biais potentiels qui peuvent affecter l’estimation du RL (et comment y remédier) :
Pour les maladies ayant un spectre de présentations cliniques, les cas qui sont portés à l’attention des autorités de santé publique et enregistrés dans les bases de données de surveillance sont généralement des personnes présentant les symptômes les plus graves, qui consultent un médecin, admises à l’hôpital ou décèdent.
Par conséquent, le RL sera généralement plus élevé chez les cas confirmés que dans l’ensemble de la population des cas, étant donné que cette dernière peut inclure des personnes présentant des symptômes légers, subcliniques et (selon certaines définitions de “cas”) asymptomatiques.
Lors d’une épidémie en cours, il y a un délai entre le moment où une personne décède et le moment où son décès est signalé. Par conséquent, à tout moment, la liste des cas contient des individus qui vont mourir et dont le décès n’est pas encore survenu ou qui est survenu mais n’a pas encore été signalé. Ainsi, la division du nombre cumulé de décès déclarés par le nombre cumulé de cas déclarés en un moment donné d’une épidémie sous-évaluera le véritable RL.
Les principaux facteurs déterminants de l’ampleur du biais sont, le taux de croissance de l’épidémie et la distribution des délais entre la déclaration des cas et la déclaration des décès ; plus les délais sont longs, plus le taux de croissance est rapide, et plus le biais est important.
Dans les sections suivantes de cet épisode du tutoriel, nous allons nous concentrer sur les solutions concernant spécifiquement ce biais en utilisant la librairie cfr.
Il est crucial d’améliorer l’estimation du RL ajusté au délais au début d’une épidémie pour déterminer sa virulence, mais aussi le niveau et les choix des interventions de santé publique et fournir des conseils au grand public.
En 2009, lors de l’épidémie de grippe porcine A (H1N1), le Mexique a effectué une estimation précoce biaisée du RL. Les premiers rapports du gouvernement mexicain faisaient état d’une infection virulente, alors que dans d’autres pays, le même virus était perçu comme bénin (TIME, 2009).
Aux États-Unis et au Canada, aucun décès n’a été attribué au virus durant les dix jours qui ont suivi la déclaration d’urgence de santé publique par l’OMS. Même dans des circonstances similaires, au début d’une pandémie mondiale, les responsables de la santé publique, les décideurs et le grand public veulent connaître la virulence d’un agent infectieux émergent.
Garske et al, 2009 évaluer les défis afin d’estimer la gravité de cette pandémie, en soulignant que le fait de recenser avec précision les cas pour le dénominateur peut améliorer la capacité à obtenir des estimations informatives du taux de létalité.
Vous trouverez plus d’informations concernant l’effet des délais dans
l’estimation du RL dans cette section de la vignette
de la librairie {cfr}.
RL ajusté au délai
Nishiura et al, 2009 ont développé une méthode de calcul du RL qui prend en compte les délais entre l’apparition des symptômes et le décès.
Durant certaines phases d’une épidémie en cours, il peut arriver que
le nombre de décès soit insuffisant pour déterminer la distribution du
temps entre l’apparition des symptômes et le décès. Par conséquent, nous
pouvons obtenir une estimation de la distribution de ce délai à
partir d’épidémies antérieures ou en réutilisant celles qui sont
accessibles via des librairies R tels que epiparameter ou
{epireview} qui les collectent à partir de la littérature
scientifique publiée. Lisez l’épisode accéder aux délais épidémiologiques de ce
tutoriel pour de plus amples informations.
Obtenons la distribution du délai entre la date d’apparition des symptômes et la date de décès via la librairie epiparameter.
R
# obtenir la distribution du délai
onset_to_death_ebola <- epiparameter::epiparameter_db(
disease = "Ebola",
epi_name = "onset_to_death",
single_epiparameter = TRUE
)
# visualiser la distribution du délai
plot(onset_to_death_ebola, xlim = c(0, 40))
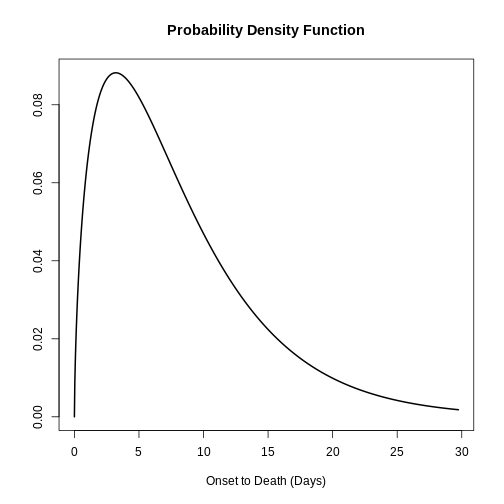
Pour prendre en compte la distribution du délai lors du calcul le RL
ajusté au délai, nous devons fournir à l’arguemt
delay_density de la fonction cfr::cfr_static()
la valeur correspondante.
R
# calculer le RL ajusté au délai pour les 30 premiers jours
cfr::cfr_static(
data = ebola_30days,
delay_density = function(x) density(onset_to_death_ebola, x)
)
SORTIE
severity_estimate severity_low severity_high
1 0.9502 0.881 0.9861Le RL ajusté au délai indique que la gravité globale de la maladie à la fin de l’épidémie ou selon les récentes données disponibles à ce moment-là est 0.9502 avec un intervalle de confiance de 95% entre 0.881 et 0.9861, légèrement supérieure à la valeur naïve.
Pour corriger le biais résultant des cas dont les résultats ne sont pas encore connus au moment de l’estimation, {cfr} tient compte de la probabilité que le résultat d’un cas soit connu après un certain délai.
Pour ce faire, il relie \(D_t\) à la fonction d’incidence \(c_t\) (c’est-à-dire le nombre de nouveaux cas confirmés au jour t) et à la fonction de densité de probabilité conditionnelle \(f_s\) du temps écoulé entre l’apparition de la maladie et le décès, étant donné le décès.
\[ D_t = p_t \times \sum_{i = 0}^t\sum_{j = 0}^\infty c_i f_{j - i} \]
Ici, \(D_t\) est le nombre cumulé de décès jusqu’au moment t, et \(p_t\) est la proportion réalisée de cas confirmés qui décèdent des suites de l’infection (c’est-à-dire le risque de létalité non biaisé, ou CFR) .
Le terme \(\sum_{i = 0}^t\sum_{j =
0}^\infty c_i f_{j - i}\) représente le nombre total
prévu de cas dont l’issue est connue au moment t.
Il additionne tous les cas incidents \(c_i\), chacun pondéré par la fonction de
densité de probabilité \(f_{j−i}\) que
leur issue soit connue après un délai de \(j−i\) jours.
Chaque jour d’analyse, cfr calcule, pour chaque cas,
le nombre attendu de résultats à l’instant
t. Lorsque vous utilisez des objets de classe
<epiparameter>, la fonction density()
peut être appliquée pour obtenir la fonction de densité de probabilité
correspondante pour chaque cas et chaque jour.
Par exemple, au jour 1, les résultats attendus sont égaux à :
- le nombre de cas observés au jour 1 multiplié par la densité au jour 0.
R
# Au jour 1, les résultats attendus sont :
ebola_30days$cases[1] *
density(onset_to_death_ebola, at = 0)
SORTIE
[1] 0Au jour 2, les résultats attendus sont égaux à :
- le nombre de cas observés au jour 1 multiplié par la densité au jour 1, plus
- le nombre de cas observés au jour 2 multiplié par la densité au jour 0
R
# Au jour 2, les résultats attendus sont les suivants :
ebola_30days$cases[1] *
density(onset_to_death_ebola, at = 1) +
ebola_30days$cases[2] *
density(onset_to_death_ebola, at = 0)
SORTIE
[1] 0.06495664Au troisième jour, les résultats attendus sont égaux à :
- le nombre de cas observés au premier jour multiplié par la densité au deuxième jour, plus
- le nombre de cas observés au deuxième jour multiplié par la densité au premier jour, plus
- le nombre de cas observés au troisième jour multiplié par la densité au jour 0.
R
# Au troisième jour, les résultats attendus sont :
ebola_30days$cases[1] *
density(onset_to_death_ebola, at = 2) +
ebola_30days$cases[2] *
density(onset_to_death_ebola, at = 1) +
ebola_30days$cases[3] *
density(onset_to_death_ebola, at = 0)
SORTIE
[1] 0.08295091Notez que les cas observés les plus récemment commencent la
distribution des délais à partir de 0, les autres
continuent avec le jour suivant.
Étant donné que la valeur d’entrée dans at varie selon
le jour pour chaque cas (at = 0, at = 1,
at = 2, …), la fonction density() doit être
exprimée en fonction de x. cfr tirera alors les valeurs
en conséquence, comme indiqué ci-dessous :
R
# {cfr} utilise la densité de la distribution à différentes valeurs de x
function(x) density(onset_to_death_ebola, at = x)
En interne, la fonction cfr::estimate_outcomes()
effectue ce calcul :
R
cfr::estimate_outcomes(
data = ebola_30days,
delay_density = function(x) density(onset_to_death_ebola, at = x)
) %>%
slice_head(n = 3) %>%
pull(estimated_outcomes)
SORTIE
[1] 0.00000000 0.06495664 0.08295091Utilisation des objets de la classe epiparameter
Lorsque vous utilisez un object de la classe
<epiparameter>, vous pouvez utiliser cette expression
comme modèle :
function(x) density(<NOM_OBJECT_EPIPARAMETER>, x)
Pour les fonctions de distribution dont les paramètres ne sont pas disponibles dans epiparameter nous vous proposons deux alternatives :
Créer un objet de la classe
<epiparameter>pour l’intégrer dans d’autres packages R d’un pipeline d’analyse épidémiologique. Lisez l’article document de référence deepiparameter::epiparameter()pour plus de clarifications.Liser la vignette de cfr portant sur l’utilisation des distributions des délais.
Pour la fonction cfr_static() et les autres de la
famille cfr_*(), les distributions les plus appropriées
sont les distributions discrets. Ceci en raison du fait
que nous travaillerons avec des données d’incidence quotidiennes sur le
nombre de cas et de décès.
Nous pouvons supposer que l’évaluation de la fonction de distribution de probabilité (FDP) d’une distribution continue est équivalente à la fonction de masse de probabilité (FMP) de la distribution discrète correspondante.
Toutefois, cette hypothèse pourrait être inappropriée en présence de
distributions présentant des pics énormes. C’est le cas, par exemple,
des maladies dont la distribution du délai entre la date d’apparition
des symptômes et la date du décès présente un pic très élevé et une
faible variance. Dans ce cas, la disparité moyenne entre la FDP et la
FMP devrait être plus prononcée que pour les distributions avec de
larges variances. Une façon d’y remédier est de discrétiser la
distribution continue en appliquant la fonction
epiparameter::discretise() à un objet de la classe
<epiparameter>.
R
onset_to_death_ebola %>%
epiparameter::discretise() %>%
plot(xlim = c(0, 40))
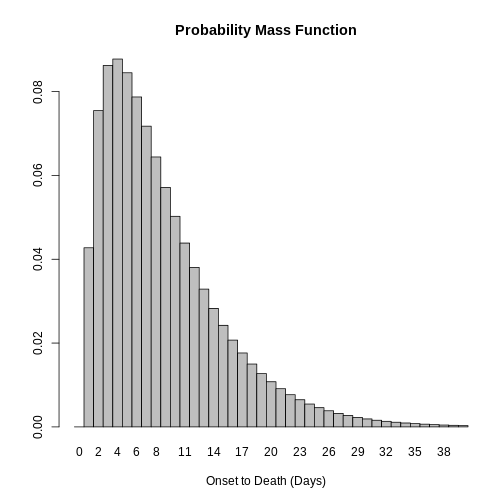
Défi
Utilisez le même fichier (sarscov2_cases_deaths.csv) que celui du défi précédent pour:
- Estimer le RL ajusté au délai en utilisant la distribution de délai adéquate.
- Comparer les résultats du RL naïf et du RL ajusté au délai.
- Trouver l’objet de la classe
<epiparameter>approprié pour ces données.
Nous utiliserons la librairie epiparameter pour accéder à une distribution des délais pour les données d’incidence du SARS-CoV-2.
R
library(epiparameter)
sarscov2_delay <- epiparameter::epiparameter_db(
disease = "covid",
epi_name = "onset to death",
single_epiparameter = TRUE
)
Les données seront importées dans R à l’aide de la fonction
readr::read_csv(). Cette fonction reconnaît que la colonne
date est de type <Date>.
R
# importer les donnees
# supposons que le chemin d'accès au fichier est: data/raw-data/ebola_cases.csv
sarscov2_input <- readr::read_csv(
file = here::here("data", "raw-data", "sarscov2_cases_deaths.csv")
)
R
# voir un apperçu des donnees
sarscov2_input
SORTIE
# A tibble: 93 × 3
date cases_jpn deaths_jpn
<date> <dbl> <dbl>
1 2020-01-20 1 0
2 2020-01-21 1 0
3 2020-01-22 0 0
4 2020-01-23 1 0
5 2020-01-24 1 0
6 2020-01-25 3 0
7 2020-01-26 3 0
8 2020-01-27 4 0
9 2020-01-28 6 0
10 2020-01-29 7 0
# ℹ 83 more rowsNous pouvons utiliser la fonction
cleanepi::standardize_column_names() pour renommer les noms
des colonnes de sorte qu’elles soient conforment à la fonction
cfr::cfr_static().
R
# renommer les noms des colonnes avant d'estimer le RL ajusté au délai
sarscov2_input %>%
cleanepi::standardize_column_names(
rename = c(cases = "cases_jpn", deaths = "deaths_jpn")
) %>%
cfr::cfr_static(
delay_density = function(x) density(sarscov2_delay, x)
)
SORTIE
severity_estimate severity_low severity_high
1 0.0734 0.071 0.0759Comparer et interpréter les estimations du RL naïfs et ajusté au délais.
Pour ajuster le RL, Nishiura et al. 2009 ont utilisé les incidences des cas et des décès pour estimer le nombre de cas dont les pronostiques vitaux sont connus :
\[ u_t = \dfrac{\sum_{i = 0}^t \sum_{j = 0}^\infty c_{i - j} f_{j}}{\sum_{i = 0} c_i}, \]
où :
- \(c_{t}\) est l’incidence quotidienne des cas à l’instant \(t\),
- \(f_{t}\) est la valeur de la fonction de masse de probabilité (FMP) de la distribution des délais entre l’apparition des symptômes et le décès, et
- \(u_{t}\) représente le facteur de sous-estimation des statuts vitals connus.
\(u_{t}\) est utilisé pour
ajuster l’échelle du nombre cumulé de cas au niveau du
dénominateur dans le calcul du RL. Ce calcul est effectué en interne à
l’aide de la fonction estimate_outcomes().
L’estimateur du RL peut être écrit comme suit :
\[p_{t} = \frac{b_{t}}{u_{t}}\]
où \(p_{t}\) est la proportion réelle de cas confirmés qui meurent de l’infection (ou le RL non biaisé), et \(b_{t}\) est l’estimation brute et biaisée du RL (ou RL naïf).
D’après cette dernière équation, nous observons que le RL non biaisé \(p_{t}\) est plus élevé que le RL biaisé \(b_{t}\), car le numérateur dans \(u_{t}\) est plus petit que le dénominateur (notez que \(f_{t}\) est la distribution de probabilité de la distribution des délais entre l’apparition des symptômes et le décès). Par conséquent, \(b_{t}\) est considérer comme l’estimateur biaisé du RL.
Lorsque nous observons toute l’évolution d’une épidémie (de \(t \rightarrow \infty\)), \(u_{t}\) tend vers 1, ce qui fait que \(b_{t}\) tend à \(p_{t}\) et devient un estimateur sans biais (Nishiura et al., 2009).
Estimation du RL au début d’une épidémie
L’estimation du RL naïf est utile pour obtenir une estimation globale de la gravité d’une épidémie (jusqu’au moment \(t\)). À la fin de l’épidémie ou lorsqu’on atteint un niveau où on a de plus en plus de décès sont signalés, le RL estimé sera alors plus proche du “véritable” RL non biaisé.
Par ailleurs, la valeur RL ajusté au délai estimée au début d’une épidémie refléte mieux la gravité d’une maladie infectieuse émergente que le RL biaisé ou naïf obtenu au cours de l’épidémie.
Nous pouvons calculer le RL ajusté au délai au début d’une
épidémie à l’aide de la fonction cfr::cfr_rolling().
À noter
cfr::cfr_rolling() est une fonction utilitaire qui
calcule automatiquement le RL à chaque jour de l’épidémie à l’aide des
données disponibles au jour de l’estimation, permettant ainsi à
l’utilisateur de gagner du temps.
cfr::cfr_rolling() montre le RL estimé à chaque jour de
l’épidémie, étant donné que les données futures sur les nombres de cas
et de décès ne sont pas disponibles à ce moment-là. Pour un même jeu de
données, la valeur finale de cfr::cfr_rolling() est
identique à celle de cfr::cfr_static().
R
# Calculer le RL naïf quotidien à chacun des 73 jours dans un jeu de donnees
# d'Ebola
rolling_cfr_naive <- cfr::cfr_rolling(data = ebola1976)
SORTIE
`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.R
# Calculer le RL quotidien ajusté au délai à chacun des 73 jours dans un jeu de
# donnees d'Ebola
rolling_cfr_adjusted <- cfr::cfr_rolling(
data = ebola1976,
delay_density = function(x) density(onset_to_death_ebola, x)
)
SORTIE
`cfr_rolling()` is a convenience function to help understand how additional data influences the overall (static) severity. Use `cfr_time_varying()` instead to estimate severity changes over the course of the outbreak.SORTIE
Some daily ratios of total deaths to total cases with known outcome are below 0.01%: some CFR estimates may be unreliable.FALSEAvec la fonction utils::tail() nous pouvons monter les
dernières estimations du RL. On voit que les intervalles de confiance à
95% des valeurs naïves et corrigées se chevauchent.
R
# voir un aperçu des dernieres valeurs du RL
utils::tail(rolling_cfr_naive)
utils::tail(rolling_cfr_adjusted)
Visualisons maintenant les deux résultats dans une série chronologique. Quelle serait la performance des estimations naïves et ajustées au délai en temps réel ?
R
# concatener les deux resultats
dplyr::bind_rows(
list(
naive = rolling_cfr_naive,
adjusted = rolling_cfr_adjusted
),
.id = "method"
) %>%
# visualiser les valeurs journalieres du RL naif et corrige
ggplot() +
geom_ribbon(
aes(
date,
ymin = severity_low,
ymax = severity_high,
fill = method
),
alpha = 0.2, show.legend = FALSE
) +
geom_line(
aes(date, severity_estimate, colour = method)
)
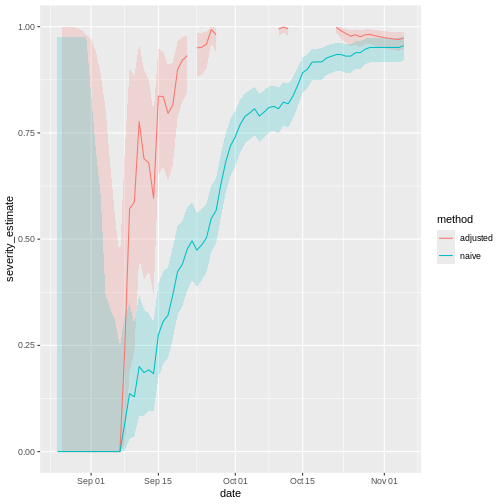
Les lignes rouges et bleues représentent respectivement le RL journalier ajusté au délai et naïf tout au long de l’épidémie. Les bandes autour d’elles représentent les intervalles de confiance à 95% (IC 95%).
Notez que le calcul du RL ajusté au délai est particulièrement utile lorsqu’une courbe épidémique de cas confirmés est la seule donnée disponible (c’est-à-dire lorsque les données concernant le temps entre l’apparition des symptômes jusqu’au décès ne sont pas disponibles, comme c’est le cas au début de l’épidémie). Lorsqu’il y a peu ou pas de décès, une hypothèse sur la distribution des délais entre l’apparition des symptômes et le décès doit être formulée, par exemple à partir de la littérature basée sur les épidémies précédentes. Nishiura et al. 2009 illustrent ce phénomène dans les figures à l’aide de données relatives à l’épidémie de SARS survenue à Hong Kong en 2003.
Les figures A et B montrent les nombres cumulés de cas et de décès dus au SARS, et la figure C montre les estimations observées (biaisées) du RL en fonction du temps, c’est-à-dire le nombre cumulé de décès par rapport au nombre de cas à l’instant \(t\). En raison du délai entre l’apparition des symptômes et le décès, l’estimation biaisée du RL au temps \(t\) est inférieure au RL obtenu à la fin de l’épidémie (302/1755 = 17,2 %).
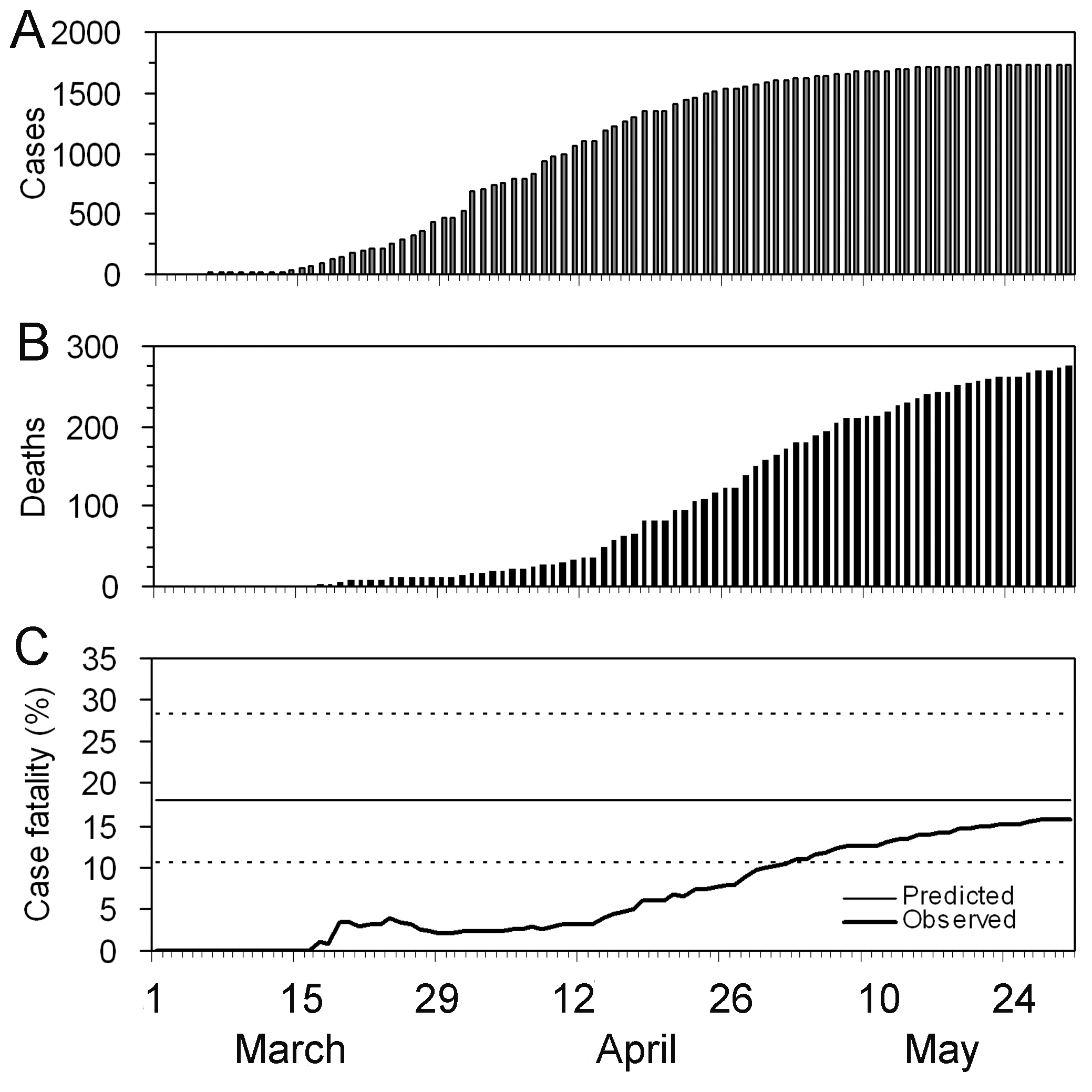
Néanmoins, même en n’utilisant que les données observées sur la
période du 19 mars au 2 avril, cfr::cfr_static() peut
produire une prédiction appropriée (figure D), par exemple le RL ajusté
au délai au 27 mars est de 18,1% (IC 95% : 10,5 - 28,1). Une
surestimation est notée au tout début de l’épidémie, mais les limites de
l’intervalle de confiance à 95% pour les phases ultérieures incluent le
RL réel (c’est-à-dire 17,2 %).
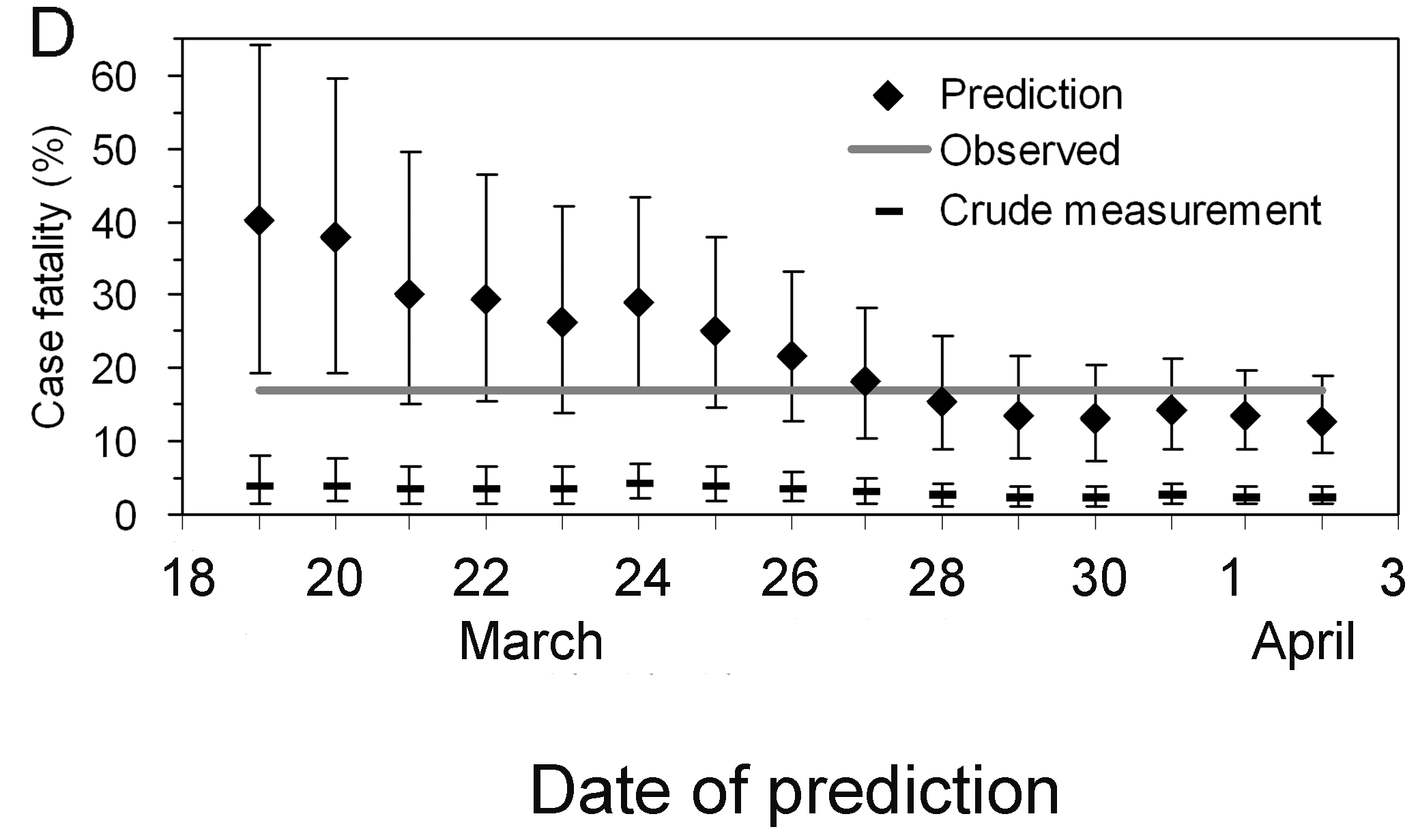
Interpréter l’estimation du RL au début de l’épidémie
Sur la base de la figure ci-dessus :
- Quelle est la différence, en jours, entre la date à laquelle l’IC à 95% du RL ajusté aux délais et du RL naïf se croisent avec le RL estimé à la fin de l’épidémie ?
Discutez-en :
- En quoi le fait de disposer d’un RL ajusté aux délai peut-il influer sur les stratégies de santé publique ?
Nous pouvons soit inspecter visuellement ou analyser les tableaux des données de sortie.
Il y a presque un mois de différence.
Notez que l’estimation présente une incertitude considérable au début de la série chronologique. Après deux semaines, le RL corrigé au délai se rapproche de l’estimation globale du RL à la fin de l’épidémie.
Ce schéma est-il similaire à celui d’autres épidémies ? Nous vous invitons à utiliser les ensembles de données dans les défis de cet épisode pour le découvrir.
Liste de vérification
Avec cfr nous estimons le RL comme la proportion de décès parmi les cas confirmés.
En n’utilisant que les cas confirmés il est clair que tous les cas qui ne cherchent pas de traitement médical ou qui ne sont pas notifiés ne sont pas pris en compte, de même que tous les cas asymptomatiques. Cela signifie que le RL estimé est plus élevé que la proportion de décès parmi l’ensemble des personnes infectées.
La méthode de la librairie cfr vise à obtenir un estimateur non biaisé “bien avant” d’observer toute l’évolution de l’épidémie. Pour ce faire, cfr utilise le facteur de sous-estimation \(u_{t}\) pour estimer le RL non biaisé \(p_{t}\) à l’aide de la méthode du maximum de vraisemblance, étant donné le processus d’échantillonnage défini par Nishiura et al, 2009.

Nous connaissons le nombre cumulé de cas confirmés et de décès \(C_{t}\) et \(D_{t}\) à l’instant \(t\) à partir des données d’incidence agrégées et souhaitons estimer le RL non biaisé \(\pi\) au moyen du facteur de sous-estimation \(u_{t}\).
Si nous connaissions le facteur de sous-estimation \(u_{t}\) nous pourrions préciser la taille de la population des cas confirmés qui ne sont plus à risque (\(u_{t}C_{t}\), ombré), bien que nous ne sachions pas quels individus survivants appartiennent à ce groupe. Une proportion \(\pi\) de ceux qui font partie du groupe de cas encore à risque (taille \((1- u_{t})C_{t}\), non ombré) devrait mourir.
Parce que chaque cas qui n’est plus à risque avait une probabilité indépendante de mourir, \(\pi\) le nombre de décès, \(D_{t}\) est un échantillon d’une distribution binomiale avec une taille d’échantillon de \(u_{t}C_{t}\) et la probabilité de décès \(p_{t}\) = \(\pi\).
Ceci est représenté par la fonction de vraisemblance suivante permettant d’obtenir l’estimation du maximum de vraisemblance du RL non biaisé \(p_{t}\) = \(\pi\):
\[ {\sf L}(\pi | C_{t},D_{t},u_{t}) = \log{\dbinom{u_{t}C_{t}}{D_{t}}} + D_{t} \log{\pi} + (u_{t}C_{t} - D_{t})\log{(1 - \pi)}, \]
Ce calcule est réalisé par la fonction interne
?cfr:::estimate_severity().
- Le RL ajusté aux délais ne prend pas en charge toutes les sources d’erreur dans les données, telle que la non-détection de toutes les personnes infectées.
Challenges
Autres mesures de sévérité
Supposons que nous ayons besoin d’évaluer la gravité clinique de l’épidémie dans un contexte autre aue la surveillance épidémiologique, comme la gravité parmi les cas qui arrivent à l’hôpital ou les cas que vous avez recueillis lors d’une enquête sérologique représentative.
En utilisant cfr nous pouvons modifier les valeurs du
numérateur (cases) et du dénominateur (deaths)
pour estimer des mesures plus sévères comme le risque d’infection
mortelle (RIM) ou le risque d’hospitalisation mortelle (RHM). Nous
pouvons suivre analogie ci-après :
Si pour le risque de décès (RL) d’un cas, nous exigeons :
- les données sur l’incidence des cas et des décès, avec une
- distribution des délais entre les cas et les décès (ou une approximation proche, comme le délai entre l’apparition des symptômes et le décès).
Dans ce cas, le risque d’infection mortelle (RIM) nécessite :
- les données sur l’incidence des infections et des décès, avec une
- distribution des délais entre l’exposition et le décès (ou une approximation proche).
De la même manière, le risque d’hospitalisation mortelle requière :
- les données d’incidence des cas d’hospitalisation et de décès, ainsi qu’une
- distribution des délais entre l’hospitalisation et le décès.
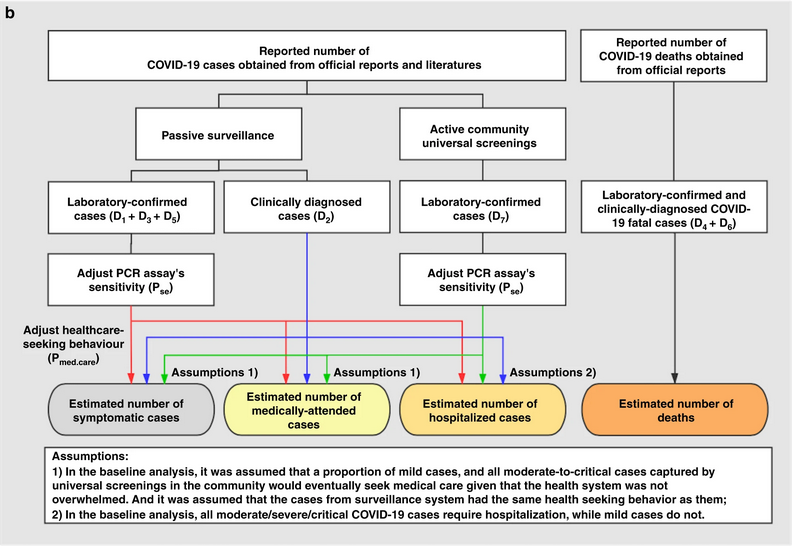
Yang et al, 2020 résume les différentes définitions et sources de données :
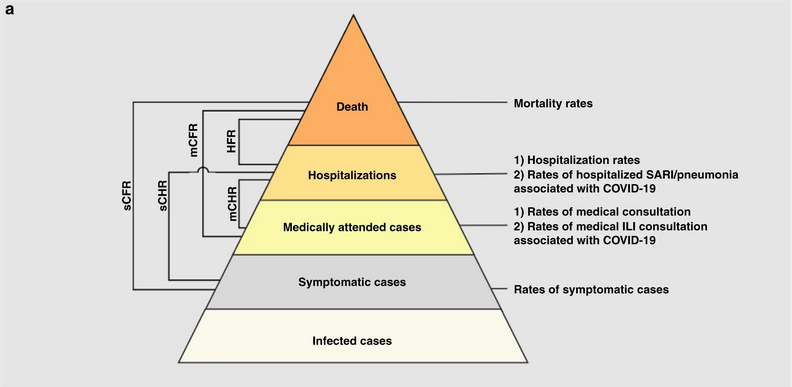
- sCFR risque de létalité des cas symptomatiques (sRL),
- sCHR risque d’hospitalisation des cas symptomatiques (sRH),
- mCFR risque de létalité des cas médicalement pris en charge (mRL),
- mCHR risque d’hospitalisation d’un cas médicalement pris en charge (mRH),
- HFR risque d’hospitalisation mortelle (RHM).
Les données agrégées diffèrent des données de cas individuels (linelist)
Les données d’incidence agrégées diffèrent des linelist où chaque observation contient des données concernant un cas individuel.
R
outbreaks::ebola_sierraleone_2014 %>% as_tibble()
SORTIE
# A tibble: 11,903 × 8
id age sex status date_of_onset date_of_sample district chiefdom
<int> <dbl> <fct> <fct> <date> <date> <fct> <fct>
1 1 20 F confirmed 2014-05-18 2014-05-23 Kailahun Kissi Teng
2 2 42 F confirmed 2014-05-20 2014-05-25 Kailahun Kissi Teng
3 3 45 F confirmed 2014-05-20 2014-05-25 Kailahun Kissi Tonge
4 4 15 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
5 5 19 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
6 6 55 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
7 7 50 F confirmed 2014-05-21 2014-05-26 Kailahun Kissi Teng
8 8 8 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
9 9 54 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
10 10 57 F confirmed 2014-05-22 2014-05-27 Kailahun Kissi Teng
# ℹ 11,893 more rowsUtilisez {incidence2} pour réorganiser vos données
Comment réorganiser les données d’entrée ?
Le réorganisation des données d’entrée durant le processus d’analyse des données peut prendre beaucoup de temps. Pour obtenir des données d’incidence agrégées prêtes à être analysées nous vous encourageons à utiliser le package incidence2.
Tout d’abord, consultez la vignette Get
started de la librairie incidence2 pour savoir
comment utiliser l’argument date_index lors de la lecture
d’un linelist contenant plusieurs colonnes de type
<Date>.
Ensuite, référez-vous au
manuel de référence sur la façon d’utiliser la fonction
cfr::prepare_data() sur les objets de classe
<incidence2>.
R
# charger les packages
library(cfr)
library(epiparameter)
library(incidence2)
library(outbreaks)
library(tidyverse)
# Acceder a la distribution des delais
mers_delay <- epiparameter::epiparameter_db(
disease = "mers",
epi_name = "onset to death",
single_epiparameter = TRUE
)
# lire le linelist
mers_korea_2015$linelist %>%
as_tibble() %>%
select(starts_with("dt_"))
SORTIE
# A tibble: 162 × 6
dt_onset dt_report dt_start_exp dt_end_exp dt_diag dt_death
<date> <date> <date> <date> <date> <date>
1 2015-05-11 2015-05-19 2015-04-18 2015-05-04 2015-05-20 NA
2 2015-05-18 2015-05-20 2015-05-15 2015-05-20 2015-05-20 NA
3 2015-05-20 2015-05-20 2015-05-16 2015-05-16 2015-05-21 2015-06-04
4 2015-05-25 2015-05-26 2015-05-16 2015-05-20 2015-05-26 NA
5 2015-05-25 2015-05-27 2015-05-17 2015-05-17 2015-05-26 NA
6 2015-05-24 2015-05-28 2015-05-15 2015-05-17 2015-05-28 2015-06-01
7 2015-05-21 2015-05-28 2015-05-16 2015-05-17 2015-05-28 NA
8 2015-05-26 2015-05-29 2015-05-15 2015-05-15 2015-05-29 NA
9 NA 2015-05-29 2015-05-15 2015-05-17 2015-05-29 NA
10 2015-05-21 2015-05-29 2015-05-16 2015-05-16 2015-05-29 NA
# ℹ 152 more rowsR
# utiliser {incidence2} pour determiner les incidences journalieres
mers_incidence <- mers_korea_2015$linelist %>%
# convertir en objet incidence2
incidence2::incidence(date_index = c("dt_onset", "dt_death")) %>%
# completer les dates du début a la fin
incidence2::complete_dates()
# voir un aperçu des donnees d'incidence
mers_incidence
SORTIE
# incidence: 72 x 3
# count vars: dt_death, dt_onset
date_index count_variable count
<date> <chr> <int>
1 2015-05-11 dt_death 0
2 2015-05-11 dt_onset 1
3 2015-05-12 dt_death 0
4 2015-05-12 dt_onset 0
5 2015-05-13 dt_death 0
6 2015-05-13 dt_onset 0
7 2015-05-14 dt_death 0
8 2015-05-14 dt_onset 0
9 2015-05-15 dt_death 0
10 2015-05-15 dt_onset 0
# ℹ 62 more rowsR
# Preparer les donnees d'incidence pour utilisation dans {cfr}
mers_incidence %>%
cfr::prepare_data(
cases_variable = "dt_onset",
deaths_variable = "dt_death"
)
SORTIE
date deaths cases
1 2015-05-11 0 1
2 2015-05-12 0 0
3 2015-05-13 0 0
4 2015-05-14 0 0
5 2015-05-15 0 0
6 2015-05-16 0 0
7 2015-05-17 0 1
8 2015-05-18 0 1
9 2015-05-19 0 0
10 2015-05-20 0 5
11 2015-05-21 0 6
12 2015-05-22 0 2
13 2015-05-23 0 4
14 2015-05-24 0 2
15 2015-05-25 0 3
16 2015-05-26 0 1
17 2015-05-27 0 2
18 2015-05-28 0 1
19 2015-05-29 0 3
20 2015-05-30 0 5
21 2015-05-31 0 10
22 2015-06-01 2 16
23 2015-06-02 0 11
24 2015-06-03 1 7
25 2015-06-04 1 12
26 2015-06-05 1 9
27 2015-06-06 0 7
28 2015-06-07 0 7
29 2015-06-08 2 6
30 2015-06-09 0 1
31 2015-06-10 2 6
32 2015-06-11 1 3
33 2015-06-12 0 0
34 2015-06-13 0 2
35 2015-06-14 0 0
36 2015-06-15 0 1R
# Estimer le RL ajuste au delai
mers_incidence %>%
cfr::prepare_data(
cases_variable = "dt_onset",
deaths_variable = "dt_death"
) %>%
cfr::cfr_static(delay_density = function(x) density(mers_delay, x))
SORTIE
severity_estimate severity_low severity_high
1 0.1377 0.0716 0.2288Hétérogénéité de la gravité
Le RL peut varier d’une population à l’autre (par exemple en fonction de l’âge, l’espace géographique, du traitement, etc) ; la quantification de ces hétérogénéités peut aider à mobiliser les ressources de manière appropriée et à comparer différents régimes de soins (Cori et al., 2017).
Utilisez le tableau de données cfr::covid_data pour
estimer un RL ajusté aux délais, stratifié par pays.
Une façon d’effectuer une analyse stratifiée consiste à
appliquer un modèle à des données imbriquées. Cette vignette
de la librairie {tidyr} vignette vous montre comment
appliquer la méthode dplyr::group_by() +
tidyr::nest() aux données de imbriquées, puis
dplyr::mutate() + purrr::map() pour appliquer
le modèle.
R
library(cfr)
library(epiparameter)
library(tidyverse)
covid_data %>% dplyr::glimpse()
SORTIE
Rows: 20,786
Columns: 4
$ date <date> 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2020-01-03, 2…
$ country <chr> "Argentina", "Brazil", "Colombia", "France", "Germany", "India…
$ cases <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ deaths <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…R
delay_onset_death <- epiparameter::epiparameter_db(
disease = "covid",
epi_name = "onset to death",
single_epiparameter = TRUE
)
covid_data %>%
dplyr::group_by(country) %>%
tidyr::nest() %>%
dplyr::mutate(
temp = purrr::map(
.x = data,
.f = cfr::cfr_static,
delay_density = function(x) density(delay_onset_death, x)
)
) %>%
tidyr::unnest(cols = temp)
SORTIE
# A tibble: 19 × 5
# Groups: country [19]
country data severity_estimate severity_low severity_high
<chr> <list> <dbl> <dbl> <dbl>
1 Argentina <tibble> 0.0133 0.0133 0.0133
2 Brazil <tibble> 0.0195 0.0195 0.0195
3 Colombia <tibble> 0.0225 0.0224 0.0226
4 France <tibble> 0.0044 0.0044 0.0044
5 Germany <tibble> 0.0045 0.0045 0.0045
6 India <tibble> 0.0119 0.0119 0.0119
7 Indonesia <tibble> 0.024 0.0239 0.0241
8 Iran <tibble> 0.0191 0.0191 0.0192
9 Italy <tibble> 0.0075 0.0075 0.0075
10 Mexico <tibble> 0.0461 0.046 0.0462
11 Peru <tibble> 0.0502 0.0501 0.0504
12 Poland <tibble> 0.0186 0.0186 0.0187
13 Russia <tibble> 0.0182 0.0182 0.0182
14 South Africa <tibble> 0.0254 0.0253 0.0255
15 Spain <tibble> 0.0087 0.0087 0.0087
16 Turkey <tibble> 0.006 0.006 0.006
17 Ukraine <tibble> 0.0204 0.0203 0.0205
18 United Kingdom <tibble> 0.009 0.009 0.009
19 United States <tibble> 0.0111 0.0111 0.0111C’est génial ! Vous pouvez maintenant utiliser un code similaire pour stratifier vos analyses en fonction de l’âge, des régions ou autres facteurs utiles.
Mais comment interpréter le fait qu’on ait une variabilité nationale de la gravité clinique pour un même agent pathogène diagnostiqué ?
Des facteurs locaux tels que la capacité de test, la définition de cas et le régime d’échantillonnage peuvent influer sur la déclaration des cas et des décès, et donc sur la détermination de la grvité clinique. Jetez un coup d’œil à la vignette de cfr sur Estimation de la proportion de cas confirmés au cours d’une épidémie.
Annexe
La librairie cfr possède une fonction appelée
cfr_time_varying() dont la fonctionnalité diffère de celle
de cfr_rolling().
Quand doit-on utiliser cfr_rolling() ?
cfr::cfr_rolling() calcule le RL estimé à chaque jour de
l’épidémie, vue que les données futures sur les cas et les décès ne sont
pas disponibles à ce moment-là. La valeur finale de
cfr_rolling() est identique à celle de
cfr_static() pour les mêmes données.
Rappelez-vous, comme indiqué ci-dessus, cfr_rolling()
est utile pour obtenir des estimations du RL à un stade précoce de
l’épidémie et vérifier si l’estimation du RL d’une épidémie s’est
stabilisée. C’est pourquoi, cfr_rolling() n’est pas
sensible à la durée ou à la taille de l’épidémie.
Quand doit-on utiliser
cfr_time_varying() ?
D’autre part, cfr::cfr_time_varying(), utilisée pour
calculer le RL mobile (RL par intervalle de temps régulier), aide à
comprendre les variations du RL dues à des changements durant
l’épidémie, comme par exemple en raison d’un nouveau variant du
pathogène ou d’une immunité accrue due à la vaccination.
Cependant, cfr_time_varying() est sensible à
l’incertitude de l’échantillonnage. Son résultat est donc sensible à la
taille de l’épidémie. Plus le nombre de cas dont on connaitra le
pronostique au moment de l’estimation est élevé, plus nous obtiendrons
des estimations raisonnables du RL variable par intervalle de temps
consécutif.
Par exemple, avec 100 cas, le taux de létalité estimé aura, grosso
modo, un intervalle de confiance de 95% ± 10% de la valeur moyenne (IC
binomial). Donc, si le nombre de cas dont on connaitra le pronostique à
un jour donné est supérieur 100, nous pouvons obtenir des
estimations raisonnables du RL mobile. Mais si nous disposons que de
>100 cas sur toute la durée de l’épidémie nous devrons
probablement nous appuyer sur la fonction cfr_rolling() qui
utilise les données cumulées.
Nous vous invitons à lire la vignette
sur la fonction cfr_time_varying().
Points clés
Utilisez la librairie cfr pour estimer la gravité clinique
Utilisez la fonction
cfr::cfr_static()pour estimer le RL global à l’aide des plus récentes données disponibles.Utilisez la fonction
cfr::cfr_rolling()pour obtenir les estimations du RL durant chaque jour de l’épidémie.Utiliser l’argument
delay_densitypour ajuster les valeurs du RL au délai épidémiologique en fonction de la distribution des délais correspondants.
