Tenir compte du phénomène hypercontagieux

Dernière mise à jour le 2025-10-24 | Modifier cette page

Durée estimée : 32 minutes

Vue d'ensemble

Questions

  • Comment peut-on estimer la variation de la transmission au niveau individuel (c’est-à-dire le potentiel de super propagation) à partir des données de traçage des contacts ?
  • Quelles sont les implications de la variation de la transmission pour la prise de décision ?

Objectifs

  • Estimez la distribution de descendance (c’est-à-dire le nombre de cas secondaires) à partir des données de l’épidémie à l’aide de epicontacts.
  • Estimez l’ampleur de la variation au niveau individuel (c’est-à-dire le paramètre de dispersion) de la distribution de la descendance à l’aide de fitdistrplus.
  • Estimez la proportion de la transmission liée à des “événements de super propagation” à l’aide de superspreading.

Pré-requis

Les apprenants doivent se familiariser avec les concepts suivants avant de suivre ce tutoriel :

Statistiques: distributions de probabilités courantes, en particulier Poisson et binôme négatif.

Théorie épidémique Le nombre de reproduction, R.

R packages installés: epicontacts, fitdistrplus, superspreading, outbreaks, tidyverse.

Installer les packages si elles ne le sont pas déjà:

R 

# si {pak} n'est pas disponible, exécutez : install.packages("pak")
pak::pak("epicontacts")
pak::pak("fitdistrplus")
pak::pak("superspreading")
pak::pak("outbreaks")
pak::pak("tidyverse")

Si vous recevez un message d’erreur, rendez-vous sur la page principale de configuration.

Introduction

De la variole au coronavirus du syndrome respiratoire aigu sévère 2 (SRAS-CoV-2), certaines personnes infectées transmettent l’infection à un plus grand nombre de personnes que d’autres. La transmission de la maladie est le résultat d’une combinaison de facteurs biologiques et sociaux, et ces facteurs s’équilibrent dans une certaine mesure au niveau de la population lors d’une grande épidémie. C’est pourquoi les chercheurs utilisent souvent les moyennes de la population pour évaluer le potentiel de propagation de la maladie. Toutefois, au début ou à la fin d’une épidémie, les différences individuelles en matière de contagiosité peuvent être plus importantes. En particulier, elles augmentent le risque d’événements de super propagation (ESS), qui peuvent déclencher des épidémies explosives et influencer les chances de contrôler la transmission (Lloyd-Smith et al., 2005).

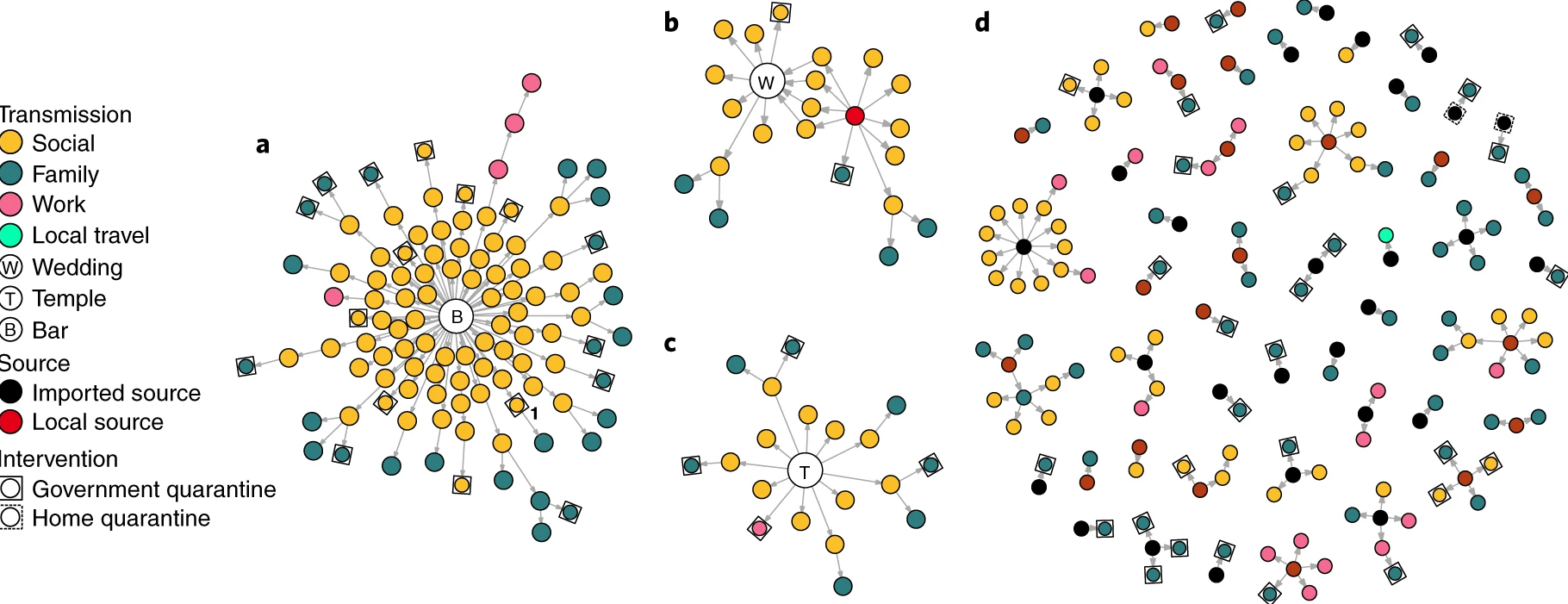
Chaînes de transmission du SRAS-CoV-2 à Hong Kong initiées par des cas locaux ou importés. (a), réseau de transmission d’un groupe de cas remontant à un ensemble de quatre bars de Hong Kong (n = 106). (b), réseau de transmission associé à un mariage sans paires infectrices-infectieuses claires, mais lié à une réunion sociale précédente et à une source locale (n = 22). (c), réseau de transmission associé à un groupe de temples de source indéterminée (n = 19). (d), tous les autres groupes d’infections par le SRAS-CoV-2 dont la source et la chaîne de transmission ont pu être déterminées (Adam et al., 2020).
Chaînes de transmission du SRAS-CoV-2 à Hong Kong initiées par des cas locaux ou importés. (a), réseau de transmission d’un groupe de cas remontant à un ensemble de quatre bars de Hong Kong (n = 106). (b), réseau de transmission associé à un mariage sans paires infectrices-infectieuses claires, mais lié à une réunion sociale précédente et à une source locale (n = 22). (c), réseau de transmission associé à un groupe de temples de source indéterminée (n = 19). (d), tous les autres groupes d’infections par le SRAS-CoV-2 dont la source et la chaîne de transmission ont pu être déterminées (Adam et al., 2020).

Le nombre de reproduction de base, \(R_{0}\) mesure le nombre moyen de cas causés par un individu infectieux dans une population entièrement susceptible. Les estimations de \(R_{0}\) sont utiles pour comprendre la dynamique moyenne d’une épidémie au niveau de la population, mais elles peuvent masquer des variations individuelles considérables dans la contagiosité. Cela a été mis en évidence lors de l’émergence mondiale du SRAS-CoV-2 par de nombreux “événements de super propagation” au cours desquels certains individus infectieux ont généré un nombre anormalement élevé de cas secondaires (LeClerc et al, 2020).

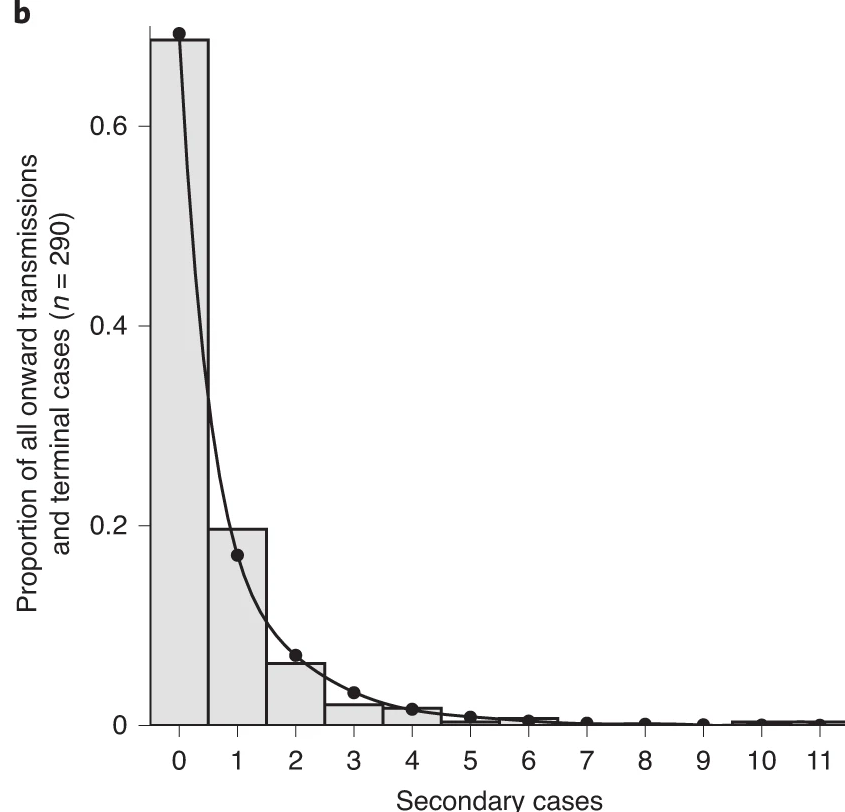
Distribution du nombre de cas secondaires de SRAS-CoV-2 observée à Hong Kong. N = 91 infectés par le SRAS-CoV-2, N = 153 infectés en phase terminale et N = 46 cas locaux sporadiques. Les barres de l’histogramme indiquent la proportion du nombre de cas secondaire generés. La ligne correspond à une distribution binomiale négative ajustée (Adam et al., 2020).
Distribution du nombre de cas secondaires de SRAS-CoV-2 observée à Hong Kong. N = 91 infectés par le SRAS-CoV-2, N = 153 infectés en phase terminale et N = 46 cas locaux sporadiques. Les barres de l’histogramme indiquent la proportion du nombre de cas secondaire generés. La ligne correspond à une distribution binomiale négative ajustée (Adam et al., 2020).

Dans ce tutoriel, nous allons quantifier la variation individuelle de la transmission, et donc estimer le potentiel d’événements d’hypercontagion. Nous utiliserons ensuite ces estimations pour explorer les implications de l’hypercontagion pour les interventions de recherche de contacts.

Nous allons utiliser les données de l’étude outbreaks et gérer la liste des lignes et les données sur les contacts à l’aide de l’outil epicontacts et estimer les paramètres de distribution avec fitdistrplus. Enfin, nous allons utiliser superspreading pour explorer les implications de la variation de la transmission sur la prise de décision.

Nous utiliserons le tuyau %>% pour relier certaines des fonctions de ces packages, donc appelons aussi le package tidyverse .

R 

library(outbreaks)
library(epicontacts)
library(fitdistrplus)
library(superspreading)
library(tidyverse)

Le double point-virgule

Le double point-virgule :: dans R vous permettent d’appeler une fonction spécifique d’un package sans charger le package entier dans l’environnement actuel.

Par exemple, vous pouvez appeler une fonction spécifique d’un package sans charger le package entier dans l’environnement actuel, dplyr::filter(data, condition) utilise filter() à partir de l’outil dplyr package.

Cela nous permet de nous souvenir des fonctions du package et d’éviter les conflits d’espace de noms.

Le numéro de reproduction individuel

Le nombre de reproduction individuel est défini comme le nombre de cas secondaires causés par un individu infecté.

Au début d’une épidémie, nous pouvons utiliser les données de contact pour reconstruire les chaînes de transmission (c’est-à-dire qui a infecté qui) et calculer le nombre de cas secondaires générés par chaque individu. Cette reconstruction des événements de transmission liés à partir des données de contact peut permettre de comprendre comment différents individus ont contribué à la transmission au cours d’une épidémie (Cori et al., 2017).

Mettons cela en pratique en utilisant l’outil mers_korea_2015 et les données de contact de la base de données outbreaks et les intégrons à l’application epicontacts pour calculer la distribution des cas secondaires lors de l’épidémie de MERS-CoV de 2015 en Corée du Sud (Campbell, 2022) :

R 

## first, make an epicontacts object
epi_contacts <-
  epicontacts::make_epicontacts(
    linelist = outbreaks::mers_korea_2015$linelist,
    contacts = outbreaks::mers_korea_2015$contacts,
    directed = TRUE
  )

Avec l’argument directed = TRUE nous configurons un graphe orienté. Ces directions intègrent notre hypothèse de la paire “infecteur-infecté”.

R 

# visualise contact network
plot(epi_contacts)

Les données de contact d’une chaîne de transmission peuvent fournir des informations sur les personnes infectées qui sont entrées en contact avec d’autres. Nous nous attendons à ce que l’infecteur (from) et la personne infectée (to), ainsi que des colonnes supplémentaires de variables liées à leur contact, telles que le lieu (exposure) et la date du contact.

À la suite de mettre de l’ordre dans les données l’unité d’observation dans notre cadre de données de contact est la paire infecteur-infecté. Bien qu’un infecteur puisse infecter plusieurs personnes, les enquêtes de recherche de contacts peuvent enregistrer des contacts liés à plus d’un infecteur (par exemple, au sein d’un ménage). Mais nous devrions nous attendre à avoir des paires infecteur-infecté uniques, car chaque personne infectée a généralement contracté l’infection auprès d’une seule autre personne.

Pour garantir l’unicité de ces paires, nous pouvons vérifier les réplicats pour les personnes infectées :

R 

# no infector-infectee pairs are replicated
epi_contacts %>%
  purrr::pluck("contacts") %>%
  dplyr::group_by(to) %>%
  dplyr::filter(dplyr::n() > 1)

SORTIE 

# A tibble: 5 × 4
# Groups:   to [2]
  from  to     exposure       diff_dt_onset
  <chr> <chr>  <fct>                  <int>
1 SK_16 SK_107 Emergency room            17
2 SK_87 SK_107 Emergency room             2
3 SK_14 SK_39  Hospital room             16
4 SK_11 SK_39  Hospital room             13
5 SK_12 SK_39  Hospital room             12

Notre objectif est d’obtenir le nombre de cas secondaires causés par les individus infectés observés. Dans la base de données des contacts, lorsque chaque paire infecteur-infecté est unique, le nombre de lignes par infecteur correspond au nombre de cas secondaires générés par cet individu.

R 

# count secondary cases per infector in contacts
epi_contacts %>%
  purrr::pluck("contacts") %>%
  dplyr::count(from, name = "secondary_cases")

SORTIE 

     from secondary_cases
1    SK_1              26
2   SK_11               1
3  SK_118               1
4   SK_12               1
5  SK_123               1
6   SK_14              38
7   SK_15               4
8   SK_16              21
9    SK_6               2
10  SK_76               2
11  SK_87               1

Mais cette sortie ne contient que le nombre de cas secondaires pour les infectieux déclarés dans les données de contact, et non pour les cas de tous les individus de l’ensemble des <epicontacts> l’objet.

Au lieu de cela, à partir de epicontacts nous pouvons utiliser la fonction epicontacts::get_degree(). L’argument type = "out" permet d’obtenir la valeur de degré de sortie de chaque nœud dans le réseau de contact à partir du <epicontacts> objet de la classe. Dans un réseau dirigé, le degré de sortie est le nombre d’arêtes sortantes (infectés) émanant d’un nœud (infecteur) (Nykamp DQ, consulté le : 2025).

De même, l’argument only_linelist = TRUE n’inclura que les individus figurant dans le cadre de données de la liste de référence. Lors des enquêtes sur les épidémies, nous nous attendons à ce qu’un registre de toutes les les personnes infectées observées dans les données de la liste de référence. Cependant, toute personne qui n’est pas liée à un infecteur ou un infecté potentiel n’apparaîtra pas dans les données de contact. Par conséquent, l’argument only_linelist = TRUE nous permettra de ne pas manquer ce dernier groupe d’individus lorsque nous compterons le nombre de cas secondaires causés par tous les individus infectés observés. Ils apparaîtront dans les <integer> sous la forme 0 cas secondaires.

R 

# Count secondary cases per subject in contacts and linelist
all_secondary_cases <- epicontacts::get_degree(
  x = epi_contacts,
  type = "out",
  only_linelist = TRUE
)

Caution

À epicontacts::get_degree() nous utilisons l’argument only_linelist = TRUE. Il s’agit de compter le nombre de cas secondaires causés par toutes les personnes infectées observées, ce qui inclut les individus figurant dans les bases de données des contacts et des listes de diffusion.

L’hypothèse selon laquelle “la liste de référence inclura toutes les personnes figurant dans les contacts et la liste de référence”. peut ne pas fonctionner dans toutes les situations.

Par exemple, si au cours du registre des infections observées, les données de contact comprenaient plus de sujets que ceux disponibles dans les données de la liste de référence, vous ne devez prendre en compte que les individus figurant dans les données de contact. Dans ce cas, vous devez prendre en compte uniquement les personnes figurant dans les données de contact, à epicontacts::get_degree() nous utilisons l’argument only_linelist = FALSE.

Vous trouverez ici une version imprimée exemple reproductible:

R 

# Three subjects on linelist
sample_linelist <- tibble::tibble(
  id = c("id1", "id2", "id3")
)

# Four infector-infectee pairs with Five subjects in contact data
sample_contact <- tibble::tibble(
  from = c("id1","id1","id2","id4"),
  to = c("id2","id3","id4","id5")
)

# make an epicontacts object
sample_net <- epicontacts::make_epicontacts(
  linelist = sample_linelist,
  contacts = sample_contact,
  directed = TRUE
)

# count secondary cases per subject from linelist only
epicontacts::get_degree(x = sample_net, type = "out", only_linelist = TRUE)
#> id1 id2 id3 
#>   2   1   0

# count secondary cases per subject from contact only
epicontacts::get_degree(x = sample_net, type = "out", only_linelist = FALSE)
#> id1 id2 id4 id3 id5 
#>   2   1   1   0   0

A partir d’un histogramme des all_secondary_cases de l’objet, nous pouvons identifier les variation au niveau individuel dans le nombre de cas secondaires. Trois cas étaient liés à plus de 20 cas secondaires, tandis que les cas complémentaires comptaient moins de cinq ou aucun cas secondaire.

<La visualisation du nombre de cas secondaires sur un histogramme nous aidera à faire le lien avec la distribution statistique à ajuster : –>

R 

## plot the distribution
all_secondary_cases %>%
  tibble::enframe() %>%
  ggplot(aes(value)) +
  geom_histogram(binwidth = 1) +
  labs(
    x = "Number of secondary cases",
    y = "Frequency"
  )

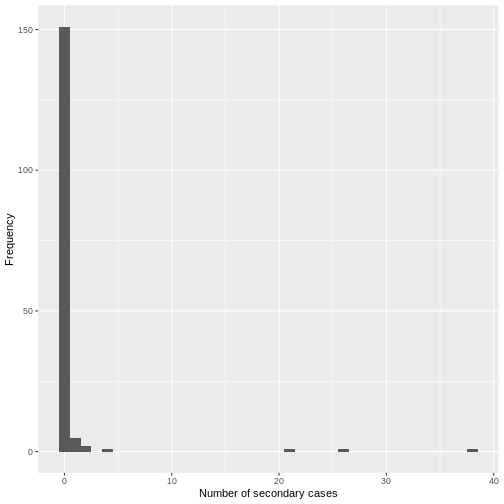
Le nombre de cas secondaires peut être utilisé pour estimer de manière empirique la distribution de la descendance qui est le nombre de cas secondaires causées par chaque cas. Une distribution statistique candidate utilisée pour modéliser la distribution de la descendance est la distribution binomiale négative avec deux paramètres :

  • Moyenne qui représente la \(R_{0}\) le nombre moyen de cas (secondaires) produits par un seul individu dans une population entièrement sensible, et

  • Dispersion exprimée par \(k\) qui représente la variation au niveau individuel de la transmission par des individus isolés.

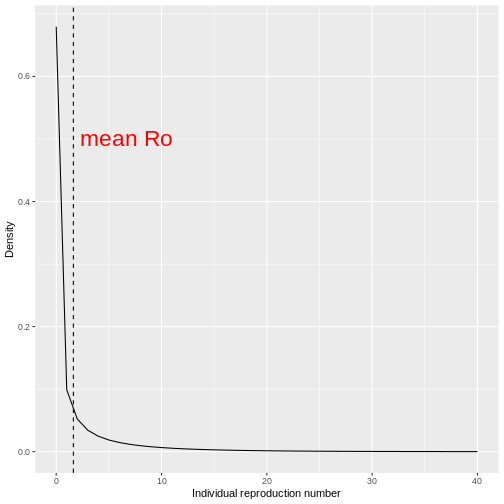
L’histogramme et le diagramme de densité montrent que la distribution de la descendance est fortement asymétrique, soit surdispersée. Dans ce cadre, les événements de surdispersion (ESS) ne sont pas arbitraires ou exceptionnels, mais simplement des réalisations de la queue droite de la distribution de la descendance, que nous pouvons quantifier et analyser (Lloyd-Smith et al., 2005).

Récapitulation terminologique

  • A partir de la liste des lignes et des données de contact, nous calculons le nombre de cas secondaires causés par les personnes infectées observées.
  • Alors que \(R_{0}\) représente la transmission moyenne au sein de la population, nous pouvons définir l’indicateur nombre de reproduction individuel comme le nombre d’infections secondaires causées par un individu infecté spécifique, qui varie d’un individu à l’autre.
  • En raison des effets stochastiques de la transmission, le nombre d’infections secondaires causées par chaque personne infectée est décrit par la distribution de la descendance.
  • La distribution des descendants peut être modélisée par l’équation suivante binomiale négative avec une moyenne \(R_{0}\) et un paramètre de dispersion \(k\), estimés à partir du nombre observé de cas secondaires.

Pour les occurrences d’événements discrets associés, nous pouvons utiliser Poisson ou des distributions binomiales négatives.

Dans une distribution de Poisson, la moyenne est égale à la variance. Mais lorsque la variance est supérieure à la moyenne, on parle de surdispersion. Dans les applications biologiques, la surdispersion se produit et une binomiale négative peut donc être considérée comme une alternative à la distribution de Poisson.

La distribution binomiale négative est particulièrement utile pour les données discrètes sur un intervalle positif non borné dont la variance de l’échantillon dépasse la moyenne de l’échantillon. En d’autres termes, les observations sont surdispersées par rapport à une distribution de Poisson, pour laquelle la moyenne est égale à la variance.

En épidémiologie, binôme négatif ont été utilisées pour modéliser la transmission de maladies infectieuses pour lesquelles le nombre probable d’infections ultérieures peut varier considérablement d’un individu à l’autre et d’un environnement à l’autre, en tenant compte de toutes les variations dans les antécédents infectieux des individus, y compris les propriétés des circonstances biologiques (c’est-à-dire le degré d’excrétion virale) et environnementales (par exemple, le type et le lieu de contact).

Défi

Calculez la distribution des cas secondaires d’Ebola à l’aide de la méthode des ebola_sim_clean objet de outbreaks package.

  • La distribution de la descendance d’Ebola est-elle asymétrique ou surdispersée ?

⚠️ Étape facultative : Cet ensemble de données a 5829 cas. Exécution plot(<epicontacts>) peut prendre plusieurs minutes et utiliser beaucoup de mémoire pour les grandes épidémies telles que la liste des cas d’Ebola. Si vous utilisez un ordinateur plus ancien ou plus lent, vous pouvez sauter cette étape.

R 

## first, make an epicontacts object
ebola_contacts <-
  epicontacts::make_epicontacts(
    linelist = outbreaks::ebola_sim_clean$linelist,
    contacts = outbreaks::ebola_sim_clean$contacts,
    directed = TRUE
  )

# count secondary cases per subject in contacts and linelist
ebola_secondary <- epicontacts::get_degree(
  x = ebola_contacts,
  type = "out",
  only_linelist = TRUE
)

## plot the distribution
ebola_secondary %>%
  tibble::enframe() %>%
  ggplot(aes(value)) +
  geom_histogram(binwidth = 1) +
  labs(
    x = "Number of secondary cases",
    y = "Frequency"
  )

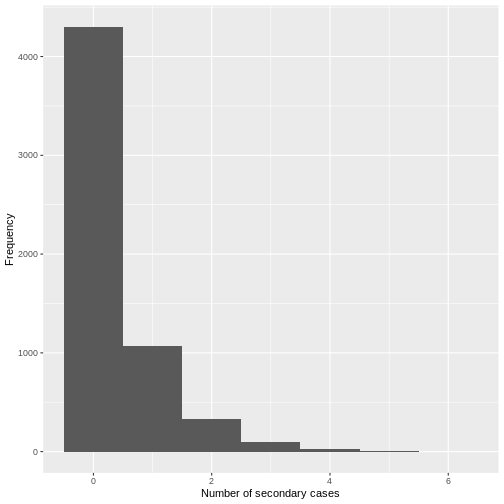
D’après une inspection visuelle, la distribution des cas secondaires pour l’ensemble des données relatives à Ebola en ebola_sim_clean montre une distribution asymétrique avec des cas secondaires inférieurs ou égaux à 6. Nous devons compléter cette observation par une analyse statistique afin d’évaluer la surdispersion.

Estimez le paramètre de dispersion

Pour estimer empiriquement le paramètre de dispersion \(k\) nous pourrions ajuster une distribution binomiale négative au nombre de cas secondaires.

Nous pouvons ajuster des distributions aux données à l’aide de la fonction fitdistrplus qui fournit des estimations du maximum de vraisemblance.

R 

library(fitdistrplus)

R 

## fit distribution
offspring_fit <- all_secondary_cases %>%
  fitdistrplus::fitdist(distr = "nbinom")

offspring_fit

SORTIE 

Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
       estimate  Std. Error
size 0.02039807 0.007278299
mu   0.60452947 0.337893199

Nom des paramètres

A partir de la fitdistrplus sortie :

  • Le size fait référence au paramètre de dispersion estimé \(k\) estimé, et
  • L’objet mu se réfère à la moyenne estimée, qui représente l’ensemble de la population. \(R_{0}\),

À partir de la distribution du nombre de cas secondaires, nous avons estimé un paramètre de dispersion \(k\) de 0.02 avec un intervalle de confiance à 95% de 0.006 à 0.035. Comme la valeur de \(k\) est nettement inférieure à un, nous pouvons conclure qu’il existe un potentiel considérable pour les événements de superposition.

Nous pouvons superposer les valeurs de densité estimées de la distribution binomiale négative ajustée et l’histogramme du nombre de cas secondaires :

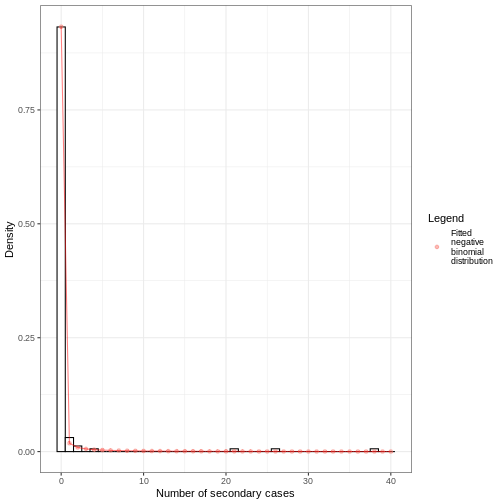
Variation de la transmission au niveau individuel

La variation de la transmission au niveau individuel est définie par la relation entre la moyenne (\(R_{0}\)), la dispersion (\(k\)) et la variance d’une distribution binomiale négative.

Le modèle binomial négatif a \(variance = R_{0}(1+\frac{R_{0}}{k})\), de sorte que les plus petites valeurs de \(k\) indiquent une plus grande variance et, par conséquent, une plus grande variation au niveau individuel de la transmission.

\[\uparrow variance = R_{0}(1+\frac{R_{0}}{\downarrow k})\]

Lorsque \(k\) s’approche de l’infini (\(k \rightarrow \infty\)), la variance est égale à la moyenne (parce que \(\frac{R_{0}}{\infty}=0\)). Cela fait du modèle de Poisson classique un cas particulier du modèle binomial négatif.

Défi

À partir de l’épreuve précédente, utilisez la distribution des cas secondaires de l’épreuve de la ebola_sim_clean de l’objet de outbreaks package.

Ajustez une distribution binomiale négative pour estimer la moyenne et le paramètre de dispersion de la distribution de la descendance. Essayez d’estimer l’incertitude du paramètre de dispersion à partir de l’erreur standard et des intervalles de confiance à 95 %.

  • Le paramètre de dispersion estimé d’Ebola fournit-il des preuves d’une variation de la transmission au niveau individuel ?

Revoyez comment nous avons ajusté une distribution binomiale négative à l’aide de la fonction fitdistrplus::fitdist() fonction.

R 

ebola_offspring <- ebola_secondary %>%
  fitdistrplus::fitdist(distr = "nbinom")

ebola_offspring

SORTIE 

Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters:
      estimate  Std. Error
size 0.8539443 0.072505326
mu   0.3675993 0.009497097

R 

## extract the "size" parameter
ebola_mid <- ebola_offspring$estimate[["size"]]

## calculate the 95% confidence intervals using the
## standard error estimate and
## the 0.025 and 0.975 quantiles of the normal distribution.

ebola_lower <- ebola_mid + ebola_offspring$sd[["size"]] * qnorm(0.025)
ebola_upper <- ebola_mid + ebola_offspring$sd[["size"]] * qnorm(0.975)

# ebola_mid
# ebola_lower
# ebola_upper

À partir de la distribution du nombre de cas secondaires, nous avons estimé un paramètre de dispersion \(k\) de 0.85 avec un intervalle de confiance à 95% de 0.71 à 1.

Pour les estimations du paramètre de dispersion supérieures à un, nous obtenons une faible variance de la distribution, et donc une faible variation de la transmission au niveau individuel.

Mais cela signifie-t-il que la distribution des cas secondaires ne présente pas d’événements de super propagation (ESS) ? Vous rencontrerez plus tard une difficulté supplémentaire : comment définir un seuil d’ESS pour Ebola ?

Nous pouvons utiliser les estimations du maximum de vraisemblance de fitdistrplus pour comparer différents modèles et évaluer la performance de l’ajustement à l’aide d’estimateurs tels que l’AIC et le BIC. Pour en savoir plus, lisez la vignette sur Estimer la transmission au niveau individuel et utilisez l’outil superspreading fonction d’aide ic_tbl() pour cela !

Le paramètre de dispersion entre les maladies

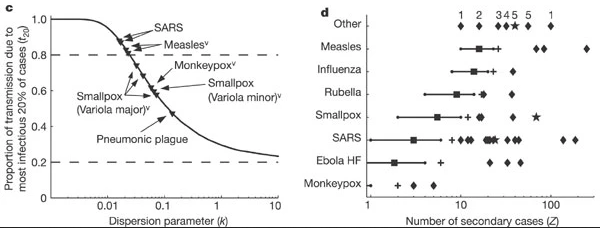
La recherche sur les maladies sexuellement transmissibles et à transmission vectorielle a précédemment suggéré une règle “20/80”, 20 % des individus contribuant à au moins 80 % du potentiel de transmission (Woolhouse et al).

En soi, le paramètre de dispersion \(k\) est difficile à interpréter intuitivement, et sa conversion en un résumé proportionnel peut faciliter la comparaison. Si l’on considère un éventail plus large d’agents pathogènes, on constate qu’il n’existe pas de règle absolue pour le pourcentage qui génère 80 % de la transmission, mais que la variation apparaît comme une caractéristique commune des maladies infectieuses.

  • Lorsque les 20 % de cas les plus infectieux contribuent à 80 % de la transmission (ou plus), on observe une forte variation de la transmission au niveau individuel, avec une distribution de la descendance fortement surdispersée (\(k<0.1\)), par exemple dans le cas du SRAS-1.

  • Lorsque les 20 % de cas les plus infectieux contribuent à environ 50 % de la transmission, la variation de la transmission au niveau individuel est faible et la distribution de la descendance est modérément dispersée (\(k > 0.1\)), par exemple la peste pulmonaire.

Preuve de la variation du nombre d’individus reproducteurs(Gauche, c) Proportion de transmission attendue à partir des 20 % de cas les plus infectieux, pour 10 ensembles de données d’épidémies ou de surveillance (triangles). Les lignes en pointillé indiquent les proportions attendues selon la règle des 20/80 (en haut) et l’homogénéité (en bas). (Droite, d), Événements de super propagation signalés (SSE ; losanges) par rapport au nombre reproductif estimé R (carrés) pour douze infections directement transmissibles. Les croix indiquent le 99e centile proposé comme seuil pour les ESS. (Pour plus de détails sur les figures, voir Lloyd-Smith et al. 2005)
Preuve de la variation du nombre d’individus reproducteurs(Gauche, c) Proportion de transmission attendue à partir des 20 % de cas les plus infectieux, pour 10 ensembles de données d’épidémies ou de surveillance (triangles). Les lignes en pointillé indiquent les proportions attendues selon la règle des 20/80 (en haut) et l’homogénéité (en bas). (Droite, d), Événements de super propagation signalés (SSE ; losanges) par rapport au nombre reproductif estimé R (carrés) pour douze infections directement transmissibles. Les croix indiquent le 99e centile proposé comme seuil pour les ESS. (Pour plus de détails sur les figures, voir Lloyd-Smith et al. 2005)

Contrôle de la superspreading avec la traçabilité des contacts

Lors d’une épidémie, il est courant d’essayer de réduire la transmission en identifiant les personnes qui ont été en contact avec une personne infectée, puis en les mettant en quarantaine au cas où elles s’avéreraient infectées par la suite. Cette recherche de contacts peut être déployée de plusieurs manières. La recherche des contacts “en amont” cible les contacts en aval susceptibles d’avoir été infectés par une infection nouvellement identifiée (c’est-à-dire le “cas index”). La recherche “en amont” vise plutôt le cas primaire en amont qui a infecté le cas index (ou un lieu ou un événement au cours duquel le cas index a été infecté), par exemple en retraçant l’historique des contacts jusqu’au point d’exposition probable. Cela permet d’identifier d’autres personnes qui ont également été potentiellement infectées par ce cas primaire antérieur.

En présence d’une variation de la transmission au niveau individuel, c’est-à-dire avec une distribution de la descendance surdispersée, si ce cas primaire est identifié, une plus grande partie de la chaîne de transmission peut être détectée en remontant l’historique de chacun des contacts de ce cas primaire (Endo et al., 2020).

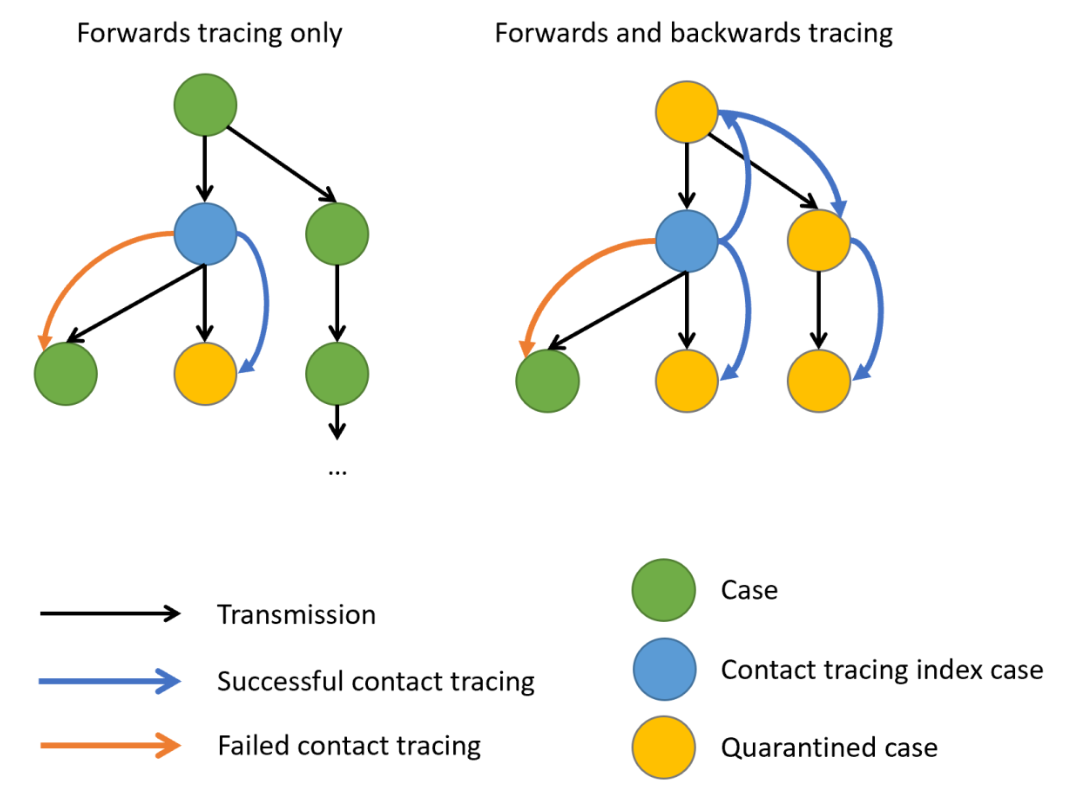
Représentation schématique des stratégies de recherche de contacts. Les flèches noires indiquent le sens de la transmission, les flèches bleues et orange indiquent respectivement une recherche de contact réussie ou échouée. Lorsqu’il existe des preuves d’une variation de la transmission au niveau individuel, entraînant souvent une superspreading, la recherche de contacts en amont du cas index (cercle bleu) augmente la probabilité de trouver le cas primaire (cercle vert) ou des grappes avec une plus grande fraction de cas, augmentant potentiellement le nombre de cas en quarantaine (cercles jaunes). Claire Blackmore, 2021
Représentation schématique des stratégies de recherche de contacts. Les flèches noires indiquent le sens de la transmission, les flèches bleues et orange indiquent respectivement une recherche de contact réussie ou échouée. Lorsqu’il existe des preuves d’une variation de la transmission au niveau individuel, entraînant souvent une superspreading, la recherche de contacts en amont du cas index (cercle bleu) augmente la probabilité de trouver le cas primaire (cercle vert) ou des grappes avec une plus grande fraction de cas, augmentant potentiellement le nombre de cas en quarantaine (cercles jaunes). Claire Blackmore, 2021

Lorsqu’il existe des preuves de variation au niveau individuel (c’est-à-dire de surdispersion), qui se traduisent souvent par ce que l’on appelle des événements de superspreading, une grande proportion d’infections peut être liée à une petite proportion de grappes d’origine. Par conséquent, la recherche et le ciblage des grappes d’origine, combinés à la réduction des infections ultérieures, peuvent considérablement améliorer l’efficacité des méthodes de dépistage (Endo et al., 2020).

Des données empiriques axées sur l’évaluation de l’efficacité de la recherche rétrospective ont permis d’identifier 42 % de cas supplémentaires par rapport à la recherche prospective, ce qui plaide en faveur de sa mise en œuvre lorsqu’une suppression rigoureuse de la transmission est justifiée (Raymenants et al, 2022)

Probabilité de cas dans un groupe donné

En utilisant superspreading nous pouvons estimer la probabilité d’avoir une grappe d’infections secondaires causées par un cas primaire identifié par traçage rétrospectif de taille \(X\) ou plus (Endo et al., 2020).

R 

# Set seed for random number generator
set.seed(33)

# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
  R = offspring_fit$estimate["mu"],
  k = offspring_fit$estimate["size"],
  cluster_size = c(5, 10, 25)
)

SORTIE 

          R          k prop_5 prop_10 prop_25
1 0.6045295 0.02039807  87.9%   74.6%   46.1%

Même si nous disposons d’un \(R<1\) une distribution de la descendance fortement surdispersée (\(k=0.02\)) signifie que si nous détectons un nouveau cas, il y a un risque d’erreur dans la distribution de la descendance. 46.1% probabilité qu’il provienne d’un groupe de 25 infections ou plus. Par conséquent, en suivant une stratégie rétrospective, les efforts de recherche des contacts augmenteront la probabilité de réussir à contenir et à mettre en quarantaine ce grand nombre de personnes précédemment infectées, plutôt que de se concentrer simplement sur le nouveau cas, qui est susceptible de n’avoir infecté personne (parce qu’il n’a pas été infecté). \(k\) est très faible).

Nous pouvons également utiliser ce nombre pour empêcher les rassemblements de certaines tailles afin de réduire l’épidémie en prévenant les événements potentiels de surpopulation. Les interventions peuvent viser à réduire le nombre de reproductions afin de réduire la probabilité d’avoir des groupes de cas secondaires.

Recherche rétrospective des contacts pour Ebola

Utilisez les paramètres estimés pour Ebola pour ebola_sim_clean à partir de outbreaks package.

Calculez la probabilité d’avoir un groupe d’infections secondaires causées par un cas primaire identifié par traçage rétrospectif de taille 5, 10, 15 ou plus.

La mise en œuvre d’une stratégie de traçage en amont à ce stade de l’épidémie d’Ebola augmenterait-elle la probabilité de contenir et de mettre en quarantaine un plus grand nombre de cas en aval ?

Examinez comment nous avons estimé la probabilité d’avoir des grappes de taille fixe, compte tenu de la moyenne de la distribution de la descendance et des paramètres de dispersion, à l’aide de la méthode des superspreading::proportion_cluster_size() fonction.

R 

# estimate the probability of
# having a cluster size of 5, 10, or 25
# secondary cases from a primary case,
# given known reproduction number and
# dispersion parameter.
superspreading::proportion_cluster_size(
  R = ebola_offspring$estimate["mu"],
  k = ebola_offspring$estimate["size"],
  cluster_size = c(5, 10, 25)
)

SORTIE 

          R         k prop_5 prop_10 prop_25
1 0.3675993 0.8539443  2.64%      0%      0%

La probabilité d’avoir des grappes de cinq personnes est de 1,8 %. À ce stade, compte tenu des paramètres de distribution de la descendance, une stratégie rétrospective n’augmentera peut-être pas la probabilité de contenir et de mettre en quarantaine davantage de cas en amont.

Défis

Le virus Ebola se propage-t-il à grande échelle ?

La notion d’“événement de surpopulation” peut revêtir des significations différentes selon les personnes. Lloyd-Smith et al, 2005 ont proposé un protocole général pour définir un événement de super propagation (ESS). Si le nombre d’infections secondaires causées par chaque cas, \(Z\) suit une distribution binomiale négative (\(R, k\)) :

  • Nous définissons une ESS comme tout individu infecté qui infecte plus de \(Z(n)\) autres, où \(Z(n)\) est le nième percentile de l’échantillon de \(Poisson(R)\) distribution.
  • Un SSE du 99e centile est donc tout cas causant plus d’infections qu’il n’en surviendrait dans 99 % des histoires infectieuses d’une population homogène.

À l’aide de la fonction de distribution correspondante, estimez le seuil d’ESS pour définir un ESS pour les estimations de la distribution de la descendance d’Ebola pour l’ensemble de la population. ebola_sim_clean objet de outbreaks package.

Dans une distribution de Poisson, lambda ou tau sont égaux à la valeur estimée du paramètre moyenne d’une distribution binomiale négative. Vous pouvez étudier cette question dans Le zoo de la distribution une application brillante.

Pour obtenir la valeur du quantile pour le 99ème centile, nous devons utiliser la fonction fonction de densité de la distribution de Poisson dpois().

R 

# get mean
ebola_mu_mid <- ebola_offspring$estimate["mu"]

# get 99th-percentile from poisson distribution
# with mean equal to mu
stats::qpois(
  p = 0.99,
  lambda = ebola_mu_mid
)

SORTIE 

[1] 2

Comparez ces valeurs avec celles rapportées par Lloyd-Smith et al, 2005. Voir la figure ci-dessous :

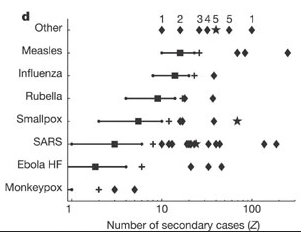
Événements de surmultiplication signalés (diamants) par rapport au nombre de reproduction estimé R (carrés) pour douze infections directement transmissibles. Les lignes indiquent les percentiles 5-95 du nombre de cas secondaires suivant une distribution de Poisson avec lambda égal au nombre de reproduction (Z∼Poisson(R)), et les croix indiquent le 99e centile proposé comme seuil pour les ESS. Les étoiles représentent les ESS causés par plus d’un cas source. Les “autres” maladies sont les suivantes 1, streptocoque du groupe A ; 2, fièvre de Lassa ; 3, pneumonie à mycoplasme ; 4, peste pulmonaire ; 5, tuberculose. R n’est pas indiqué pour les “autres” maladies et est hors échelle pour la variole.
Événements de surmultiplication signalés (diamants) par rapport au nombre de reproduction estimé R (carrés) pour douze infections directement transmissibles. Les lignes indiquent les percentiles 5-95 du nombre de cas secondaires suivant une distribution de Poisson avec lambda égal au nombre de reproduction (\(Z∼Poisson(R)\)), et les croix indiquent le 99e centile proposé comme seuil pour les ESS. Les étoiles représentent les ESS causés par plus d’un cas source. Les “autres” maladies sont les suivantes 1, streptocoque du groupe A ; 2, fièvre de Lassa ; 3, pneumonie à mycoplasme ; 4, peste pulmonaire ; 5, tuberculose. R n’est pas indiqué pour les “autres” maladies et est hors échelle pour la variole.

Proportion attendue de transmission

Quelle est la proportion de cas responsables de 80 % de la transmission ?

L’utilisation superspreading et comparez les estimations pour MERS en utilisant les paramètres de distribution de la descendance de cet épisode du didacticiel, avec les estimations pour le SRAS-1 et Ebola accessibles via le paramètre de distribution de la descendance epiparameter R.

Pour utiliser superspreading::proportion_transmission() nous vous recommandons de lire le Estimer quelle proportion de cas provoque une certaine proportion de transmission le manuel de référence.

Actuellement, epiparameter a des distributions de descendants pour SARS, Smallpox, Mpox, Pneumonic Plague, Hantavirus Pulmonary Syndrome, Ebola Virus Disease. Accédons à la distribution des descendants mean et dispersion pour SARS-1 :

R 

# Load parameters
sars <- epiparameter::epiparameter_db(
  disease = "SARS",
  epi_name = "offspring distribution",
  single_epiparameter = TRUE
)
sars_params <- epiparameter::get_parameters(sars)
sars_params

SORTIE 

      mean dispersion
      1.63       0.16

R 

#' estimate for ebola --------------

ebola_epiparameter <- epiparameter::epiparameter_db(
  disease = "Ebola",
  epi_name = "offspring distribution",
  single_epiparameter = TRUE
)
ebola_params <- epiparameter::get_parameters(ebola_epiparameter)
ebola_params

SORTIE 

      mean dispersion
       1.5        5.1

R 

# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
  R = ebola_params[["mean"]],
  k = ebola_params[["dispersion"]],
  prop_transmission = 0.8
)

SORTIE 

    R   k prop_80
1 1.5 5.1   43.2%

R 

#' estimate for sars --------------

# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
  R = sars_params[["mean"]],
  k = sars_params[["dispersion"]],
  prop_transmission = 0.8
)

SORTIE 

     R    k prop_80
1 1.63 0.16     13%

R 

#' estimate for mers --------------

# estimate
# proportion of cases that
# generate 80% of transmission
superspreading::proportion_transmission(
  R = offspring_fit$estimate["mu"],
  k = offspring_fit$estimate["size"],
  prop_transmission = 0.8
)

SORTIE 

          R          k prop_80
1 0.6045295 0.02039807   2.13%

Le MERS présente le pourcentage le plus faible de cas (2,1 %) responsables de 80 % de la transmission, ce qui est représentatif d’une distribution très dispersée de la descendance.

Le virus Ebola présente le pourcentage le plus élevé de cas (43 %) responsables de 80 % de la transmission. Ce pourcentage est représentatif des distributions de descendance dont les paramètres de dispersion sont élevés.

inverse-dispersion ?

Le paramètre de dispersion \(k\) peut être exprimé différemment dans la littérature.

  • Dans la page Wikipédia consacrée à la binomiale négative, ce paramètre est défini sous sa forme réciproque (voir la rubrique équation de la variance).
  • Dans le cas d’une le zoo de distribution shiny app, le paramètre de dispersion \(k\) est appelé “Inverse-dispersion” mais il est égal au paramètre estimé dans cet épisode. Nous vous invitons à explorer cette piste !

hétérogénéité ?

La variation de la transmission au niveau individuel est également appelée hétérogénéité de la transmission ou degré d’hétérogénéité de la transmission. Lloyd-Smith et al, 2005 l’infectiosité hétérogène dans les Campbell et al, 2018 lors de l’introduction de la {outbreaker2} package. De même, un réseau de contacts peut stocker des contacts épidémiologiques hétérogènes, comme dans la documentation de l’étude epicontacts package (Nagraj et al., 2018).

Lisez ces articles de blog

Tracer la variole du singe de la JUNIPER montre l’utilité des modèles de réseau pour la recherche de contacts.

Devenir viral d’Adam Kucharski présente les conditions qui déclenchent la contagion en ligne : viralité sur YouTube, épidémies et campagnes de marketing.

Points clés

  • Utiliser epicontacts pour calculer le nombre de cas secondaires causés par une personne particulière à partir de la liste de diffusion et des données de contact.
  • Utiliser fitdistrplus pour estimer empiriquement la distribution de la descendance à partir de la distribution du nombre de cas secondaires.
  • Utilisez superspreading pour estimer la probabilité d’avoir des grappes d’une taille donnée à partir des cas primaires et informer les efforts de recherche de contacts.